1. Introduction
As large amounts of mobile devices such as Internet of things (IoT) devices or smartphones are utilized, the contradiction between limited storage space and sharply increasing data deluge becomes increasingly serious in the era of big data [
1,
2]. This exceedingly massive data makes the conventional data storage mechanisms inadequate within a tolerable time, and therefore the data storage is one of the major challenges in big data [
3]. Note that storing all the data becomes more and more dispensable nowadays, and it is also not conducive to reduce data transmission costs [
4,
5]. In fact, data compression storage is widely adopted in many applications, such as IoT [
2], industrial data platform [
6], bioinformatics [
7], wireless networking [
8]. Thus, the research on data compression storage becomes increasingly paramount and compelling nowadays.
In conventional source coding, data compression is carried out by removing the data redundancy, where short descriptions are assigned to the most frequent class [
9]. Based on it, the tight bounds for lossless data compression are given. In order to further increase the compression rate, one needs to use more information. A quintessential example is to use some side information [
10]. Another possible solution is to compress the data with quite a few losses first and then reconstruct them with acceptable distortion, which is referred to as lossy compression [
11,
12,
13]. Some adaptive compressions are adopted extensively. For example, Reference [
14] proposed an adaptive compression scheme in IoT systems, and Reference [
15] investigated the backlog-adaptive source coding system in terms of age of information. In fact, most of the previous compression methods usually carried out compression by means of contextual data or leveraging data transformation techniques [
4].
Although these previous methods of data compression perform satisfactorily in their respective application scenarios, there is still much room for improvement when facing rapidly growing large-scale data. Moreover, they also do not take the data value into account. This paper focuses on the problem of how to further compress data with acceptable distortion to implement the specified requirements in data storage when the storage size is still not enough to guarantee the lossless storage after the conventional lossless data compression. This paper will realize this goal by reallocating storage space based on the data value which represents the subjective assessment of users. Here, we take the importance-aware weighting in the weighted reconstruction error to measure the total cost in data storage with unequal costs.
Generally, users prefer to care about the crucial part of data that attracts their attention rather than the whole data itself. In many real-world applications, such as cost-sensitive learning [
16,
17,
18] and unequal error protection [
19,
20], different errors bring different costs. To be specific, the distortion in the data that users care about may be catastrophic if the loss of some data being insignificant for users is allowed. Similar to coresets [
21], the data needing to be processed was reduced to those users as the main focus rather than the whole data set. Unlike coresets, the data needing to be processed in this paper no longer pursues approximately representing the raw data, and it is expected to minimize the storage cost with respect to the importance weighting value. In fact, although the data deluge sharply increases, the significant data that users care about is still rare in a lot of scenarios of big data. In this sense, it can be regarded as the sparse representation from the perspective of the data value, and we can use it to compress data.
Alternatively, it is interesting to achieve data compression by storing a fraction of data, which preserves as much information as possible regarding the data that users care about [
22,
23]. This paper also employs this strategy. However, there are subtle but critical differences between the compression storage strategy proposed in this paper with those in Reference [
22,
23]. In fact, Reference [
22] focused on Pareto-optimal data compression, which presents the trade-off between retained entropy and class information. However, this paper puts forward an optimal compression storage strategy for digital data from the viewpoint of message importance, and it gives the trade-off between the relative weighted reconstruction error (RWRE) and the available storage size. Furthermore, the compression method based on message importance was preliminarily discussed in Reference [
23] to solve the big data storage problem in wireless communications, while this paper will aim to discuss the optimal storage space allocation strategy with limited storage space, in general, based on message importance. Moreover, the constraints are also different. That is, the available storage size is limited in this paper, while the total code length of all the events is given in Reference [
23].
From users’ attention viewpoint, the data value can be considered as the subjective assessment of users on the importance of data. Actually, much of the research in the last decade suggested that the study from the perspective of message importance is rewarding to obtain new findings [
20,
24,
25]. Thus, there may be effective performance improvement in storage systems when taking message importance into account. For example, Reference [
26] discussed the lossy image compression method with the aid of a content-weighted importance map. Since any quantity can be seen as important if it agrees with the intuitive characterization of the user’s subjective degree of concern of data, the cost in data reconstruction for specific user preferences is regarded as the importance in this paper, which will be used as the weight in the weighted reconstruction error.
Since we desire to achieve data compression by keeping only a small portion of important data and abandoning less important data, this paper mainly focuses on the case where only a fraction of data take up the vast majority of the users’ interests. Actually, these scenarios are not rare in big data. A quintessential example should be cited that the minority subset detection is overwhelmingly paramount in intrusion detection [
27,
28]. Moreover, this phenomenon is also exceedingly typical in financial crime detection systems for the fact that only a few illicit identities catch our eyes to prevent financial frauds [
29]. Actually, when a certain degree of information loss can be acceptable, people prefer to take high-probability events for granted and abandon them to maximize the compressibility. These cases are referred to as
small-probability event scenarios in this paper. In order to depict the message importance in small-probability event scenarios, message importance measure (MIM) was proposed in Reference [
30]. Furthermore, MIM is fairly effective in many applications of big data, such as IoT [
31], mobile edge computing [
32]. In addition, Reference [
33] expanded MIM to the general case, and it presented that MIM can be adopted as a special weight in designing the recommendation system. Since there is no universal data value model, we might as well take the case where the MIM describes the cost of the error as a quintessential example to analyze the property of the optimal storage space allocation strategy.
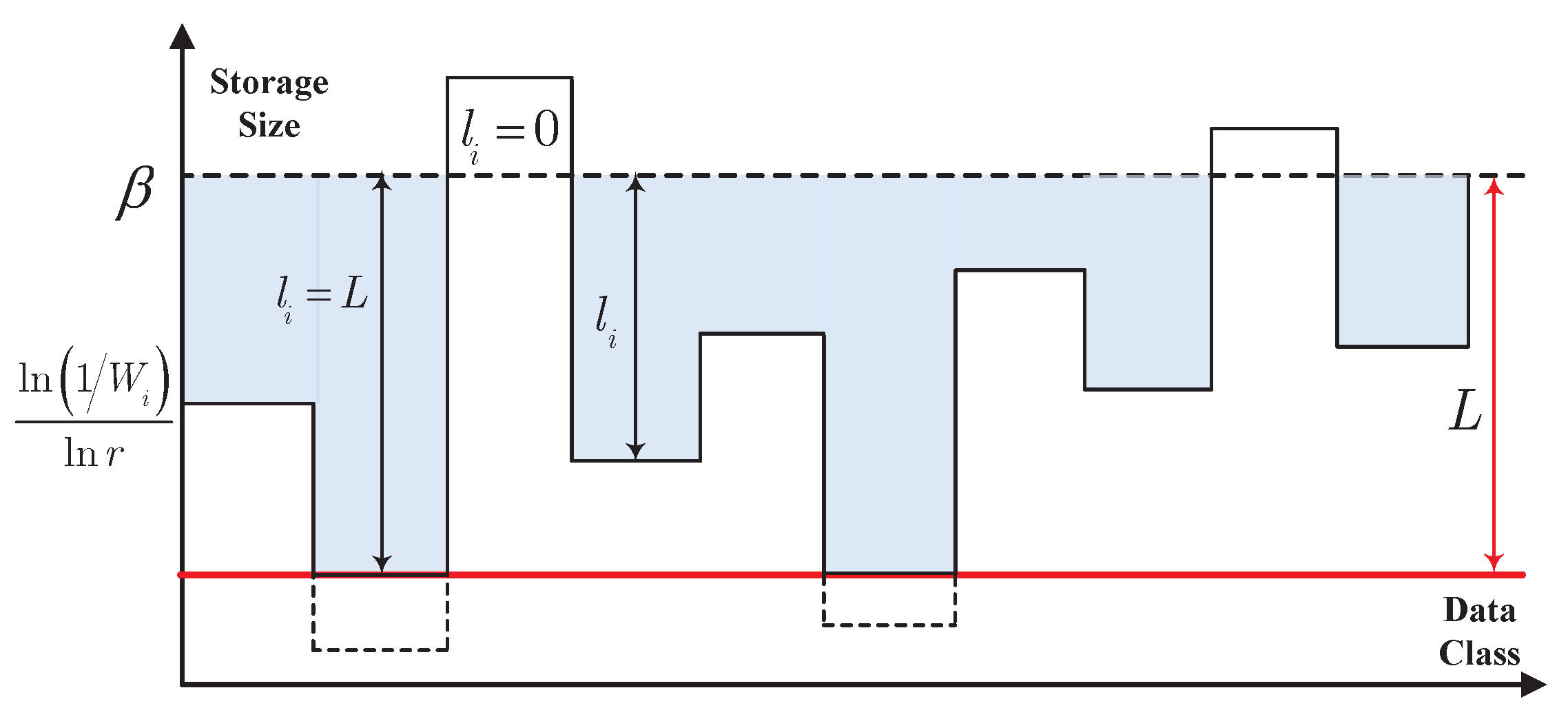
In this paper, we firstly propose a particular storage space allocation strategy for digital data on the best effort in minimizing the importance-weighted reconstruction error when the total available storage size is provided. For digital data, we formulate this problem as an optimization problem, and present the optimal storage strategy by means of a kind of restrictive water-filling. For the given available storage size, the storage size is mainly determined by the values of message importance and probability distribution of event class in a data sequence. In fact, this optimal allocation strategy adaptively prefers to provide more storage size for crucial data classes in order to make the rational use of resources, which is in accord with the cognitive mechanism of human beings.
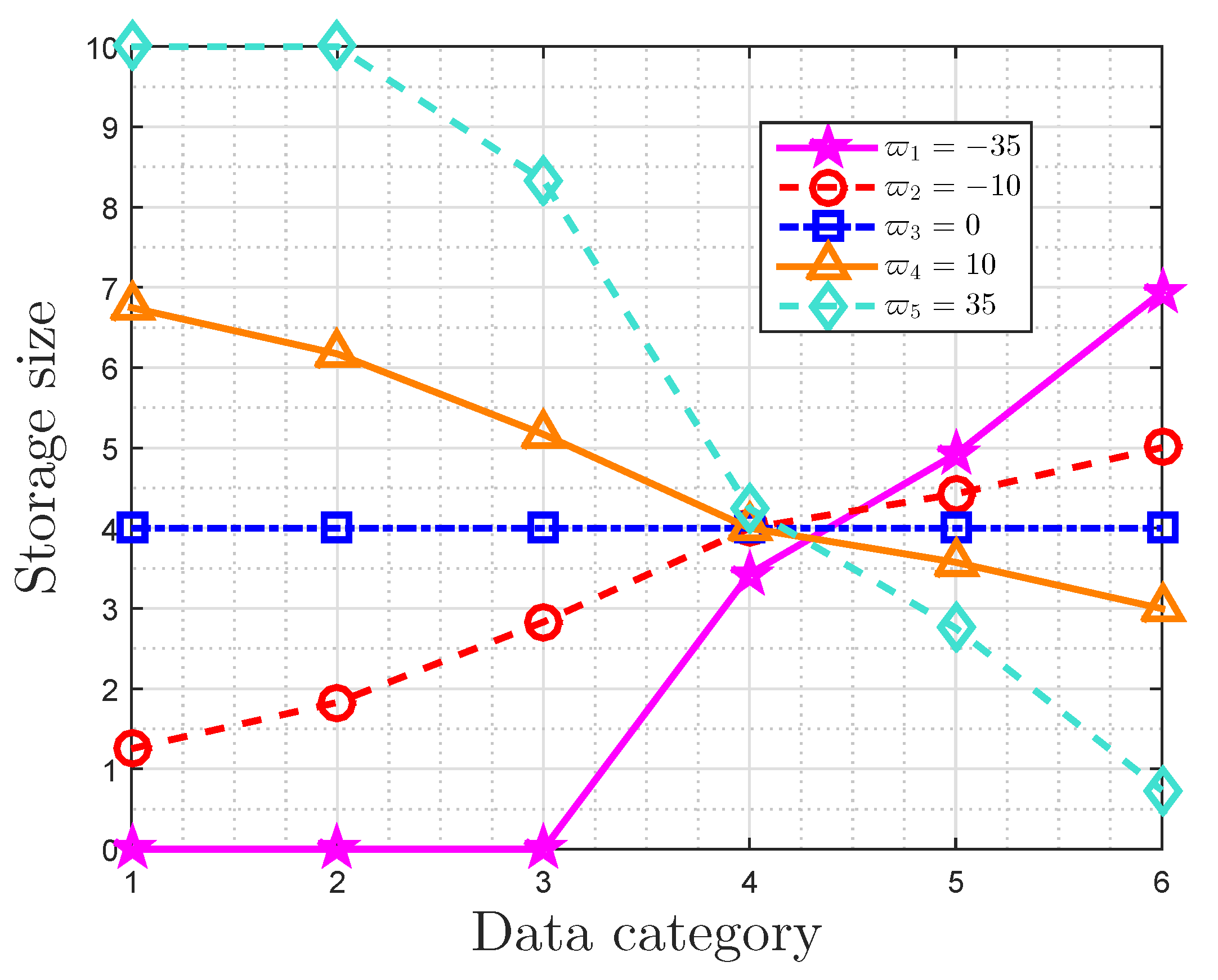
Afterward, we focus on the properties of this optimal storage space allocation strategy when the importance weights are characterized by MIM. It is noted that there is a trade-off between the RWRE and the available storage size. The constraints on the performance of this storage system are true, and they depend on the importance coefficient and the probability distribution of events classes. On the one hand, the RWRE increases with the increasing of the absolute value of importance coefficient for the fact that the overwhelming majority of important information will gather in a fraction of data as the importance coefficient increases to negative/positive infinity, which suggests the influence of users’ preferences. On the other hand, the compression performance is also affected by probability distribution of event classes. In fact, the more closely the probability distribution matches the requirement of the small-probability event scenarios, the more effective this compression strategy becomes. Furthermore, it is also obtained that the RWRE in a uniform distribution is larger than any other distributions for the same available storage size. In this regard, the uniform distribution is incompressible from the perspective of optimal storage space allocation based on data value, which is consistent with the conclusion in information theory [
34].
The main contributions of this paper can be summarized as follows. (1) It proposes a new digital data compression strategy taking message importance into account, which can help improve the design of a big data storage system. (2) We illuminate the properties of this new method, which can characterize the trade-off between the RWRE and the available storage size. (3) It shows that the data with highly clustered message importance is beneficial to compression storage, and it also finds that the data with a uniform information distribution is incompressible from the perspective of optimal storage space allocation based on data value, which is consistent with that in information theory.
The rest of this paper is organized as follows. The system model is introduced in
Section 2, including the definition of weighted reconstruction error, distortion measure, and problem formulation. In
Section 3, we solve the problem of optimal storage space allocation in three kinds of system models and give the solutions. The properties of this optimal storage space allocation strategy based on MIM are fully discussed in
Section 4. The effects of the importance coefficient and the probability of event classes on RWRE are also investigated in detail.
Section 5 illuminates the properties of this optimal storage strategy when the importance weight is characterized by Non-parametric MIM. The numerical results are shown and discussed in
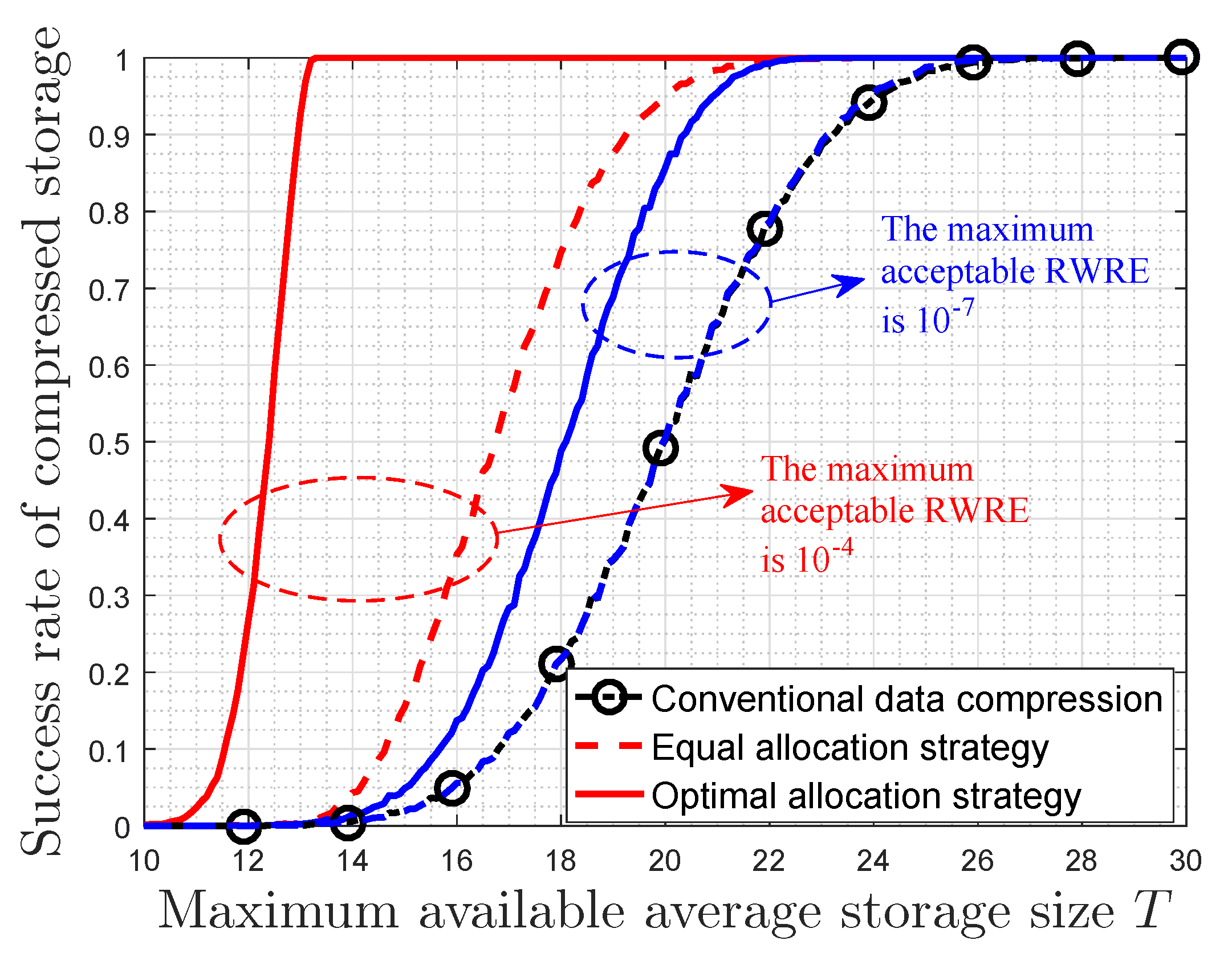
Section 6, which verifies the validity of the developed theoretical results in this paper. Finally, we give the conclusion in
Section 7.
2. System Model
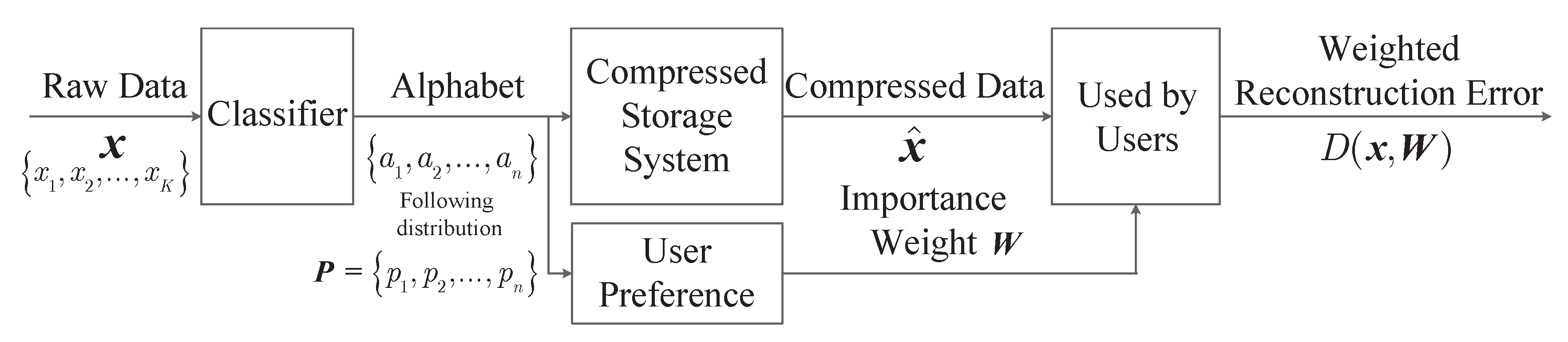
This section introduces the system model, including the definition of the weighted reconstruction error, the modeling of distortion measure, in order to illustrate how we formulate the lossy compression problem as an optimization problem for digital data based on message importance. In order to make the formulation and discussion more clear, the main notations in this paper are listed in
Table 1.
2.1. Modeling Weighted Reconstruction Error Based on Message Importance
The data storage system may lack storage space frequently when facing a super-large scale of data to store. When the storage size is still not enough after the lossless conventional data compression, the optimum allocation of storage space based on data value may be imperative. For this purpose, we consider the following storage system, which stores K pieces of data. Let be the sequence of raw data. Assume that all the data redundancy have been removed after the lossless conventional data compression, and each data needs to take up storage space with size of if this data can be recovered without any distortion. However, in many scenarios of big data, the storage size is still not enough in this case. That is to say, the actual required storage space is larger than the maximum available storage space , where T is the maximum available average storage size.
In fact, users prefer to care about the paramount part of data that attracts their attention rather than the whole data itself. In this perspective, storing all data without distortion may be unnecessary. Considering that the natural distribution of storage space is not invariably reasonable and the high value data in big data is usually sparse, the rational storage space allocation by minimizing the loss of data value may solve the above problem of insufficient storage space, if a certain amount of data value is allowed to be lost. After the data compression by means of the rational storage space allocation, we use to denote the compressed data sequence, and assume that the compressed data takes up storage space with size of in practice for .
The lossy data compression usually pursues the least the storage cost while retaining as much information users required as possible [
22]. In the lossless conventional data compression, the costs of different data are assumed to be the same. However, different kinds of errors may result in unequal costs in many real-world applications [
16,
17,
18,
19]. In this model, we use the notation
to denote the error cost for the reconstructed data. Namely,
is with respect to the data value of data
, and it is regarded as the message importance in this paper. Here, we define the weighted reconstruction error to describe the total cost in data storage with unequal costs, which is given by
where
characterizes the distortion between the raw data and the compressed data in data reconstruction, which characterizes the loss degree of data value with allocated storage size.
Consider the situation where the data is stored according to its category for easier retrieval, which can also make the recommendation system based on it more effective [
33]. Since data classification is becoming increasingly convenient and accurate nowadays due to the rapid development of machine learning [
35,
36], this paper assumes that the event class can be easily detected and known in the storage system. Moreover, assume the data that belongs to the same class has the same importance-weight and occupies the same storage size. Hence,
can be seen as a sequence of
K symbols from an alphabet
where
represents event class
i. This storage model is summarized and shown in
Figure 1. In this case, the weighted reconstruction error based on importance is formulated as
where
is the number of times the
i-class occurs in the sequence
. Let
denote the probability of event class
i in data sequence
.
2.2. Modeling Distortion between the Raw Data and the Compressed Data
We focus on the formula of
in this part, which characterizes the distortion between the raw data and the compressed data with specified storage size. Usually, there is no universal characterization of distortion measure, especially in speech coding and image coding [
34]. In fact,
should characterize the loss degree of data value with allocated storage size. In this respect, the conventional distortion measures are not appropriate since they do not take unequal costs into account. In order to facilitate the analysis and design, this paper proposes an exponential distortion measure to discuss the following special case.
We assume that the data is digital and ignore the storage formats and standards in concrete application environments. On its application fields, it may be useful in some scenarios with counting systems, such as finance, or medicine, as the general merchandise. Let the description of the raw data
be
bits, and
where
r is radix (
). Actually, the radix represents the base of the system in practical application, such as
in a binary system. In particular,
will approach the infinite number if
is an arbitrary real number. When the storage size is still not enough after the lossless conventional data compression, there is only
bits assigned to it in order to compress data further based on the message importance. For convenience, the smaller
numbers are discarded in this process. When restoring the compressed data, the discarded digits are set to the same pre-specified number or random numbers in the actual system. Let
be the
-th discarded digit for
, and assume that
is a random number in
. In this case, the compressed data is
. As a result, the absolute error is
, which meets
When
, which means there is no information stored, the supremum of absolute error reaches the maximum and it is
. In order to better weigh the different costs, we define the relative error by normalizing the absolute error to the interval
based on the above maximum absolute error
. Moreover, we adopt the supremum of this relative error as the distortion measure
, which is given by
In particular, we obtain
and
. Moreover, it is easy to check that
and
decreases with the increasing of
. In fact,
can be regarded as the percentage of data value loss in this case. Thus, the weighted reconstruction error in Equation (
1) represents the total cost in data storage based on the loss degree.
In this stored procedure, the compression rate is , and the total saving storage size is . Actually, K denotes the number of data, and it is extremely big due to the sharply increasing data deluge in the era of big data. Therefore, although is not always large, the saving storage size is still exceedingly substantial since K is exceedingly large.
Furthermore, to simplify the comparisons under different conditions, the weighted reconstruction error is also normalized to the relative weighted reconstruction error (RWRE). In fact, the RWRE characterizes the relative total cost in the data compression, and it is given by
where
and
.
2.3. Problem Formulation
2.3.1. General Storage System
In fact, the actual storage size of each data after the compression can then be expressed as
. For each given maximum available storage space constraint
, where
T denotes the maximum available average storage size, we shall optimize the storage resources allocation strategy of this system by minimizing the RWRE, which can be expressed as
The storage systems, which can be characterized by Problem , are referred to as the general storage system.
Remark 1. In fact, this paper focuses on allocating resources by category with taking message importance into account, while the conventional source coding searches the shortest average description length of a random variable.
2.3.2. Ideal Storage System
In practice, the storage size of raw data is usually assigned to be the same for ease of use. Thus, we mainly consider the case where the original storage size of each data is the same, and use
L to denote it (i.e.,
for
). As a result, we have
Thus, the problem
can be rewritten as
For convenience, we use the ideal storage system to represent the storage systems, which can be described by Problem . Moreover, we will mainly focus on the characteristics of the solutions in Problem in this paper.
2.3.3. Quantification Storage System
A
quantification storage system quantizes and stores the real data acquired from sensors in the real world. The data is usually a real number, which requires an infinite number of bits to describe it accurately. That is, the original storage size of each class approaches the infinite number, (i.e.,
for
), in this case. As a result, the RWRE can be rewritten as
Therefore, the problem
in this case is reduced to
5. Property of Optimal Storage Strategy Based on Non-Parametric Message Importance Measure
In this section, we define the importance weight based on the form of non-parametric message importance measure (NMIM) to characterize the relative weighted reconstruction error (RWRE) [
23]. Then, the importance weight of
i-th class in this section is given by
Due to Equation (
22), the optimal storage size in the ideal storage system by this importance weight is given by
For two probabilities and , if , then we will have . In this case, we obtain according to Theorem 2.
Assume
and ignore rounding, due to Equation (
23), we obtain
Let
in this case, we find
Generally, this constraint does not invariably hold, and therefore we usually do not have
.
For the quantification storage system as shown in
in this section, if the maximum available average storage size satisfies
, an arbitrary probability distribution will make Equation (
50) hold, which means
. In this case, substituting Equation (
47) in Equation (
9), the RWRE can be expressed as
where
, which is defined as the NMIM [
23].
It is noted
as
T approaches positive infinity. Since
, we find
. Furthermore, since that
according to Reference [
23], we obtain
. Let
, we have
Obviously, for a given RWRE, the minimum average required storage size for the quantification storage system decreases with increasing of
. That is to say, the data with large NMIM will get a large compression ratio. In fact, the NMIM in the typical small-probability event scenarios is generally large according to Reference [
23]. Thus, this compression strategy is effective in the typical small-probability event scenarios.
Furthermore, due to Reference [
23],
when
is small. Hence, for small
, the RWRE in this case can be reduced to
It is easy to check that
increases as
increases in this case.
7. Conclusions
In this paper, we focused on the problem of lossy compression storage when the storage size is still not enough after conventional lossless data compression. By means of the message importance to characterize the data value, we define the weighted reconstruction error to describe the total cost in data storage. Based on it, we presented an optimal storage space allocation strategy for digital data from the perspective of data value by the exponential distortion measure, which pursues the least error with respect to the data value for restricted storage size. We gave the solutions by a kind of restrictive water-filling, which presented an alternative way to design an effective storage space allocation strategy. In fact, this optimal allocation strategy prefers to provide more storage size for crucial event classes in order to make the rational use of resources, which agrees with the individuals’ cognitive mechanism.
Then, we presented the properties of this strategy based on the message importance measure (MIM) detailedly. It is obtained that there is a trade-off between the relative weighted reconstruction error (RWRE) and available storage size. In fact, if a small quantity of loss of total data value is accepted by users, this strategy will further compress data based on the conventional methods of data compression. Moreover, the compression performance of this storage system improves as the absolute value of importance coefficient increases. This is due to the fact that a fraction of data can contain the overwhelming majority of useful information that exerts a tremendous fascination on users as the importance coefficient approaches negative/positive infinity, which suggests that the users’ interest is highly-concentrated. On the other hand, the probability distribution of event classes also has an effect on the compression results. When the useful information is only highly enriched in a small portion of raw data naturally from the viewpoint of users, such as the small-probability event scenarios, it is obvious that we can compress the data greatly with the aid of these characteristics of distribution. Furthermore, the properties of storage size and RWRE based on non-parametric MIM were also discussed. In fact, the RWRE in the data with a uniform distribution was invariably the largest in any case. Therefore, this paper harbors the idea that the data with uniform information distribution is incompressible from the perspective of optimal storage size allocation based on data value, which is consistent with the well known conclusion in information theory in a sense.
Proposing a more general distortion measure between the raw data and the compressed data, which no longer only applies to digital data, and using it to acquire the high-efficiency lossy data compression systems from the perspective of message importance are of our future interests. In addition, we are also interested in using this optimal storage space allocation strategy in a real application with a real data stream in the future.