Cryptanalysis and Improvement of a Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion
Abstract
1. Introduction
2. Related Work
2.1. The Involved Chaotic Maps
2.1.1. Generalized Arnold’s Cat Map
2.1.2. Chebyshev Map
2.2. Image Encryption Algorithm
2.2.1. Permutation Stage
2.2.2. Diffusion Stage
2.3. Image Decryption Algorithm
3. Cryptanalysis
3.1. Security Weaknesses
3.1.1. Equivalent Classes in Keyspace
3.1.2. Low Sensitivity to the Change of Plaintext
3.2. Chosen-Plaintext Attack
3.2.1. Extraction of the Permutation Matrix
- Construct a special plain image , such that
- Encrypt using CIES-UBPRPD to obtain the corresponding cipher image . We denote the image after permutation stage as (an intermediate product during the execution of the whole encryption process).
- Let us use R channel as an example: select two different positions and , where and construct another special plain image , such thatwhere
- Encrypt to obtain its cipher image . From Section 3.1.2, we knew that and share the same parameters used in ACM; thus, they have the same permutation mapping. Let us denote the first position of different values that occurred in and , following the raster-scan order, as . It means that , such that , which means either or will be moved to the position after performing the permutation stage. This property reveals some information regarding the permutation behavior of CIES-UBPRPD. We define as a tuple of constraints.
- Choose a different or , repeat Step 3 to Step 4 several times and collect all of the produced constraint tuples, and then define the associated collection of constraint tuples as a set .
- Construct a matrix , by setting the chosen positions (a, b) and (x, y), used in Step 2, with different positive integers and all other positions with value 0. For example, assume there are two constraint tuples and in , we can now set , , , and .
- Using the brute-force searching algorithm, denoted as Algorithm 1 in the following, to find and for all of the above chosen plain images, where . In the specifically considered case, all of the images are of size , and are equivalent in the permutation stage. Actually, we do not need to know what exactly is, but only its last eight bits. If Algorithm 1 outputs more than one candidate pair, let us go back to Step 3 to collect more constrained tuples and iterate this step until only one pair is left.
- Making changes to G and B channels, repeat the procedures listed in Step 3 to Step 7 and obtain , , , and , where and .
- Extract , , and by usingWe denote these three values as , and , respectively, for convenience.
3.2.2. Extraction of the Diffusion Matrix
3.2.3. Recovering the Original Plain Image
- Transform , , and into three 1D arrays , , and , respectively, in row major ordering.
- Calculate the required parameters, as follows.
- Reconstruct , and according towhereand . Subsequently, transform these three arrays into two-dimensional (2D) arrays , , and , respectively.
- Reconstruct , and by using ACM, but now the scanning sequence is from right to left and from bottom to top.
4. Improved CIES-UBPRPD Algorithm
4.1. The Weaknesses of the Original CIES-UBPRPD
- Misuse of the modulo operation. A value’s remainder divided by 256 equals to the last eight bits in its binary representation. This operation makes the last eight bits of the value more important than the rest parts. This unequal importance in bits gives us a large number of clues for finding the equivalent classes of parameters in CIES-UBPRPD.
- The parameters used in ACM are not very sensitive to the initial plain images. As we pointed out in Section 3.1.2, images that have the same , , and share the same system parameters. Thus, it is vulnerable to differential attacks.
- The diffusion matrix (process) depends only on secret keys, but not the plain images. Once we cracked one cipher image and extracted the diffusion matrix, we can use it to decrypt the other cipher images.
4.2. The Enhanced CIES-UBPRPD
4.2.1. Secret Key Formulation
4.2.2. Image Encryption Algorithm
Permutation Stage
- Use as the initial value and iterate the Chebyshev map times, discard the first elements to avoid the harmful effect, and obtain the chaotic sequences , which contain 131 elements. That is,
- Generate another sequence by
- Calculate the parameters by following equations:
- Permute using the following three-dimensional (3D) cat map:where , and is used to indicate the color channel. The scanning sequence is from R channel to B channel, from left to right and from top to bottom. After this step, we get the permuted image .
Diffusion Stage
- Transform , , and into three 1D arrays , and by row-major ordering.
- Use as the new initial value and iterate the Chebyshev map times, discard the first n0 elements and generate another chaotic sequence , which contains elements. That is,
- Calculate the diffusion matrices , , and according to:
- Calculate , and by usingwhere and .
- Transform , and into three grayscale images with size , and then merge them into color cipher image with size .
Image Decryption Algorithm
- Transform , and into three 1D arrays , and respectively, by row-major ordering.
- Calculate the chaotic sequence in the same way as the encryption process.
- Calculate the parameters in the same way as the encryption process.
- Calculate the diffusion matrices , and in the same way as the encryption process.
- Reconstruct , and by usingwhere and . Subsequently, transform these three arrays into 2D arrays , and respectively.
- Reconstruct , and by using 3D cat map in Equation (15), but now the scanning sequence is from B channel to R channel, from right to left, and from bottom to top.
5. Experimental Results
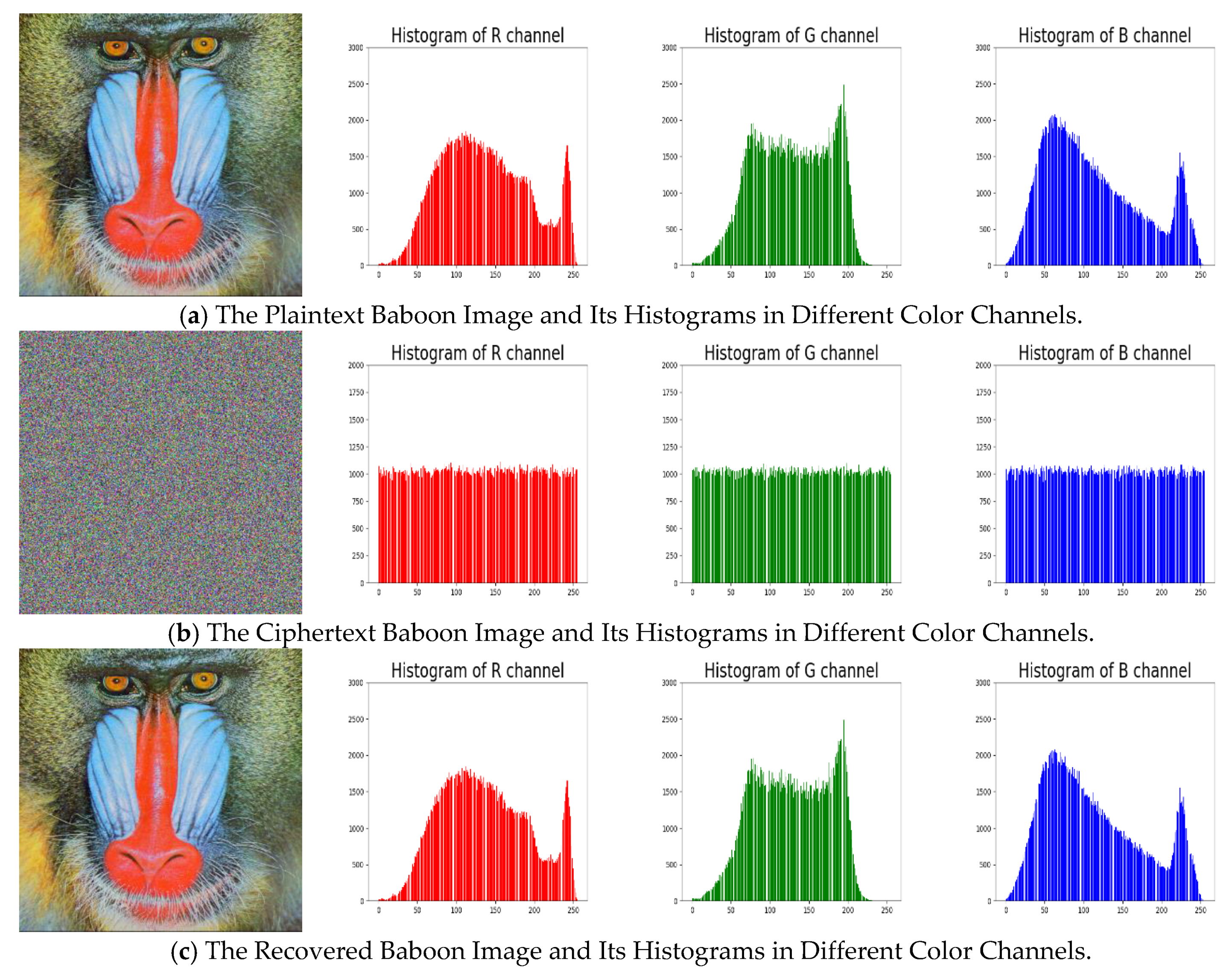
5.1. Verification of Encryption and Decryption Algorithms
5.2. Security Analyses
5.2.1. KeySpace Analysis
5.2.2. Histogram Analysis
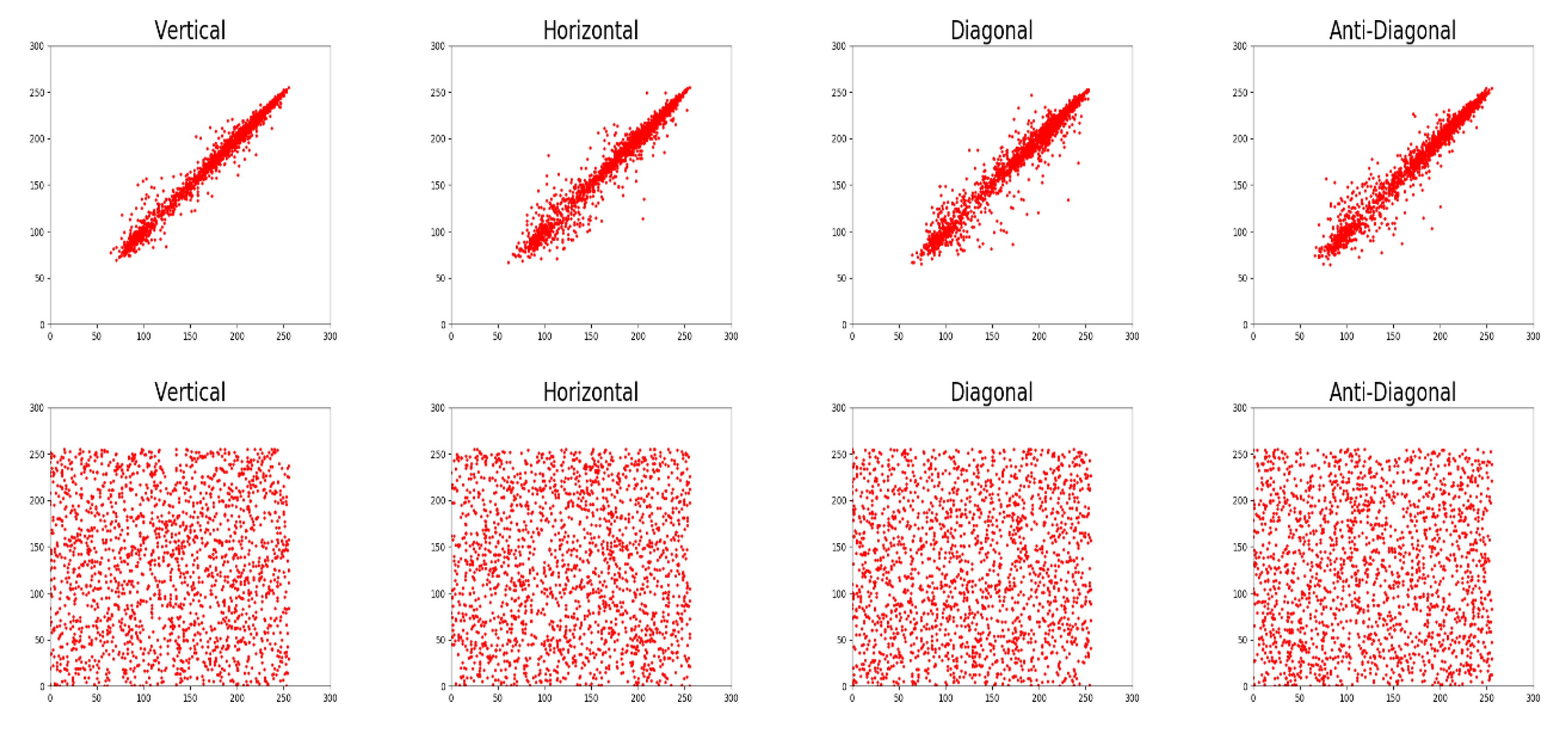
5.2.3. Correlation Analysis
5.2.4. Key Sensitivity Analysis
5.2.5. Plaintext Sensitivity Analysis
5.3. Robustness Analyses
6. Discussions and Conclusions
6.1. Discussions
6.2. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumari, M.; Gupta, S.; Sardana, P. A Survey of Image Encryption Algorithms. 3D Res. 2017, 8. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, F.; Jiang, X.; Liu, X.; Liu, Y. A Novel Image Encryption Algorithm Based on Plaintext-related Hybrid Modulation Map. J. Internet Technol. 2019, 20, 2141–2155. [Google Scholar]
- Kyamakya, K.; Halang, W.A.; Unger, H.; Chedjou, J.C.; Rulkov, N.C.; Li, Z. (Eds.) Recent Advances in Nonlinear. In Dynamics and Synchronization: Theory and Applications, Studies in Computational Intelligence 254; Springer: Berlin, Heidelberg, 2009. [Google Scholar]
- Fridrich, J. Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Priya, R.; Vidhyapriya, R.; Seifedine, K.; Robertas, D.; Tomas, B. An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic-Tent Map. Entropy 2019, 21, 656. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, G.; Zhu, C. A Secure and Fast Image Encryption Scheme based on Double Chaotic S-Boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Sun, X. Chaos-based fast colour image encryption scheme with true random number keys from environmental noise. IET Image Process. 2017, 11, 324–332. [Google Scholar] [CrossRef]
- Li, Q.; Qian, G. A New Image Encryption Algorithm Based on Chaotic Maps. In Proceedings of the 9th International Conference on Signal Processing Systems, Auckland, New Zealand, 27–30 November 2017; pp. 65–69. [Google Scholar]
- Zhu, S.; Zhu, C.; Wang, W. A New Image Encryption Algorithm Based on Chaos and Secure Hash SHA-256. Entropy 2018, 20, 716. [Google Scholar] [CrossRef]
- Huang, L.; Cai, S.; Xiao, M.; Xiong, X. A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy 2018, 20, 535. [Google Scholar] [CrossRef]
- Arnold, V.I.; Avez, A. Problèmes Ergodiques de la Mécanique Classique; Benjamin: New York, NY, USA, 1967. (In French) [Google Scholar]
- He, D.; He, C.; Jiang, L.-G.; Zhu, H.-W.; Hu, G.-R. Chaotic characteristics of a one-dimensional iterative map with infinite collapses. IEEE Trans. Circuits Syst. I Regul. Pap. 2001, 48, 900–906. [Google Scholar] [CrossRef]
- Schneier, B. A self-study course in block-cipher cryptanalysis. Cryptologia 2000, 24, 18–33. [Google Scholar] [CrossRef]
- Wu, C.-P.; Kuo, C.-C. Design of integrated multimedia compression and encryption systems. IEEE Trans. Multimed. 2005, 7, 828–839. [Google Scholar] [CrossRef]
- Grangetto, M.; Magli, E.; Olmo, G. Multimedia Selective Encryption by Means of Randomized Arithmetic Coding. IEEE Trans. Multimed. 2006, 8, 905–917. [Google Scholar] [CrossRef]
- Zhou, J.; Liang, Z.; Chen, Y.; Au, O.C. Security Analysis of Multimedia Encryption Schemes Based on Multiple Huffman Table. IEEE Signal Process. Lett. 2007, 14, 201–204. [Google Scholar] [CrossRef]
- Nagaraj, N.; Vaidya, P.G.; Bhat, K.G. Arithmetic coding as a non-linear dynamical system. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1013–1020. [Google Scholar] [CrossRef]
- El-Arsh, H.Y.; Mohasseb, Y.Z. A New Light-Weight JPEG2000 Encryption Technique Based on Arithmetic Coding. In Proceedings of the MILCOM 2013—2013 IEEE Military Communications Conference, Institute of Electrical and Electronics Engineers (IEEE). San Diego, CA, USA, 18–20 November 2013; pp. 1844–1849. [Google Scholar]
- Mostafa, M.; Fakhr, M.W. Joint image compression and encryption based on compressed sensing and entropy coding. In Proceedings of the 2017 IEEE 13th International Colloquium on Signal Processing & its Applications (CSPA), Penang, Malaysia, 10–12 March 2017; pp. 129–134. [Google Scholar] [CrossRef]
- Guo, L.; Li, J.; Xue, Q. Joint image compression and encryption algorithm based on SPIHT and crossover operator. In Proceedings of the 2017 14th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Institute of Electrical and Electronics Engineers (IEEE). Chengdu, China, 15–17 December 2017; pp. 185–188. [Google Scholar]
- Shehata, A.E.R.; El-Arsh, H.Y. Lightweight Joint Compression-Encryption-Authentication-Integrity Framework Based on Arithmetic Coding. arXiv 2018, arXiv:1804.04300. [Google Scholar]
- Tsai, C.-J.; Wang, H.-C.; Wu, J.-L. Three Techniques for Enhancing Chaos-Based Joint Compression and Encryption Schemes. Entropy 2019, 21, 40. [Google Scholar] [CrossRef]
- Xie, Y.; Yu, J.; Guo, S.; Ding, Q.; Wang, E. Image Encryption Scheme with Compressed Sensing Based on New Three-Dimensional Chaotic System. Entropy 2019, 21, 819. [Google Scholar] [CrossRef]
- Liao, X.; Guo, S.; Yin, J.; Wang, H.; Li, X.; Sangaiah, A.K. New cubic reference table based image steganography. Multimed. Tools Appl. 2017, 77, 10033–10050. [Google Scholar] [CrossRef]
- Liao, X.; Yin, J.; Guo, S.; Li, X.; Sangaiah, A.K. Medical JPEG image steganography based on preserving inter-block dependencies. Comput. Electr. Eng. 2018, 67, 320–329. [Google Scholar] [CrossRef]

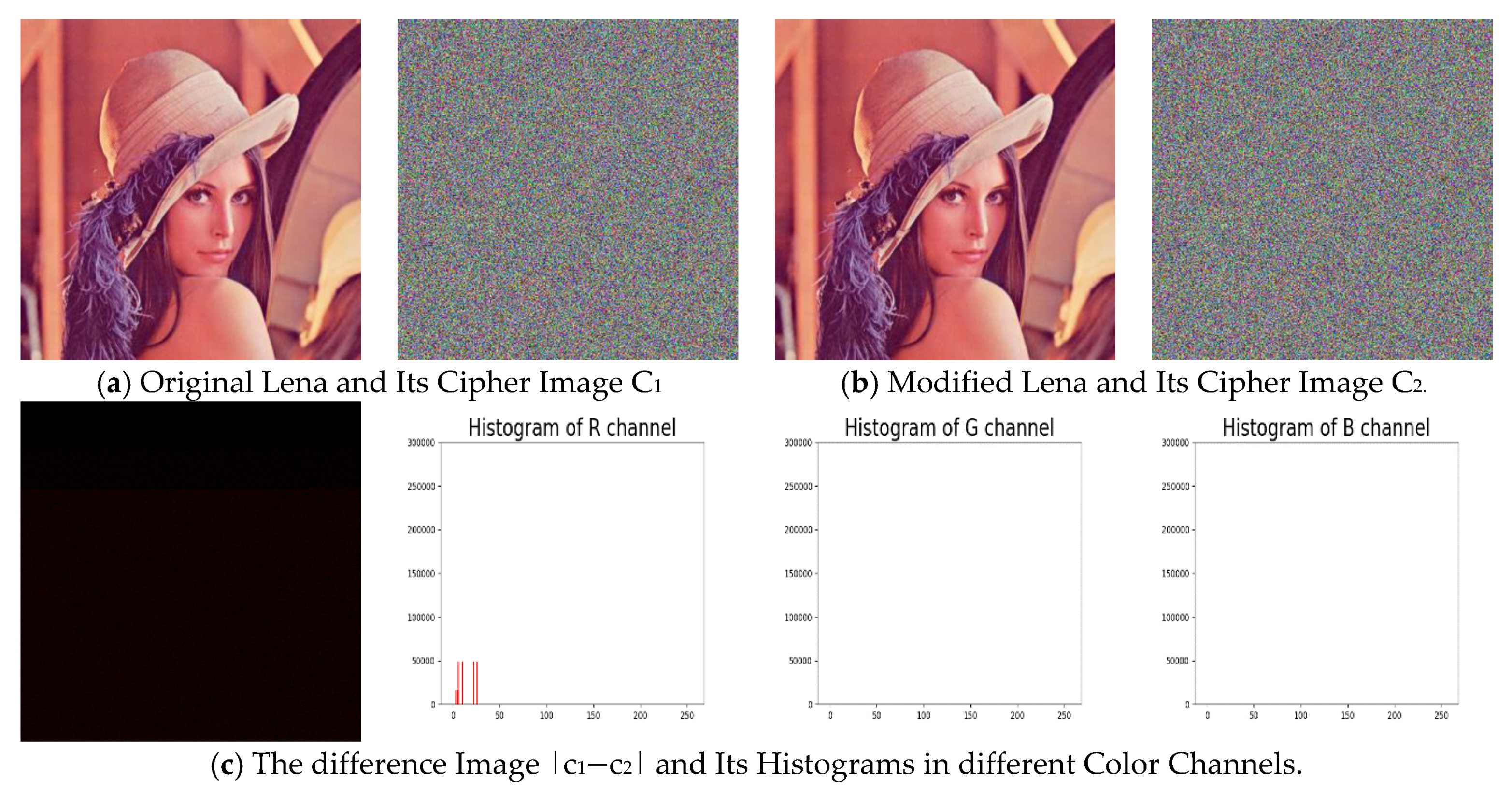










| R | G | B | |
|---|---|---|---|
| NPCR (%) | 86.5371 | 0 | 0 |
| UACI (%) | 4.8464 | 0 | 0 |
| Plain Image | Cipher Image | ||||||
|---|---|---|---|---|---|---|---|
| R | G | B | R | G | B | ||
| Lena | V | 0.9893 | 0.9823 | 0.9574 | 0.0015 | −0.0017 | −0.0023 |
| H | 0.9797 | 0.9689 | 0.9325 | −0.008 | −0.0014 | −0.0013 | |
| D | 0.9696 | 0.9554 | 0.9180 | −0.003 | −0.0011 | −0.0011 | |
| A | 0.9777 | 0.9652 | 0.9252 | −0.006 | −0.0005 | −0.0002 | |
| baboon | V | 0.8659 | 0.7650 | 0.8808 | 0.0004 | −0.0017 | 0.006 |
| H | 0.9230 | 0.8654 | 0.9073 | 0.0005 | 0.0027 | 0.0019 | |
| D | 0.8543 | 0.7347 | 0.8398 | 0.0004 | −0.0026 | 0.0014 | |
| A | 0.8518 | 0.7249 | 0.8424 | −0.0015 | −0.0017 | 0.002 | |
| NPCR (%) | UACI (%) | |||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Lena | 99.6094 | 99.6084 | 99.6096 | 33.4673 | 33.4630 | 33.4662 |
| baboon | 99.6075 | 99.6081 | 99.6086 | 33.4606 | 33.4646 | 33.4684 |
| fruits | 99.6081 | 99.6103 | 99.6095 | 33.4612 | 33.4620 | 33.4689 |
| airplane | 99.6094 | 99.6071 | 99.6101 | 33.4669 | 33.4595 | 33.4564 |
| peppers | 99.6099 | 99.6109 | 99.6092 | 33.4649 | 33.4641 | 33.4702 |
| Added Noise Density | PSNR of the De-Ciphered Image |
|---|---|
| 0.1 (10% of the image frame) | 17.6748 (dB) |
| 0.2 | 14.9988 (dB) |
| 0.3 | 13.5375 (dB) |
| Data Occlusion Loss | PSNR of the De-Ciphered Image |
|---|---|
| Pixel values in the bottom half = 0 | 11.6397 (dB) |
| Pixel values in the center square = 0 | 14.6680 (dB) |
| Pixel values in center row-rectangle = 0 | 14.6726 (dB) |
| Pixel values in center column-rectangle = 0 | 14.6285 (dB) |
| Original CIES-UBPRPD | Enhanced CIES-UBPRPD | |
|---|---|---|
| 512 512 (image size) | 3.3557 (s) | 3.7944 (s) |
| 256 256 (image size) | 0.8355 (s) | 0.9165 (s) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-Y.; Wu, J.-L. Cryptanalysis and Improvement of a Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy 2020, 22, 589. https://doi.org/10.3390/e22050589
Lin C-Y, Wu J-L. Cryptanalysis and Improvement of a Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy. 2020; 22(5):589. https://doi.org/10.3390/e22050589
Chicago/Turabian StyleLin, Cheng-Yi, and Ja-Ling Wu. 2020. "Cryptanalysis and Improvement of a Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion" Entropy 22, no. 5: 589. https://doi.org/10.3390/e22050589
APA StyleLin, C.-Y., & Wu, J.-L. (2020). Cryptanalysis and Improvement of a Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy, 22(5), 589. https://doi.org/10.3390/e22050589








