Rigid Shape Registration Based on Extended Hamiltonian Learning
Abstract
1. Introduction
2. Geometry of Special Euclidean Groups
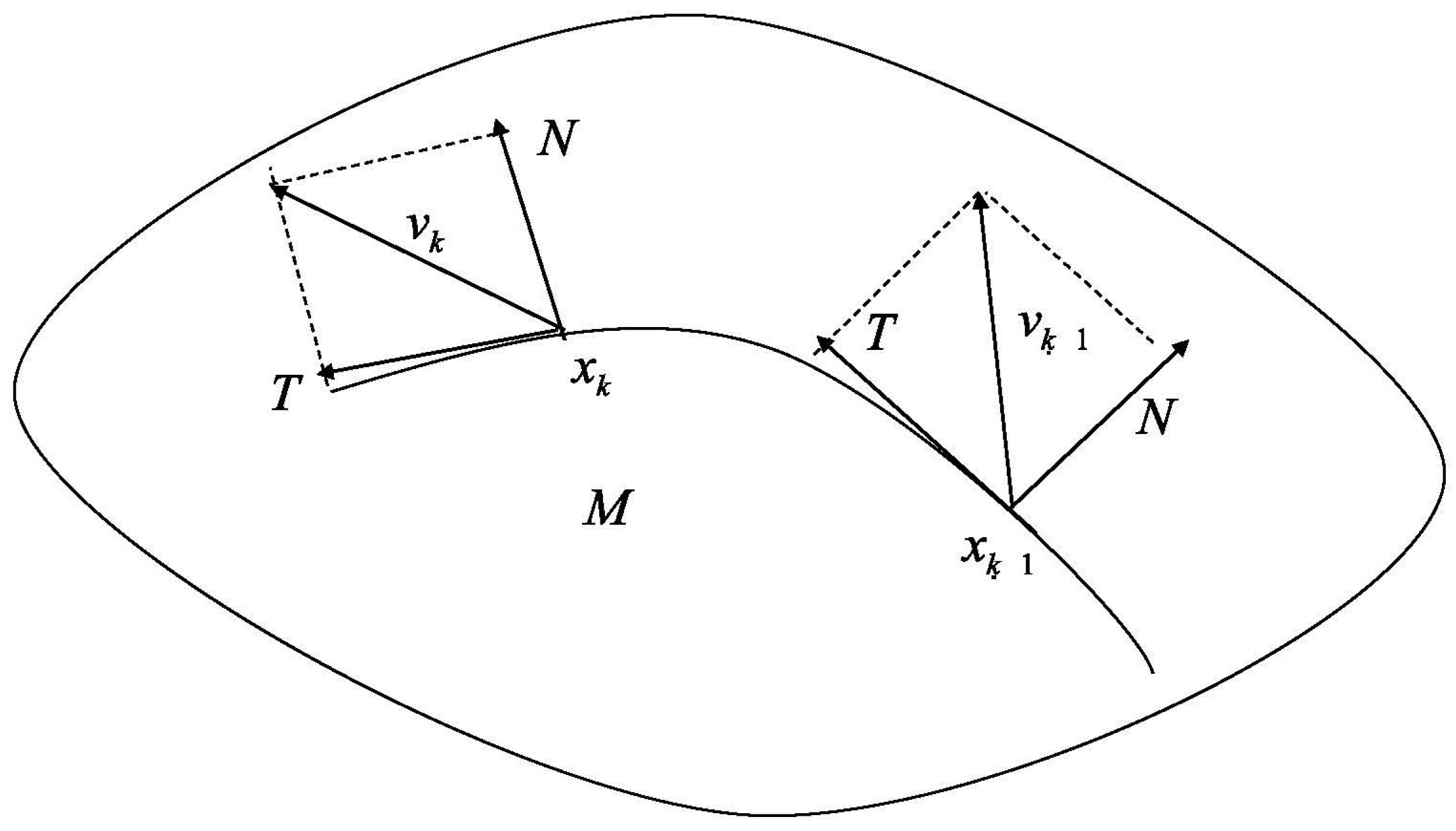
3. Extended Hamiltonian Learning on SE(n)
4. 2D/3D Rigid Shape Registration Based on Extended Hamiltonian Learning
| Algorithm 1 EHL-ICP Algorithm |
| Input: Initial Data ; Target Data Output: Rotation ; Translation ; Registration Error ;
|
5. Numerical Results
5.1. 2D Rigid Shape Registration
5.2. 3D Shape Registration
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Cheng, P.; Menq, C.H. Real-Time Continuous Image Registration Enabling Ultraprecise 2D Motion Tracking. IEEE Trans. Image Process. 2013, 22, 2081–2090. [Google Scholar] [CrossRef] [PubMed]
- Chandrashekara, R.; Mohiaddin, R.H.; Rueckert, D. Cardiac Motion Tracking in Tagged MR Images Using a 4D B-Spline Motion Model and Nonrigid Image Registration. In Proceedings of the IEEE International Symposium on Biomedical Imaging: Nano to Macro, Arlington, VA, USA, 18 April 2004. [Google Scholar]
- Silva, T.D.; Uneri, A.; Ketcha, M.D.; Reaungamornrat, S.; Kleinszig, G.; Vogt, S.; Aygun, N.; Lo, S.; Wolinsky, J.P.; Siewerdsen, J.H. 3D-2D Image Registration for Target Localization in Spine Surgery: Investigation of Similarity Metrics Providing Robustness to Content Mismatch. Phys. Med. Biol. 2016, 61, 3009–3025. [Google Scholar] [CrossRef] [PubMed]
- Vandewalle, P.; Susstrunk, S.; Vetterli, M. A Frequency Domain Approach to Registration of Aliased Images with Application to Super-resolution. EURASIP J. Adv. Signal Process. 2006, 1, 071459. [Google Scholar] [CrossRef]
- Majumdar, J.; Vinay, S.; Selvi, S. Registration and Mosaicing for Images Obtained from UAV. In Proceedings of the IEEE International Conference on Signal Processing and Communications, Bangalore, India, 11–14 December 2005. [Google Scholar]
- Roche, A.; Pennec, X.; Malandain, G.; Ayache, N. Rigid Registration of 3D Ultrasound With MR Images: A New Approach Combining Intensity and Gradient Information. IEEE Trans. Med. Imaging 2001, 20, 1038–1049. [Google Scholar] [CrossRef]
- Rueckert, D.; Sonoda, L.I.; Hayes, C.; Hill, D.L.; Leach, M.O.; Hawkes, D.J. Nonrigid Registration Using Free-Form Deformations: Application to Breast MR Images. IEEE Trans. Med. Imaging 1999, 18, 712–721. [Google Scholar] [CrossRef]
- Maintz, J.B.; Viergever, M.A. A Survey of Medical Image Registration. Comput. Digit. Eng. 2009, 33, 140–144. [Google Scholar] [CrossRef]
- Wyawahare, M.W.; Patil, P.M.; Abhyankar, H.K. Image Registration Techniques: An Overview. Int. J. Signal Process. Image Process. Pattern Recognit. 2009, 2, 11–28. [Google Scholar]
- Wan, R.; Li, M. An Overview of Medical Image Registration. In Proceedings of the IEEE International Conference on Computational Intelligence and Multimedia Applications, Xi’an, China, 27–30 September 2003. [Google Scholar]
- Zitova, B.; Flusser, J.; Sroubek, F. Image Registration: A Survey and Recent Advances. In Proceedings of the International Conference Image Processing, Genoa, Italy, 11–14 September 2005. [Google Scholar]
- Salvi, J.; Matabosch, C.; Fofi, D.; Forest, J. A Review of Recent Range Image Registration Methods with Accuracy Evaluation. Image Vis. Comput. 2007, 25, 578–596. [Google Scholar] [CrossRef]
- Zha, H.; Ikuta, M.; Hasegawa, T. Registration of Range Images with Different Scanning Resolutions. In Proceedings of the IEEE International Conference on Systems, Nashville, TN, USA, 8–11 October 2000. [Google Scholar]
- Chui, H.; Rangarajan, A. A New Point Matching Algorithm for Non-Rigid Registration. Comput. Vis. Image Underst. 2003, 89, 114–141. [Google Scholar] [CrossRef]
- Zhu, J.; Du, S.; Yuan, Z.; Liu, Y.; Ma, L. Robust Affine Iterative Closest Point Algorithm with Bidirectional Distance. IET Comput. Vis. 2012, 6, 252–261. [Google Scholar] [CrossRef]
- Du, S.; Zheng, N.; Meng, G.; Yuan, Z. Affine Registration of Point Sets Using ICP and ICA. IEEE Signal Process. Lett. 2008, 15, 689–692. [Google Scholar]
- Ying, S.; Peng, J.; Du, S.; Qiao, H. A Scale Stretch Method Based on ICP for 3D Data Registration. IEEE Trans. Autom. Sci. Eng. 2009, 6, 559–565. [Google Scholar] [CrossRef]
- Ying, S.; Peng, J.; Du, S.; Qiao, H. Lie Group Framework of Iterative Closest Point Algorithm for n-D Data Registration. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 1201–1220. [Google Scholar] [CrossRef]
- Du, S.; Zheng, N.; Xiong, L.; Ying, S.; Xue, J. Scaling Iterative Closest Point Algorithm for Registration of m-D Point Sets. J. Vis. Commun. Image Represent. 2010, 21, 442–452. [Google Scholar] [CrossRef]
- Ying, S.; Lin, W.; Peng, J.; Peng, J. Soft Shape Registration Under Lie Group Frame. IET Comput. Vis. 2013, 7, 437–447. [Google Scholar]
- Ying, S.; Peng, Y.; Wen, Z. Iwasawa Decomposition: A New Approach to 2D Affine Registration Problem. Pattern Anal. Appl. 2011, 14, 127–137. [Google Scholar] [CrossRef]
- Celledoni, E.; Eidnes, S.; Eslitzbichler, M.; Schmeding, A. Shape analysis on Lie groups and homogeneous spaces. In Proceedings of the International Conference on Geometric Science of Information, Paris, France, 7–9 November 2017; pp. 49–56. [Google Scholar]
- Celledoni, E.; Eidnes, S.; Schmeding, A. Shape analysis on homogeneous spaces: A generalised SRVT framework. In Proceedings of the Abel Symposium, Rosendal, Norway, 16–19 August 2016; pp. 187–220. [Google Scholar]
- Brigant, A.L. A discrete framework to find the optimal matching between manifold-valued curves. J. Math. Imaging Vis. 2019, 61, 40–70. [Google Scholar] [CrossRef]
- Pennec, X.; Ayache, N.; Thirion, J.-P. Landmark-based registration using features identified through differential geometry. In Handbook of Medical Imaging—Processing and Analysis; Wiley-VCH: Hoboken, NJ, USA, 2000; pp. 499–513. [Google Scholar]
- Chirikjian, G.S.; Kyatkin, A.B. Harmonic Analysis for Engineers and Applied Scientists: Updated and Expanded Edition; Courier Dover Publications: New York, NY, USA, 2016. [Google Scholar]
- Gower, J.; Dijksterhuis, G. Procrustes Problems; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Kanatani, K. Statistical Optimization for Geometric Computation: Theory and Practice; Courier Dover Publications: New York, NY, USA, 2005. [Google Scholar]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Barbaresco, F. Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning. Entropy 2018, 20, 840. [Google Scholar] [CrossRef]
- Barbaresco, F. Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics. Entropy 2014, 16, 4521–4565. [Google Scholar] [CrossRef]
- Fiori, S. Extended Hamiltonian Learning on Riemannian manifolds: Theoretical Aspects. IEEE Trans. Neural Netw. 2011, 22, 687–700. [Google Scholar] [CrossRef]
- Fiori, S. Extended Hamiltonian Learning on Riemannian manifolds: Numerical Aspects. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 7–21. [Google Scholar] [CrossRef]
- Selig, J.M. Lie Algebra. In Geometric Fundamentals of Robotics; Springer: New York, NY, USA, 2005; pp. 52–71. [Google Scholar]
- Kumar, V.; Croke, C.B. On the generation of smooth three-dimensional rigid body motions. IEEE Trans. Robot. Autom. 1998, 14, 576–589. [Google Scholar]
- Hall, B.C. Lie Algebras and the Exponential Mapping. In Lie Groups, Lie Algebras, and Representations: An Elementary Introduction; Springer: New York, NY, USA, 2003; pp. 27–58. [Google Scholar]
- Do Carmo, M. Differential Geometry of Curves and Surfaces; Prentice-Hall: Upper Saddle River, NJ, USA, 1976; pp. 238–260. [Google Scholar]
- Feydy, J.; Charlier, B.; Vialard, F.; Peyré, G. Optimal transport for diffeomorphic registration. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017; pp. 291–299. [Google Scholar]
- Kolouri, S.; Park, S.; Thorpe, M.; Slepcev, D.; Rohde, G.K. Transport-based analysis, modeling, and learning from signal and data distributions. arXiv 2016, arXiv:1609.04767. [Google Scholar]
- Keszei, A.; Berkels, B.; Deserno, T. Survey of non-rigid registration tools in medicine. J. Digit. Imaging 2017, 30, 102–116. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Yang, J.; Lai, Y.; Guo, D. Robust non-rigid registration with reweighted position and transformation sparsity. IEEE Trans. Vis. Comput. Graph. 2018, 25, 2255–2269. [Google Scholar] [CrossRef] [PubMed]
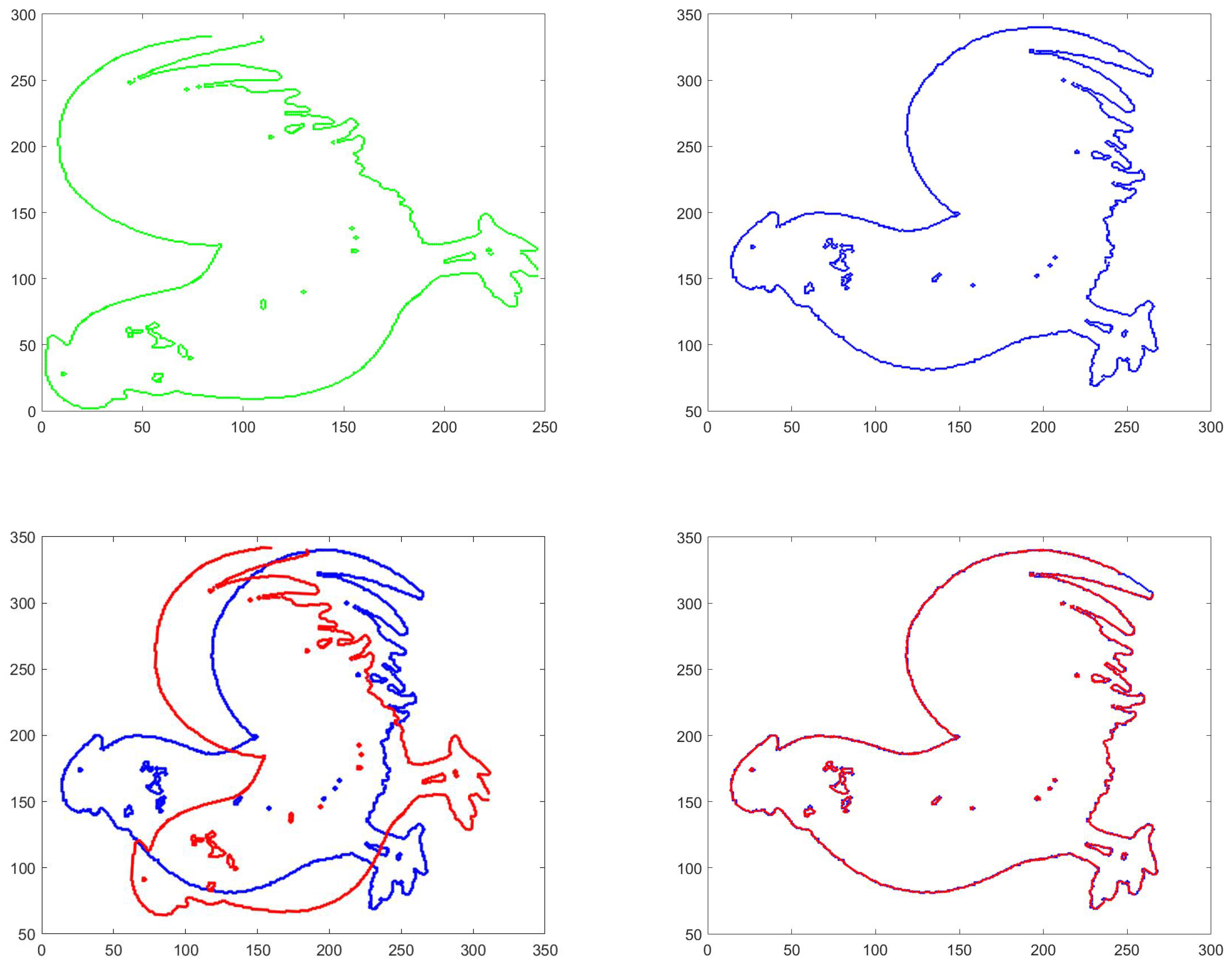
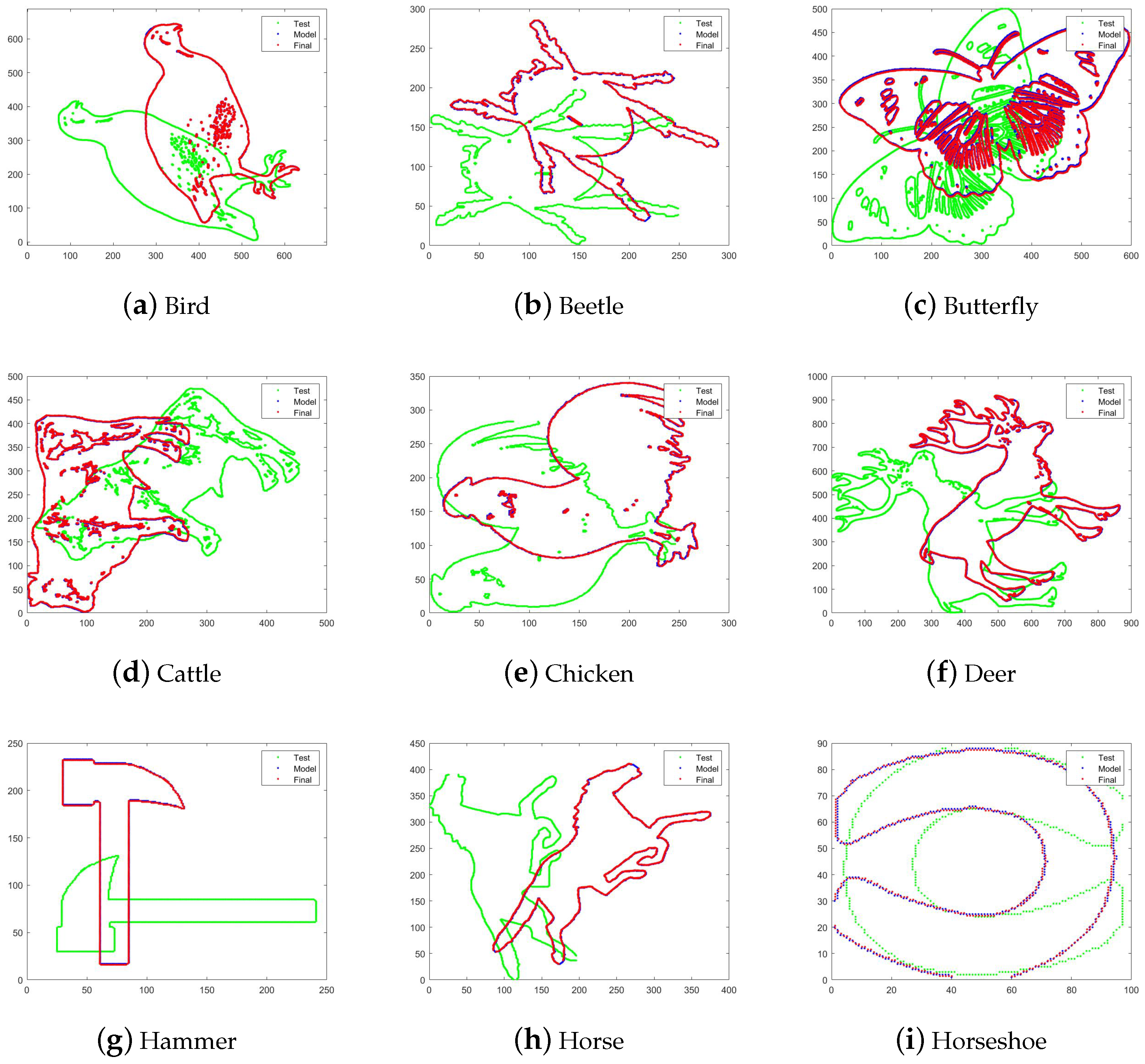

| Group | Model | Test | SVD | ID | LGO | EHL-ICP |
|---|---|---|---|---|---|---|
| (1) | bird-3 | bird-4 | 0.5841 | 0.9996 | 0.5690 | 0.4048 |
| (2) | deer-1 | deer-4 | 0.5263 | 2.7598 | 0.5272 | 2.8826 |
| (3) | horse-3 | horse-4 | 0.5107 | 1.4278 | 0.5112 | 0.3880 |
| (4) | beetle-7 | beetle-8 | 0.8749 | 0.8746 | 0.5242 | 0.4730 |
| (5) | cattle-1 | cattle-20 | 22.8580 | 28.3719 | 22.5155 | 1.1656 |
| (6) | hammer-4 | hammer-5 | 0.4846 | 0.8037 | 0.4232 | 0.3043 |
| (7) | chicken-2 | chicken-3 | 0.5484 | 2.7 843 | 0.5471 | 0.5202 |
| (8) | butterfly-1 | butterfly-2 | 18.1726 | 34.3588 | 6.9691 | 2.9062 |
| (9) | horseshoe-9 | horseshoe-17 | 0.5425 | 0.5690 | 0.5873 | 0.3577 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, J.; Zhang, S.; Cao, Y.; Zhang, E.; Sun, H. Rigid Shape Registration Based on Extended Hamiltonian Learning. Entropy 2020, 22, 539. https://doi.org/10.3390/e22050539
Yi J, Zhang S, Cao Y, Zhang E, Sun H. Rigid Shape Registration Based on Extended Hamiltonian Learning. Entropy. 2020; 22(5):539. https://doi.org/10.3390/e22050539
Chicago/Turabian StyleYi, Jin, Shiqiang Zhang, Yueqi Cao, Erchuan Zhang, and Huafei Sun. 2020. "Rigid Shape Registration Based on Extended Hamiltonian Learning" Entropy 22, no. 5: 539. https://doi.org/10.3390/e22050539
APA StyleYi, J., Zhang, S., Cao, Y., Zhang, E., & Sun, H. (2020). Rigid Shape Registration Based on Extended Hamiltonian Learning. Entropy, 22(5), 539. https://doi.org/10.3390/e22050539





