Neural Computing Enhanced Parameter Estimation for Multi-Input and Multi-Output Total Non-Linear Dynamic Models
Abstract
1. Introduction
1.1. Literature Survey
1.2. Motivation and Contributions
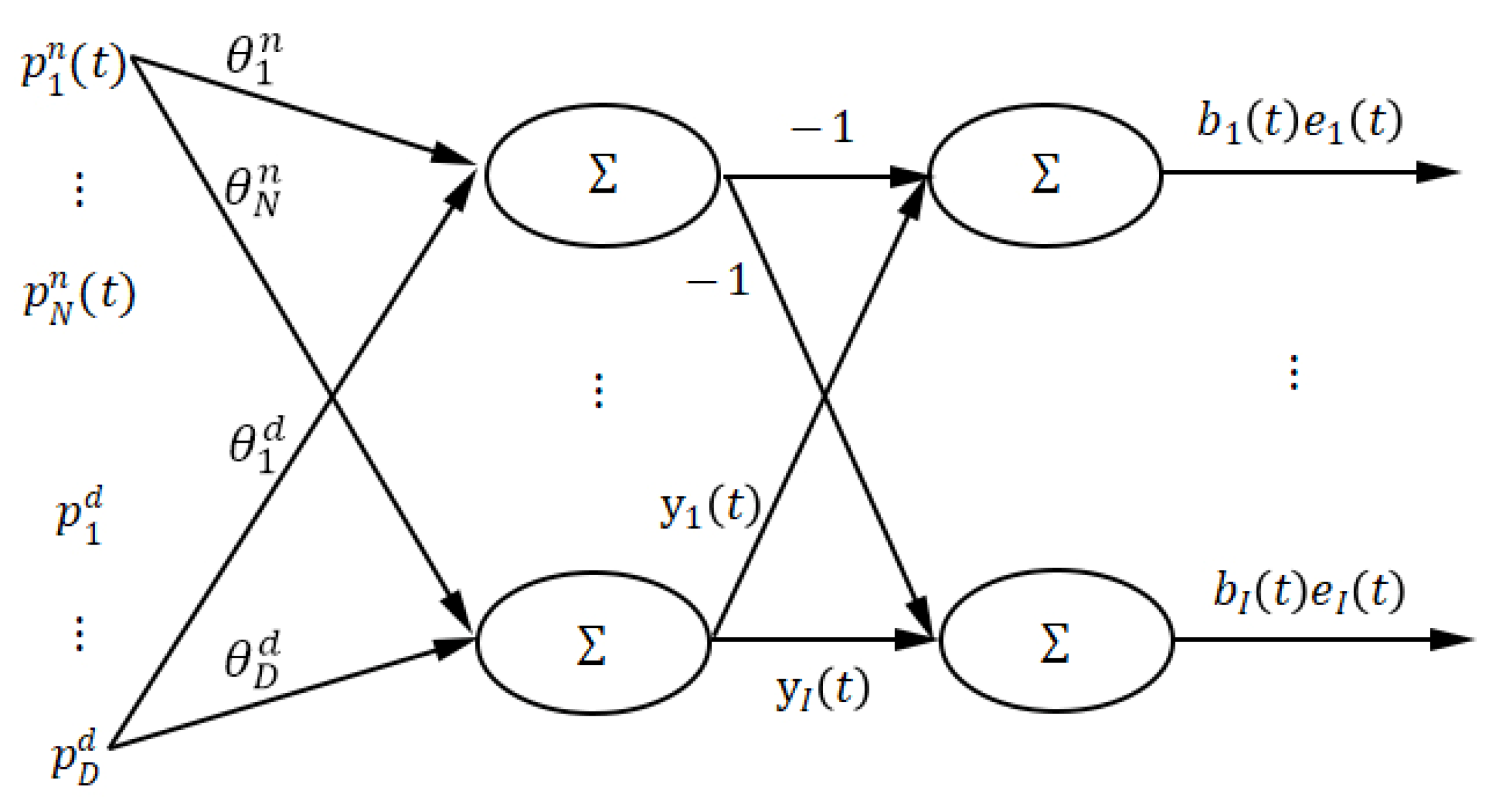
2. Total Non-Linear Model
- (i)
- The input layer consists of regression terms and ; here, a neuron in the hidden layer is not connected to all the neurons in the input layer, that is, the network is a non-completely connected feedforward neural network.
- (ii)
- The action function of the neurons in the hidden layer is linear, and the output of the hidden layer neurons is or .
- (iii)
- The action function of the output layer neurons is linear, and the output of the ith output layer neuron is .
- (iv)
- The connection weights between the input layer neurons and the hidden layer neurons are the parameters and of the model.
- (v)
- The connection weight between the hidden layer neurons and the ith output layer neurons are and the observed output .
- (i)
- By setting parameter , Zhu’s [18] model can be a special case of the model in Formula (1).
- (ii)
- The model is non-linear in parameters and regression terms, which was caused by denominator polynomials.
- (iii)
- When the denominator of the model is close to 0, the output deviation would be large. In this paper, considering this point, division operation was avoided in the action function of the neuron when the neural network model was being built.
- (iv)
- The structure of the neural network corresponding to the total non-linear model is a non-completely connected feedforward neural network, or a partially connected feedforward neural network. Therefore, the convergence of the network becomes a big problem, which is the difficulty of this paper.
- (v)
- The model has a wide range of application prospects. In many non-linear system modeling and control applications, the total non-linear model has been gradually adopted. Some non-linear models, such as the exponential model , which describes the change of dynamic rate constant with temperature, cannot be directly used. The exponential model can be firstly transformed into a non-linear model (), and then, system identification can be implemented [19,21,22].
3. Gradient Descent Calculation of Parameter Estimation
| Algorithm 1. Gradient Descent Algorithm |
| 1: Initialization: The weights of the neural network (parameters of a total non-linear model) are set as random little numbers with uniform distribution; the average value is zero, and the variance is small. Set the maximum number of iterations T, the minimum error ε, and the maximum number of samples . 2: Generate training sample set {,} of the neural network according to Formula (1), where , = {}, {,,…,,}, ={}. 3: Input a training sample p to the neural network. 4: Calculate the output value , and of the neurons in the hidden layer and the output layer according to Formulas (2), (3), and (4), respectively. 5: Adjust the weight of the neural network according to Formulas (10) and (13). 6: Calculate the error according to Formula (4) and calculate the total error according to Formula (14). 7: 8: If p > P, then t = t + 1; otherwise, run step 3. 9: If ε or , stop training; otherwise, run step 3. |
4. Model Structure Detection
| Algorithm 2. Knock-Out Algorithm |
| 1: Using the network structure shown in Figure 1, all the items contained in the whole items set are taken as the input of the network. 2: The algorithm in Section 3 is used to train the network, and network error is obtained. 3: A new network structure is obtained by randomly removing a network input. The algorithm in Section 3 is used to train the new network, and network error is obtained. If , then . Otherwise, this operation should be invalid (the input is reserved). 4: Another input is selected, and step 3 is executed again until all the input items are executed once. 5: The N connection weights between the input layer and the hidden layer are sorted in descending order. The first n weights are selected to make the significance reach 95%. Meanwhile, Formulas (15) and (16) are met, and the network input items corresponding to the first n weights are retained. |
5. Convergence Analysis of the Algorithm
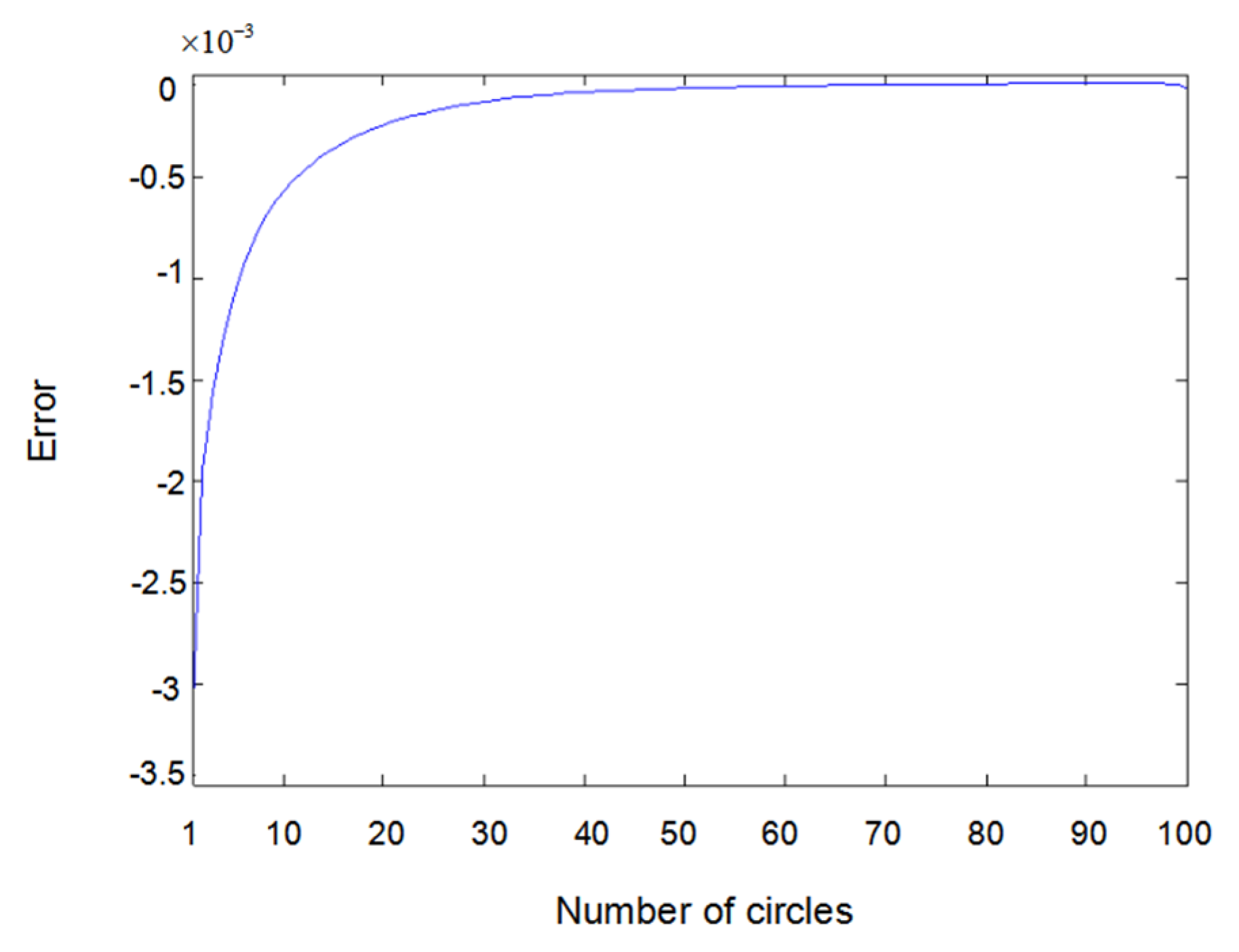
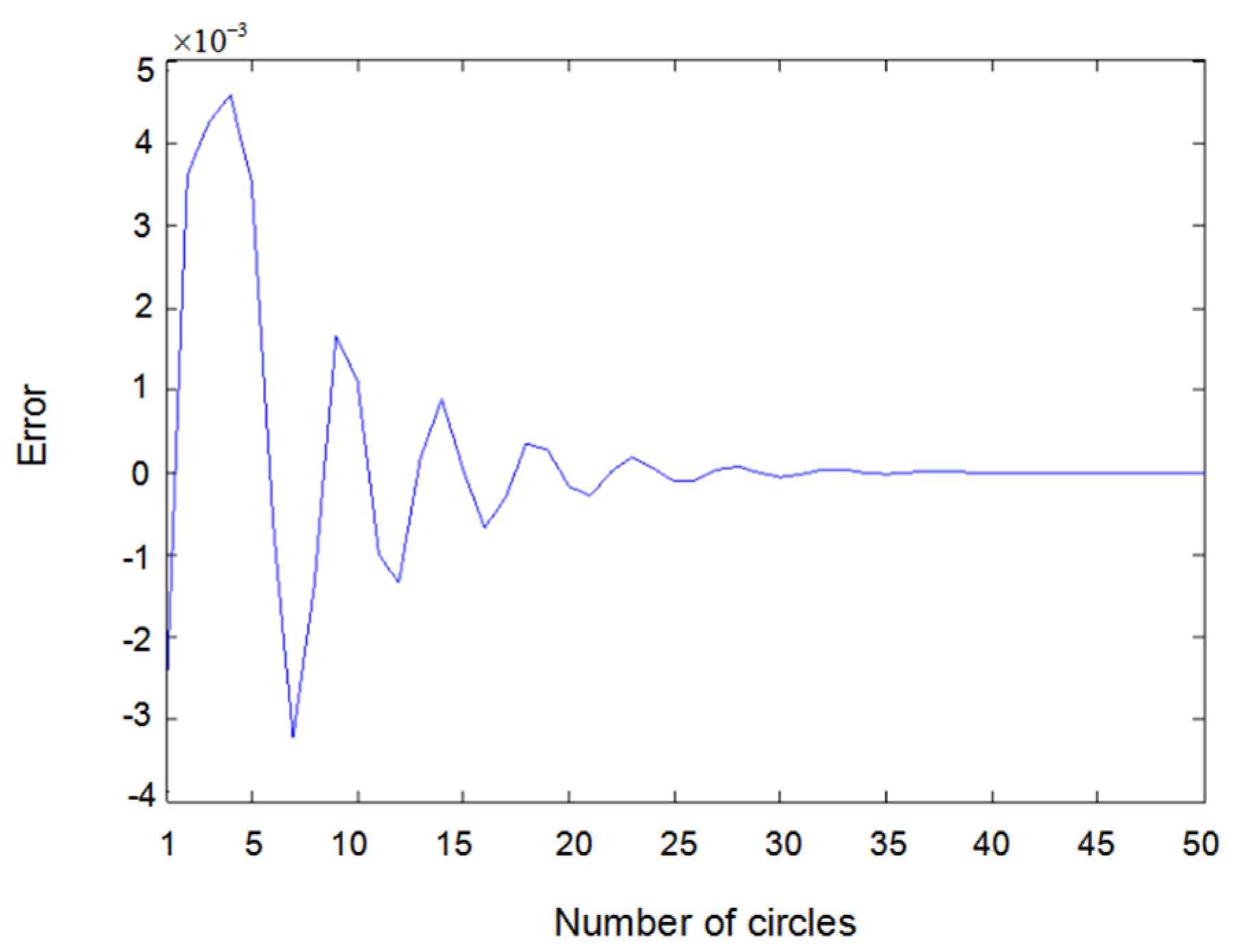
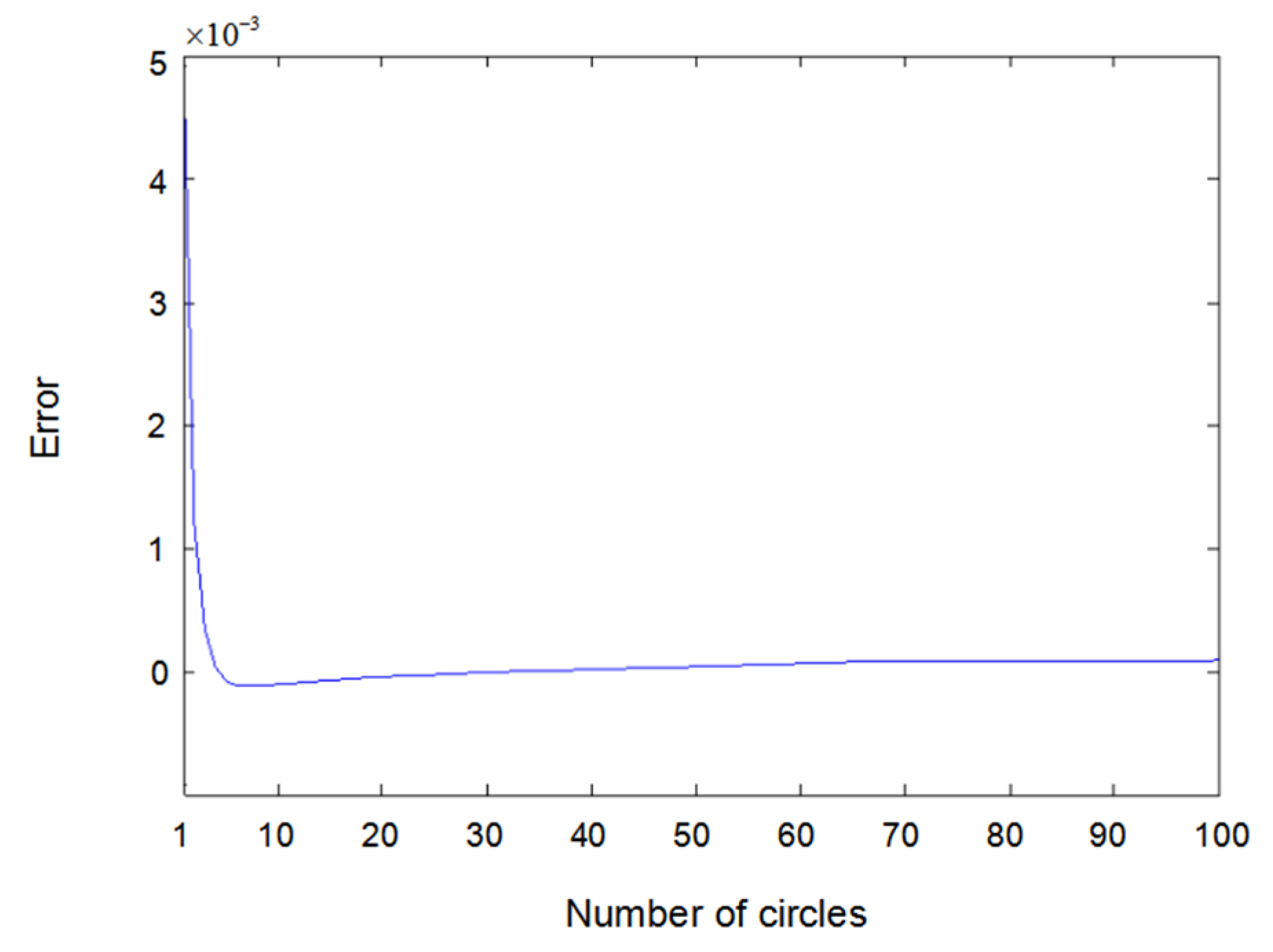
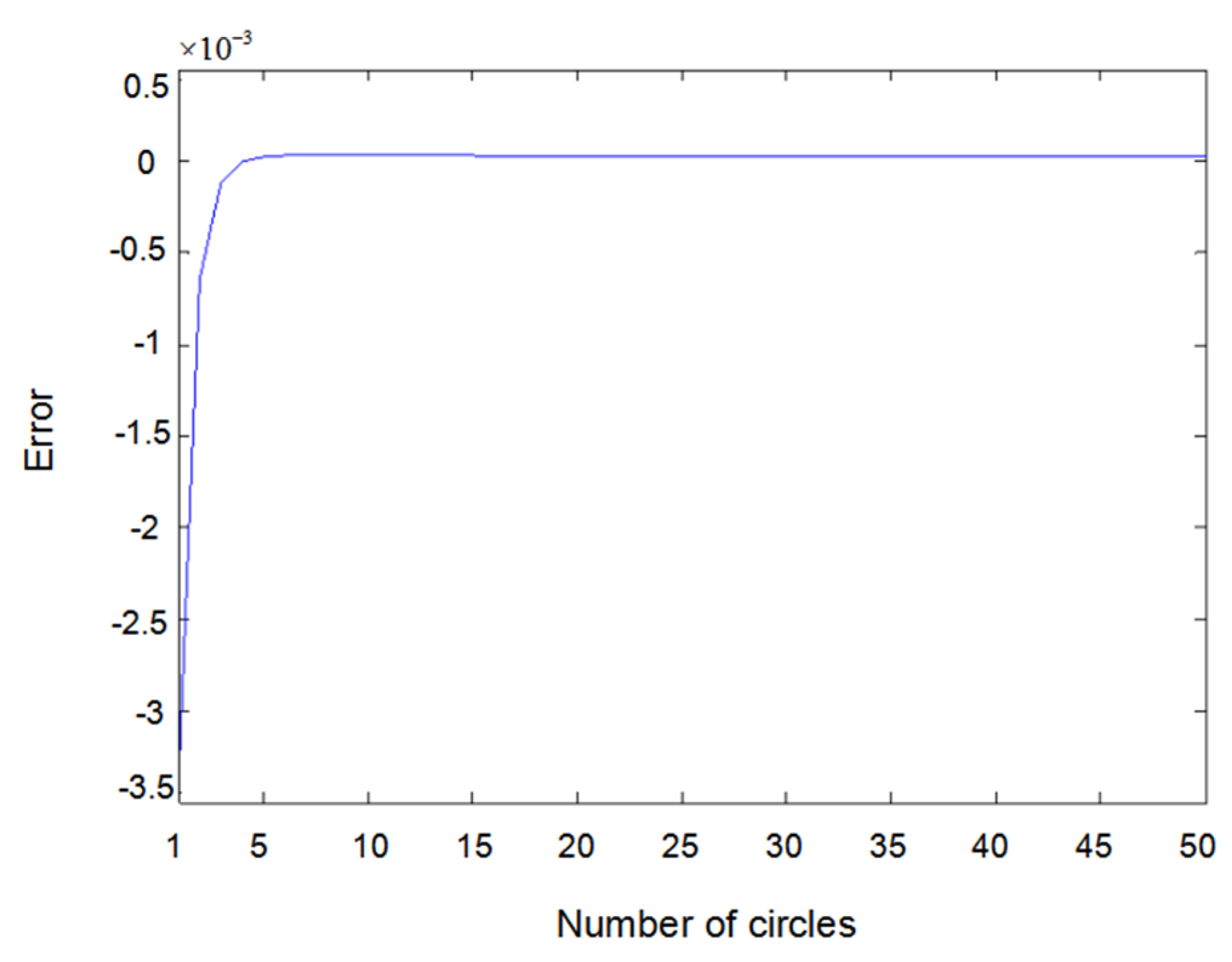
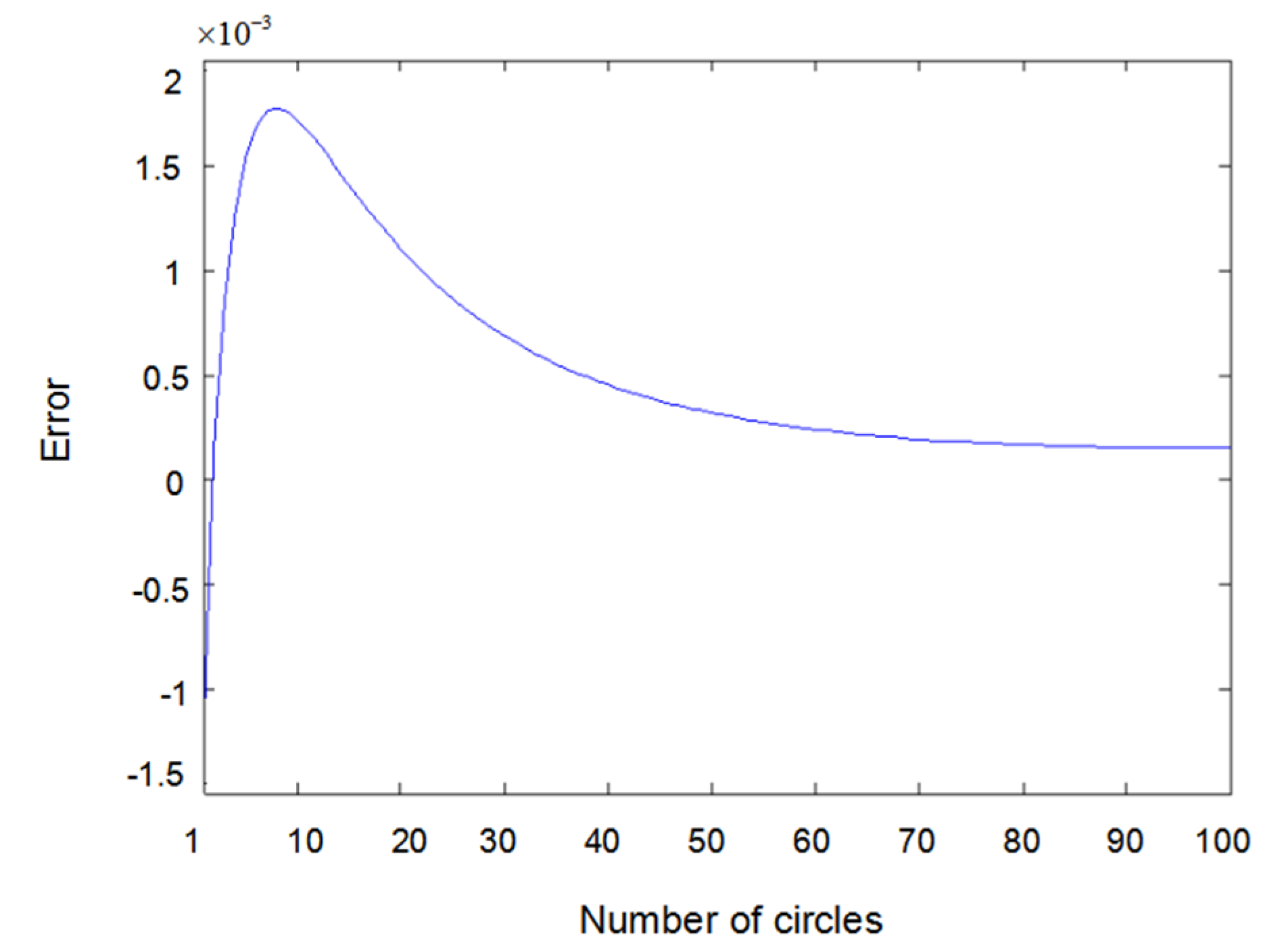
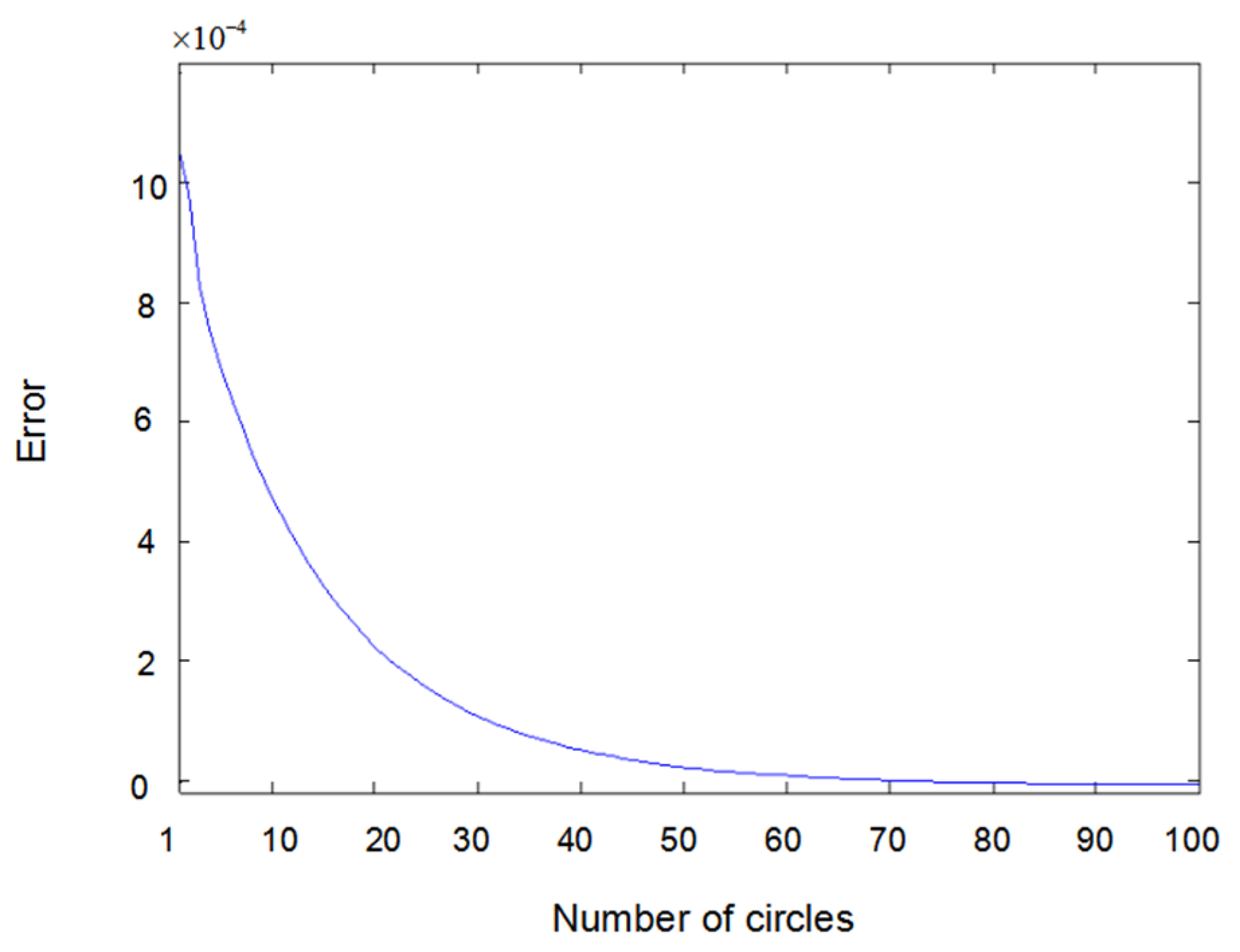
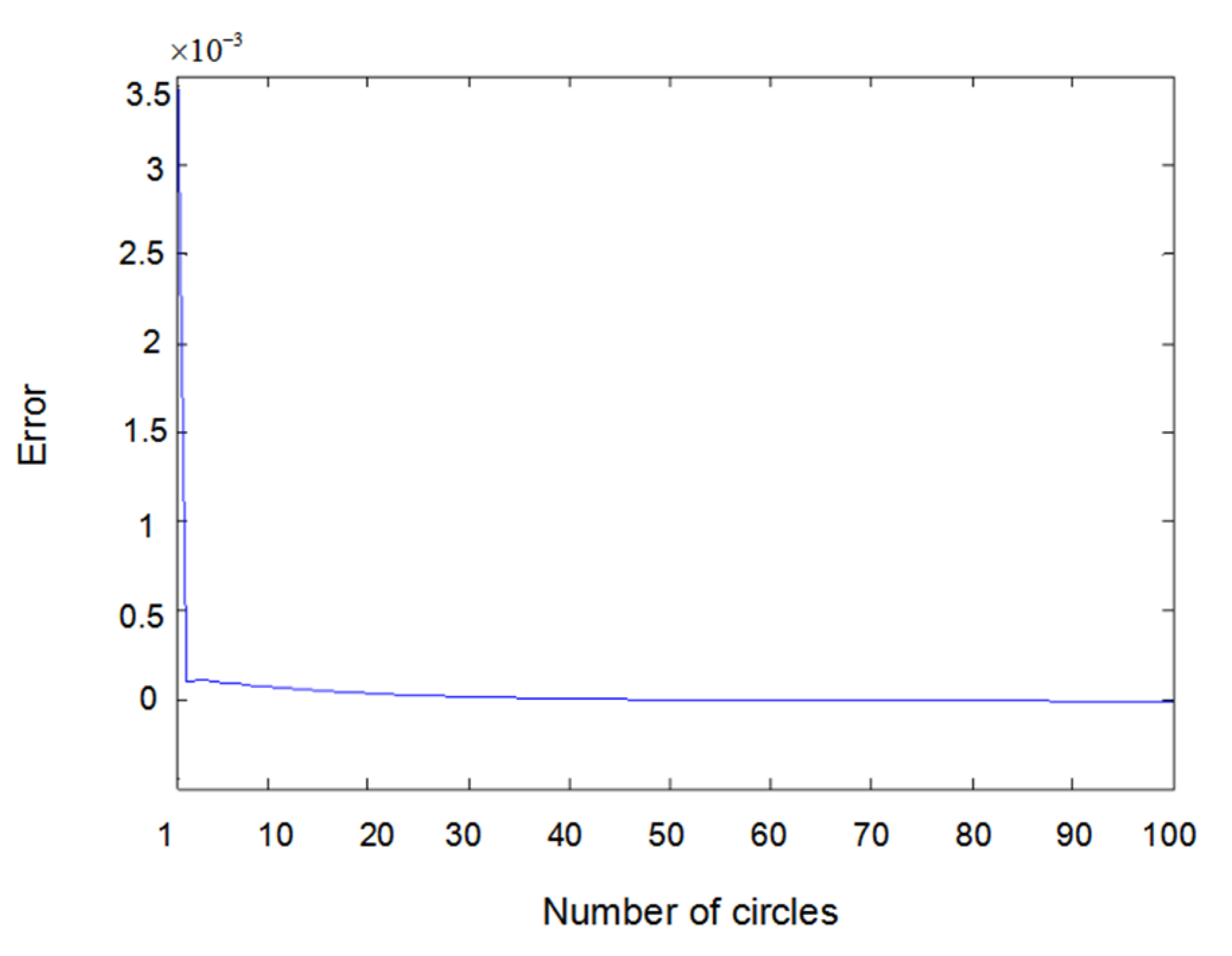
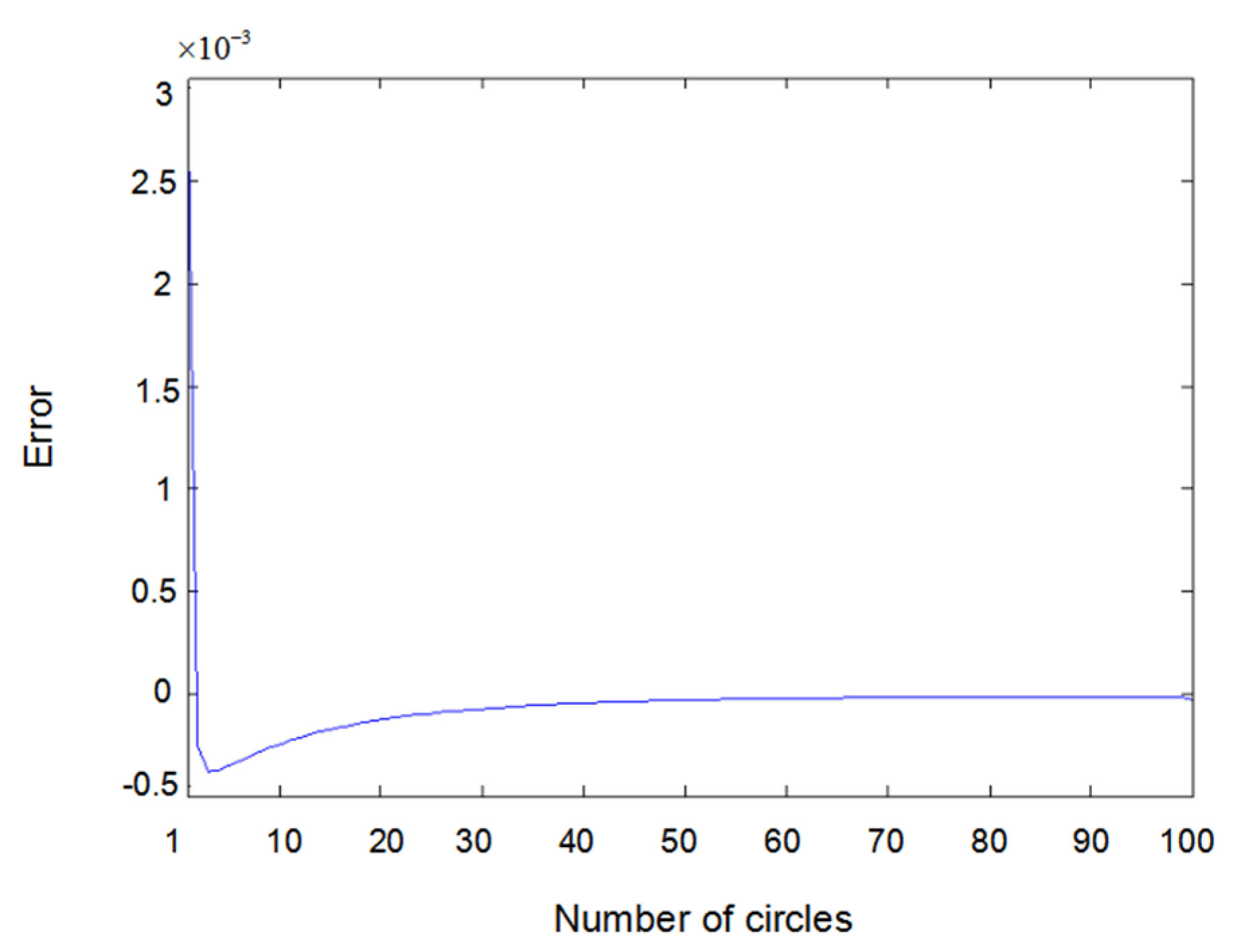
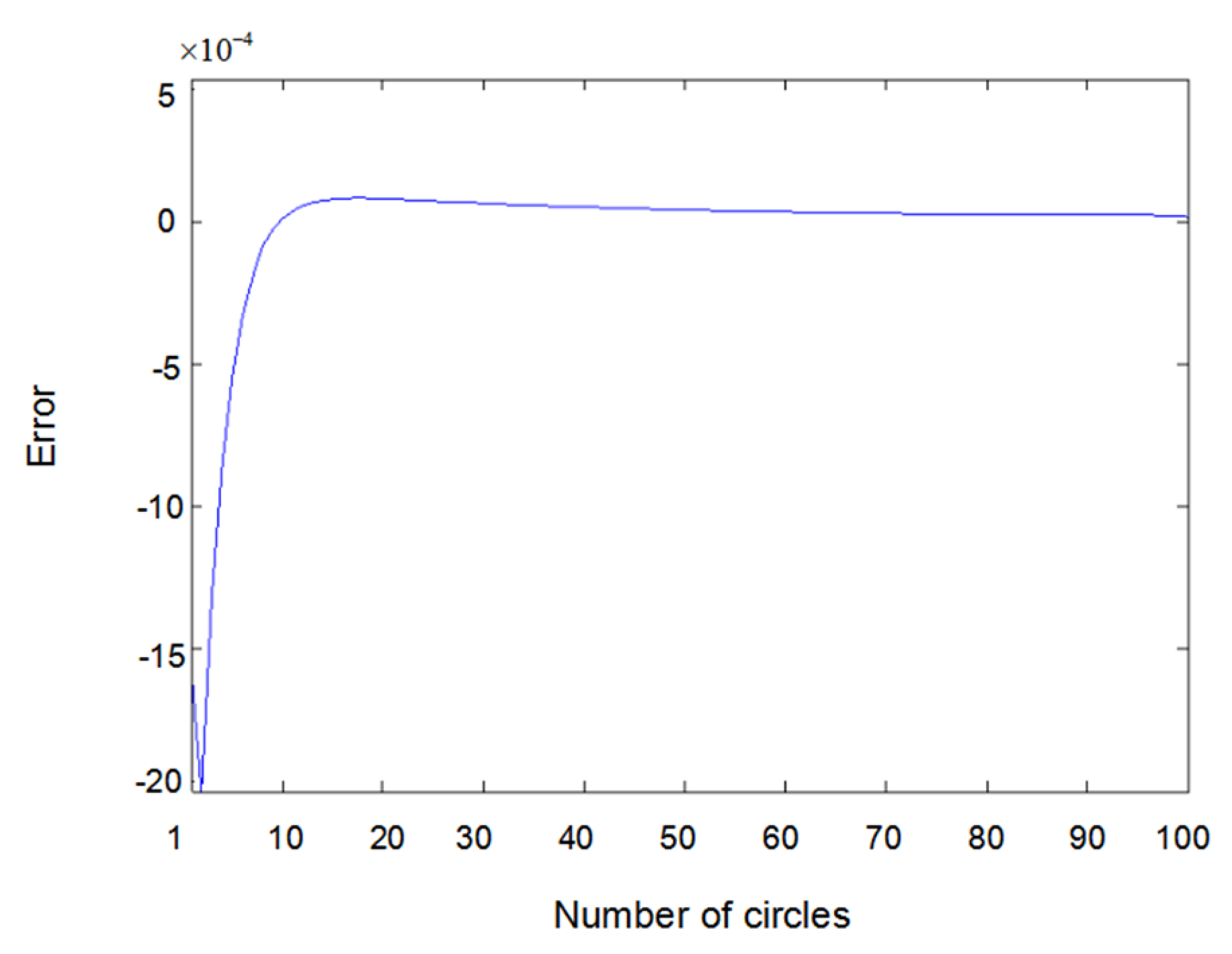
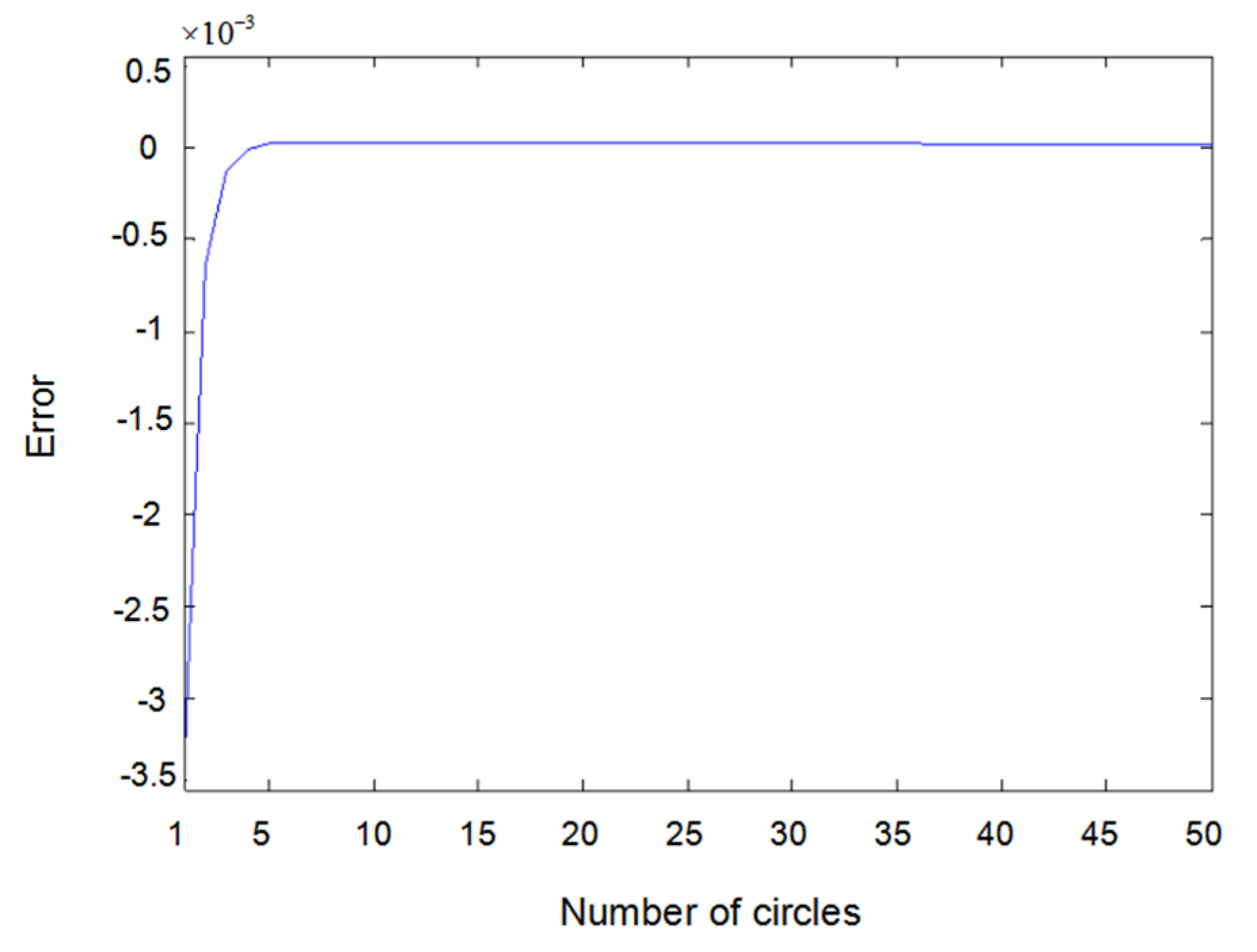
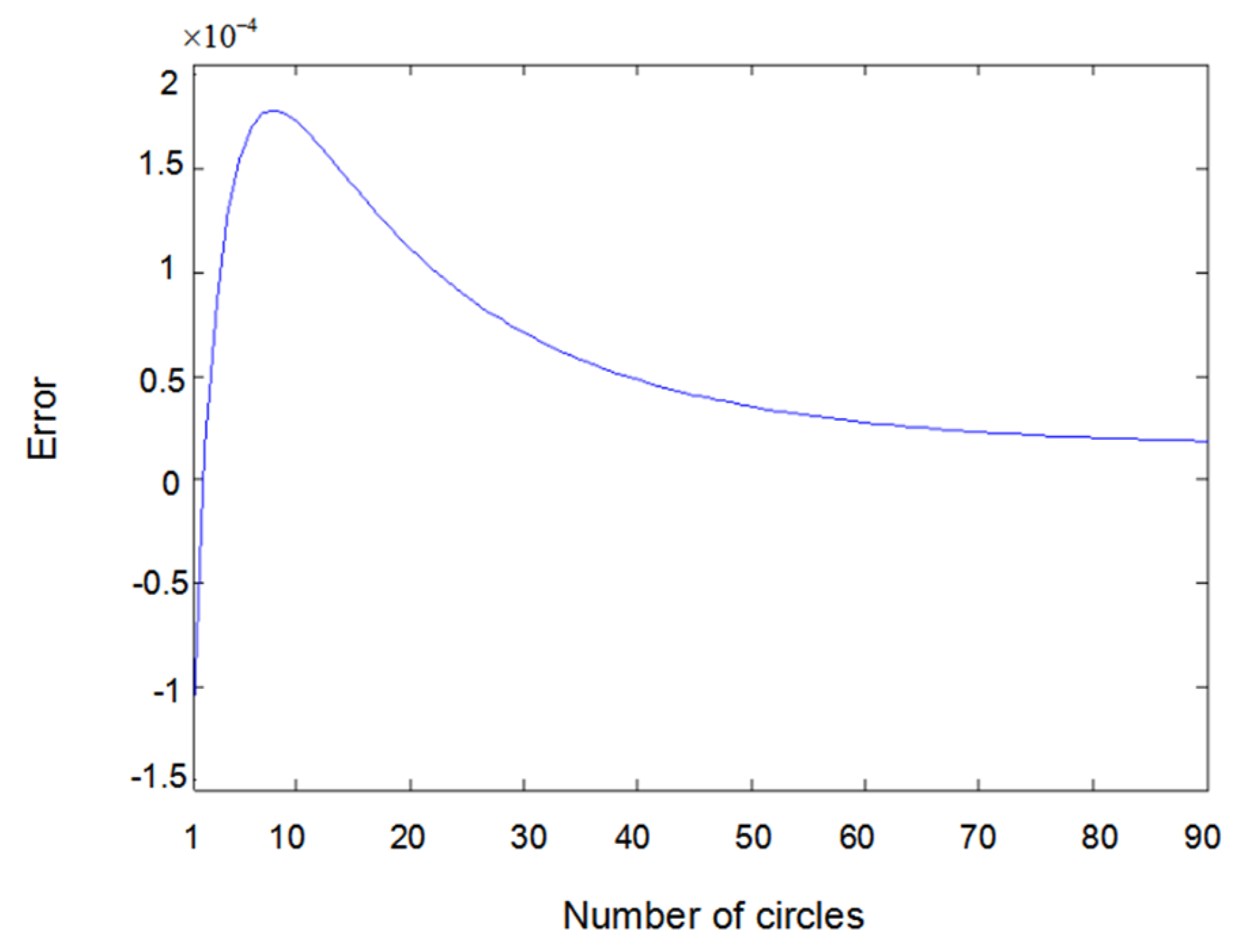
6. Simulation Results and Discussions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Billings, S.A.; Chen, S. Identification of non-linear rational systems using a prediction-error estimation algorithm. Int. J. Syst. Sci. 1989, 20, 467–494. [Google Scholar] [CrossRef]
- Billings, S.A.; Zhu, Q.M. Rational model identification using an extended least-squares algorithm. Int. J. Control 1991, 54, 529–546. [Google Scholar] [CrossRef]
- Sontag, E.D. Polynomial Response Maps. Lecture Notes in Control & Information Sciences; Springer: Berlin/Heidelberg, Germany, 1979; Volume 13. [Google Scholar]
- Narendra, K.S.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 2002, 1, 4–27. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.M.; Ma, Z.; Warwick, K. Neural network enhanced generalised minimum variance self-tuning controller for nonlinear discrete-time systems. IEE Proc. Control Theory Appl. 1999, 146, 319–326. [Google Scholar] [CrossRef]
- Billings, S.A.; Zhu, Q.M. A structure detection algorithm for nonlinear dynamic rational models. Int. J. Control 1994, 59, 1439–1463. [Google Scholar] [CrossRef]
- Zhu, Q.M.; Billings, S.A. Recursive parameter estimation for nonlinear rational models. J. Syst. Eng. 1991, 1, 63–67. [Google Scholar]
- Zhu, Q.M.; Billings, S.A. Parameter estimation for stochastic nonlinear rational models. Int. J. Control 1993, 57, 309–333. [Google Scholar] [CrossRef]
- Aguirre, L.A.; Barbosa, B.H.G.; Braga, A.P. Prediction and simulation errors in parameter estimation for nonlinear systems. Mech. Syst. Signal Process. 2010, 24, 2855–2867. [Google Scholar] [CrossRef]
- Huo, M.; Duan, H.; Luo, D.; Wang, Y. Parameter Estimation for a VTOL UAV Using Mutant Pigeon Inspired Optimization Algorithm with Dynamic OBL Strategy. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; pp. 669–674. [Google Scholar]
- Zhu, Q.M.; Yu, D.; Zhao, D. An Enhanced Linear Kalman Filter (EnLKF) algorithm for parameter estimation of nonlinear rational models. Int. J. Syst. Sci. 2016, 48, 451–461. [Google Scholar] [CrossRef]
- Türksen, Ö.; Babacan, E.K. Parameter Estimation of Nonlinear Response Surface Models by Using Genetic Algorithm and Unscented Kalman Filter. In Chaos, Complexity and Leadership 2014; Erçetin, S., Ed.; Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Billings, S.A.; Mao, K.Z. Structure detection for nonlinear rational models using genetic algorithms. Int. J. Syst. Sci. 1998, 29, 223–231. [Google Scholar] [CrossRef]
- Plakias, S.; Boutalis, Y.S. Lyapunov Theory Based Fusion Neural Networks for the Identification of Dynamic Nonlinear Systems. Int. J. Neural Syst. 2019, 29, 1950015. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Srivastava, S.; Gupta, J.R.P.; Mohindru, A. Diagonal recurrent neural network based identification of nonlinear dynamical systems with lyapunov stability based adaptive learning rates. Neurocomputing 2018, 287, 102–117. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Y. Robust Distributed Parameter Estimation of Nonlinear Systems with Missing Data over Networks. IEEE Trans. Aerosp. Electron. Syst. 2019. [Google Scholar] [CrossRef]
- Zhu, Q.M. An implicit least squares algorithm for nonlinear rational model parameter estimation. Appl. Math. Model. 2005, 29, 673–689. [Google Scholar] [CrossRef]
- Zhu, Q.M. A back propagation algorithm to estimate the parameters of non-linear dynamic rational models. Appl. Math. Model. 2003, 27, 169–187. [Google Scholar] [CrossRef]
- Zhu, Q.M.; Wang, Y.; Zhao, D.; Li, S.; Billings, S.A. Review of rational (total) nonlinear dynamic system modelling, identification, and control. Int. J. Syst. Sci. 2015, 46, 2122–2133. [Google Scholar] [CrossRef]
- Leung, H.; Haykin, S. Rational function neural network. Neural Comput. 1993, 5, 928–938. [Google Scholar] [CrossRef]
- Jain, R.; Narasimhan, S.; Bhatt, N.P. A priori parameter identifiability in models with non-rational functions. Automatica 2019, 109, 108513. [Google Scholar] [CrossRef]
- Kambhampati, C.; Mason, J.D.; Warwick, K. A stable one-step-ahead predictive control of nonlinear systems. Automatica 2000, 36, 485–495. [Google Scholar] [CrossRef]
- Kumar, R.; Srivastava, S.; Gupta, J.R.P. Lyapunov stability-based control and identification of nonlinear dynamical systems using adaptive dynamic programming. Soft Comput. 2017, 21, 4465–4480. [Google Scholar] [CrossRef]
- Ge, H.W.; Du, W.L.; Qian, F.; Liang, Y.C. Identification and control of nonlinear systems by a time-delay recurrent neural network. Neurocomputing 2009, 72, 2857–2864. [Google Scholar] [CrossRef]
- Verdière, N.; Zhu, S.; Denis-Vidal, L. A distribution input–output polynomial approach for estimating parameters in nonlinear models. Application to a chikungunya model. J. Comput. Appl. Math. 2018, 331, 104–118. [Google Scholar] [CrossRef]
- Li, F.; Jia, L. Parameter estimation of hammerstein-wiener nonlinear system with noise using special test signals. Neurocomputing 2019, 344, 37–48. [Google Scholar] [CrossRef]
- Chen, C.Y.; Gui, W.H.; Guan, Z.H.; Wang, R.L.; Zhou, S.W. Adaptive neural control for a class of stochastic nonlinear systems with unknown parameters, unknown nonlinear functions and stochastic disturbances. Neurocomputing 2017, 226, 101–108. [Google Scholar] [CrossRef]

| MSE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sine | sine | 0.5002 | 0.8025 | 1.0003 | 1.0034 | 1.0000 | 0.2006 | 0.5010 | 1.0004 | 1.0018 | 0.9991 | 2.351E-06 |
| sine | square | 0.5000 | 0.8000 | 1.0000 | 1.0000 | 1.0000 | 0.1996 | 0.4982 | 1.0182 | 0.9677 | 1.0473 | 0.0003 |
| square | square | 0.4973 | 0.8760 | 1.0110 | 1.0031 | 1.0153 | 0.2013 | 0.5072 | 1.0354 | 0.9744 | 1.0840 | 0.0015 |
| MSE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sine | sine | 0.5003 | 0.8041 | 1.0005 | 1.0054 | 1.0001 | 0.2008 | 0.5014 | 1.0005 | 1.0016 | 0.9987 | 5.342E-06 |
| sine | square | 0.5000 | 0.8001 | 1.0000 | 1.0001 | 1.0000 | 0.2045 | 0.5019 | 1.073 | 1.1364 | 1.0898 | 0.0032 |
| square | square | 0.4953 | 0.8765 | 1.0085 | 1.0327 | 1.0095 | 0.2969 | 0.7030 | 0.9971 | 1.0007 | 0.9953 | 0.0058 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ma, D.; Azar, A.T.; Zhu, Q. Neural Computing Enhanced Parameter Estimation for Multi-Input and Multi-Output Total Non-Linear Dynamic Models. Entropy 2020, 22, 510. https://doi.org/10.3390/e22050510
Liu L, Ma D, Azar AT, Zhu Q. Neural Computing Enhanced Parameter Estimation for Multi-Input and Multi-Output Total Non-Linear Dynamic Models. Entropy. 2020; 22(5):510. https://doi.org/10.3390/e22050510
Chicago/Turabian StyleLiu, Longlong, Di Ma, Ahmad Taher Azar, and Quanmin Zhu. 2020. "Neural Computing Enhanced Parameter Estimation for Multi-Input and Multi-Output Total Non-Linear Dynamic Models" Entropy 22, no. 5: 510. https://doi.org/10.3390/e22050510
APA StyleLiu, L., Ma, D., Azar, A. T., & Zhu, Q. (2020). Neural Computing Enhanced Parameter Estimation for Multi-Input and Multi-Output Total Non-Linear Dynamic Models. Entropy, 22(5), 510. https://doi.org/10.3390/e22050510






