How Complexity and Uncertainty Grew with Algorithmic Trading
Abstract
1. Introduction
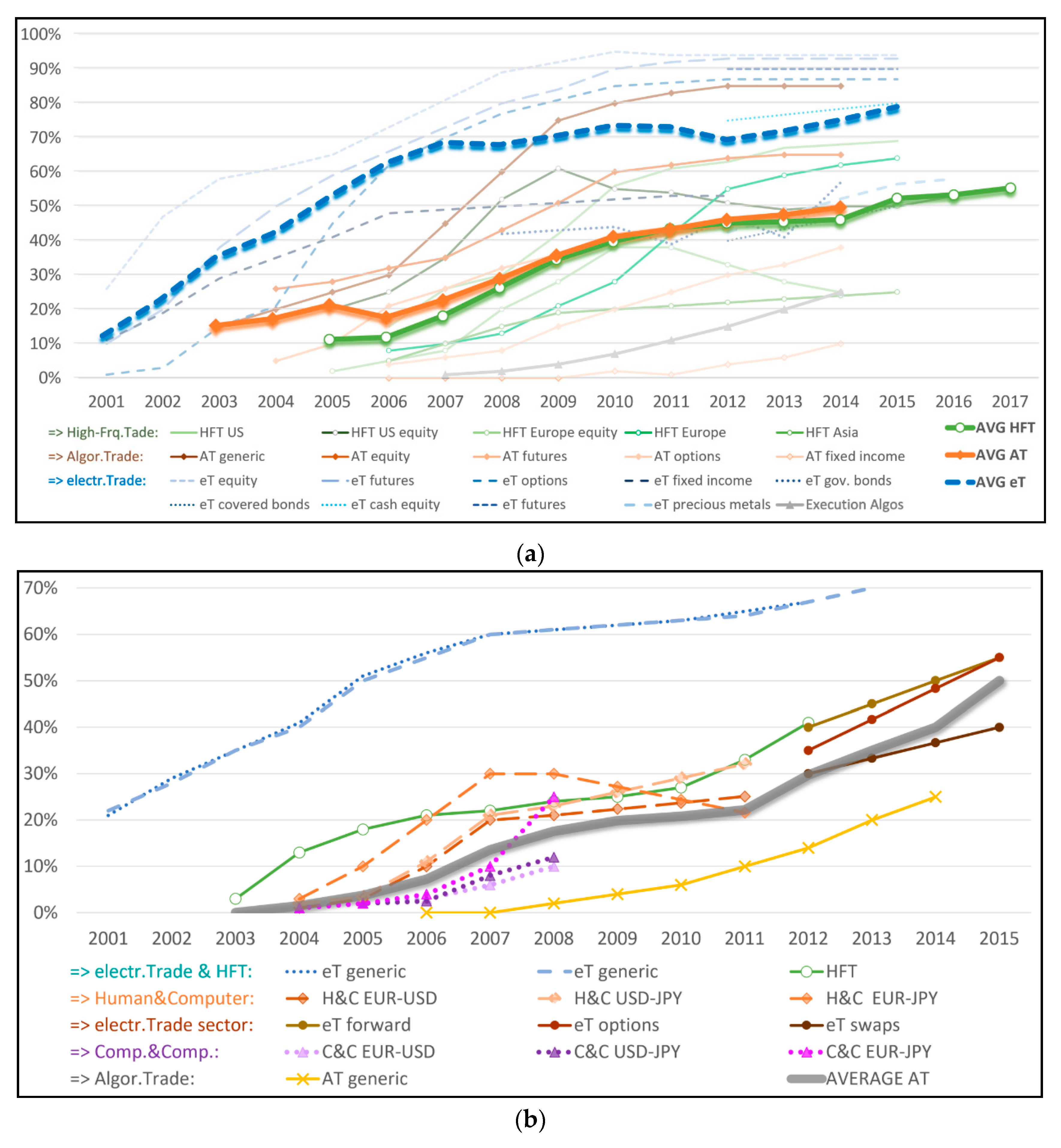
2. The Rise of Algorithmic Trading
3. Hypothesized Effects
3.1. Complexity (H1)
3.2. Uncertainty (H2)
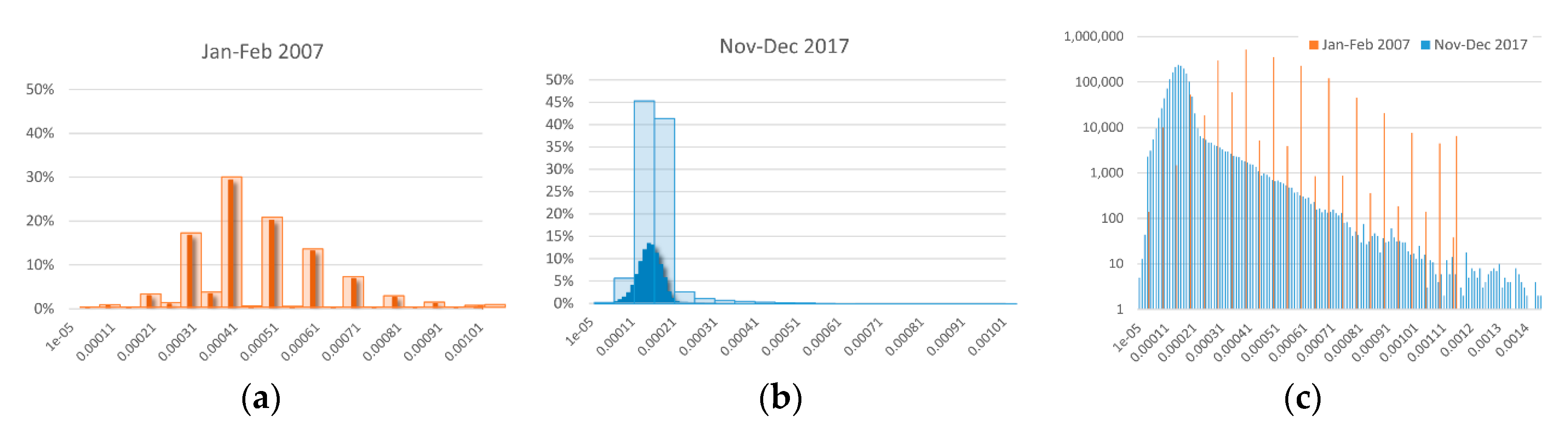
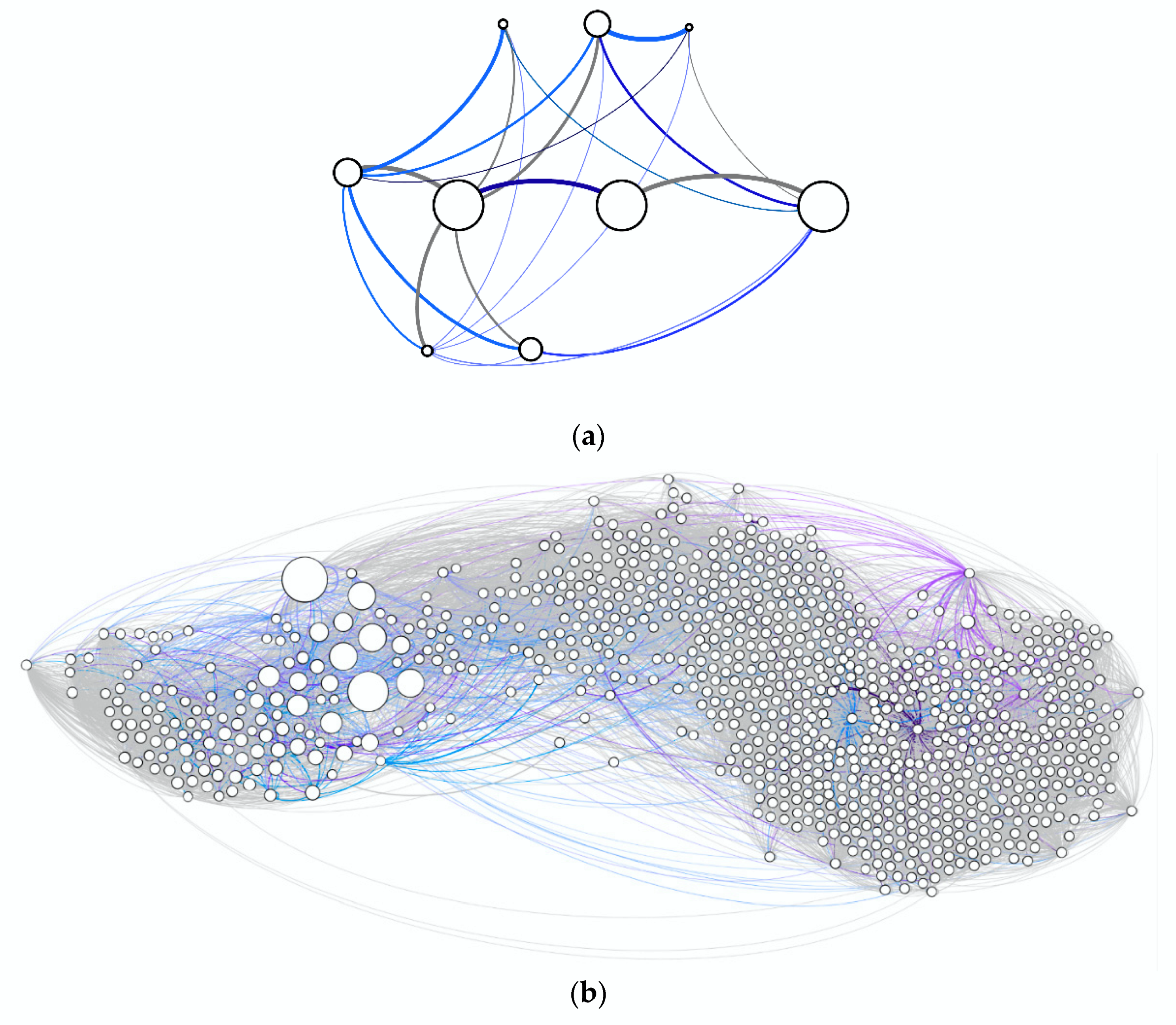
4. Data
4.1. Dependent Variables
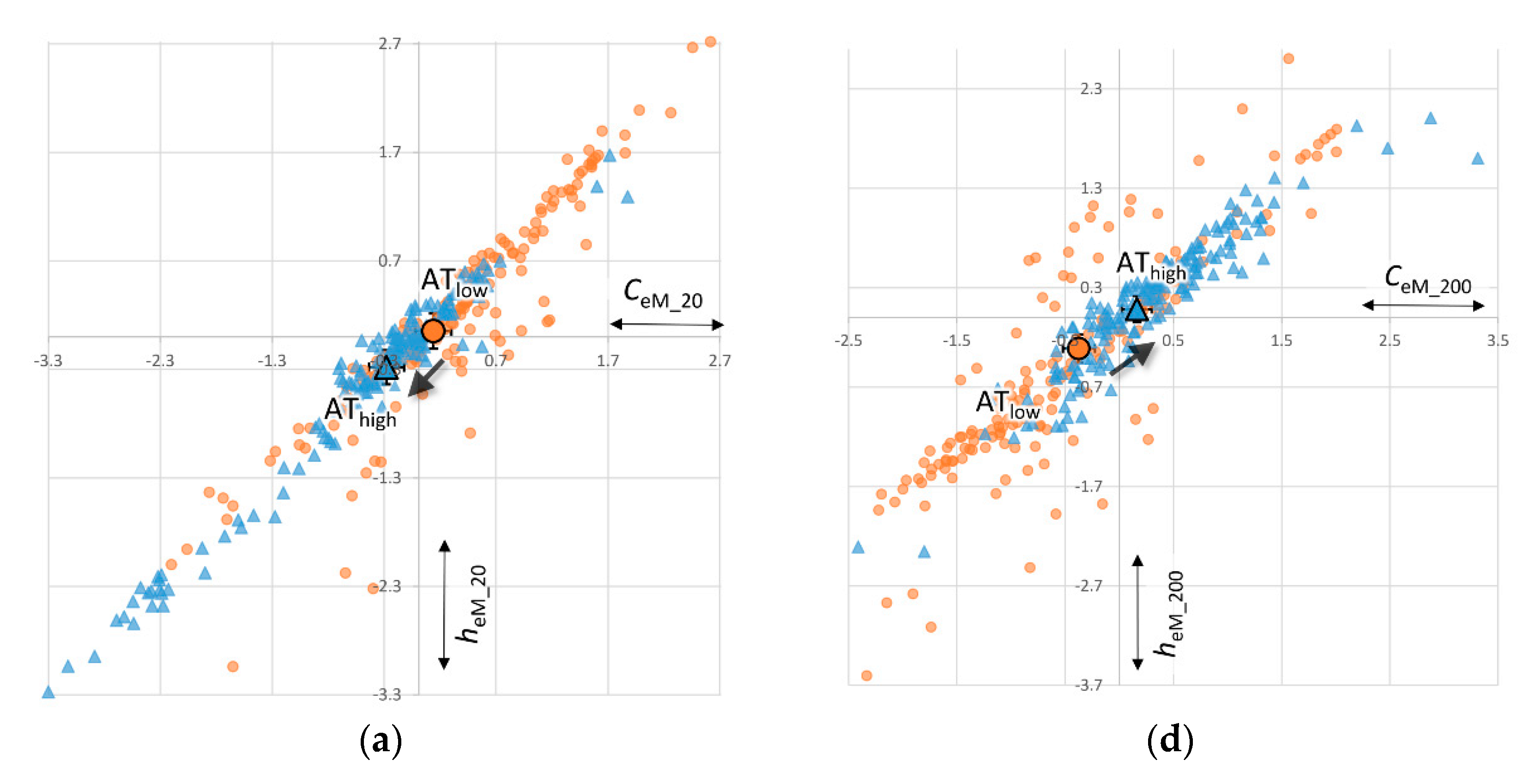
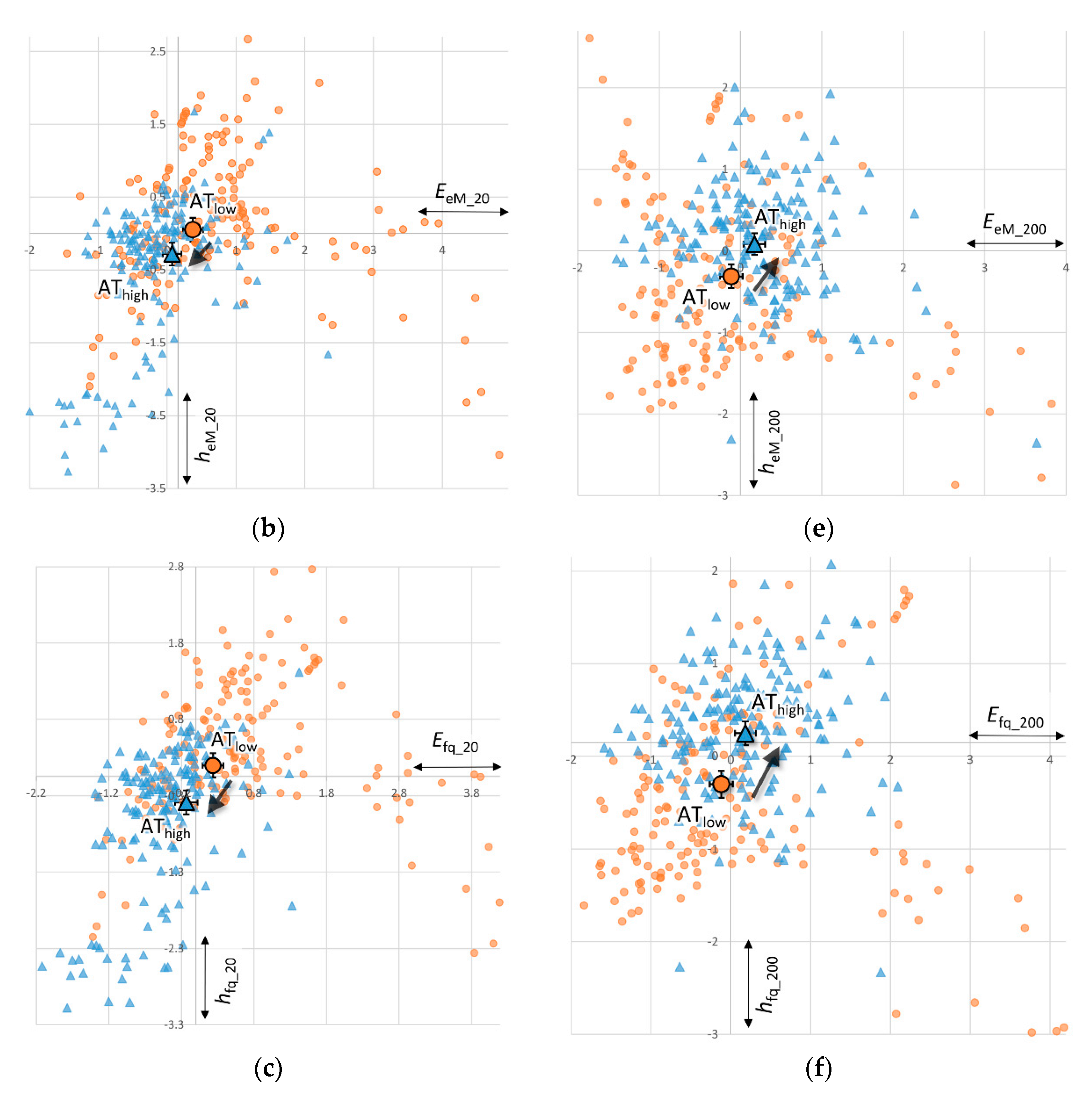
4.1.1. Complexity
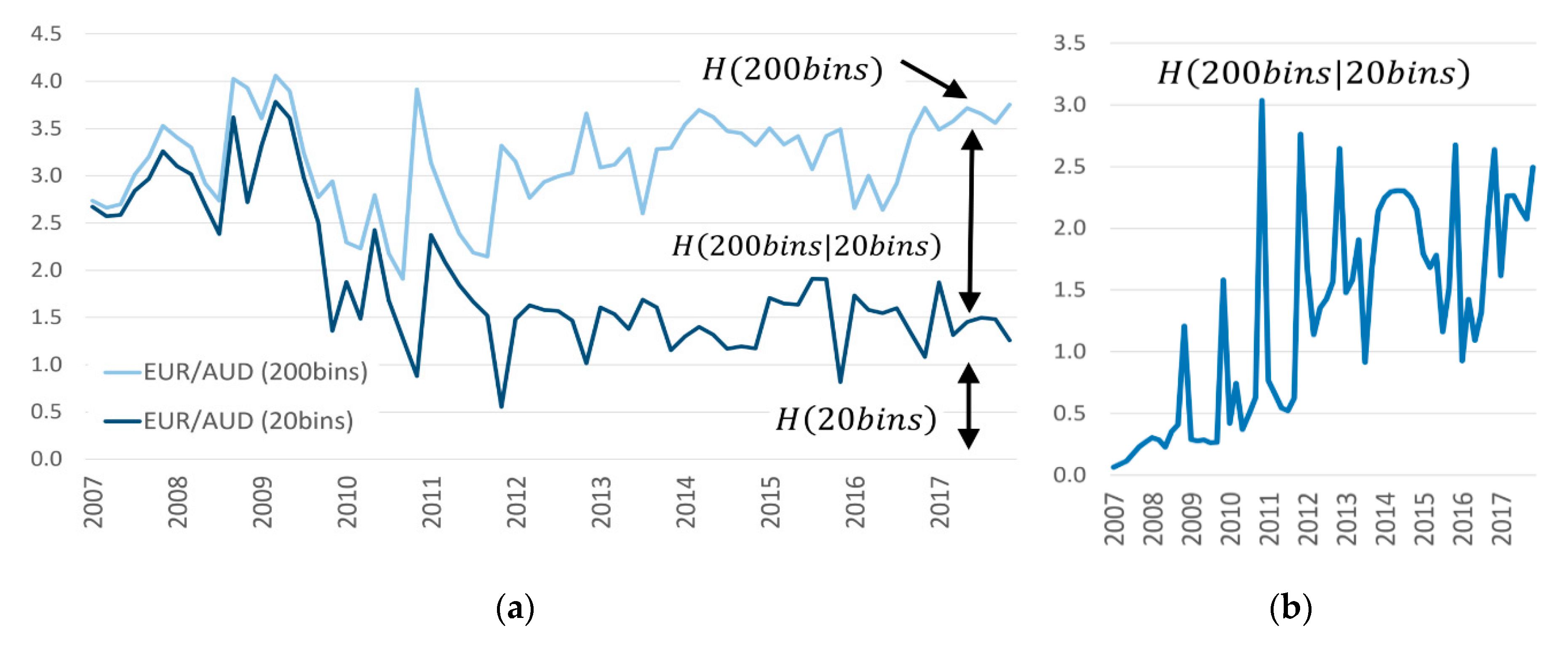
4.1.2. Remaining Uncertainty
4.1.3. Derivation of Measures
4.2. Independent Variables
4.2.1. Algorithmic Trading
4.2.2. Control Variables
4.2.3. Variable Versions
- Three dependent variables (DVs). We derive different versions of our three summary measures, namely from ϵ-machines (epsilon-machine, eM) and from frequency counts (fq), calculated on basis of coarse-grained 20 bins (_20) and more fine-grained 200 bins (_200).
- ○
- predictable information (EeM_20, Efq_20 and EeM_200, Efq_200)
- ○
- predictive complexity (CeM_20 and CeM_200)
- ○
- remaining uncertainty (heM_20, hfq_20 and heM_200, hfq_200)
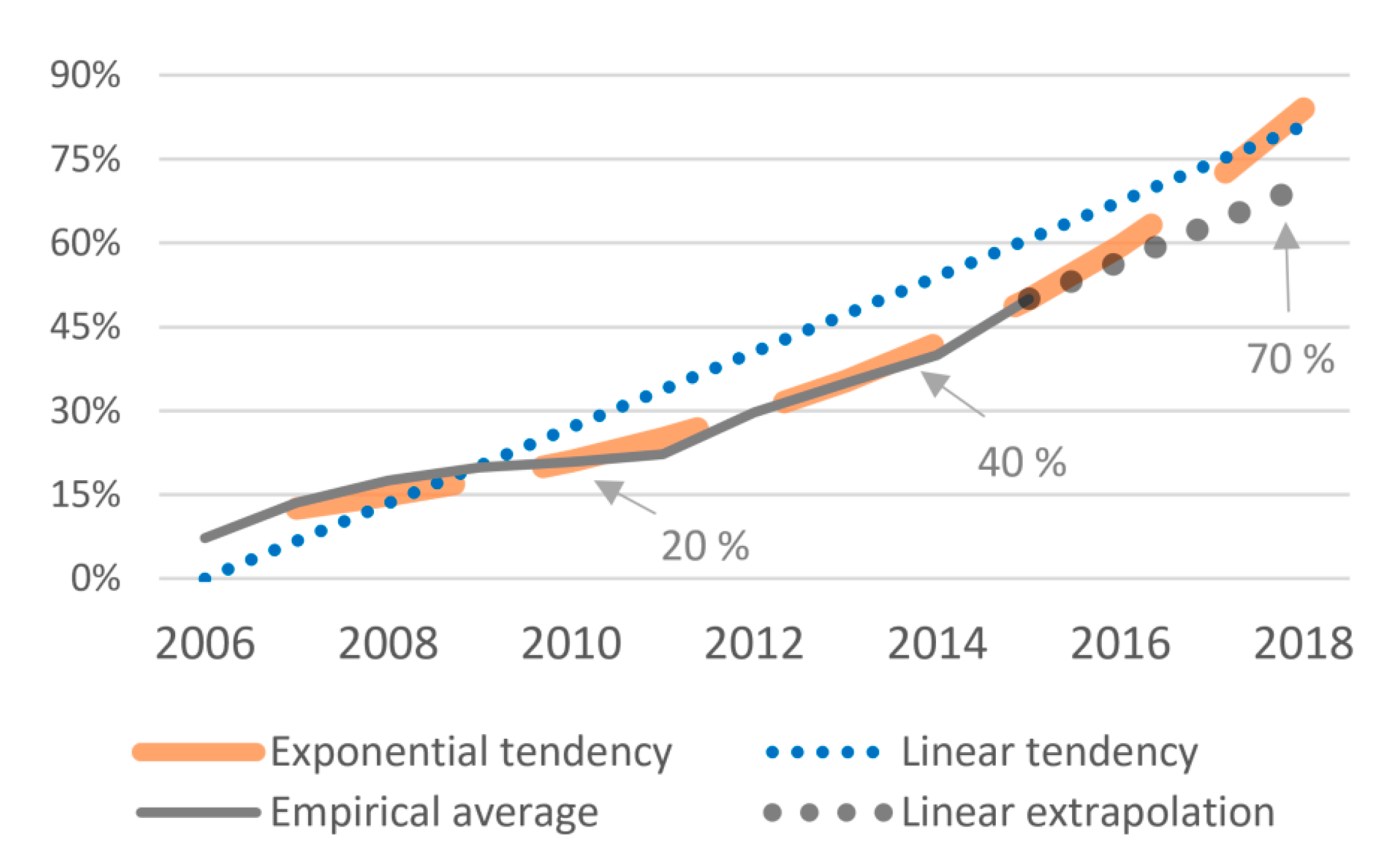
- Six independent variables (IVs). Our main variable of algorithmic trading is estimated in three different ways (see Figure 3).
- ○
- algorithmic trading
- ▪
- empirical with linear extrapolation (ATemp)
- ▪
- linear tendency (ATlin)
- ▪
- exponential tendency (ATexp)
- ○
- lagged dependent variable (dept−1)
- ○
- GDP growth rate (GDPr)
- ○
- inflation rate (infl)
- ○
- interest rate (intr)
- ○
- unemployment rate (unpl)
5. Results
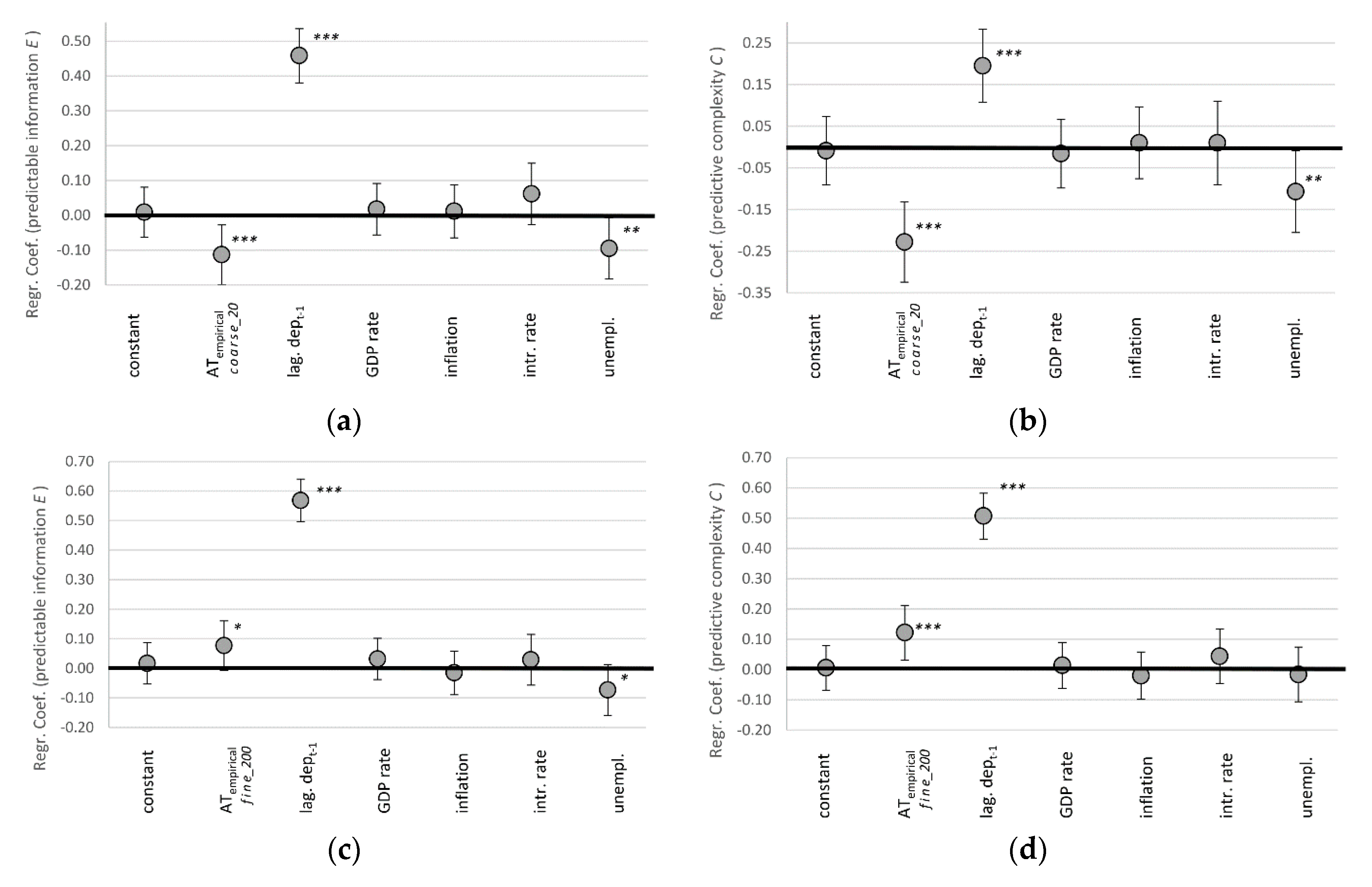
5.1. Increasing Complexity (H1)
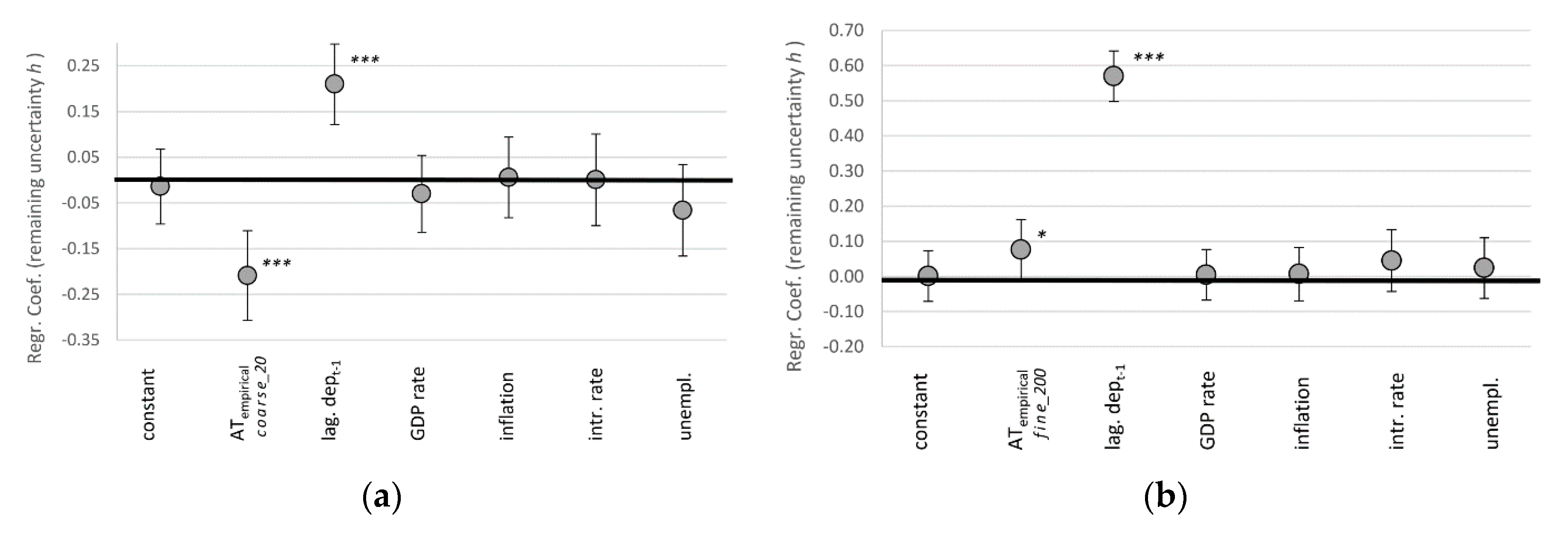
5.2. Decreasing Uncertainty (H2)
5.3. Robustness of Results for Complexity and Uncertainty (H1 & H2)
6. Discussion and Interpretation
6.1. There’s Plenty of Room at the Bottom
6.2. Digging Deeper: The Chain Rule of Entropy
6.3. The More You Know, the More Uncertain You Get
7. Conclusions
7.1. Infinitely More Levels of Uncertainty?
7.2. Limitations and Future Outlooks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agrawal, A.; Gans, J.; Goldfarb, A. Prediction Machines: The Simple Economics of Artificial Intelligence; Harvard Business Press: Brighton, MA, USA, 2018. [Google Scholar]
- Brookshear, J.G. Computer Science: An Overview, 10th ed.; Addison Wesley: Boston, MA, USA, 2009. [Google Scholar]
- Johnson, N.; Zhao, G.; Hunsader, E.; Qi, H.; Johnson, N.; Meng, J.; Tivnan, B. Abrupt rise of new machine ecology beyond human response time. Sci. Rep. 2013, 3, 2627. [Google Scholar] [CrossRef] [PubMed]
- Farmer, J.D.; Skouras, S. An ecological perspective on the future of computer trading. Quant. Financ. 2013, 13, 325–346. [Google Scholar] [CrossRef]
- Golub, A.; Dupuis, A.; Olson, R.B. High-Frequency Trading in FX Markets. In High-frequency Trading: New Realities for Traders, Markets and Regulators; Easley, D., Prado, M.M.L.D., O’Hara, M., Eds.; Risk Books: London, UK, 2013; pp. 21–44. ISBN 978-1-78272-009-6. [Google Scholar]
- Mahmoodzadeh, S. Essays on Market Microstructure and Foreign Exchange Market. Ph.D. Thesis, Simon Fraser University, Department of Economics, Burnaby, BC, Canada, 2015. [Google Scholar]
- Hendershott, T.; Jones, C.M.; Menkveld, A.J. Does Algorithmic Trading Improve Liquidity? J. Financ. 2011, 66, 1–33. [Google Scholar] [CrossRef]
- Menkveld, A.J. High frequency trading and the new market makers. J. Financ. Mark. 2013, 16, 712–740. [Google Scholar] [CrossRef]
- Chaboud, A.P.; Chiquoine, B.; Hjalmarsson, E.; Vega, C. Rise of the Machines: Algorithmic Trading in the Foreign Exchange Market. J. Financ. 2014, 69, 2045–2084. [Google Scholar] [CrossRef]
- Dasar, M.; Sankar, S. Technology Systems in the Global FX Market | Celent. 2011. Available online: https://www.celent.com/insights/698289644 (accessed on 21 April 2020).
- Schmidt, A.B. Ecology of the Modern Institutional Spot FX: The EBS Market in 2011; Social Science Research Network: Rochester, NY, USA, 2012. [Google Scholar]
- Aite Group. Algo Trading Will Make Up 25% of FX Volume by 2014, Aite Says. Available online: https://www.euromoney.com/article/b12kjb9hbvjsj8/algo-trading-will-make-up-25-of-fx-volume-by-2014-aite-says (accessed on 21 April 2020).
- BIS, (Bank for International Settlements) Electronic Trading in Fixed Income Markets. Available online: https://www.bis.org/publ/mktc07.htm (accessed on 21 April 2020).
- Glantz, M.; Kissell, R. Chapter 8—Algorithmic Trading Risk. In Multi-Asset Risk Modeling; Glantz, M., Kissell, R., Eds.; Academic Press: San Diego, CA, 2014; pp. 247–304. [Google Scholar]
- Lee, S.; Tierney, D. The Trade Surveillance Compliance: Market and the Battle for Automation; Aite Group: Boston, MA, USA, 2013. [Google Scholar]
- Rennison, J.; Meyer, G.; Bullock, N. How high-frequency trading hit a speed bump. Financial Times. 2018. Available online: https://www.ft.com/content/d81f96ea-d43c-11e7-a303-9060cb1e5f44 (accessed on 21 April 2020).
- SEC, (U.S. Securities and Exchange Commission); BCG, (Boston Consulting Group). Organizational Study and Reform; Bethesda, MD, USA, 2011; Available online: https://www.sec.gov/news/studies/2011/967study.pdf (accessed on 21 April 2020).
- The Economist. The fast and the furious. The Economist. 25 February 2012. Available online: https://www.economist.com/special-report/2012/02/25/the-fast-and-the-furious (accessed on 21 April 2020).
- High-Frequency Trading in the Foreign Exchange Market. Available online: https://www.bis.org/publ/mktc05.pdf (accessed on 21 April 2020).
- Granham, P. Rise of Electronic FX Trading Won’t Silence Voice Brokers; Euromoney: London, UK, 2013; Available online: https://www.euromoney.com/article/b12kjx172lr4mn/rise-of-electronic-fx-trading-wont-silence-voice-brokers (accessed on 21 April 2020).
- Breedon, F.; Chen, L.; Ranaldo, A.; Vause, N. Judgement Day: Algorithmic Trading Around the Swiss Franc Cap Removal. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3126136 (accessed on 21 April 2020).
- Das, R.; Hanson, J.E.; Kephart, J.O.; Tesauro, G. Agent-human Interactions in the Continuous Double Auction. In Proceedings of the 17th International Joint Conference on Artificial Intelligence—Volume 2; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2001; pp. 1169–1176. [Google Scholar]
- Chakravorty, G. Execution Algorithms: How Can We Get the Best Price for Our Trade? 2017. Available online: https://slides.com/gchak/execution-algorithms#/ (accessed on 21 April 2020).
- Jovanovic, B.; Menkveld, A.J. Middlemen in Limit Order Markets; Social Science Research Network: Rochester, NY, USA, 2016. [Google Scholar]
- Mishra, S.; Daigler, R.T.; Holowczak, R. The Effect of High-Frequency Market Making on Option Market Liquidity. J. Trading 2016, 11, 56–76. [Google Scholar] [CrossRef]
- McGowan, M. The Rise of Computerized High Frequency Trading: Use and Controversy. Duke Law Technol. Rev. 2010, 9, 1–25. [Google Scholar]
- Hendershott, T.; Moulton, P.C. Automation, speed, and stock market quality: The NYSE’s Hybrid. J. Financ. Mark. 2011, 14, 568–604. [Google Scholar] [CrossRef]
- Simon, H.A. Theories of bounded rationality. Decis. Organ. 1972, 1, 161–176. [Google Scholar]
- Wolpert, D.H. The Lack of A Priori Distinctions Between Learning Algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Tsvetkova, M.; García-Gavilanes, R.; Floridi, L.; Yasseri, T. Even good bots fight: The case of Wikipedia. PLoS ONE 2017, 12, e0171774. [Google Scholar] [CrossRef] [PubMed]
- Park, J.B.; Won Lee, J.; Yang, J.-S.; Jo, H.-H.; Moon, H.-T. Complexity analysis of the stock market. Physica A 2007, 379, 179–187. [Google Scholar] [CrossRef]
- Ng, A. What Artificial Intelligence Can and Can’t Do Right Now. Harvard Business Review. 9 November 2016. Available online: https://hbr.org/2016/11/what-artificial-intelligence-can-and-cant-do-right-now (accessed on 21 April 2020).
- Hilbert, M. Big Data requires Big Visions for Big Change; TEDxUCL, x=independently organized TED talks: London, UK, 2014; Available online: https://www.martinhilbert.net/big-data-requires-big-visions-for-big-change-tedxucl/ (accessed on 21 April 2020).
- Madsen, A.K.; Flyverbom, M.; Hilbert, M.; Ruppert, E. Big Data: Issues for an International Political Sociology of Data Practices. Int. Political Sociol. 2016, olw010. [Google Scholar] [CrossRef]
- Cvitanic, J.; Kirilenko, A.A. High Frequency Traders and Asset Prices; Social Science Research Network: Rochester, NY, USA, 2010. [Google Scholar]
- Dukascopy Bank. Historical Data Feed Swiss Forex Bank; Swiss FX trading platform; Dukascopy Bank SA: Geneva, Switzerland, 2018; Available online: https://www.dukascopy.com/swiss/english/marketwatch/historical/ (accessed on 21 April 2020).
- Smirnovs, J.; Hilbert, M. Personal email communication with Dukascopy representative, 2019.
- Marton, K.; Shields, P.C. Entropy and the Consistent Estimation of Joint Distributions. Ann. Probab. 1994, 22, 960–977. [Google Scholar] [CrossRef]
- Lewis, M. Flash Boys: A Wall Street Revolt; W. W. Norton & Company: New York, NY, USA, 2014; ISBN 978-0-393-24467-0. [Google Scholar]
- Pappalardo, J. New Transatlantic Cable Built to Shave 5 Milliseconds off Stock Trades. Popular Mechanics. 27 October 2011. Available online: https://www.popularmechanics.com/technology/infrastructure/a7274/a-transatlantic-cable-to-shave-5-milliseconds-off-stock-trades/ (accessed on 21 April 2020).
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; ISBN 0-471-24195-4. [Google Scholar]
- Hilbert, M.; Darmon, D. Dumb and Predictable Bots Make Largescale Communication More Complex and Unpredictable. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3464833 (accessed on 21 April 2020).
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl. Akad. Nauk SSSR. 1958, 119, 2. [Google Scholar]
- Kolmogorov, A.N. Entropy per unit time as a metric invariant of automorphisms. Dokl. Akad. Nauk SSSR 1959, 124, 754–755. [Google Scholar]
- Sinai, Y.G. On the notion of entropy of dynamical systems. Dokl. Akad. Nauk 1959, 124, 768–771. [Google Scholar]
- Crutchfield, J.P.; Feldman, D. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos Interdiscip. J. Nonlinear Sci. 2003, 13, 25–54. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P.; Ellison, C.J.; Mahoney, J.R. Time’s Barbed Arrow: Irreversibility, Crypticity, and Stored Information. Phys. Rev. Lett. 2009, 103, 094101. [Google Scholar] [CrossRef]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037109. [Google Scholar] [CrossRef]
- Yeung, R.W. A new outlook on Shannon’s information measures. IEEE Trans. Inf. Theory 1991, 37, 466–474. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Statistical Complexity of Simple 1D Spin Systems. Phys. Rev. E 1997, 55, R1239–R1242. [Google Scholar] [CrossRef]
- Lindgren, K.; Nordahl, M.G. Complexity measures and cellular automata. Complex Syst. 1988, 2, 409–440. [Google Scholar]
- Shaw, R. The Dripping Faucet as a Model Chaotic System; Aerial Press: Ann Arbor, MI, USA, 1984. [Google Scholar]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, Complexity and Learning. Neural Comput. 2001, 13, 2001. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Crutchfield, J.P. Computational Mechanics: Pattern and Prediction, Structure and Simplicity. J. Stat. Phys. 2001, 104, 817–879. [Google Scholar] [CrossRef]
- Crutchfield, J.P. Between order and chaos. Nat. Phys. 2012, 8, 17–24. [Google Scholar] [CrossRef]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics and induction. Phys. D Nonlin. Phenomena 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Hilbert, M.; James, R.G.; Gil-Lopez, T.; Jiang, K.; Zhou, Y. The Complementary Importance of Static Structure and Temporal Dynamics in Teamwork Communication. Hum. Commun. Res. 2018, 44, 427–448. [Google Scholar] [CrossRef]
- Darmon, D. Statistical Methods for Analyzing Time Series Data Drawn from Complex Social Systems. PhD Thesis, University of Maryland, College Park, MD, USA, 2015. Supervised by Michelle Girvan and William Rand. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Klinkner, K.L. Blind Construction of Optimal Nonlinear Recursive Predictors for Discrete Sequences. arXiv 2014, arXiv:cs/0406011. [Google Scholar]
- Crutchfield, J.P.; Ellison, C.J.; Riechers, P.M. Exact complexity: The spectral decomposition of intrinsic computation. Phys. Lett. A 2016, 380, 998–1002. [Google Scholar] [CrossRef]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. dit: A Python package for discrete information theory. J. Open Source Softw. 2018, 3, 738. [Google Scholar] [CrossRef]
- Beers, B. What indicators are used in exchange rate forecasting? Investopedia. 29 August 2018. Available online: https://www.investopedia.com/ask/answers/021715/what-economic-indicators-are-most-used-when-forecasting-exchange-rate.asp (accessed on 21 April 2020).
- TradingEconomics. TradingEconomics Database. Available online: https://tradingeconomics.com/ (accessed on 21 April 2020).
- Allison, P. Don’t Put Lagged Dependent Variables in Mixed Models. Statistical Horizons. 2 June 2015. Available online: https://statisticalhorizons.com/lagged-dependent-variables (accessed on 21 April 2020).
- Kahn, R.; Whited, T.M. Identification Is Not Causality, and Vice Versa. Rev. Corp. Financ. Stud. 2018, 7, 1–21. [Google Scholar] [CrossRef]
- Koopmans, T.C. Identification Problems in Economic Model Construction. Econometrica 1949, 17, 125–144. [Google Scholar] [CrossRef]
- Morgan, S.L.; Winship, C. Counterfactuals and Causal Inference: Methods and Principles for Social Research. Available online: /core/books/counterfactuals-and-causal-inference/5CC81E6DF63C5E5A8B88F79D45E1D1B7 (accessed on 3 April 2020).
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-89560-6. [Google Scholar]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 4th ed.; South-Western: Mason, OH, USA, 2008; ISBN 978-0-324-66054-8. [Google Scholar]
- Feldman, D.P.; McTague, C.S.; Crutchfield, J.P. The organization of intrinsic computation: Complexity-entropy diagrams and the diversity of natural information processing. Chaos 2008, 18, 043106. [Google Scholar] [CrossRef]
- Osborne, M.F.M. Periodic Structure in the Brownian Motion of Stock Prices. Oper. Res. 1962, 10, 345–379. [Google Scholar] [CrossRef]
- Niederhoffer, V. Clustering of Stock Prices. Oper. Res. 1965, 13, 258–265. [Google Scholar] [CrossRef]
- Harris, L. Stock Price Clustering and Discreteness. Rev. Financ. Stud. 1991, 4, 389–415. [Google Scholar] [CrossRef]
- Tseng, M.; Mahmoodzadeh, S.; Gencay, R. Impact of Algorithmic Trading on Market Quality: A Reconciliation; Social Science Research Network: Rochester, NY, USA, 2018. [Google Scholar]
- Lallouache, M.; Abergel, F. Tick size reduction and price clustering in a FX order book. Physica A 2014, 416, 488–498. [Google Scholar] [CrossRef]
- Ball, C.A.; Torous, W.N.; Tschoegl, A.E. The degree of price resolution: The case of the gold market. J. Futures Mark. 1985, 5, 29–43. [Google Scholar] [CrossRef]
- Cooney, J.W.; Van Ness, B.; Van Ness, R. Do investors prefer even-eighth prices? Evidence from NYSE limit orders. J. Bank. Financ. 2003, 27, 719–748. [Google Scholar] [CrossRef]
- Christie, W.G.; Harris, J.H.; Schultz, P.H. Why did NASDAQ Market Makers Stop Avoiding Odd-Eighth Quotes? J. Financ. 1994, 49, 1841–1860. [Google Scholar] [CrossRef]
- Christie, W.G.; Schultz, P.H. Why do NASDAQ Market Makers Avoid Odd-Eighth Quotes? J. Financ. 1994, 49, 1813–1840. [Google Scholar] [CrossRef]
- Mahmoodzadeh, S.; Gençay, R. Human vs. high-frequency traders, penny jumping, and tick size. J. Bank. Financ. 2017, 85, 69–82. [Google Scholar] [CrossRef]
- Feynman, R. There’s Plenty of Room at the Bottom: An Invitation to Enter a New Field of Physics. Available online: https://www.taylorfrancis.com/books/e/9781315217178/chapters/10.1201/9781315217178-6 (accessed on 21 April 2020).
- Crutchfield, J.P. The Origins of Computational Mechanics: A Brief Intellectual History and Several Clarifications. arXiv 2017, arXiv:1710.06832. [Google Scholar]
- Crutchfield, J.P.; Packard, N.H. Symbolic dynamics of noisy chaos. Physica D 1983, 7, 201–223. [Google Scholar] [CrossRef]
- Seth, A.K.; Dienes, Z.; Cleeremans, A.; Overgaard, M.; Pessoa, L. Measuring consciousness: Relating behavioural and neurophysiological approaches. Trends Cognit. Sci. 2008, 12, 314–321. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K.; Izhikevich, E.; Reeke, G.N.; Edelman, G.M. Theories and measures of consciousness: An extended framework. Proc. Natl. Acad. Sci. USA 2006, 103, 10799–10804. [Google Scholar] [CrossRef] [PubMed]
- Sipser, M. Introduction to the Theory of Computation, 2nd ed.; Course Technology: Boston, MA, USA, 2006; ISBN 978-0-534-95097-2. [Google Scholar]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Amblard, P.-O.; Michel, O.J.J. On directed information theory and Granger causality graphs. J. Comput. Neurosci. 2011, 30, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information Decomposition and Synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Barnett, N.; Crutchfield, J.P. Computational Mechanics of Input–Output Processes: Structured Transformations and the \epsilon-Transducer. J. Stat. Phys. 2015, 161, 404–451. [Google Scholar] [CrossRef]
- Cartlidge, J.; Szostek, C.; Luca, M.D.; Cliff, D. Too Fast Too Furious—Faster Financial-market Trading Agents Can Give Less Efficient Markets. In Proceedings of the 4th ICAART, Vilamoura, Portugal, 6–8 February 2012. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hilbert, M.; Darmon, D. How Complexity and Uncertainty Grew with Algorithmic Trading. Entropy 2020, 22, 499. https://doi.org/10.3390/e22050499
Hilbert M, Darmon D. How Complexity and Uncertainty Grew with Algorithmic Trading. Entropy. 2020; 22(5):499. https://doi.org/10.3390/e22050499
Chicago/Turabian StyleHilbert, Martin, and David Darmon. 2020. "How Complexity and Uncertainty Grew with Algorithmic Trading" Entropy 22, no. 5: 499. https://doi.org/10.3390/e22050499
APA StyleHilbert, M., & Darmon, D. (2020). How Complexity and Uncertainty Grew with Algorithmic Trading. Entropy, 22(5), 499. https://doi.org/10.3390/e22050499





