Analysis of Multifractal and Organization/Order Structure in Suomi-NPP VIIRS Normalized Difference Vegetation Index Series of Wildfire Affected and Unaffected Sites by Using the Multifractal Detrended Fluctuation Analysis and the Fisher–Shannon Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
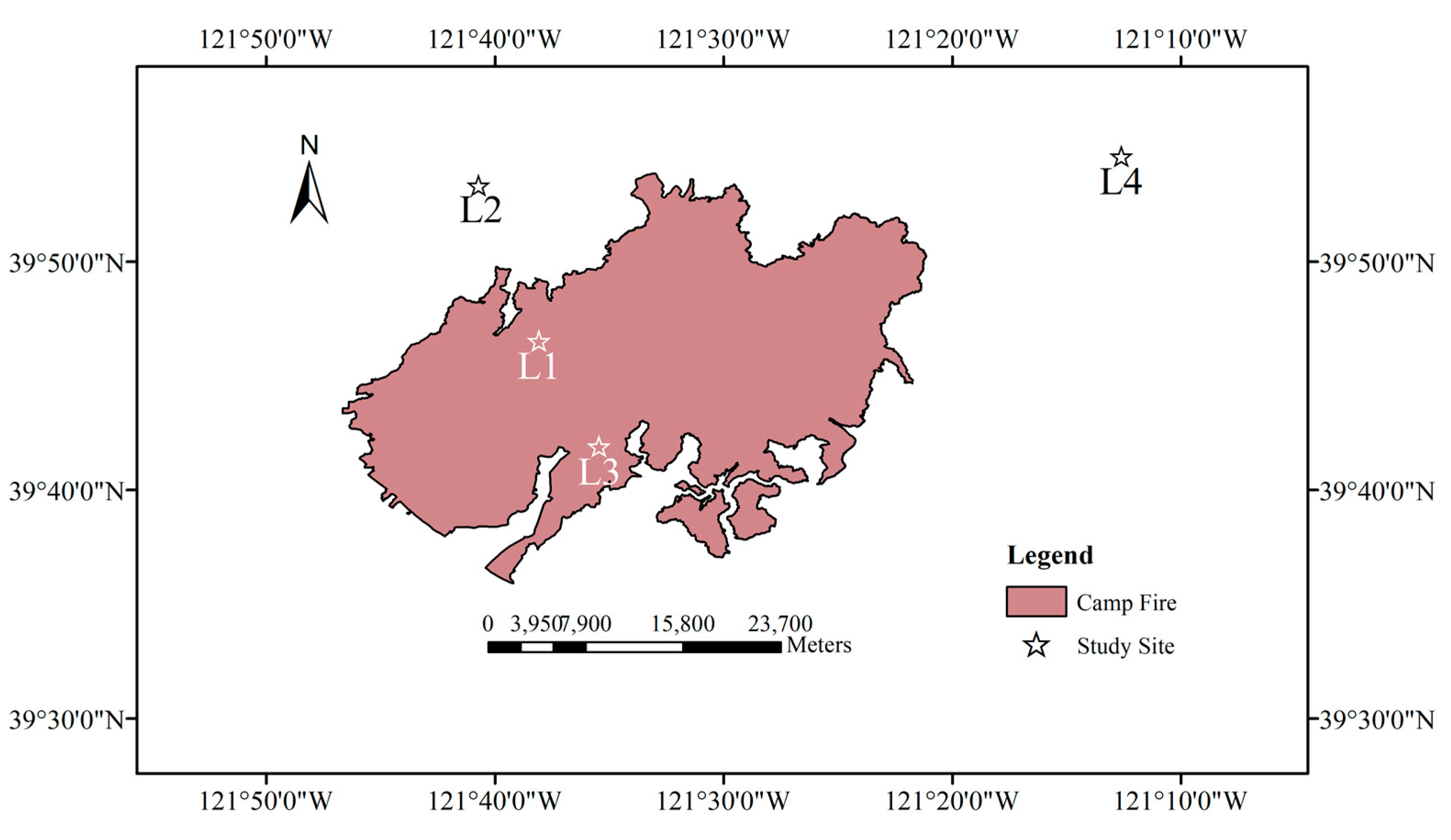
2.2. Study Sites
2.3. Methods
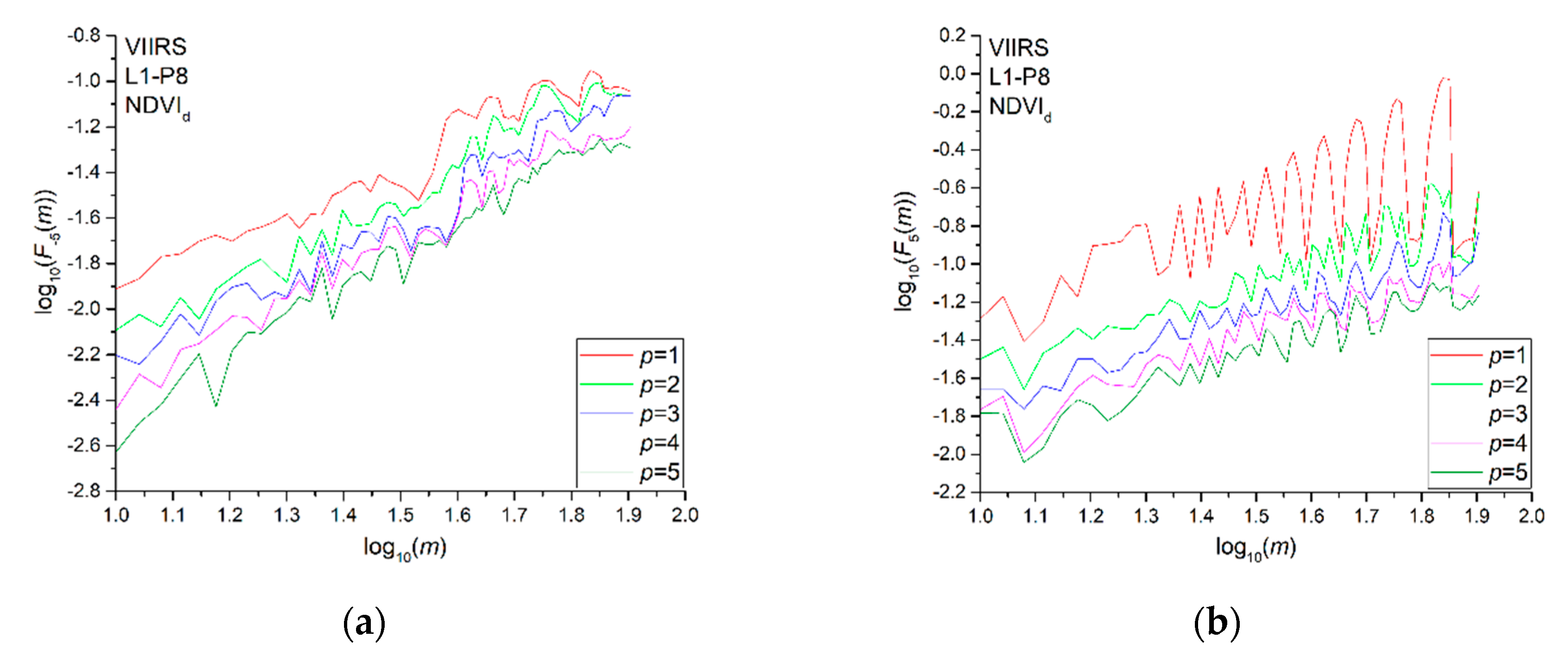
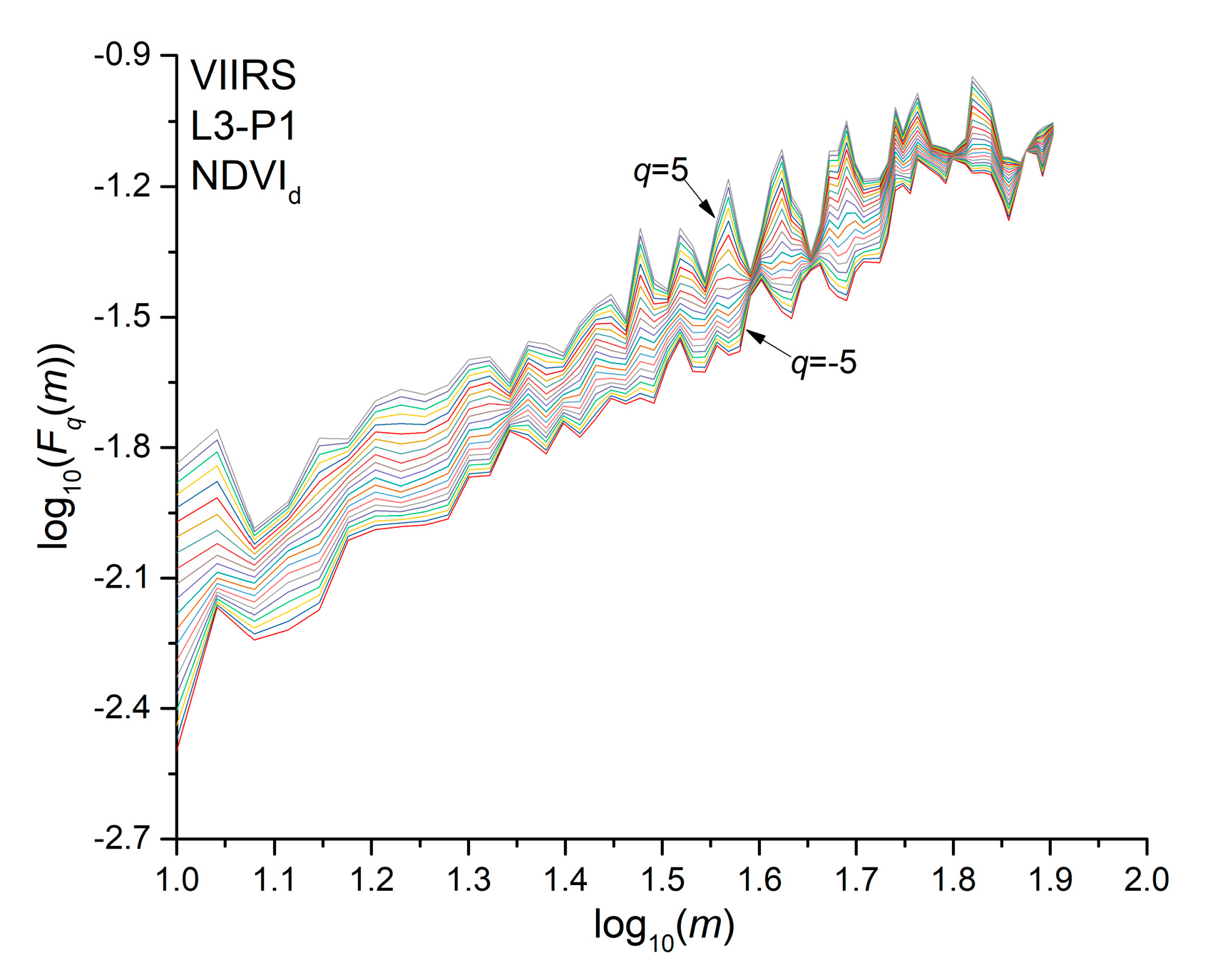
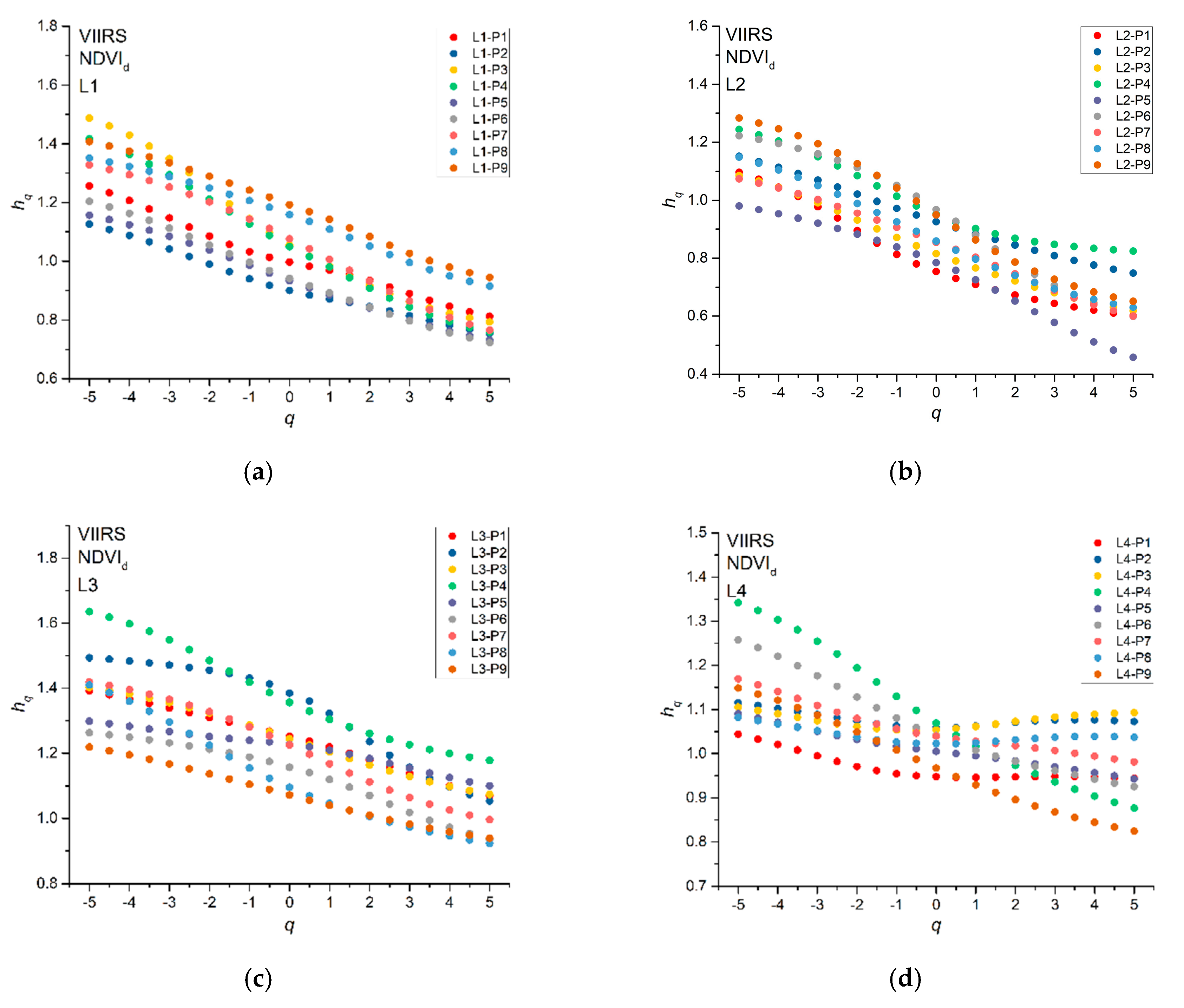
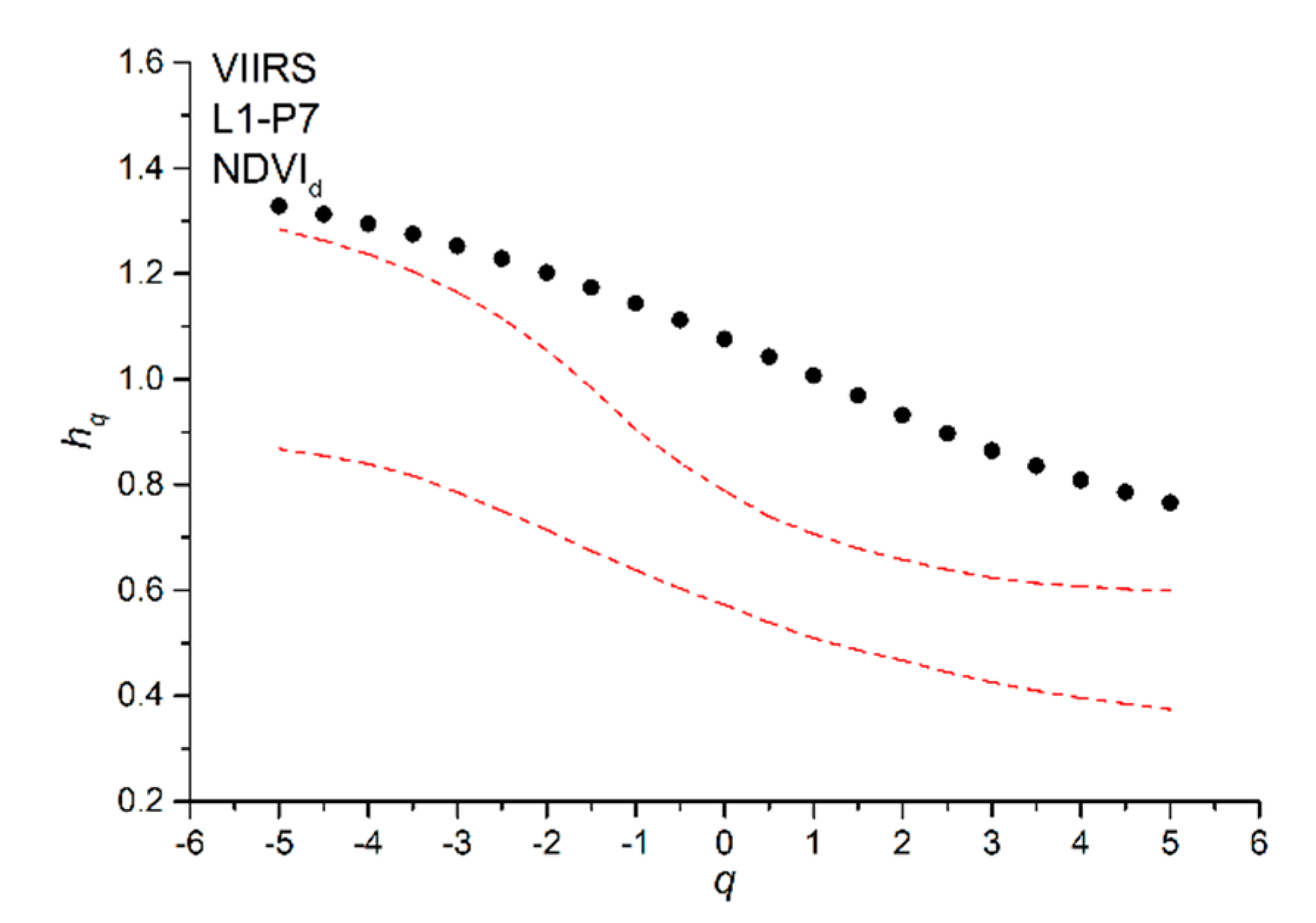
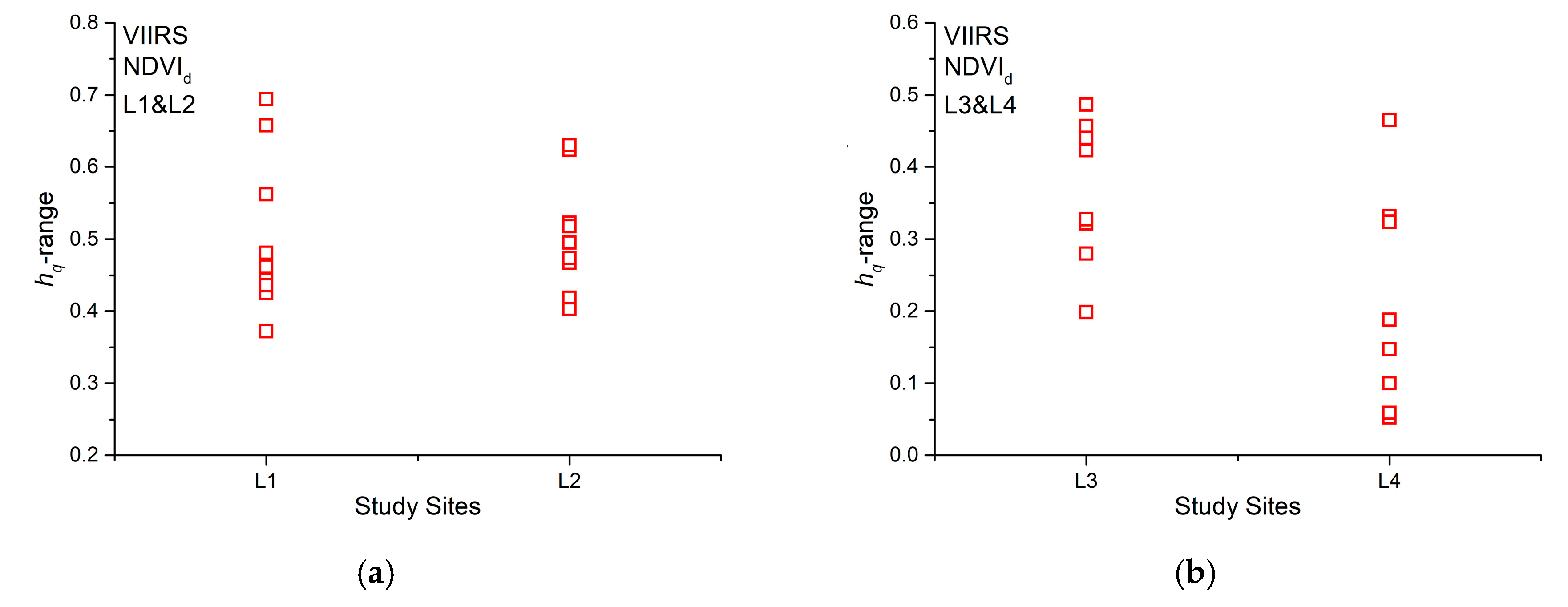
2.3.1. Multifractal Detrended Fluctuation Analysis
2.3.2. Fisher–Shannon Analysis
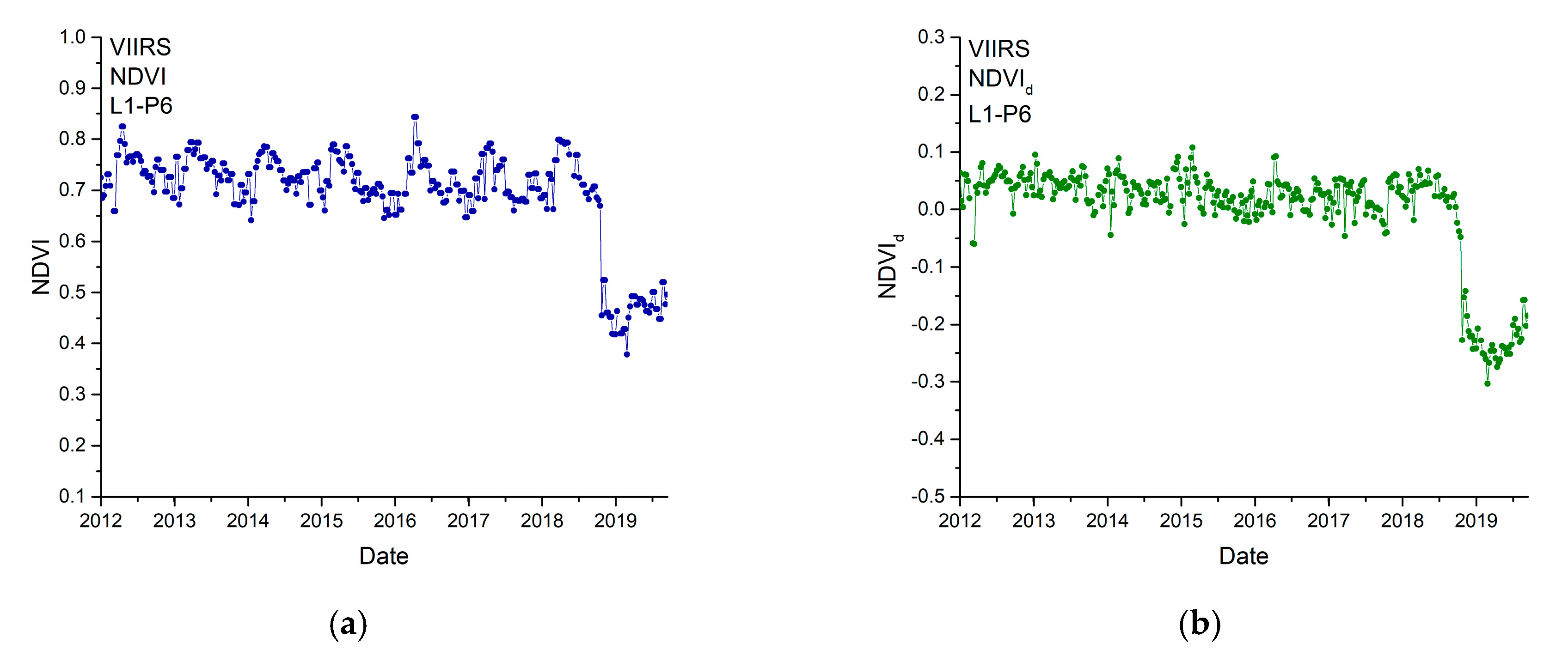
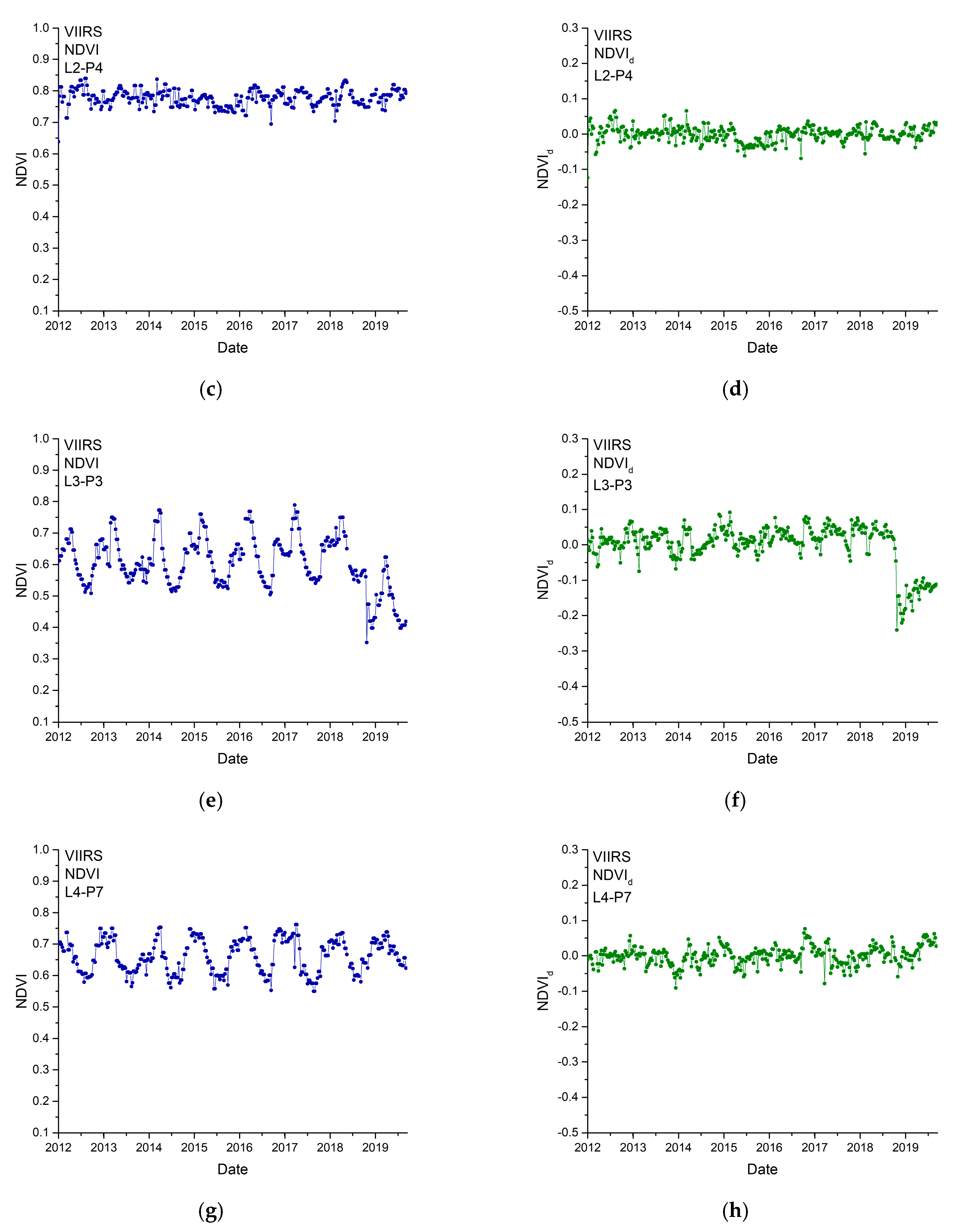
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclatures
| NDVI | Normalized Difference Vegetation Index |
| MFDFA | multifractal detrended fluctuation analysis |
| FS | Fisher-Shannon |
| VIIRS | Visible Infrared Imaging Radiometer Suite |
| Suomi-NPP | Suomi National Polar-Orbiting Partnership |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| EOS | Earth Observing System |
| VI | vegetation indices |
| ROI | region of interest |
| DFA | Detrended Fluctuation Analysis |
| FIM | Fisher Information Measure |
| SE | Shannon entropy |
| NX | Shannon entropy power |
| BRDF | bidirectional reflectance distribution function |
| SDS | science data sets |
| NDVId | departure NDVI |
| PG&E | Pacific Gas and Electric Co. |
| IGBP | International Geosphere-Biosphere Programme |
| hq | Generalized Hurst exponents |
| hq-range | range of the generalized Hurst exponent |
| FGN | Fractional Gaussian Noise |
References
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Ba, R.; Song, W.; Li, X.; Xie, Z.; Lo, S. Integration of Multiple Spectral Indices and a Neural Network for Burned Area Mapping Based on MODIS Data. Remote Sens. 2019, 11, 326. [Google Scholar] [CrossRef]
- Mukai, S. Remote Sensing of Heavy Aerosol Pollution Episodes: Smoke and Dust. In Remote Sensing of Aerosols, Clouds, and Precipitation; Elsevier: Amsterdam, The Netherlands, 2018; pp. 85–108. [Google Scholar]
- Yapp, G.; Walker, J.; Thackway, R. Linking vegetation type and condition to ecosystem goods and services. Ecol. Complex. 2010, 7, 292–301. [Google Scholar] [CrossRef]
- Lawley, V.; Lewis, M.; Clarke, K.; Ostendorf, B. Site-based and remote sensing methods for monitoring indicators of vegetation condition: An Australian review. Ecol. Indic. 2016, 60, 1273–1283. [Google Scholar] [CrossRef]
- Lentile, L.B.; Holden, Z.A.; Smith, A.M.S.; Falkowski, M.J.; Hudak, A.T.; Morgan, P.; Lewis, S.A.; Gessler, P.E.; Benson, N.C. Remote sensing techniques to assess active fire characteristics and post-fire effects. Int. J. Wildland Fire 2006, 15, 319–345. [Google Scholar] [CrossRef]
- Diaz-Delgado, R.; Llorett, F.; Pons, X. Influence of fire severity on plant regeneration by means of remote sensing imagery. Int. J. Remote. Sens. 2003, 24, 1751–1763. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Analysis of time-scaling properties in forest-fire sequence observed in Italy. Ecol. Model. 2010, 221, 90–93. [Google Scholar] [CrossRef]
- Puzachenko, Y.; Sandlersky, R.; Sankovski, A. Methods of evaluating thermodynamic properties of landscape cover using multispectral reflected radiation measurements by the Landsat satellite. Entropy 2013, 15, 3970–3982. [Google Scholar] [CrossRef]
- Ba, R.; Chen, C.; Yuan, J.; Song, W.; Lo, S. SmokeNet: Satellite Smoke Scene Detection Using Convolutional Neural Network with Spatial and Channel-Wise Attention. Remote Sens. 2019, 11, 1702. [Google Scholar] [CrossRef]
- Xie, Z.; Song, W.; Ba, R.; Li, X.; Xia, L. A Spatiotemporal Contextual Model for Forest Fire Detection Using Himawari-8 Satellite Data. Remote Sens. 2018, 10, 1992. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Wang, J.; Roudini, S.; Hyer, E.J.; Xu, X.; Zhou, M.; Garcia, L.C.; Reid, J.S.; Peterson, D.A.; da Silva, A.M. Detecting nighttime fire combustion phase by hybrid application of visible and infrared radiation from Suomi NPP VIIRS. Remote Sens. Environ. 2020, 237, 111466. [Google Scholar] [CrossRef]
- Deering, D.W. Rangeland Reflectance Characteristics Measured by Aircraft and Spacecraft Sensors. Ph.D. Thesis, Texas A&M Universtiy, College Station, TX, USA, 1978. [Google Scholar]
- Didan, A.B.K. VIIRS/NPP Vegetation Indices 16-Day L3 Global 500m SIN Grid V001; NASA EOSDIS Land Processes DAAC: Oak Ridge, TN, USA, 2018. [CrossRef]
- Guelpa, E.; Verda, V. Entropy Generation Analysis of Wildfire Propagation. Entropy 2017, 19, 433. [Google Scholar] [CrossRef]
- Telesca, L.; Lanorte, A.; Lasaponara, R. Investigating dynamical trends in burned and unburned vegetation covers using SPOT-VGT NDVI data. J. Geophys. Eng. 2007, 4, 128–138. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Discriminating dynamical patterns in burned and unburned vegetational covers by using SPOT-VGT NDVI data. Geophys. Res. Lett. 2005, 32, L21401. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Quantifying intra-annual persistent behaviour in SPOT-VEGETATION NDVI data for Mediterranean ecosystems of southern Italy. Remote Sens. Environ. 2006, 101, 95–103. [Google Scholar] [CrossRef]
- Li, X.; Lanorte, A.; Lasaponara, R.; Lovallo, M.; Song, W.; Telesca, L. Fisher–Shannon and detrended fluctuation analysis of MODIS normalized difference vegetation index (NDVI) time series of fire-affected and fire-unaffected pixels. Geomat. Nat. Hazards Risk 2017, 8, 1342–1357. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of statistical estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Frieden, B.R. Fisher information, disorder, and the equilibrium distributions of physics. Phys. Rev. A 1990, 41, 4265–4276. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Perez, J.; Plastino, A. Fisher information and nonlinear dynamics. Phys. A Stat. Mech. Its Appl. 2001, 291, 523–532. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M. Non-uniform scaling features in central Italy seismicity: A non-linear approach in investigating seismic patterns and detection of possible earthquake precursors. Geophys. Res. Lett. 2009, 36, L01308. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Martì Molist, J.; López Moreno, C.; Abella Meléndez, R. Using the Fisher–Shannon method to characterize continuous seismic signal during volcanic eruptions: Application to 2011–2012 El Hierro (Canary Islands) eruption. Terra Nova 2014, 26, 425–429. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Romano, G.; Hsu, H.-L.; Chiang, C.-W.; Chen, C.-C. Informational analysis of apparent Earth’s resistivity time series to assess the reliability of magnetotelluric measurements. J. Asian Earth Sci. 2013, 77, 77–82. [Google Scholar] [CrossRef]
- Wu, T.-H.; Chen, C.-C.; Lovallo, M.; Telesca, L. Informational analysis of Langevin equation of friction in earthquake rupture processes. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 103120. [Google Scholar] [CrossRef]
- Telesca, L.; Chamoli, A.; Lovallo, M.; Stabile, T.A. Investigating the tsunamigenic potential of earthquakes from analysis of the informational and multifractal properties of seismograms. Pure Appl. Geophys. 2015, 172, 1933–1943. [Google Scholar] [CrossRef]
- Testa, S.; Soudani, K.; Boschetti, L.; Mondino, E.B. MODIS-derived EVI, NDVI and WDRVI time series to estimate phenological metrics in French deciduous forests. Int. J. Appl. Earth Obs. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Ba, R.; Song, W.; Lo, S.; Xie, Z. Spectral Characteristic Analysis of Burned Area Based on MODIS Data. In Proceedings of Asia-Oceania Symposium on Fire Science and Technology; Springer: Singapore, 2019; pp. 391–404. [Google Scholar]
- ORNL DAAC. MODIS and VIIRS Land Products Global Subsetting and Visualization Tool; ORNL DAAC: Oak Ridge, TN, USA, 2018; (Subset obtained for VNP13A1 product at various sites in Spatial Range: N = 39.91N, S = 39.699N, E = 121.77W, W = 121.63W, time period: 2012-01-17 to 2019-09-22, and subset size: 4.5 × 4.5 km.). [CrossRef]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Pre- and post- fire behavioral trends revealed in satellite NDVI time series. Geophys. Res. Lett. 2006, 33, L14401. [Google Scholar] [CrossRef]
- Telesca, L.; Lasaponara, R. Vegetational patterns in burned and unburned areas investigated by using the detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2006, 368, 531–535. [Google Scholar] [CrossRef]
- Telesca, L.; Pierini, J.O.; Lovallo, M.; Santamaría-del-Angel, E. Spatio-temporal variability in the Brazil-Malvinas Confluence Zone (BMCZ), based on spectroradiometric MODIS-AQUA chlorophyll-a observations. Oceanologia 2018, 60, 76–85. [Google Scholar] [CrossRef]
- Camp Fire—CAL FIRE. Available online: https://www.fire.ca.gov/incidents/2018/11/8/camp-fire/ (accessed on 26 March 2020).
- Friedl, M.; Sulla-Menashe, D. MCD12Q1 MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 500m SIN Grid V006; NASA EOSDIS Land Processes DAAC: Oak Ridge, TN, USA, 2015. [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; López-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108–7116. [Google Scholar] [CrossRef] [PubMed]
- Martin, M.; Pennini, F.; Plastino, A. Fisher’s information and the analysis of complex signals. Phys. Lett. A 1999, 256, 173–180. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M. On the performance of Fisher Information Measure and Shannon entropy estimators. Phys. A Stat. Mech. Its Appl. 2017, 484, 569–576. [Google Scholar] [CrossRef]
- Devroye, L. A Course in Density Estimation; Birkhauser Boston Inc.: Cambridge, MA, USA, 1987. [Google Scholar]
- Janicki, A.; Weron, A. Simulation and Chaotic Behavior of Alpha-Stable Stochastic Processes; CRC Press: Boca Raton, FL, USA, 1993; Volume 178. [Google Scholar]
- Troudi, M.; Alimi, A.M.; Saoudi, S. Analytical plug-in method for kernel density estimator applied to genetic neutrality study. EURASIP J. Adv. Signal Process. 2008, 2008, 739082. [Google Scholar] [CrossRef]
- Raykar, V.C.; Duraiswami, R. Fast optimal bandwidth selection for kernel density estimation. In Proceedings of the 2006 SIAM International Conference on Data Mining; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; pp. 524–528. [Google Scholar]
- Vignat, C.; Bercher, J.-F. Analysis of signals in the Fisher–Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Daubenmire, R. Ecology of fire in grasslands. In Advances in Ecological Research; Elsevier: Amsterdam, The Netherlands, 1968; Volume 5, pp. 209–266. [Google Scholar]
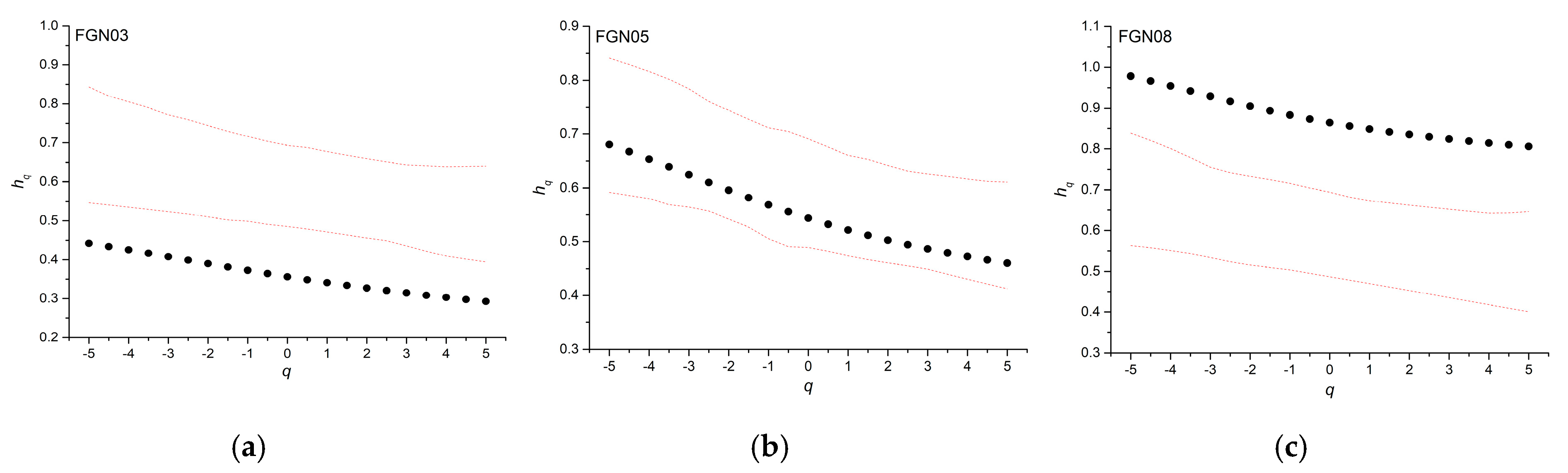
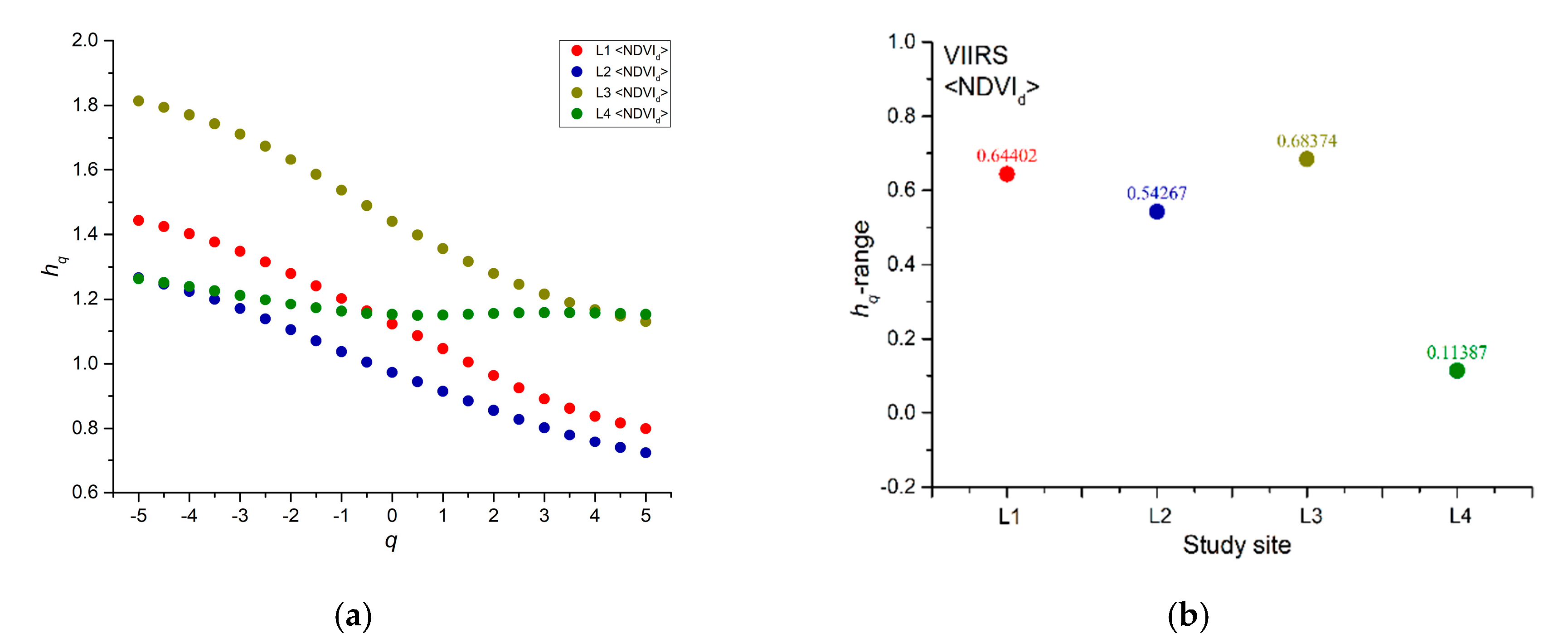

| L1–L2 | L3–L4 | |
|---|---|---|
| NX | 1.4743E−14 | 0.000431 |
| FIM | 0.000007 | 0.001475 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ba, R.; Song, W.; Lovallo, M.; Lo, S.; Telesca, L. Analysis of Multifractal and Organization/Order Structure in Suomi-NPP VIIRS Normalized Difference Vegetation Index Series of Wildfire Affected and Unaffected Sites by Using the Multifractal Detrended Fluctuation Analysis and the Fisher–Shannon Analysis. Entropy 2020, 22, 415. https://doi.org/10.3390/e22040415
Ba R, Song W, Lovallo M, Lo S, Telesca L. Analysis of Multifractal and Organization/Order Structure in Suomi-NPP VIIRS Normalized Difference Vegetation Index Series of Wildfire Affected and Unaffected Sites by Using the Multifractal Detrended Fluctuation Analysis and the Fisher–Shannon Analysis. Entropy. 2020; 22(4):415. https://doi.org/10.3390/e22040415
Chicago/Turabian StyleBa, Rui, Weiguo Song, Michele Lovallo, Siuming Lo, and Luciano Telesca. 2020. "Analysis of Multifractal and Organization/Order Structure in Suomi-NPP VIIRS Normalized Difference Vegetation Index Series of Wildfire Affected and Unaffected Sites by Using the Multifractal Detrended Fluctuation Analysis and the Fisher–Shannon Analysis" Entropy 22, no. 4: 415. https://doi.org/10.3390/e22040415
APA StyleBa, R., Song, W., Lovallo, M., Lo, S., & Telesca, L. (2020). Analysis of Multifractal and Organization/Order Structure in Suomi-NPP VIIRS Normalized Difference Vegetation Index Series of Wildfire Affected and Unaffected Sites by Using the Multifractal Detrended Fluctuation Analysis and the Fisher–Shannon Analysis. Entropy, 22(4), 415. https://doi.org/10.3390/e22040415







