1. Introduction
Since its discovery in 1975 [
1,
2], laser cooling of individually trapped atomic particles has become a standard technique in quantum optics laboratories worldwide [
3,
4]. Rapidly oscillating electric fields can be used to strongly confine charged particles, such as single ions, for relatively large amounts of time [
5]. Moreover, laser trapping provides unique means to control the dynamics of neutral particles, such as neutral atoms [
6,
7]. To cool single atomic particles, laser fields are applied which remove vibrational energy at high enough rates to transfer them down to near absolute-zero temperatures [
5]. Nowadays, ion traps are used to perform a wide range of high-precision quantum optics experiments. For example, individually trapped ions are at the heart of devices with applications in quantum technology, such as atomic and optical clocks [
8,
9], quantum computers [
10,
11,
12,
13], quantum simulators [
14,
15] and electric and magnetic field sensors [
16].
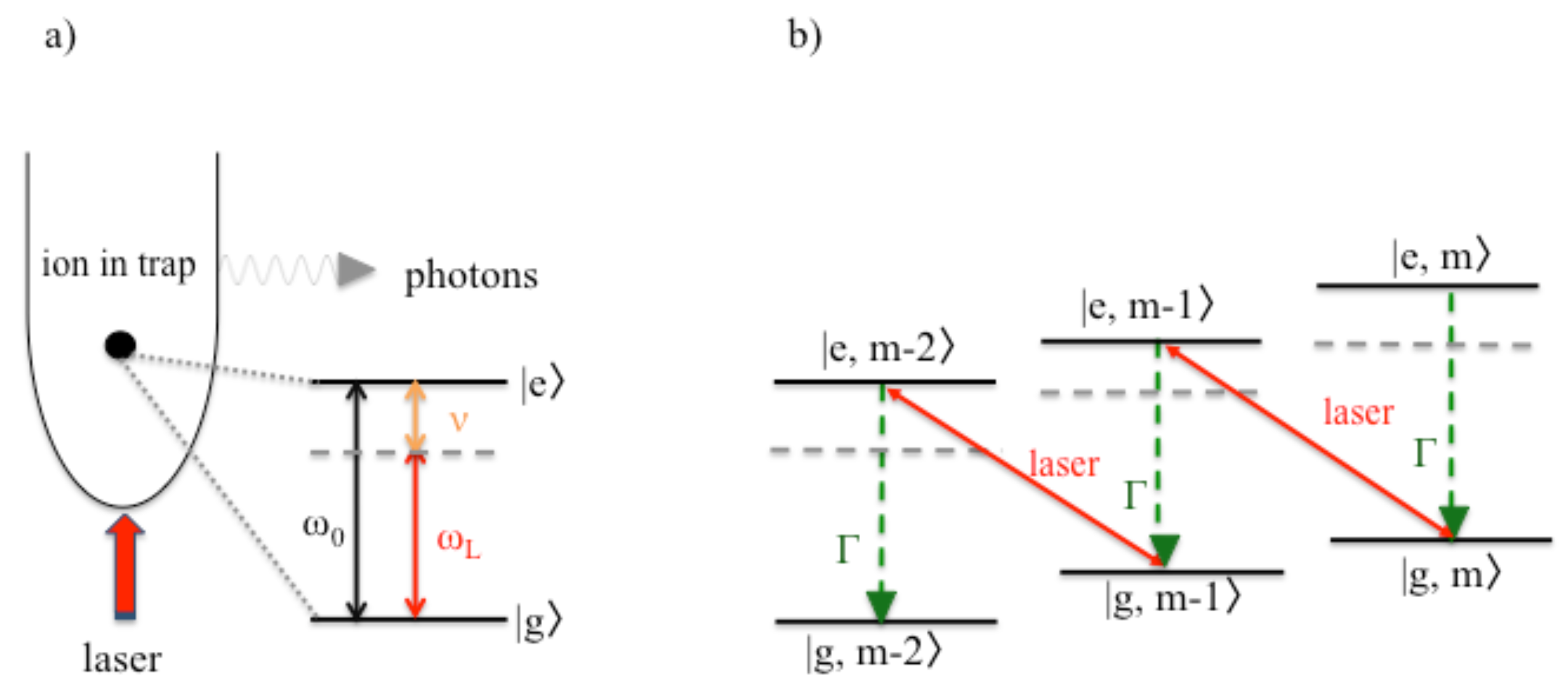
For laser cooling to be at its most efficient, the confinement of individually trapped particles should be so strong that the quantum characteristics of their motion is no longer negligible. This means that their vibrational energy is made up of energy quanta, which have been named phonons. When this applies, an externally applied laser field not only affects the electronic states of a trapped ion, but it also changes its vibrational state. Ideally, laser frequencies should be chosen such that the excitation of the ion should be most likely accompanied by the loss of a phonon. If the ion returns subsequently into its ground state via the spontaneous emission of a photon, its phonon state remains the same. Overall one phonon is permanently lost from the system which implies cooling. On average, every emitted photon lowers the vibrational energy of the trapped ion by the energy of one phonon. Eventually, the cooling process stops when the ion no longer possesses any vibrational energy.
Currently, there are many different ways of designing and fabricating ion traps [
17,
18]. However, the main requirements for the efficient conversion of vibrational energy into light on relatively short quantum optical time scales are always the same [
19,
20]:
- (1)
Individual atomic particles need to be so strongly confined that the quantum character of their motion has to be taken into account. In the following, denotes the phonon frequency and is the energy of a single phonon.
- (2)
A laser field with a frequency
below the atomic transition frequency
needs to be applied. As long as the laser detuning
and the phonon frequency
are comparable in size,
the excitation of an ion is more likely accompanied by the annihilation of a phonon than by the creation of a phonon. Transitions which result in the simultaneous excitation of an ion and the creation of a phonon are possible but are less likely to occur as long as their detuning is larger.
- (3)
When excited, the confined atomic particle needs to be able to emit a photon. In the following, we denote its spontaneous decay rate by
. This rate should not be much larger than
,
so that the cooling laser couples efficiently to atomic transitions. At the same time,
should not be too small so that de-excitation of the excited atomic state happens often via the spontaneous emission of a photon.
Given these three conditions, the applied laser field results in the conversion of the vibrational energy of individually trapped ions into photons. As mentioned already above, laser cooling can prepare individually trapped atomic particles at low enough temperatures for applications in high-precision quantum optics experiments and in quantum technology.
In this paper, we ask the question whether laser cooling could also have applications in micro-and nanoscale physics experiments. For example, nanotechnology deals with objects which have dimensions between 1 and 1000 nm and is well known for its applications in information and communication technology, as well as sensing and imaging. Increasing the speed at which information can be processed and the sensitivity of sensors is usually achieved by reducing system dimensions. However, smaller devices are usually more prone to heating as thermal resistances increase [
21]. Sometimes, large surface to volume ratios can help to off-set this problem. Another problem for nanoscale sensors is thermal noise. As sensors are reduced in size, their signal to noise ratio usually decreases and thus the thermal energy of the system can limit device sensitivity [
22]. Therefore, thermal considerations have to be taken into account and large vacuums or compact heat exchangers have already become an integral part of nanotechnology devices.
Usually, heat exchangers in micro- and nanotechnology rely on fluid flow [
23]. In this paper, we propose an alternative approach. More concretely, we propose to use heat transfer as well as a variation of laser cooling, namely cavity-mediated collective laser cooling [
24,
25,
26,
27,
28], to lower the temperature of a small device. As illustrated in
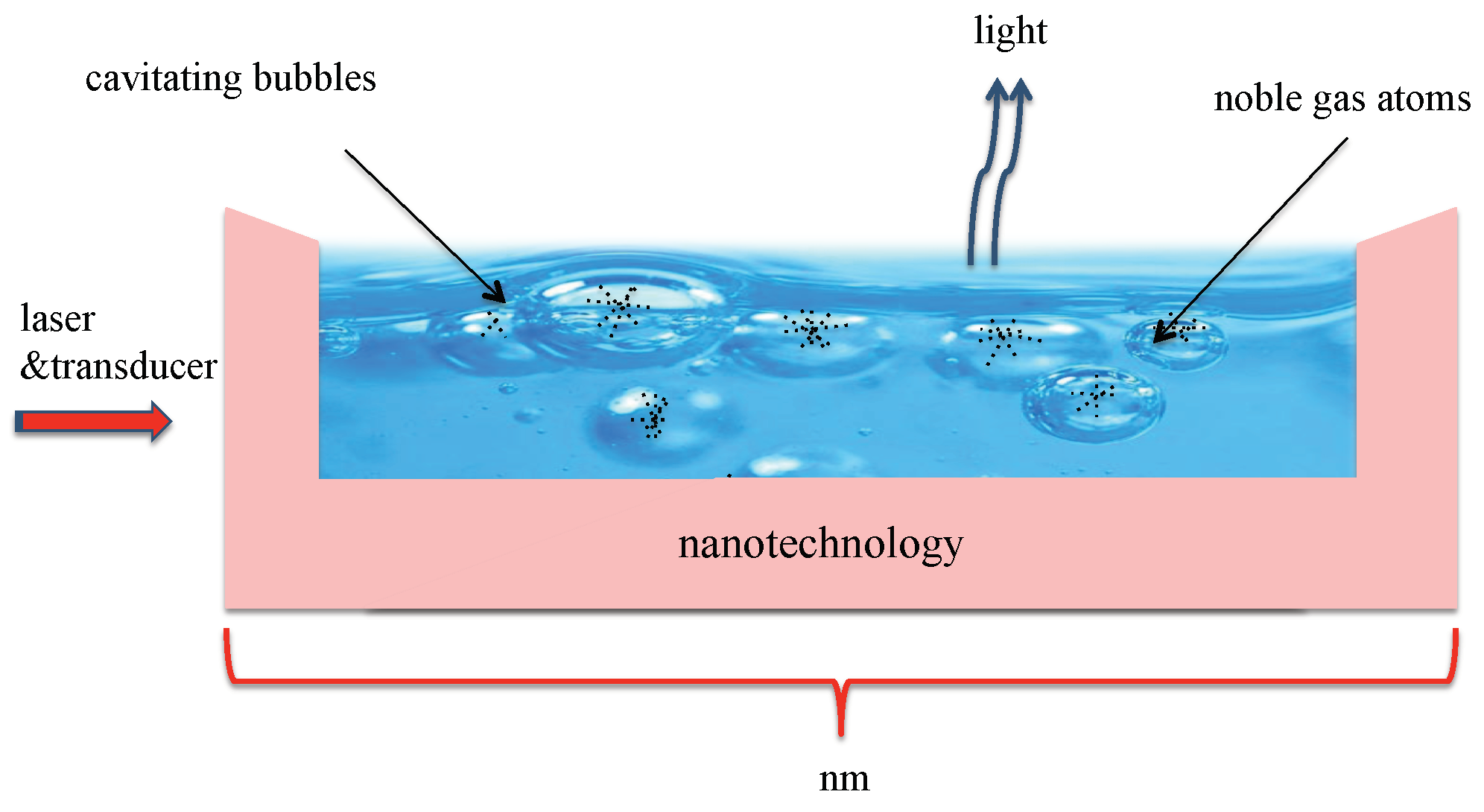
Figure 1, the proposed quantum heat exchanger mainly consist of a liquid which contains a large number of cavitating bubbles filled with noble gas atoms. Transducers constantly change the radius of these bubbles which should resemble optical cavities when they reach their minimum radius during bubble collapse phases. At this point, a continuously applied external laser field rapidly transfers vibrational energy of the atoms into light. If the surrounding liquid contains many cavitating bubbles, their surface area becomes relatively large and there can be a very efficient exchange of heat between the inside and the outside of cavitating bubbles. Any removal of thermal energy from the trapped atomic gas inside bubbles should eventually result in the cooling of the surrounding liquid and of the surface area of the device on which it is placed.
In this paper, we emphasize that cavitating bubbles can provide all of the above listed requirements for laser cooling, especially a very strong confinement of atomic particles, such as nitrogen [
29,
30]. For example, calculations based on a variation of the Rayleigh–Plesset equations show that the pressure at the location of a cavitating bubble can be significantly larger than the externally applied driving pressure [
31]. However, the strongest indication for the presence of phonon modes with sufficiently large frequencies for laser cooling to work comes from the fact that sonoluminescence experiments are well-known for converting sound into relatively large amounts of thermal energy, while producing light in the optical regime [
32,
33,
34]. During this process, the atomic gas inside a cavitating bubbles can reach very high temperatures [
35,
36], which hints at very strong couplings between electronic and vibrational degrees of freedom. In addition, the surfaces of cavitating bubbles can become opaque during the bubble collapse phase [
37], thereby creating a spherical optical cavity [
38,
39] which is an essential requirement for cavity-mediated collective laser cooling.
To initiate the cooling process, an appropriately detuned laser field needs to be applied in addition to the transducers which confine the bubbles with sound waves. Although sonoluminescence has been studied in great detail and the idea of applying laser fields to cavitating bubbles is not new [
40], not enough is known about the relevant quantum properties, such as phonon frequencies. Hence, we cannot predict realistic cooling rates for the experimental setup shown in
Figure 1. A crude estimate which borrows data from different, already available experiments suggests that it might be possible to achieve cooling rates of the order of Kelvin temperatures per millisecond for volumes of liquid on a cubic micrometer scale. Cavitating bubbles already have applications in sonochemistry, where they are used to provide energy for chemical reactions [
41]. Here, we propose to exploit the atom–phonon interactions in sonoluminescence experiments for laser cooling. In the presence of an appropriately detuned laser field, we expect other, highly-detuned heating processes to become secondary.
There are five sections in this paper. The purpose of
Section 2 is to provide an introduction to cavity-mediated collective laser cooling of an atomic gas. As we show below, this technique is a variation of standard laser cooling techniques for individually trapped atomic particles. We provide an overview of the experimental requirements and estimate achievable cooling rates.
Section 3 studies the effect of thermalization for a large collection of atoms with elastic collisions.
Section 4 reviews the main design principles of a quantum heat exchanger for nanotechnology. Finally, we summarize our findings in
Section 5.
4. A Quantum Heat Exchanger with Cavitating Bubbles
As pointed out in
Section 1, the aim of this paper is to design a quantum heat exchanger for nanotechnology. The proposed experimental setup consists of a liquid on top of the device which we aim to keep cool, a transducer and a cooling laser (cf.
Figure 1). The transducer generates cavitating bubbles which need to contain atomic particles and whose diameters need to change very rapidly in time. The purpose of the cooling laser is to stimulate the conversion of heat into light. The cooling of the atomic particles inside cavitating bubbles subsequently aids the cooling of the liquid which surrounds the bubbles and its environment via adiabatic heat transfers.
To gain a better understanding of the experimental setup in
Figure 1,
Section 4.1 describes the main characteristics of single bubble sonoluminescence experiments [
32,
33,
34,
35,
36].
Section 4.2 emphasizes that there are many similarities between sonoluminescence and quantum optics experiments [
29,
30]. From this, we conclude that sonoluminescence experiments naturally provide the main ingredients for the implementation of cavity-mediated collective laser cooling of an atomic gas [
26,
27,
28]. Finally, in
Section 4.3 and
Section 4.4, we have a closer look at the physics of the proposed quantum heat exchanger and estimate cooling rates.
4.1. Single Bubble Sonoluminescence Experiments
Sonoluminescence can be defined as a phenomenon of strong light emission from collapsing bubbles in a liquid, such as water [
32,
33,
34]. These bubbles need to be filled with noble gas atoms, such as nitrogen atoms, which occur naturally in air. Alternatively, the bubbles can be filled with ions from ionic liquids, molten salts, and concentrated electrolyte solutions [
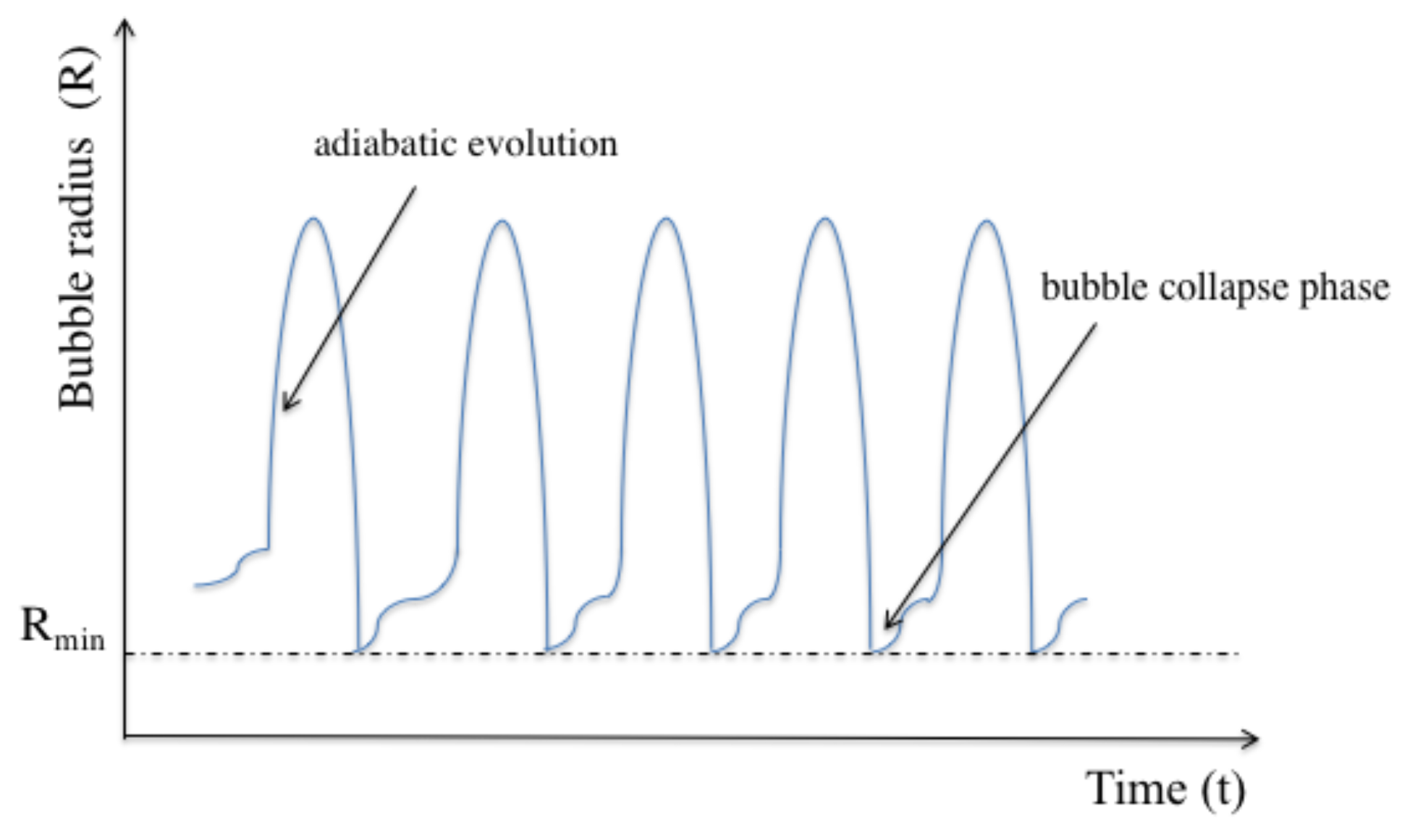
48]. Moreover, the bubbles need to be acoustically confined and periodically driven by ultrasonic frequencies. As a result, the bubble radius changes periodically in time, as illustrated in
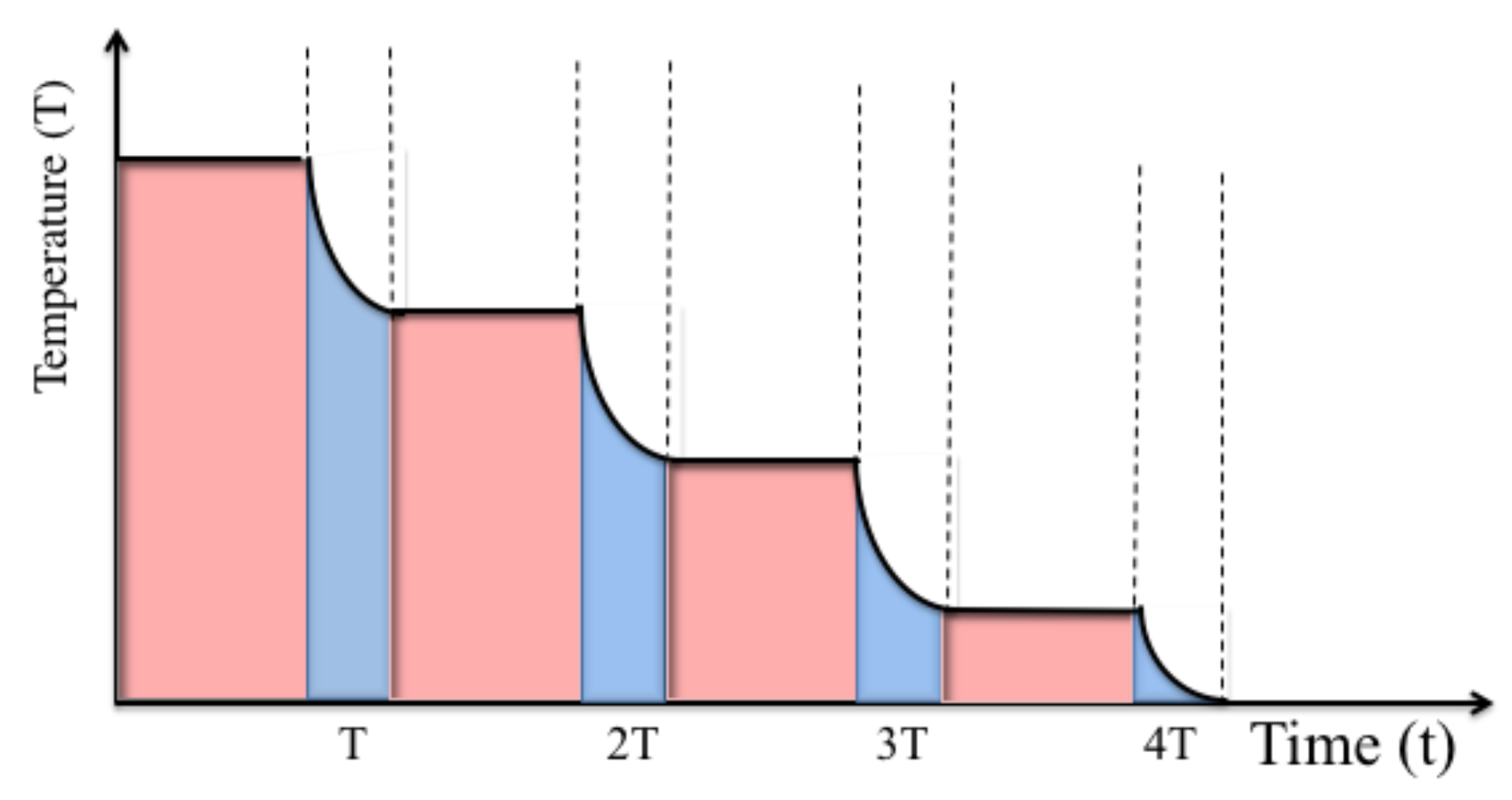
Figure 5. The oscillation of the bubble radius regenerates itself with unusual precision.
At the beginning of every expansion phase, the bubble oscillates about its equilibrium radius until it returns to its fastness. During this process, the bubble temperature changes adiabatically and there is an exchange of thermal energy between the atoms inside the bubble and the surrounding liquid. During the collapse phase of a typical single-bubble sonoluminescence, i.e., when the bubble reaches its minimum radius, its inside becomes thermally isolated from the surrounding environment and the atomic gas inside the bubble becomes strongly confined. Usually, a strong light flash occurs at this point which is accompanied by a sharp increase of the temperature of the particles. Experiments have shown that increasing the concentration of atoms inside the bubble increases the intensity of the emitted light [
35,
36].
4.2. A Quantum Optics Perspective on Sonoluminescence
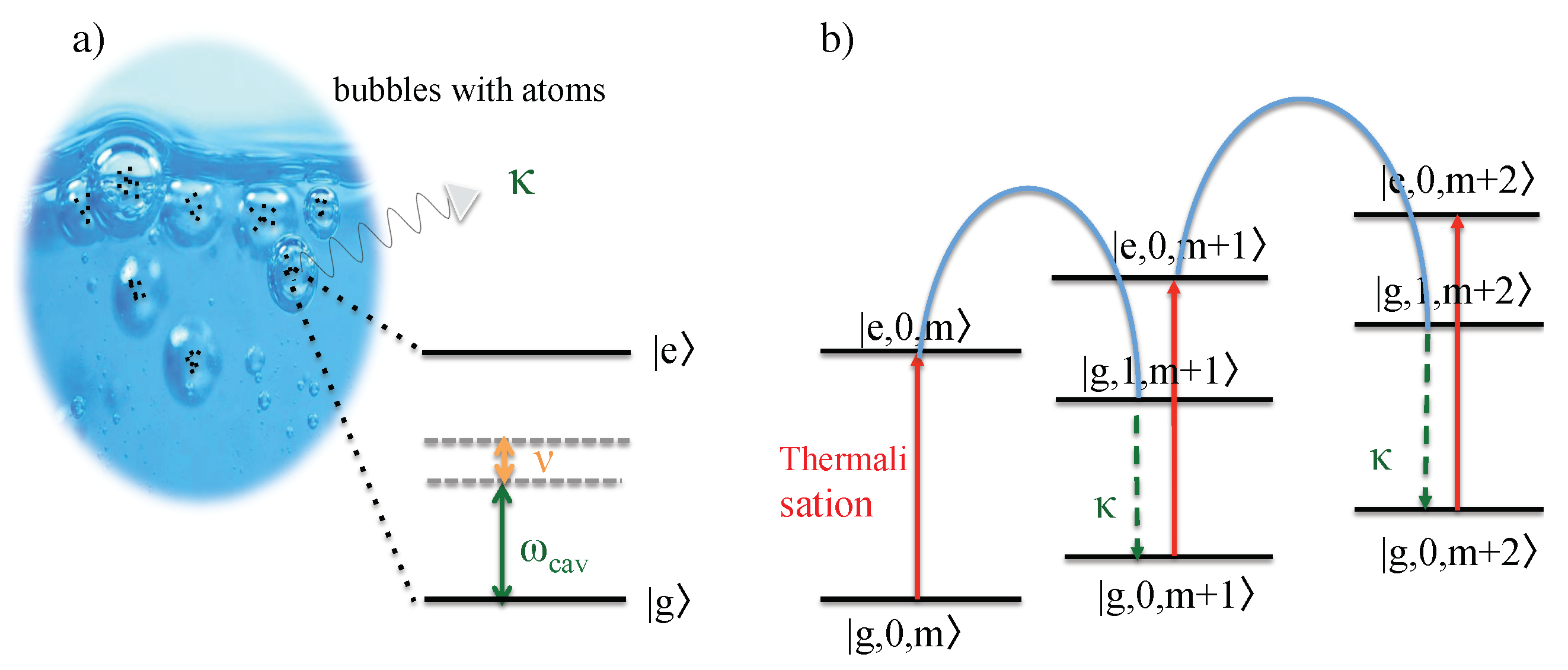
The above observations suggest many similarities between sonoluminescence and quantum optics experiments with trapped atomic particles [
29,
30]. When the bubble reaches its minimum radius, an atomic gas becomes very strongly confined [
31]. The quantum character of the atomic motion can no longer be neglected and, as in ion trap experiments (cf.
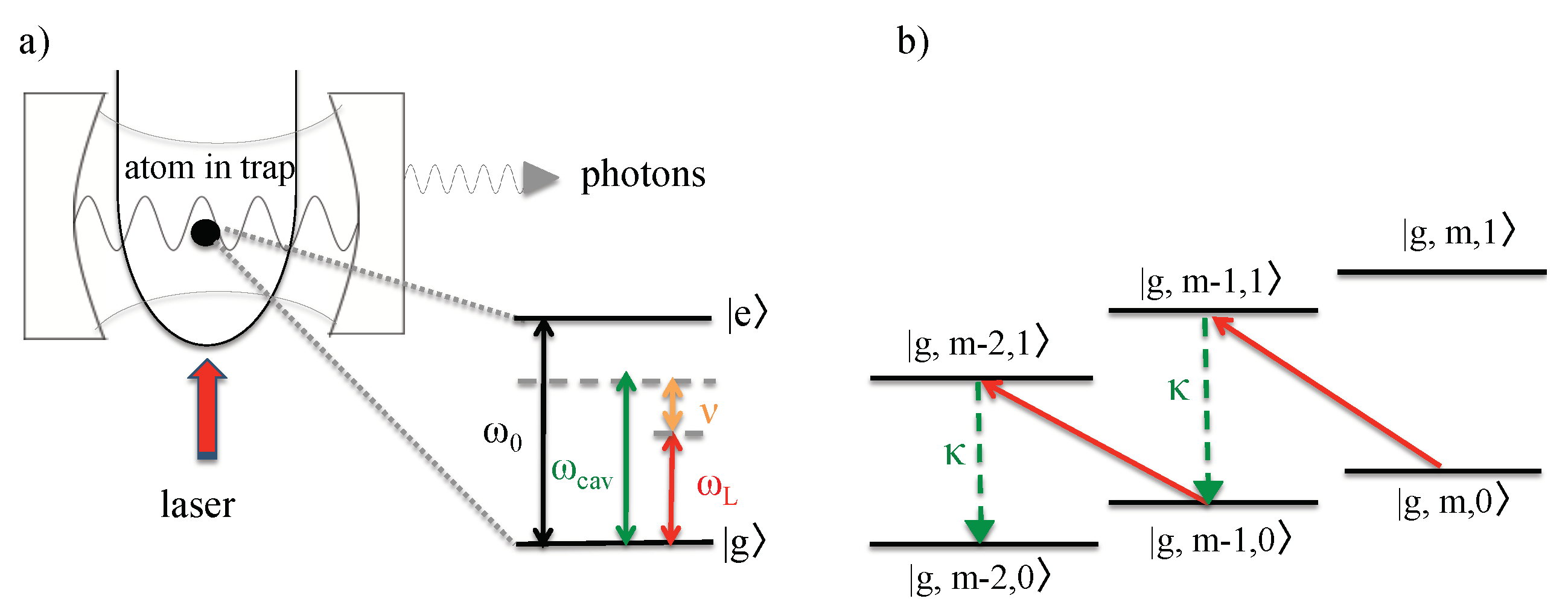
Section 2.1), the presence of phonons with different trapping frequencies
has to be taken into account. Moreover, when the bubble reaches its minimum radius, its surface can become opaque and almost metallic [
37]. When this happens, the bubble traps light inside and closely resembles an optical cavity which can be characterized by a frequency
and a spontaneous decay rate
. Since the confined particles have atomic dipole moments, they naturally couple to the quantized electromagnetic field inside the cavity. The result can be an exchange of energy between atomic dipoles and the cavity mode. The creation of photons inside the cavity is always accompanied by a change of the vibrational states of the atoms. Hence, the subsequent spontaneous emission of light in the optical regime results in a permanent change of the temperature of the atomic particles.
A main difference between sonoluminescence and cavity-mediated collective laser cooling is the absence and presence of external laser driving (cf.
Section 2.3). However, even in the absence of external laser driving, there can be a non-negligible amount of population in the excited atomic states
. This applies, for example, if the atomic gas inside the cavitating bubble is initially prepared in the thermal equilibrium state of a finite temperature
T. Once surrounded by an optical cavity, as it occurs during bubble collapse phases, excited atoms can return into their ground state via the creation of a cavity photon (cf.
Figure 6). Suddenly, an additional de-excitation channel has become available to them. As pointed out in Refs. [
29,
30], the creation a cavity photons is more likely accompanied by the creation of a phonon than the annihilation of a phonon since
Here,
B and
denote the relevant phonon annihilation and creation operators, while
denotes a state with exactly
m phonons. As one can see from Equation (
27), the normalization factor of
is slightly larger than the normalization factor of the state
. When the cavity photon is subsequently lost via spontaneous photon emission, the newly-created phonon remains inside the bubble. Hence, the light emission during bubble collapse phases is usually accompanied by heating, until the sonoluminescing bubble reaches an equilibrium.
During each bubble collapse phase, cavitating bubbles are thermally isolated from their surroundings. However, during the subsequent expansion phase, system parameters change adiabatically and there is a constant exchange of thermal energy between atomic gas inside the bubble and the surrounding liquid (cf.
Figure 5). Eventually, the atoms reach an equilibrium between heating during bubble collapse phases and the loss of energy during subsequent expansion phases. Experiments have shown that the atomic gas in side the cavitating bubble can reaches temperature of the order of
K which strongly supports the hypothesis that there is a very strong coupling between the vibrational and the electronic states of the confined particles [
35,
36].
4.3. Cavity-Mediated Collective Laser Cooling of Cavitating Bubbles
The previous subsection shows that, during each collapse phase, the dynamics of the cavitating bubbles in
Figure 1 is essentially the same as the dynamics of the experimental setup in
Figure 3 but with the single atom replaced by an atomic gas. When the bubble reaches its minimum diameter
, it forms an optical cavity which supports a discrete set of frequencies
,
where
c denotes the speed of light in air and
is an integer. As illustrated in
Figure 7, the case
corresponds to a cavity photon wavelength
. Moreover,
corresponds to
, and so on. Under realistic conditions, the cavitating bubbles are not all of the same size which is why every
j is usually associated with a range of frequencies
(cf.
Figure 7). Here, we are especially interested in the parameter
j, where the relevant cavity frequencies lie in the optical regime. All other parameters
j can be neglected, once a laser field with an optical frequency
is applied, if neighboring frequency bands are sufficiently detuned.
In addition, we know that the phonon frequency
of the collective phonon mode
B assumes its maximum
during the bubble collapse phase. Suppose the cavity detuning
of the applied laser field is chosen such that
in analogy to Equation (
2). As we have seen in
Section 2.3, in this case, the two-step transition which results in the simultaneous annihilation of a phonon and the creation of a cavity photon becomes resonant and dominates the system dynamics. If the creation of a cavity photon is followed by a spontaneous emission, the previously annihilated phonon cannot be restored and is permanently lost. Overall, we expect this cooling process to be very efficient, since the atoms are strongly confined and cavity cooling rates are collectively enhanced (cf. Equation (
17)).
To cool not only very tiny but larger volumes, the experimental setup in
Figure 1 should contain a relatively large number of cavitating bubbles. Depending on the quality of the applied transducer, the minimum diameters
of these bubbles might vary in size. Consequently, the collection of bubbles supports a finite range of cavity frequencies
(cf.
Figure 7 so that it becomes impossible to realize the ideal cooling condition
in Equation (
29) for all bubbles. However, as long as the frequency
of the cooling laser is smaller than all optical cavity frequencies
, the system dynamics will be dominated by cooling and not by heating. In general, it is important that the diameters of the bubbles does not vary by too much.
Section 2.3 also shows that cavity-mediated collective laser cooling only removes thermal energy from a single collective vibrational mode
B of the atoms. Once this mode is depleted, the cooling process stops. To efficiently cool an entire atomic gas, a mechanism is needed which rapidly re-distributes energy between different vibrational degrees of freedom, for example, via thermalization based on elastic collisions (cf.
Section 3). As shown above, between cooling stages, cavitating bubbles evolve essentially adiabatically and the atoms experience strong collisions. In other words, the expansion phase of cavitating bubbles automatically implements the intermittent thermalization stages of cavity-mediated collective laser cooling.
Finally, let us point out that it does not matter whether the cooling laser is turned on or off during thermalization stages, i.e., during bubble expansion phases. As long as optical cavities only form during the bubble collapse phases, the above-described conversion of heat into light only happens when the bubble reaches its minimum diameter. The reason for this is that noble gas atoms, such as nitrogen, have very large transition frequencies
. The direct laser excitation of atomic particles is therefore relatively unlikely, even when the cooling laser is turned on. If we could excite the atoms directly by laser driving, we could cool them even more efficiently (cf.
Section 2.1).
4.4. Cooling of the Surroundings via Heat Transfer
The purpose of the heat exchanger which we propose here is to constantly remove thermal energy from the liquid surrounding the cavitating bubbles and device on which the liquid is placed (cf.
Figure 1). As described in the previous subsection, the atomic gas inside the bubbles is cooled by very rapidly converting heat into light during each collapse phase. In between collapse phases, the cavitating bubbles evolve adiabatically and naturally cool their immediate environment via heat transfer. As illustrated in
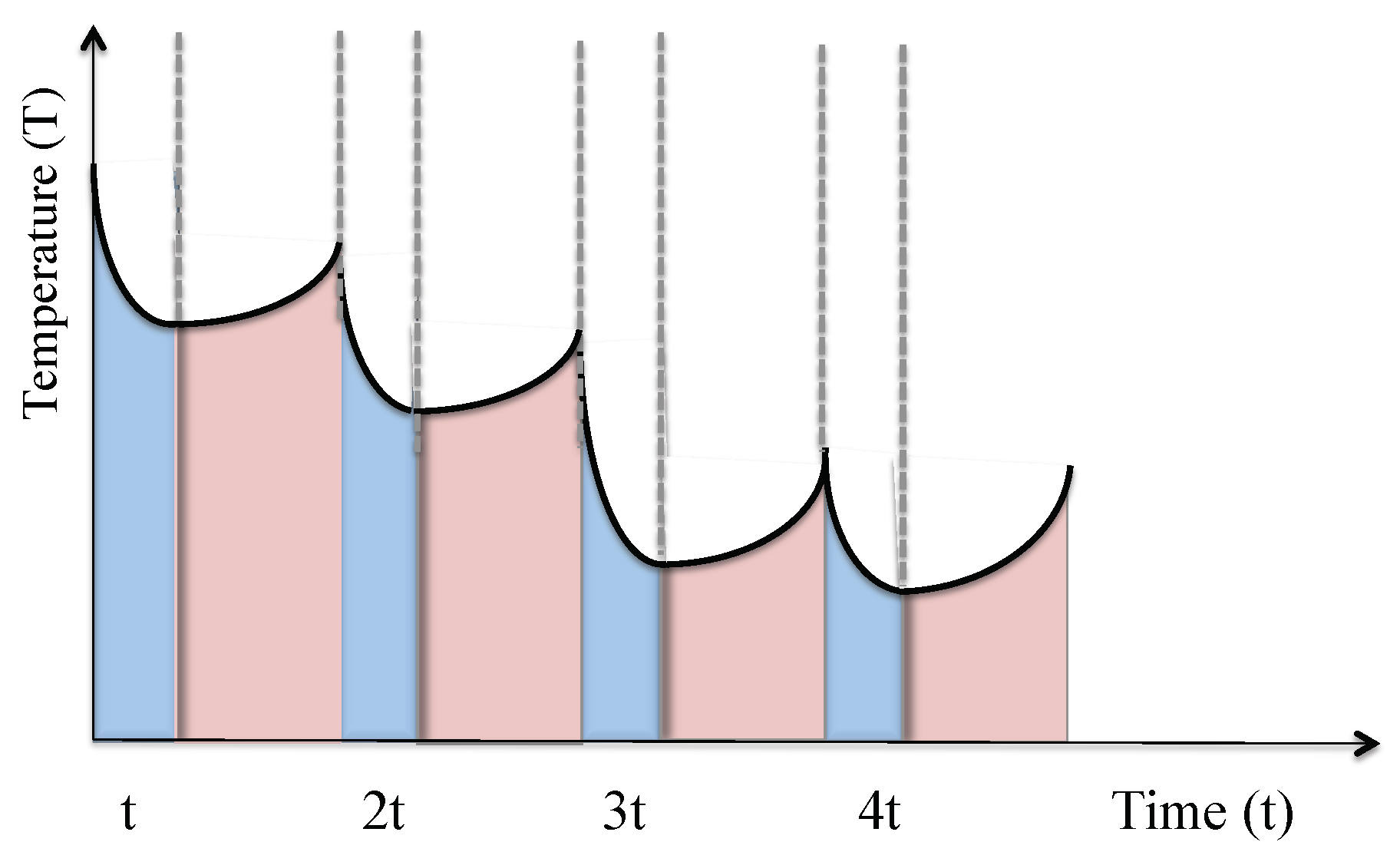
Figure 8, alternating cooling and thermalization stages (or collapse and expansion phases) is expected to implement a quantum heat exchanger, which does not require the actual transport of particles from one place to another.
Finally, let us have a closer look at achievable cooling rates for micro- and nanotechnology devices with length dimensions in the nano- and micrometer regime. Unfortunately, we do not know how rapidly heat can be transferred from the nanotechnology device to the liquid and from there to the atomic gas inside the cavitating bubbles. However, any thermal energy which is taken from the atoms comes eventually from the environment which we aim to cool. Suppose the relevant phonon frequencies are sufficiently large to ensure that every emitted photon indicates the loss of one phonon, i.e., the loss of one energy quantum . Moreover, suppose our quantum heat exchanger contains a certain amount of liquid, let us say water, of mass and heat capacity at an initial temperature . Then, we can ask the question: How many photons do we need to create in order to cool the water by a certain temperature ?
From thermodynamics, we know that the change in the thermal energy of the water equals
in this case. Moreover, we know that
Hence, the number of photons that needs to be produced is given by
The time
it would take to create this number of photons equals
where
I denotes the average single-atom photon emission rate and
is the number of atoms involved in the cooling process. When combining the above equations, we find that the cooling rate
of the proposed cooling process equals
to a very good approximations.
As an example, suppose we want to cool one cubic micrometer of water (
) at room temperature (
°C). In this case,
g and
J/gK to a very good approximation. Suppose
MHz (a typical frequency in ion trap experiments is
MHz),
s and
(a typical bubble in single bubble sonoluminescence contains about
atoms). Substituting these numbers into Equation (
33) yields a cooling rate of
Achieving cooling rates of the order of Kelvin temperatures per millisecond seems therefore experimentally feasible. As one can see from Equation (
33), to reduce cooling rates further, one can either reduce the volume that requires cooling, increase the number of atoms involved in the cooling process or increase the trapping frequency
of the atomic gas inside collapsing bubbles. All of this is, at least in principle, possible.