Theory, Analysis, and Applications of the Entropic Lattice Boltzmann Model for Compressible Flows
Abstract
1. Introduction
2. Compressible Lattice Boltzmann Models
2.1. Discrete Kinetic Equations
2.2. Thermo-Hydrodynamic Equations
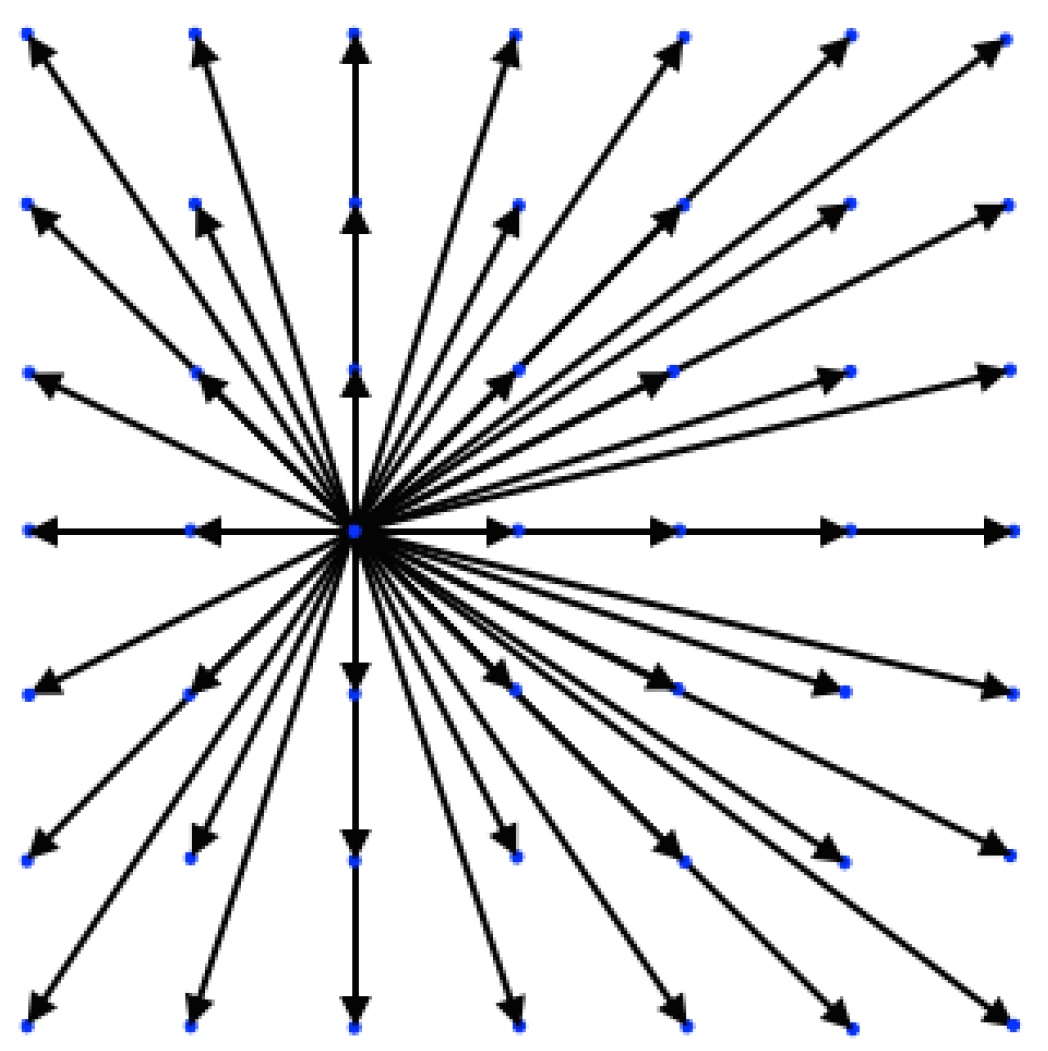
2.3. Lattices
2.4. Equilibrium
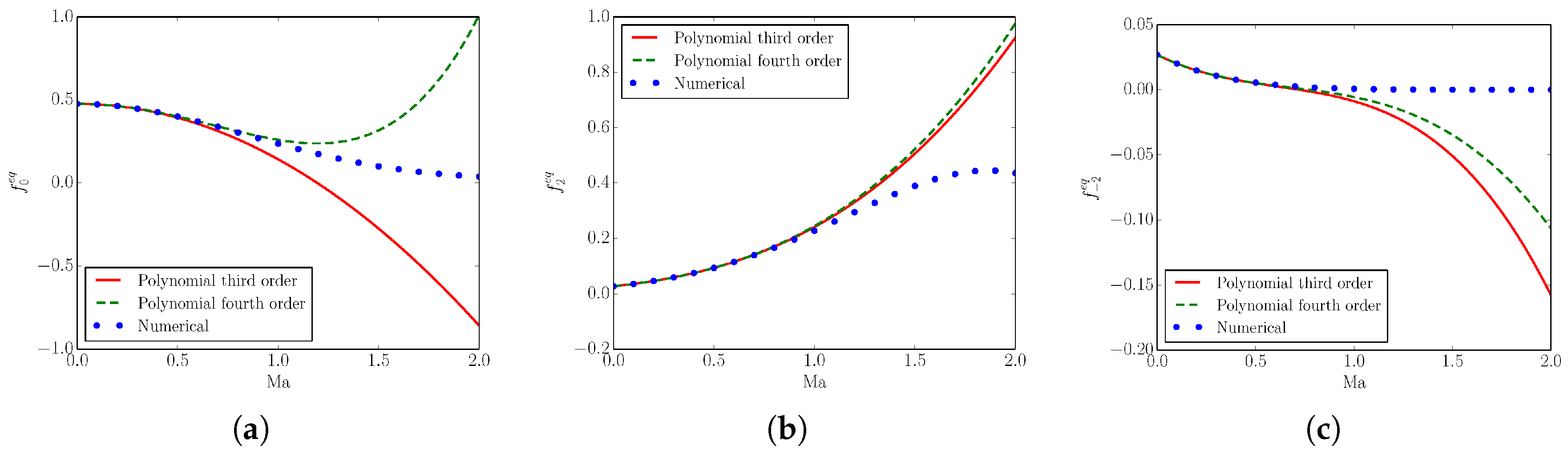
2.4.1. Equilibrium Construction
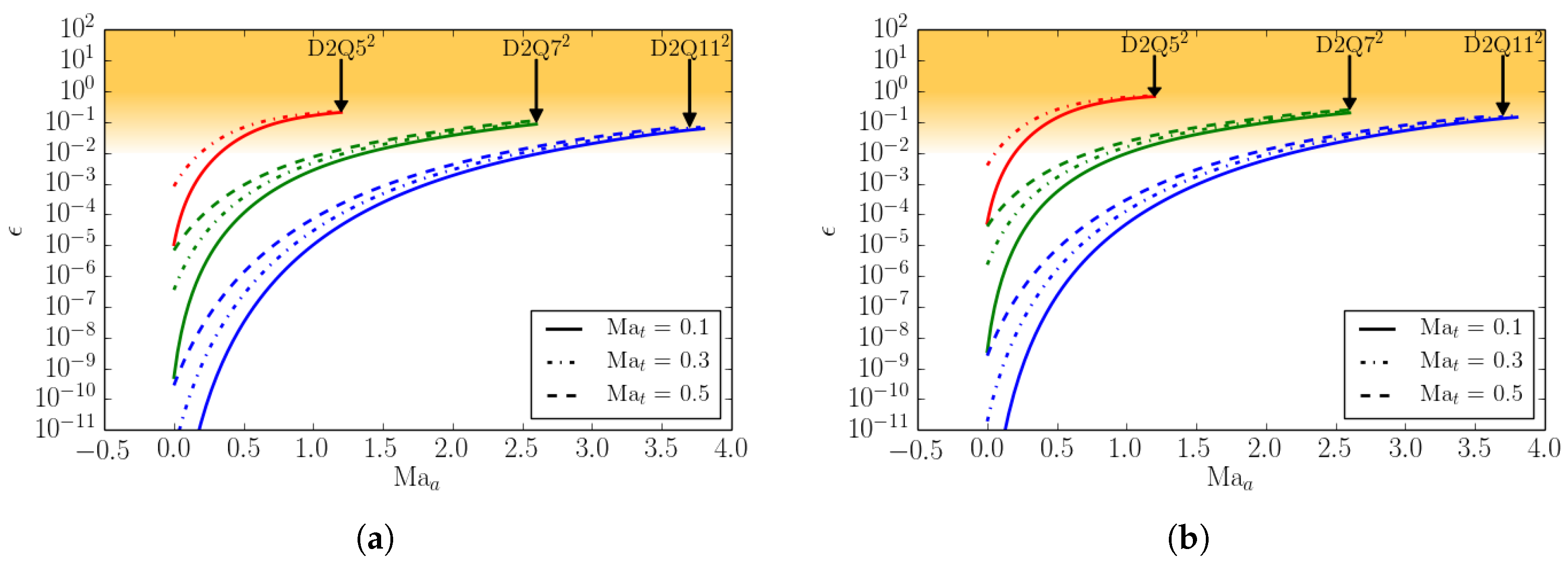
2.4.2. Computational Costs of Numerical Equilibrium
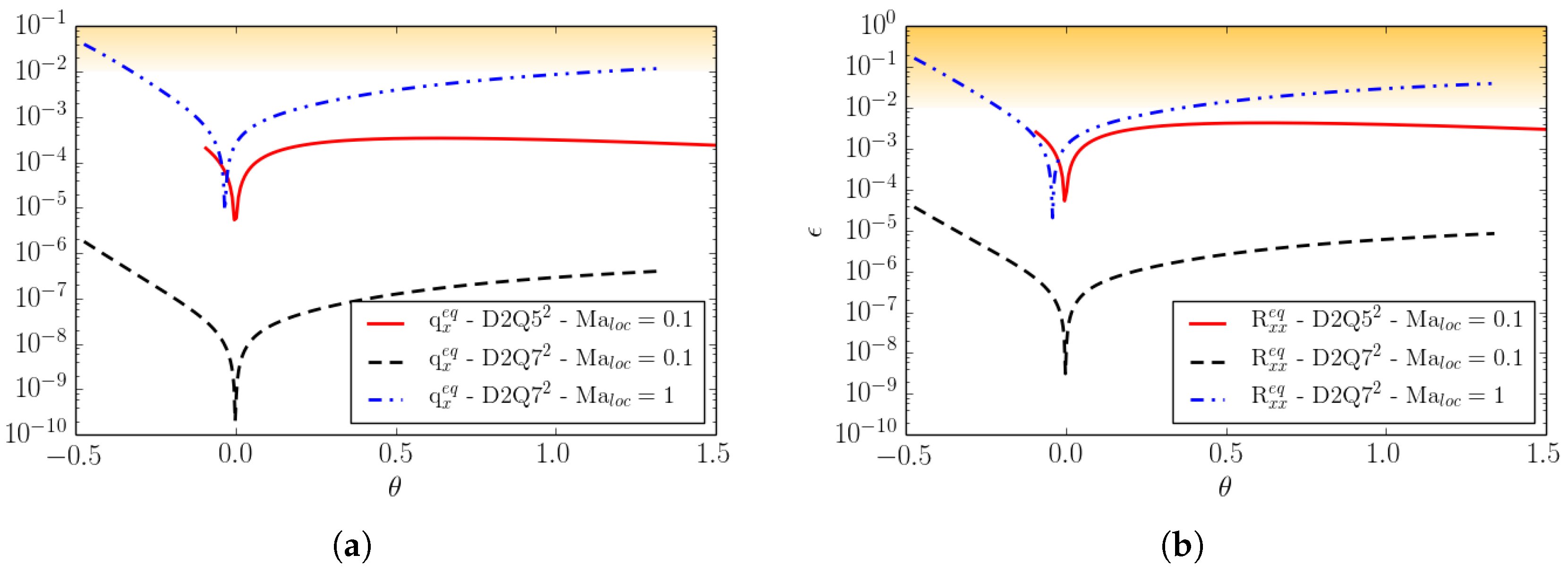
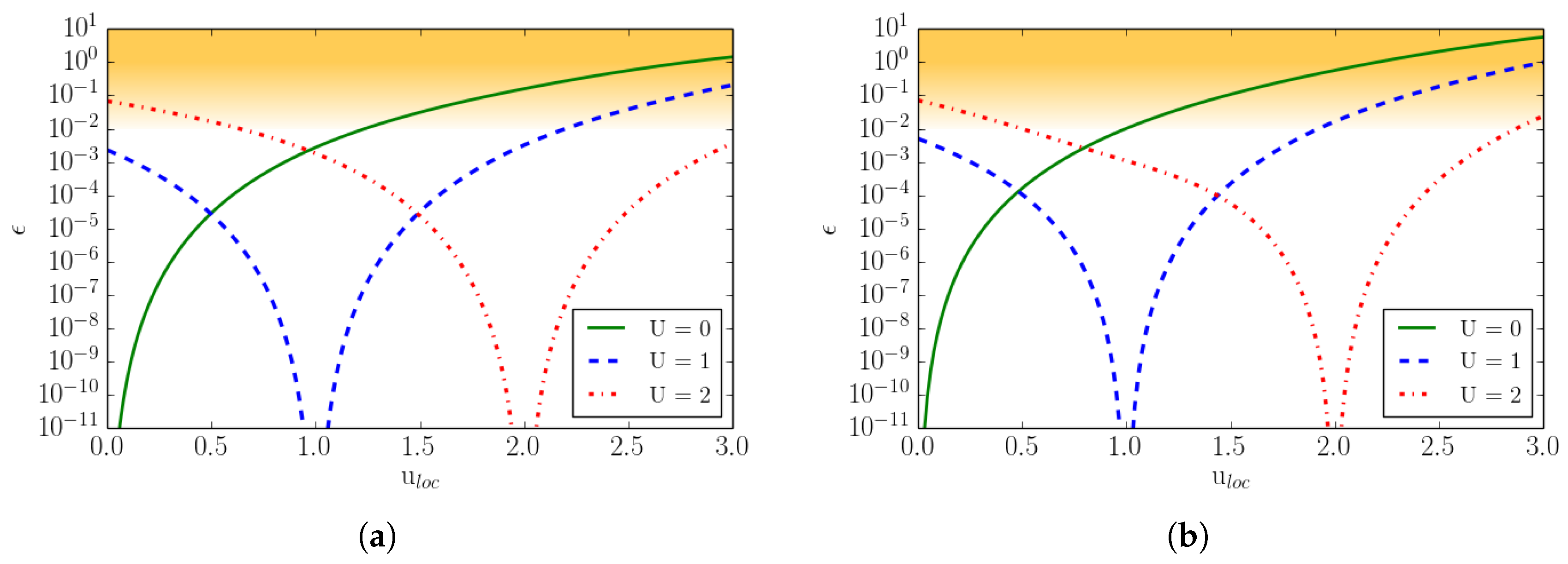
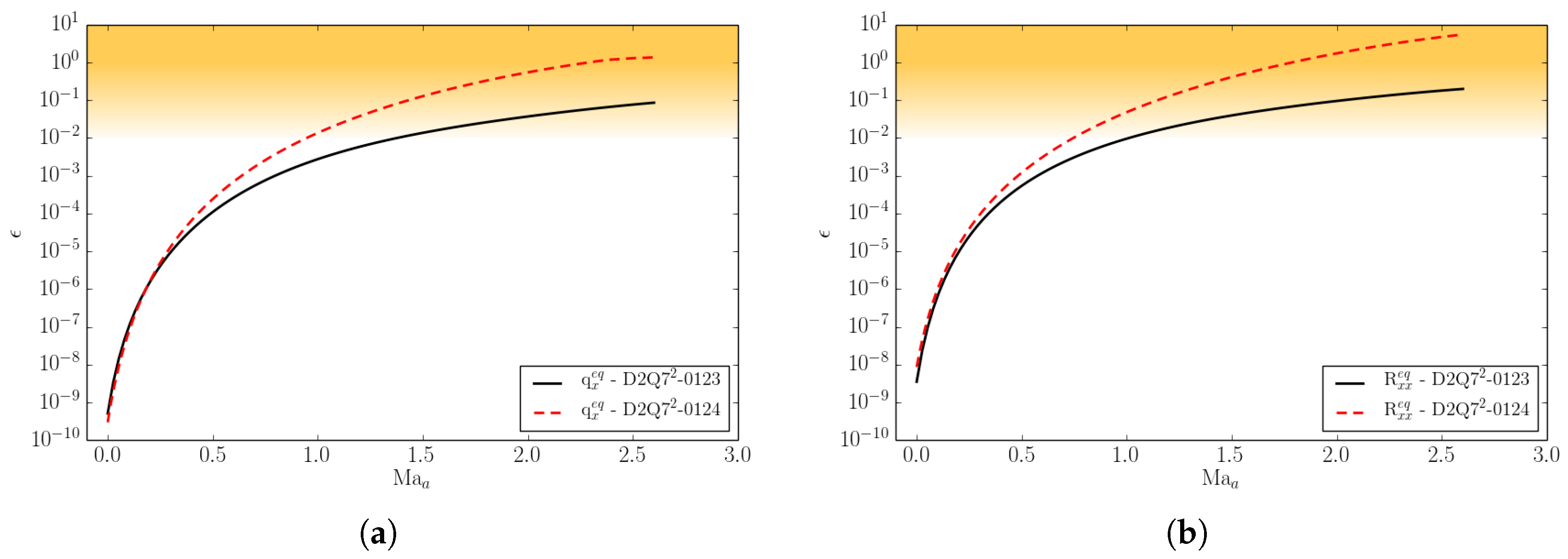
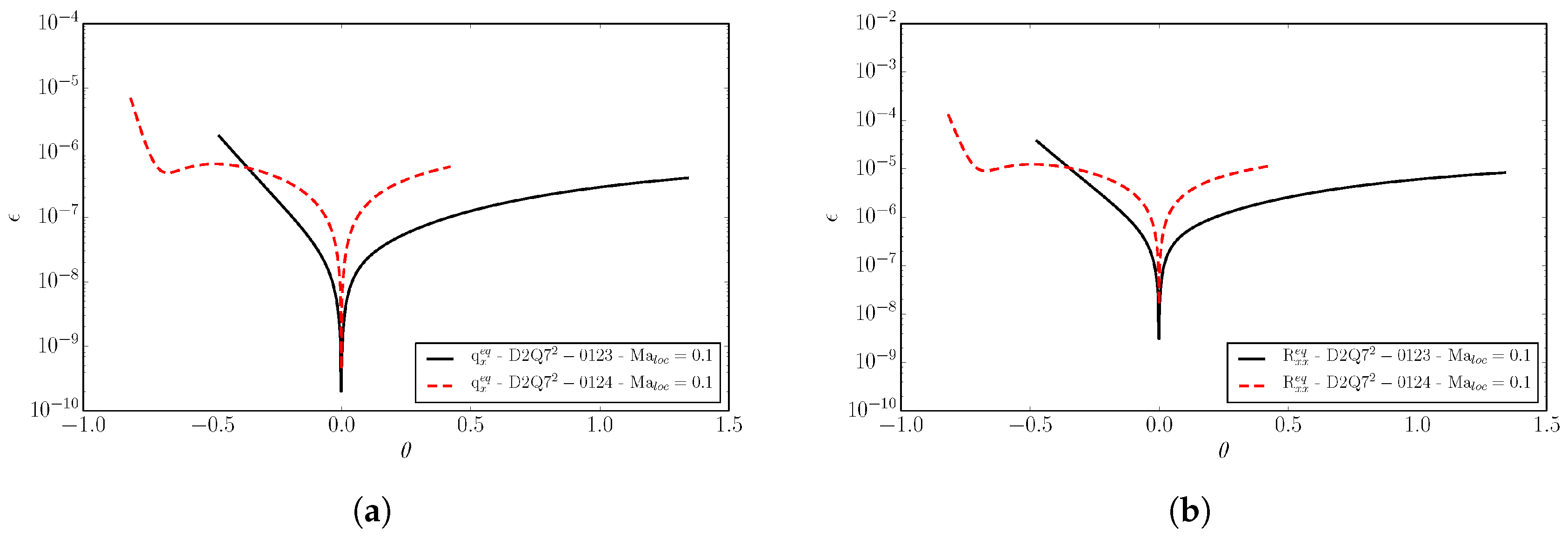
2.4.3. Numerical Equilibrium Accuracy
2.4.4. Equilibria Positivity
3. Extension of Operation Domain
3.1. Shifted Lattices
3.2. Lattices with Increased Temperature Range
4. Numerical Results
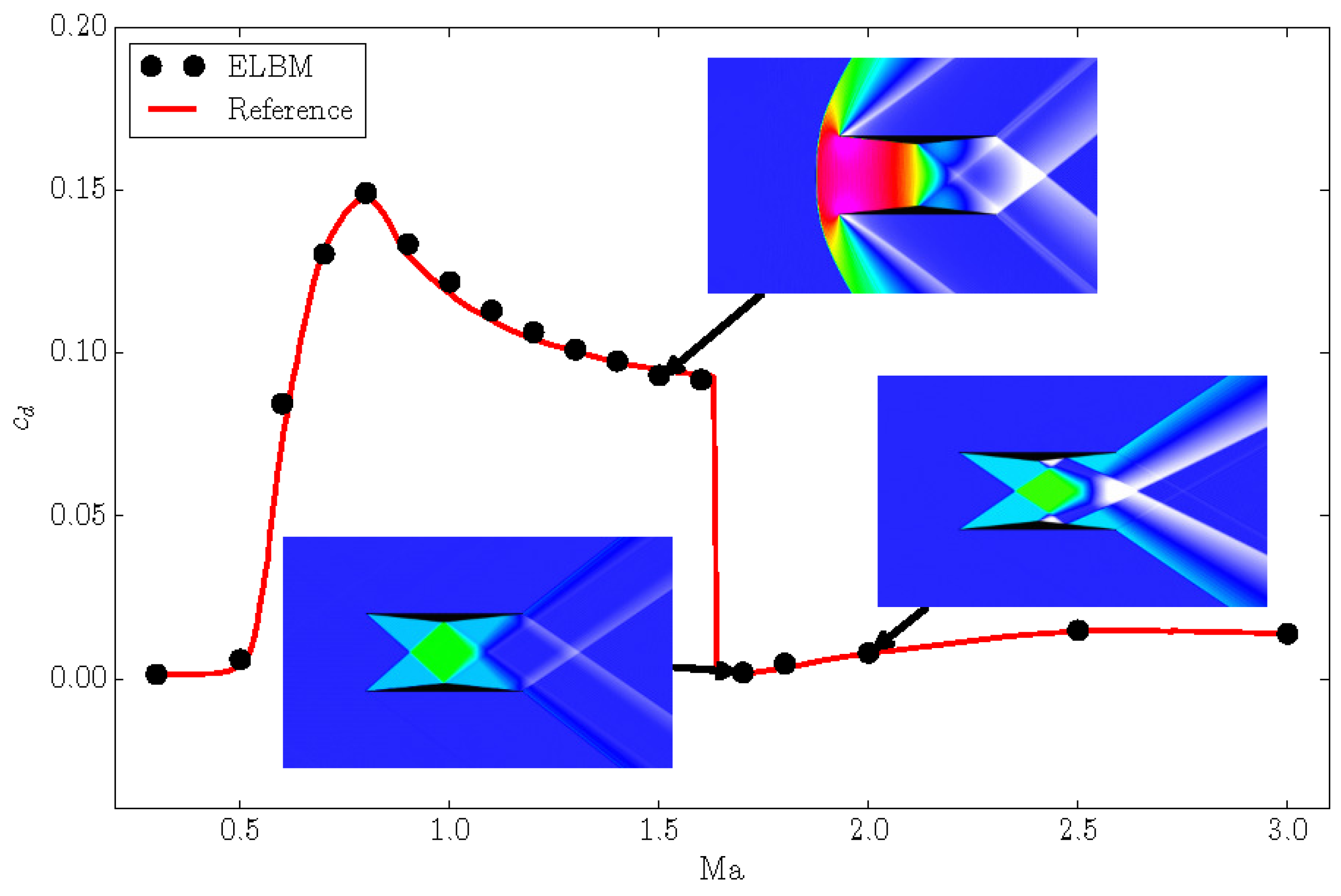
4.1. Supersonic Diamond Airfoil
4.2. Busemann Biplane
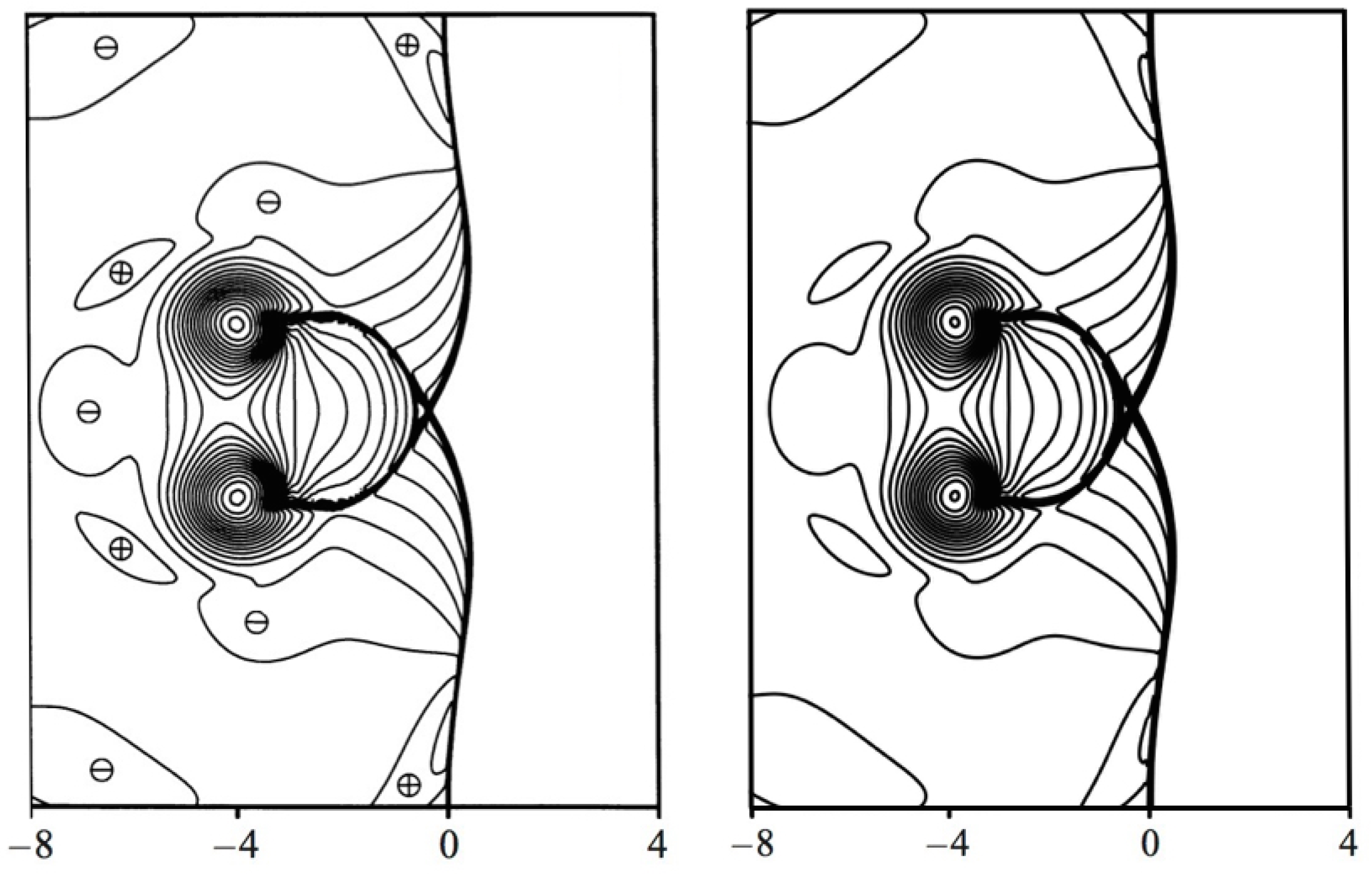
4.3. Supersonic NACA0012 Airfoil
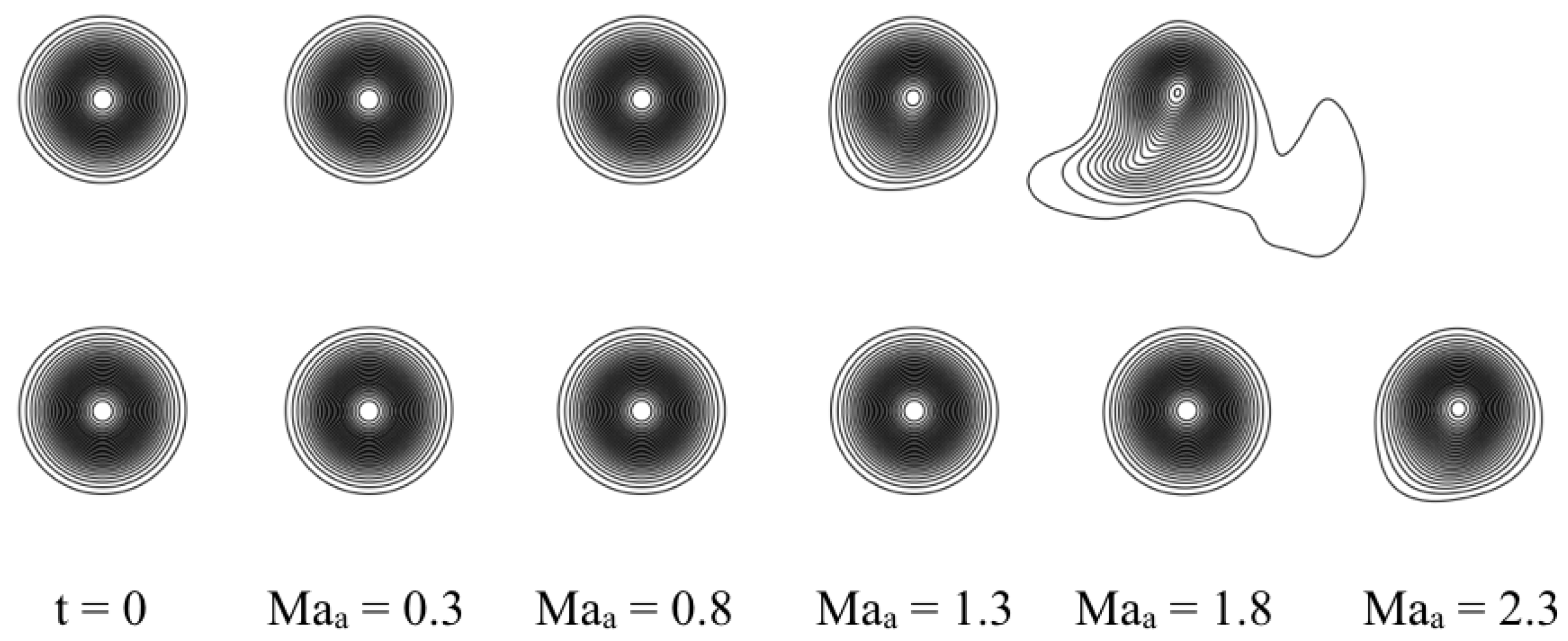
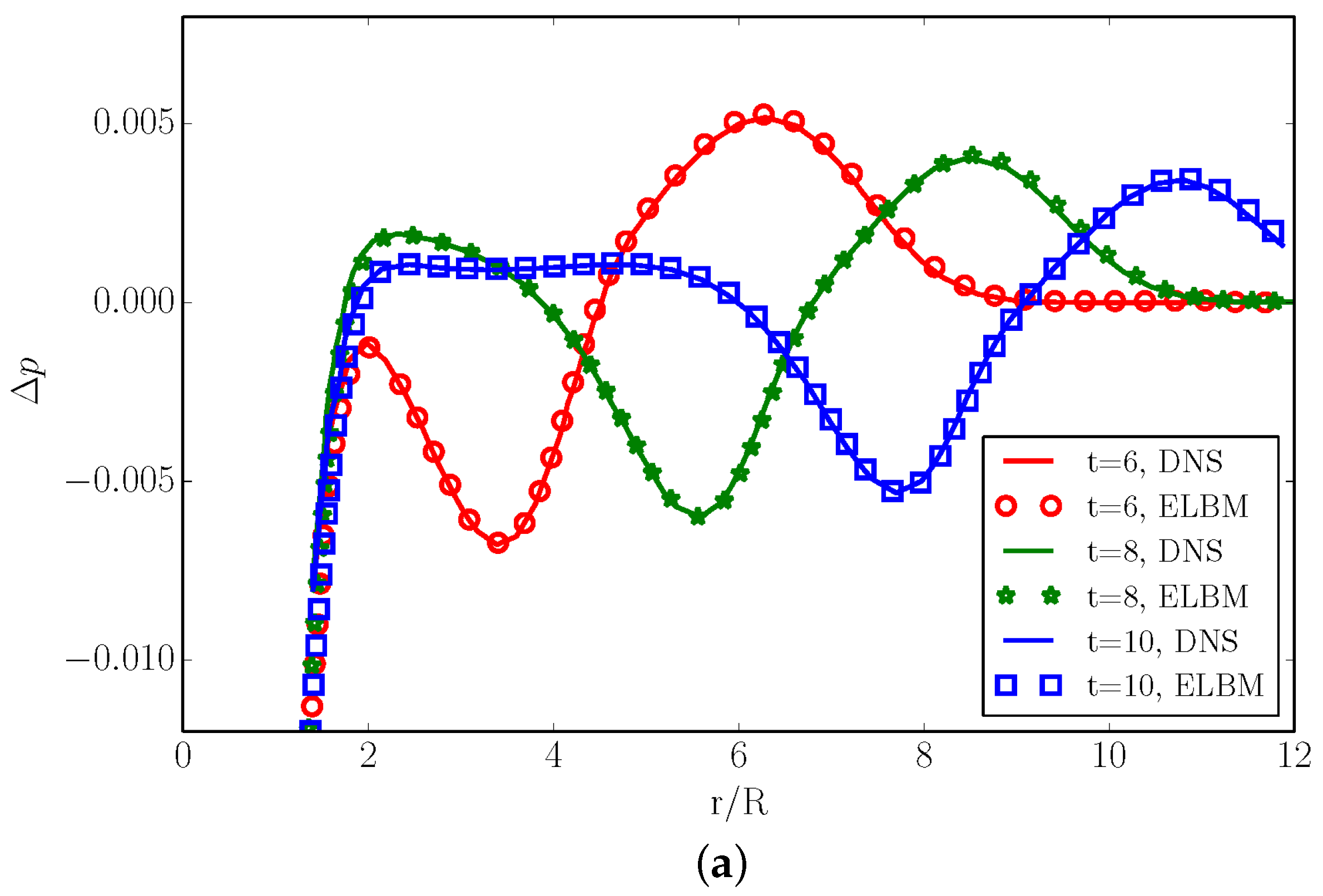
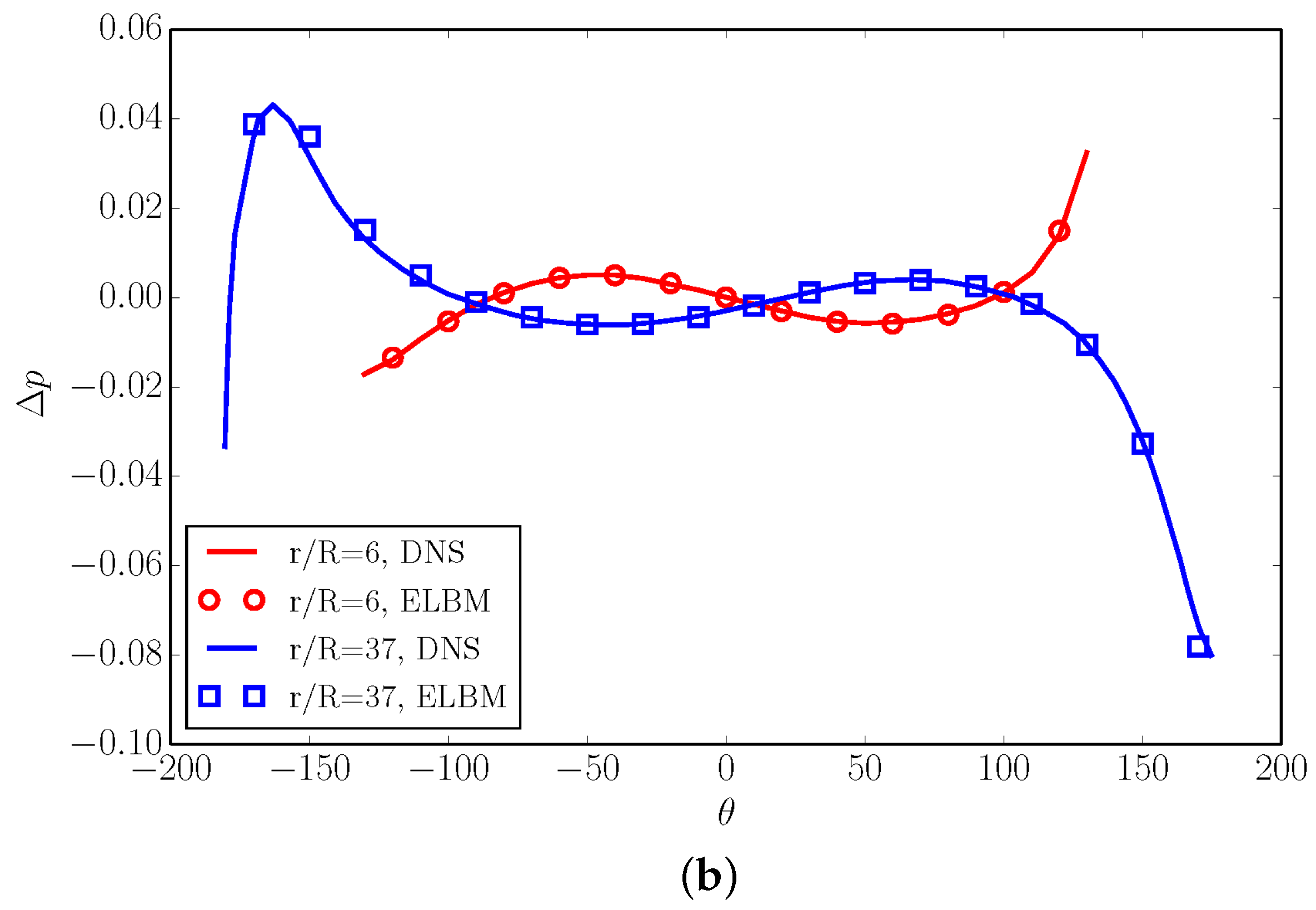
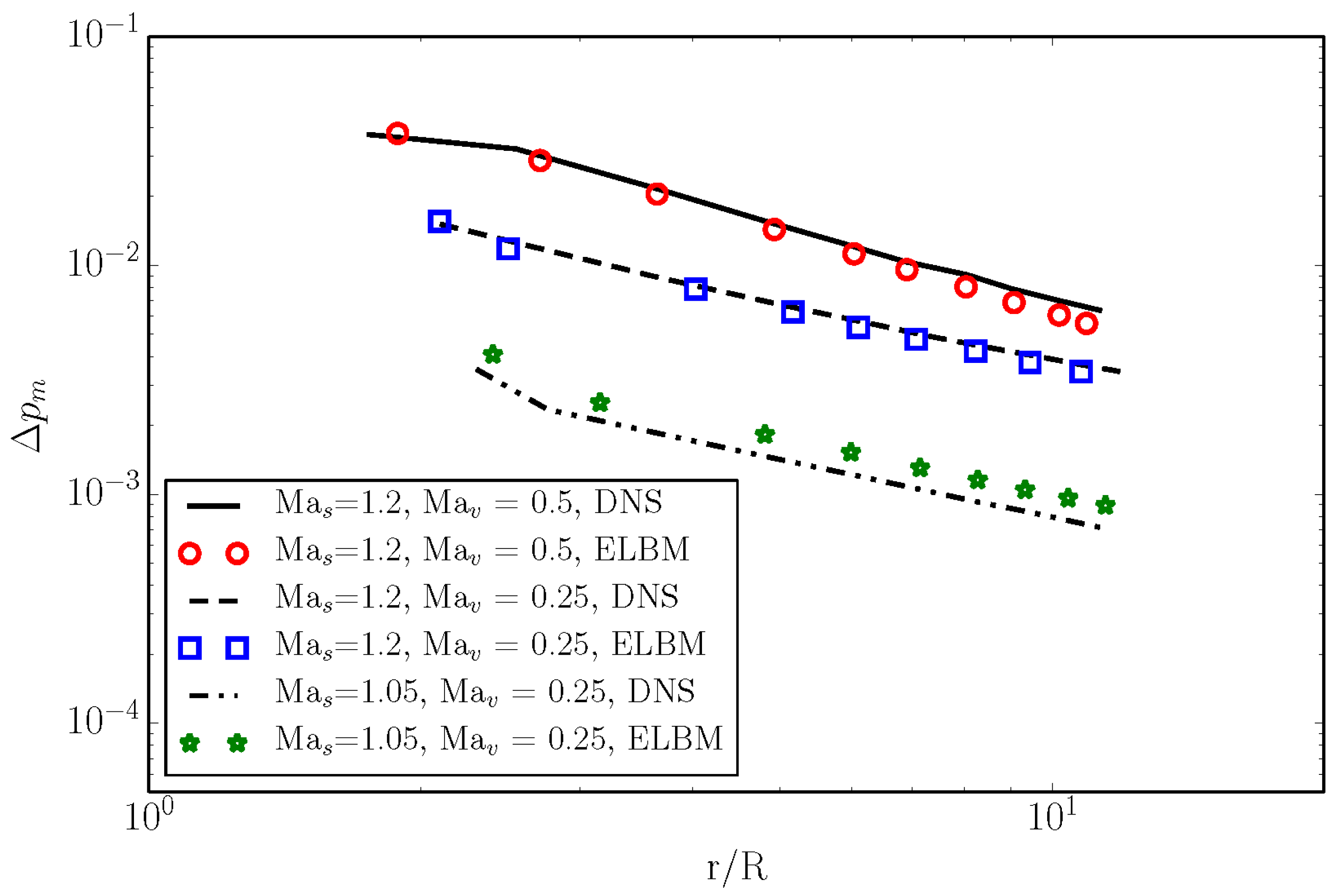
4.4. Shock–Vortex Interaction
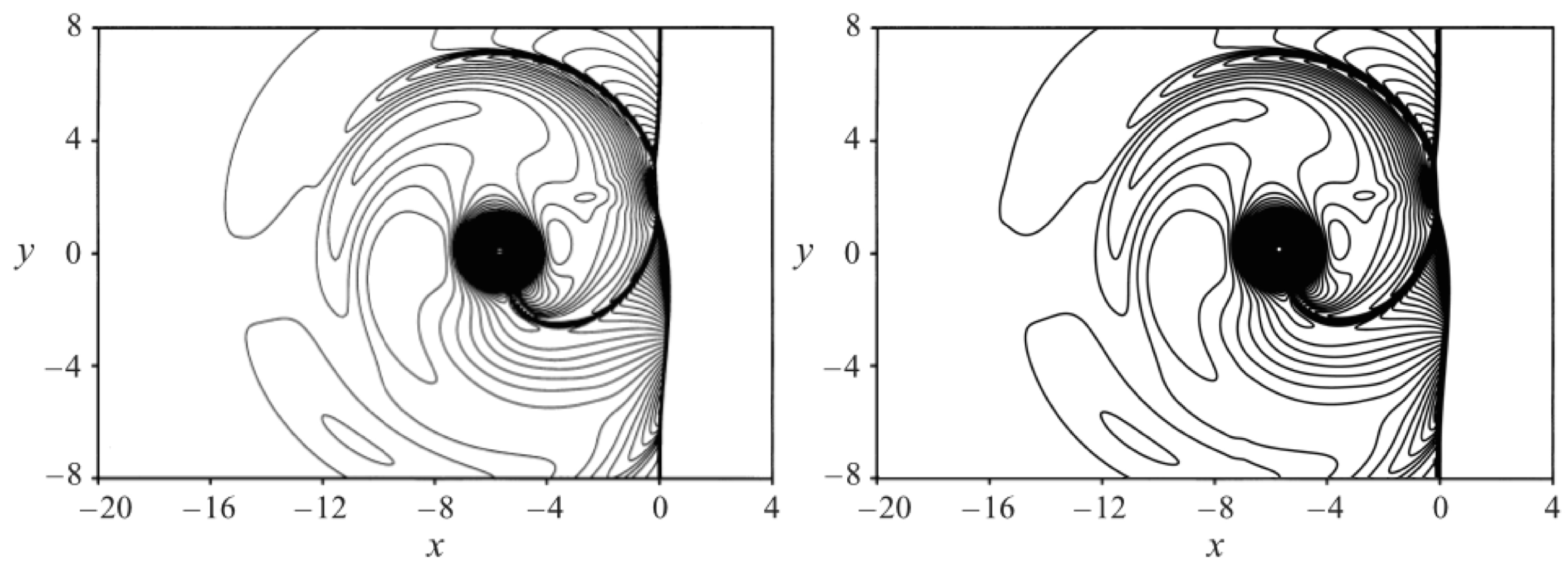
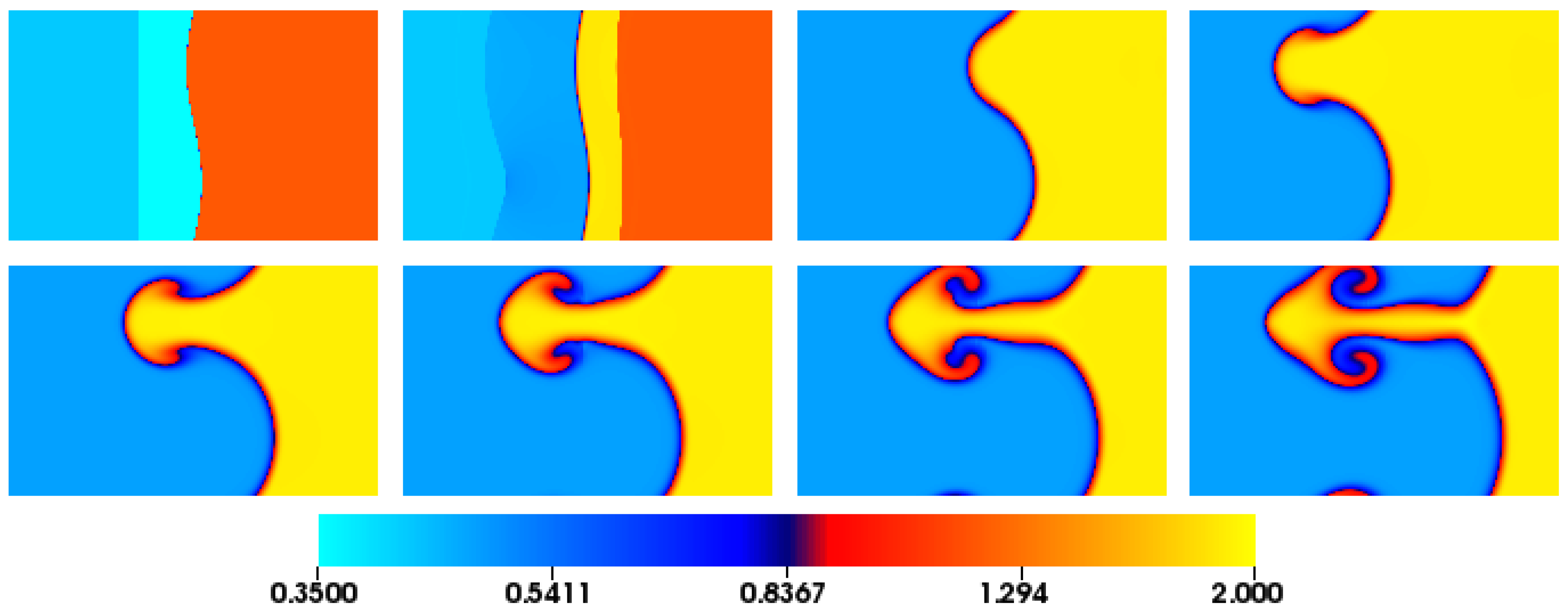
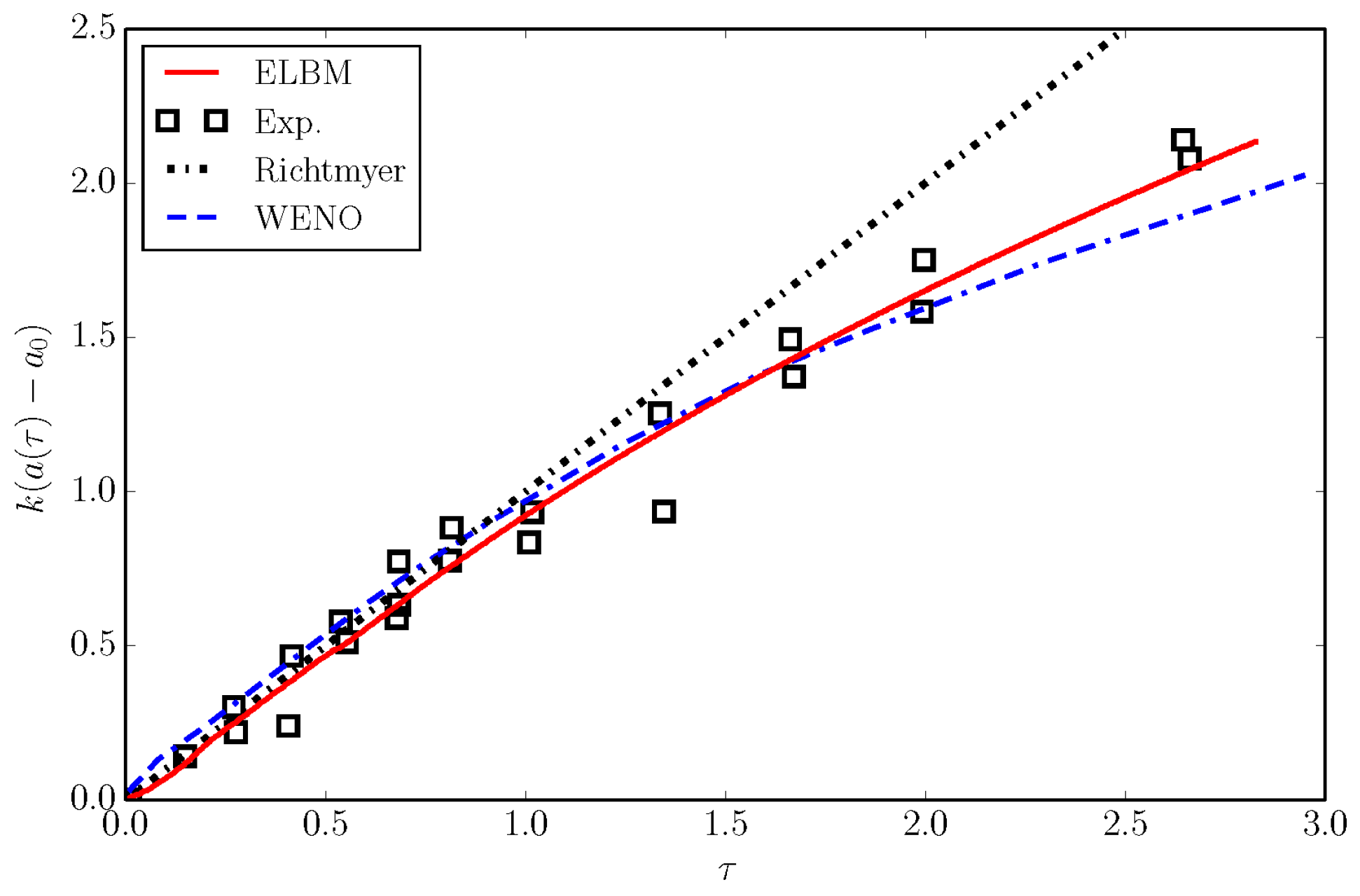
4.5. Richtmyer–Meshkov Instability
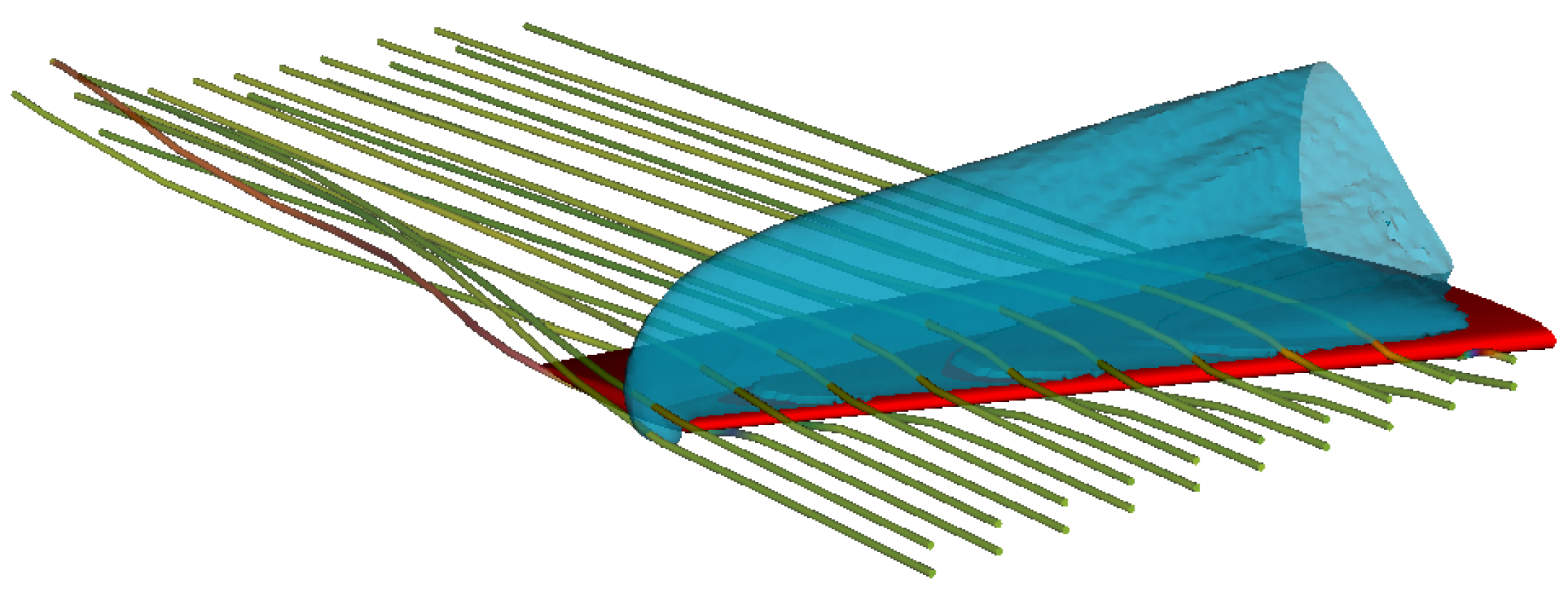
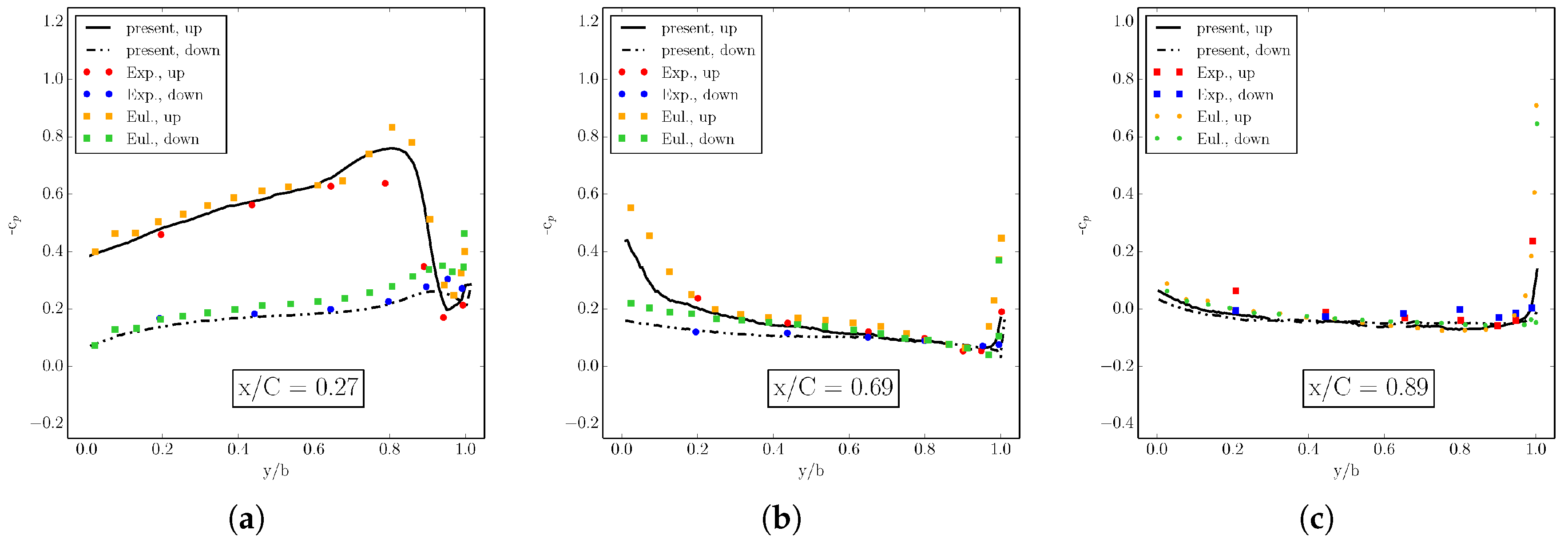
4.6. Transonic Onera M6 Wing
5. Conclusions and Outlook: Pruned Lattices and Entropic Guided Equilibrium Construction
5.1. Lattice Pruning
5.2. Entropic Guided Equilibrium
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ekaterinaris, J.A. High-order accurate, low numerical diffusion methods for aerodynamics. Progr. Aerospace Sci. 2005, 41, 192–300. [Google Scholar] [CrossRef]
- Pirozzoli, S. Numerical methods for high-speed flows. Annu. Rev. Fluid Mech. 2011, 43, 163–194. [Google Scholar] [CrossRef]
- Succi, S. The Lattice-Boltzmann Equation; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Karlin, I.; Ferrante, A.; Öttinger, H.C. Perfect entropy functions of the lattice Boltzmann method. Europhys. Lett. 1999, 47, 182. [Google Scholar] [CrossRef]
- Boghosian, B.M.; Yepez, J.; Coveney, P.V.; Wagner, A. Entropic lattice Boltzmann methods. Proc. R. Soc. Lond. Ser. A Math. 2001, 457, 717–766. [Google Scholar] [CrossRef]
- Ansumali, S.; Karlin, I.; Öttinger, H.C. Minimal entropic kinetic models for hydrodynamics. Europhys. Lett. 2003, 63, 798. [Google Scholar] [CrossRef]
- Shan, X.; He, X. Discretization of the velocity space in the solution of the Boltzmann equation. Phys. Rev. Lett. 1998, 80, 65. [Google Scholar] [CrossRef]
- Alexander, F.J.; Chen, S.; Sterling, J. Lattice Boltzmann thermohydrodynamics. Phys. Rev. E 1993, 47, R2249. [Google Scholar] [CrossRef]
- McNamara, G.R.; Garcia, A.L.; Alder, B.J. Stabilization of thermal lattice Boltzmann models. J. Stat. Phys. 1995, 81, 395–408. [Google Scholar] [CrossRef]
- Shan, X.; Yuan, X.F.; Chen, H. Kinetic theory representation of hydrodynamics: A way beyond the Navier–Stokes equation. J. Fluid Mech. 2006, 550, 413–441. [Google Scholar] [CrossRef]
- Philippi, P.C.; Hegele, L.A., Jr.; Dos Santos, L.O.; Surmas, R. From the continuous to the lattice Boltzmann equation: The discretization problem and thermal models. Phys. Rev. E 2006, 73, 056702. [Google Scholar] [CrossRef]
- Sun, C.; Hsu, A.T. Three-dimensional lattice Boltzmann model for compressible flows. Phys. Rev. E 2003, 68, 016303. [Google Scholar] [CrossRef] [PubMed]
- Chikatamarla, S.S.; Karlin, I.V. Entropy and Galilean invariance of lattice Boltzmann theories. Phys. Rev. Lett. 2006, 97, 190601. [Google Scholar] [CrossRef] [PubMed]
- Chikatamarla, S.S.; Karlin, I.V. Lattices for the lattice Boltzmann method. Phys. Rev. E 2009, 79, 046701. [Google Scholar] [CrossRef] [PubMed]
- Chikatamarla, S.; Frouzakis, C.; Karlin, I.; Tomboulides, A.; Boulouchos, K. Lattice Boltzmann method for direct numerical simulation of turbulent flows. J. Fluid Mech. 2010, 656, 298–308. [Google Scholar] [CrossRef]
- Frapolli, N.; Chikatamarla, S.; Karlin, I. Multispeed entropic lattice Boltzmann model for thermal flows. Phys. Rev. E 2014, 90, 043306. [Google Scholar] [CrossRef] [PubMed]
- Frapolli, N.; Chikatamarla, S.; Karlin, I. Entropic lattice Boltzmann model for compressible flows. Phys. Rev. E 2015, 92, 061301. [Google Scholar] [CrossRef]
- Frapolli, N.; Chikatamarla, S.; Karlin, I. Entropic lattice Boltzmann model for gas dynamics: Theory, boundary conditions, and implementation. Phys. Rev. E 2016, 93, 063302. [Google Scholar] [CrossRef]
- Frapolli, N.; Chikatamarla, S.; Karlin, I. Lattice kinetic theory in a comoving Galilean reference frame. Phys. Rev. Lett. 2016, 117, 010604. [Google Scholar] [CrossRef]
- Frapolli, N. Entropic Lattice Boltzmann Models for Thermal and Compressible Flows. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2017. [Google Scholar]
- Kataoka, T.; Tsutahara, M. Lattice Boltzmann model for the compressible Navier–Stokes equations with flexible specific-heat ratio. Phys. Rev. E 2004, 69, 035701. [Google Scholar] [CrossRef]
- Chen, F.; Xu, A.; Zhang, G.; Li, Y.; Succi, S. Multiple-relaxation-time lattice Boltzmann approach to compressible flows with flexible specific-heat ratio and Prandtl number. Europhys. Lett. 2010, 90, 54003. [Google Scholar] [CrossRef]
- Rykov, V. A model kinetic equation for a gas with rotational degrees of freedom. Fluid Dyn. 1975, 10, 959–966. [Google Scholar] [CrossRef]
- Nie, X.; Shan, X.; Chen, H. Thermal lattice Boltzmann model for gases with internal degrees of freedom. Phys. Rev. E 2008, 77, 035701. [Google Scholar] [CrossRef] [PubMed]
- Ruggeri, T.; Sugiyama, M. Rational Extended Thermodynamics beyond the Monatomic Gas; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ansumali, S.; Arcidiacono, S.; Chikatamarla, S.; Prasianakis, N.; Gorban, A.; Karlin, I. Quasi-equilibrium lattice Boltzmann method. Eur. Phys. J. B 2007, 56, 135–139. [Google Scholar] [CrossRef]
- Shakhov, E.M. Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 1968, 3, 95–96. [Google Scholar] [CrossRef]
- Karlin, I.; Asinari, P. Factorization symmetry in the lattice Boltzmann method. Phys. A Stat. Mech. Appl. 2010, 389, 1530–1548. [Google Scholar] [CrossRef]
- Liepmann, H.W.; Roshko, A. Elements of Gasdynamics; Courier Corporation: Chelmsford, MA, USA, 1957. [Google Scholar]
- Kusunose, K.; Matsushima, K.; Maruyama, D. Supersonic biplane: A review. Prog. Aerosp. Sci. 2011, 47, 53–87. [Google Scholar] [CrossRef]
- Hafez, M.; Wahba, E. Simulations of viscous transonic flows over lifting airfoils and wings. Comput. Fluid. 2007, 36, 39–52. [Google Scholar] [CrossRef]
- Inoue, O.; Hattori, Y. Sound generation by shock–vortex interactions. J. Fluid Mech. 1999, 380, 81–116. [Google Scholar] [CrossRef]
- Brouillette, M. The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 2002, 34, 445–468. [Google Scholar] [CrossRef]
- Collins, B.; Jacobs, J. PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF 6 interface. J. Fluid Mech. 2002, 464, 113–136. [Google Scholar] [CrossRef]
- Latini, M.; Schilling, O.; Don, W.S. High-resolution simulations and modeling of reshocked single-mode Richtmyer–Meshkov instability: Comparison to experimental data and to amplitude growth model predictions. Phys. Fluid. 2007, 19, 024104. [Google Scholar] [CrossRef]
- Richtmyer, R.D. Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Math. 1960, 13, 297–319. [Google Scholar] [CrossRef]
- Rizzi, A.; Eriksson, L.E. Computation of flow around wings based on the Euler equations. J. Fluid Mech. 1984, 148, 45–71. [Google Scholar] [CrossRef]
- Kuzmin, A. On the lambda-shock formation on ONERA M6 wing. Int. J. Appl. Eng. Res. 2014, 9, 7029–7038. [Google Scholar]
- Prasianakis, N.I.; Karlin, I.V. Lattice Boltzmann method for thermal flow simulation on standard lattices. Phys. Rev. E 2007, 76, 016702. [Google Scholar] [CrossRef]
- Karlin, I.V.; Succi, S. Equilibria for discrete kinetic equations. Phys. Rev. E 1998, 58, R4053. [Google Scholar] [CrossRef]
- Prasianakis, N.I.; Karlin, I.V. Lattice Boltzmann method for simulation of compressible flows on standard lattices. Phys. Rev. E 2008, 78, 016704. [Google Scholar] [CrossRef]
- Dorschner, B.; Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Grid refinement for entropic lattice Boltzmann models. Phys. Rev. E 2016, 94, 053311. [Google Scholar] [CrossRef]








| n | |||||||
|---|---|---|---|---|---|---|---|
| 3 | 2 | ∞ | |||||
| 5 | 9 | ||||||
| 7 | |||||||
| 9 | |||||||
| 11 |
| DdQ | DdQ | DdQ | |
|---|---|---|---|
| Polynomial | 1 | ||
| Numerical | |||
| Polynomial | 1 | ||
| Numerical |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |
| 1.000 | 1.047 | 1.023 | 1.059 | 1.062 | 1.070 | 1.067 |
| Up | Analytical | |||||
| ELBM | ||||||
| Error | ||||||
| Down | Analytical | |||||
| ELBM | ||||||
| Error | ||||||
| Representative Velocity | Number of Velocities | ||
|---|---|---|---|
| 0 | 0 | 1 | |
| 1 | 1 | 6 | |
| 2 | 2 | 12 | |
| 3 | 3 | 8 | |
| 4 | 2 | 6 | |
| 5 | 3 | 24 | |
| 6 | 4 | 24 | |
| 8 | 4 | 12 | |
| 9 | 3 | 6 | |
| 9 | 5 | 24 | |
| 10 | 4 | 24 | |
| 11 | 5 | 24 | |
| 12 | 6 | 8 | |
| 13 | 5 | 24 | |
| 14 | 6 | 48 | |
| 17 | 7 | 24 | |
| 18 | 6 | 12 | |
| 19 | 7 | 24 | |
| 22 | 8 | 24 | |
| 27 | 9 | 8 |
| Representative Velocity | Number of Velocities | ||
|---|---|---|---|
| 0 | 0 | 1 | |
| 1 | 1 | 6 | |
| 3 | 3 | 8 | |
| 4 | 2 | 6 | |
| 8 | 4 | 12 | |
| 9 | 3 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frapolli, N.; Chikatamarla, S.; Karlin, I. Theory, Analysis, and Applications of the Entropic Lattice Boltzmann Model for Compressible Flows. Entropy 2020, 22, 370. https://doi.org/10.3390/e22030370
Frapolli N, Chikatamarla S, Karlin I. Theory, Analysis, and Applications of the Entropic Lattice Boltzmann Model for Compressible Flows. Entropy. 2020; 22(3):370. https://doi.org/10.3390/e22030370
Chicago/Turabian StyleFrapolli, Nicolò, Shyam Chikatamarla, and Ilya Karlin. 2020. "Theory, Analysis, and Applications of the Entropic Lattice Boltzmann Model for Compressible Flows" Entropy 22, no. 3: 370. https://doi.org/10.3390/e22030370
APA StyleFrapolli, N., Chikatamarla, S., & Karlin, I. (2020). Theory, Analysis, and Applications of the Entropic Lattice Boltzmann Model for Compressible Flows. Entropy, 22(3), 370. https://doi.org/10.3390/e22030370





