Entropy as a Measure of Attractiveness and Socioeconomic Complexity in Rio de Janeiro Metropolitan Area
Abstract
1. Introduction
2. Materials and Methods
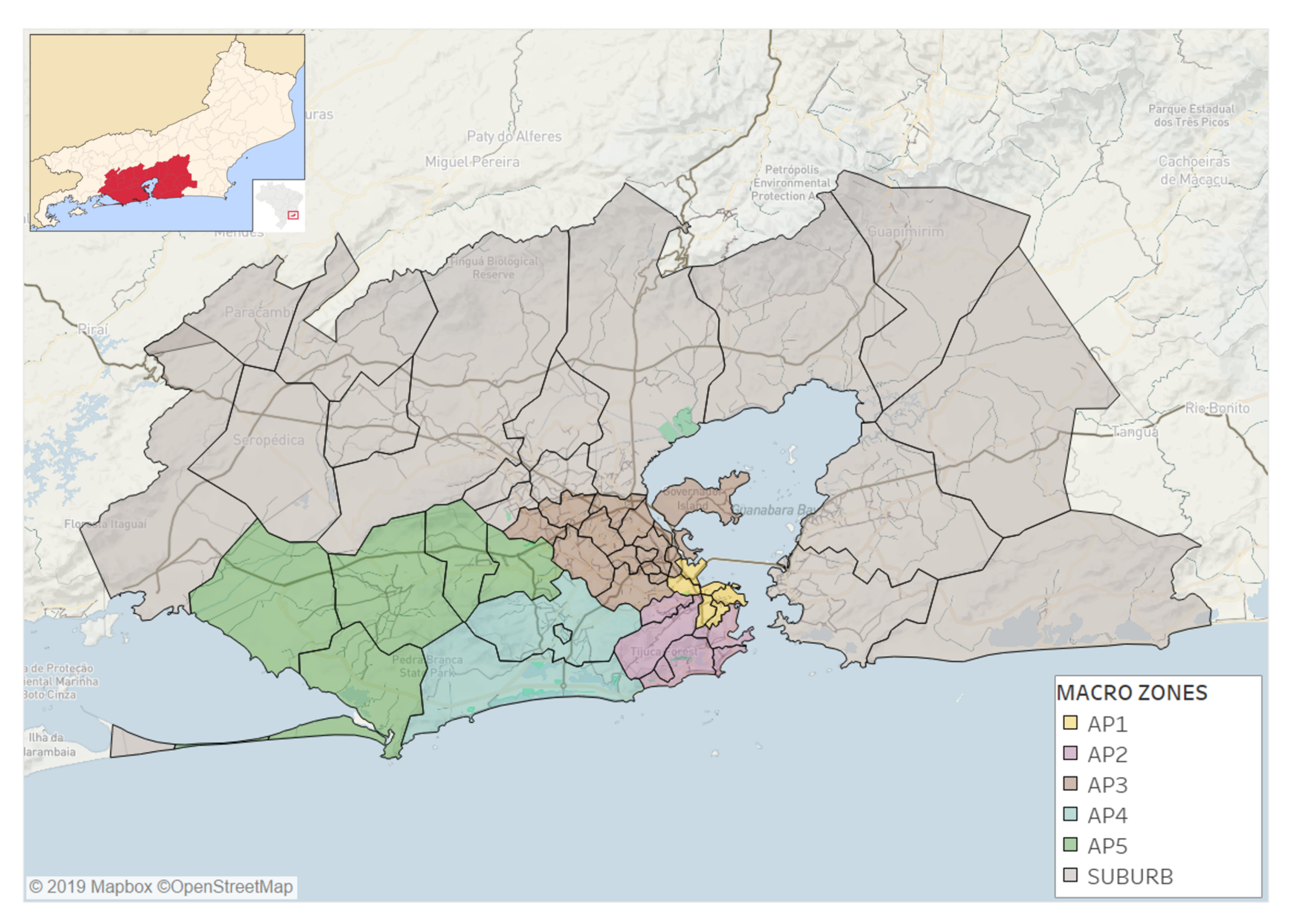
2.1. The Study Area and Dataset
2.2. Entropy as a Measure of Attractiveness
2.3. Entropy, Economic and Sociodemographic Indicators
3. Results
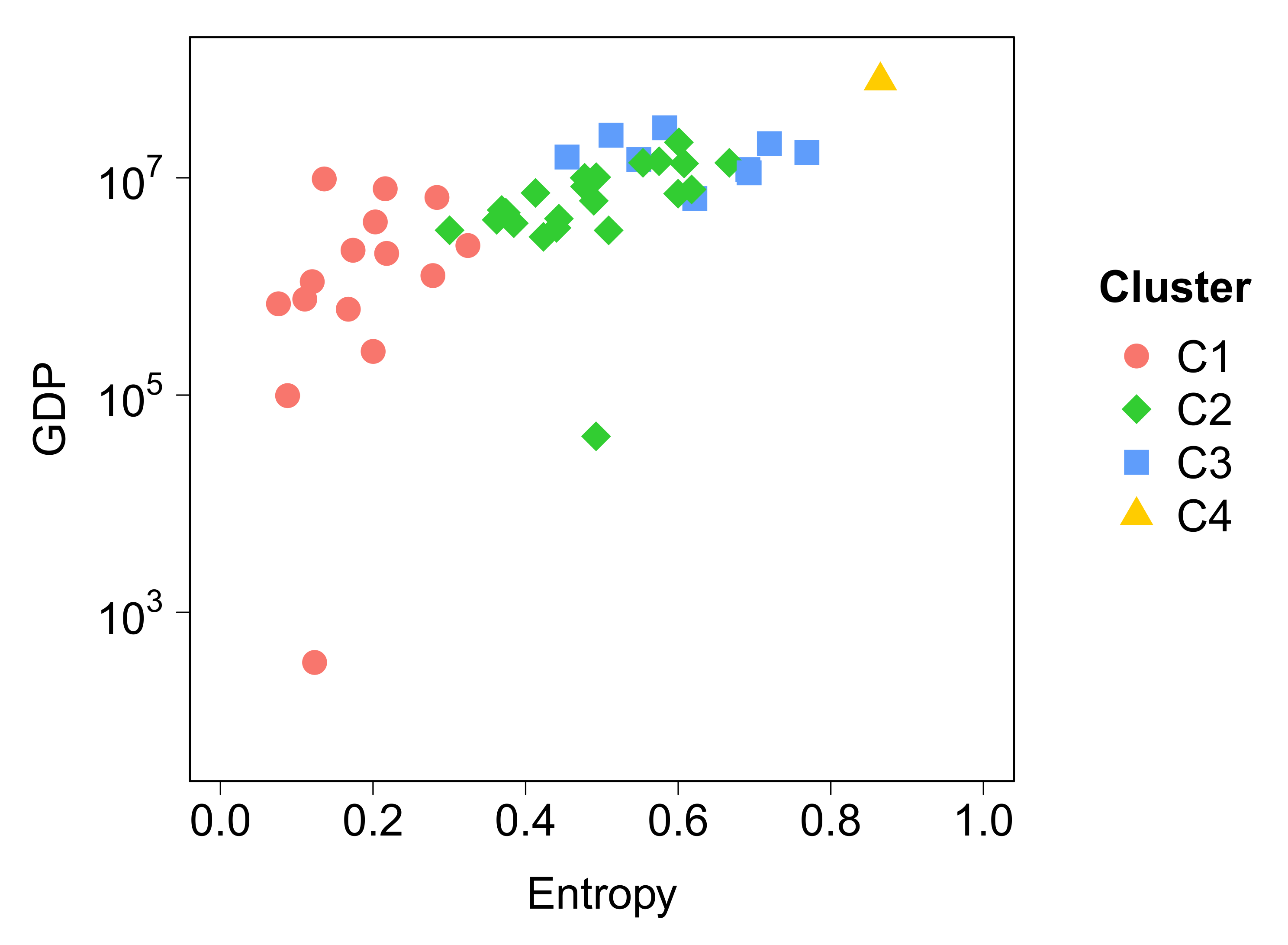
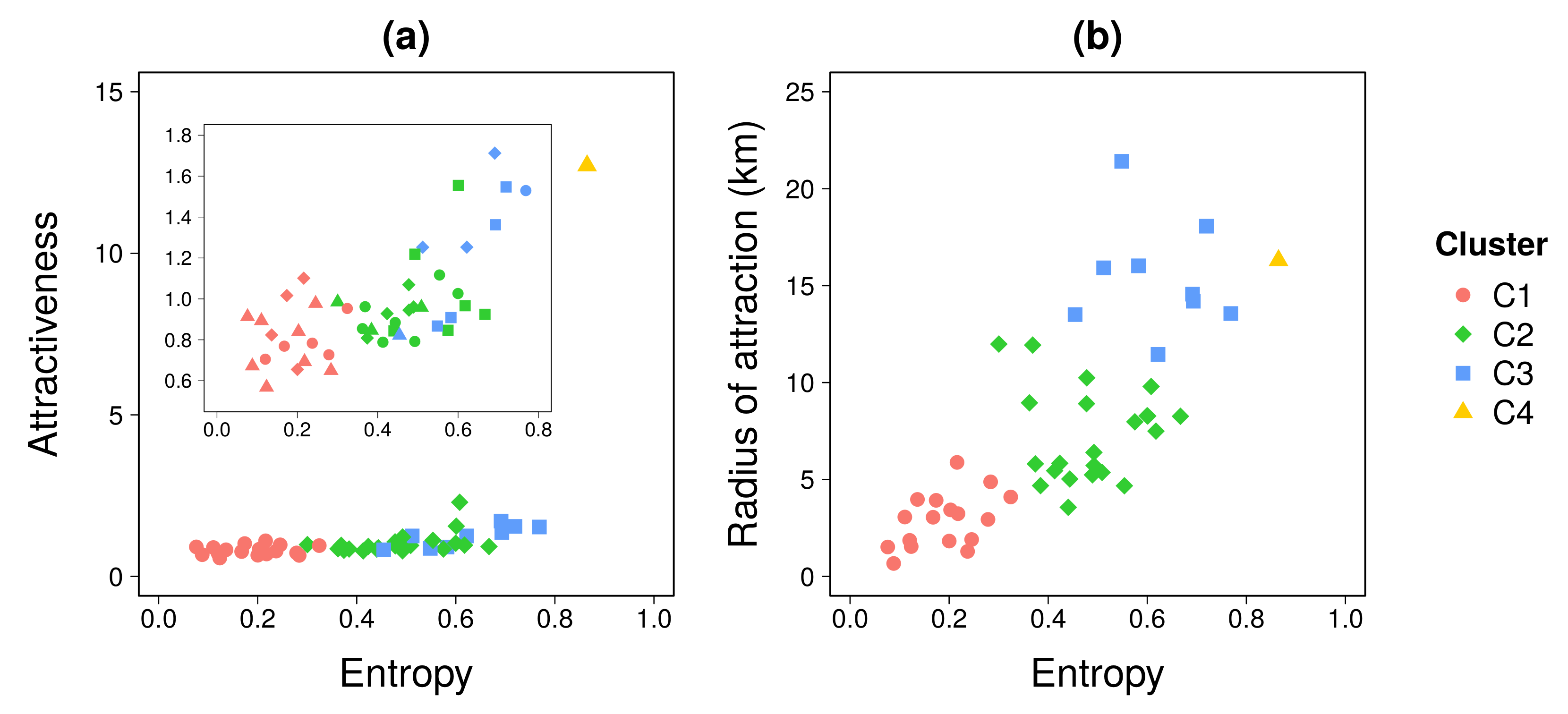
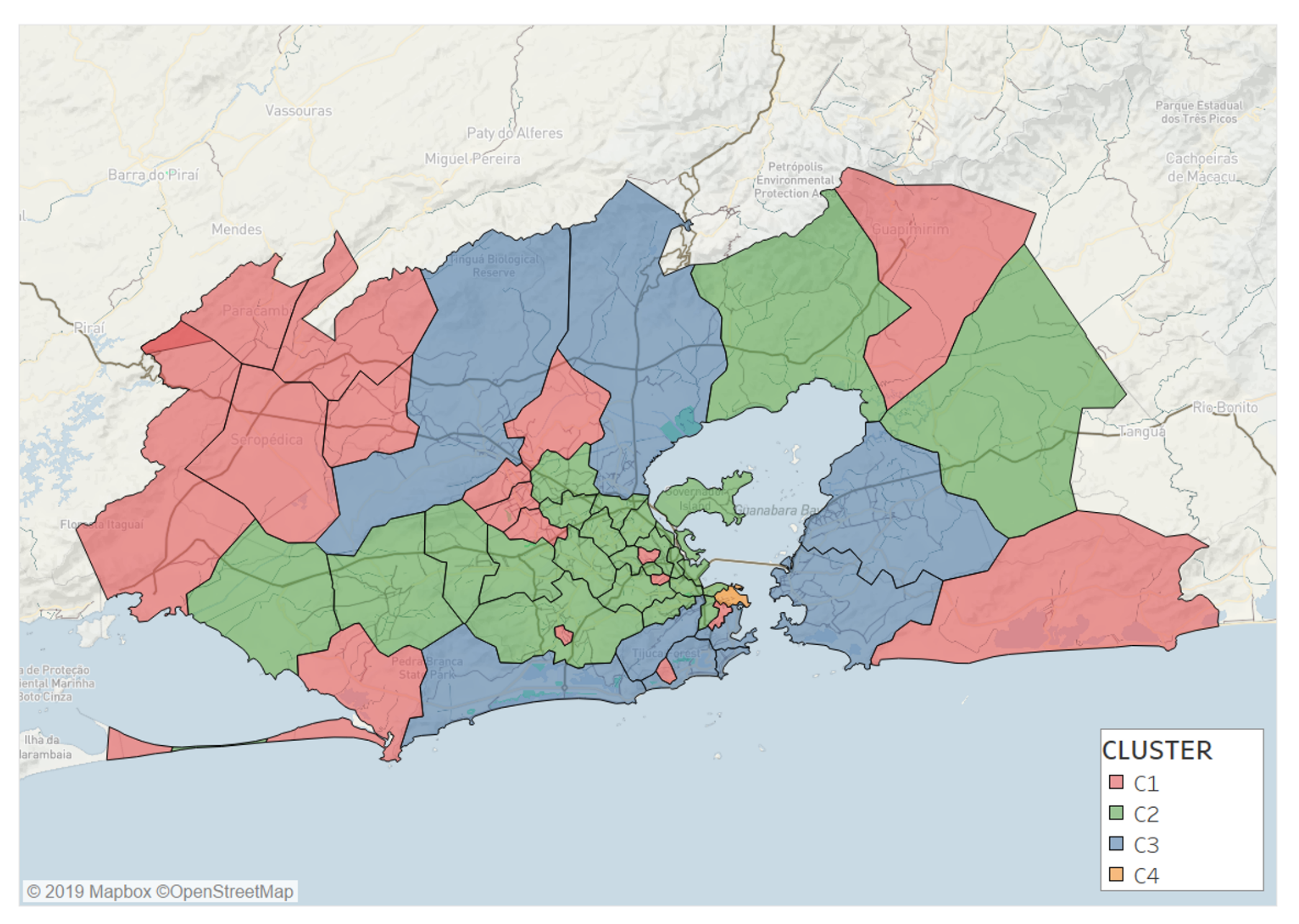
3.1. Classification of Locations According to Their Attractiveness
- C1 (red) represents a low-attractive cluster composed of 17 locations. It is characterized by a low entropy, an attractiveness ratio lower than one, and a low radius of attraction. Locations in C1 are far from the Rio city center or segregated areas inside the Capital.
- C2 (green) is a cluster of 22 locations, mostly located inside the city. This cluster is characterized by medium values of entropy of visitors and radius of attraction, while having an attractiveness ratio close to one.
- C3 (blue) is an attractive group with 8 locations mostly near to the sea inside Capital. This cluster shares high entropy values, attractiveness ratio between 1 and 2, and a large radius of attraction.
- C4 (orange) is composed of only one location that can be considered as an outlier due to its very high attractiveness. The remaining three clusters do not change if this outlier is removed before clustering. This location is the business center (Centro) of the city, and is a very attractive cluster with a very large entropy (), attractiveness ratio, and radius of attraction (). This location concentrates most of jobs and visitors from all the RJMA.
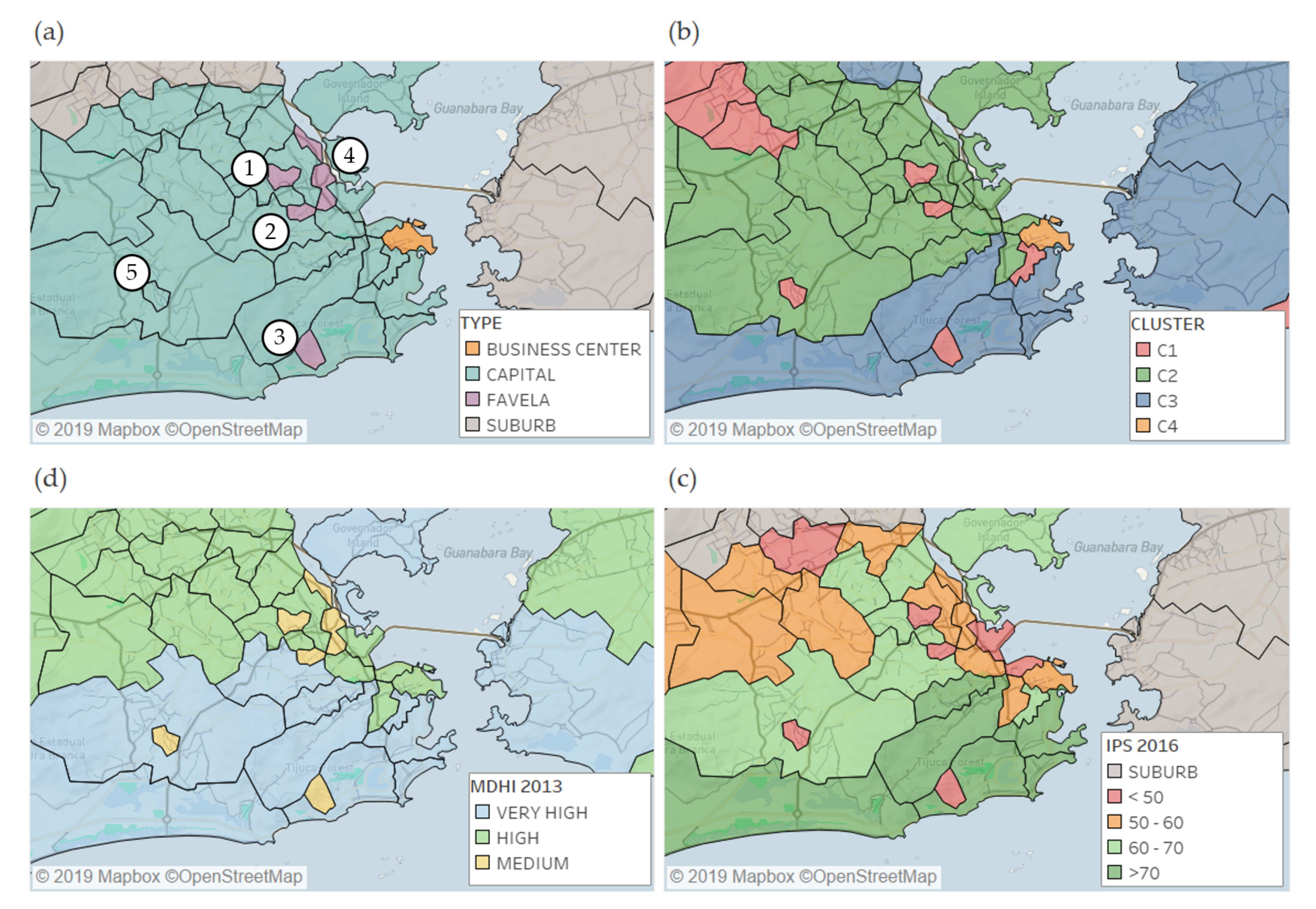
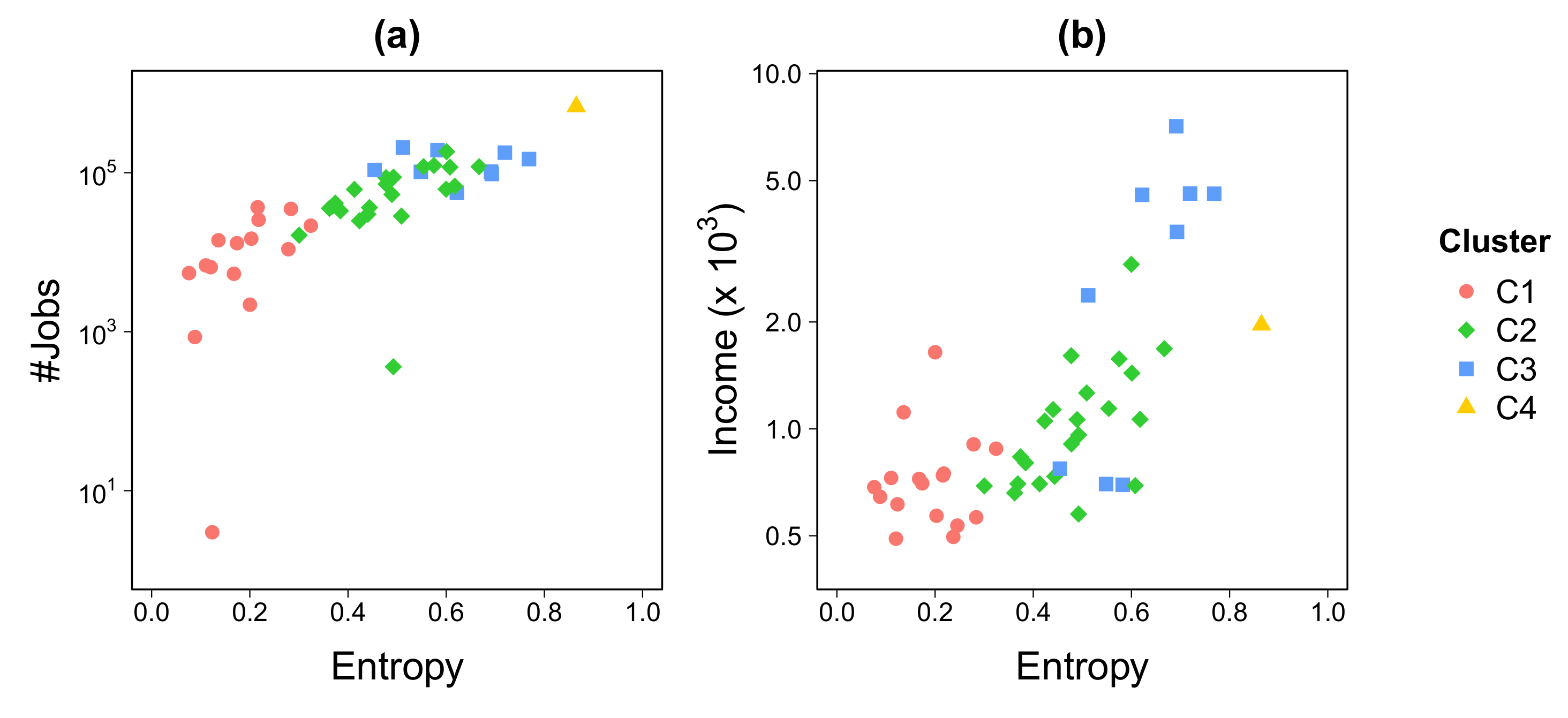
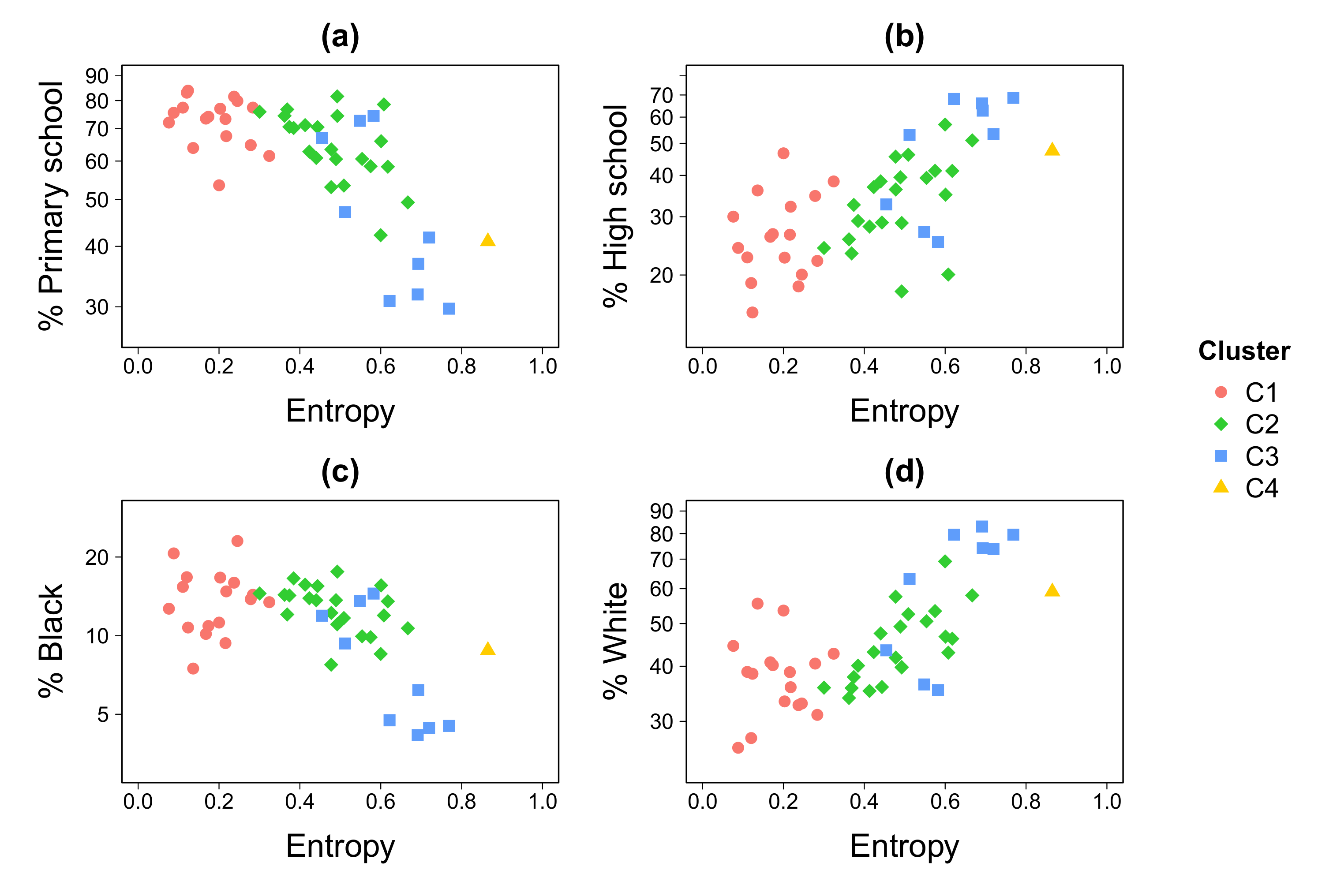
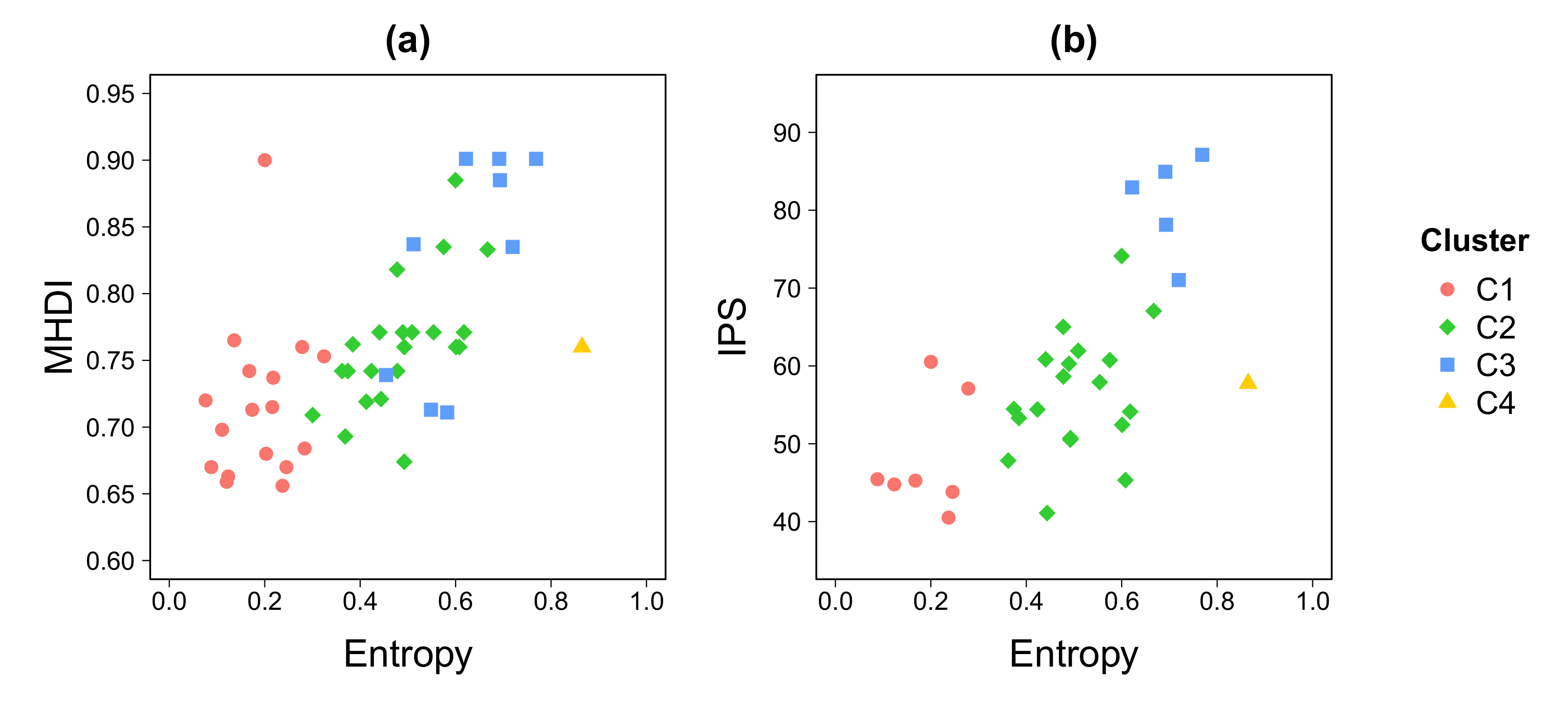
3.2. Economic Activity and Sociodemographic Factors
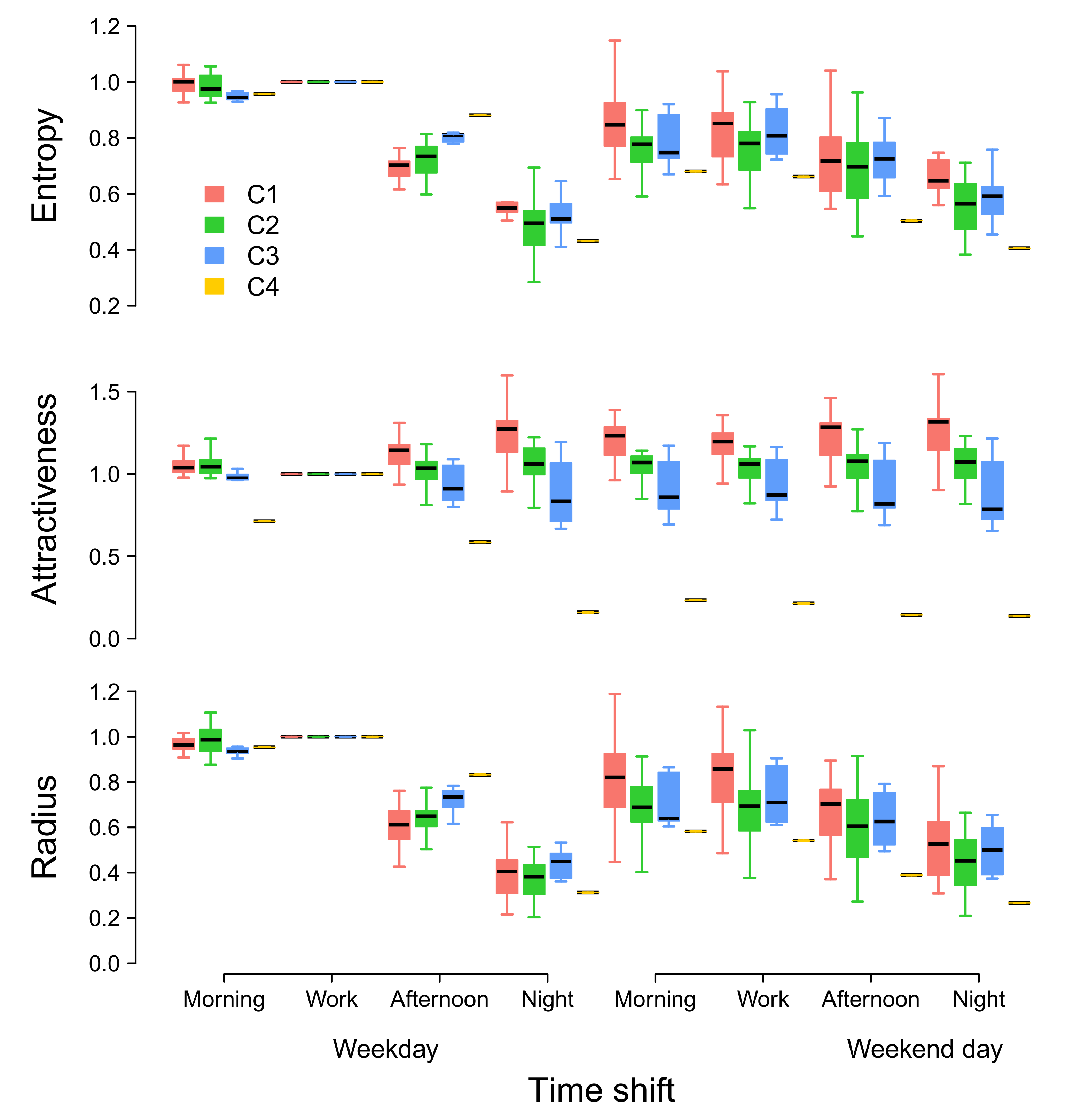
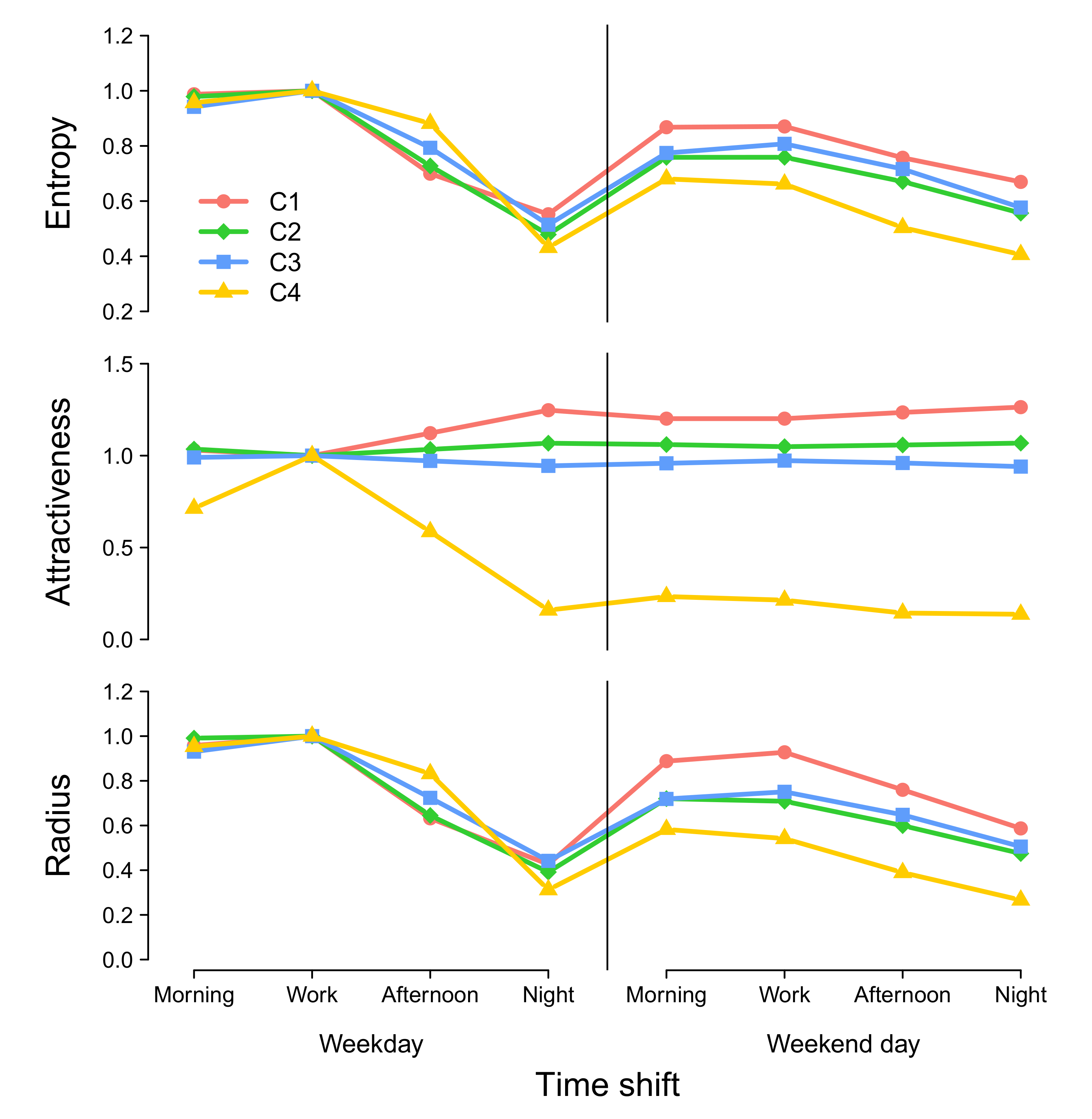
3.3. Temporal Evolution of the Attractiveness
4. Discussion
Author Contributions
Funding
Data availability
Conflicts of Interest
Appendix A. Data Preprocessing
Appendix A.1. Spatial Aggregation
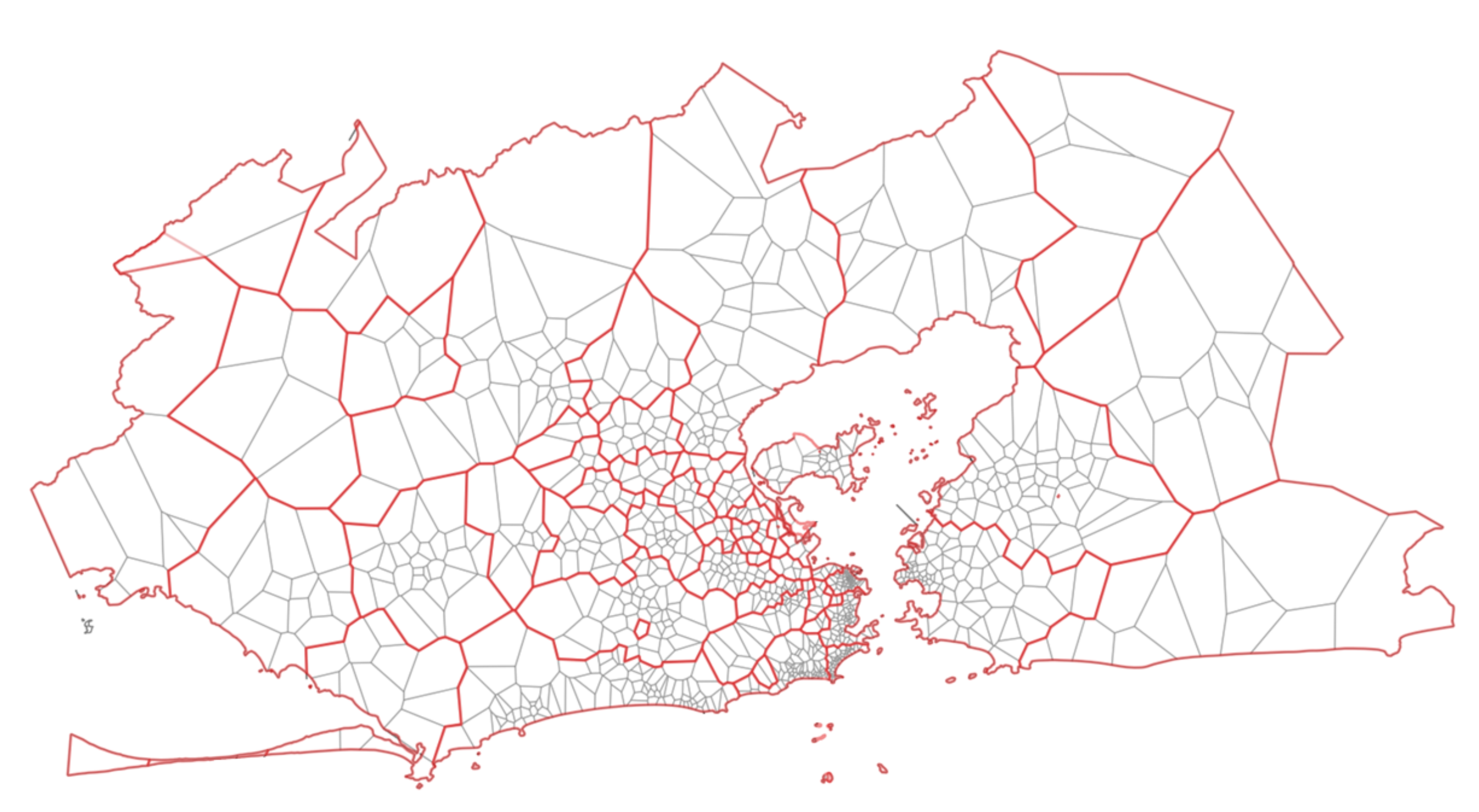
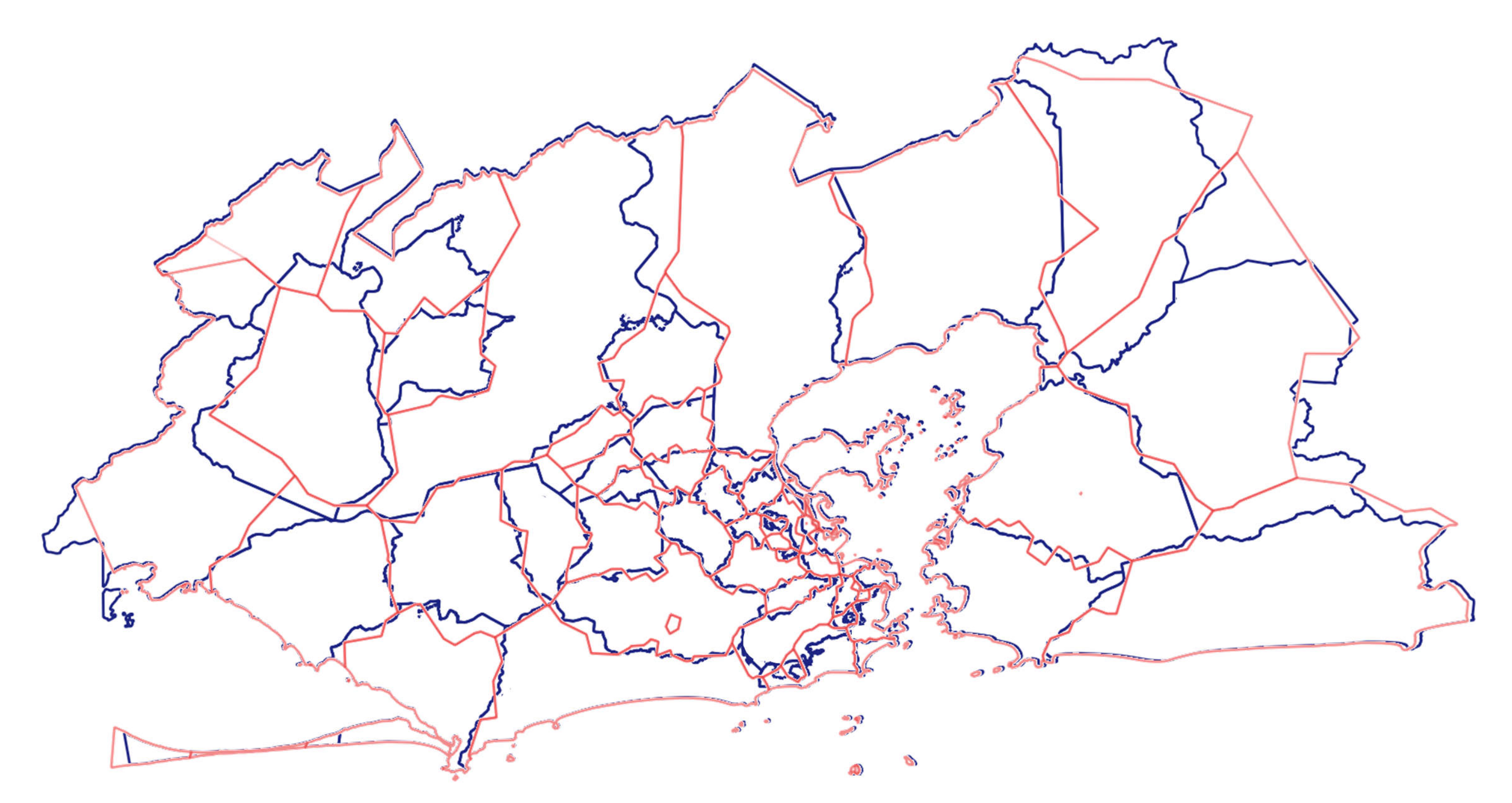
Appendix A.2. Temporal Aggregation
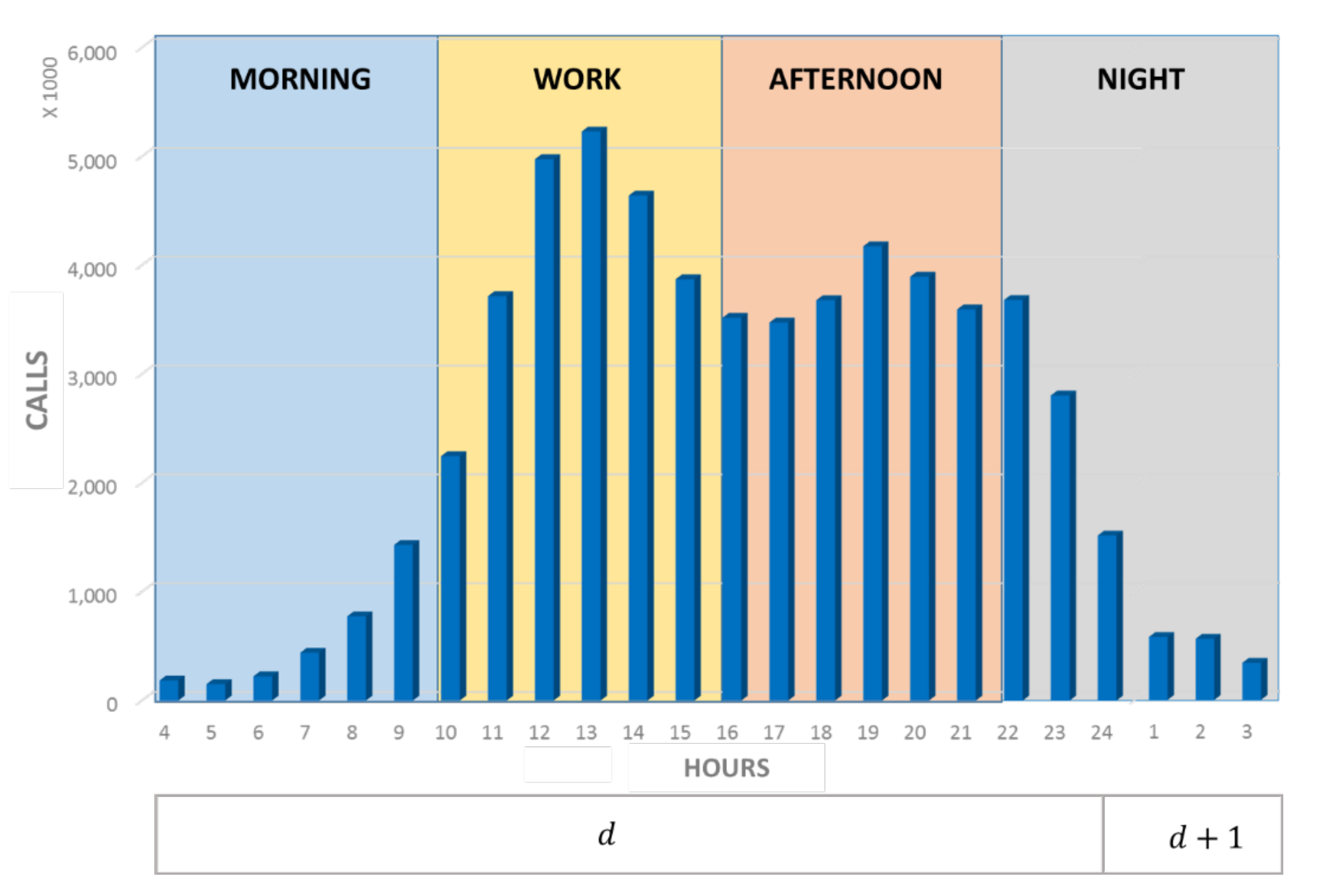
Appendix A.3. Identification of the User’s Place of Residence
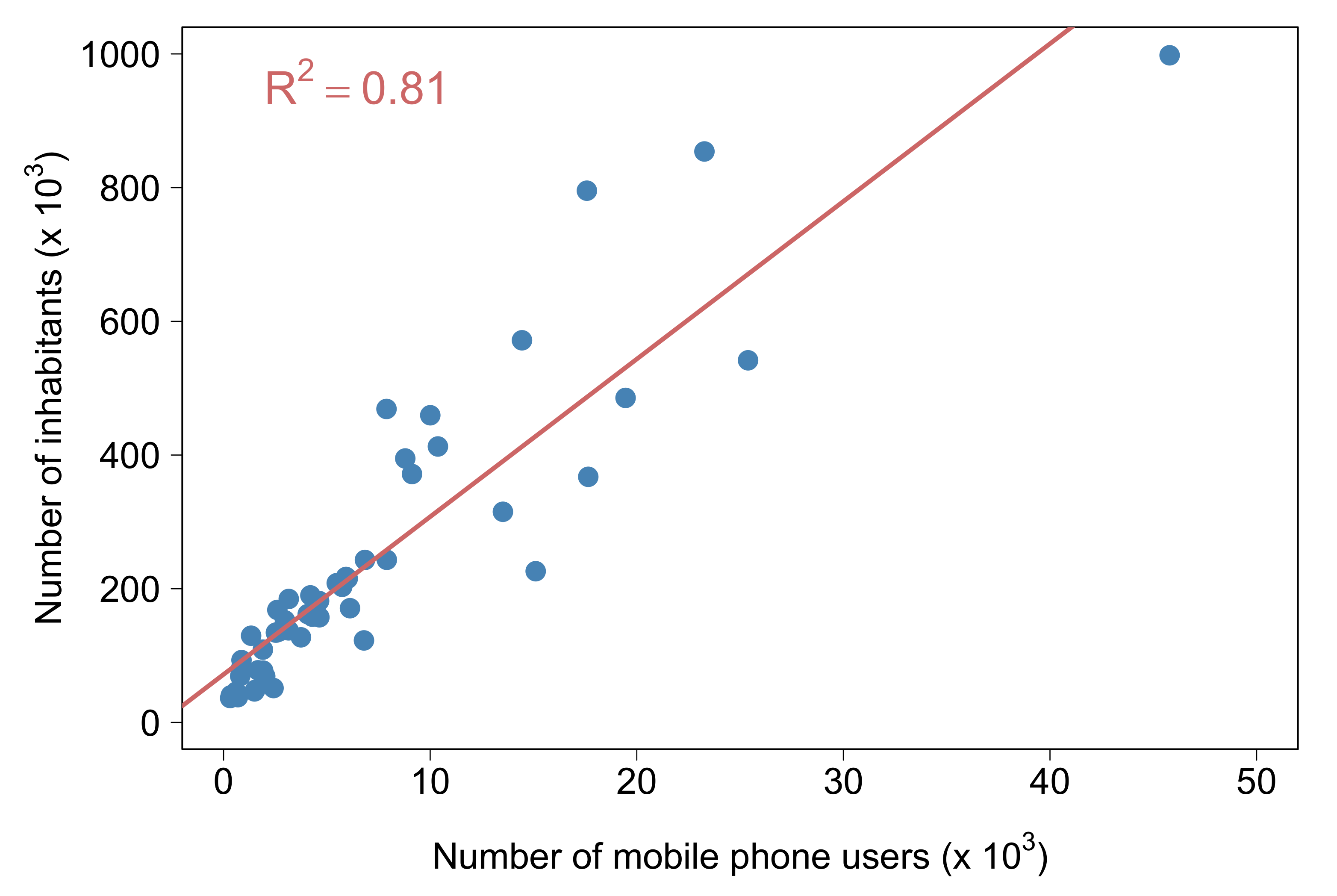
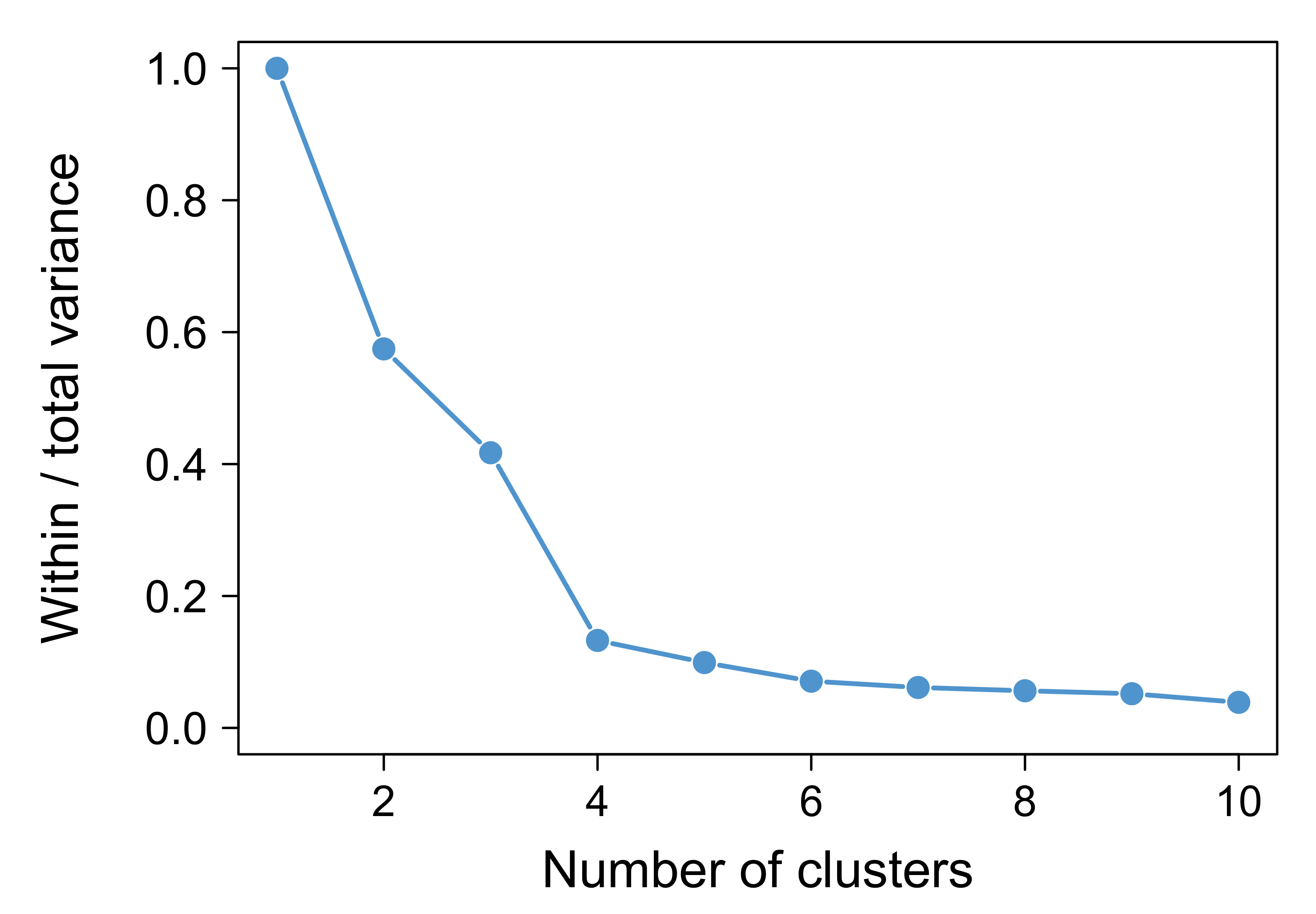
Appendix B. Clustering Analysis
Appendix C. Economic Activity
Appendix D. Temporal Evolution
References
- Alvaredo, F.; Chancel, L.; Piketty, T.; Saez, E.; Zucman, G. World Inequality Report 2018; Belknap Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ruiz-Tagle, J. A theory of socio-spatial integration: Problems, policies and concepts from a US perspective. Int. J. Urban Reg. Res. 2013, 37, 388–408. [Google Scholar] [CrossRef]
- Jargowsky, P.A. Poverty and Place: Ghettos, Barrios, and the American City; Russell Sage Foundation: New York, NY, USA, 1997. [Google Scholar]
- Massey, D.S. American apartheid: Segregation and the making of the underclass. Am. J. Sociol. 1990, 96, 329–357. [Google Scholar] [CrossRef]
- Wilson, W.J. The Truly Disadvantaged: The Inner City, the Underclass, and Public Policy; University of Chicago Press: Chicago, IL, USA, 2012. [Google Scholar]
- Cutler, D.; Glaeser, E. Are ghettos good or bad? Q. J. Econ. 1997, 112, 827–872. [Google Scholar] [CrossRef]
- Garreton, M.; Sánchez, R. Identifying an optimal analysis level in multiscalar regionalization: A study case of social distress in greater Santiago. Comput. Environ. Urban Syst. 2016, 56, 14–24. [Google Scholar] [CrossRef]
- Krieger, N. Embodying inequality: A review of concepts, measures, and methods for studying health consequences of discrimination. Int. J. Health Serv. 1999, 29, 295–352. [Google Scholar] [CrossRef]
- Massey, D.S.; Denton, N.A. The dimensions of residential segregation. Soc. Forces 1988, 67, 281–315. [Google Scholar] [CrossRef]
- Bolt, G.; Burgers, J.; Van Kempen, R. On the social significance of spatial location; spatial segregation and social inclusion. Neth. J. Hous. Built Environ. 1998, 13, 83. [Google Scholar] [CrossRef]
- Farber, S.; O’Kelly, M.; Miller, H.; Neutens, T. Measuring segregation using patterns of daily travel behavior: A social interaction based model of exposure. J. Transp. Geogr. 2015, 49, 26–38. [Google Scholar] [CrossRef]
- Farber, S.; Neutens, T.; Miller, H.; Li, X. The social interaction potential of metropolitan regions: A time-geographic measurement approach using joint accessibility. Ann. Assoc. Am. Geogr. 2013, 103, 483–504. [Google Scholar] [CrossRef]
- Forrest, R.; Kearns, A. Social cohesion, social capital and the neighbourhood. Urban Stud. 2001, 38, 2125–2143. [Google Scholar] [CrossRef]
- Louf, R.; Barthelemy, M. Patterns of residential segregation. PLoS ONE 2016, 11, e0157476. [Google Scholar] [CrossRef] [PubMed]
- Netto, V.; Brigatti, E.; Meirelles, J.; Ribeiro, F.; Pace, B.; Cacholas, C.; Sanches, P. Cities, from Information to Interaction. Entropy 2018, 20, 834. [Google Scholar] [CrossRef]
- Caldeira, T. Fortified enclaves: The new urban segregation. In The Urban Sociology Reader; Routledge: London, UK, 2012; pp. 419–427. [Google Scholar]
- Batty, M. Big data, smart cities and city planning. Dialogues Hum. Geogr. 2013, 3, 274–279. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.; Samaniego, H.; Youn, H. Professional diversity and the productivity of cities. Sci. Rep. 2014, 4, 5393. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Decuyper, A.; Krings, G. A survey of results on mobile phone datasets analysis. EPJ Data Sci. 2015, 4, 10. [Google Scholar] [CrossRef]
- Louail, T.; Lenormand, M.; Arias, J.M.; Ramasco, J.J. Crowdsourcing the Robin Hood effect in cities. Appl. Netw. Sci. 2017, 2, 11. [Google Scholar] [CrossRef]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Phys. Rep. 2018, 734, 1–74. [Google Scholar] [CrossRef]
- Onnela, J.P.; Saramäki, J.; Hyvönen, J.; Szabó, G.; Lazer, D.; Kaski, K.; Kertész, J.; Barabási, A.L. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. 2007, 104, 7332–7336. [Google Scholar] [CrossRef]
- Panigutti, C.; Tizzoni, M.; Bajardi, P.; Smoreda, Z.; Colizza, V. Assessing the use of mobile phone data to describe recurrent mobility patterns in spatial epidemic models. R. Soc. Open Sci. 2017, 4, 160950. [Google Scholar] [CrossRef]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779. [Google Scholar] [CrossRef]
- Lenormand, M.; Picornell, M.; Cantú-Ros, O.G.; Louail, T.; Herranz, R.; Barthelemy, M.; Frías-Martínez, E.; San Miguel, M.; Ramasco, J.J. Comparing and modelling land use organization in cities. R. Soc. Open Sci. 2015, 2, 150449. [Google Scholar] [CrossRef] [PubMed]
- Beiró, M.G.; Bravo, L.; Caro, D.; Cattuto, C.; Ferres, L.; Graells-Garrido, E. Shopping mall attraction and social mixing at a city scale. EPJ Data Sci. 2018, 7, 28. [Google Scholar] [CrossRef]
- Louail, T.; Lenormand, M.; Cantú-Ros, O.G.; Picornell, M.; Herranz, R.; Frias-Martinez, E.; Ramasco, J.J.; Barthelemy, M. From mobile phone data to the spatial structure of cities. Sci. Rep. 2014, 4, 5276. [Google Scholar] [CrossRef] [PubMed]
- Sotomayor-Gómez, B.; Samaniego, H. City limits in the age of smartphones and urban scaling. Comput. Environ. Urban Syst. 2020, 79, 101423. [Google Scholar] [CrossRef]
- Lamanna, F.; Lenormand, M.; Salas-Olmedo, M.H.; Romanillos, G.; Gonçalves, B.; Ramasco, J.J. Immigrant community integration in world cities. PLoS ONE 2018, 13, e0191612. [Google Scholar] [CrossRef]
- Dannemann, T.; Sotomayor-Gómez, B.; Samaniego, H. The time geography of segregation during working hours. R. Soc. Open Sci. 2018, 5, 180749. [Google Scholar] [CrossRef]
- Jiang, S.; Ferreira, J.; Gonzalez, M.C. Activity-based human mobility patterns inferred from mobile phone data: A case study of Singapore. IEEE Trans. Big Data 2017, 3, 208–219. [Google Scholar] [CrossRef]
- Motte, B.; Aguilera, A.; Bonin, O.; Nassi, C.D. Commuting patterns in the metropolitan region of Rio de Janeiro. What differences between formal and informal jobs? J. Transp. Geogr. 2016, 51, 59–69. [Google Scholar] [CrossRef]
- Rubim, B.; Leitão, S. O plano de mobilidade urbana e o futuro das cidades. Estudos avançados 2013, 27, 55–66. [Google Scholar] [CrossRef]
- Toole, J.L.; Colak, S.; Sturt, B.; Alexander, L.P.; Evsukoff, A.; González, M.C. The path most traveled: Travel demand estimation using big data resources. Transp. Res. Part C: Emerg. Technol. 2015, 58, 162–177. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Hägerstrand, T. What about people in regional science? Pap. Reg. Sci. 1970, 24, 6–21. [Google Scholar] [CrossRef]
- Schönfelder, S.; Axhausen, K.W. Activity spaces: Measures of social exclusion? Transp. Policy 2003, 10, 273–286. [Google Scholar]
- Phithakkitnukoon, S.; Smoreda, Z.; Olivier, P. Socio-geography of human mobility: A study using longitudinal mobile phone data. PLoS ONE 2012, 7, e39253. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Hsu, W.J.; Lee, Z.Q. Predictability of individuals’ mobility with high-resolution positioning data. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; pp. 381–390. [Google Scholar]
- Pappalardo, L.; Vanhoof, M.; Gabrielli, L.; Smoreda, Z.; Pedreschi, D.; Giannotti, F. An analytical framework to nowcast well-being using mobile phone data. Int. J. Data Sci. Anal. 2016, 2, 75–92. [Google Scholar] [CrossRef]
- Vanhoof, M.; Schoors, W.; Rompaey, A.V.; Ploetz, T.; Smoreda, Z. Comparing regional patterns of individual movement using corrected mobility entropy. J. Urban Technol. 2018, 25, 27–61. [Google Scholar] [CrossRef]
- Cottineau, C.; Vanhoof, M. Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities. ISPRS Int. J. -Geo-Inf. 2019, 8, 19. [Google Scholar] [CrossRef]
- Pappalardo, L.; Pedreschi, D.; Smoreda, Z.; Giannotti, F. Using big data to study the link between human mobility and socio-economic development. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 871–878. [Google Scholar]
- Lenormand, M.; Luque, S.; Langemeyer, J.; Tenerelli, P.; Zulian, G.; Aalders, I.; Chivulescu, S.; Clemente, P.; Dick, J.; van Dijk, J.; et al. Multiscale socio-ecological networks in the age of information. PLoS ONE 2018, 13, 1–16. [Google Scholar] [CrossRef]
- Wilson, A.G. The use of entropy maximising models, in the theory of trip distribution, mode split and route split. J. Transp. Econ. Policy 1969, 3, 108–126. [Google Scholar]
- Distance Matrix API. Available online: https://developers.google.com/maps/documentation/distance-matrix/ (accessed on 14 March 2020).
- Favelas na cidade do Rio de Janeiro: O quadro populacional com base no Censo 2010. (In Portuguese). Available online: http://bit.ly/2O9SEdA.
- Subnormal Agglomerates. Available online: http://bit.ly/337gQlb (accessed on 14 March 2020).
- Atlas Brasil. Available online: www.atlasbrasil.org.br (accessed on 14 March 2020).
- Data. Available online: www.data.rio (accessed on 14 March 2020).
- Duranton, G.; Puga, D. Micro-foundations of urban agglomeration economies. In Handbook of Regional and Urban Economics; Elsevier: Amsterdam, The Netherlands, 2004; Volume 4, pp. 2063–2117. [Google Scholar]
- Xu, Y.; Belyi, A.; Bojic, I.; Ratti, C. Human mobility and socioeconomic status: Analysis of Singapore and Boston. Comput. Environ. Urban Syst. 2018, 72, 51–67. [Google Scholar] [CrossRef]
- Henderson, J.V. Urban Development: Theory, Fact, and Illusion; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Sabatini, F. The Social Spatial Segregation in the Cities of Latin America; Technical report; Inter-American Development Bank: Washington, DC, USA, 2006. [Google Scholar]
- Lotero, L.; Hurtado, R.G.; Floría, L.M.; Gómez-Gardeñes, J. Rich do not rise early: Spatio-temporal patterns in the mobility networks of different socio-economic classes. R. Soc. Open Sci. 2016, 3, 150654. [Google Scholar] [CrossRef] [PubMed]
- Flores, C.A. Residential segregation and the geography of opportunites: A spatial analysis of heterogeneity and spillovers in education. Ph.D. Thesis, LBJ School of Public Affairs, University of Texas, Austin, TX, USA, 2008. [Google Scholar]
- Li, H.; Campbell, H.; Fernandez, S. Residential Segregation, Spatial Mismatch and Economic Growth across US Metropolitan Areas. Urban Stud. 2013, 50, 2642–2660. [Google Scholar] [CrossRef]
- Karasch, M.C. Slave life in Rio de Janeiro, 1808-1850; Princeton University Press: Princeton, NJ, USA, 1987; p. 448. [Google Scholar]
- Eagle, N.; Macy, M.; Claxton, R. Network diversity and economic development. Science 2010, 328, 1029–1031. [Google Scholar] [CrossRef]
- Blumenstock, J.; Cadamuro, G.; On, R. Predicting poverty and wealth from mobile phone metadata. Science 2015, 350, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, M.; Louail, T.; Barthelemy, M.; Ramasco, J.J. Is spatial information in ICT data reliable? In Proceedings of the 2016 Spatial Accuracy Conference, Montpellier, France, 5–8 July 2016. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenormand, M.; Samaniego, H.; Chaves, J.C.; da Fonseca Vieira, V.; da Silva, M.A.H.B.; Evsukoff, A.G. Entropy as a Measure of Attractiveness and Socioeconomic Complexity in Rio de Janeiro Metropolitan Area. Entropy 2020, 22, 368. https://doi.org/10.3390/e22030368
Lenormand M, Samaniego H, Chaves JC, da Fonseca Vieira V, da Silva MAHB, Evsukoff AG. Entropy as a Measure of Attractiveness and Socioeconomic Complexity in Rio de Janeiro Metropolitan Area. Entropy. 2020; 22(3):368. https://doi.org/10.3390/e22030368
Chicago/Turabian StyleLenormand, Maxime, Horacio Samaniego, Júlio César Chaves, Vinícius da Fonseca Vieira, Moacyr Alvim Horta Barbosa da Silva, and Alexandre Gonçalves Evsukoff. 2020. "Entropy as a Measure of Attractiveness and Socioeconomic Complexity in Rio de Janeiro Metropolitan Area" Entropy 22, no. 3: 368. https://doi.org/10.3390/e22030368
APA StyleLenormand, M., Samaniego, H., Chaves, J. C., da Fonseca Vieira, V., da Silva, M. A. H. B., & Evsukoff, A. G. (2020). Entropy as a Measure of Attractiveness and Socioeconomic Complexity in Rio de Janeiro Metropolitan Area. Entropy, 22(3), 368. https://doi.org/10.3390/e22030368




