1. Introduction
A knowledge of the way of infiltration of water into the ground is crucially important for predicting disasters, such as river floods and landslides, when heavy rain attacks. A classical mathematical model for describing the fluid motion in unsaturated zone in a porous medium is the Richards equation, a nonlinear degenerate advection-diffusion equation. Two main research directions arose recently for the Richards equation. One is to find exact solutions by finding a specific form of coefficient functions so as to make the equation completely integrable. An exact solution helps to clearly capture the physical mechanism of the phenomena and to pursue controllability [
1,
2,
3]. The other research direction is to seek an approximate solution by numerical methods, for coefficient functions to match with a practical situation. Finite elements, finite difference or finite volumes methods are carried out in [
4,
5] and the reference therein. The above schemes commonly used fully implicit schemes based on a backward Euler format. Adaptive time stepping is studied in [
6,
7]. In these studies, some conservative schemes are devised and numerical tests show that they have good stability and some order accuracy, but no theoretical proof is given.
So far, we have only known one paper to prove the stability for the mixed finite element discretization of the Richards equation in [
8,
9]. In [
8], they introduced an implicit mixed element scheme and applied the Kirchhoff transformation to deal with the degeneracy of the Richards equation. The Kirchhoff transformation could be used in the continuous inner product, but we have to take the discrete inner product in the analysis for the difference scheme, so we take a new way which is by adding a perturbation to the coefficient function of parabolic term to overcome the degeneracy.
In [
8], the scheme they used is implicit, the stability condition is certainly superior to the explicit scheme. So they do not pay attention to the stability condition in the analysis for the implicit scheme. However, the explicit numerical schemes always are stable only in rigorous restriction for mesh ratio. To improve the stability condition, we introduced an extra term in the difference scheme to relax the time step restriction for improving the stability condition. Also, the theoretical analysis for the implicit numerical schemes and the explicit difference scheme is completely different.
As we know, these early attempts are all implicit schemes based on backward Euler difference scheme and the central difference scheme, although in certain case, the implicit scheme may have to be used to avoid instability. However a strongly nonlinear algebraic system must be solved at each time level, even though these iterative methods [
10,
11] are used, it still needs huge calculation. Explicit scheme is a good choice to improve the computation efficiency, but the classical explicit scheme cannot be used for the Richards equation due to its degeneracy and the severe time step length restriction.
The main purpose of this work is to provide an efficient explicit numerical scheme for the Richards equation and prove the stability. The key objectives of this work are threefold: First, we add a perturbation to the coefficient function of parabolic term to overcome the degeneracy. Secondly, we introduce a stabilization term with constant coefficient in the difference scheme to relax the stability restriction on the time step. Please note that a similar technique has been used in the simulation of the Cahn–Hilliard equation [
12] and the MBE models [
13]. The Cahn–Hilliard equation and the MBE models are fourth-order parabolic partial differential equations, so they introduced a second-order stabilization term in the Fourier spectral scheme and finite element scheme respectively. The Richards equation is a second-order equation, so the stabilization term which is added in the explicit difference scheme is completely different. Finally, we prove the stability by induction method and perform some numerical experiments.
The organization of the paper as follows. In
Section 2, an explicit difference scheme is given for the Richards equation. In
Section 3, we prove the stability of such scheme. In
Section 4, some numerical experiments are given. We conclude the paper in
Section 5.
2. Richards Equation and the Explicit Difference Scheme
The Richards equation could be written in three equivalent forms, with either pressure head or moisture content as the dependent variable. We recall that the hydraulic head is partitioned into the pressure head and the gravity head z, the vertical coordinate increasing upwards, with the pressure p normalized by the gravity force. Here is the mass density of the fluid and g is the gravity acceleration. The constitutive relationship between and allows the conversion from one to another. The three forms can be identified as h-based, -based, and mixed:
where the real-valued functions , , and respectively denote the specific moisture capacity function , the unsaturated hydraulic conductivity and the unsaturated diffusivity . The coefficient describes the ease with which water can move through pore spaces, and depends on the intrinsic permeability of the material, degree of saturation, and the density and the viscosity of the fluid. The porous medium is assumed to be isotropic.
We consider the
h-based form with the datum reported by Haverkamp et al. [
14,
15] which is used to solve an example of infiltration into soil column.
where
represents the moisture content.
and
are initial and saturated moisture content respectively. Moreover,
, simple calculations show that
For the given
and
, we consider the following data [
16].
These data provide some real numbers from an example of infiltration into soil column. From the data, we can verify that there are upper bounds for and easily, i.e., for . This is to be used in the stability proof.
Let be the uniform step length, where M is a positive integer. We divide the domain of time T with N segments, let be the uniform time length. Then for a function , denote , where , and , . Let be the mesh ratios.
Define the following difference operators
Now, we introduce the discrete
inner product as
and the coresponding discrete
norm is
. Moreover, the discrete
seminorm
and the discrete maximum norm
are defined as
A classical first-order explicit difference scheme is
For the degeneracy of the Richards equation, a special trick to handle the nonlinear parabolic term is devised. We add a positive constant
to
in (
7) (in fact,
can be seen as a small positive bound of
). Then modified first-order explicit scheme is of the form
With the Richards equation featured by a convection dominated diffusion problems, numerical experiments show that the stability of (
8) is restricted by the mesh ratio, meaning that the scheme is stable only in very tiny time step, as is expected. So we add extra diffusion terms in (
8) to improve the stability condition so that relax the restriction of the time step.
where
is a positive constant to be determined so as to improve the stability condition.
Remark 1. In [17], for the one-dimensional Richards equation, we also established a linearized semi-implicit finite difference scheme and analyzed the stability. Compared to the scheme of [17], the explicit difference scheme (9) is to avoid solving a linear algebraic equations at every time step. If we divide the domain of time with N segments, the explicit difference scheme could reduce the computational cost to of that. So the explicit difference scheme (9) is more concise and the speed of its numerical simulation is faster. 4. Numerical Experiments
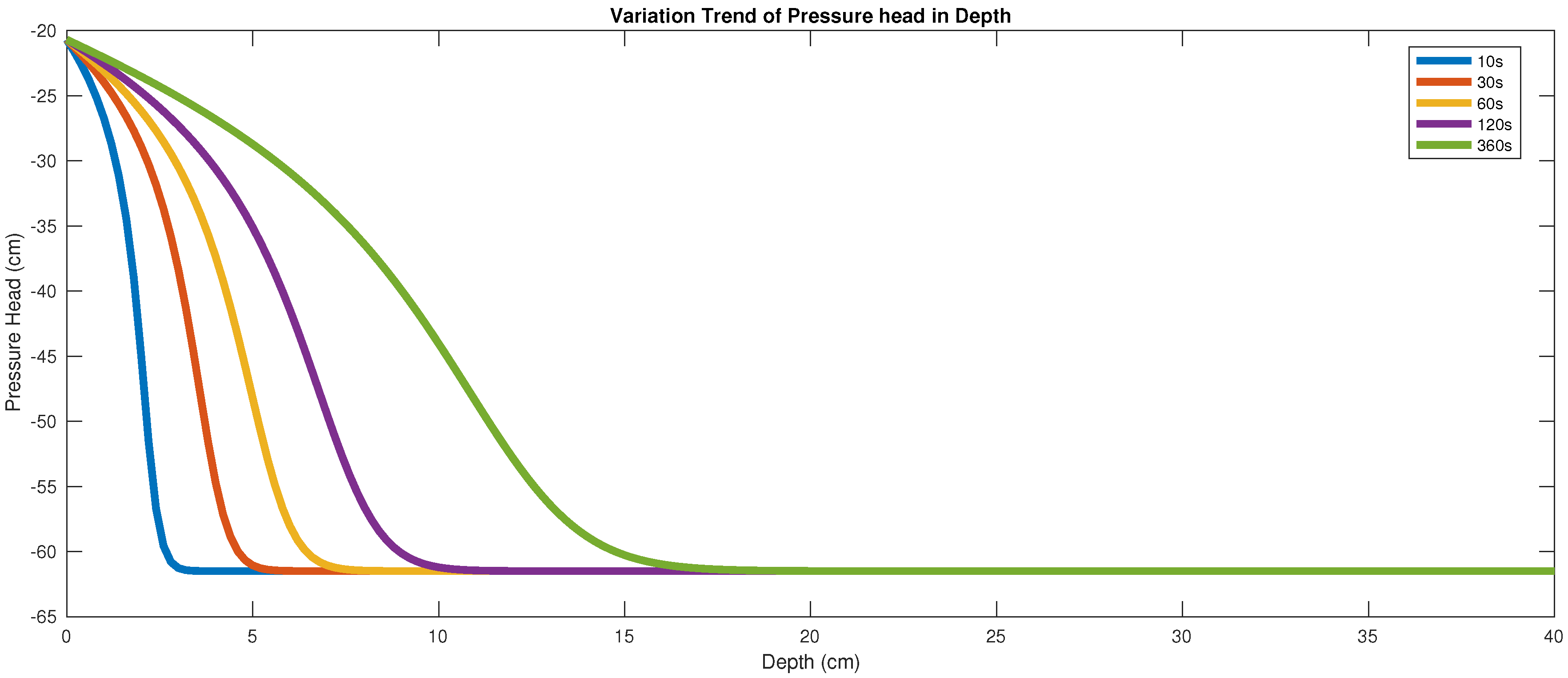
In this section, we illustrate the numerical stability by a numerical experiment of the infiltration process based on a generalized
h-based Richards equation. Since it is difficult to obtain the exact solution of this model, to verify the theoretical results, we take the following non-homogeneous model,
where the boundary conditions remain unchanged as (
6). If we suppose an exact solution
, a simple calculation shows that
By using the scheme (
9), we show, in
Figure 1, the variation trend of the pressure head with depth for the time interval from 10 s to 360 s, with the choice of
and
.
In [
14], the authors used an implicit numerical scheme, and took a large time step, for instance, 10 s, 30 s and 120 s, to save the computational workload. In this paper, we take the time step as small as
s. Correspondingly the space steps that they used are much larger than ours. The different scheme and the large grid gap may bring some but tolerable discrepancy.
We take
s and
to test the stability of the scheme with different time steps and different choices of
. The results are listed in
Table 1. It is evident that the improvement in the stability by use of the extra terms is significant. Moreover, in
Table 2, we set
and
s, and confirm that the expected order of convergence is obtained.
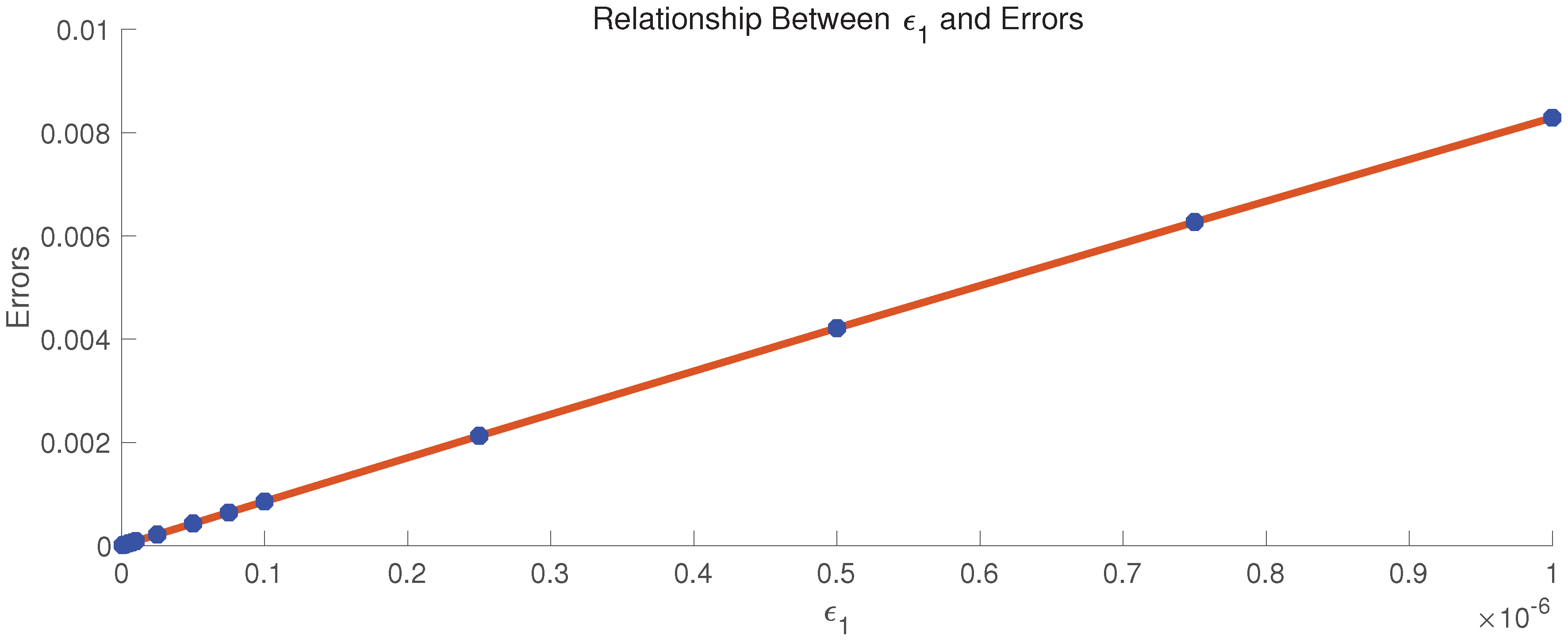
Figure 2 shows the linear relationship between
and errors.