Entropy as a Robustness Marker in Genetic Regulatory Networks
Abstract
1. Introduction
2. Materials and Methods
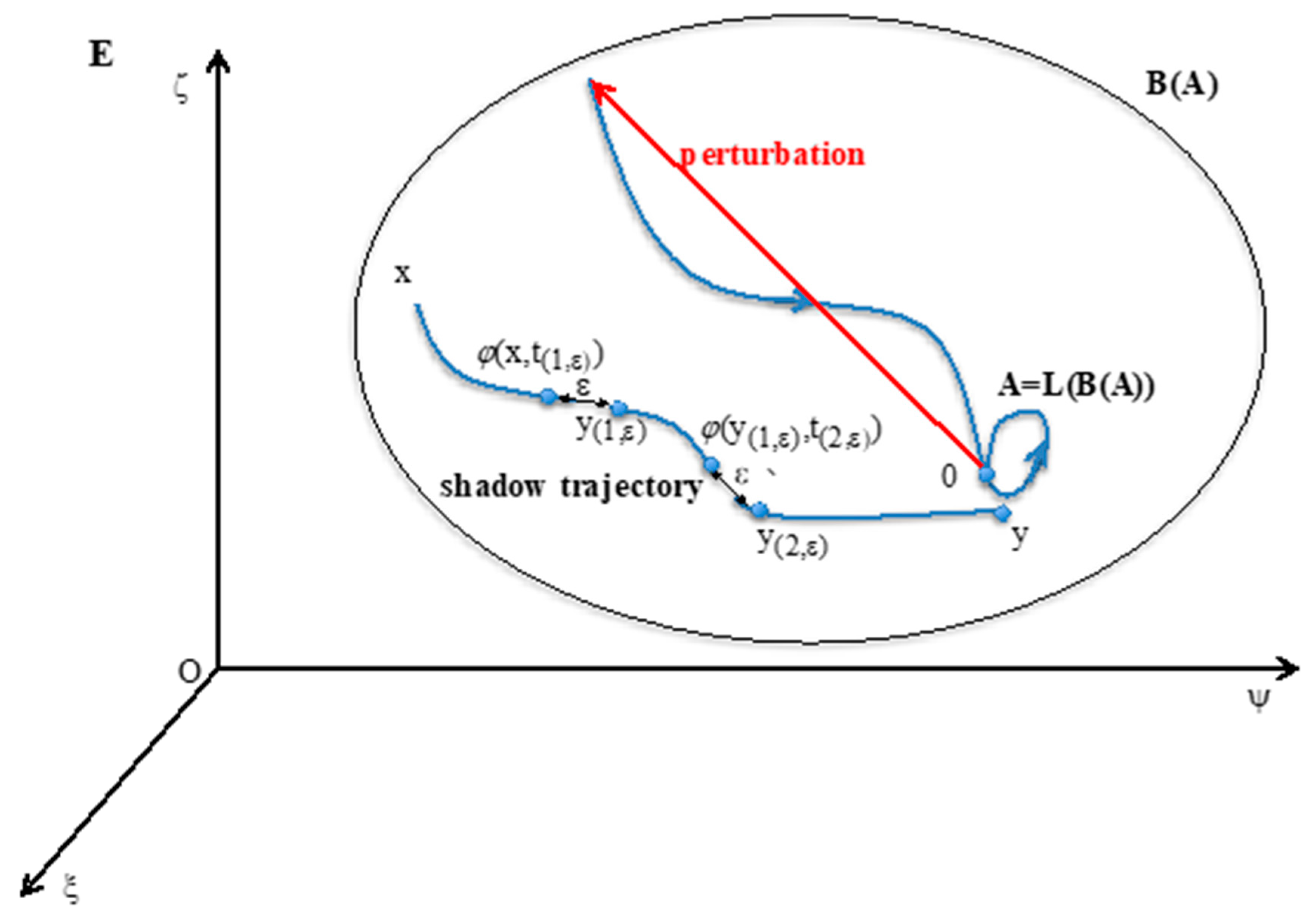
2.1. Definitions
- (i)
- A = LoB(A).
- (ii)
- There is no set A’ containing strictly A and shadow-connected to A.
- (iii)
- There is no set A” strictly contained in A verifying (i) and (ii).
2.2. Hopfield Dynamics
- -
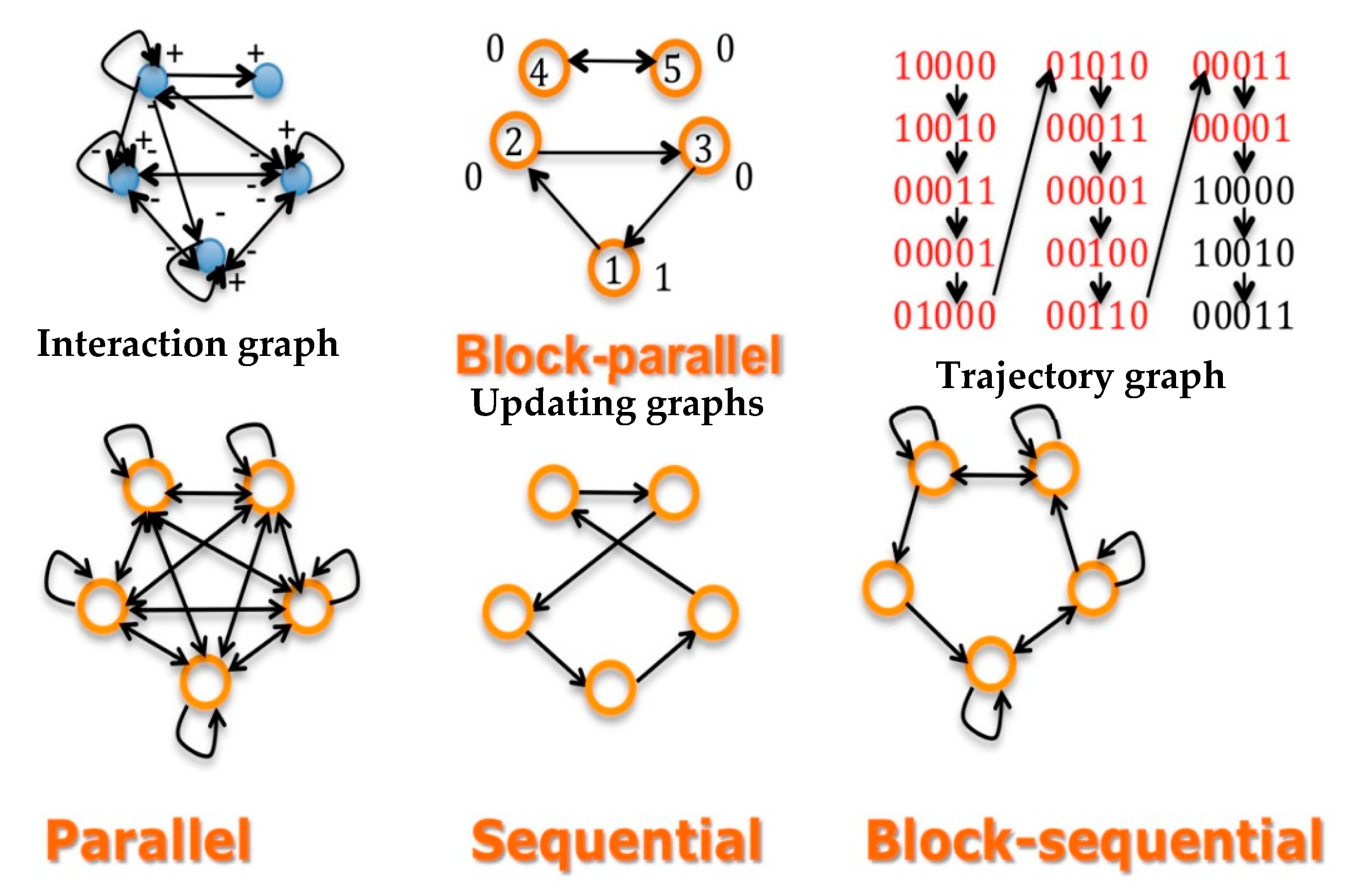
- Interaction matrix W: Its coefficient wij corresponds to the action of the gene j on the gene i. W is analogue to a discrete Jacobian matrix. Signed Jacobian matrix A is defined as follows: αij=1, if wij > 0, αij = −1, if wij > 0 and αij=0, if wij=0. Its associated directed graph is the interaction graph G;
- -
- Updating matrix S: sij = 1, if j is updated before or with i, else sij = 0;
- -
- Flow matrix Φ: ϕbc = 1, where b and c belong to E, if and only if b = φ(c,1); else ϕbc = 0.
- -
- Concerning W, the dependence is called the Hebbian dynamics: if the two vectors {xi(s)}s<t and {xj(s)}s<t have a correlation coefficient j(t)≠0, then the dependence is expressed through the equation: wij(t + 1) = wij(t) + hij(t), with h > 0, corresponding to a reinforcement of the absolute value of interactions wij(t) having succeeded to increase the xi(s)’s, if wij(t) is positive, and conversely to decrease the xi(s)’s, if wij(t) is negative.
- -
- Concerning S, the updating can be state dependent or not. If all sij equal one, the updating schedule is called parallel; if there exists a sequence of indices of the n nodes of the network, i1,…, such as sikik+1 = 1, the other sij’s being equal to 0, the updating is called sequential. Between these two extreme schedules, the updating modes are called block-sequential, i.e., they are parallel in a block, the blocks being updated sequentially. A more realistic schedule in genetic and metabolic networks is called block parallel [50]: These networks are composed of blocks made of genes sequentially updated, these blocks being updated in parallel (Figure 2 Top middle). Some interactions between these blocks can exist (i.e., there are wij ≠ 0, with i and j belonging to 2 different blocks), but because the block sizes are different, the time at which the first attractor state is reached in a block is not necessarily synchronized with the corresponding times in other blocks: the synchronization expected as asymptotic behavior of the dynamics depends on the intra-block as well as on the inter-block interactions, which explains that states of genes in a block serving as the clock for the network are highly dependent on states of genes in other blocks connected to them (e.g., acting as transcription factors of the clock genes).
- -
- Concerning Φ, the transition operator is Markov, and hence autonomous in time.
3. Results
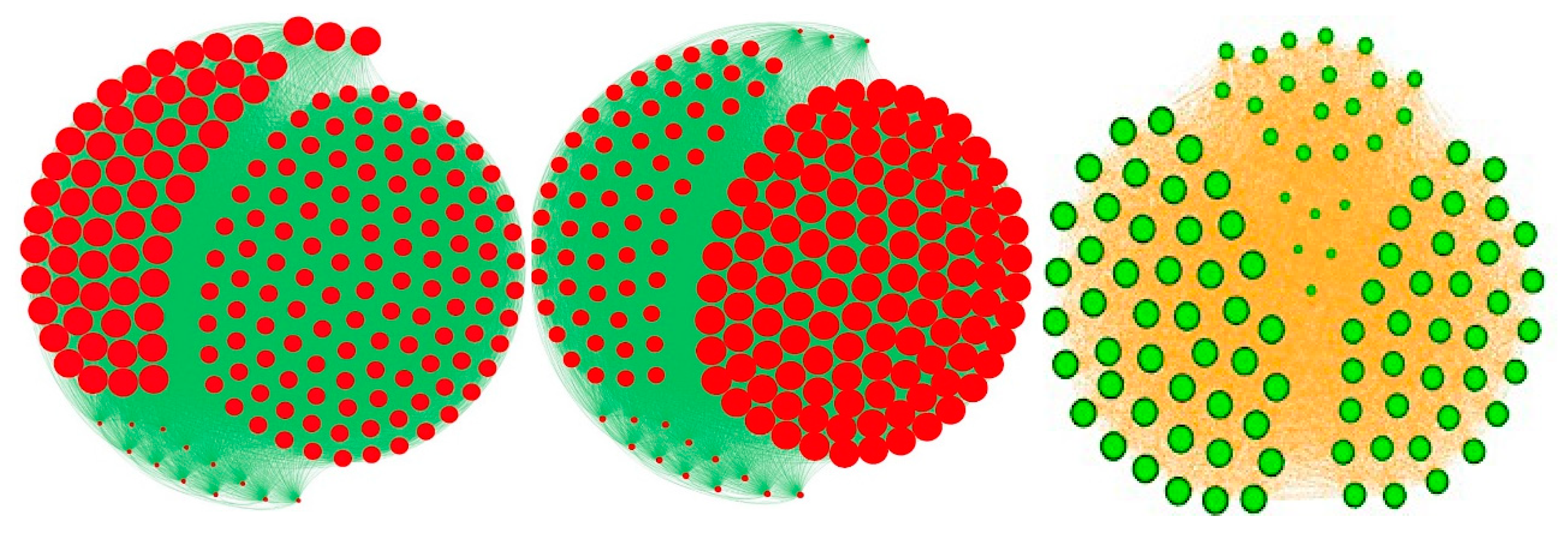
3.1. Attractor Entropy and Isochronal Entropy, Indices of Complexity and Synchronizability
3.2. Energy, Frustration and Dynamic Entropy
3.3. Dynamic Entropy, Index of Robustness
= (Σi,j=1,n αijxixj/T)μx − Σy∊E (Σi,j=1,n αijyiyj/T)μyμx,
= μx (Ex(G) – Ev(G))
- (1)
- The Proposition 2 still holds when we replace c, the absolute value of weights wij, by the temperature T, and we have: ∂Eµ/∂T = Varµ(F)/T3.
- (2)
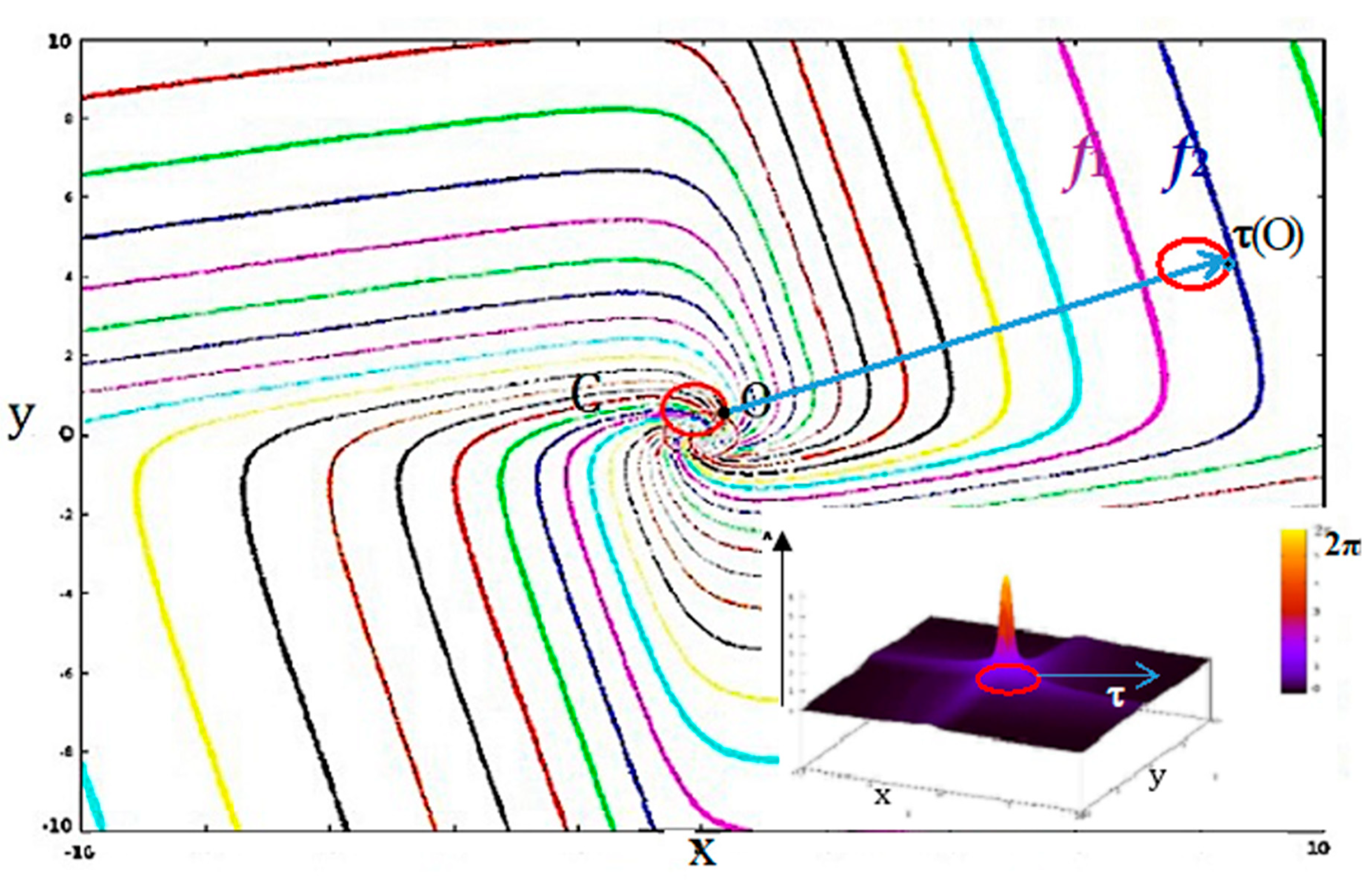
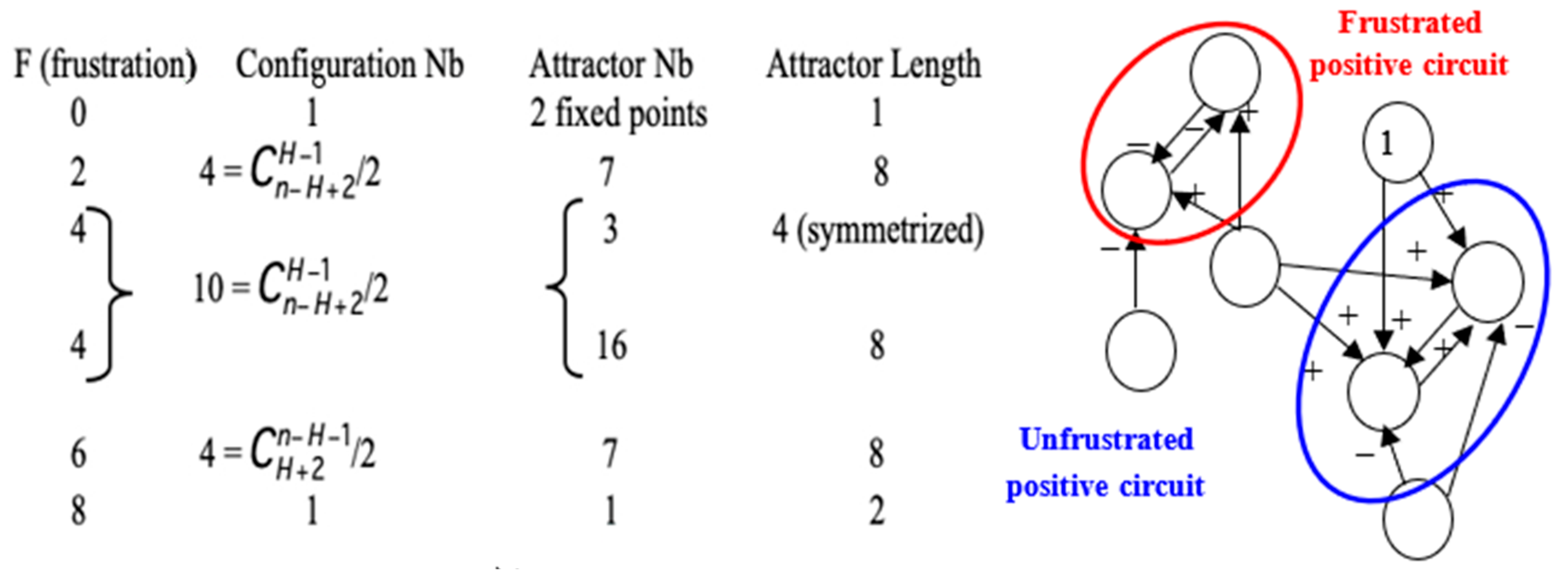
- The Proposition 2 shows that there is a close relationship between the robustness (or structural stability) with respect to variations of the parameter c and the global dynamic frustration F. This global dynamic frustration F is in general easy to calculate. For the configuration x of the genetic network controlling the flowering of Arabidopsis thaliana [37], there is only one frustrated pair; hence, F(x) = 2 (Figure 5 Right). More generally, all the thermodynamic functions introduced here are calculable in theory and could serve to quantifying the trajectory (Lyapunov) stability and the structural stability. If the number of states of a discrete state space E is too large, or if integrals on a continuous state space E are too difficult to calculate, it is possible to use Monte Carlo procedures for getting the values of the variance of the global frustration and of the dynamic entropy.
3.4. Entropy Centrality of Nodes
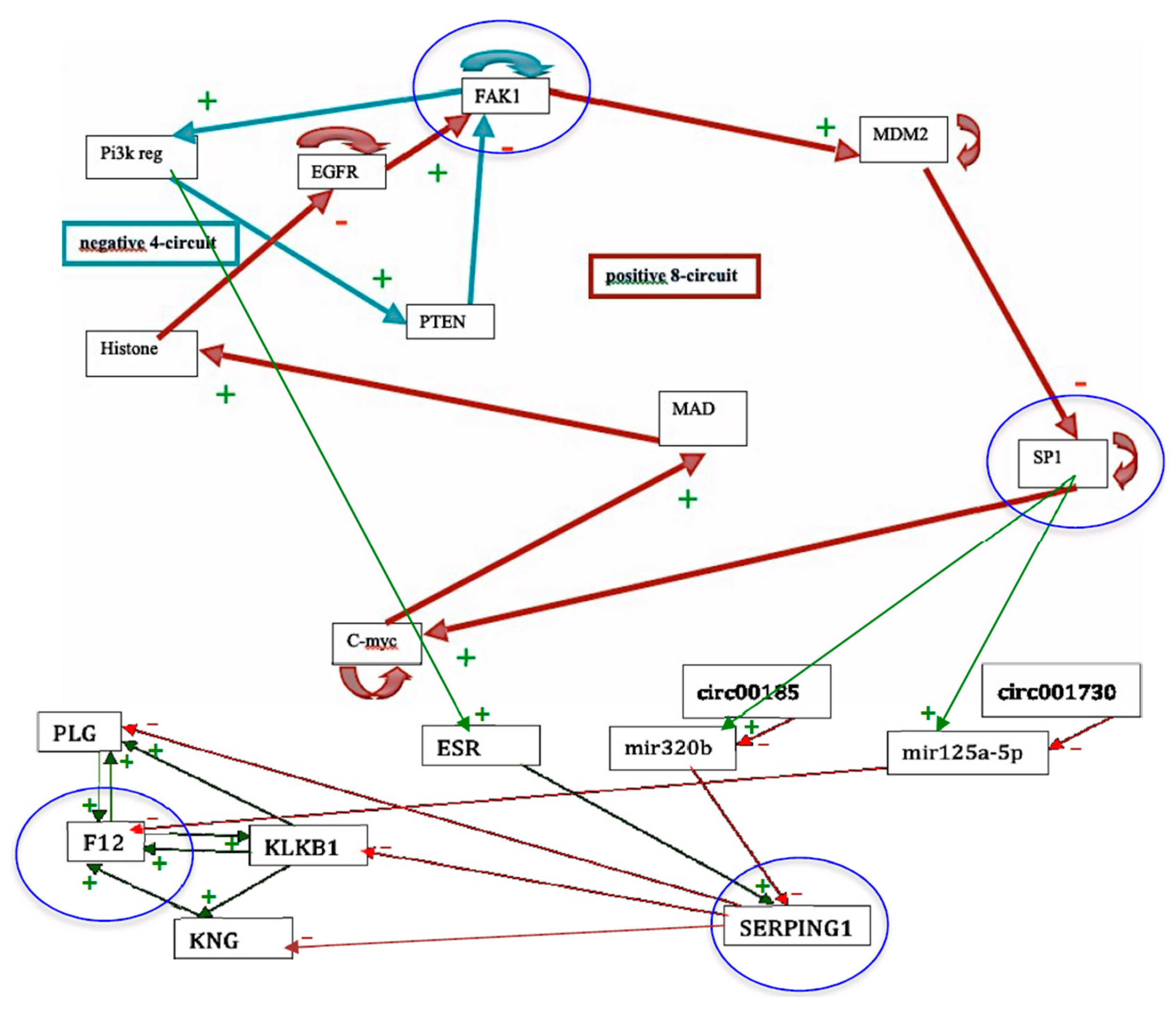
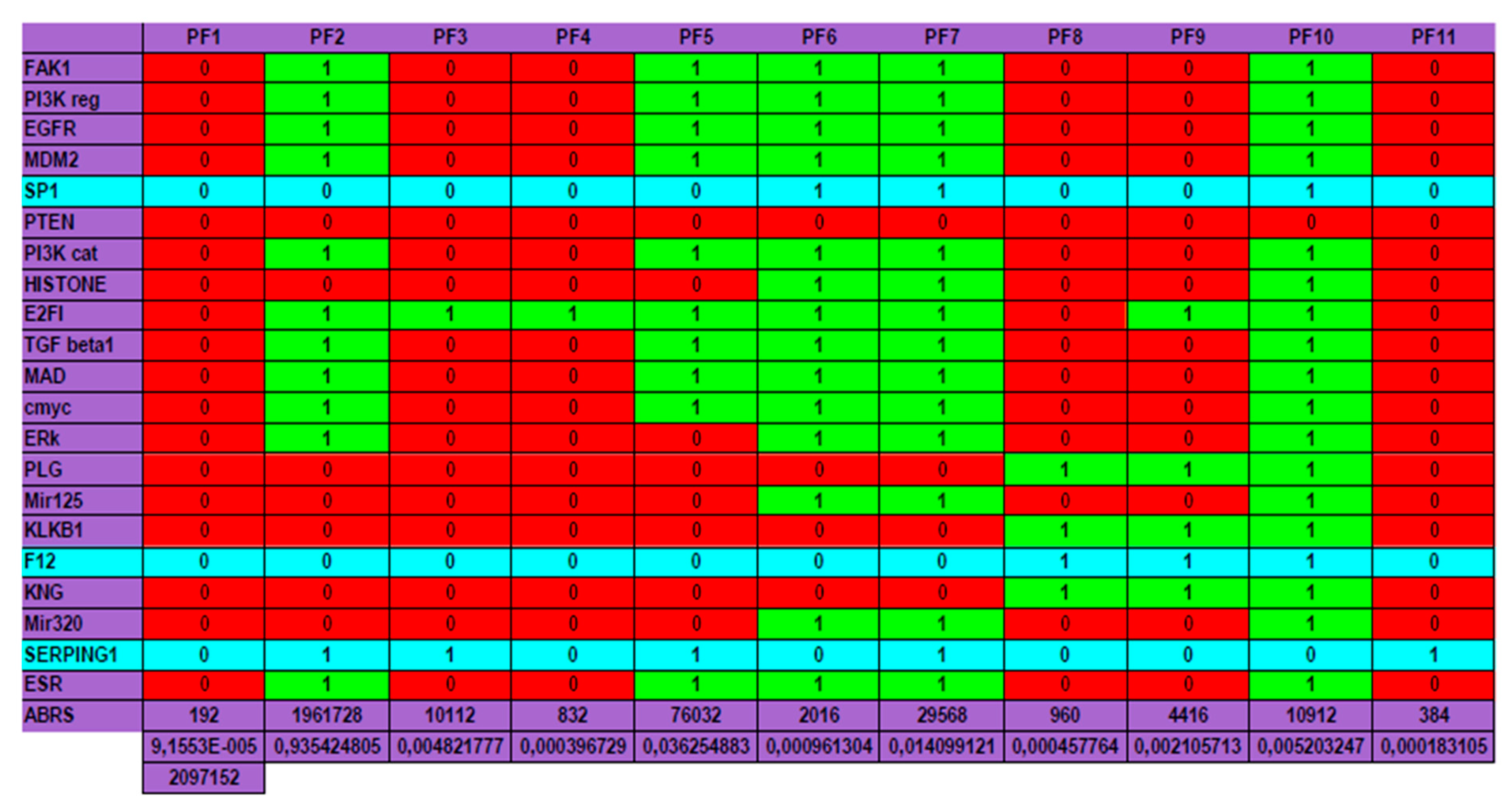
4. Application to a Real Genetic Network
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Demongeot, J.; Jezequel, C.; Sené, S. Asymptotic behavior and phase transition in regulatory networks. I. Theoretical results. Neural Netw. 2008, 21, 962–970. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Sené, S. Asymptotic behavior and phase transition in regulatory networks. II. Simulations. Neural Netw. 2008, 21, 971–979. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Elena, A.; Sené, S. Robustness in neural and genetic networks. Acta Biotheor. 2008, 56, 27–49. [Google Scholar] [CrossRef] [PubMed]
- Goles, E.; Olivos, J. Comportement itératif des fonctions à multiseuil. Inf. Control 1980, 45, 300–313. [Google Scholar] [CrossRef]
- Goles, E. Sequential iteration of threshold functions. Springer Ser. Synerg. 1981, 9, 64–70. [Google Scholar]
- Fogelman-Soulié, F.; Goles, E.; Weisbuch, G. Specific roles of the different Boolean mappings in random networks. Bull. Math. Biol. 1982, 44, 715–730. [Google Scholar] [CrossRef]
- Goles, E. Dynamics of positive automata networks. Theor. Comp. Sci. 1985, 41, 19–32. [Google Scholar] [CrossRef][Green Version]
- Goles, E.; Fogelman-Soulie, F.; Pellegrin, D. Decreasing energy functions as a tool for studying threshold networks. Discrete Appl. Math. 1985, 12, 261–277. [Google Scholar] [CrossRef]
- Cosnard, M.; Goles, E.; Moumida, D. Bifurcation structure of a discrete neuronal equation. Discret. Appl. Math. 1988, 21, 21–34. [Google Scholar] [CrossRef][Green Version]
- Demongeot, J.; Jacob, C. Confineurs: Une approche stochastique. Comptes Rendus Acad. Sci. Série I 1989, 309, 699–702. [Google Scholar]
- Demongeot, J.; Benaouda, D.; Jezequel, C. “Dynamical confinement” in neural networks and cell cycle. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Wentzell, A.D.; Freidlin, M.I. On small random perturbations of dynamical systems. Russ. Math. Surv. 1970, 25, 1–55. [Google Scholar]
- Donsker, M.D.; Varadhan, S.R.S. Asymptotic evaluation of certain Markov process expectations for large time. Comm. Pure Appl. Math. 1975, 28, 1–47. [Google Scholar] [CrossRef]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Demetrius, L. Statistical mechanics and population biology. J. Stat. Phys. 1983, 30, 709–753. [Google Scholar] [CrossRef]
- Demetrius, L.; Demongeot, J. A thermodynamic approach in the modeling of the cellular cycle. Biometrics 1984, 40, 259–260. [Google Scholar]
- Demongeot, J.; Demetrius, L. La dérive démographique et la sélection naturelle: Etude empirique de la France (1850–1965). Population 1989, 2, 231–248. [Google Scholar]
- Demetrius, L. Directionality principles in thermodynamics and evolution. Proc. Natl. Acad. Sci. USA 1997, 94, 3491–3498. [Google Scholar] [CrossRef]
- Demetrius, L. Thermodynamics and evolution. J. Theor. Biol. 2000, 206, 1–16. [Google Scholar] [CrossRef]
- Demetrius, L.; Gundlach, M.; Ochs, G. Complexity and demographic stability in population models. Theor. Popul. Biol. 2004, 65, 211–225. [Google Scholar] [CrossRef]
- Demetrius, L.; Manke, T. Robustness and network evolution-an entropic principle. Phys. A Stat. Mech. Its Appl. 2005, 346, 682–696. [Google Scholar] [CrossRef]
- Manke, T.; Demetrius, L.; Vingron, M. An entropic characterization of protein interaction networks and cellular robustness. J. R. Soc. Interface 2006, 3, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Demetrius, L.; Ziehe, M. Darwinian fitness. Theor. Popul. Biol. 2007, 72, 323–345. [Google Scholar] [CrossRef] [PubMed]
- Rochlin, V.A. Exact endomorphisms of Lebesgue spaces. Am. Math. Soc. Transl. 1964, 39, 1–36. [Google Scholar]
- Rochlin, V.A. Lectures on the theory of entropy of transformations with invariant measure. Russ. Math. Surv. 1967, 22, 1–52. [Google Scholar] [CrossRef]
- Wichert, A.; Moreira, C.; Peter Bruza, P. Balanced Quantum-Like Bayesian Networks. Entropy 2020, 22, 170. [Google Scholar] [CrossRef]
- Downarowicz, T. Symbolic extensions of smooth interval maps. Probab. Surv. 2010, 7, 84–104. [Google Scholar] [CrossRef]
- Ferenczi, S. Complexity of sequences and dynamical systems. Discret. Math. 1999, 206, 145–154. [Google Scholar] [CrossRef]
- Ferenczi, S. Substitution dynamical systems on infinite alphabets. Ann. l’Institut Fourier 2006, 56, 2315–2343. [Google Scholar] [CrossRef]
- Hernández-Orozco, S.; Kiani, N.A.; Zenil, H. Algorithmically probable mutations reproduce aspects of evolution, such as convergence rate, genetic memory and modularity. R. Soc. Open Sci. 2018, 5, 180399. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.A.; Marabita, F.; Deng, Y.; Elias, S.; Schmidt, A.; Ball, G.; Tegnér, J. An Algorithmic Information Calculus for Causal Discovery and Reprogramming Systems. iScience 2019, 19, 1160–1172. [Google Scholar] [CrossRef]
- Delbrück, M. Discussions, In: Unités biologiques douées de continuité génétique. Colloques Int. CNRS 1949, 8, 33–35. [Google Scholar]
- Thomas, R. Boolean formalization of genetic control circuits. J. Theor. Biol. 1973, 42, 563–585. [Google Scholar] [CrossRef]
- Thomas, R. On the relation between the logical structure of systems and their ability to generate multiple steady states or sustained oscillations. Springer Ser. Synerg. 1981, 9, 180–193. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Ben Amor, H.; Gillois, P.; Noual, M.; Sené, S. Robustness of regulatory networks. A generic approach with applications at different levels: Physiologic, metabolic and genetic. Int. J. Mol. Sci. 2009, 10, 4437–4473. [Google Scholar] [CrossRef]
- Demongeot, J.; Goles, E.; Morvan, M.; Noual, M.; Sené, S. Attraction basins as gauges of environmental robustness against boundary conditions in biological complex systems. PLoS ONE 2010, 5, e11793.2. [Google Scholar] [CrossRef]
- Demongeot, J.; Elena, A.; Noual, M.; Sené, S.; Thuderoz, F. Immunetworks, intersecting circuits and dynamics. J. Theor. Biol. 2011, 280, 19–33. [Google Scholar] [CrossRef]
- Demongeot, J.; Waku, J. Robustness in biological regulatory networks. I–IV. Comptes Rendus Mathématique 2012, 350, 221–228, 289–298. [Google Scholar] [CrossRef]
- Demongeot, J.; Noual, M.; Sené, S. Combinatorics of Boolean automata circuits dynamics. Discret. Appl. Math. 2012, 160, 398–415. [Google Scholar] [CrossRef]
- Demongeot, J.; Cohen, O.; Henrion-Caude, A. MicroRNAs and Robustness in Biological Regulatory Networks. A Generic Approach with Applications at Different Levels: Physiologic, Metabolic, and Genetic. Springer Ser. Biophys. 2013, 16, 63–114. [Google Scholar]
- Demongeot, J.; Ben Amor, H.; Hazgui, H.; Waku, J. Stability, complexity and robustness in population dynamics. Acta Biotheor. 2014, 62, 243–284. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Demetrius, L. Complexity and Stability in Biological Systems. Int. J. Bifurc. Chaos 2015, 25, 40013. [Google Scholar] [CrossRef]
- Demongeot, J.; Hazgui, H.; Henrion Caude, A. Genetic regulatory networks: Focus on attractors of their dynamics. In Computational Biology, Bioinformatics & Systems Biology; Tran, Q.N., Arabnia, H.R., Eds.; Elsevier: New York, NY, USA, 2015; pp. 135–165. [Google Scholar]
- Demongeot, J.; Elena, A.; Taramasco, C. Social Networks and Obesity. Application to an interactive system for patient-centred therapeutic education. In Metabolic Syndrome: A Comprehensive Textbook; Ahima, R.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 287–307. [Google Scholar]
- Demongeot, J.; Jelassi, M.; Taramasco, C. From Susceptibility to Frailty in social networks: The case of obesity. Math. Pop. Studies 2017, 24, 219–245. [Google Scholar] [CrossRef]
- Demongeot, J.; Jelassi, M.; Hazgui, H.; Ben Miled, S.; Bellamine Ben Saoud, N.; Taramasco, C. Biological Networks Entropies: Examples in Neural Memory Networks, Genetic Regulation Networks and Social Epidemic Networks. Entropy 2018, 20, 36. [Google Scholar] [CrossRef]
- Demongeot, J.; Sené, S. Phase transitions in stochastic non-linear threshold Boolean automata networks on ℤ2: The boundary impact. Adv. Appl. Math. 2018, 98, 77–99. [Google Scholar] [CrossRef]
- Demongeot, J.; Hazgui, H.; Thellier, M. Memory in plants: Boolean modelling of the learning and store/recall mnesic functions in response to environmental stimuli. J. Theor. Biol. 2019, 467, 123–133. [Google Scholar] [CrossRef]
- Demongeot, J.; Sené, S. About block-parallel Boolean networks: A position paper. Nat. Comput. 2020, 19. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A. On random graphs. Pub. Math. 1959, 6, 290–297. [Google Scholar]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1959, 286, 509–512. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Banerji, C.R.S.; Miranda-Saavedra, D.; Severini, S.; Widschwendter, M.; Enver, T.; Zhou, J.X.; Teschendorff, A.E. Cellular network entropy as the energy potential in Waddington’s differentiation landscape. Sci. Rep. 2013, 3, 3039. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Mason, S.P.; Barabasi, A.L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef]
- Gómez-Gardeñes, J.; Latora, V. Entropy rate of diffusion processes on complex networks. Phys. Rev. E 2008, 78, 065102. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wang, B.H.; Wang, W.X.; Zhou, T. Network Entropy Based on Topology Configuration and Its Computation to Random Networks. Chin. Phys. Lett. 2008, 25, 4177–4180. [Google Scholar] [CrossRef]
- Teschendorff, A.E.; Severini, S. Increased entropy of signal transduction in the cancer metastasis phenotype. BMC Syst. Biol. 2010, 4, 104. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Banerji, C.R.S.; Severini, S.; Kuehn, R.; Sollich, P. Increased signaling entropy in cancer requires the scale-free property of protein interaction networks. Sci. Rep. 2014, 2, 802. [Google Scholar]
- Teschendorff, A.E.; Sollich, P.; Kuehn, R. Signalling entropy: A novel network theoretical framework for systems analysis and interpretation of functional omic data. Methods 2014, 67, 282–293. [Google Scholar] [CrossRef]
- West, J.; Bianconi, G.; Severini, S.; Teschendorff, A. Differential network entropy reveals cancer hallmarks. Sci. Rep. 2012, 2, 802. [Google Scholar] [CrossRef]
- Chen, B.S.; Wong, S.W.; Li, C.W. On the Calculation of System Entropy in Nonlinear Stochastic Biological Networks. Entropy 2015, 17, 6801–6833. [Google Scholar] [CrossRef]
- Cosnard, M.; Demongeot, J. Attracteurs: Une approche déterministe. Comptes Rendus Acad. Sci. Maths. Série I 1985, 300, 551–556. [Google Scholar]
- Cosnard, M.; Demongeot, J. On the definitions of attractors. Lect. Notes Maths. 1985, 1163, 23–31. [Google Scholar]
- Szabó, K.G.; Tél, T. Thermodynamics of attractor enlargement. Phys. Rev. E 1994, 50, 1070–1082. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xu, L.; Wang, E. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA 2008, 105, 12271–12276. [Google Scholar] [CrossRef] [PubMed]
- Menck, P.J.; Heitzig, J.; Marwan, N.; Kurths, J. How basin stability complements the linear-stability paradigm. Nat. Phys. 2013, 9, 89–92. [Google Scholar] [CrossRef]
- Kurz, F.T.; Kembro, J.M.; Flesia, A.G.; Armoundas, A.A.; Cortassa, S.; Aon, M.A.; Lloyd, D. Network dynamics: Quantitative analysis of complex behavior in metabolism, organelles, and cells, from experiments to models and back. Wiley Interdiscipl. Rev. Syst. Biol. Med. 2017, 9, e1352. [Google Scholar] [CrossRef] [PubMed]
- Bowen, R. ω-limit sets for Axiom A diffeomorphisms. J. Diff. Equ. 1978, 18, 333–339. [Google Scholar] [CrossRef]
- Williams, R.F. Expanding attractors. Publ. Math. l’IHÉS 1974, 43, 169–203. [Google Scholar] [CrossRef]
- Ruelle, D. Small random perturbations and the definition of attractors. Comm. Math. Phys. 1981, 82, 137–151. [Google Scholar] [CrossRef]
- Haraux, A. Attractors of asymptotically compact processes and applications to nonlinear partial differential equations. Commun. Partial Differ. Equ. 1988, 13, 1383–1414. [Google Scholar] [CrossRef]
- Glade, N.; Forest, L.; Demongeot, J. Liénard systems and potential-Hamiltonian decomposition. III Applications in biology. Comptes Rendus Mathématique 2007, 344, 253–258. [Google Scholar] [CrossRef]
- Tonnelier, A.; Meignen, S.; Bosch, H.; Demongeot, J. Synchronization and desynchronization of neural oscillators: Comparison of two models. Neural Netw. 1999, 12, 1213–1228. [Google Scholar] [CrossRef]
- Robert, F. Discrete Iterations: A Metric Study, Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Ben Amor, H.; Glade, N.; Lobos, C.; Demongeot, J. The isochronal fibration: Characterization and implication in biology. Acta Biotheor. 2010, 58, 121–142. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J.; Kaufmann, M.; Thomas, R. Positive feedback circuits and memory. Comptes Rendus Acad. Sci. Paris Life Sci. 2000, 323, 69–79. [Google Scholar] [CrossRef]
- Toulouse, G. Theory of the frustration effect in spin glasses: I. Commun. Phys. 1977, 2, 115–119. [Google Scholar]
- Waddington, C.H. Organizers & Genes; Cambridge University Press: Cambridge, UK, 1940. [Google Scholar]
- Gardner, M.R.; Ashby, W.R. Connectance of large dynamic systems: Critical values for stability. Nature 1970, 228, 784. [Google Scholar] [CrossRef]
- Thom, R. Structural Stability and Morphogenesis; CRC Press: Boca Raton, FL, USA, 1972. [Google Scholar]
- Wagner, A. Robustness and Evolvability in Living Systems; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Gunawardena, S. The robustness of a biochemical network can be inferred mathematically from its architecture. Biol. Syst. Theory 2010, 328, 581–582. [Google Scholar]
- Demongeot, J.; Elena, A.; Weil, G. Potential-Hamiltonian decomposition of cellular automata. Application to degeneracy of genetic code and cyclic codes III. Comptes Rendus Biol. 2006, 329, 953–962. [Google Scholar] [CrossRef]
- Barthélémy, M. Betweenness centrality in large complex networks. Eur. Phys. J. B 2004, 38, 163–168. [Google Scholar] [CrossRef]
- Negre, C.F.A.; Morzan, U.N.; Hendrickson, H.P.; Pal, R.; Lisi, G.P.J.; Loria, P.; Rivalta, I.; Ho, J.; Batista, V.S. Eigenvector centrality for characterization of protein allosteric pathways. Proc. Natl. Acad. Sci. USA 2018, 115, 12201–12208. [Google Scholar] [CrossRef]
- Ghazi, A.; Grant, J.A. Hereditary angioedema: Epidemiology, management, and role of icatibant. Biol. Targets Ther. 2013, 7, 103–113. [Google Scholar] [CrossRef]
- Charignon, D.; Ponard, D.; de Gennes, C.; Drouet, C.; Ghannam, A. SERPING1 and F12 combined variants in a hereditary angioedema family. Ann. Allergy Asthma Immunol. 2018, 121, 500–502. [Google Scholar] [CrossRef] [PubMed]
- Cinquin, O.; Demongeot, J. Positive and negative feedback: Striking a balance between necessary antagonists. J. Theor. Biol. 2002, 216, 229–241. [Google Scholar] [CrossRef] [PubMed]
- Fatès, N. A tutorial on elementary cellular automata with fully asynchronous updating. Nat. Comput. 2020, 19. [Google Scholar] [CrossRef]
- Mason, O.; Verwoerd, M. Graph theory and networks in Biology. IET Syst. Biol. 2007, 1, 89–119. [Google Scholar] [CrossRef] [PubMed]
- Gosak, M.; Markovi, R.; Dolenšek, J.; Rupnik, M.S.; Marhl, M.; Stožer, A.; Perc, M. Network science of biological systems at different scales: A review. Phys. Life Rev. 2017, 1571, 0645. [Google Scholar] [CrossRef]
- Christakis, N.A.; Fowler, J.H. The Spread of Obesity in a Large Social Network over 32 Years. N. Engl. J. Med. 2007, 357, 370–379. [Google Scholar] [CrossRef] [PubMed]
- Federer, C.; Zylberberg, J. A self-organizing memory network. BioRxiv 2017. [Google Scholar] [CrossRef]
- Grillner, S. Biological Pattern Generation: The Cellular and Computational Logic of Networks in Motion. Neuron 2006, 52, 751–766. [Google Scholar] [CrossRef] [PubMed]
- Naitoh, Y.; Sugino, K. Ciliary Movement and Its Control in Paramecium. J. Eukaryot. Microbiol. 2007, 31, 31–40. [Google Scholar]
- Guerra, S.; Peressotti, A.; Peressotti, F.; Bulgheroni, F.M.; Baccinelli, W.; D’Amico, E.; Gómez, A.; Massaccesi, S.; Ceccarini, F.; Castiello, U. Flexible control of movement in plants. Sci. Rep. 2019, 9, 16570. [Google Scholar] [CrossRef]
- Young, L.S. Some large deviation results for dynamical systems. Trans. Amer. Math. Soc. 1990, 318, 525–535. [Google Scholar] [CrossRef]
- Weaver, D.C.; Workman, C.T.; Stormo, G.D. Modeling regulatory networks with weight matrices. Pac. Symp. Biocomput. 1999, 4, 112–123. [Google Scholar]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 2 | 2 | 3 | 3 | 5 | 5 | 8 | 10 |
| 2 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 8 | 10 |
| 3 | 1 | 2 | 1 | 3 | 3 | 6 | 5 | 8 | 8 |
| 4 | 1 | 1 | 2 | 1 | 3 | 4 | 5 | 11 | 10 |
| 5 | 1 | 2 | 2 | 3 | 1 | 5 | 5 | 8 | 10 |
| 6 | 1 | 1 | 1 | 3 | 3 | 1 | 5 | 8 | 8 |
| 7 | 1 | 2 | 2 | 3 | 3 | 5 | 1 | 8 | 10 |
| 8 | 1 | 1 | 2 | 1 | 3 | 4 | 5 | 1 | 10 |
| 9 | 1 | 2 | 1 | 3 | 3 | 6 | 5 | 8 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rachdi, M.; Waku, J.; Hazgui, H.; Demongeot, J. Entropy as a Robustness Marker in Genetic Regulatory Networks. Entropy 2020, 22, 260. https://doi.org/10.3390/e22030260
Rachdi M, Waku J, Hazgui H, Demongeot J. Entropy as a Robustness Marker in Genetic Regulatory Networks. Entropy. 2020; 22(3):260. https://doi.org/10.3390/e22030260
Chicago/Turabian StyleRachdi, Mustapha, Jules Waku, Hana Hazgui, and Jacques Demongeot. 2020. "Entropy as a Robustness Marker in Genetic Regulatory Networks" Entropy 22, no. 3: 260. https://doi.org/10.3390/e22030260
APA StyleRachdi, M., Waku, J., Hazgui, H., & Demongeot, J. (2020). Entropy as a Robustness Marker in Genetic Regulatory Networks. Entropy, 22(3), 260. https://doi.org/10.3390/e22030260







