Thermodynamic and Transport Properties of Equilibrium Debye Plasmas
Abstract
1. Introduction
2. Results
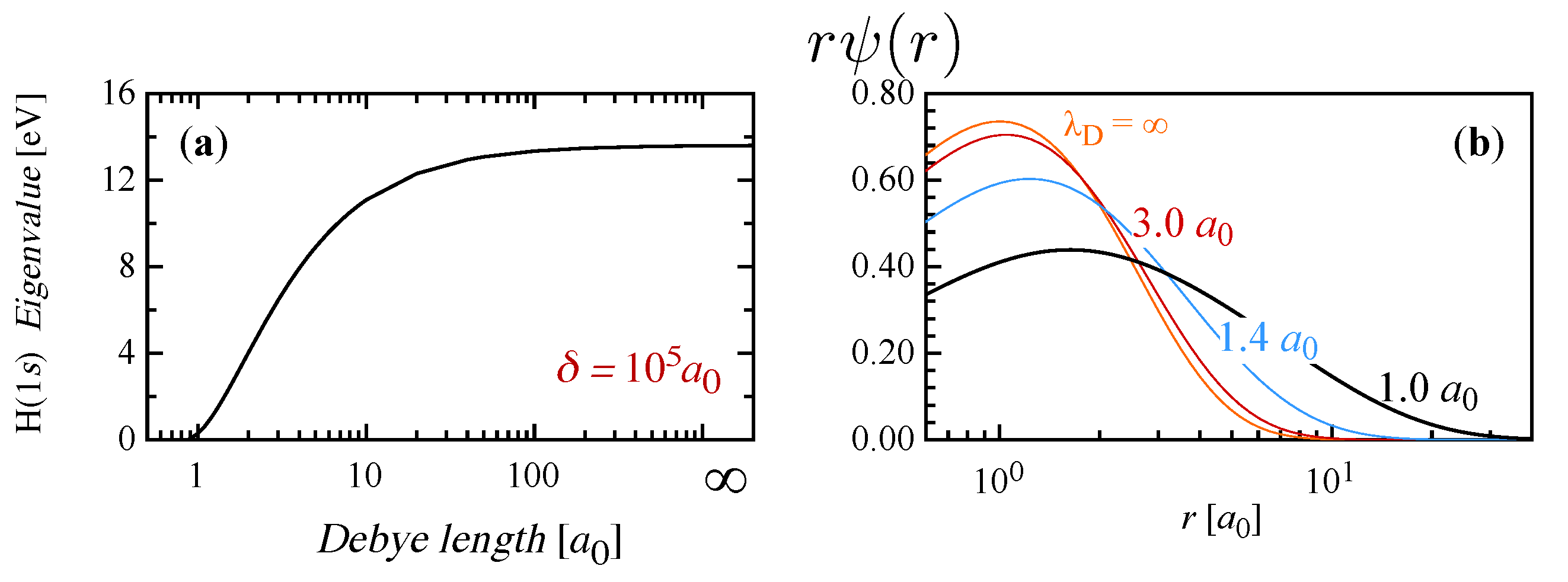
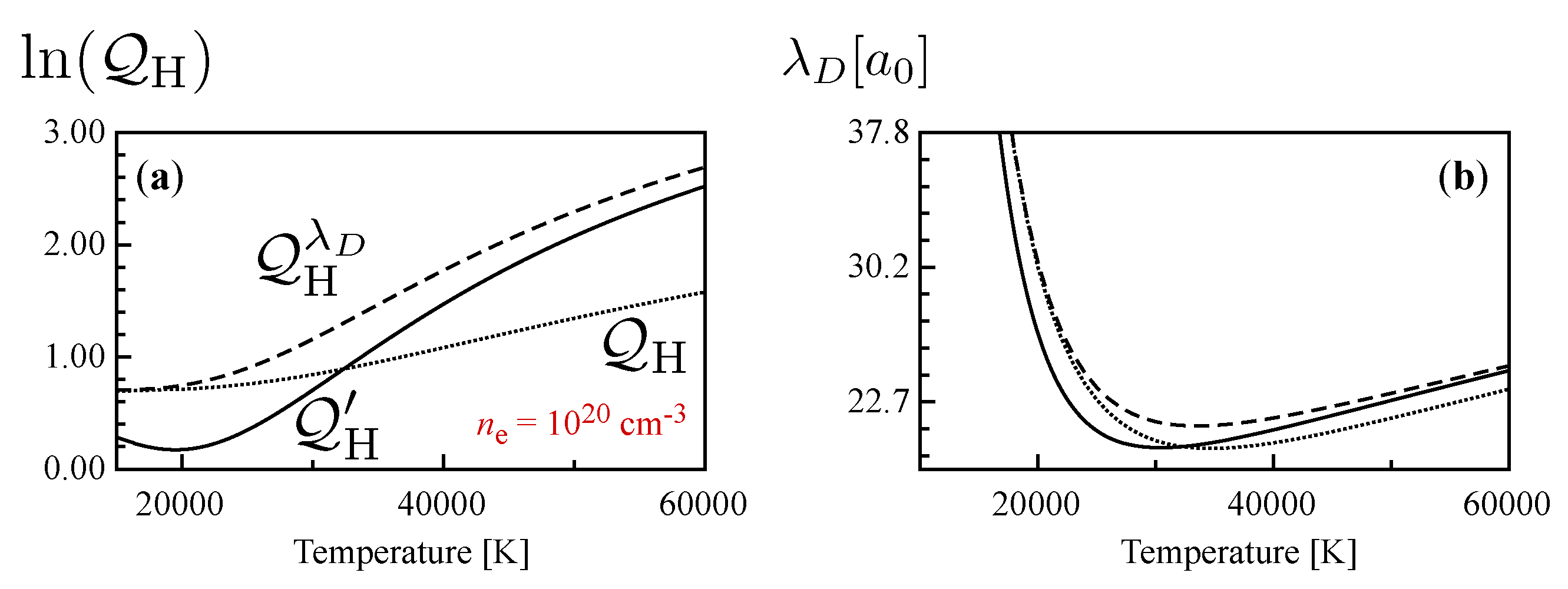
2.1. Thermodynamics
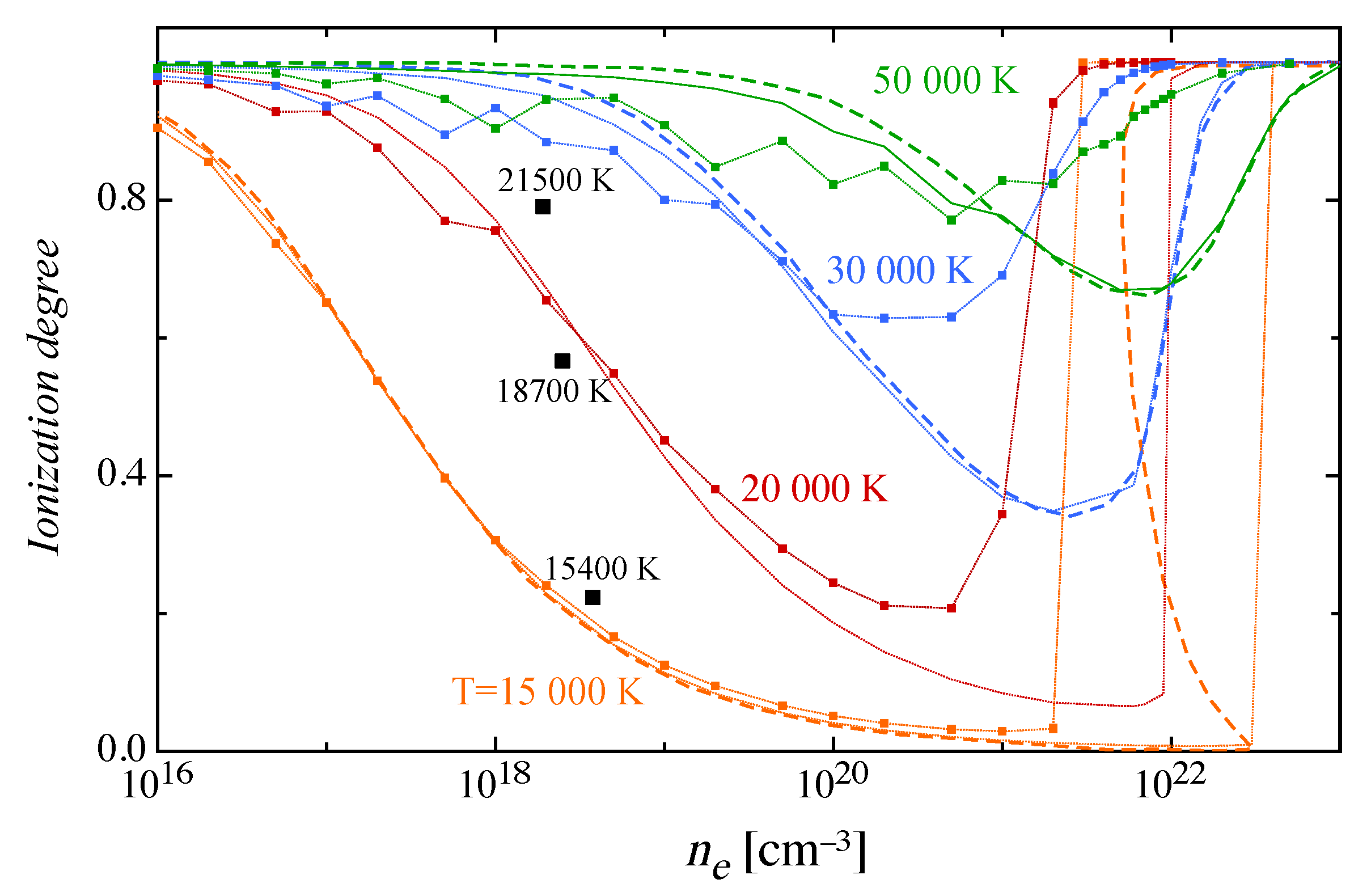
2.2. Transport: The Electrical Conductivity
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sako, T.; Diercksen, G.H.F. Confined quantum systems: A comparison of the spectral properties of the two-electron quantum dot, the negative hydrogen ion and the helium atom. J. Phys. B: At. Molec. Opt. Phys. 2003, 36, 1681–1702. [Google Scholar] [CrossRef]
- Merkt, U.; Huser, J.; Wagner, M. Energy spectra of two electrons in a harmonic quantum dot. Phys. Rev. B 1991, 43, 7320–7323. [Google Scholar] [CrossRef] [PubMed]
- Dutt, R.; Mukherjee, A.; Varshni, Y.P. Dipole polarizability of hydrogen atom at high pressures. Phys. Lett. A 2001, 280, 318–324. [Google Scholar] [CrossRef]
- Hummer, D.G.; Mihalas, D. The equation of state for stellar envelopes. I - an occupation probability formalism for the truncation of internal partition functions. Astrophys. J. 1988, 331, 794–814. [Google Scholar] [CrossRef]
- Graboske, H.C., Jr.; Harwood, D.J.; Rogers, F.J. Thermodynamic properties of nonideal gases. I. Free-energy minimization method. Phys. Rev. 1969, 186, 210. [Google Scholar] [CrossRef]
- Ebeling, W.; Kraeft, W.D.; Kremp, D. Theory of Bound States and Ionization Equilibrium in Plasmas and Solids; Akademie-Verlag: Berlin, Germany, 1977. [Google Scholar]
- Kremp, D.; Schlanges, M.; Kraeft, W.D. Quantum Statistic of Nonideal Plasmas; Springer: Berlin, Germany, 2005. [Google Scholar]
- Capitelli, M.; Giordano, D. Energy levels of atomic hydrogen in a closed box: A natural cutoff criterion of the electronic partition function. Phys. Rev. A 2009, 80, 032113. [Google Scholar] [CrossRef]
- Zaghloul, M.R. On the ionization equilibrium of hot hydrogen plasma and thermodynamic consistency of formulating finite internal partition functions. Phys. Plasmas 2010, 17, 062701. [Google Scholar] [CrossRef]
- Nikolaev, D.; Pyalling, A.; Kvitov, S.; Fortov, V. Temperature measurements and hydrogen transformation under dynamic compression up to 150 GPA. In Proceedings of the AIP Conference, Chicago, IL, USA, 26 June–1 July 2011. [Google Scholar] [CrossRef]
- Saumon, D.; Chabrier, G.; Van Horn, H. An equation of state for low-mass stars and giant planets. Astrophys. J. Suppl. Ser. 1995, 99, 713. [Google Scholar] [CrossRef]
- Knudson, M.; Desjarlais, M. High-precision shock wave measurements of deuterium: Evaluation of exchange-correlation functionals at the molecular-to-atomic transition. Phys. Rev. Lett. 2017, 118, 035501. [Google Scholar] [CrossRef]
- Saha, J.; Mukherjee, T.; Mukherjee, P.; Fricke, B. Hyperpolarizability of hydrogen atom under spherically confined Debye plasma. Eur. Phys. J. D 2011, 62, 205–211. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, J.; Janev, R. Static dipole polarizability of hydrogenlike ions in Debye plasmas. Phys. Rev. A 2009, 80, 032502. [Google Scholar] [CrossRef]
- Das, M. Transition energies and polarizabilities of hydrogen like ions in plasma. Phys. Plasmas 2012, 19, 092707. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, Y.; Wang, J.; Qu, Y. The generalized oscillator strengths of hydrogenlike ions in Debye plasmas. Phys. Plasmas 2009, 16, 023502. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Bray, I. Convergent-close-coupling calculations for excitation and ionization processes of electron-hydrogen collisions in Debye plasmas. Phys. Rev. A 2010, 82, 052705. [Google Scholar] [CrossRef]
- Laricchiuta, A.; Colonna, G.; Capitelli, M.; Kosarim, A.; Smirnov, B.M. Resonant charge exchange for H-H+ in Debye plasmas. Eur. Phys. J. D 2017, 71, 265. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.G.; Krstic, P.S.; Janev, R.K. Oscillation structures in elastic and electron capture cross-sections for H+-H collisions in Debye plasmas. J. Phys. B: At. Mol. Opt. Phys. 2010, 43, 201003. [Google Scholar] [CrossRef]
- Jung, Y.D. Collective effects on the symmetric resonant charge transfer in partially ionized hydrogen plasma. Appl. Phys. Lett. 2005, 86, 021502. [Google Scholar] [CrossRef]
- Murillo, M.S.; Weisheit, J.C. Dense plasmas, screened interactions, and atomic ionization. Phys. Rep. 1998, 302, 1–65. [Google Scholar] [CrossRef]
- Capitelli, M.; Colonna, G.; D’Angola, A. Fundamental Aspects of Plasma Chemical Physics: Thermodynamics, in Springer Series on Atomic, Optical, and Plasma Physics; Springer: New York, NY, USA, 2016. [Google Scholar]
- Jung, Y.D. Plasma-screening effects on the electron-impact excitation of hydrogenic ions in dense plasmas. Phys. Fluids B: Plasma Phys. 1993, 5, 3432–3440. [Google Scholar] [CrossRef]
- Yoon, J.S.; Jung, Y.D. Antiscreening channels for ion–ion collisional excitations in dense plasmas. Phys. Plasmas 1997, 4, 3477–3481. [Google Scholar] [CrossRef]
- Yoon, J.S.; Jung, Y.D. Dynamic screening effects on antiscreening excitations for ion–ion collisions in dense plasma. Phys. Plasmas 1998, 5, 889–894. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.G.; He, B.; Qiu, Y.B.; Janev, R.K. Charge exchange and ionization in hydrogen atom-fully stripped ion collisions in Debye plasmas. Phys. Plasmas 2007, 14, 053505. [Google Scholar] [CrossRef]
- Jakimovski, D.; Janev, R. Polarization of Balmer alpha radiation resulting from H++ H collisions in Debye plasmas. Phys. Plasmas 2015, 22, 103301. [Google Scholar] [CrossRef]
- Holst, B.; Redmer, R.; Desjarlais, M.P. Thermophysical properties of warm dense hydrogen using quantum molecular dynamics simulations. Phys. Rev. B 2008, 77, 184201. [Google Scholar] [CrossRef]
- Holst, B.; French, M.; Redmer, R. Electronic transport coefficients from ab initio simulations and application to dense liquid hydrogen. Phys. Rev. B 2011, 83, 235120. [Google Scholar] [CrossRef]
- Clérouin, J. The viscosity of dense hydrogen: From liquid to plasma behaviour. J. Phys.: Condens. Matter 2002, 14, 9089. [Google Scholar] [CrossRef]
- Shalenov, E.O.; Dzhumagulova, K.N.; Ramazanov, T.S.; Reinholz, H.; Röpke, G. Influence of dynamic screening on the conductivity of hydrogen plasma including electron–electron collisions. Contrib. Plasma Phys. 2019, 59, e201900024. [Google Scholar] [CrossRef]
- Jung, Y.D. Influence of the dynamic plasma shielding on the elastic electron-ion collision in turbulent plasmas. Appl. Phys. Lett. 2012, 100, 074109. [Google Scholar] [CrossRef]
- Jung, Y.D. Dynamic screening effects on semiclassical ionization probabilities for electron–ion collisions in weakly coupled plasmas. Phys. Plasmas 1998, 5, 536–540. [Google Scholar] [CrossRef]
- Kim, C.G.; Jung, Y.D. Dynamic plasma screening effects on semiclassical electron captures from hydrogenic ions by protons in weakly coupled plasmas. Phys. Plasmas 1998, 5, 3493–3496. [Google Scholar] [CrossRef]
- Rogers, F.; Graboske, H., Jr.; Harwood, D. Bound eigenstates of the static screened Coulomb potential. Phys. Rev. A 1970, 1, 1577. [Google Scholar] [CrossRef]
- Son, S.K.; Thiele, R.; Jurek, Z.; Ziaja, B.; Santra, R. Quantum-mechanical calculation of ionization- potential lowering in dense plasmas. Phys. Rev. X 2014, 4, 031004. [Google Scholar] [CrossRef]
- Reinholz, H.; Redmer, R.; Nagel, S. Thermodynamic and transport properties of dense hydrogen plasmas. Phys. Rev. E 1995, 52, 5368. [Google Scholar] [CrossRef]
- Ott, T.; Bonitz, M.; Stanton, L.G.; Murillo, M.S. Coupling strength in Coulomb and Yukawa one-component plasmas. Phys. Plasmas 2014, 21, 113704. [Google Scholar] [CrossRef]
- Bernu, B.; Wallenbom, J.; Zehnlé, V. On the transport properties of a dense fully-ionized hydrogen plasma. II. Quantum analysis. J. Phys. 1988, 49, 1161–1171. [Google Scholar] [CrossRef][Green Version]
- Capitelli, M.; Giordano, D.; Colonna, G. The role of Debye-Hückel electronic energy levels on the thermodynamic properties of hydrogen plasmas including isentropic coefficients. Phys. Plasmas 2008, 15, 082115. [Google Scholar] [CrossRef]
- Filinov, V.S.; Levashov, P.R.; Bonitz, M.; Fortov, V.E. Thermodynamics of Hydrogen and Hydrogen-Helium Plasmas: Path Integral Monte Carlo Calculations and Chemical Picture. Contrib. Plasma Phys. 2005, 45, 258–265. [Google Scholar] [CrossRef]
- Radtke, R.; Günther, K. Electrical conductivity of highly ionized dense hydrogen plasma. I. Electrical measurements and diagnostics. J. Phys. D: Appl. Phys. 1976, 9, 1131. [Google Scholar] [CrossRef]
- Levashov, P.R.; Filinov, V.S.; Fortov, V.E.; Bonitz, M. Thermodynamic properties of nonideal strongly degenerate hydrogen plasma. In Proceedings of the AIP Conference, Atlanta, GA, USA, 24–29 June 2001. [Google Scholar]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. Molecular Theory of Gases and Liquids; John Wiley & Sons: New York, NY, USA, 1966. [Google Scholar]
- Bruno, D.; Catalfamo, C.; Capitelli, M.; Colonna, G.; De Pascale, O.; Diomede, P.; Gorse, C.; Laricchiuta, A.; Longo, S.; Giordano, D.; et al. Transport properties of high-temperature Jupiter atmosphere components. Phys. Plasmas 2010, 17, 112315. [Google Scholar] [CrossRef]
- Mason, E.A.; Munn, R.J.; Smith, F.J. Transport Coefficients of Ionized Gases. Phys. Fluids 1967, 10, 1827. [Google Scholar] [CrossRef]
- Hahn, H.S.; Mason, E.A.; Smith, F.J. Quantum transport cross-sections in a completely ionized gas. Phys. Fluids 1971, 14, 278–287. [Google Scholar] [CrossRef]
- D’Angola, A.; Colonna, G.; Gorse, C.; Capitelli, M. Thermodynamic and transport properties in equilibrium air plasmas in a wide pressure and temperature range. Eur. Phys. J. D 2008, 46, 129–150. [Google Scholar] [CrossRef]
- Schlanges, M.; Kremp, D.; Keuer, H. Kinetic approach to the electrical conductivity in a partially ionized hydrogen plasma. Ann. Phys. 1984, 496, 54–66. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colonna, G.; Laricchiuta, A. Thermodynamic and Transport Properties of Equilibrium Debye Plasmas. Entropy 2020, 22, 237. https://doi.org/10.3390/e22020237
Colonna G, Laricchiuta A. Thermodynamic and Transport Properties of Equilibrium Debye Plasmas. Entropy. 2020; 22(2):237. https://doi.org/10.3390/e22020237
Chicago/Turabian StyleColonna, Gianpiero, and Annarita Laricchiuta. 2020. "Thermodynamic and Transport Properties of Equilibrium Debye Plasmas" Entropy 22, no. 2: 237. https://doi.org/10.3390/e22020237
APA StyleColonna, G., & Laricchiuta, A. (2020). Thermodynamic and Transport Properties of Equilibrium Debye Plasmas. Entropy, 22(2), 237. https://doi.org/10.3390/e22020237





