Leveraging Blockchain Technology for Secure Energy Trading and Least-Cost Evaluation of Decentralized Contributions to Electrification in Sub-Saharan Africa
Abstract
1. Introduction
- Is there any feasible long-term cost-effective energy planning model for energy generation in SSA?
- Are there any solutions to historical antipathy or lack of trust and security that can jeopardize the process of regional decentralized energy cooperation in SSA?
- Are there any technologies that provide a secure trade arrangement for cross-border electricity, which can effectively solve the problem of fair energy trading and payment in SSA?
- This paper proposes a secure BDES that addresses the issue of historical antipathy (i.e., lack of trust) and security in order to establish decentralized electrification in SSA.
- A blockchain-based mechanism for the trading and payment of energy in SSA is proposed to ensure fair regional and cross-border energy trade. New methods of self-consumption and self-sufficiency are included in the proposed energy trading mechanism to enhance energy trading for regional energy producers.
- A cost-effective energy planning model is proposed to quantify the impact of energy reliability on generation costs. The proposed energy planning model is used to compare the economic energy generation costs between CES and DES in SSA.
- Energy trading price negotiation and incentive mechanisms are also proposed to encourage more participation of energy users in energy trading and payment. Also, a mechanism for cryptocurrency trading is introduced to reduce excess rewards and alleviates the electricity debt of customers.
2. Literature Review
2.1. Energy Management in SG
2.2. Blockchain for SG
2.3. Least-Cost Evaluation for Decentralized Electrification in SG
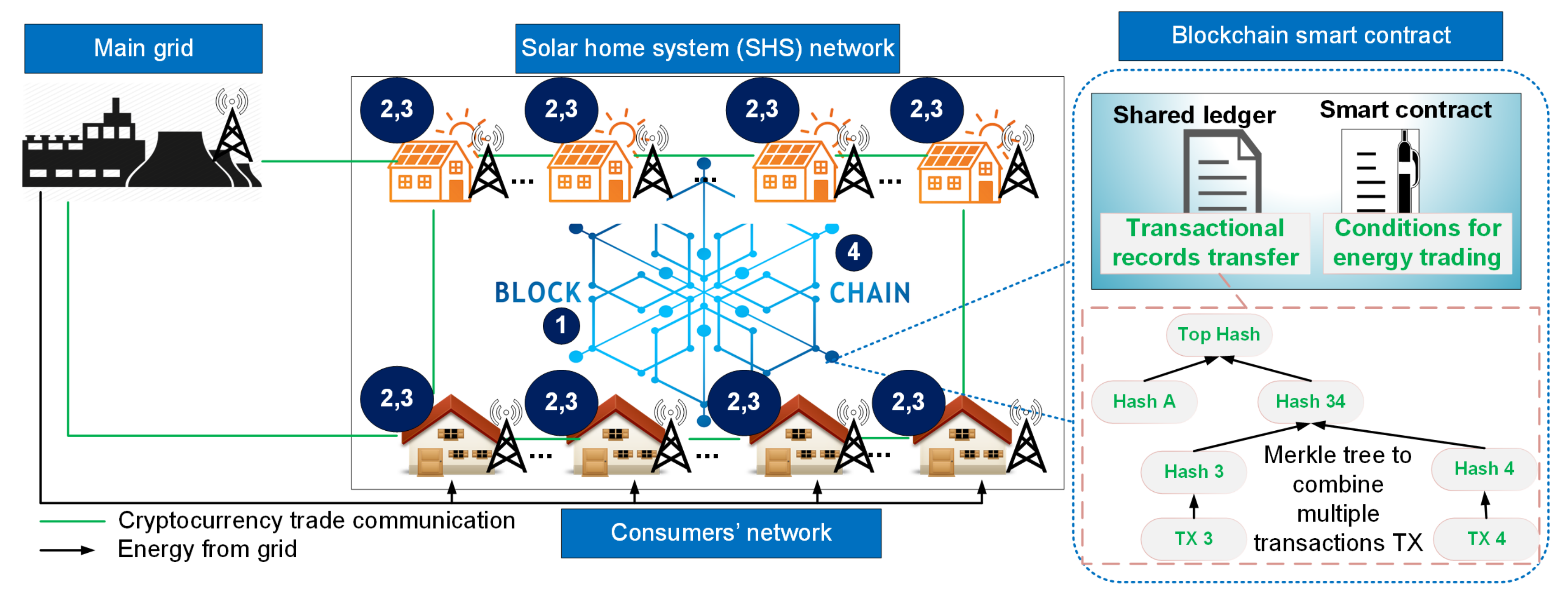
3. Proposed Framework
- The blockchain user creates a new transaction, which is visible to other nodes in the network.
- Each node validates each transaction at a certain period. Invalid transactions are discarded. Contrarily, valid transactions are packed into a new block through the mining process.
- Before a block is committed to the blockchain, a notification is sent to all mining nodes within the blockchain network. Mining nodes, which receive the committed block, will verify the validity of the block with a hashing mechanism [45]. If the block passes the verification test by the majority of mining nodes, then it will be chained at the end of the current blockchain. Thus, a consensus is established. In this paper, proof of authority consensus mechanism is used [46]. The total usage of energy is measured and recorded with the help of smart meter and it indicates the first proof of their work for all prosumers.
3.1. Structure of the Blockchain
3.1.1. Prosumers
3.1.2. Energy Consumers
3.1.3. Smart Contract
3.1.4. Financial Mode
3.1.5. Metering Mode
3.1.6. Trading Platform
3.1.7. Industrial Standard
3.2. Problem Formulations
3.3. The Isoreliability Curve
3.3.1. BDES
3.3.2. CES
3.3.3. DES
3.4. Modeling the Types of Prosumers
| Algorithm 1: Smart contract for SHS |
 |
3.5. Energy Trading of Prosumers in SSA
3.5.1. Regional Sellers of Energy
3.5.2. Regional Buyers of Energy
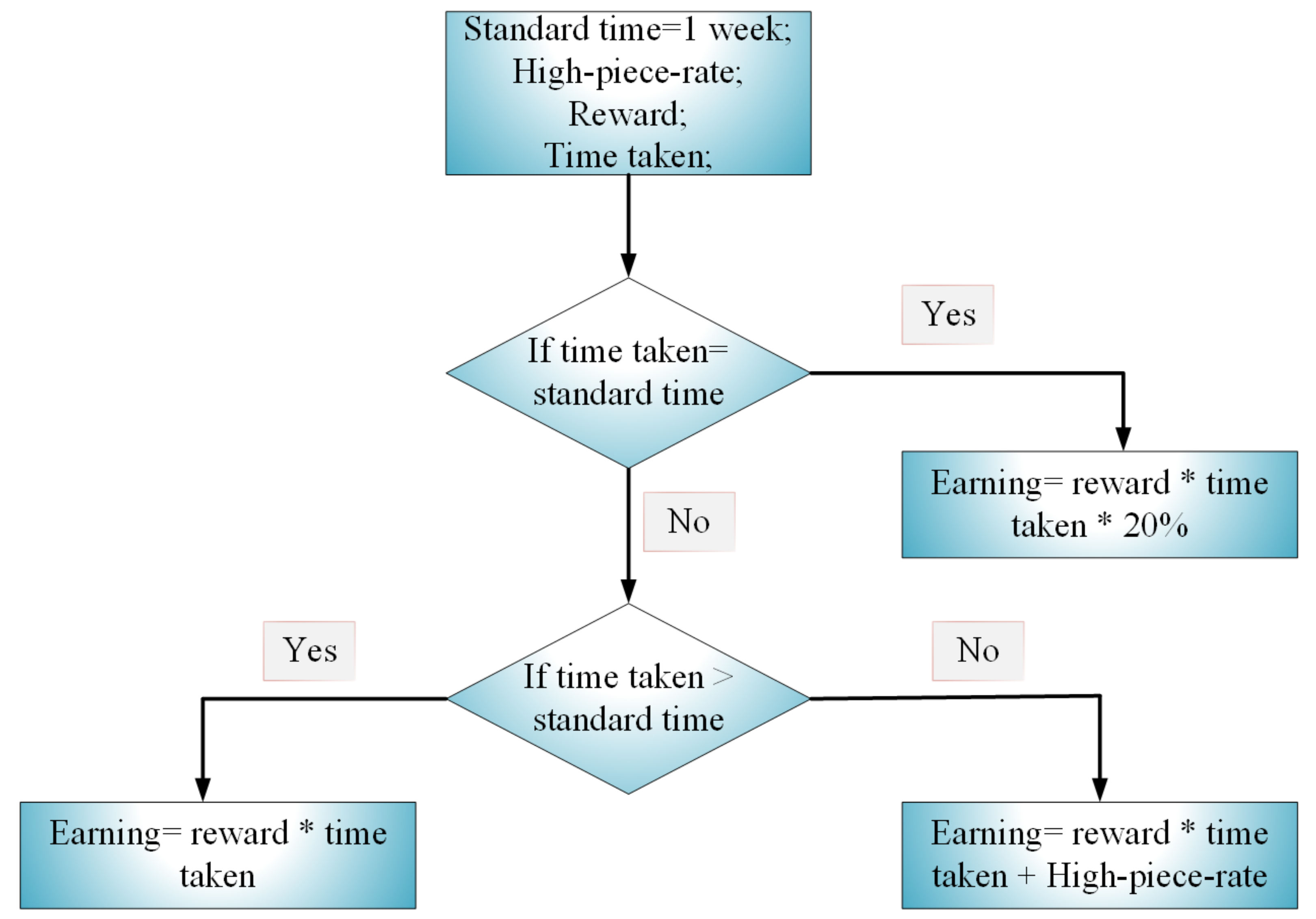
3.6. Blockchain Incentive Mechanism
3.7. Cryptocurrency Trading
- Scope: it includes all the financial levels of prosumers and consumers and the type of RES.
- Capital allocation: it determines the WC and the electricity bill reduction rate. It also determines the length of time that the cryptocurrency will stay relevant.
- Offset policy: it determines whether the offset is necessary to be used in the scheme, what type of offset is allowed and the limit or amount of offset required.
- Trading: it specifies the rules for cryptocurrency trading and the compliance policy.
- Expansion potentials: it is flexible to accommodate larger number of participants and should be compatible with other monetary exchange.
3.8. WC Formulation
4. Simulations and Discussions
4.1. Simulation Parameters
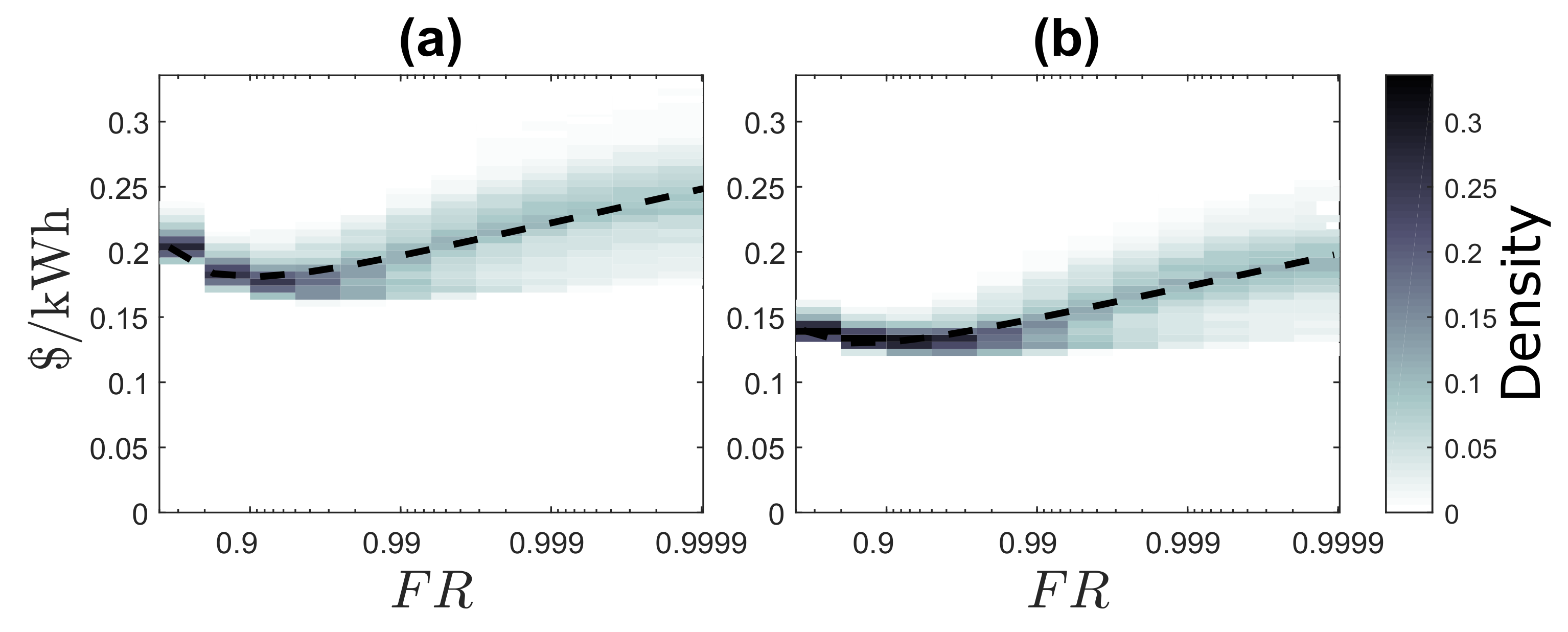
4.2. Evaluation of the Impact of Energy Reliability on Generation Cost based on FR
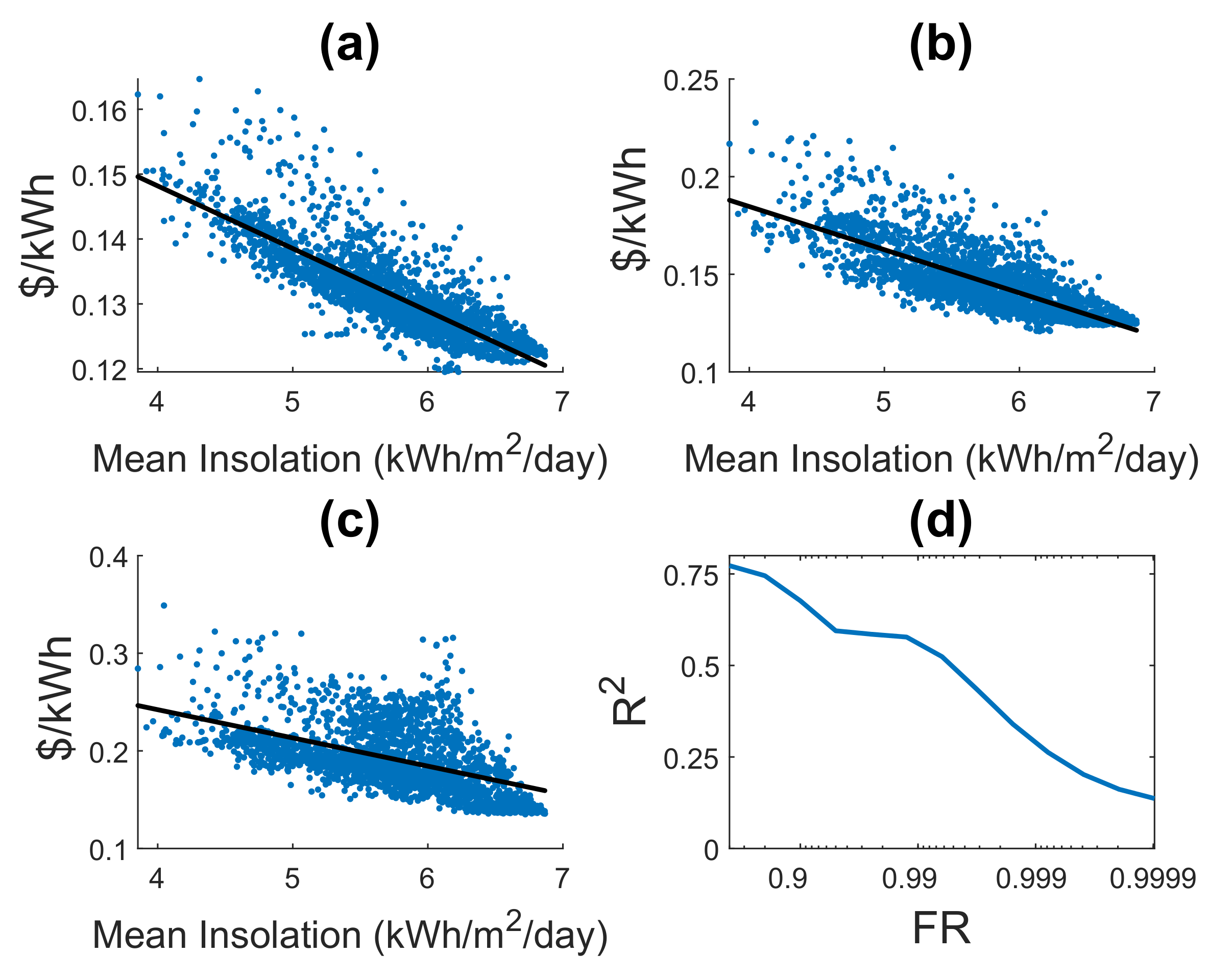
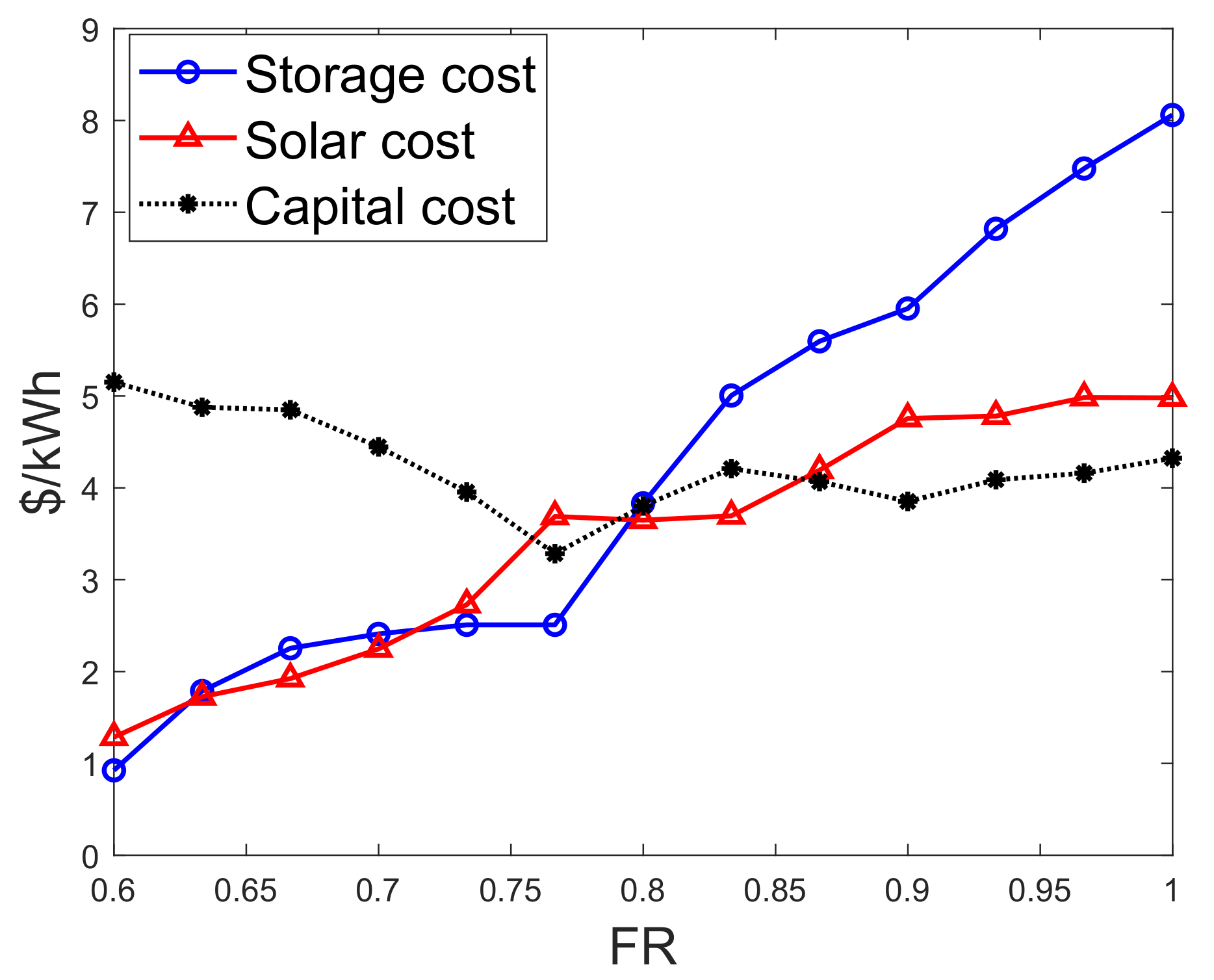
4.2.1. Evaluation of the Energy Cost between Solar Modules and Battery Storage
4.2.2. Comparison between of Isolation and Solar System Using Least-Cost System
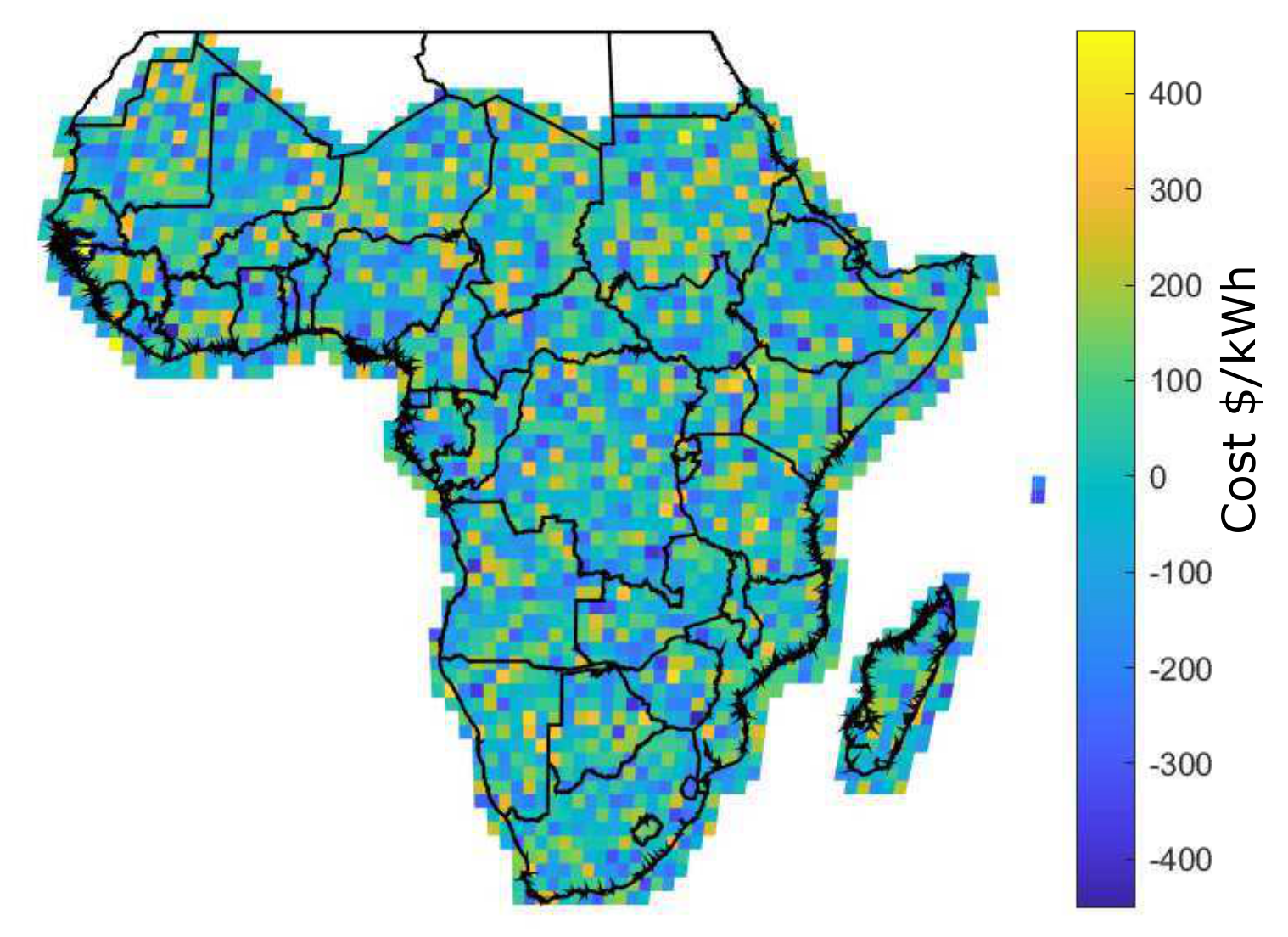
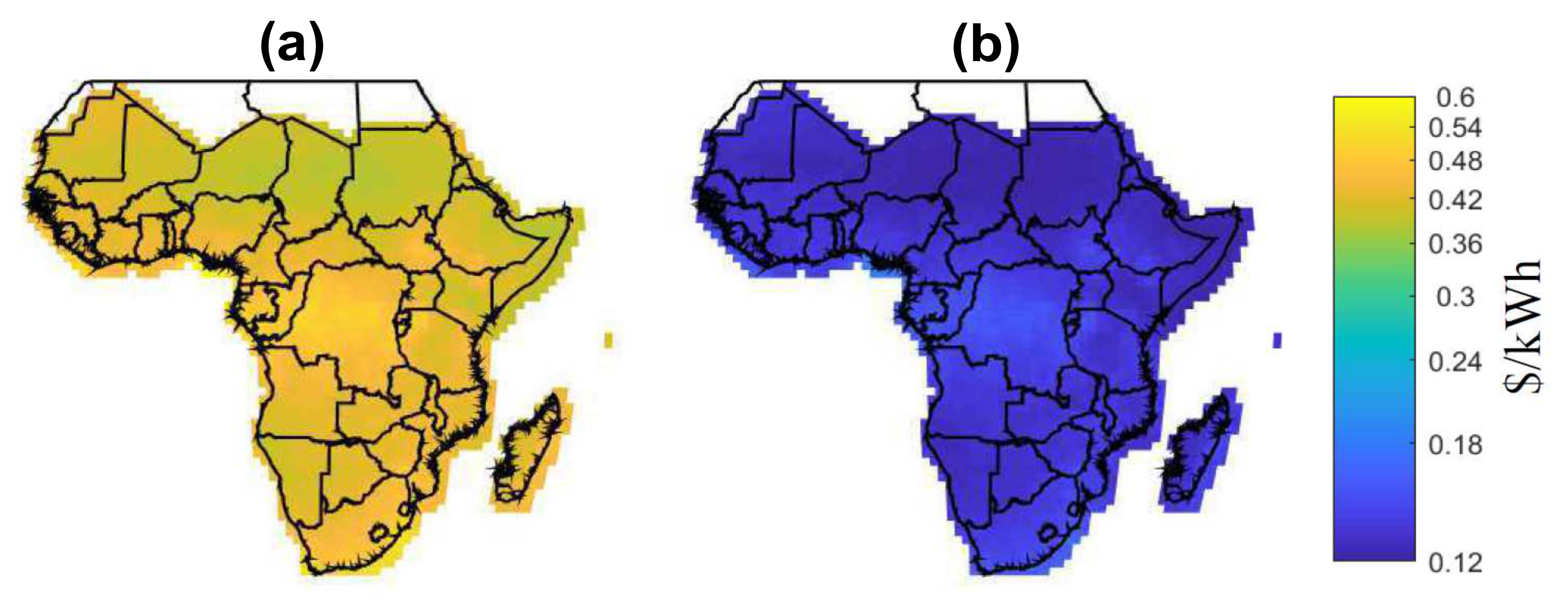
4.2.3. Evaluation of Energy Reliability Premium in SSA
4.2.4. Variation of Load Demand with Respect to FR
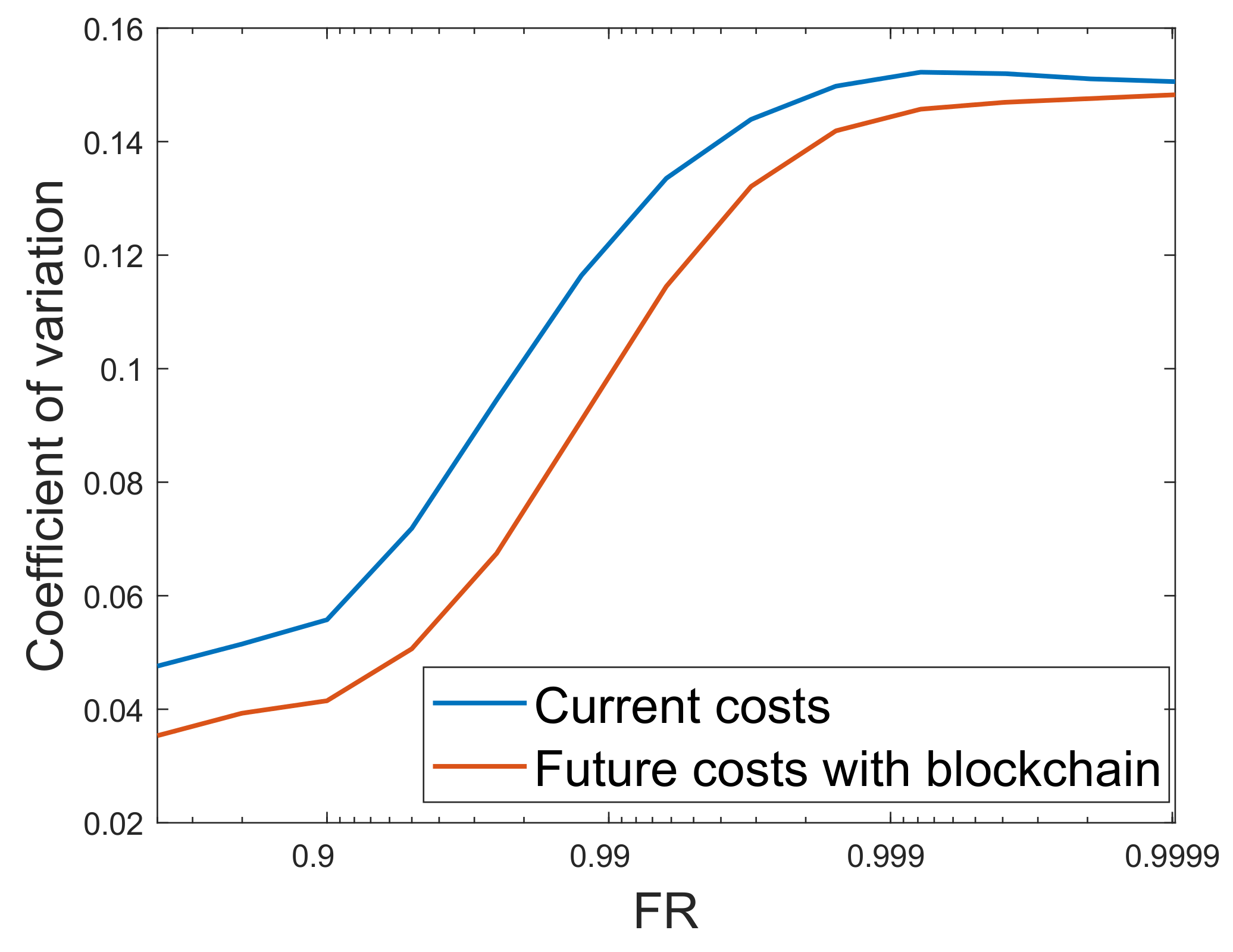
4.2.5. Prediction of the Future Costs with Respect to Isoreliability
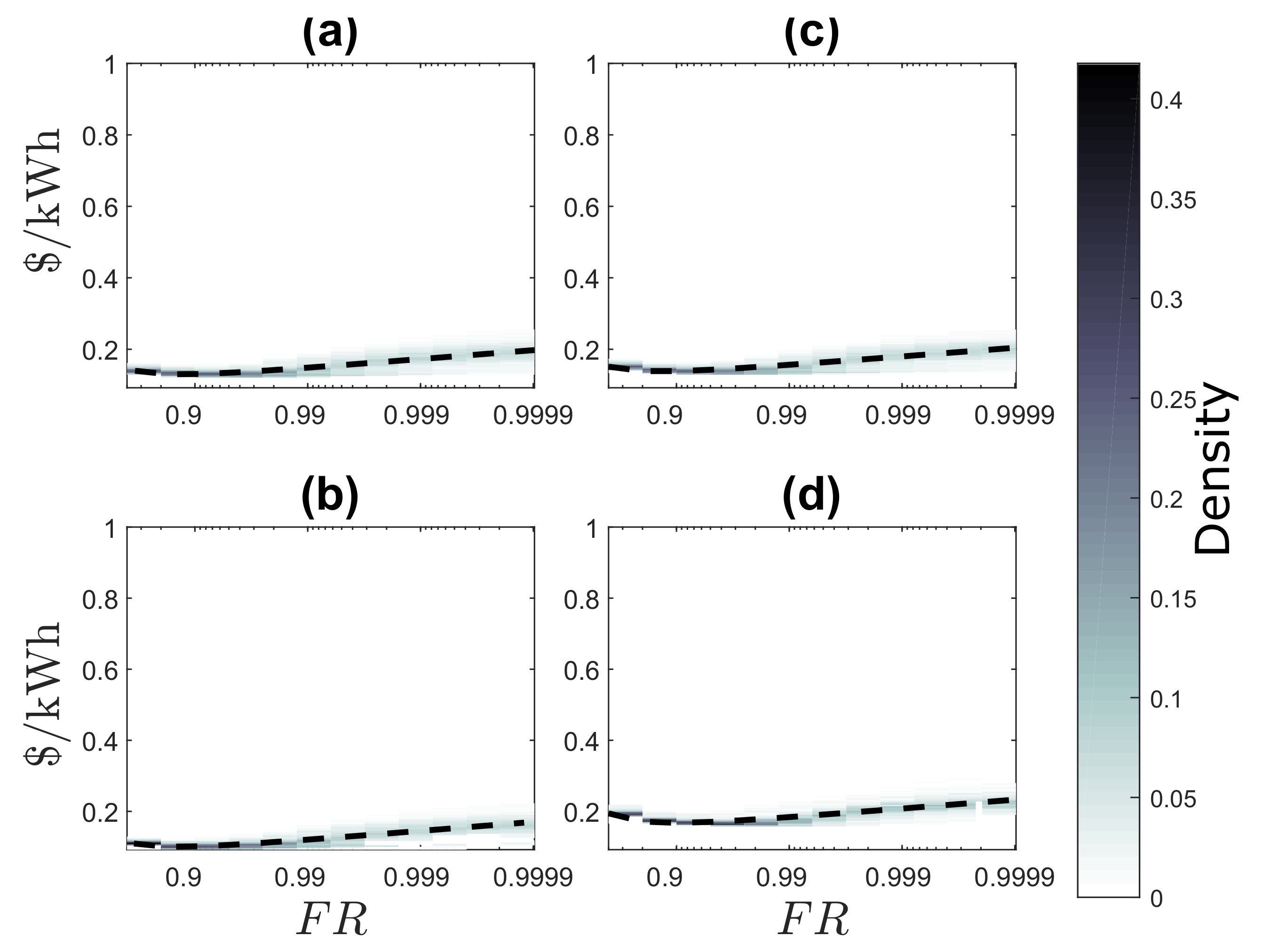
4.2.6. Comparison of the Different Cost Systems
4.2.7. Least-Cost Evaluation for CES, DES, and BDES Contributions to Electrification in SSA
4.3. Evaluation of Blockchain-Based Energy Trading in SSA
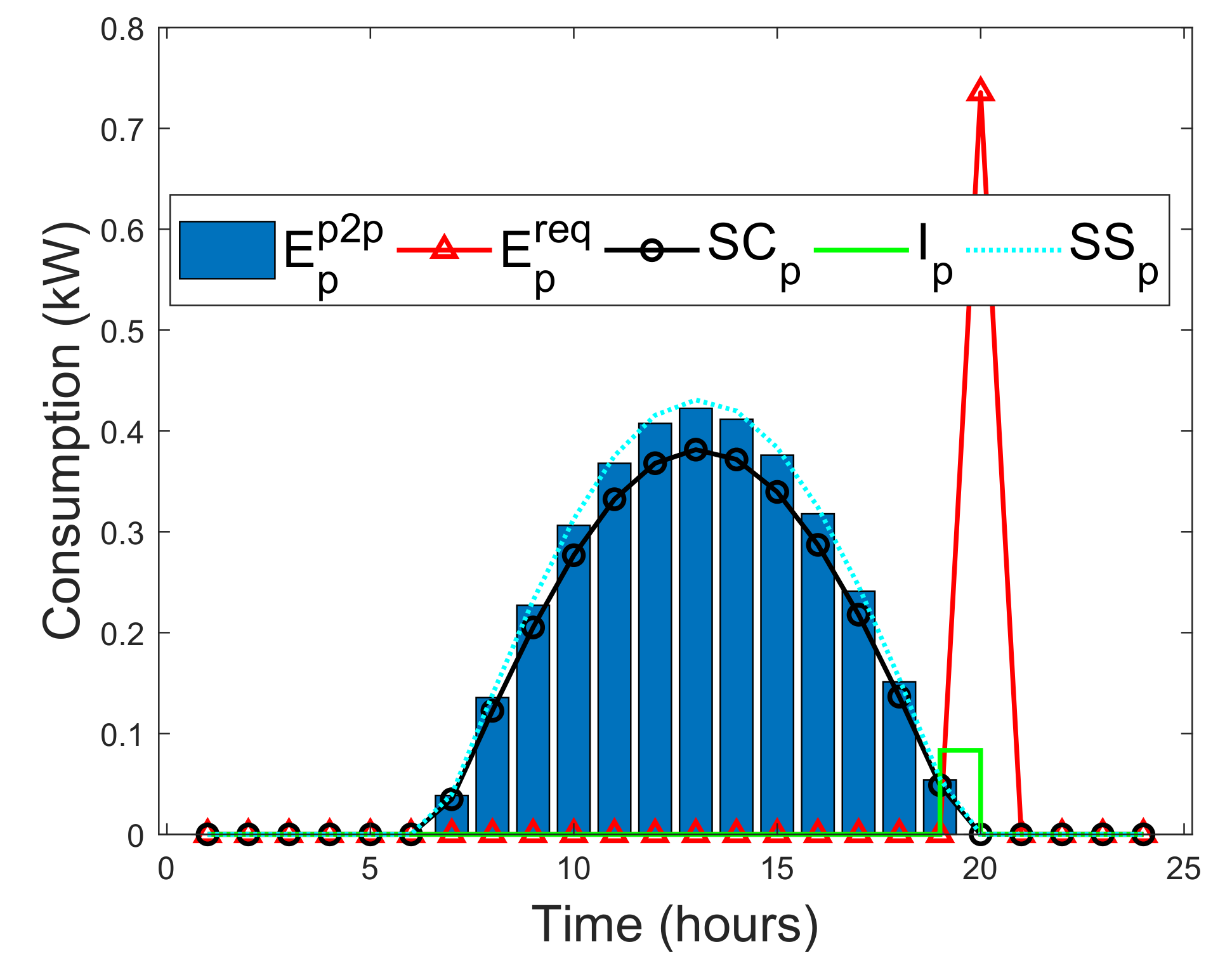
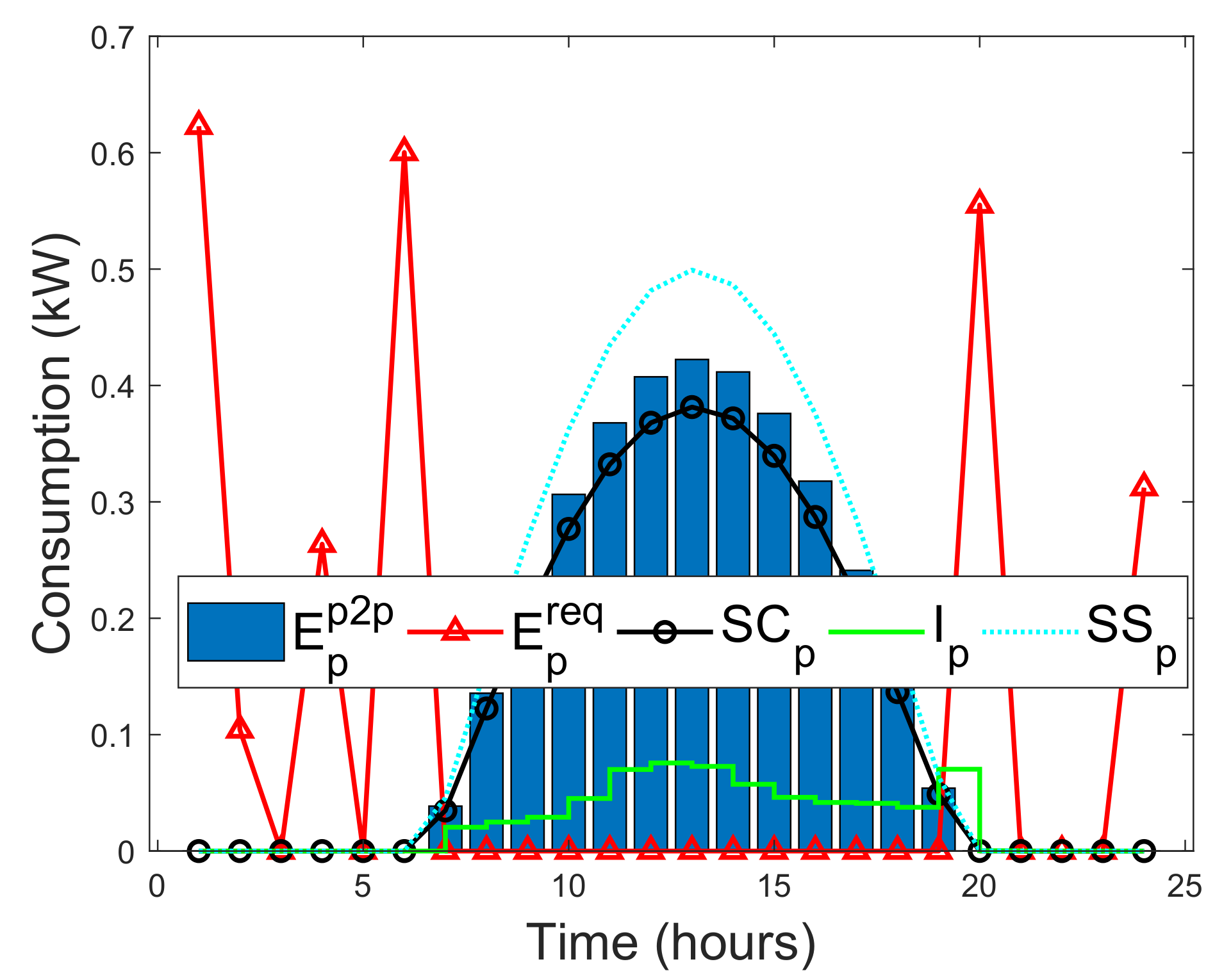
4.3.1. Evaluation of Different Unmet Loads for Blockchain-Based Energy Trading
4.3.2. Comparison between Selling Cost and Buying Cost for Blockchain-Based Energy Trading
5. Research Implications
6. Conclusions
- Is there any feasible long-term cost-effective energy planning model for energy generation in SSA? The framework proposed in this paper provides energy cost planning model that quantifies the impact of reliability on energy cost based on FR. Also, the proposed model estimates the future energy generation cost for 20 years to be 0.049 $/kWh as compared to 0.11 $/kWh for the existing scheme.
- Are there any solutions to historical antipathy or lack of trust and security that can jeopardize the process of regional decentralized energy cooperation in SSA? The proposed framework ensures that a trustful and secure environment is established for cooperation among regional decentralized energy providers. Also, with blockchain smart contract, historical antipathy among regions is eliminated.
- Are there any technologies that provide a trade arrangement for cross-border electricity and can effectively solve the problem of fair energy distribution and payment of electricity bill in SSA? The proposed framework ensures that blockchain-based cross-border energy trading is achieved. Also, the use of cryptocurrency as means of payment is encouraged, which minimizes the vetting process and eliminates the third party system.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BLCOE | Blockchain-based levelized cost of energy |
| BDES | greenBlockchain-based decentralized energy system |
| CP | Critical prosumer |
| CES | Centralized energy system |
| DSM | Demand side management |
| DES | Decentralized energy system |
| DER | Distributed energy resource |
| FR | Fill rate |
| LCOE | Levelized cost of energy |
| NCP | Non-critical prosumer |
| OM | Operation and maintenance cost |
| P2P | Peer-to-peer |
| PV | Photovoltaic |
| RES | Renewable energy source |
| SHS | Solar home system |
| SSA | Sub-Sahara Africa |
| SG | Smart grid |
| SL | Service level |
| WC | Working capital |
| WCR | Working capital ratio |
References
- Ng, E.J.; El-Shatshat, R.A. Multi-microgrid control systems (MMCS). In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar] [CrossRef]
- Bruck, M.; Sandborn, P.; Goudarzi, N. A Levelized Cost of Energy (LCOE) model for wind farms that include Power Purchase Agreements (PPAs). Renew. Energy 2018, 122, 131–139. [Google Scholar] [CrossRef]
- Levin, T.; Thomas, V.M. Least-cost network evaluation of centralized and decentralized contributions to global electrification. Energy Policy 2012, 41, 286–302. [Google Scholar] [CrossRef]
- Bhatti, H.J.; Danilovic, M. Making the World More Sustainable: Enabling Localized Energy Generation and Distribution on Decentralized Smart Grid Systems. World J. Eng. Technol. 2018, 6, 350. [Google Scholar] [CrossRef]
- Patel, N.; Srinivasan, B.; Srinivasan, R. Non-intrusive Appliance Load Monitoring for Electrical Energy Systems Simulation and Analysis-A case study in India. Comput. Aided Chem. Eng. 2016, 38, 2061–2066. [Google Scholar] [CrossRef]
- Energypedia. Solar Home System. Available online: https://energypedia.info/wiki/Solar_Home_Systems_(SHS) (accessed on 1 August 2019).
- International Energy Agency. World Energy Outlook. Available online: http://www.worldenergyoutlook.org/resources/energydevelopment/energyaccessdatabase/ (accessed on 5 August 2019).
- Blimpo, M.P.; Cosgrove-Davies, M. Electricity access in Sub-Saharan Africa: Uptake, reliability, and complementary factors for economic impact. World Bank Publ. 2019, 1, 1–167. [Google Scholar]
- Lowitzsch, J. Financing Renewables While Implementing Energy Efficiency Measures through Consumer Stock Ownership Plans (CSOPs)-The H2020 Project Score; IOP Publishing: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- Meierding, E. Energy security and sub-Saharan Africa. Inst. Dev. Policy Rev. Intern. Politique Dev. 2011, 2, 2. [Google Scholar] [CrossRef]
- Prasad, J.; Samikannu, R. Barriers to implementation of smart grids and virtual power plant in sub-saharan region-focus Botswana. Energy Rep. 2018, 4, 119–128. [Google Scholar]
- Chang, G.; Jones, C.A.; Roberts, J.D.; Neary, V.S. A comprehensive evaluation of factors affecting the levelized cost of wave energy conversion projects. Renew. Energy 2018, 127, 344–354. [Google Scholar] [CrossRef]
- Tu, Q.; Betz, R.; Mo, J.; Fan, Y.; Liu, Y. Achieving grid parity of wind power in China–Present levelized cost of electricity and future evolution. Appl. Energy 2019, 250, 1053–1064. [Google Scholar] [CrossRef]
- Shea, R.P.; Ramgolam, Y.K. Applied levelized cost of electricity for energy technologies in a small island developing state: A case study in Mauritius. Renew. Energy 2019, 132, 1415–1424. [Google Scholar] [CrossRef]
- Hulio, Z.H.; Jiang, W. Assessment of the apparent performance characterization along with levelized cost of energy of wind power plants considering real data. Energy Explor. 2018, 36, 1708–1728. [Google Scholar] [CrossRef]
- Mendicino, L.; Menniti, D.; Pinnarelli, A.; Sorrentino, N. Corporate power purchase agreement: Formulation of the related levelized cost of energy and its application to a real life case study. Appl. Energy 2019, 253, 113577. [Google Scholar] [CrossRef]
- Hwang, S.H.; Kim, M.K.; Ryu, H.S. Real Levelized Cost of Energy with Indirect Costs and Market Value of Variable Renewables: A Study of the Korean Power Market. Energies 2019, 12, 2459. [Google Scholar] [CrossRef]
- Gioutsos, D.M.; Blok, K.; Velzen, L.; Moorman, S. Cost-optimal electricity systems with increasing renewable energy penetration for islands across the globe. Appl. Energy 2019, 226, 437–449. [Google Scholar] [CrossRef]
- Lee, J.T.; Callaway, D.S. The cost of reliability in decentralized solar power systems in sub-Saharan Africa. Nat. Energy 2018, 3, 960. [Google Scholar] [CrossRef]
- Bazilian, M.; Sagar, A.; Detchon, R.; Yumkella, K. More heat and light. Energy Policy 2010, 38, 5409–5412. [Google Scholar] [CrossRef]
- Samuel, O.; Javaid, N.; Rabiya, K.; Muhammad, I.; Moshen, G. Case Study of Direct Communication based Solar Power Systems in Sub-Saharan Africa for Levelled Energy Cost Using Blockchain. In Proceedings of the IEEE International Conference on Communications, Dublin, Ireland, 7–11 June 2020. [Google Scholar]
- Morstyn, T.; Teytelboym, A.; McCulloch, M.D. Bilateral contract networks for peer-to-peer energy trading. IEEE Trans. Smart Grid 2018, 10, 2026–2035. [Google Scholar] [CrossRef]
- Nazari, M.H.; Costello, Z.; Feizollahi, M.J.; Grijalva, S.; Egerstedt, M. Distributed frequency control of prosumer-based electric energy systems. IEEE Trans. Power Syst. 2014, 29, 2934–2942. [Google Scholar] [CrossRef]
- Morstyn, T.; Farrell, N.; Darby, S.J.; McCulloch, M.D. Using peer-to-peer energy-trading platforms to incentivize prosumers to form federated power plants. Nat. Energy 2018, 3, 94. [Google Scholar] [CrossRef]
- Khalid, A.; Javaid, N.; Mateen, A.; Ilahi, M.; Saba, T.; Rehman, A. Enhanced time-of-use electricity price rate using game theory. Electronics 2019, 8, 48. [Google Scholar] [CrossRef]
- Iria, J.P.; Soares, F.J.; Matos, M.A. Trading small prosumers flexibility in the energy and tertiary reserve markets. IEEE Trans. Smart Grid 2018, 10, 2371–2382. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Liddell, P.; Bean, R.; Poor, H.V. Peer-to-peer energy trading with sustainable user participation: A game theoretic approach. IEEE Access 2018, 6, 62932–62943. [Google Scholar] [CrossRef]
- Paudel, A.; Chaudhari, K.; Long, C.; Gooi, H.B. Peer-to-Peer Energy Trading in a Prosumer-Based Community Microgrid: A Game-Theoretic Model. IEEE Trans. Ind. Electron. 2018, 66, 6087–6097. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Morstyn, T.; McCulloch, M.D.; Poor, H.V.; Wood, K.L. A motivational game-theoretic approach for peer-to-peer energy trading in the smart grid. Appl. Energy 2019, 243, 10–20. [Google Scholar] [CrossRef]
- Livingston, D.; Sivaram, V.; Freeman, M.; Fiege, M. Applying Block chain Technology to Electric Power Systems. Discuss. Pap. 2018, 1, 1–37. [Google Scholar]
- Coinfox. European Utilities to Test Blockchain-Based Energy Trading. Available online: http://www.coinfox.info/news/7037-european-utilities-to-test-blockchain-based-energy-trading (accessed on 29 November 2019).
- Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets: A case study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
- Münsing, E.; Mather, J.; Moura, S. Blockchains for decentralized optimization of energy resources in microgrid networks. In Proceedings of the IEEE Conference on Control Technology and Applications (CCTA), Mauna Lani, HI, USA, 27–30 August 2017; pp. 2164–2171. [Google Scholar]
- Mylrea, M.; Gourisetti, S.N.G. Blockchain for smart grid resilience: Exchanging distributed energy at speed, scale and security. In Proceedings of the Resilience Week (RWS), Wilmington, DE, USA, 18–22 September 2017. [Google Scholar] [CrossRef]
- Khatoon, A.; Verma, P.; Southernwood, J.; Massey, B.; Corcoran, P. Blockchain in Energy Efficiency: Potential Applications and Benefits. Energies 2019, 12, 3317. [Google Scholar] [CrossRef]
- Thomason, J.; Ahmad, M.; Bronder, P.; Hoyt, E.; Pocock, S.; Bouteloupe, J.; Donaghy, K.; Huysman, D.; Willenberg, T.; Joakim, B.; et al. Blockchain—Powering and Empowering the Poor in Developing Countries. Transforming Climate Finance and Green Investment with Blockchains; Academic Press: San Francisco, CA, USA, 2018; pp. 137–152. [Google Scholar]
- Chelley-Steeley, P.; Lambertides, N.; Savva, C.S. Sentiment, order imbalance, and co-movement: An examination of shocks to retail and institutional trading activity. Eur. Financ. Manag. 2019, 25, 116–159. [Google Scholar] [CrossRef]
- Wu, J.; Tran, N. Application of blockchain technology in sustainable energy systems: An overview. Sustainability 2018, 10, 3067. [Google Scholar] [CrossRef]
- Li, W. Reliability Assessment of Electric Power Systems Using Monte Carlo Methods; Springer US: New York, NY, USA, 2013; pp. 1–361. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Y.; Niyato, D.; Wang, P.; Han, Z. When mobile blockchain meets edge computing. IEEE Commun. Mag. 2018, 56, 33–39. [Google Scholar] [CrossRef]
- Sultana, T.; Almogren, A.; Akbar, M.; Zuair, M.; Ullah, I.; Javaid, N. Data Sharing System Integrating Access Control Mechanism using Blockchain-Based Smart Contracts for IoT Devices. Appl. Sci. 2020, 10, 488. [Google Scholar] [CrossRef]
- Alghamdi, T.A.; Ali, I.; Javaid, N.; Shafiq, M. Secure Service Provisioning Scheme for Lightweight IoT Devices with a Fair Payment System and an Incentive Mechanism based on Blockchain; IEEE Access: Piscataway, NJ, USA, 2019; pp. 82–93. [Google Scholar] [CrossRef]
- Naz, M.; Al-zahrani, F.A.; Khalid, R.; Javaid, N.; Qamar, A.M.; Afzal, M.K.; Shafiq, M. A Secure Data Sharing Platform Using Blockchain and Interplanetary File System. Sustainability 2019, 11, 7054. [Google Scholar] [CrossRef]
- Rehman, M.; Javaid, N.; Awais, M.; Imran, M.; Naseer, N. Cloud based secure service providing for IoTs using blockchain. In Proceedings of the IEEE Global Communications Conference: Communication Information Systems Security, Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Samuel, O.; Javaid, N.; Awais, M.; Ahmed, Z.; Imran, M.; Guizani, M. A Blockchain Model for Fair Data Sharing in Deregulated Smart Grids. In Proceedings of the IEEE Global Communications Conference: Communication Information Systems Security, Waikoloa, HI, USA, 9–13 December 2019. [Google Scholar]
- Wu, J.; Hu, J.; Ai, X.; Zhang, Z.; Hu, H. Multi-time scale energy management of electric vehicle model-based prosumers by using virtual battery model. Appl. Energy 2019, 251, 113312. [Google Scholar] [CrossRef]
- Hou, J.; Wang, H.; Liu, P. Applying the blockchain technology to promote the development of distributed photovoltaic in China. Int. J. Energy Res. 2018, 42, 2050–2069. [Google Scholar] [CrossRef]
- Aujla, G.S.; Kumar, N.; Singh, M.; Zomaya, A.Y. Energy trading with dynamic pricing for electric vehicles in a smart city environment. J. Parallel Distrib. Comput. 2019, 127, 169–183. [Google Scholar] [CrossRef]
- Xu, M.; Niu, J.; Lin, Y. An efficient method for fractional nonlinear differential equations by quasi-Newton’s method and simplified reproducing kernel method. Math. Methods Appl. Sci. 2018, 41, 5–14. [Google Scholar] [CrossRef]
- Thomas, L.; Long, C.; Burnap, P.; Wu, J.; Jenkins, N. Automation of the supplier role in the GB power system using blockchain-based smart contracts. In Proceedings of the 24th International Conference Exhibition on Electricity Distribution (CIRED), Glasgow, UK, 12–15 June 2017; pp. 2619–2623. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef]
- Merei, G.; Moshövel, J.; Magnor, D.; Sauer, D.U. Optimization of self-consumption and techno-economic analysis of PV-battery systems in commercial applications. Appl. Energy 2016, 168, 171–178. [Google Scholar] [CrossRef]
- Streatfeild, J.E. Low Electricity Supply in Sub-Saharan Africa: Causes, Implications, and Remedies. J. Int. Commer. Econ. 2018, 1, 1–16. [Google Scholar]
- Business Jargons. Types of Incentive Schemes. Available online: https://https://businessjargons.com/types-of-incentive-schemes.html/ (accessed on 31 October 2019).
- Lighting Africa. Off-Grid Solar Market Trends Report. Available online: https://www.lightingafrica.org/wp-content/uploads/2018/02/2018_Off_Grid_Solar_Market_Trends_Report_Full.pdf (accessed on 12 July 2019).
- Ikram, A.; Su, Q.; Fiaz, M. Pakistan’s persistent energy crisis and performance of private power producers. Int. J. Bus. Perform. Manag. 2018, 19, 237–252. [Google Scholar] [CrossRef]
- Business Dictionary. What Is Negative Cash Flow. Available online: http://www.businessdictionary.com/definition/negative-cash-flow.html (accessed on 22 August 2019).
- National Aeronautics and Space Administration. Power Project Data Sets. Available online: https://power.larc.nasa.gov/ (accessed on 31 October 2019).
- Energypedia. Burkina Faso Energy Situation. Available online: https://energypedia.info/wiki/Burkina_Faso_Energy_Situation (accessed on 4 December 2019).
- International Trade Administration. Gambia-Energy. Available online: https://www.export.gov/article?id=Gambia-Energy (accessed on 4 December 2019).
- Surroop, D.; Raghoo, P. Renewable energy to improve energy situation in African island states. Renew. Sustain. Energy Rev. 2018, 88, 176–183. [Google Scholar] [CrossRef]
- Salif, S.; Sarkodie, O.W.; Gnamien, C.K. Renewable Energy Technology Assessment: Case Study of Senegal, Ghana & Cote d’Ivoire. Available online: https://energypedia.info/images/c/c5/Renewable_Energy_Technology_Assessment_Case_Study_of_Senegal_Ghana_and_CC3B4te_dE28099Ivoire.pdf (accessed on 4 December 2019).
- United States Agency for International Development. Liberia Power Africa Fact Sheet. Available online: https://www.usaid.gov/powerafrica/liberia (accessed on 4 December 2019).
- Touré, A.F.; Addouche, S.A.; Danioko, F.; Diourté, B.; Mhamedi, A.E. Hybrid Systems Optimization: Application to Hybrid Systems Photovoltaic Connected to Grid. A Mali Case Study. Sustainability 2019, 11, 2356. [Google Scholar] [CrossRef]
- Asumadu-Sarkodie, S.; Owusu, P.A. A multivariate analysis of carbon dioxide emissions, electricity consumption, economic growth, financial development, industrialization, and urbanization in Senegal. Energy Sources Part B Econ. Plan. Policy 2017, 12, 77–84. [Google Scholar] [CrossRef]
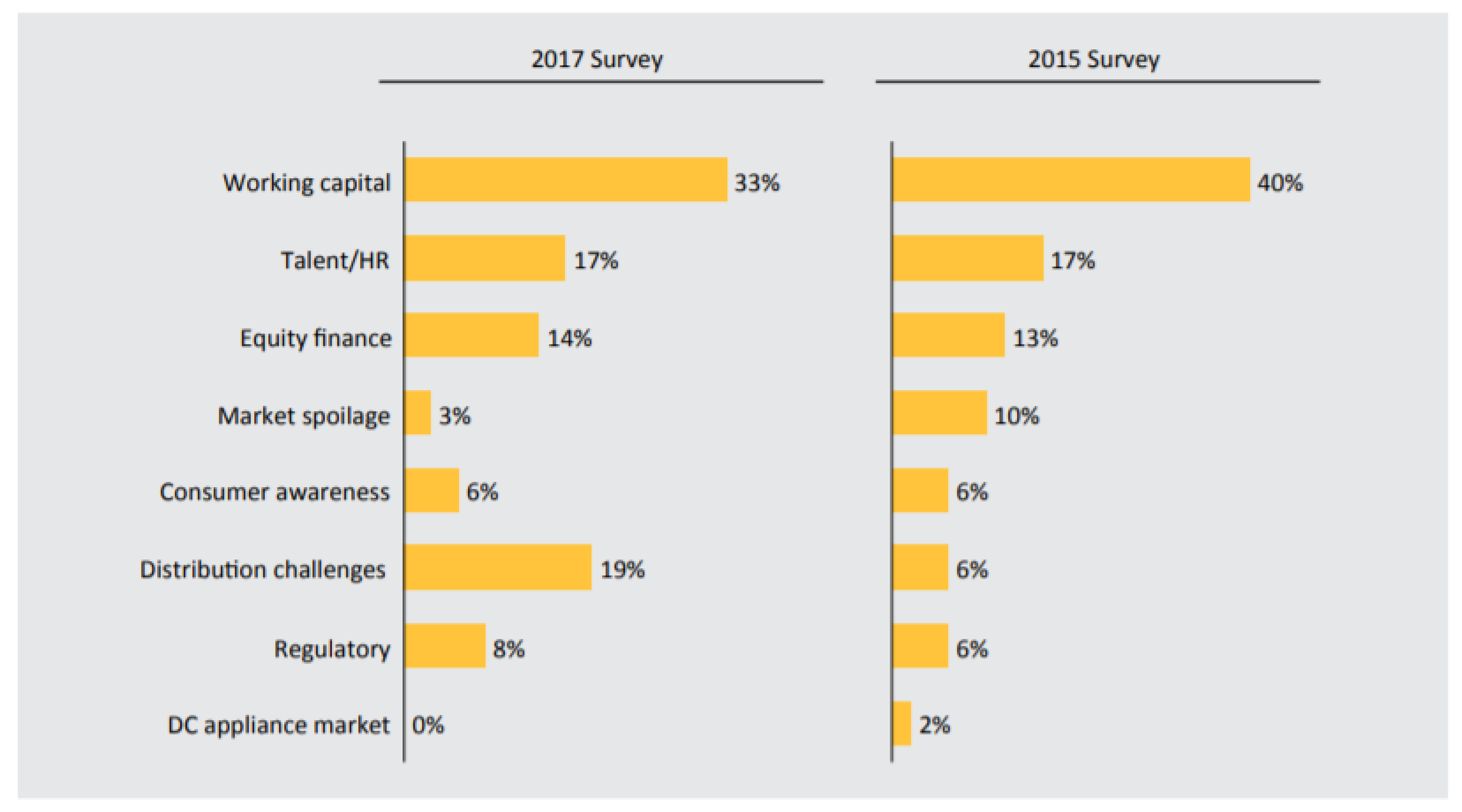

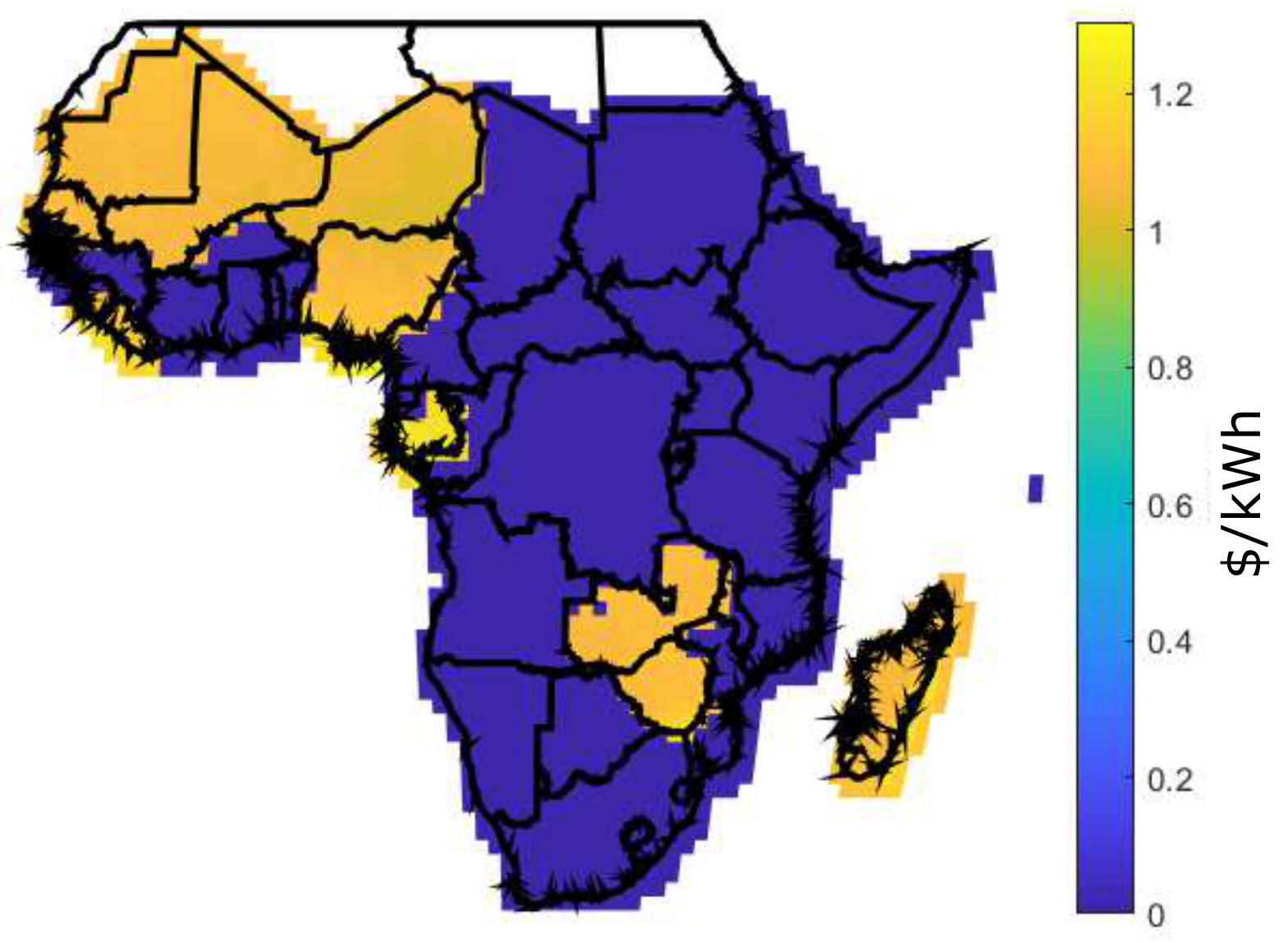
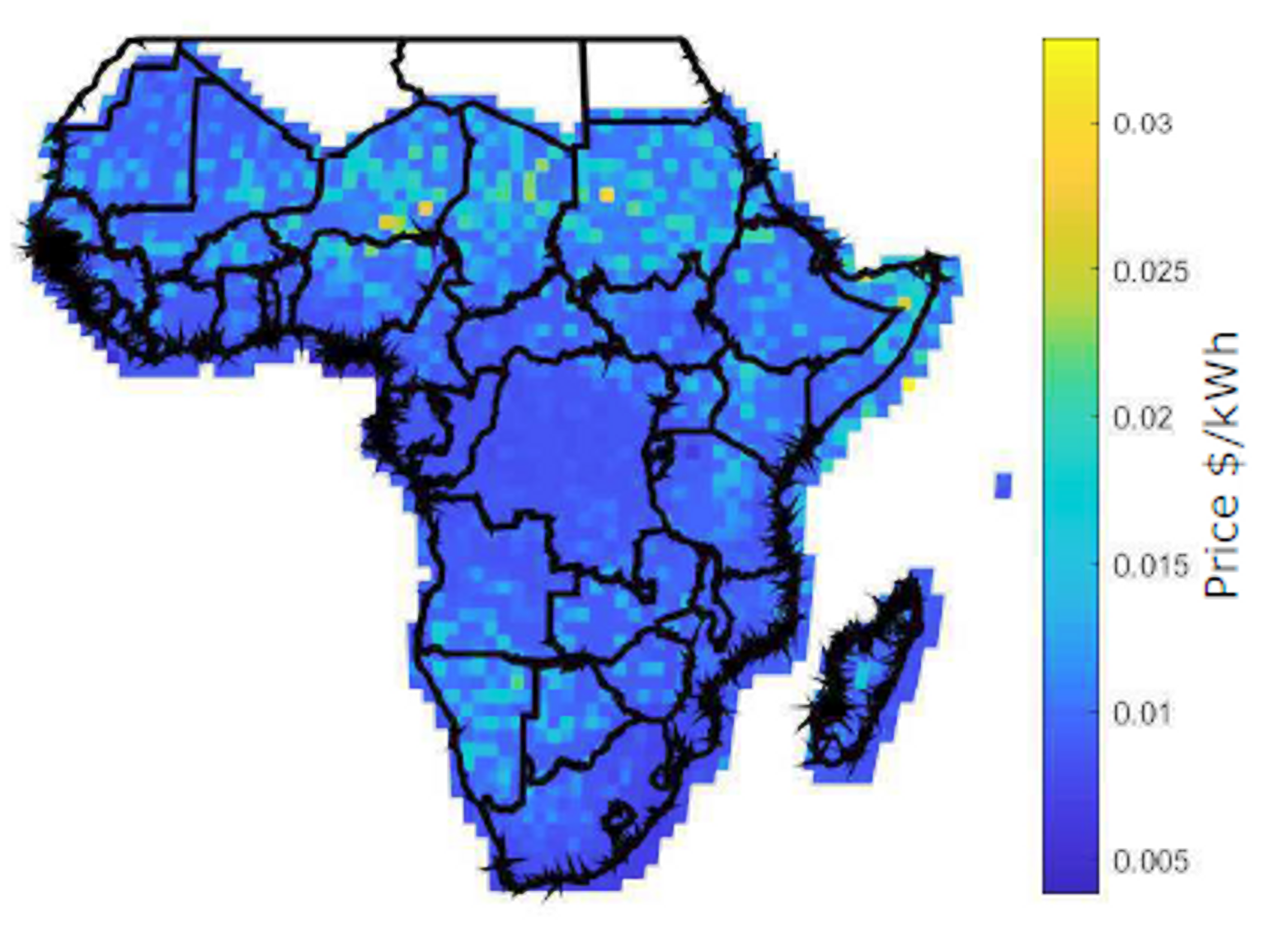

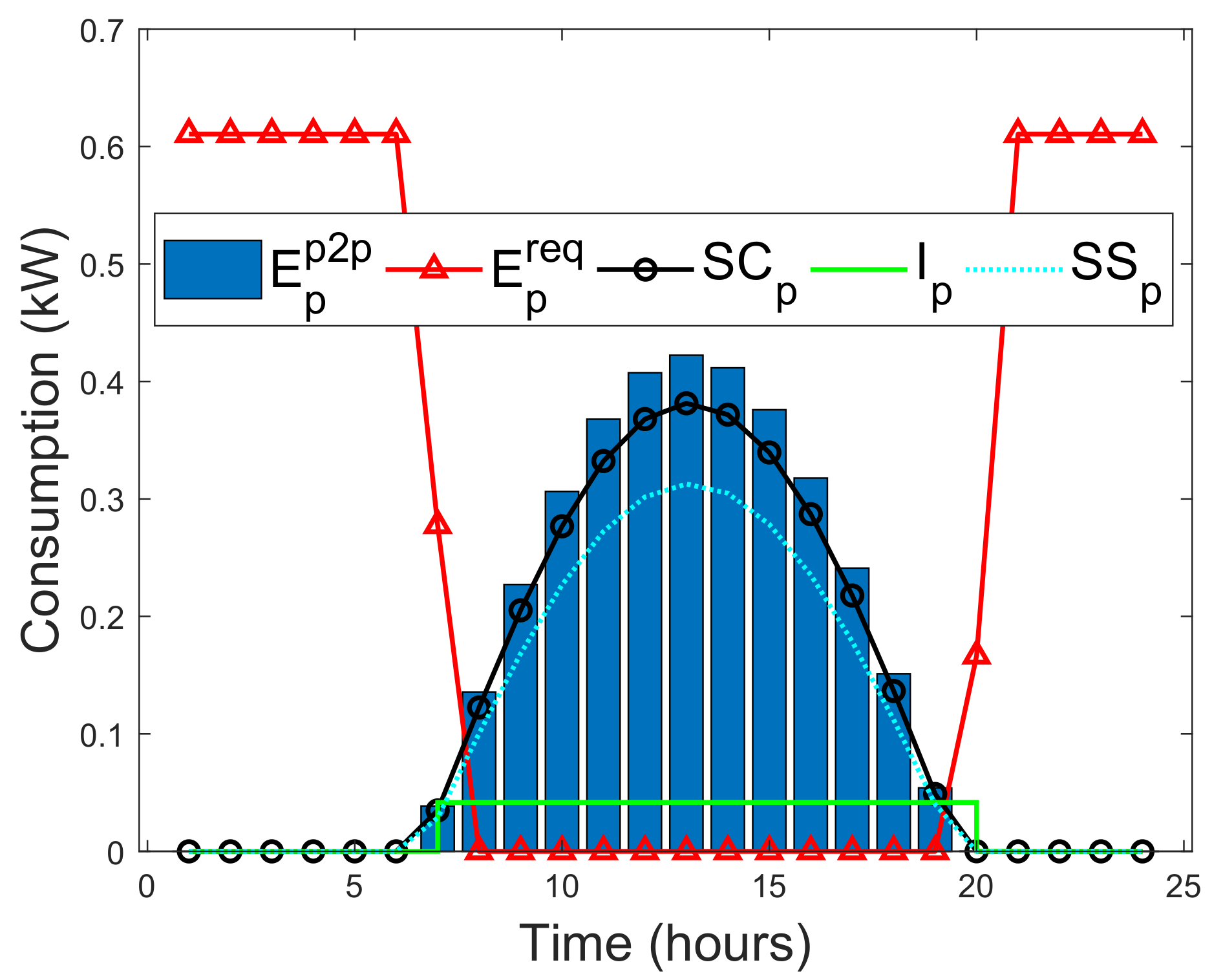
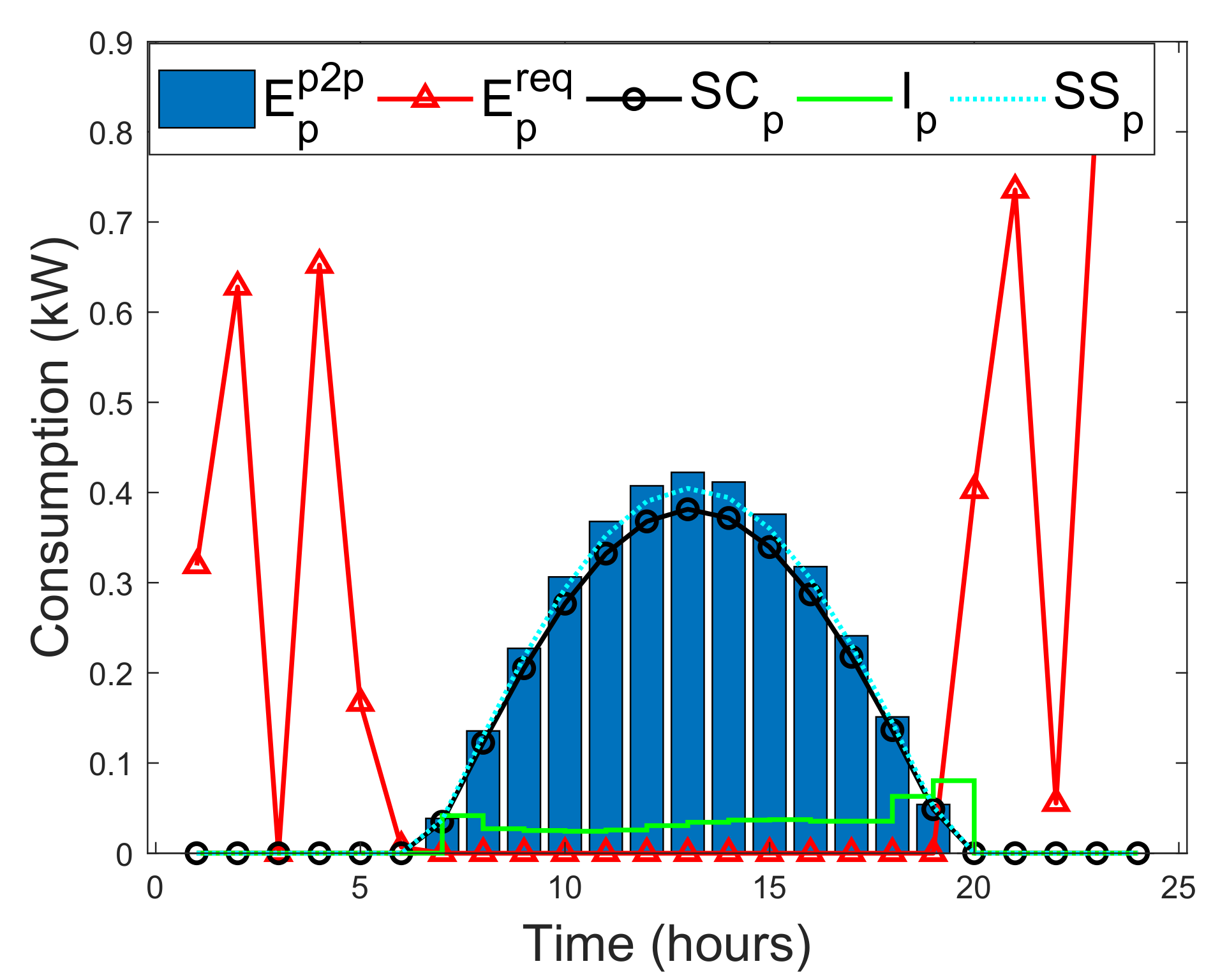
| Capital Utilization | Values ($) | Capital Source | Values ($) |
|---|---|---|---|
| Receivable funding | 3350–3725 | Operating cash | 900–1000 |
| Inventories funding | 1275–1425 | Change in payable | 225–250 |
| Capital expenditure | 475–550 | External debt | 2600–2850 |
| External equity | 1175–1325 | ||
| External grants | 200–275 |
| 2017 | Future (2022) | |
|---|---|---|
| Costs of solar | ||
| Module + d.c balance of system | 1.00 | 0.50 |
| Charge controller | 0.20 | 0.10 |
| Total ($/W) | 1.20 | 0.60 |
| Costs of battery | ||
| Total ($/kW) | 400 | 100 |
| Costs of load | ||
| Inverter | 0.30 | 0.15 |
| Soft costs + d.c balance of system | 1.00 | 0.50 |
| Total ($/W) | 1.30 | 0.65 |
| Other assumptions | ||
| Operation and Maintenance | 100 $/kW | |
| Length of project | 20 years | |
| Battery replacement | 10 years | |
| Discount | 10% |
| Country | Retail Price at 100 kWh/month | FR | CES ($/kWh) | DES ($/kWh) | BDES ($/kWh) | |||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | |||
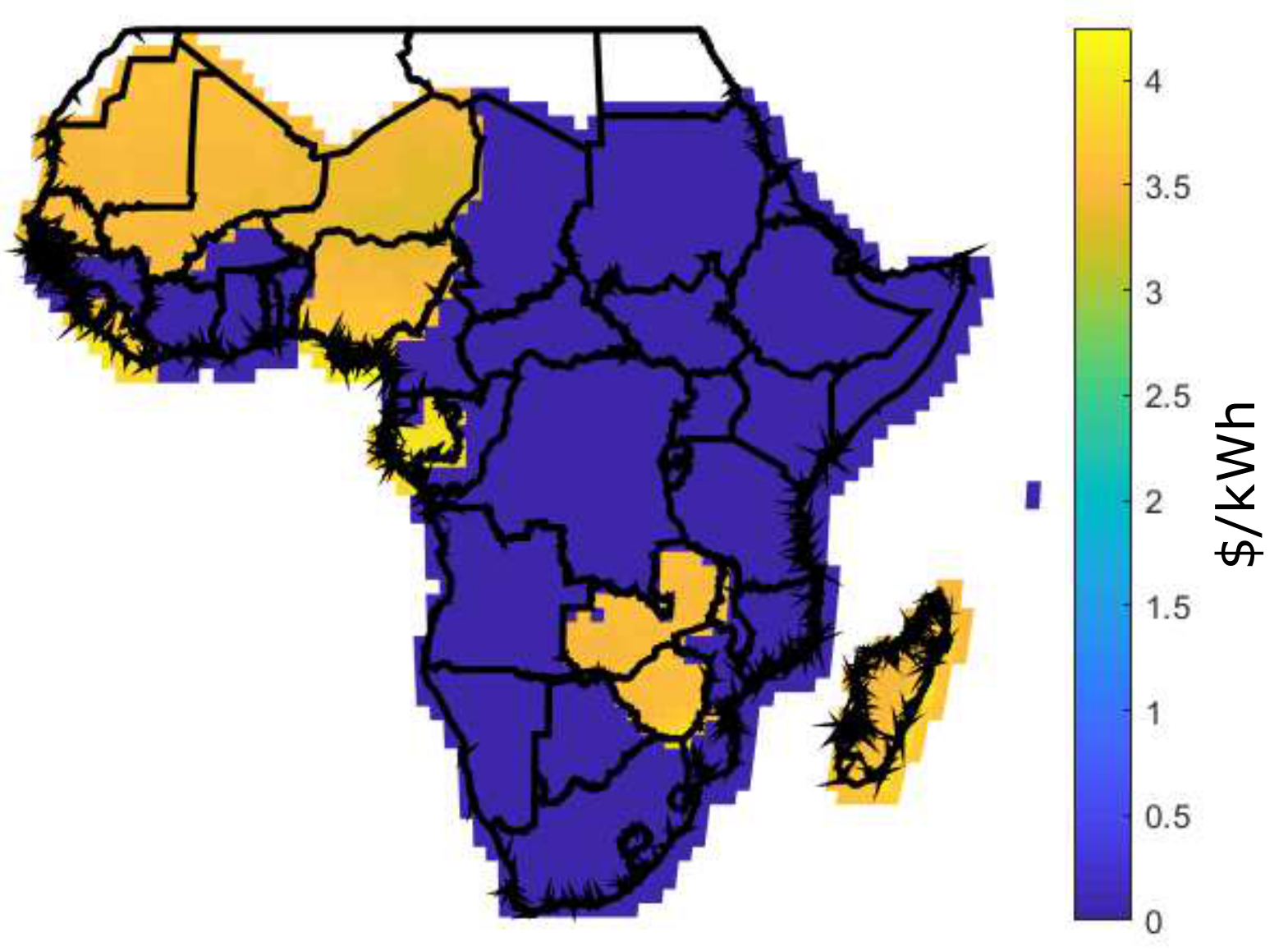
| Angola | 0.04 | 0.6000 | 0.0681 | 0.2424 | 0.1629 | 0.5805 | 0.0834 | 0.2971 |
| Benin | 0.30 | 0.6000 | 0.4519 | 0.6431 | 0.7998 | 1.0977 | 0.4093 | 0.5617 |
| Botswana | 0.10 | 0.6000 | 0.1445 | 0.3678 | 0.3056 | 0.7761 | 0.1564 | 0.3972 |
| Burkina Faso | 0.31 | 0.6000 | 0.9129 | 1.2008 | 0.8218 | 1.0667 | 0.4205 | 0.5459 |
| Burundi | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Cameroon | 0.10 | 0.6000 | 0.2921 | 0.5823 | 0.5239 | 0.9731 | 0.2681 | 0.4980 |
| Central African Republic | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Chad | 0.18 | 0.6000 | 0.1665 | 0.5073 | 0.2102 | 0.6362 | 0.1075 | 0.3256 |
| Congo | 0.00 | 0.6000 | 0.6634 | 1.0723 | 0.6988 | 1.1298 | 0.3576 | 0.5782 |
| Congo drc | 0.12 | 0.6000 | 0.0862 | 0.2702 | 0.2071 | 0.6488 | 0.1060 | 0.3320 |
| Co´te d’ivoire | 0.27 | 0.6000 | 0.6105 | 1.4788 | 0.3595 | 0.8475 | 0.1840 | 0.4337 |
| Djibouti | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Equatorial Guinea | 0.00 | 0.6000 | 1.4697 | 1.2170 | 1.5458 | 1.2802 | 0.7911 | 0.6552 |
| Eritrea | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Ethiopia | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Gabon | 0.25 | 0.6000 | 2.3482 | 0.0067 | 2.4458 | 0.0557 | 1.2517 | 0.0285 |
| Gambia | 0.23 | 0.6000 | 2.4512 | 0.1038 | 2.2143 | 0.0048 | 1.1332 | 0.0024 |
| Ghana | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Guinea-bissau | 0.03 | 0.6000 | 0.9486 | 1.3969 | 0.7975 | 1.0964 | 0.4081 | 0.5611 |
| Guinea | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Kenya | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lesotho | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Liberia | 0.51 | 0.6000 | 4.03005 | 0.9974 | 2.4216 | 0.0482 | 1.2393 | 0.0246 |
| Madagascar | 0.17 | 0.6000 | 1.6689 | 0.0107 | 2.2543 | 0.0878 | 1.1537 | 0.0449 |
| Malawi | 0.08 | 0.6000 | 0.1950 | 0.3828 | 0.4673 | 0.9171 | 0.2391 | 0.4693 |
| Mali | 0.27 | 0.6000 | 2.2928 | 0.5049 | 2.1995 | 0.0288 | 1.1256 | 0.0147 |
| Mauritania | 0.13 | 0.6000 | 1.3109 | 0.2583 | 2.2187 | 0.0305 | 1.1354 | 0.0156 |
| Mozambique | 0.11 | 0.6000 | 0.1224 | 0.3430 | 0.2608 | 0.7299 | 0.1335 | 0.3735 |
| Namibia | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Niger | 0.17 | 0.6000 | 1.6632 | 0.2075 | 2.1390 | 0.0309 | 1.0947 | 0.0158 |
| Nigeria | 0.14 | 0.6000 | 1.1007 | 0.0144 | 2.3019 | 0.1188 | 1.1780 | 0.0608 |
| Rwanda | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Senegal | 0.24 | 0.6000 | 2.4818 | 0.0059 | 2.1963 | 0.0486 | 1.1240 | 0.0249 |
| Seychelles | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Sierra Leone | 0.11 | 0.6000 | 2.0141 | 0.0029 | 2.3958 | 0.0244 | 1.2261 | 0.0124 |
| Somalia | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| South Africa | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| South Sudan | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Sudan | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Tanzania | 0.12 | 0.6000 | 0.0171 | 0.1261 | 0.0411 | 0.3025 | 0.0210 | 0.1548 |
| Uganda | 0.00 | 0.6000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Zambia | 010 | 0.6000 | 0.9585 | 0.0666 | 2.2224 | 0.0155 | 1.1374 | 0.0079 |
| Zimbabwe | 0.07 | 0.6000 | 1.0946 | 0.00599 | 2.2522 | 0.0491 | 1.1526 | 0.0251 |
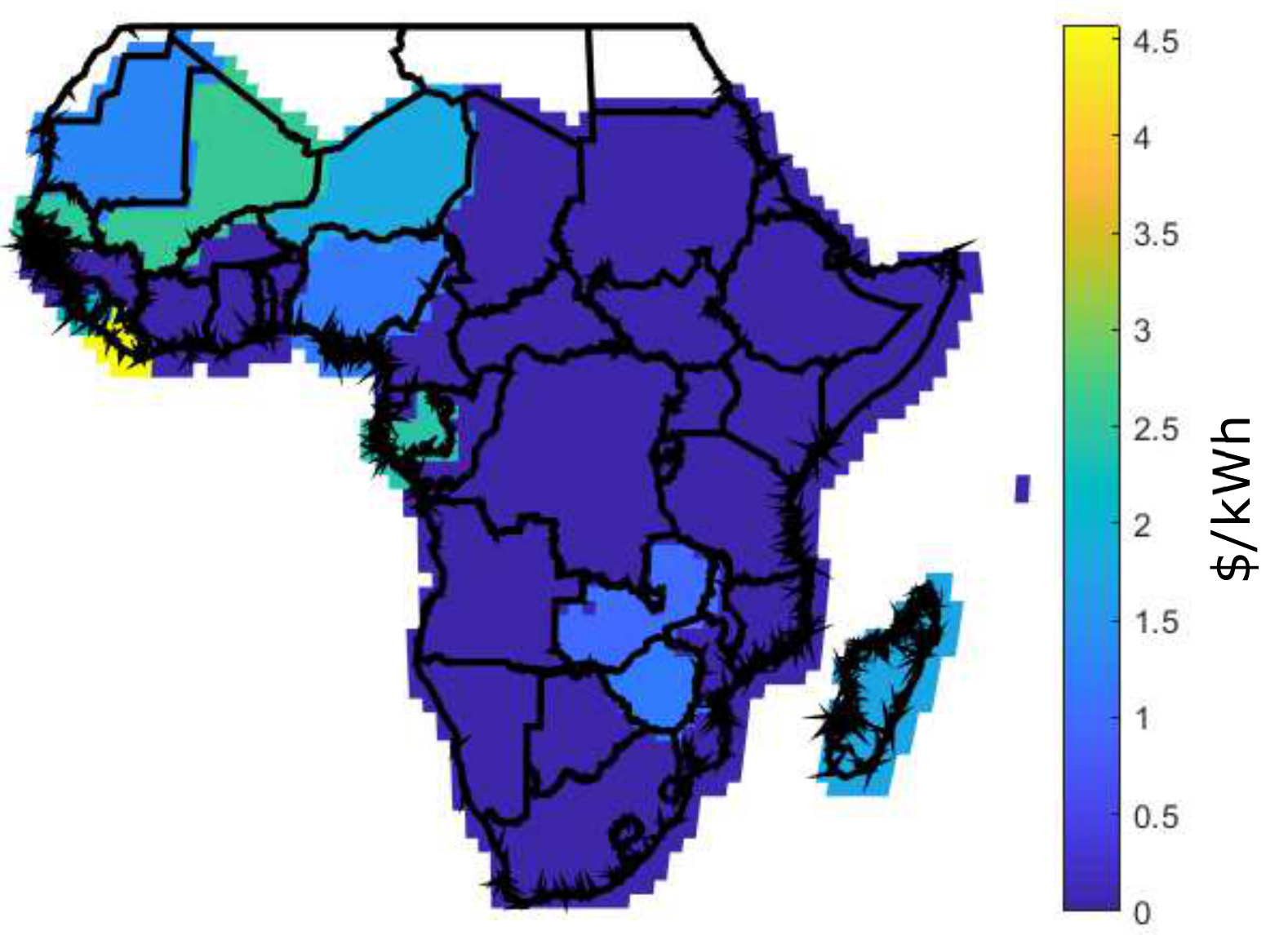
| Country | Retail Price at 100 kWh/month | FR | CES ($/kWh) | DES ($/kWh) | BDES ($/kWh) | |||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | |||
| Angola | 0.04 | 0.9999 | 0.1994 | 0.4465 | 0.4203 | 1.5036 | 0.1290 | 0.4617 |
| Benin | 0.30 | 0.9999 | 0.6326 | 0.7953 | 2.0352 | 2.8217 | 0.6250 | 0.8665 |
| Botswana | 0.10 | 0.9999 | 0.2971 | 0.5454 | 0.9009 | 2.3057 | 0.2766 | 0.7081 |
| Burkina Faso | 0.31 | 0.9999 | 1.0526 | 1.3810 | 1.9672 | 2.5577 | 0.6041 | 0.7854 |
| Burundi | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Cameroon | 0.10 | 0.9999 | 0.4922 | 0.7051 | 1.3447 | 2.5277 | 0.4129 | 0.7762 |
| Central African Republic | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Chad | 0.18 | 0.9999 | 0.1993 | 0.6057 | 0.4789 | 1.4517 | 0.1470 | 0.4458 |
| Congo | 0.00 | 0.9999 | 0.7927 | 1.2815 | 1.7594 | 2.8487 | 0.5403 | 0.8748 |
| Congo drc | 0.12 | 0.9999 | 0.1232 | 0.3860 | 0.5102 | 1.5988 | 0.1566 | 0.4909 |
| Co´te d’ivoire | 0.27 | 0.9999 | 0.6730 | 1.6236 | 0.8720 | 2.0597 | 0.2677 | 0.6325 |
| Djibouti | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Equatorial Guinea | 0.00 | 0.9999 | 1.7695 | 1.4660 | 4.003 | 3.3391 | 1.2295 | 1.0254 |
| Eritrea | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Ethiopia | 0.02 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Gabon | 0.25 | 0.9999 | 2.8847 | 0.0547 | 6.8447 | 0.4488 | 2.1019 | 0.1378 |
| Gambia | 0.23 | 0.9999 | 3.0637 | 0.1164 | 7.2366 | 0.5049 | 2.2223 | 0.1550 |
| Ghana | 0.12 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Guinea-bissau | 0.03 | 0.9999 | 1.1014 | 1.5934 | 2.0505 | 2.8264 | 0.6297 | 0.8680 |
| Guinea | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Kenya | 0.23 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Lesotho | 0.11 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Liberia | 0.51 | 0.9999 | 4.6311 | 1.0641 | 7.3504 | 1.3603 | 2.2572 | 0.4177 |
| Madagascar | 0.17 | 0.9999 | 2.3126 | 0.1468 | 7.5331 | 1.2039 | 2.3134 | 0.3697 |
| Malawi | 0.08 | 0.9999 | 0.2727 | 0.5354 | 1.1043 | 2.1687 | 0.3391 | 0.6660 |
| Mali | 0.27 | 0.9999 | 2.8391 | 0.5060 | 6.6791 | 1.0373 | 2.0511 | 0.3185 |
| Mauritania | 0.13 | 0.9999 | 2.9692 | 1.7231 | 7.6160 | 0.5423 | 2.3388 | 0.1665 |
| Mozambique | 0.11 | 0.9999 | 0.2890 | 0.5375 | 0.8074 | 2.2921 | 0.2479 | 0.7039 |
| Namibia | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Niger | 0.17 | 0.9999 | 2.0298 | 0.2237 | 5.1456 | 0.6384 | 1.5802 | 0.1960 |
| Nigeria | 0.14 | 0.9999 | 2.5753 | 1.6047 | 6.1936 | 1.4354 | 1.9020 | 0.4408 |
| Rwanda | 0.23 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Senegal | 0.24 | 0.9999 | 3.0648 | 0.0908 | 6.9773 | 0.7445 | 2.1427 | 0.2286 |
| Seychelles | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Sierra Leone | 0.11 | 0.9999 | 2.6199 | 0.1308 | 7.3634 | 1.0733 | 2.2612 | 0.3296 |
| Somalia | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| South Africa | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| South Sudan | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Sudan | 0.00 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Tanzania | 0.12 | 0.9999 | 0.1243 | 0.3525 | 0.1003 | 0.7374 | 0.0308 | 0.2264 |
| Uganda | 0.22 | 0.9999 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Zambia | 0.10 | 0.9999 | 1.9092 | 1.3817 | 5.9182 | 0.6693 | 1.8174 | 0.2055 |
| Zimbabwe | 0.07 | 0.9999 | 2.6770 | 1.6369 | 7.0274 | 0.7195 | 2.1581 | 0.2209 |
| Unmet loads | Selling Cost ($/kWh) | Buying Cost ($/kWh) | Offer Price ($/kWh) | Blockchain Price ($/kWh) |
|---|---|---|---|---|
| Constant load | 2.05 | 153.86 | 6.60 | 0.088 |
| Medium load | 2.60 | 386.23 | 7.58 | 0.051 |
| Heavy night load | 4.53 | 226.91 | 9.84 | 0.096 |
| Business daily load | 8.82 | 119.94 | 23.63 | 0.095 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samuel, O.; Almogren, A.; Javaid, A.; Zuair, M.; Ullah, I.; Javaid, N. Leveraging Blockchain Technology for Secure Energy Trading and Least-Cost Evaluation of Decentralized Contributions to Electrification in Sub-Saharan Africa. Entropy 2020, 22, 226. https://doi.org/10.3390/e22020226
Samuel O, Almogren A, Javaid A, Zuair M, Ullah I, Javaid N. Leveraging Blockchain Technology for Secure Energy Trading and Least-Cost Evaluation of Decentralized Contributions to Electrification in Sub-Saharan Africa. Entropy. 2020; 22(2):226. https://doi.org/10.3390/e22020226
Chicago/Turabian StyleSamuel, Omaji, Ahmad Almogren, Atia Javaid, Mansour Zuair, Ibrar Ullah, and Nadeem Javaid. 2020. "Leveraging Blockchain Technology for Secure Energy Trading and Least-Cost Evaluation of Decentralized Contributions to Electrification in Sub-Saharan Africa" Entropy 22, no. 2: 226. https://doi.org/10.3390/e22020226
APA StyleSamuel, O., Almogren, A., Javaid, A., Zuair, M., Ullah, I., & Javaid, N. (2020). Leveraging Blockchain Technology for Secure Energy Trading and Least-Cost Evaluation of Decentralized Contributions to Electrification in Sub-Saharan Africa. Entropy, 22(2), 226. https://doi.org/10.3390/e22020226






