Adapting Logic to Physics: The Quantum-Like Eigenlogic Program
Abstract
1. Introduction and Motivation
- prop. A: “the electron is detected at position x ”
- prop. B: “the electron went through slit 1”
- prop. C: “the electron went through slit 2”
2. Eigenlogic
| eigenvalues | ↔ | logical truth values |
| operators | ↔ | logical connectives |
| eigenvectors | ↔ | logical interpretations |
2.1. Boolean Eigenlogic Using Zero and One
2.2. Involution Eigenlogic Using the Numbers +1 and −1
2.3. Eigenlogic Operators and Quantum Computing Gates
2.4. Operators for Many-Valued Logic Using Lagrange Interpolation and the Cayley–Hamilton Theorem
3. Probabilities and Fuzzy Eigenlogic
3.1. Probability Theory: The Views of Boole and Poincaré
3.2. Fuzzy Eigenlogic and Quantum Probabilities
4. Operators in Logic: Projectors, Quaternions, Pauli Matrices and the Heisenberg Group
4.1. Von Neumann’s ‘Projections as Propositions’
- is a projection operator iff (they commute)
- is a projection operator iff or
- is a projection operator iff or
4.2. Quaternions and Their Logical Interpretation by George Boole
4.3. Pauli and Weyl–Heisenberg Operators and Their Semantic and Syntactic Interpretation in Logic
5. Logical Conjectures on Universality, Predicate Logic, Normal Forms and Combinatory Logic
5.1. Truth Table Method and the Eigenlogic Interpretation of Universal Quantum Gates
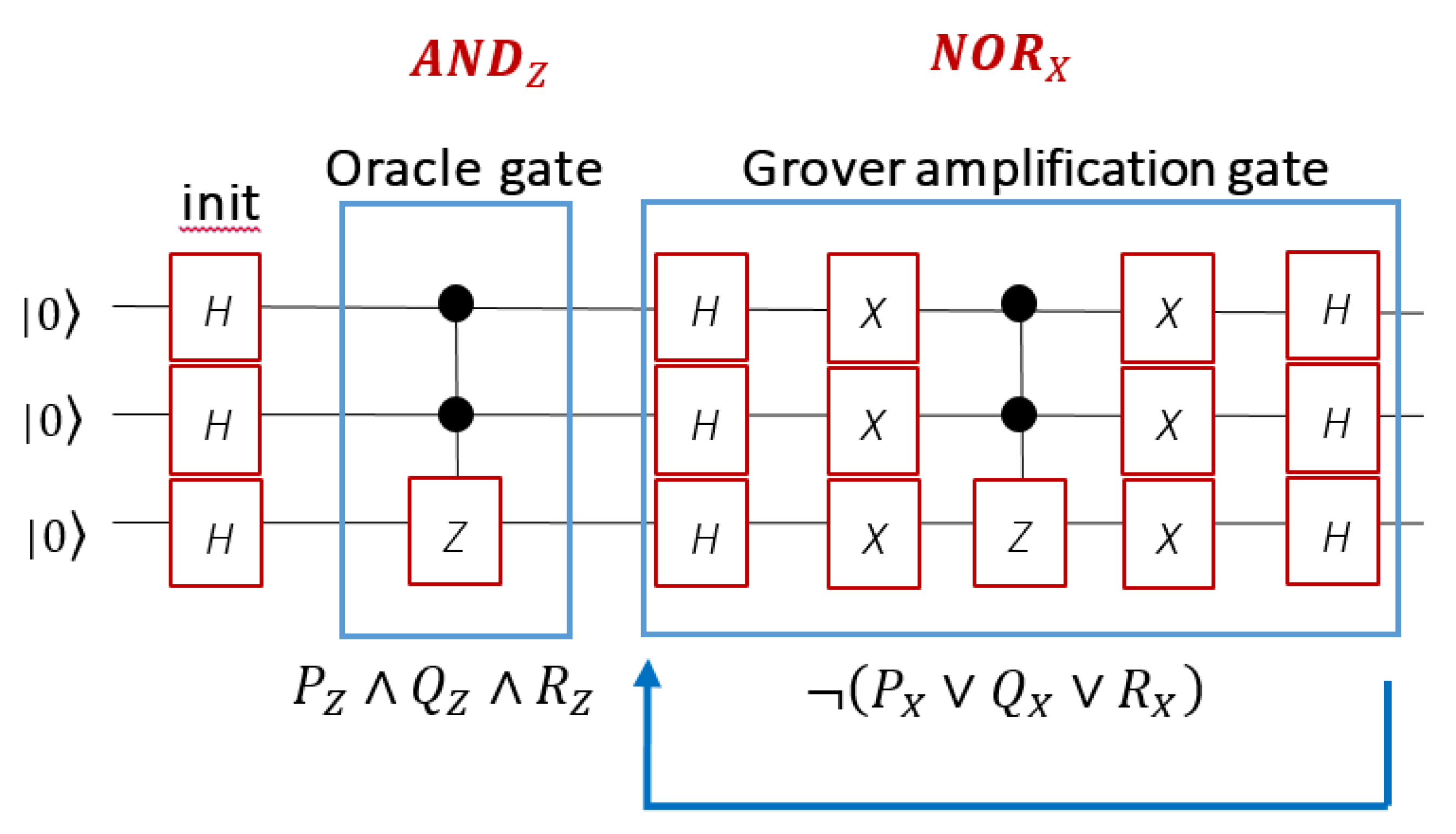
5.2. Towards First Order Eigenlogic: A Link with Grover’s Algorithm
5.3. The Production Systems of Emil Post and the Role of Non-Commutativity
5.4. Qauntum-Like Combinatory Logic
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Neumann, J.V. Mathematical Foundations of Quantum Mechanics; Princeton Univ. Press: Princeton, NJ, USA, 1955; p. 247, (transl. Neumann, J.V. From Grundlehren der Mathematischen Wissenschaften; 38nd ed., Springer: Berlin/Heidelberg, Germany, 1932). [Google Scholar]
- Birkhoff, G.; Neumann, J.V. The Logic of Quantum Mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Girard, J.-Y. Ch 1 Existence vs. Essence, 1.3 Gödel and after. In The Blind Spot: Lectures on Logic; European Mathematical Society: Zürich, Switzerland, 2011; p. 11. [Google Scholar] [CrossRef]
- Dalla Chiara, M.L.; Giuntini, R.; Leporini, R.; Sergioli, G. Quantum Computation and Logic—How Quantum Computers Have Inspired Logical Investigations; Trends in Logic (Book 48); Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Boole, G. The Mathematical Analysis of Logic: Being an Essay to a Calculus of Deductive Reasoning; Macmillan, Barclay & Macmillan: Cambridge, UK, 1847. [Google Scholar]
- Dubois, F.; Toffano, Z. Eigenlogic: A Quantum View for Multiple-Valued and Fuzzy Systems. Quantum Interaction. QI 2016. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2017; pp. 239–251. [Google Scholar] [CrossRef]
- Benioff, P. The Representation of Numbers in Quantum Mechanics. Algorithmica 2002, 34, 529–559. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Łukasiewicz, J. On three-valued logic. Ruch Filozoficzny 1920, 5, 170–171. [Google Scholar]
- Post, E.L. Introduction to a General Theory of Elementary Propositions. Am. J. Math. 1921, 43, 163–185. [Google Scholar] [CrossRef]
- Miller, D.M.; Thornton, M.A. Multiple Valued Logic: Concepts and Representations. Synth. Lect. Digit. Circuits Syst. 2007, 2, 1–127. [Google Scholar] [CrossRef]
- Boole, G. An Investigation of the Laws of Thought on Which Are Founded the Mathematical Theories of Logic and Probabilities; Macmillan, Barclay & Macmillan: Cambridge, UK, 1854. [Google Scholar]
- Montanaro, A.; Osborne, T.J. Quantum Boolean Functions. CJTCS 2010, 1, 1–45. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. A 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Mermin, D. Quantum Computer Science: An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Toffano, Z.; Dubois, F. Interpolating Binary and Multivalued Logical Quantum Gates. Proceedings 2018, 2, 152. [Google Scholar] [CrossRef]
- Formanek, E. Polynomial identities and the Cayley-Hamilton theorem. Math. Intell. 1989, 11, 37–39. [Google Scholar] [CrossRef]
- Poincaré, H. Calcul des Probabilités; Gauthier-Villars: Paris, France, 1912. [Google Scholar]
- Benioff, P. Quantum Robots and Environments. Phys. Rev. A 1988, 58, 893–904. [Google Scholar] [CrossRef]
- Cunha, R.A.F.; Sharma, N.; Toffano, Z.; Dubois, F. Fuzzy Logic Behavior of Quantum-Controlled Braitenberg Vehicle Agents. In Quantum Interaction. QI 2018. Lecture Notes in Computer Science; Lambert-Mogiliansky, A., Ed.; Springer: Cham, Switzerland, 2019; Volume 11690, pp. 111–122. [Google Scholar] [CrossRef]
- Toffano, Z.; Dubois, F. Quantum eigenlogic observables applied to the study of fuzzy behaviour of Braitenberg vehicle quantum robots. Kybernetes 2019, 48, 2307–2324. [Google Scholar] [CrossRef]
- Khrennikov, A. Ubiquitous Quantum Structure: From Psychology to Finances; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Boole, G. Notes on quaternions. Philos. Mag. 1848, 33, 278–280. [Google Scholar] [CrossRef]
- Altmann, S.L. Rotations, Quaternions, and Double Groups; Clarendon Press: Oxford, UK, 1986. [Google Scholar] [CrossRef]
- Johansson, N.; Larsson, J.-A. Quantum Simulation Logic, Oracles, and the Quantum Advantage. Entropy 2019, 21, 800. [Google Scholar] [CrossRef]
- Durt, T.; Englert, B.-G.; Bengtsson, I.; Życzkowski, K. On Mutually Unbiased Bases. Int. J. Quantum Inf. 2010, 8, 535–640. [Google Scholar] [CrossRef]
- Lawrence, J.; Brukner, Č.; Zeilinger, A. Mutually unbiased binary observable sets on N qubits. Phys. Rev. A 2002, 65, 032320. [Google Scholar] [CrossRef]
- Majumdar, R.; Basu, S.; Ghosh, S.; Sur-Kolay, S. Quantum error-correcting code for ternary logic. Phys. Rev. A 2018, 97, 052302. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, Philadelphia, PL, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Post, E.L. Formal reductions of the general combinatorial decision problem. Am. J. Math. 1943, 65, 197–268. [Google Scholar] [CrossRef]
- Potapov, I.; Semukhin, P.; ACM. Decidability of the Membership Problem for 2 × 2 integer matrices. In Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, Barcelona, Spain, January 2017; pp. 170–186. [Google Scholar] [CrossRef]
- Schönfinkel, M. Über die Bausteine der mathematischen Logik. Math. Ann. 1924, 92, 305–316. [Google Scholar] [CrossRef]
- Curry, H.B.; Feys, R. Combinatory Logic; North-Holland Co: Amsterdam, The Netherlands, 1958; Volume I. [Google Scholar]
- Di Pierro, A. On Reversible Combinatory Logic. Electron. Notes Theor. Comput. Sci. 2006, 135, 25–35. [Google Scholar] [CrossRef][Green Version]
- Haven, E.; Khrennikov, A. Quantum Social Science; Cambridge Univ. Press: Cambridge, UK, 2013. [Google Scholar]
- Barros, J.; Toffano, Z.; Meguebli, Y.; Doan, B.L. Contextual Query Using Bell Tests. In Quantum Interaction. QI 2013. Lecture Notes in Computer Science; Atmanspacher, H., Haven, E., Kitto, K., Raine, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8369, pp. 110–121. [Google Scholar] [CrossRef]
- Galofaro, F.; Toffano, Z.; Doan, B.L. A quantum-based semiotic model for textual semantics. Kybernetes 2018, 47, 307–320. [Google Scholar] [CrossRef]
- Sergioli, G. Quantum and quantum-like machine learning: A note on differences and similarities. In Soft Computing; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–9. [Google Scholar] [CrossRef]
| Truth Table {F,T} , | |||
|---|---|---|---|
| 0 | |||
| − | |||
| . | |||
| = | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toffano, Z.; Dubois, F. Adapting Logic to Physics: The Quantum-Like Eigenlogic Program. Entropy 2020, 22, 139. https://doi.org/10.3390/e22020139
Toffano Z, Dubois F. Adapting Logic to Physics: The Quantum-Like Eigenlogic Program. Entropy. 2020; 22(2):139. https://doi.org/10.3390/e22020139
Chicago/Turabian StyleToffano, Zeno, and François Dubois. 2020. "Adapting Logic to Physics: The Quantum-Like Eigenlogic Program" Entropy 22, no. 2: 139. https://doi.org/10.3390/e22020139
APA StyleToffano, Z., & Dubois, F. (2020). Adapting Logic to Physics: The Quantum-Like Eigenlogic Program. Entropy, 22(2), 139. https://doi.org/10.3390/e22020139




