Consciousness Detection in a Complete Locked-in Syndrome Patient through Multiscale Approach Analysis
Abstract
1. Introduction
2. Materials and Methods
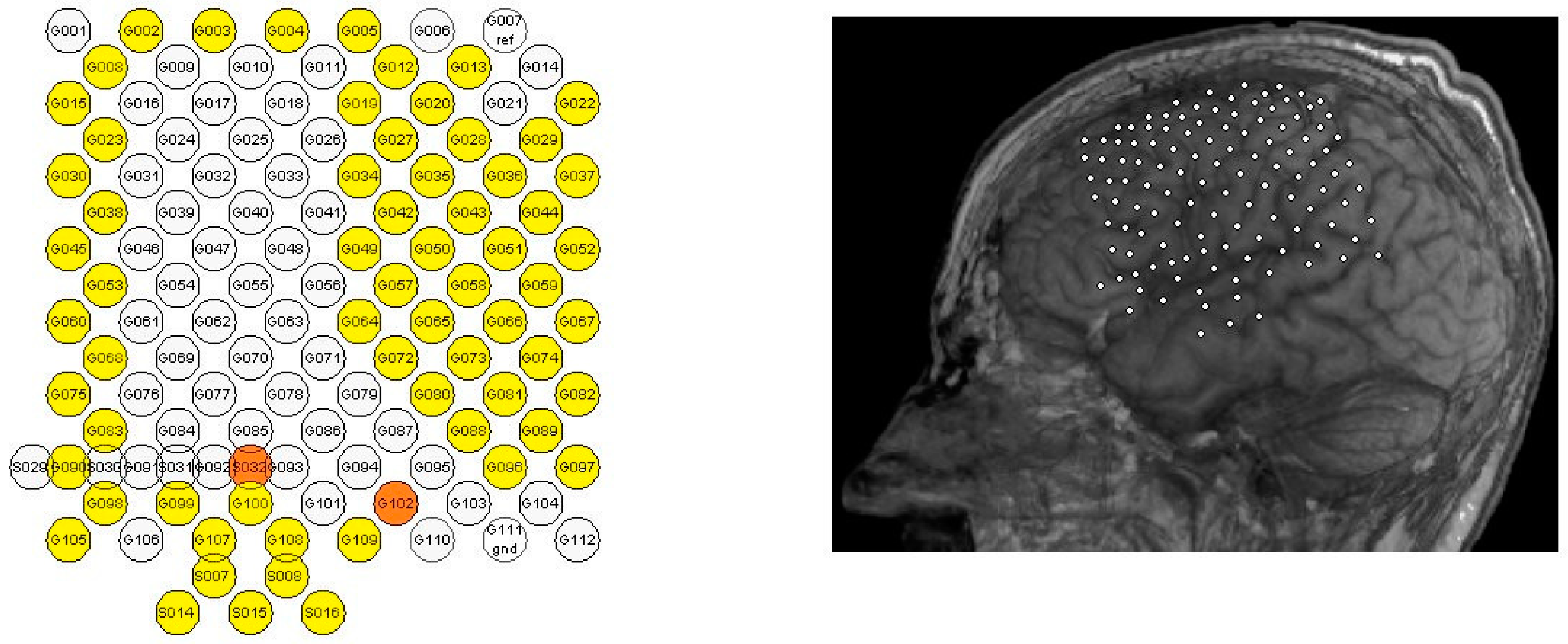
2.1. Dataset
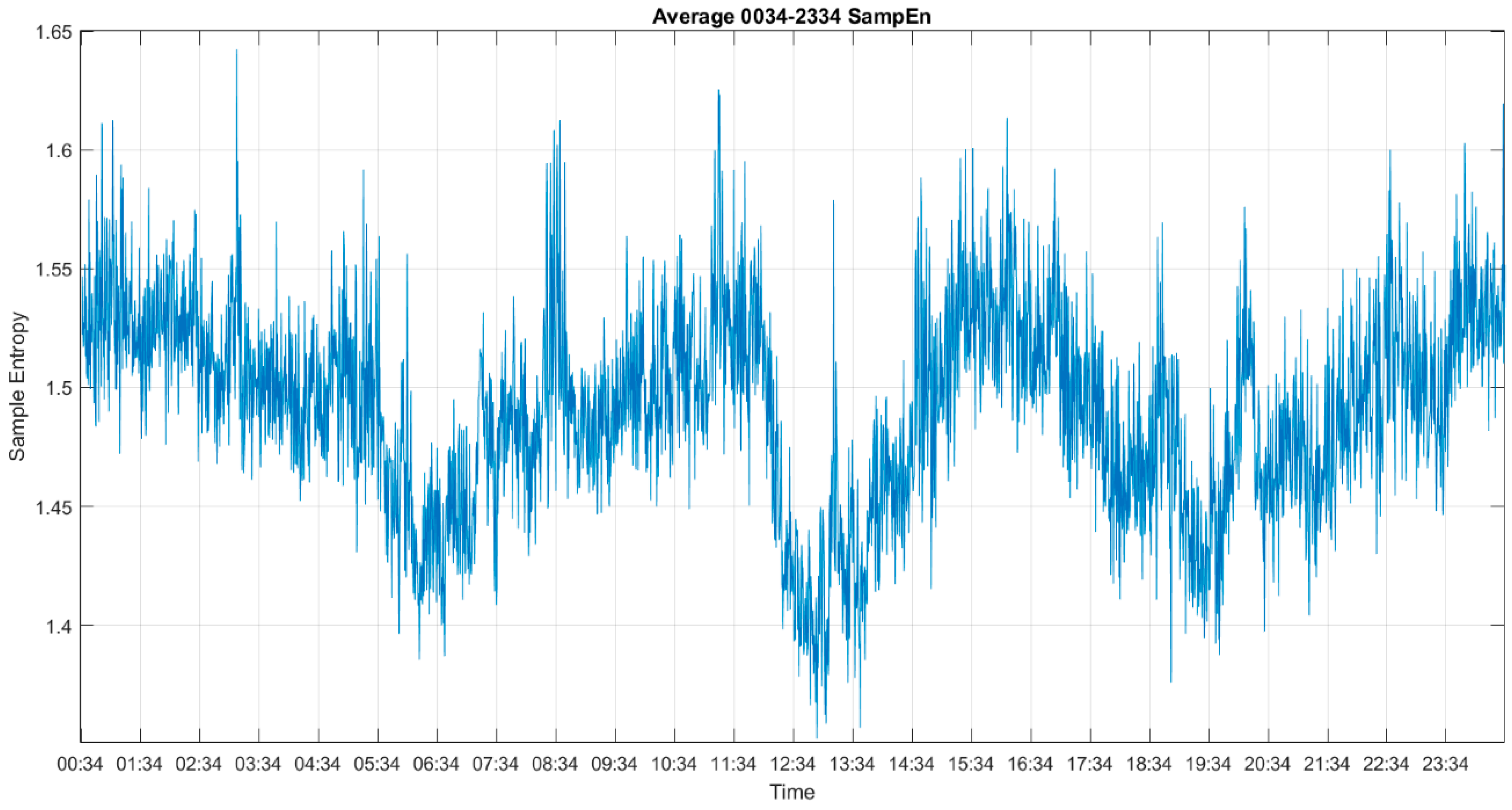
2.2. Sample Entropy
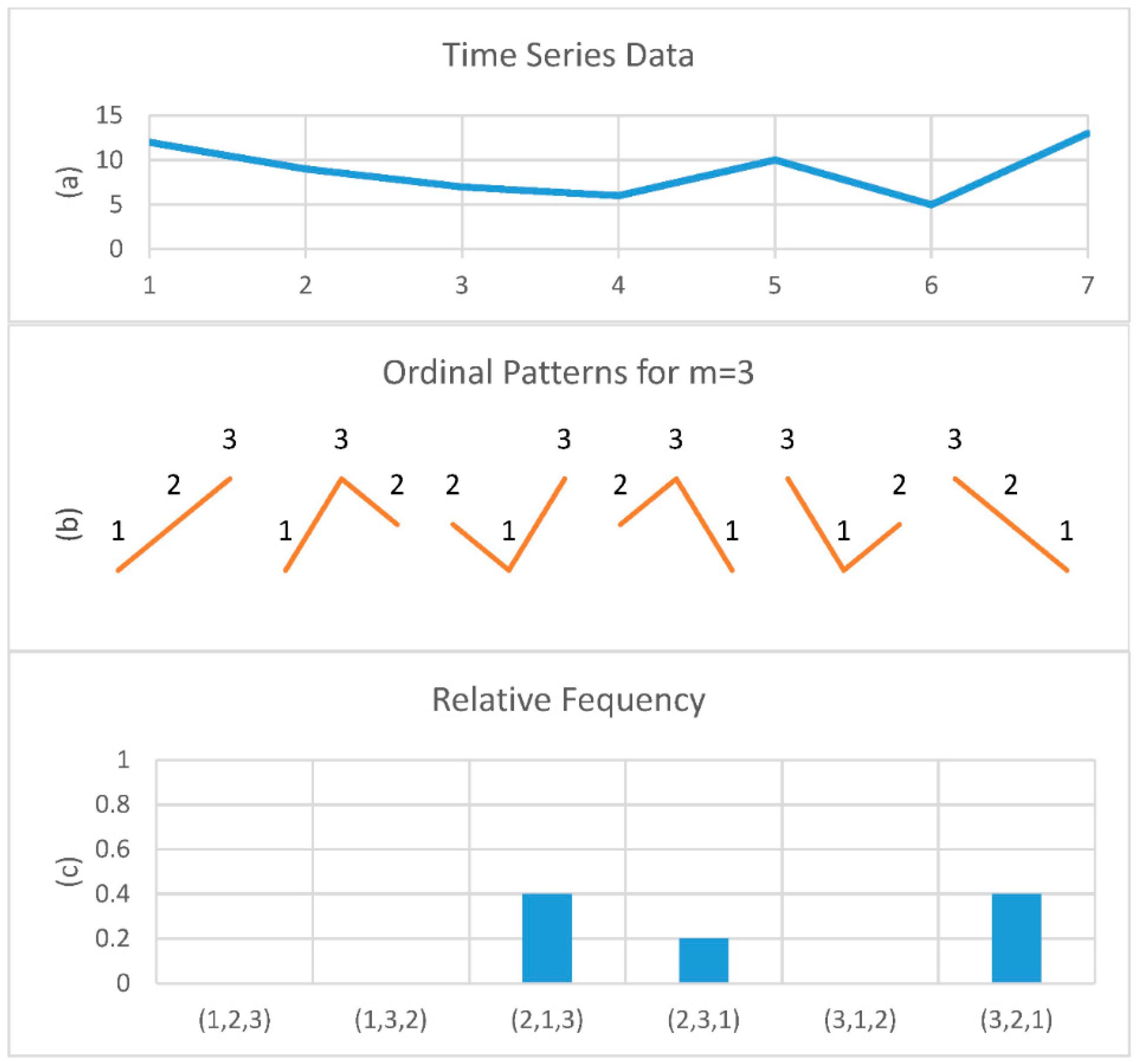
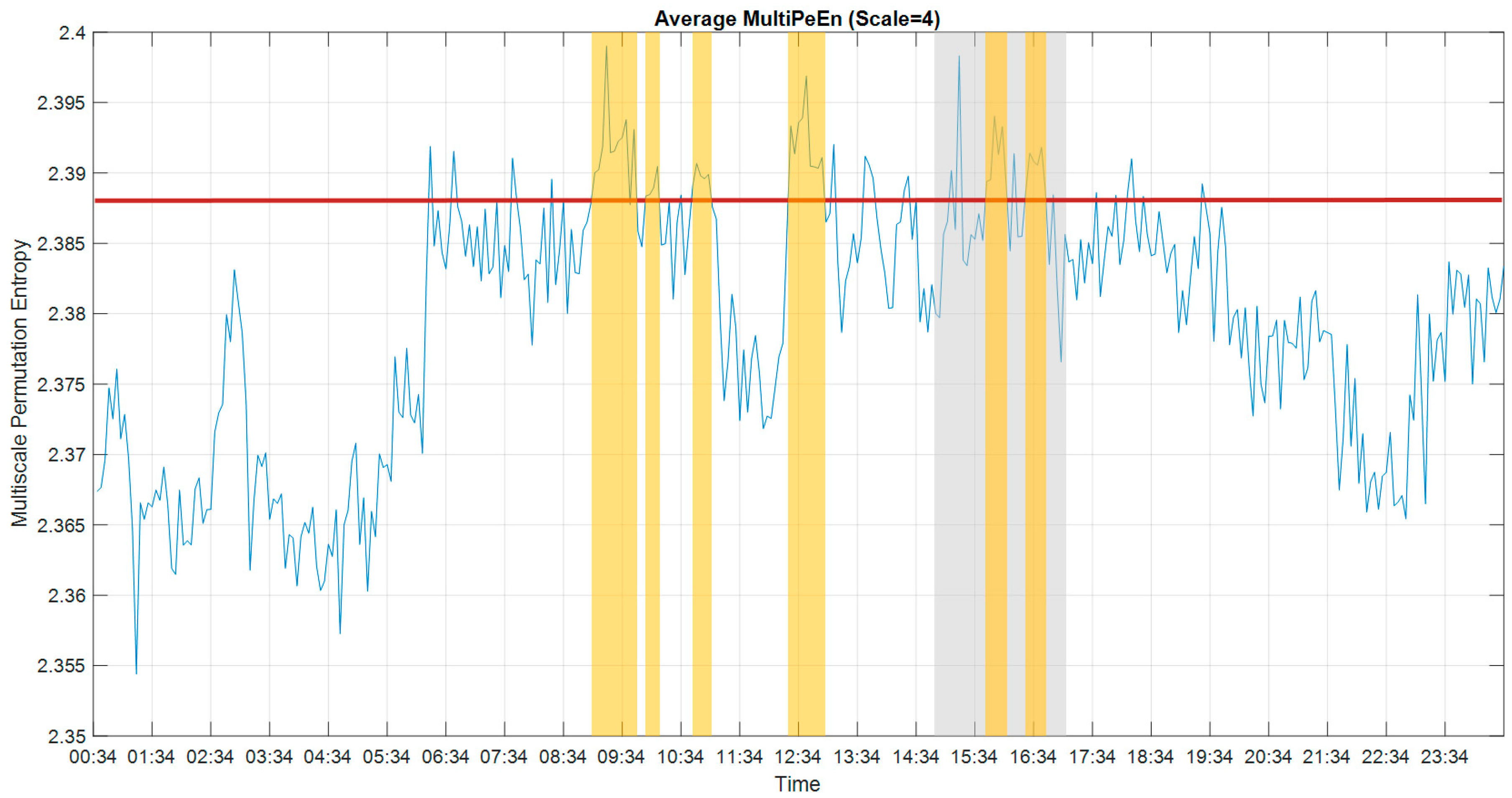
2.3. Permutation Entropy
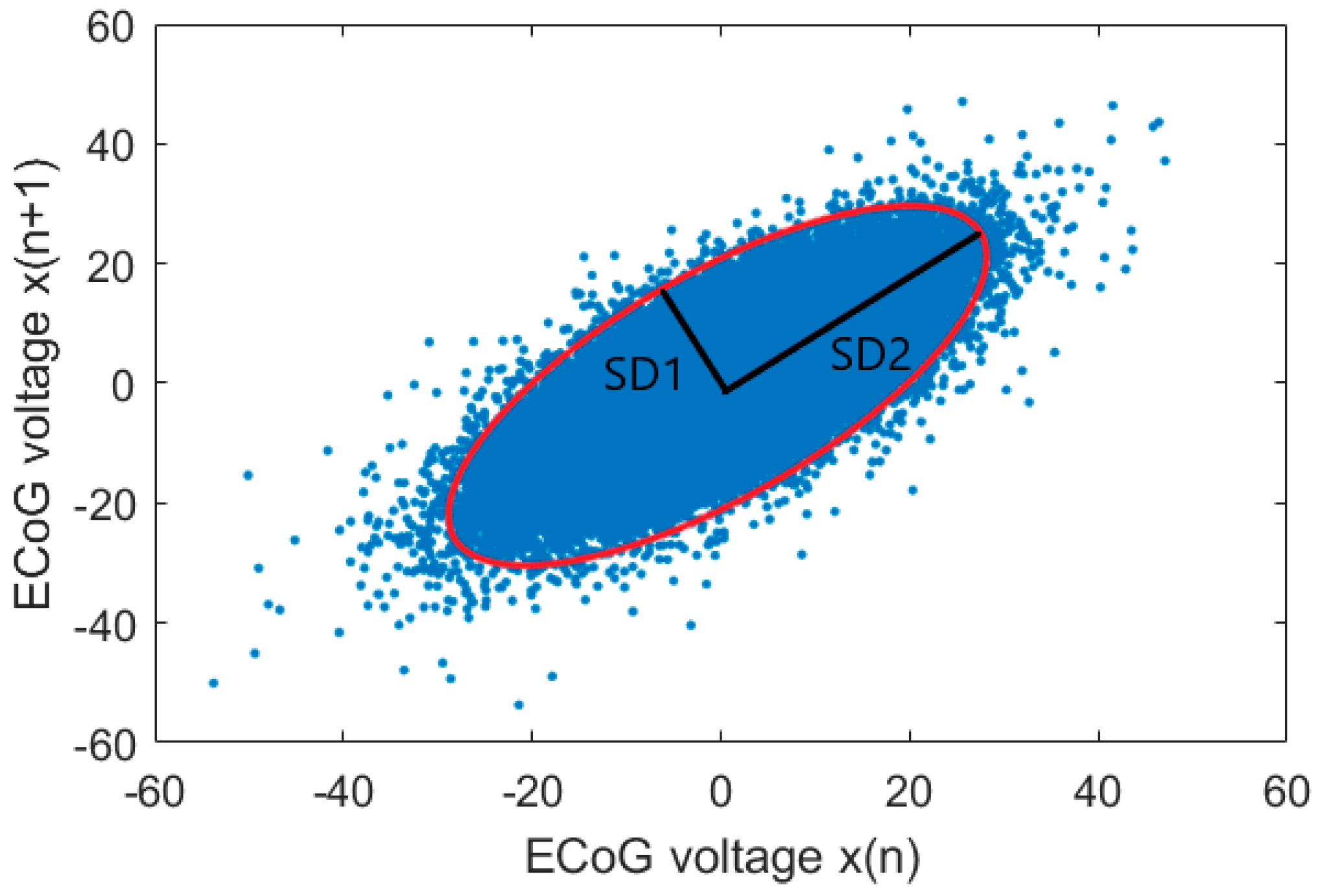
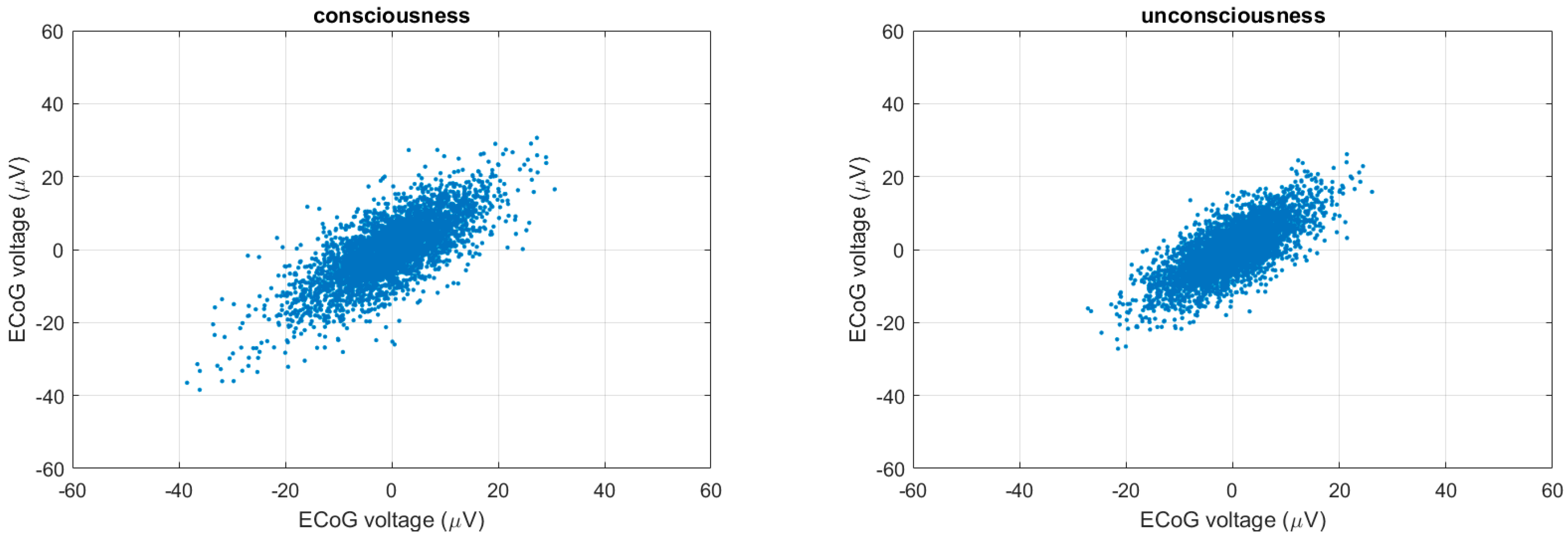
2.4. Poincaré Plot
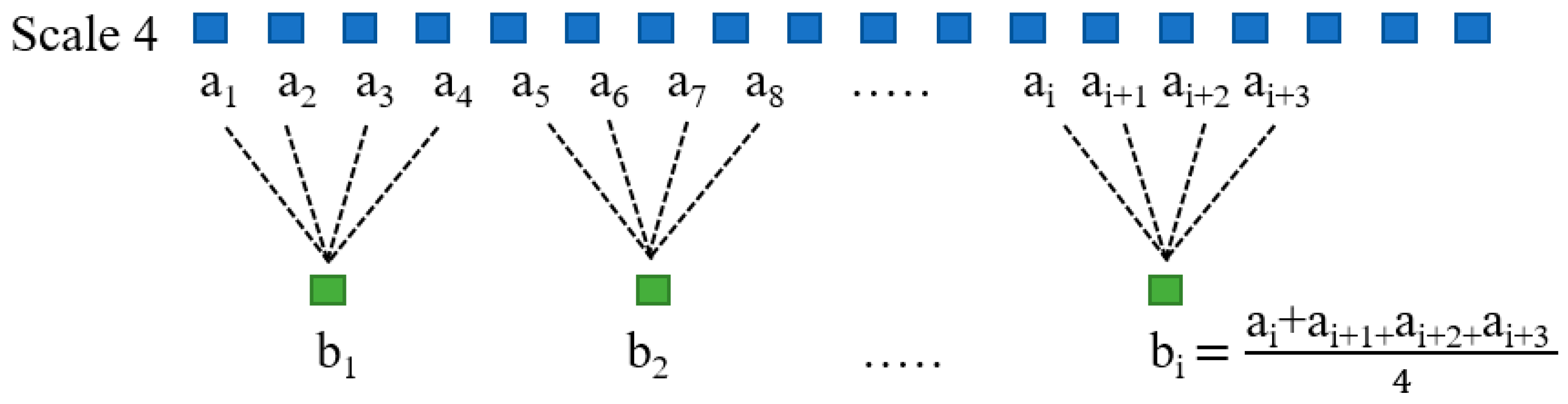
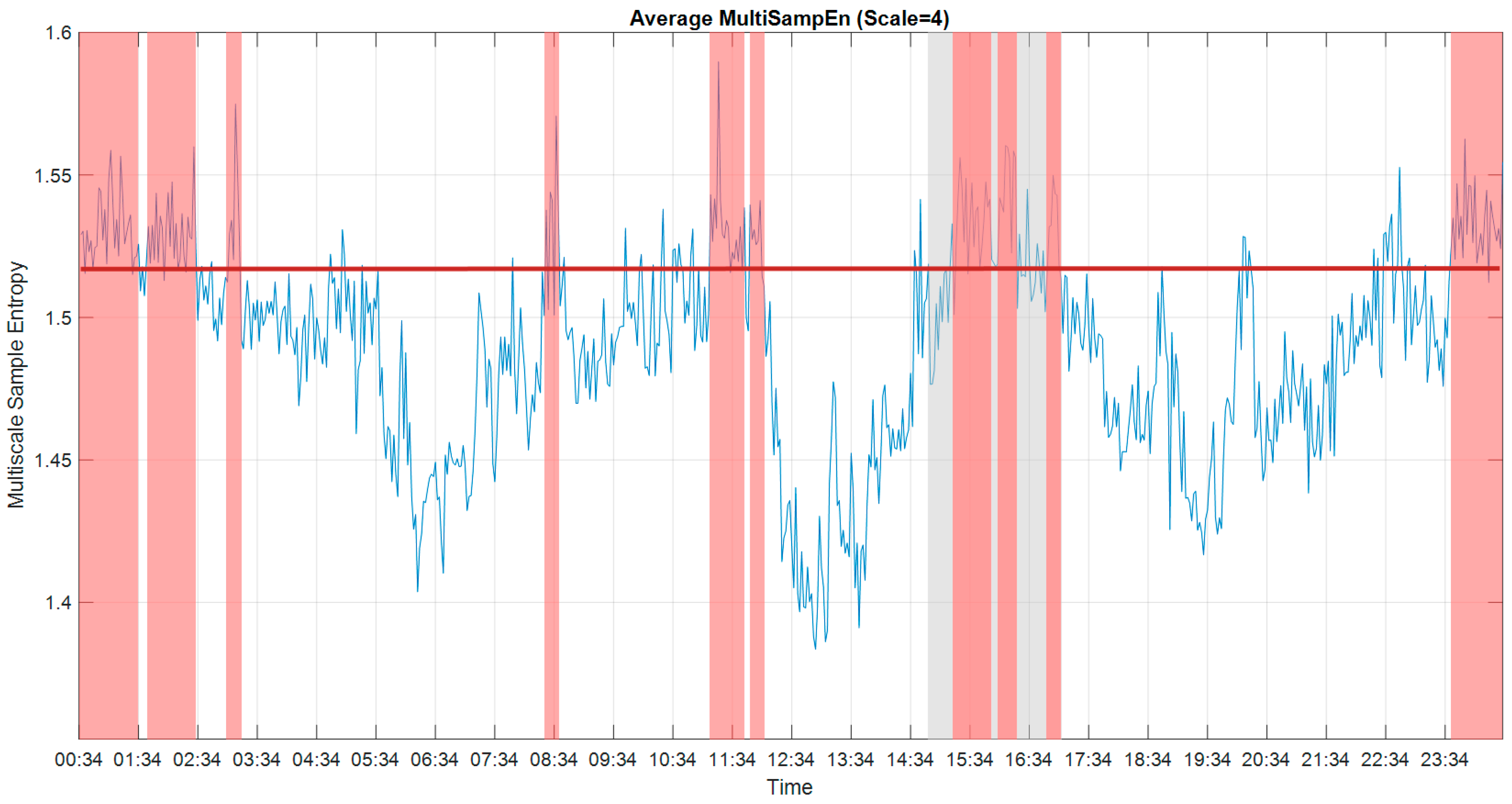
2.5. Multiscale Approach
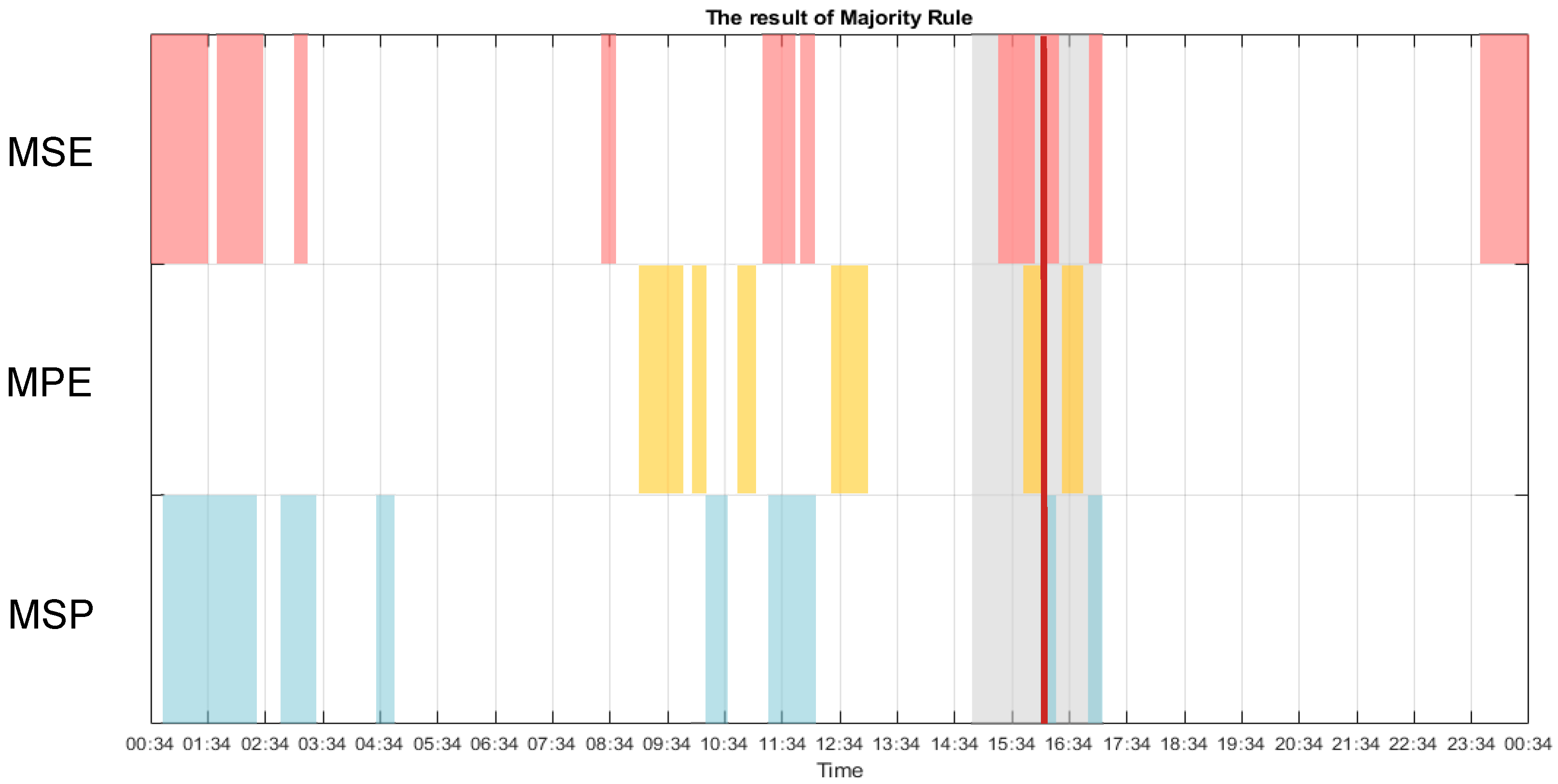
3. Results
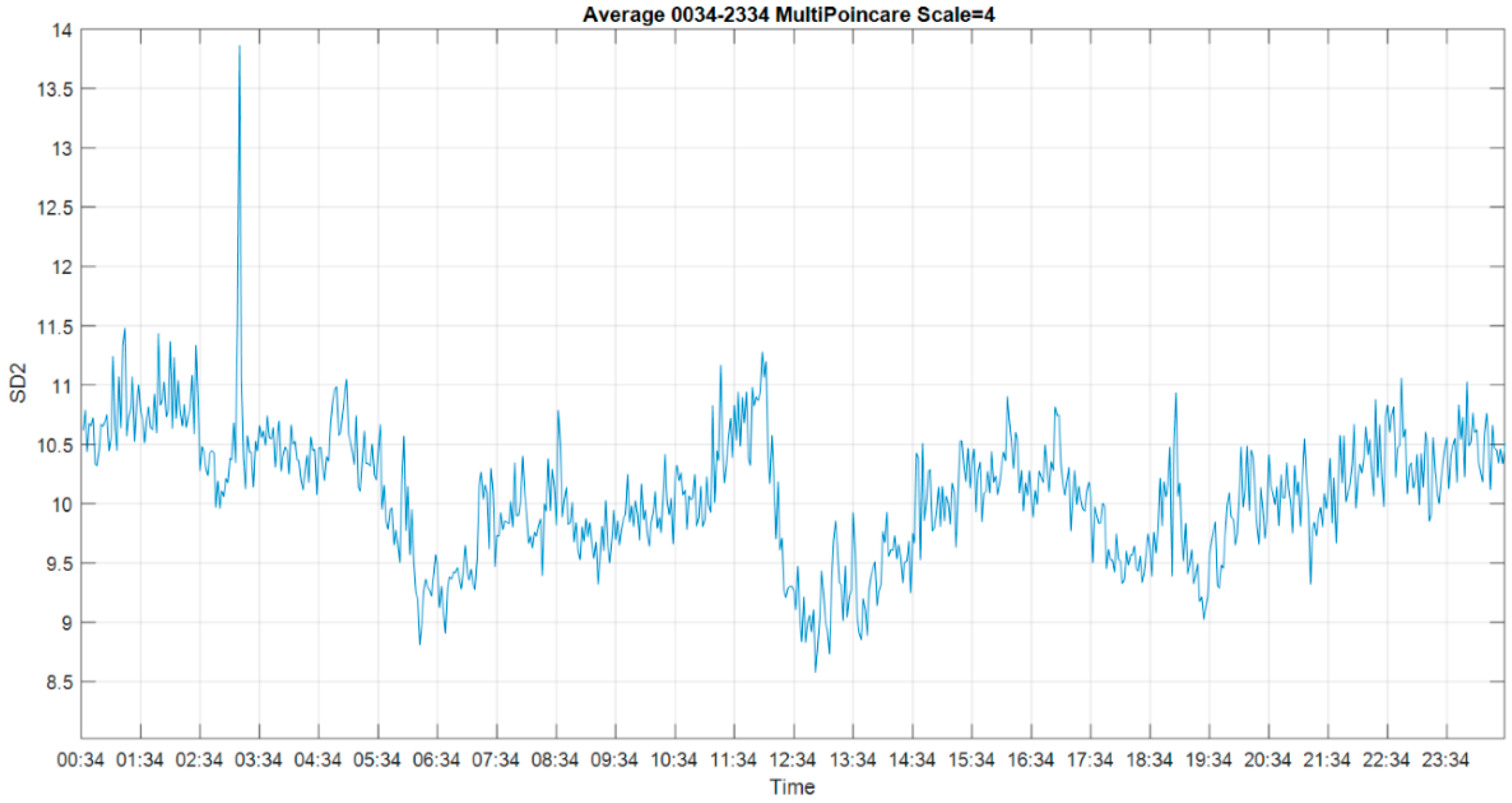
3.1. Multiscale Approach
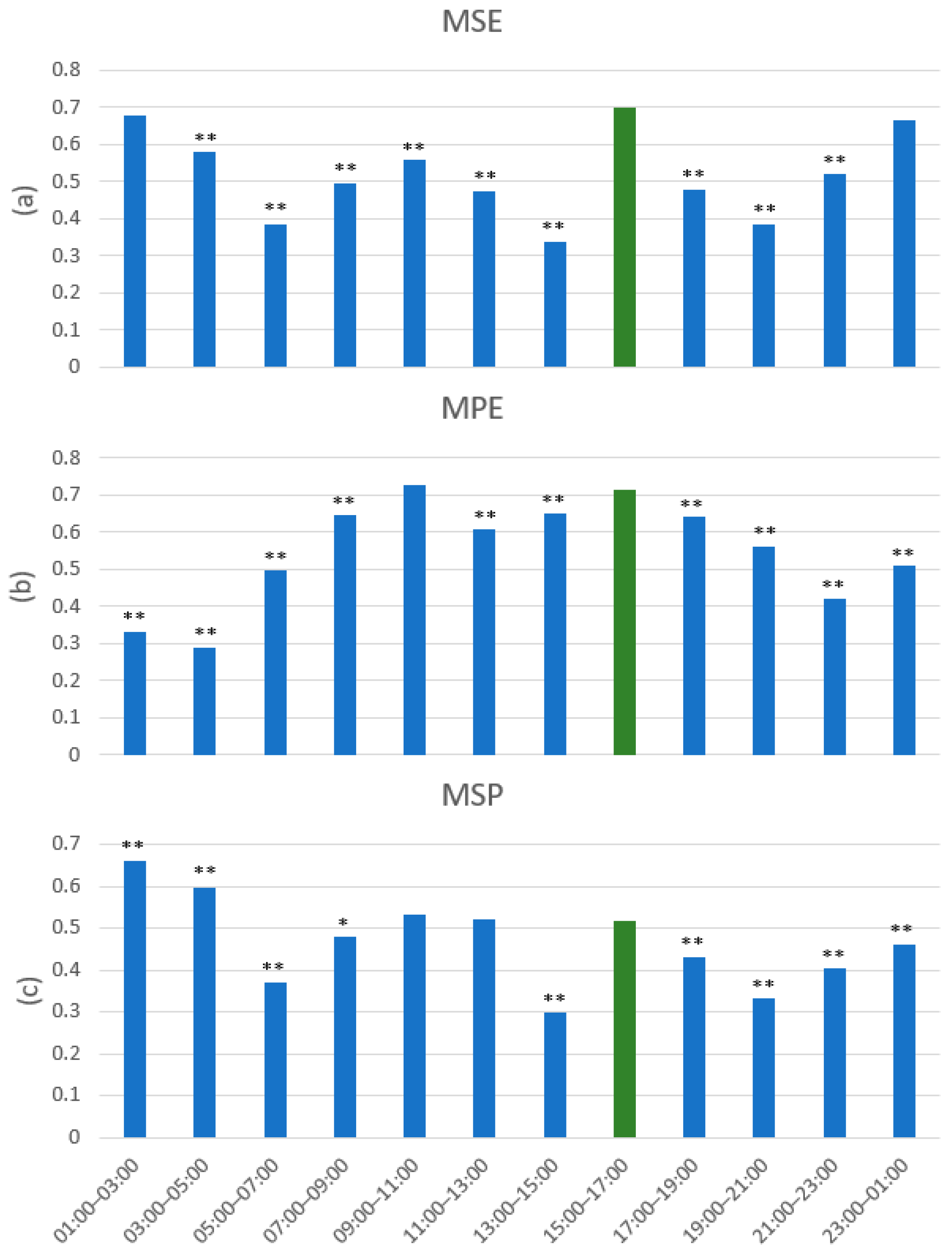
3.2. Multiscale Sample Entropy
3.3. Multiscale Permutation Entropy
3.4. Multiscale Poincaré (MSP) Plots
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vanhaudenhuyse, A.; Charland-Verville, V.; Thibaut, A.; Chatelle, C.; Tshibanda, J.-F.L.; Maudoux, A.; Faymonville, M.-E.; Laureys, S.; Gosseries, O. Conscious While Being Considered in an Unresponsive Wakefulness Syndrome for 20 Years. Front. Neurol. 2018, 9. [Google Scholar] [CrossRef]
- Ramos-Murguialday, A.; Hill, J.; Bensch, M.; Martens, S.; Halder, S.; Nijboer, F.; Schoelkopf, B.; Birbaumer, N.; Gharabaghi, A. Transition from the locked in to the completely locked-in state: A physiological analysis. Clin. Neurophysiol. 2011, 122, 925–933. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, U.; Xia, B.; Silvoni, S.; Cohen, L.G.; Birbaumer, N. Brain–Computer Interface–Based Communication in the Completely Locked-In State. PLoS Biol. 2017, 15, e1002593. [Google Scholar] [CrossRef] [PubMed]
- Gallegos-Ayala, G.; Furdea, A.; Takano, K.; Ruf, C.A.; Flor, H.; Birbaumer, N. Brain communication in a completely locked-in patient using bedside near-infrared spectroscopy. Neurology 2014, 82, 1930–1932. [Google Scholar] [CrossRef] [PubMed]
- Spüler, M. Questioning the evidence for BCI-based communication in the complete locked-in state. PLoS Biol. 2019, 17, e2004750. [Google Scholar] [CrossRef] [PubMed]
- The PLOS Biology Editors. Retraction: Brain–Computer Interface–Based Communication in the Completely Locked-In State. PLoS Biol. 2019, 17, e3000607. [Google Scholar] [CrossRef]
- Owen, A.M.; Coleman, M.R.; Boly, M.; Davis, M.H.; Laureys, S.; Pickard, J.D. Detecting Awareness in the Vegetative State. Science 2006, 313, 1402. [Google Scholar] [CrossRef]
- Casali, A.G.; Gosseries, O.; Rosanova, M.; Boly, M.; Sarasso, S.; Casali, K.R.; Casarotto, S.; Bruno, M.-A.; Laureys, S.; Tononi, G.; et al. A Theoretically Based Index of Consciousness Independent of Sensory Processing and Behavior. Sci. Transl. Med. 2013, 5, 198ra105. [Google Scholar] [CrossRef]
- Laureys, S. The neural correlate of (un)awareness: Lessons from the vegetative state. Trends Cogn. Sci. 2005, 9, 556–559. [Google Scholar] [CrossRef]
- Luauté, J.; Morlet, D.; Mattout, J. BCI in patients with disorders of consciousness: Clinical perspectives. Ann. Phys. Rehabil. Med. 2015, 58, 29–34. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Li, Y.; Fan, S.-Z.; Liu, Q.; Abbod, M.F.; Lu, C.-W.; Lin, T.-Y.; Jen, K.-K.; Wu, S.-J.; Shieh, J.-S. A critical care monitoring system for depth of anaesthesia analysis based on entropy analysis and physiological information database. Australas. Phys. Eng. Sci. Med. 2014, 37, 591–605. [Google Scholar] [CrossRef] [PubMed]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Kreuzer, M.; Kochs, E.F.; Schneider, G.; Jordan, D. Non-stationarity of EEG during wakefulness and anaesthesia: Advantages of EEG permutation entropy monitoring. J. Clin. Monit. 2014, 28, 573–580. [Google Scholar] [CrossRef]
- Hayashi, K.; Mukai, N.; Sawa, T. Poincaré analysis of the electroencephalogram during sevoflurane anesthesia. Clin. Neurophysiol. 2015, 126, 404–411. [Google Scholar] [CrossRef]
- Hayashi, K.; Yamada, T.; Sawa, T. Comparative study of Poincaré plot analysis using short electroencephalogram signals during anaesthesia with spectral edge frequency 95 and bispectral index. Anaesthesia 2014, 70, 310–317. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef]
- Soekadar, S.; Born, J.; Birbaumer, N.; Bensch, M.; Halder, S.; Murguialday, A.R.; Gharabaghi, A.; Nijboer, F.; Schölkopf, B.; Martens, S. Fragmentation of Slow Wave Sleep after Onset of Complete Locked-In State. J. Clin. Sleep Med. 2013, 9, 951–953. [Google Scholar] [CrossRef]
- Bensch, M.; Martens, S.; Halder, S.; Hill, J.; Nijboer, F.; Ramos-Murguialday, A.; Birbaumer, N.; Bogdan, M.; Kotchoubey, B.; Rosenstiel, W.; et al. Assessing attention and cognitive function in completely locked-in state with event-related brain potentials and epidural electrocorticography. J. Neural Eng. 2014, 11. [Google Scholar] [CrossRef]
- Adama, V.S.; Wu, S.-J.; Nicolaou, N.; Bogdan, M. Extendable Hybrid. Approach to Detect. Conscious. States in a CLIS Patient Using Machine Learning; EUROSIM: Logroño, Spain, 2019. [Google Scholar]
- Pincus, S. Approximate entropy: A complexity measure for biological time series data. In Proceedings of the 1991 IEEE Seventeenth Annual Northeast Bioengineering Conference, Hartford, CT, USA, 4–5 April 1991. [Google Scholar]
- Yeragani, V.K.; Pohl, R.; Mallavarapu, M.; Balon, R. Approximate entropy of symptoms of mood: An effective technique to quantify regularity of mood. Bipolar Disord. 2003, 5, 279–286. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-J.; Chen, N.-T.; Jen, K.-K. Application of Improving Sample Entropy to Measure the Depth of Anesthesia. In Proceedings of the International Conference on Advanced Manufacturing (ICAM), Chiayi, Taiwan, 30 September–3 October 2014. [Google Scholar]
- Wu, S.-J.; Chen, N.-T.; Jen, K.-K.; Fan, S.-Z. Analysis of the Level of Consciousness with Sample Entropy: A comparative study with Bispectral Index study with Bispectral Index. Eur. J. Anaesthesiol. 2015, 32, 11. [Google Scholar]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. Heart Circ. Physiol. 1994, 266, H1643–H1656. [Google Scholar] [CrossRef] [PubMed]
- Kuntzelman, K.; Rhodes, L.J.; Harrington, L.N.; Miskovic, V. A practical comparison of algorithms for the measurement of multiscale entropy in neural time series data. Brain Cogn. 2018, 123, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Henriques, T.; Mariani, S.; Burykin, A.; Rodrigues, F.; Silva, T.F.; Goldberger, A.L. Multiscale Poincaré plots for visualizing the structure of heartbeat time series. BMC Med. Inform. Decis. Mak. 2015, 16, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Golińska, A.K. Poincaré Plots in Analysis of Selected Biomedical Signals. Stud. Logic. Gramm. Rhetor. 2013, 35, 117–127. [Google Scholar] [CrossRef]
- Bolanos, J.D.; Vallverdú, M.; Caminal, P.; Valencia, D.F.; Borrat, X.; Gambús, P.; Valencia, J.F. Assessment of sedation-analgesia by means of poincaré analysis of the electroencephalogram. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC); Institute of Electrical and Electronics Engineers (IEEE), Orlando, FL, USA, 16–20 August 2016; pp. 6425–6428. [Google Scholar]
- Wu, S.-J.; Bogdan, M. Application of Sample Entropy to Analyze Consciousness in CLIS Patients; Springer Science and Business Media LLC: Berlin, Germany, 2020; Volume 176, pp. 521–531. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.-J.; Nicolaou, N.; Bogdan, M. Consciousness Detection in a Complete Locked-in Syndrome Patient through Multiscale Approach Analysis. Entropy 2020, 22, 1411. https://doi.org/10.3390/e22121411
Wu S-J, Nicolaou N, Bogdan M. Consciousness Detection in a Complete Locked-in Syndrome Patient through Multiscale Approach Analysis. Entropy. 2020; 22(12):1411. https://doi.org/10.3390/e22121411
Chicago/Turabian StyleWu, Shang-Ju, Nicoletta Nicolaou, and Martin Bogdan. 2020. "Consciousness Detection in a Complete Locked-in Syndrome Patient through Multiscale Approach Analysis" Entropy 22, no. 12: 1411. https://doi.org/10.3390/e22121411
APA StyleWu, S.-J., Nicolaou, N., & Bogdan, M. (2020). Consciousness Detection in a Complete Locked-in Syndrome Patient through Multiscale Approach Analysis. Entropy, 22(12), 1411. https://doi.org/10.3390/e22121411




