Scattering as a Quantum Metrology Problem: A Quantum Walk Approach
Abstract
1. Introduction
2. Quantum Walks with Inhomogeneous On-Site Energies
3. Tools of Local Quantum Estimation Theory
4. Scattering in the Presence of an Obstacle
4.1. Scattering States
4.2. Gaussian Wave Packets
4.3. Scattering with Gaussian Wave Packets
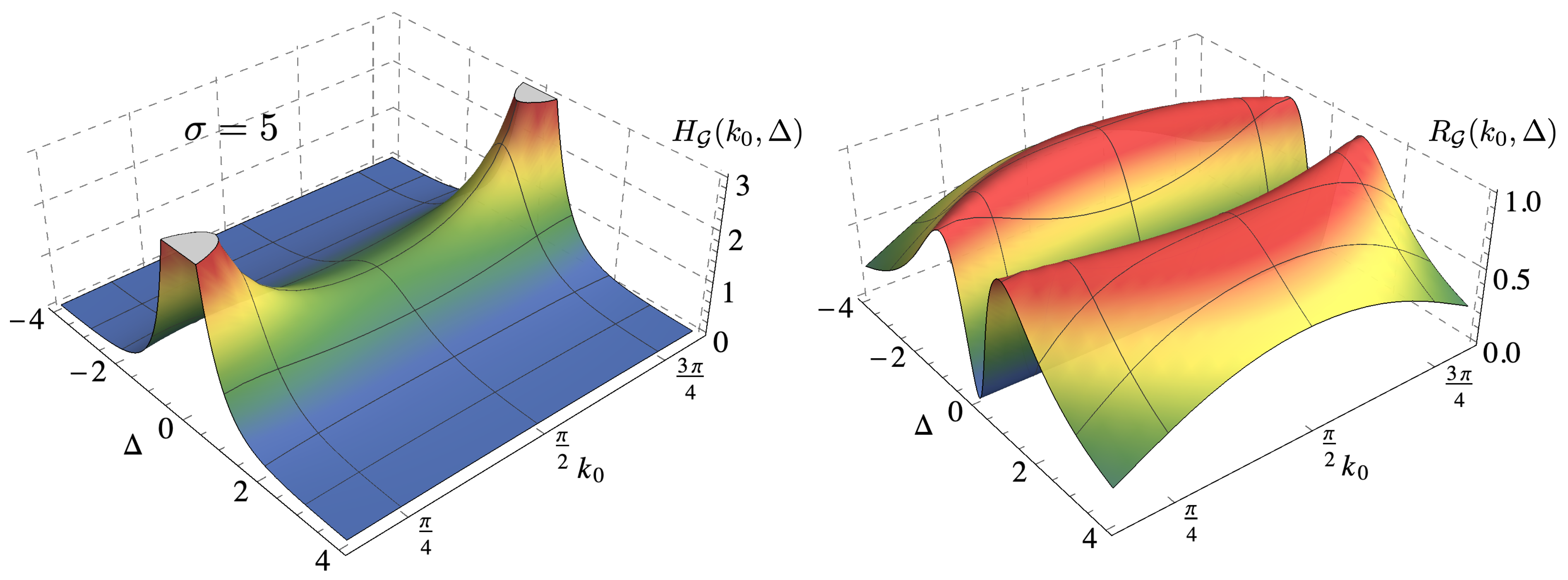
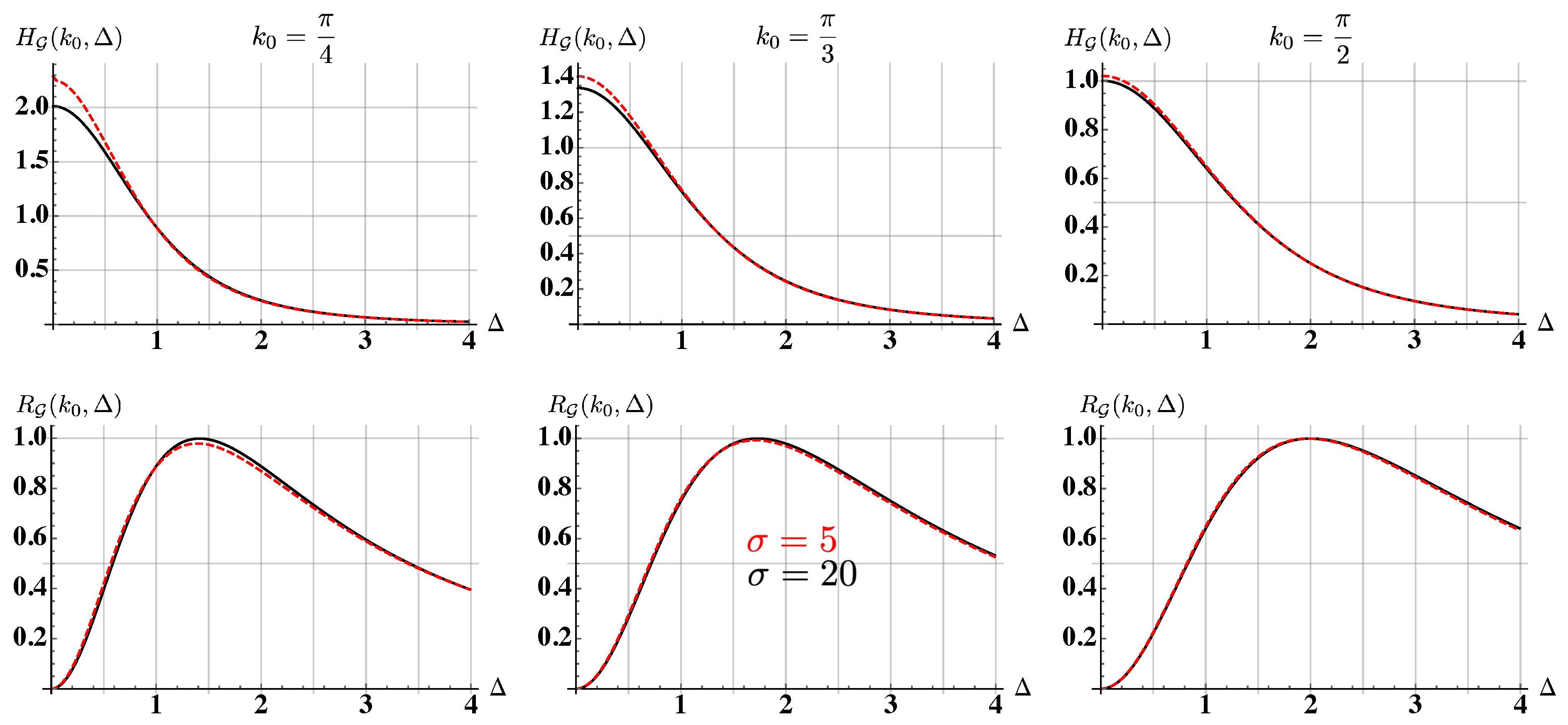
5. Quantum Estimation of a Scattering Potential
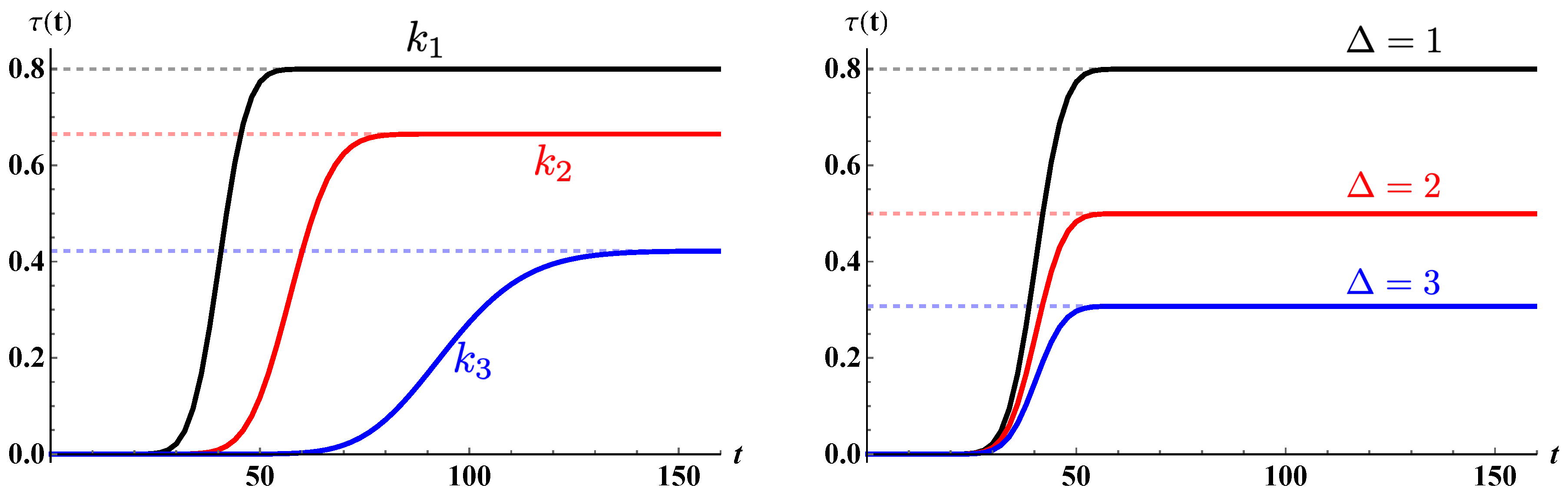
Dichotomic Position Measurement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CTQW | Continuous-time quantum walk |
| CR | Cramér–Rao |
| FI | Fisher information |
| QFI | Quantum Fisher information |
| QSNR | Quantum signal-to-noise ratio |
Appendix A. Gaussian Wave Packet in K-Space
Appendix B. The Explicit Expression of the Functions gH (Δ, k0) and gF (Δ, k0)
References
- Rutherford, E.F. LXXIX. The scattering of α and β particles by matter and the structure of the atom. Philos. Mag. Ser. 1911, 21, 669–688. [Google Scholar] [CrossRef]
- Franklin, R. Influence of the Bonding Electrons on the Scattering of X-Rays by Carbon. Nature 1950, 165, 71–72. [Google Scholar] [CrossRef] [PubMed]
- Chamberlain, O.; Segrè, E.; Wiegand, C.; Ypsilantis, T. Observation of Antiprotons. Phys. Rev. 1955, 100, 947–950. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Gebbia, F.; Benedetti, C.; Benatti, F.; Floreanini, R.; Bina, M.; Paris, M.G.A. Two-qubit quantum probes for the temperature of an Ohmic environment. Phys. Rev. A 2020, 101, 032112. [Google Scholar] [CrossRef]
- Tamascelli, D.; Benedetti, C.; Breuer, H.P.; Paris, M. Quantum probing beyond pure dephasing. New J. Phys. 2020, 22, 083027. [Google Scholar] [CrossRef]
- Salari Sehdaran, F.; Bina, M.; Benedetti, C.; Paris, M. Quantum Probes for Ohmic Environments at Thermal Equilibrium. Entropy 2019, 21, 486. [Google Scholar] [CrossRef]
- Mirkin, N.; Larocca, M.; Wisniacki, D. Quantum metrology in a non-Markovian quantum evolution. Phys. Rev. A 2020, 102, 022618. [Google Scholar] [CrossRef]
- Wu, W.; Shi, C. Quantum parameter estimation in a dissipative environment. Phys. Rev. A 2020, 102, 032607. [Google Scholar] [CrossRef]
- Seveso, L.; Benedetti, C.; Paris, M. The walker speaks its graph: Global and nearly-local probing of the tunnelling amplitude in continuous-time quantum walks. J. Phys. A Math. Theor. 2019, 52, 105304. [Google Scholar] [CrossRef]
- Tamascelli, D.; Benedetti, C.; Olivares, S.; Paris, M.G.A. Characterization of qubit chains by Feynman probes. Phys. Rev. A 2016, 94, 042129. [Google Scholar] [CrossRef]
- Razzoli, L.; Ghirardi, L.; Siloi, I.; Bordone, P.; Paris, M.G.A. Lattice quantum magnetometry. Phys. Rev. A 2019, 99, 062330. [Google Scholar] [CrossRef]
- Benedetti, C.; Paris, M. Characterization of classical Gaussian processes using quantum probes. Phys. Lett. A 2014, 378, 2495–2500. [Google Scholar] [CrossRef]
- Schreiber, A.; Cassemiro, K.N.; Potoček, V.; Gábris, A.; Jex, I.; Silberhorn, C. Decoherence and Disorder in Quantum Walks: From Ballistic Spread to Localization. Phys. Rev. Lett. 2011, 106, 180403. [Google Scholar] [CrossRef]
- Izaac, J.A.; Wang, J.B.; Li, Z.J. Continuous-time quantum walks with defects and disorder. Phys. Rev. A 2013, 88, 042334. [Google Scholar] [CrossRef]
- Li, Z.J.; Izaac, J.A.; Wang, J.B. Position-defect-induced reflection, trapping, transmission, and resonance in quantum walks. Phys. Rev. A 2013, 87, 012314. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J. Single-point position and transition defects in continuous time quantum walks. Sci. Rep. 2015, 5, 13585. [Google Scholar] [CrossRef]
- de Falco, D.; Tamascelli, D. Noise-assisted quantum transport and computation. J. Phys. A Math. Theor. 2013, 46, 225301. [Google Scholar] [CrossRef]
- Chakraborty, S.; Novo, L.; Di Giorgio, S.; Omar, Y. Optimal Quantum Spatial Search on Random Temporal Networks. Phys. Rev. Lett. 2017, 119, 220503. [Google Scholar] [CrossRef]
- Cattaneo, M.; Rossi, M.A.C.; Paris, M.G.A.; Maniscalco, S. Quantum spatial search on graphs subject to dynamical noise. Phys. Rev. A 2018, 98, 052347. [Google Scholar] [CrossRef]
- Morley, J.G.; Chancellor, N.; Bose, S.; Kendon, V. Quantum search with hybrid adiabatic–quantum-walk algorithms and realistic noise. Phys. Rev. A 2019, 99, 022339. [Google Scholar] [CrossRef]
- Benedetti, C.; Rossi, M.A.C.; Paris, M.G.A. Continuous-time quantum walks on dynamical percolation graphs. EPL 2019, 124, 60001. [Google Scholar] [CrossRef]
- Boykin, T.B.; Klimeck, G. The discretized Schrödinger equation and simple models for semiconductor quantum wells. Eur. J. Phys. 2004, 25, 503–514. [Google Scholar] [CrossRef]
- Tarasov, V.E. Exact discretization of Schrödinger equation. Phys. Lett. A 2016, 380, 68–75. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915–928. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Wong, T.G.; Tarrataca, L.; Nahimov, N. Laplacian versus adjacency matrix in quantum walk search. Quantum Inf. Proc. 2016, 15, 4029–4048. [Google Scholar] [CrossRef]
- Simon, S.H. The Oxford Solid State Basics; The Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Paris, M.G.A. Quantum estimation for quantum technology. Int. J. Quantum Inf. 2009, 7, 125–137. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zatelli, F.; Benedetti, C.; Paris, M.G.A. Scattering as a Quantum Metrology Problem: A Quantum Walk Approach. Entropy 2020, 22, 1321. https://doi.org/10.3390/e22111321
Zatelli F, Benedetti C, Paris MGA. Scattering as a Quantum Metrology Problem: A Quantum Walk Approach. Entropy. 2020; 22(11):1321. https://doi.org/10.3390/e22111321
Chicago/Turabian StyleZatelli, Francesco, Claudia Benedetti, and Matteo G. A. Paris. 2020. "Scattering as a Quantum Metrology Problem: A Quantum Walk Approach" Entropy 22, no. 11: 1321. https://doi.org/10.3390/e22111321
APA StyleZatelli, F., Benedetti, C., & Paris, M. G. A. (2020). Scattering as a Quantum Metrology Problem: A Quantum Walk Approach. Entropy, 22(11), 1321. https://doi.org/10.3390/e22111321




