2. Model
We consider an XXZ spin chain of length
L with the following Hamiltonian
where
are the raising and lowering operators acting on site
i and
is a Pauli spin matrix.
J and
denote the tunneling strength and magnitude of the nearest neighbor interaction, respectively. We use
for the local magnetic field. On each site, the local magnetic field
can only take the two discrete values
. Therefore, there are
possible shapes of magnetic field potential.
The chain is coupled to two spin baths at the edges and we model the evolution via a Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) master equation [
16,
17] for the system density matrix as [
3,
12,
18,
19,
20,
21,
22,
23,
24]
where the
are the jump operators given by
Here, describes the system-reservoir coupling strength and () is the left (right) dissipation bias. We choose a symmetric driving at the boundaries, i.e., . Thus, is the dissipative boundary driving bias, due to the reservoirs. In the limiting case with , so that and , the left reservoir tries to impose spin up to spin down conversions, while the right reservoir would do the opposite, only converting spins down to spins up. For the rest of the paper, in the study of our systems, we will be using , which is the largest possible bias , and we will refer to this as the strong driving regime.
For
, the system relaxes to a current carrying non-equilibrium steady state (NESS)
at long times. The spin current
can be obtained from the continuity equation for local magnetisation
,
resulting in
, where
. In the steady state, the current is independent of the chosen site
i. For all systems considered in this study, the steady state density matrix
is computed by setting the time derivative to zero in Equation (
2) and using exact diagonalization with a number conserving numerical approach described in [
25], which allows for studying open spin systems up to 14 spins. From the point of view of numerical computations, we stress that, to simulate with exact diagonalization the density matrix for
L spins, one would require storing a state with
elements, which corresponds to simulating the unitary dynamics of a system with
spins. This poses a severe limit to the system sizes that one can compute in reasonable time. In the following, we work in units, for which
J and
ℏ are 1.
3. Results
Interactions in the XXZ chain can significantly alter the spin transport in a boundary driven chain. For instance, in the absence of any field and for
, the spin current is ballistic for
(weakly interacting), super diffusive for
, and insulating for
(strongly interacting). The insulating behavior at large bias results in the interesting phenomenon of negative differential conductance in strongly interacting (
) XXZ chains [
5,
6]. The insulating behavior is attributed to the formation of two oppositely polarized ferromagnetic domains in the chain, each half of the chain acquiring the polarisation of the reservoir to which it is connected. The two domains inhibit the spin flips that result in the reduction of current in the chain. The main focus of this paper is to explore the potential advantages of these ferromagnetic domains in device applications. To this end, we apply a local magnetic field in all of the possible shapes of magnetic field potential configurations, as presented in Equation (
1) to the XXZ chain and study the spin transport.
We start by considering, in
Figure 1, the spin current
versus interaction
for all of the
configurations of the magnetic field. We highlight that the presence of fewer lines as compared to
in these panels is due to the fact that some different configurations of magnetic fields result in the same current. For instance, there are only 10 plots in
Figure 1a, and this is due to the fact that there are six pairs of magnetic field configurations that yield the same
versus
profile within the pair. In the following, we use the following notation in order to indicate the magnetic fields direction: we write a + for a site with magnetic field
and − for a site with field
. For instance,
corresponds to the magnetic field configuration
. For the case in which the magnetic field is
h in the first half of the chain, and
in the second half of the chain, we refer to it as
, the magnetic field, which is
in the first half of the chain and
in the second half, we refer to it as
. Note that the configuration
is highlighted by the red dotted line, while its reflection symmetric configuration
is depicted by the blue dashed line while all the other configurations by represented by grey lines. For
large enough we observe that the configurations corresponding to the blue and the red lines are either the ones with the largest or the lowest currents. This is very clearly observed for system sizes
to 8.
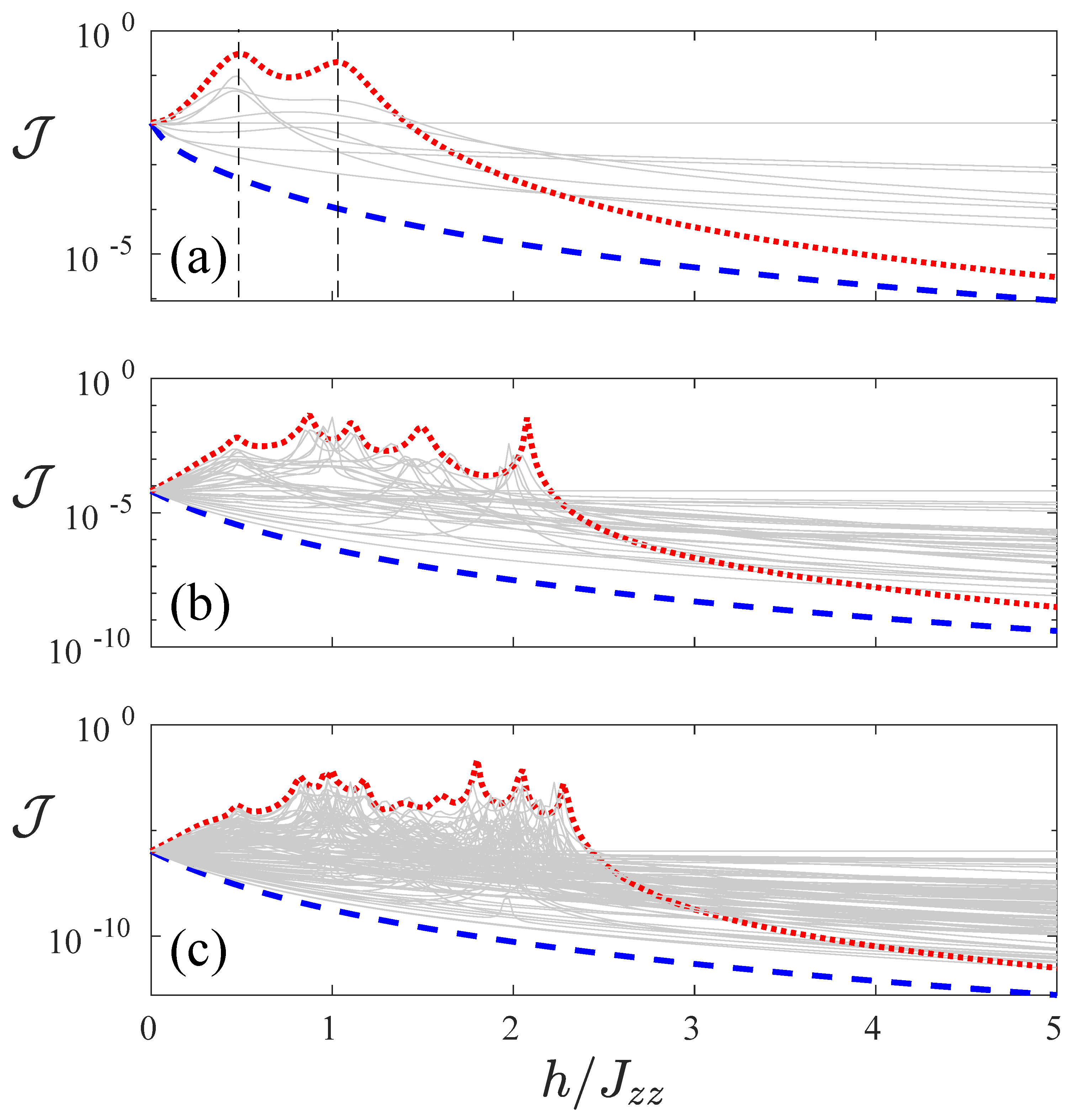
In
Figure 1, we consider a large local field
. However, it is insightful to fix the interaction to be large, e.g.,
and study the current as we vary
h. This is depicted in
Figure 2. The configuration
corresponds (blue dashed line) to the lowest current, while the configuration
corresponds, for smaller
h, to the largest currents. It also presents some resonant-like structures, and its current decreases for larger values of
h. Given this seemingly antithetic effect of the
and
configurations, which are reflection symmetric of each other, in the following we study the effectiveness of all the different magnetic field configurations in order to result in a large spin current rectification effect.
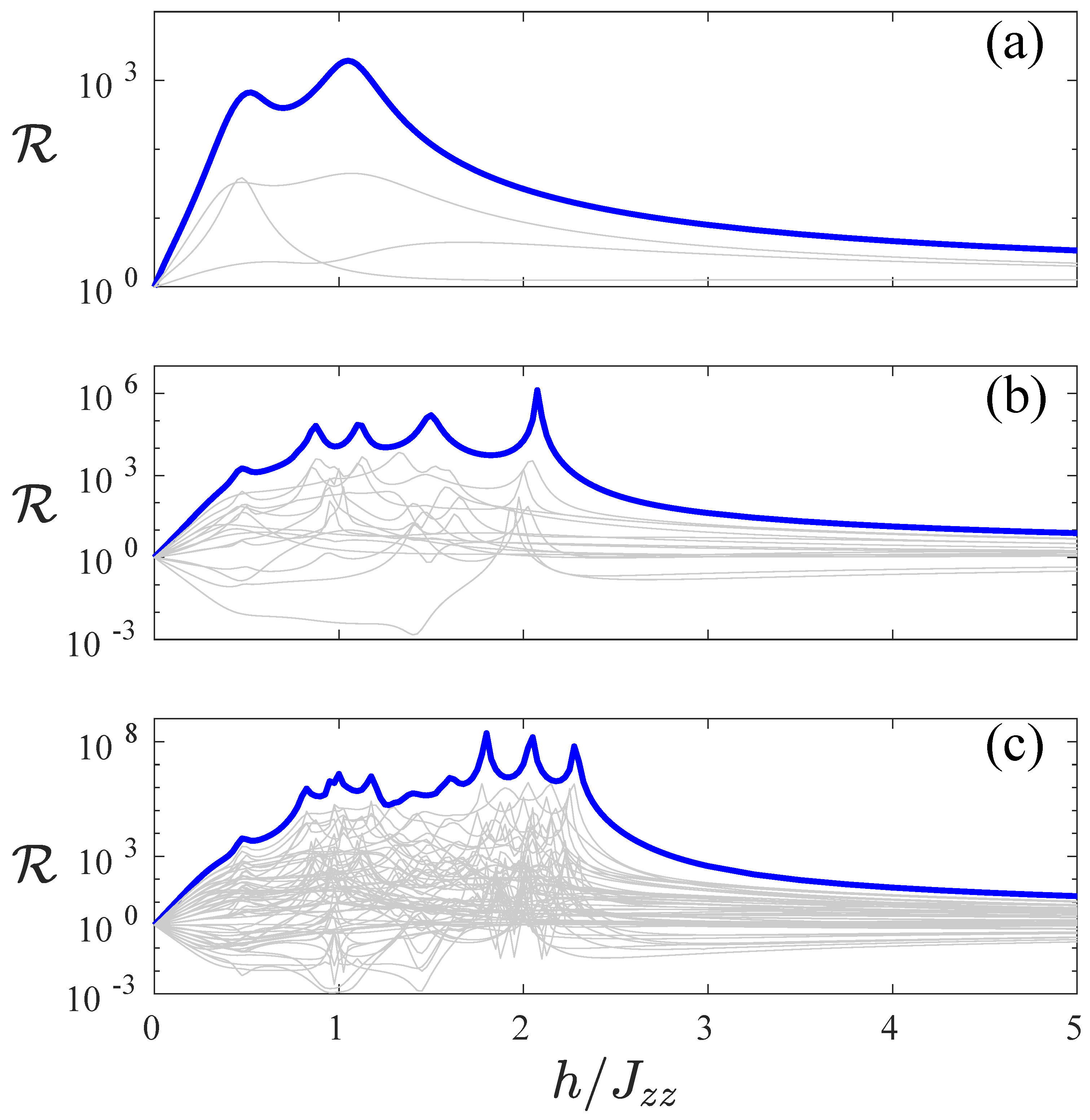
Thus, we investigate the rectification in
Figure 3. Here, the rectification is quantified using
[
7,
26,
27,
28], where
and
are referred to as forward and reverse currents and are computed, respectively, for a configuration of the magnetic field and its reflection symmetric one, e.g.,
and
. We note that this is equivalent to fixing a configuration and switching the driving bias (i.e.,
, forward direction to
, reverse direction). When
, there is no rectification as the forward and reverse currents are equal, e.g., for symmetric magnetic fields configurations. Perfect diodes are signalled by
or 0 (the latter is obtained when the forward current tends to 0, but the reverse current is finite). In
Figure 3, there are less lines when compared to
Figure 1 and
Figure 2, and this is due to the fact that each line corresponds to a pair of magnetic field configurations: one is a configuration and the other is the reflection symmetric one. Importantly, each pair is considered only once, e.g., we plot the rectification considering the
configuration to give the forward current
and
to give the reverse current
, and we do not plot the opposite combination, because it does not give extra information, resulting in a
rectification. This is particularly relevant, because, in
Figure 3, we use a log-lin plot, and the reverse combination of magnetic field configurations would simply result in a curve symmetric around
. The blue thick line presented in
Figure 3 corresponds to the combination
, for
, and
, for
, and it gives clearly the strongest rectification. We remind the reader that a small value of
corresponds to a large rectification in the opposite direction, yet clearly the blue thick line corresponds to the largest possible current rectifications. In
Figure 3, we also note that, for larger systems, one can obtain even larger rectifications, for example, showing a rectification of
for the
chain. We will also return to this point in a later part of the paper.
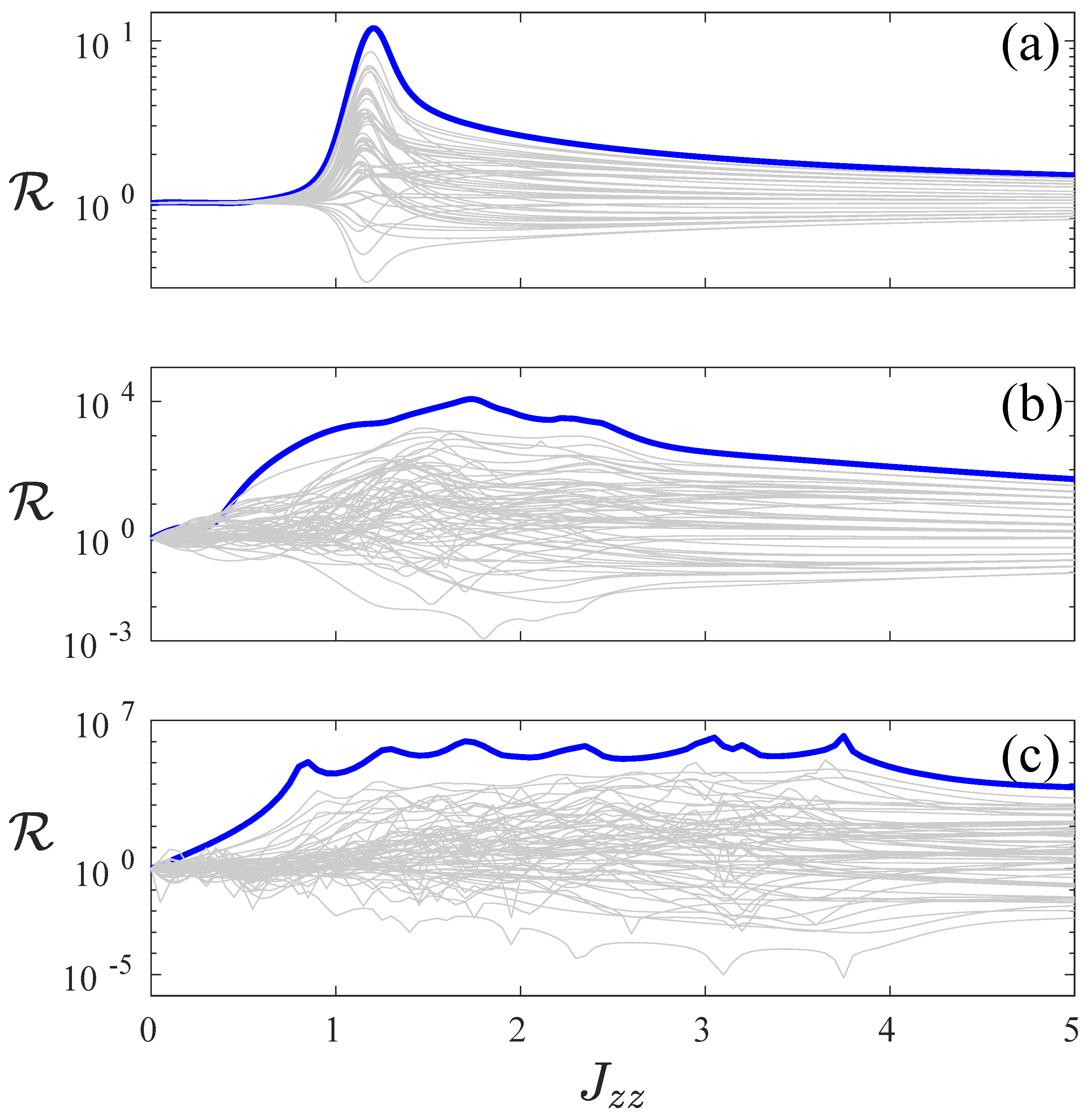
In
Figure 4, rectification
is plotted as a function of interaction
. Similar to
Figure 3, each line corresponds to a pair of magnetic field configurations, which are the reflection symmetric of each other. Highlighted in blue thick line is the
,
configuration pair which yields the strongest rectification. Here, we highlight the role of interaction
in causing large rectification. In panel (a) of
Figure 4, where
, we observe the sharp transition to a steep increase in rectification occuring near
, where the quantum phase transition occurs. This transition occurs at smaller values of
for increasing
h, as we observe for
in panel (b) and
in panel (c). With increasing
h, the system behaviour deviates further from that of the XXZ spin chain system, and it is thus natural that the values of
, for which an enhancement of rectification occur, deviates further from
.
Figure 4 thus highlights the importance of the interplay of kinetic, interactive, and dissipative terms in the master Equation (
2) of the set-up.
In
Figure 1,
Figure 2,
Figure 3 and
Figure 4, we have observed resonances, which correspond to peaks of currents and the largest rectifications. We now aim to gain an insight into this. The mechanism for the emergence of such resonances, and of the strong rectifications, can be understood by studying the configuration
, where the field is in the positive direction in first half of the chain and negative in the other half of the chain (the configuration corresponding to the largest rectification). To give a clear idea of the mechanism, we focus on the case of
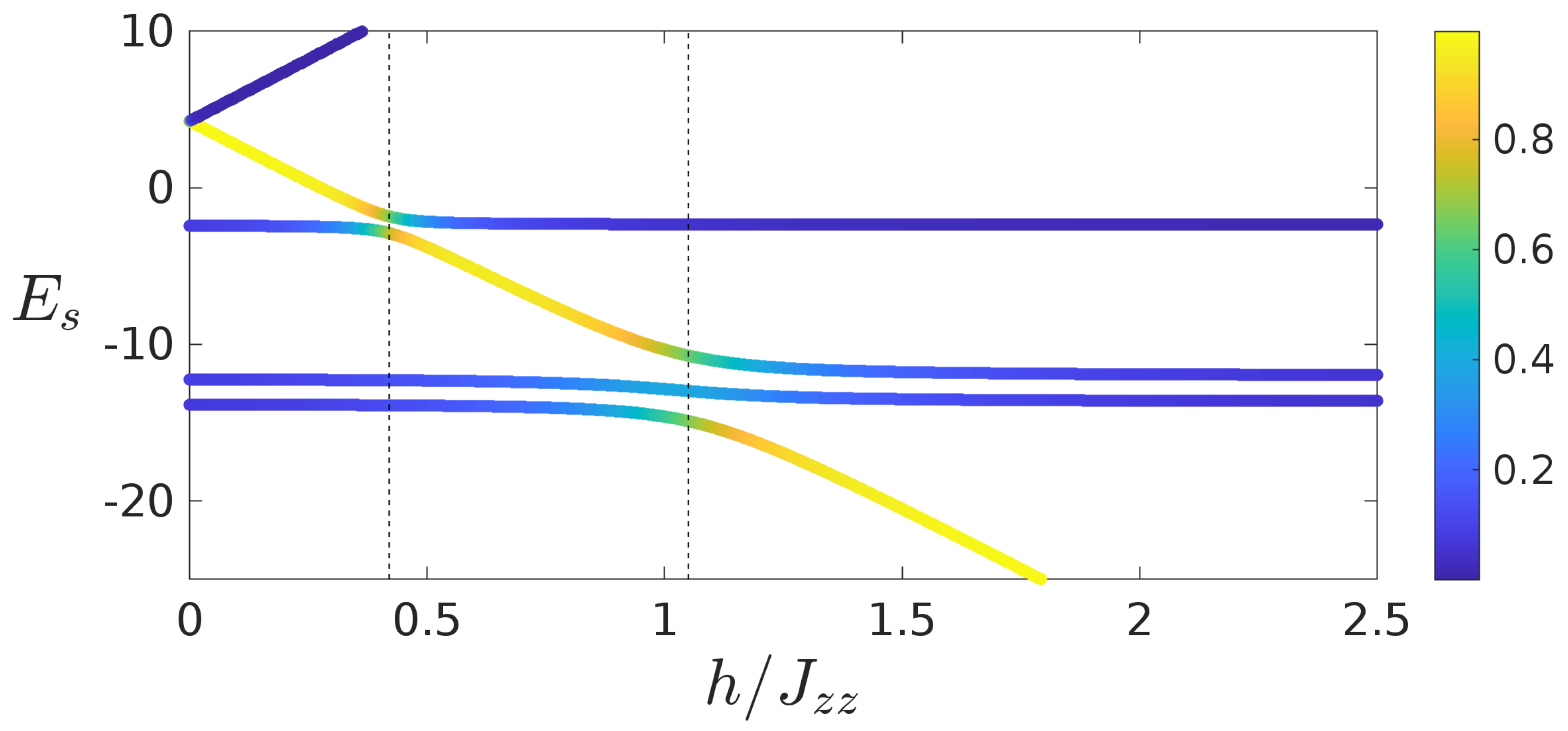
. In
Figure 5, we show the energy spectrum as a function of
h for
. For each magnitude
h, the value of the energy is indicated by a point in the plot. Different colors of each point corresponds to the values of the overlap of the corresponding eigenvector
with the state
, i.e.,
. The vertical dashed lines show the position of the peaks of current for system size
, as taken from
Figure 2. It is clear from the figure that the avoided crossings in the spectrum matches with the maxima of the current. At these points, given the proximity in energy between different energy eigenstates, it is easier for the steady state to be in a mixture of different eigenstates, thus resulting in the possibility of larger currents (note that each energy eigenstate carries 0 current). The presence of avoided crossings for the peaks in
Figure 1,
Figure 2 and
Figure 3 has been checked for all system sizes and parameters tested.
Thus, we have shown that an XXZ chain with large enough interaction
and a magnetic field in the configuration
results in a highly performing spin-current diode. It is however important to investigate the performance at larger sizes of this diode. At this point we should stress that computing the steady state in regimes of very low currents is extremely demanding, because the equations are ill-conditioned. Thus, we resort to a different, yet very insightful approach. In order to understand the robustness of the effect for larger system sizes, we study the inverse participation ratio (
) of the Hamiltonian of the system with the local magnetic field configuration
in
Figure 6. The
for a given state
over the energy eigenstates
is given by
. A value of
means that the state
is well distributed over all the eigenstates
, while
means that
almost exactly corresponds to a single energy eigenstate. The study of this quantity can be done simply by diagonalizing the Hamiltonian, which we do for system sizes up to
.
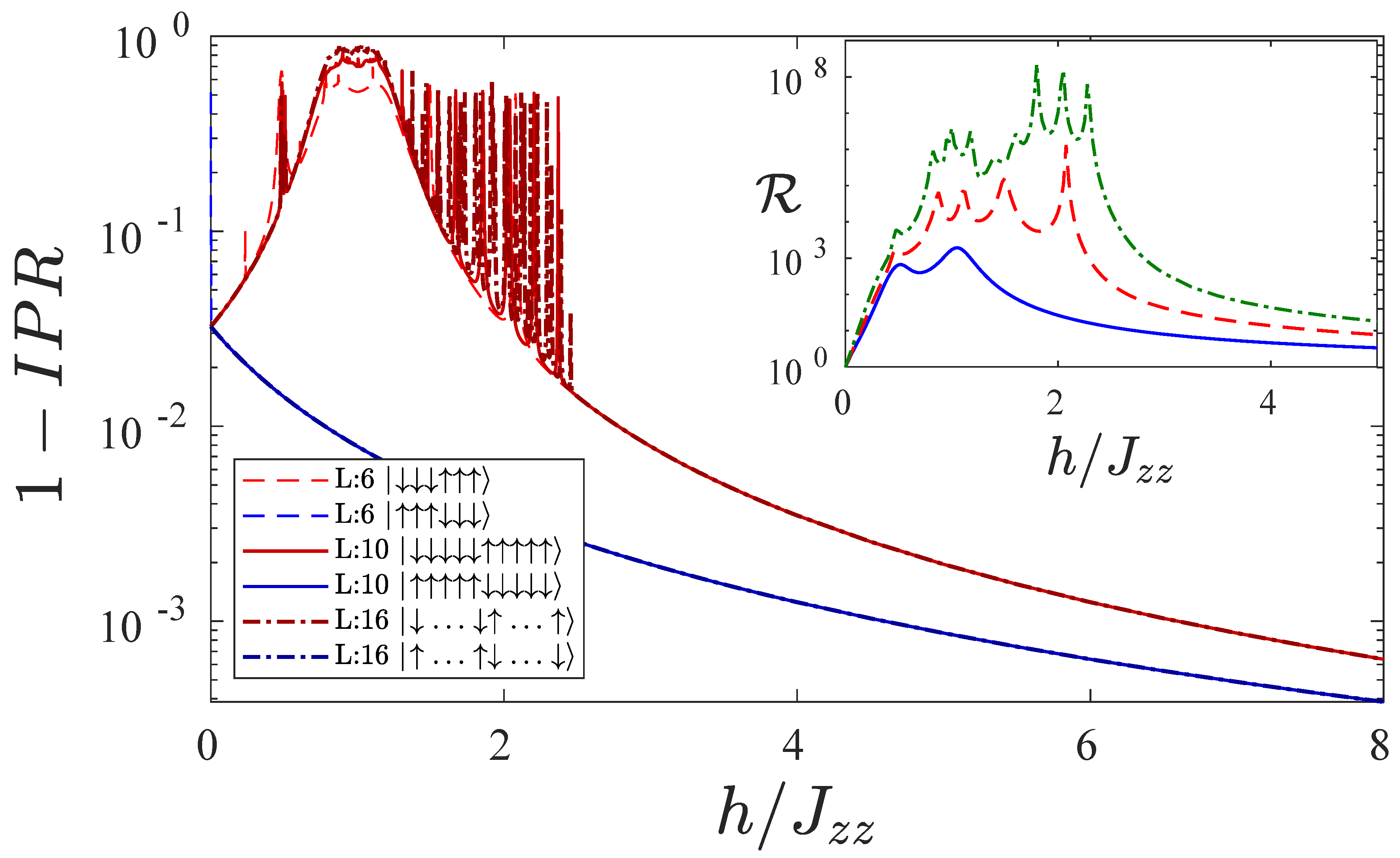
In
Figure 6, we plot
as a function of the ratio of local field strength and interaction
for the state
(red plots) and for the state
(blue plots). For the state
,
quickly becomes small and it continues to decrease as
h increases. This means that the state that is favored by the dissipator in reverse bias,
, is almost entirely an eigenstate of the Hamiltonian. Hence, the steady state would be well approximated by this
current-carrying state. We note that the blue solid, dashed, and dot-dashed curves relative to this state, each for a different system size, are almost completely identical.
For the state
, the physics is very different. For
well approximates the highest energetic state, together with
. However, while
approximates better and better the highest energetic state as
h increases, for large enough magnetic field
h, the state
well approximates the ground state. Hence, this state is bound to go through numerous avoided crossings, at the occurrence of which transport is favored and rectification can be very large. In particular, we observe that, for the state
,
is close to 1 for
, and
increases with the system sizes. This is because of the presence of a energy band of state that are crossed for
. Beyond this energy band, there can be other avoided crossings which can result in even larger rectification. For instance, in the inset of
Figure 6, we illustrate the rectification for different system sizes, showing a significant increase in the rectification power as the system size increases, even up to
(
blue continuous line,
red dashed line, and
green dot-dashed line). The exact position of the last avoided crossings depends on the parameters of the system. For large enough
, they occur for
. This can be computed analytically, in fact, setting
one realizes that the energy of state
is, for large enough system sizes
L, given by
while the energy of the first excited state (at large enough
h), is
. These two energies coincide for
. For finite values of
J and smaller ratios
, the last resonance is moved to larger values of
h, as in the cases analyzed in this work.
In
Figure 7, we plot the steady state Von Neumann entropy
. In the reverse bias case (lines with ∘), the entropy decreases rapidly as
h increases, because the steady state approaches more closely a pure state. This mirrors the results presented in
Figure 6, where
in the reverse bias is favoured by the dissipator and is almost entirely an eigenstate of the Hamiltonian. In the case with magnetic field configuration
(lines without symbols), the steady state is mixed and has much larger entropy, particularly at the avoided crossing where the current and the rectification are largest. For even larger magnitude of the magnetic field
h, the steady state also approximates a pure state and the entropy decreases.