Estimation of the Reliability of a Stress–Strength System from Poisson Half Logistic Distribution
Abstract
1. Introduction
2. Estimation of R in General Case
2.1. Maximum Likelihood Estimation
2.2. Asymptotic Distribution and Confidence Interval
2.3. Bootstrap Confidence Intervals for R
- Generate independent samples from PGHLD1, and from PGHLD2. The samples can be generated from (2) by sampling p from uniform distribution i.e., .
- Generate an independent bootstrap sample and taken with replacement from the given samples above in the first step. Based on the bootstrap sample compute the maximum likelihood estimates of say as well as the MLE of .
- Repeat step 2 to 3 B-times to obtain a set of bootstrap samples of R say , .
2.3.1. Percentile Bootstrap Confidence Interval :
2.3.2. Student’s t Bootstrap Confidence Interval ():
3. Estimation of R with Common Scale Parameter
3.1. Maximum Likelihood Estimation
3.2. Asymptotic Distribution and Confidence Intervals
4. Bayes Estimation of R
4.1. Bayes Estimation of R in General Case
- Step 1: Start with initial guess
- Step 2: Set
- Step 3: Use the Metropolis–Hastings algorithm to generate from and from
- Step 4: Use the Metropolis–Hastings algorithm to generate from and from
- Step 5: Compute from Equation (7)
- Step 6: Set
- Step 7: Repeat step 3 to 6, T times.
4.2. Bayes Estimation of R with Common Scale Parameter
- Step 1: Start with initial guess
- Step 2: Set
- Step 3: Use the Metropolis–Hastings algorithm to generate from and from
- Step 4: Use the Metropolis–Hastings algorithm to generate from
- Step 5: Compute from Equation (14)
- Step 6: Set
- Step 7: Repeat step 3 to 6, T times.
5. Simulation
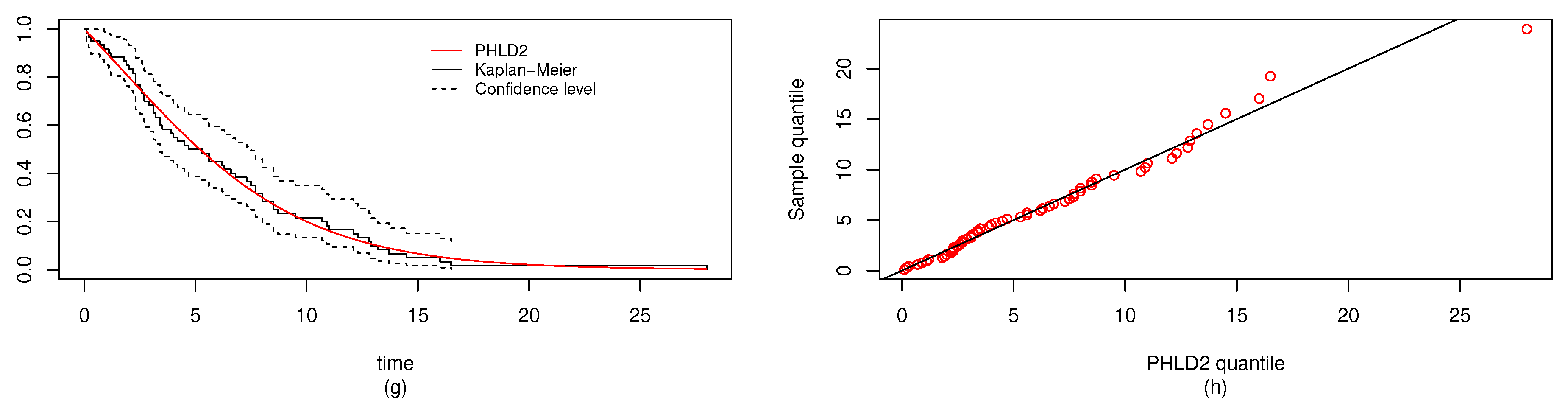
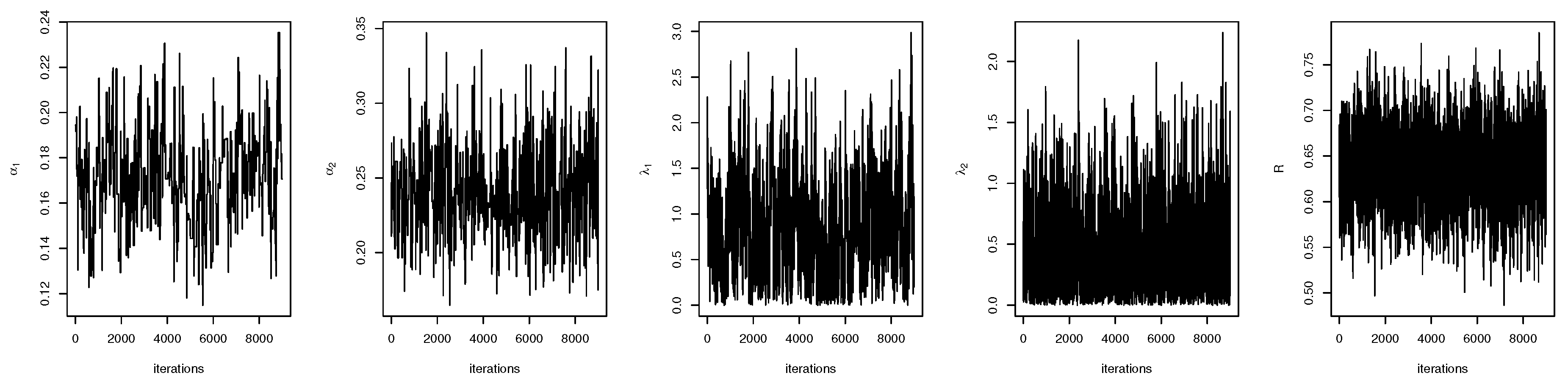
6. Real Data Study
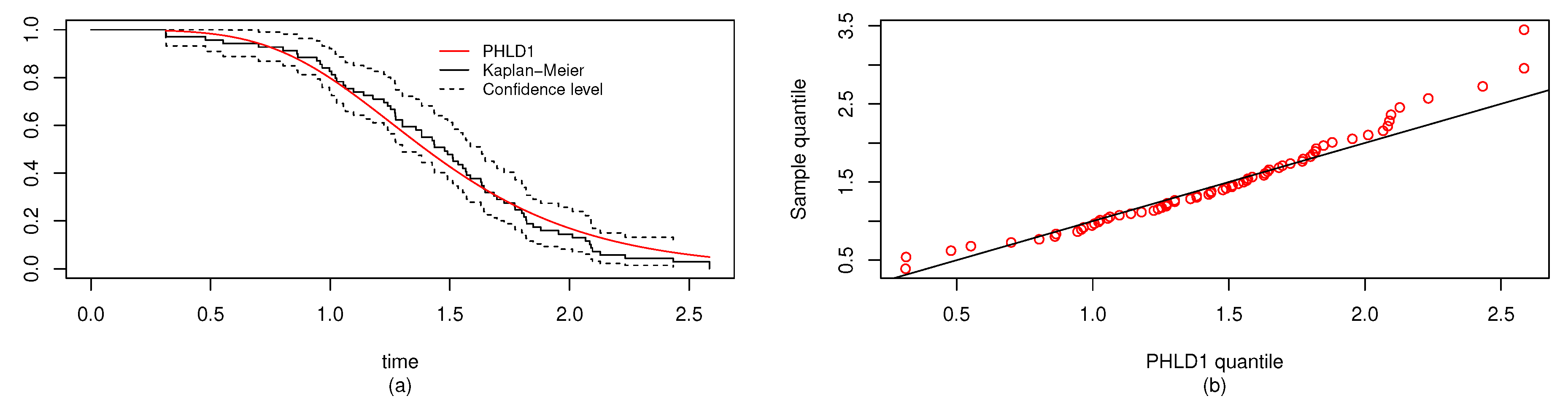
6.1. Real Data Study 1
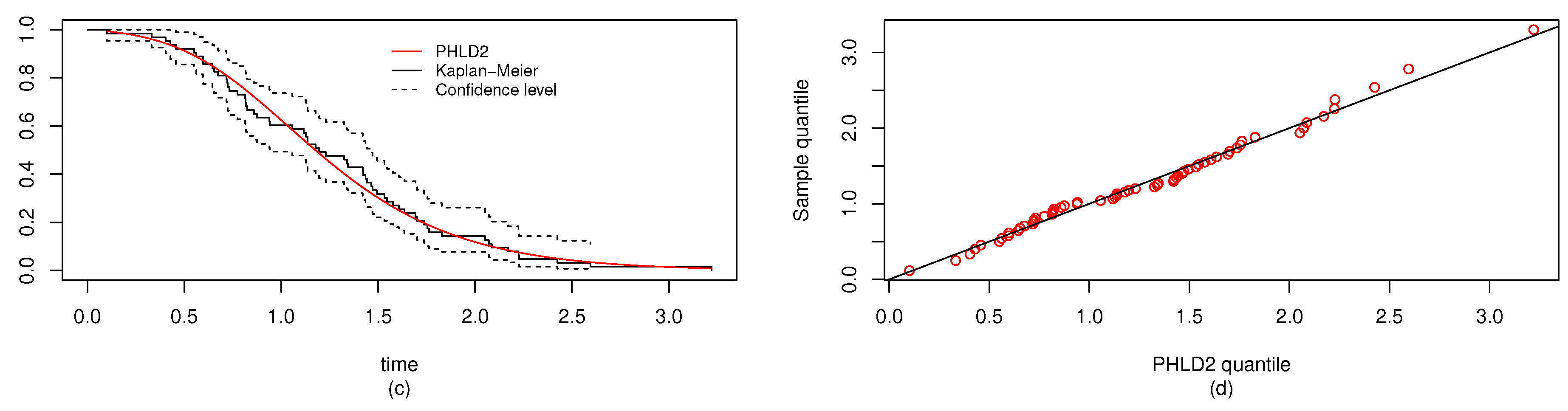
6.2. Real Data Study 2
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AEL | absolute error loss function |
| ALCI | average length of confidence interval |
| asymptotic confidence interval | |
| BE | Bayes estimation |
| percentile bootstrap confidence interval | |
| student’s bootstrap confidence interval | |
| CI | confidence interval |
| CP | coverage probability |
| GEL | general entropy loss function |
| HPD | highest posterior density |
| Fisher information matrix | |
| KS | Kolmogorov-Smirnov |
| L | log-likelihood |
| LINEX | linear exponential loss function |
| MAP | maximum a posteriori |
| MLE | maximum likelihood estimation |
| MSE | mean square error |
| PHLD | Poisson half logistic distribution |
| R | stress-strength parameter |
| SEL | square error loss function |
Appendix A
References
- Wolfe, D.A.; Hogg, R.V. On constructing statistics and reporting data. Am. Stat. 1971, 25, 27–30. [Google Scholar]
- Lloyd, D.K.; Lipow, M. Reliability, Management, Methods and Mathematics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Guttman, I.; Johnson, R.A.; Bhattacharyya, G.K.; Reiser, B. Confidence limits for stress-strength models with explanatory variables. Technometrics 1988, 30, 161–168. [Google Scholar] [CrossRef]
- Kotz, S.; Lumelskii, Y.; Pensky, M. The Stress–Strength Model and Its Generalizations: Theory and Applications; World Scientific: Singapore, 2003. [Google Scholar]
- Ratnam, R.R.L.; Rosaiah, K.; Anjaneyulu, M.S.R. Estimation of reliability in multicomponent stress-strength model: Half logistic distribution. IAPQR Trans. 2000, 25, 43–52. [Google Scholar]
- Kim, D.H.; Kang, S.G.; Cho, J.S. Noninformative priors for stress-strength system in the Burr-type X model. J. Korean Stat. Soc. 2000, 29, 17–27. [Google Scholar]
- Guo, H.; Krishnamoorthy, K. New approximate inferential methods for the relia- bility parameter in a stress-strength model: The normal case. Commun. Stat. Theory Methods 2004, 33, 1715–1731. [Google Scholar] [CrossRef]
- Barbiero, A. Confidence intervals for reliability of stress-strength models in the normal case. Commun. Stat. Simul. Comput. 2011, 40, 907–925. [Google Scholar] [CrossRef]
- Gupta, R.C.; Brown, N. Reliability studies of the skew-normal distribution and its application to a strength-stress model. Commun. Stat. Theory Methods 2001, 30, 2427–2445. [Google Scholar] [CrossRef]
- Azzalini, A.; Chiogna, M. Some results on the stress-strength model for skew-normal variates. Metron 2004, 62, 315–326. [Google Scholar]
- Shawky, A.I.; El Sayed, H.S.; Nassar, M.M. On stress-strength reliability model in generalized gamma case. IAPQR Trans. 2001, 26, 1–8. [Google Scholar]
- Khan, M.A.; Islam, H.M. On strength reliability for generalized gamma distributed stress. J. Stat. Theory Appl. 2009, 8, 115–124. [Google Scholar]
- Nadarajah, S. Reliability for logistic distributions. Elektron. Model. 2004, 26, 65–82. [Google Scholar]
- Asgharzadeh, A.; Valiollahi, R.; Raqab, M.Z. Estimation of the stress-strength reliability for the generalized logistic distribution. Stat. Meth. 2013, 15, 73–94. [Google Scholar] [CrossRef]
- Nadarajah, S. Reliability for Laplace distributions. Math. Prob. Eng. 2004, 2, 169–183. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D. Estimation of P(Y < X) for generalized exponential distribution. Metrika 2005, 61, 291–308. [Google Scholar]
- Krishnamoorthy, K.; Mukherjee, S.; Guo, H. Inference on reliability in two- parameter exponential stress-strength model. Metrika 2007, 65, 261–273. [Google Scholar] [CrossRef]
- Baklizi, A. Interval estimation of the stress-strength reliability in the two-parameter exponential distribution based on records. J. Stat. Comput. Simul. 2014, 84, 2670–2679. [Google Scholar] [CrossRef]
- Baklizi, A.; El-Masri, A.Q. Shrinkage estimation of P(X<Y) in the exponential case with common location parameter. Metrika 2004, 59, 163–171. [Google Scholar]
- Kayid, M.; Elbatal, I.; Merovci, F. A new family of generalized quadratic hazard rate distribution with applications. J. Test. Eval. 2016, 44. [Google Scholar] [CrossRef]
- Abbas, K.; Tang, Y. Objective Bayesian analysis of the Fréchet stress-strength model. Stat. Prob. Lett. 2014, 84, 169–175. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Mutairi, D.K.; Aboukhamseen, S.M. Estimation of the reliability of a stress-strength system from power Lindley distributions. Commun. Stat. Simul. Comput. 2015, 44, 118–136. [Google Scholar] [CrossRef]
- Okasha, H.M.; Kayid, M.; Abouammoh, M.A.; Elbatal, I. A new family of quadratic hazard rate-geometric distributions with reliability applications. J. Test. Eval. 2016, 44, 1937–1948. [Google Scholar] [CrossRef]
- Nadarajah, S.; Bagheri, S.; Alizadeh, M.; Samani, E. Estimation of the Stress Strength Parameter for the Generalized Exponential-Poisson Distribution. J. Test. Eval. 2018, 46, 2184–2202. [Google Scholar] [CrossRef]
- Nadarajah, S. Reliability for some bivariate beta distributions. Math. Prob. Eng. 2005, 1, 101–111. [Google Scholar] [CrossRef]
- Shrahili, M.; Elbatal, I.; Muhammad, I.; Muhammad, M. Properties and applications of beta Erlang-truncated exponential distribution. J. Math. Comput. Sci. JM 2020, 22, 16–37. [Google Scholar] [CrossRef]
- Muhammad, M.; Lixia, L. A New Extension of the Generalized Half Logistic Distribution with Applications to Real Data. Entropy 2019, 21, 339. [Google Scholar] [CrossRef]
- Ahmad, K.E.; Jaheen, Z.F.; Yousef, M.M. Inference on Pareto distribution as stress- strength model based on generalized order statistics. J. Appl. Stat. Sci. 2010, 17, 247–257. [Google Scholar]
- Krishnamoorthy, K.; Lin, Y. Confidence limits for stress-strength reliability involv- ing Weibull models. J. Stat. Plan. Infer. 2010, 140, 1754–1764. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D. Estimation of P[Y < X] for Weibull distributions. IEEE Trans. Reliab. 2006, 55, 270–280. [Google Scholar]
- Asgharzadeh, A.; Valiollahi, R.; Raqab, M.Z. Stress-strength reliability of Weibull distribution based on progressively censored samples. SORT 2011, 35, 103–124. [Google Scholar]
- Asgharzadeh, A.; Kazemi, M.; Kundu, D. Estimation of P(X<Y) for Weibull distribution based on hybrid censored samples. Int. J. Syst. Assur. Eng. Manag. 2015. [Google Scholar] [CrossRef]
- Valiollahi, R.; Asgharzadeh, A.; Raqab, M.Z. Estimation of P(Y<X) for Weibull distribution under progressive type-II censoring. Commun. Stat. Theory Methods 2013, 42, 4476–4498. [Google Scholar]
- Asgharzadeh, A.; Valiollahi, R.; Raqab, M.Z. Estimation of Pr(Y<X) for the two- parameter generalized exponential records. Commun. Stat. Simul. Comput. 2017, 46, 371–394. [Google Scholar]
- Kohansal, A. Bayesian and classical estimation of R=P(X<Y) based on Burr type XII distribution under hybrid progressive censored samples. Commun. Stat. Theory Methods 2019. [Google Scholar] [CrossRef]
- Yadav, A.S.; Singh, S.K.; Singh, U. Bayesian estimation of stress–strength reliability for Lomax distribution under type-II hybrid censored data using asymmetric loss function. Life Cycle Reliab. Saf. Eng. 2019, 8, 257–267. [Google Scholar] [CrossRef]
- Alaa, H.; Properties, A.-H. Estimations and Predictions for a Poisson- Half-Logistic Distribution Based on Progressively Type-II Censored Samples. Appl. Math. Model. 2016. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer: New York, NY, USA, 2006. [Google Scholar]
- Muhammad, M.; Yahaya, M.A. The Half Logistic-Poisson Distribution. Asian J. Math. Appl. 2017, 2017. [Google Scholar]
- Muhammad, M. Generalized Half Logistic Poisson Distributions. Commun. Stat. Appl. Methods 2017, 24, 1–14. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to Bootstrap; Chapman & Hall Inc.: New York, NY, USA, 1993. [Google Scholar]
- Calabria, R.; Pulcini, G. Point estimation under asymmetric loss function for left truncated exponential samples. Commun. Stat. Theory Meth. 1996, 25, 285–600. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. Equations of state calculations by fast computing machine. J. Chem. Phys. 1953, 21, 1087–1091. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their appli- cations. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Smith, A.F.M. Sampling-based approaches to calculating marginal densities. J. Am. Stat. Assoc. 1990, 85, 398–409. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian Credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar]
- Meredith, M.; Kruschke, J. HDInterval: Highest (Posterior) Density Intervals. R Package Version 0.2.0. 2018. Available online: https://CRAN.R-project.org/package=HDInterval (accessed on 11 October 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 11 October 2020).
- Al-Mutairi, D.K.; Ghitany, M.E.; Kundu, D. Inferences on stress-strength reliability from weighted lindley distributions. Commun. Stat. Theory Meth. 2015, 44, 4096–4113. [Google Scholar] [CrossRef]
- Badar, M.G.; Priest, A.M. Statistical aspects of fibre and bundle strength in hybrid composites. In Progress in Science and Engineering Composites; Hayashi, T., Kawata, K., Umekawa, S., Eds.; ICCM-IV: Tokyo, Japan, 1982; pp. 1129–1136. [Google Scholar]
- Raqab, M.Z.; Kundu, D. Comparison of different estimators of P(Y<X) for a scaled Burr Type X distribution. Commun. Stat. Simul. Comput. 2005, 34, 465–483. [Google Scholar]
- Surles, J.G.; Padgett, W.J. Inference for Reliability and Stress-Strength for a Scaled Burr-Type X Distribution. Lifetime Data Anal. 1998, 7, 187–200. [Google Scholar] [CrossRef]
- Surles, J.G.; Padgett, W.J. Inference for P(Y<X) in the Burr-Type X Model. J. Appl. Stat. Sci. 2001, 7, 225–238. [Google Scholar]
- Al-Mutairi, D.K.; Ghitany, M.E.; Kundu, D. Inferences on stress-strength reliability from lindley distributions. Commun. Stat. Theory Meth. 2013, 42, 1443–1463. [Google Scholar] [CrossRef]
- Ali, S. On the mean residual life function and stress and strength analysis under different loss function for lindley distribution. J. Qual. Reliab. Eng. 2013. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Sharma, V.K. Estimation on system reliabilityin generalized Lindley stress-strength model. J. Stat. Appl. Prob. 2014, 3, 61–75. [Google Scholar] [CrossRef]
- Sadek, A. Mostafa Mohie Eldin and Shaimaa Elmeghawry. Estimation of Stress-Strength Reliability for Quasi Lindley Distribution. Adv. Syst. Sci. Appl. 2018, 18, 39–51. [Google Scholar]
- Lindley, D.V. Fiducial distributions and bayes theorem. J. R. Stat. Soc. 1958, 20, 102–107. [Google Scholar] [CrossRef]




| R | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| 4 | ||||||||||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| R | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |||||||||||||
| ALCI | CP | ALCI | CP | ALCI | CP | ALCI | CP | |||||||||||||
| L | |||||
|---|---|---|---|---|---|
| MLE | |||||
| Bayes | − | ||||
| KS | |||||
| p-value |
| R | ||||||
| CI | ||||||
| LCI |
| L | |||||
|---|---|---|---|---|---|
| MLE | |||||
| Bayes | − | ||||
| KS | |||||
| p-value |
| R | ||||||
| CI | ||||||
| LCI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, I.; Wang, X.; Li, C.; Yan, M.; Chang, M. Estimation of the Reliability of a Stress–Strength System from Poisson Half Logistic Distribution. Entropy 2020, 22, 1307. https://doi.org/10.3390/e22111307
Muhammad I, Wang X, Li C, Yan M, Chang M. Estimation of the Reliability of a Stress–Strength System from Poisson Half Logistic Distribution. Entropy. 2020; 22(11):1307. https://doi.org/10.3390/e22111307
Chicago/Turabian StyleMuhammad, Isyaku, Xingang Wang, Changyou Li, Mingming Yan, and Miaoxin Chang. 2020. "Estimation of the Reliability of a Stress–Strength System from Poisson Half Logistic Distribution" Entropy 22, no. 11: 1307. https://doi.org/10.3390/e22111307
APA StyleMuhammad, I., Wang, X., Li, C., Yan, M., & Chang, M. (2020). Estimation of the Reliability of a Stress–Strength System from Poisson Half Logistic Distribution. Entropy, 22(11), 1307. https://doi.org/10.3390/e22111307





