Noise Reduction in Spur Gear Systems
Abstract
:1. Introduction
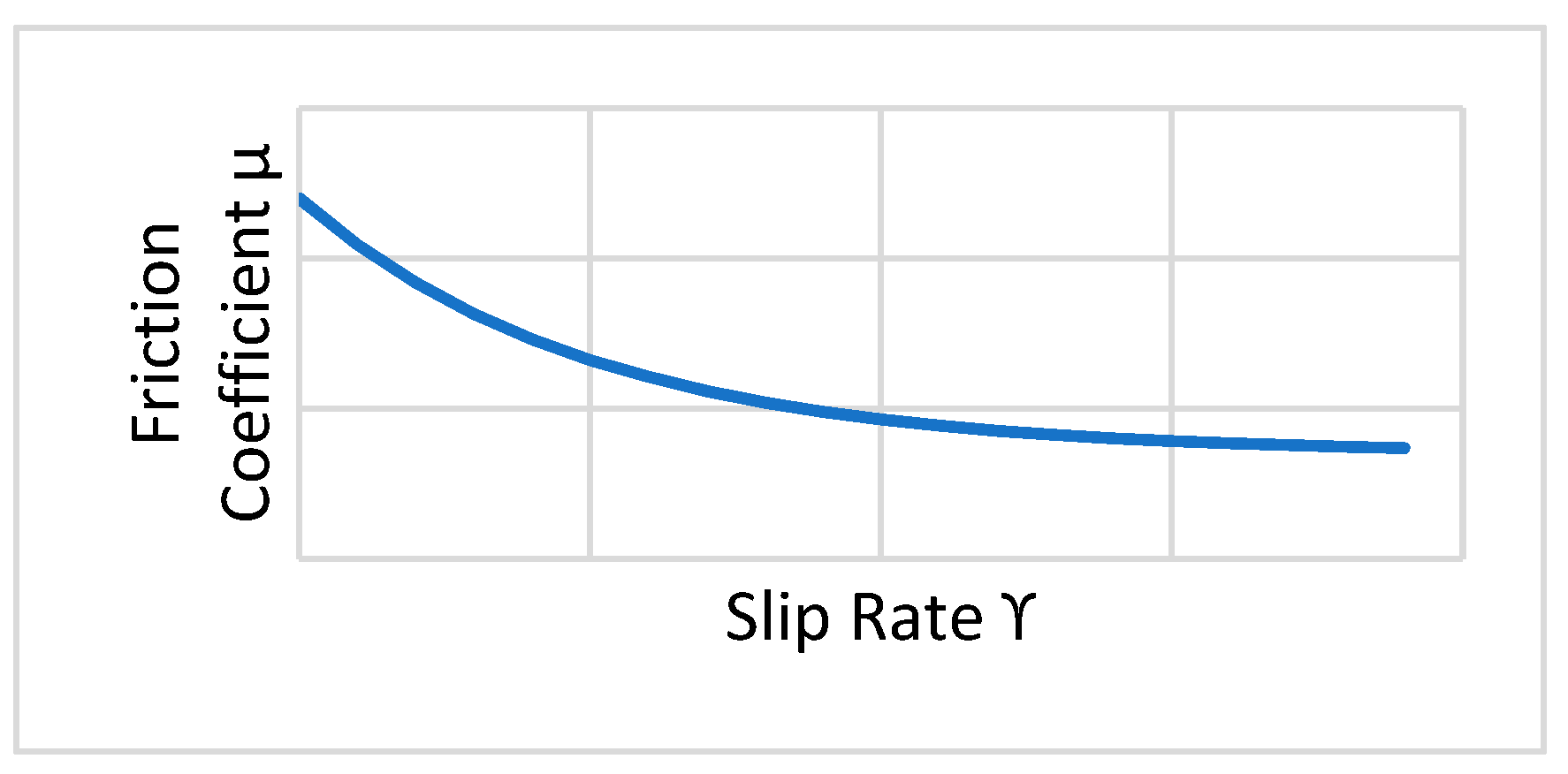
2. Materials and Methods
FEM Static Analysis of a Spur Gear Pair
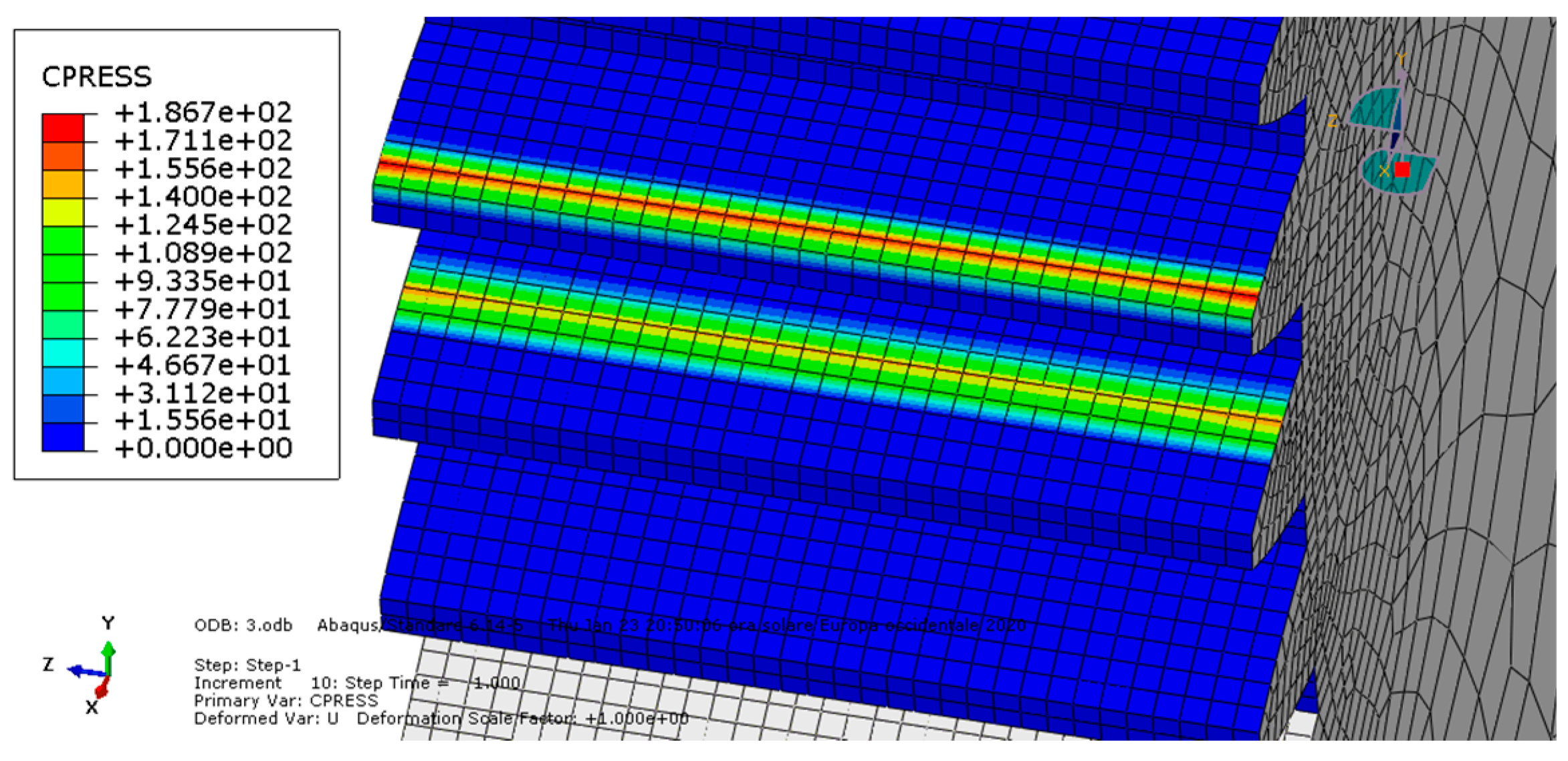
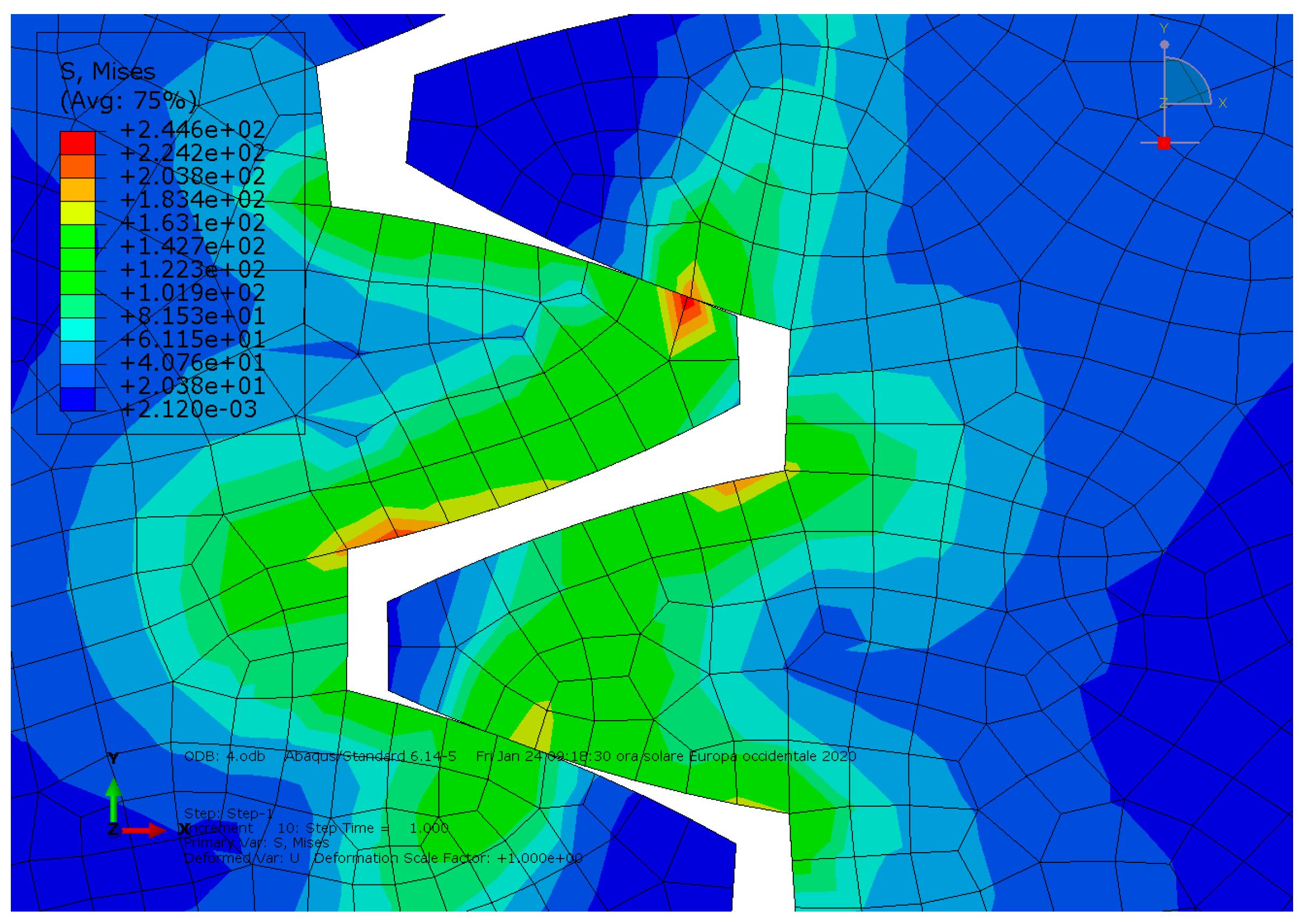
3. Results
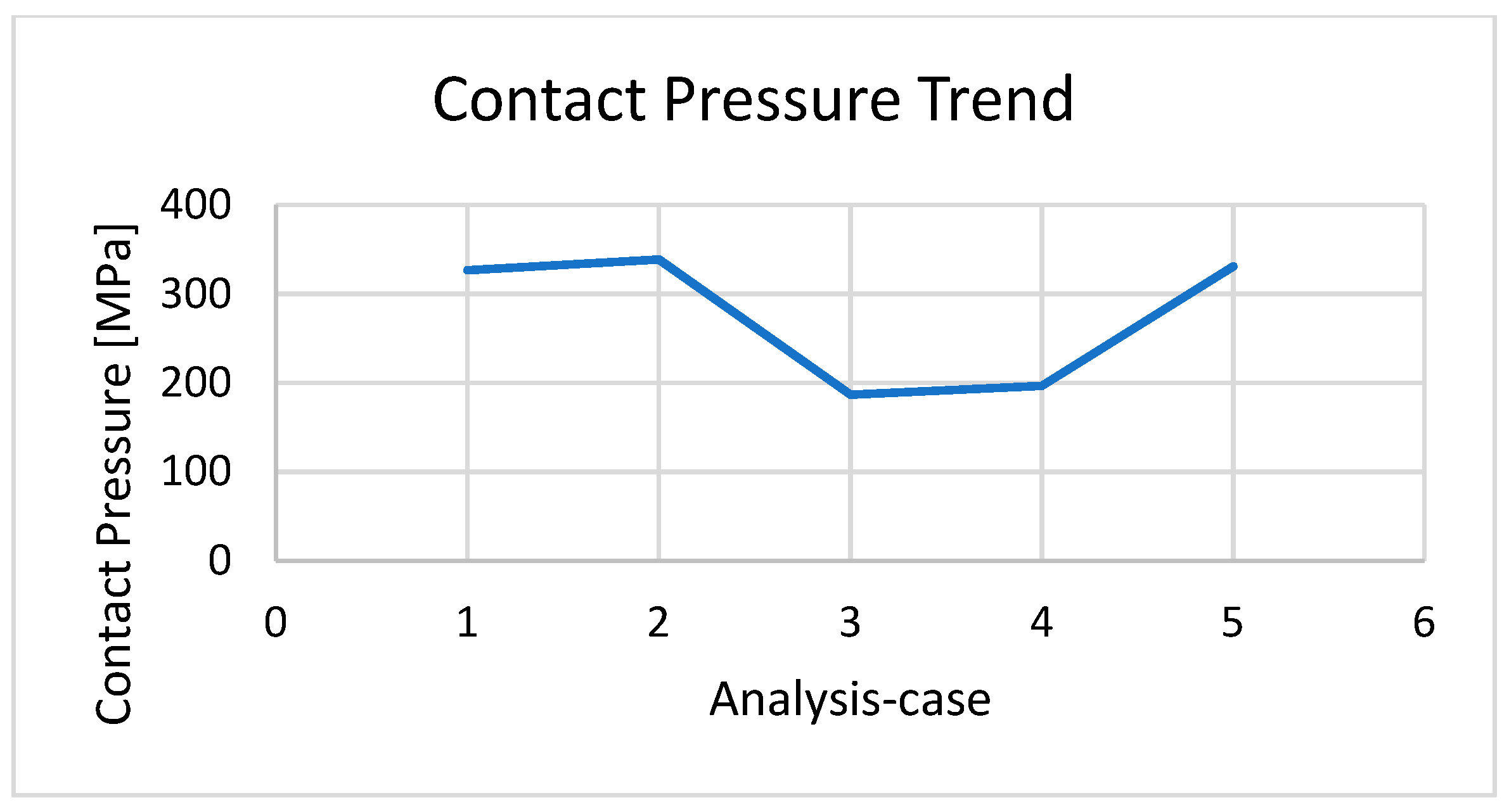
3.1. Comparisons
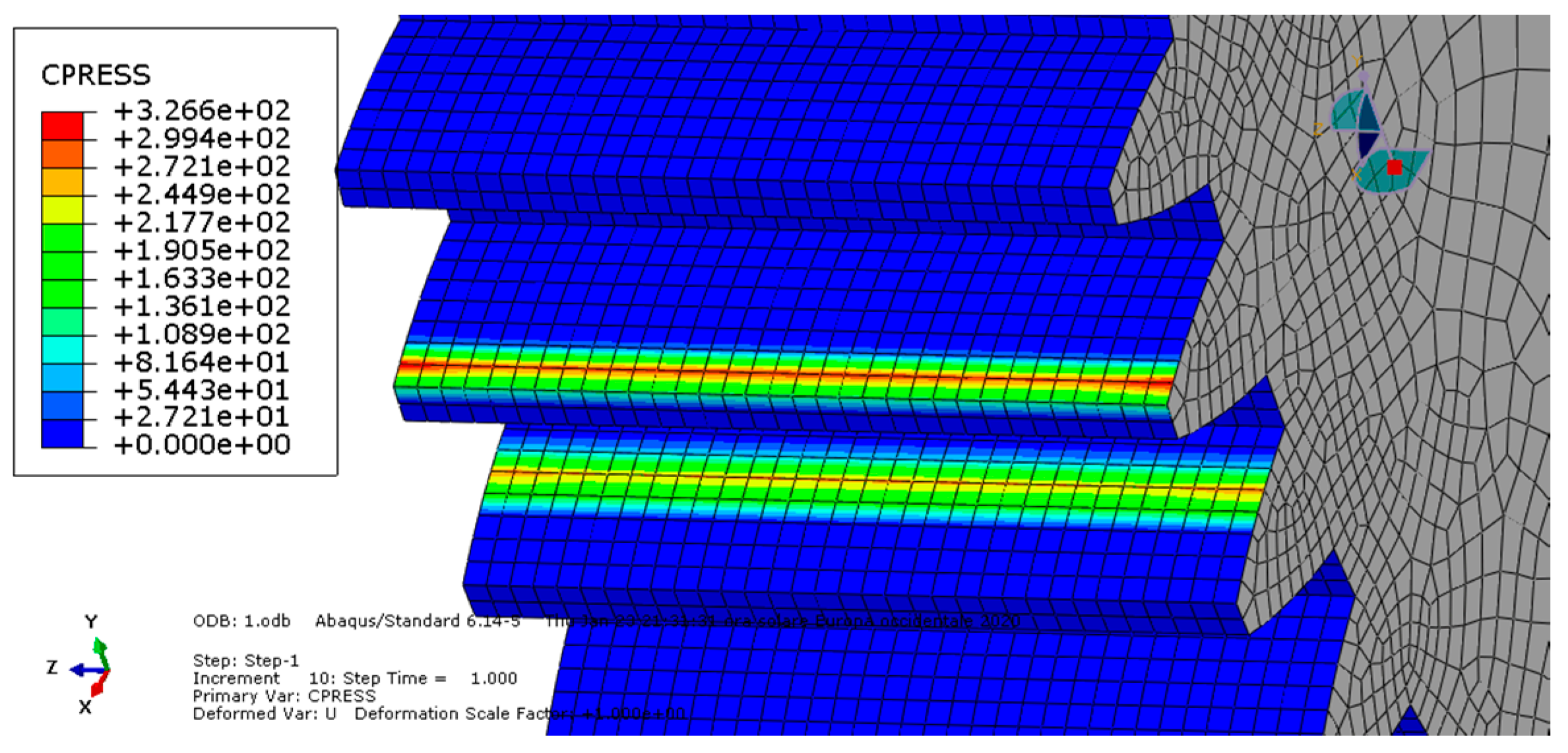
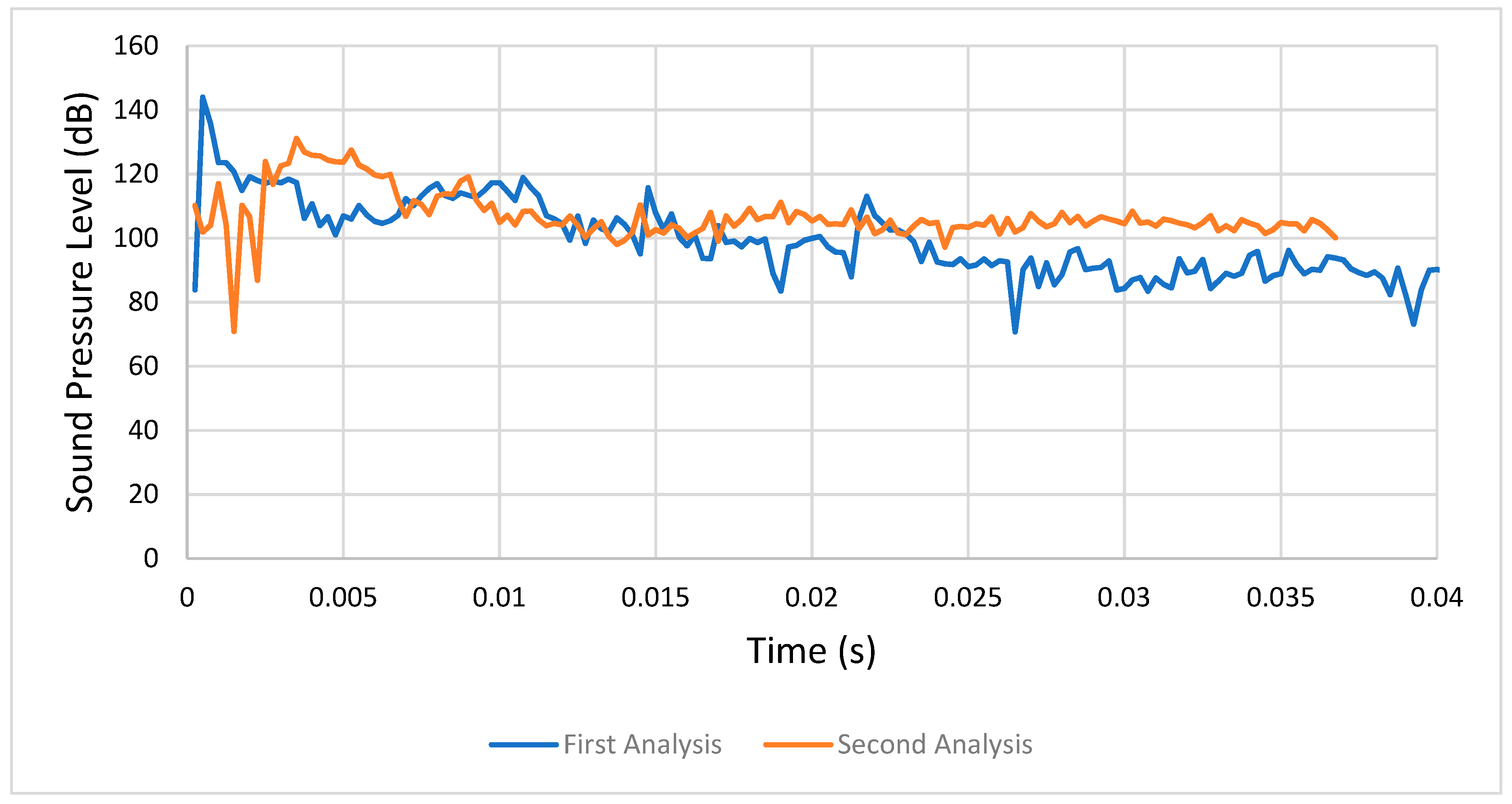
The second analysis (condition B) showed higher von Mises stress and contact pressure values than the first one, so the presence of friction made the stress increase together with the sound excitation, as previously mentioned for this parameter.
Third Analysis (Condition C) versus Fourth Analysis (Condition D)
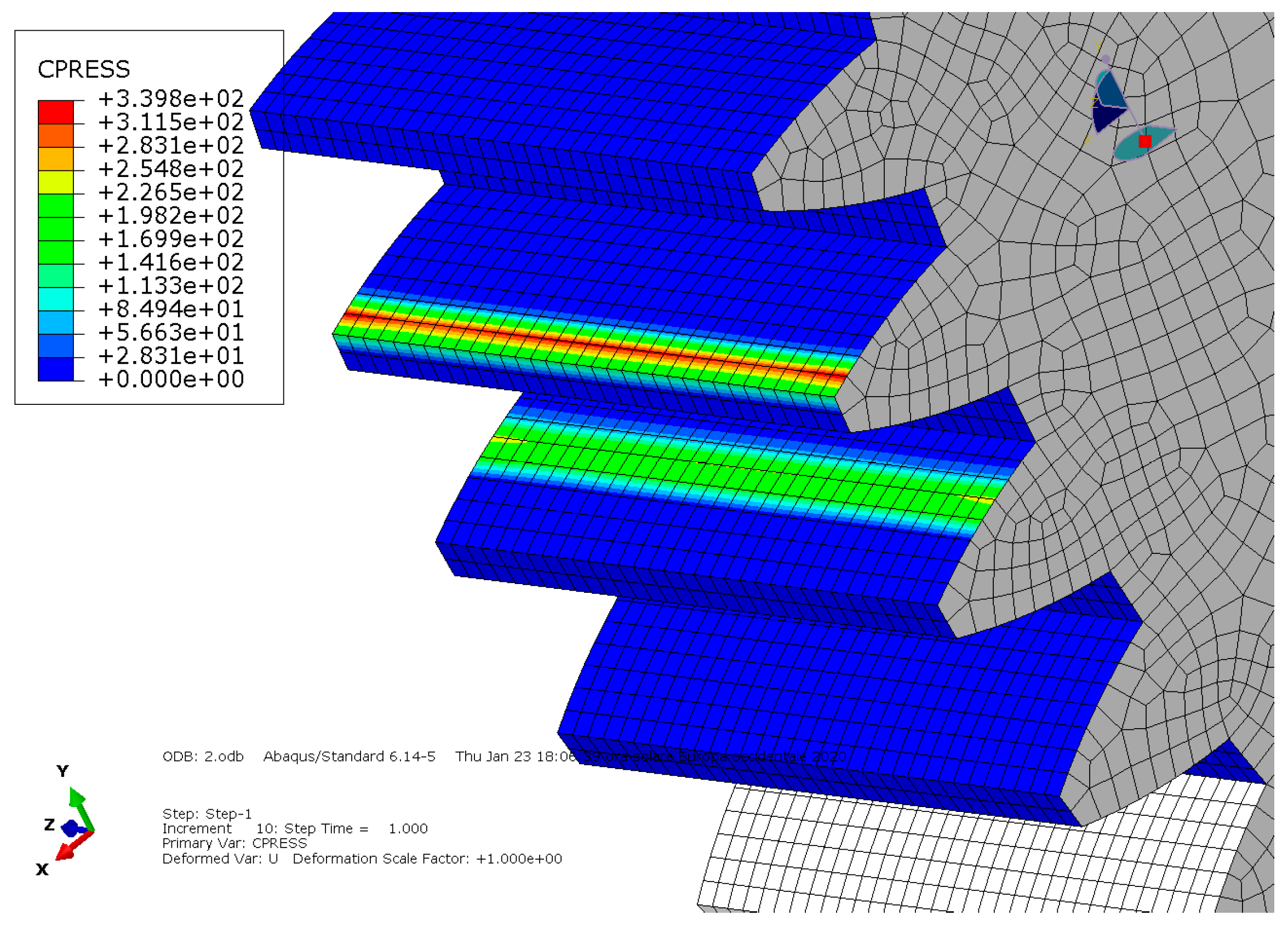
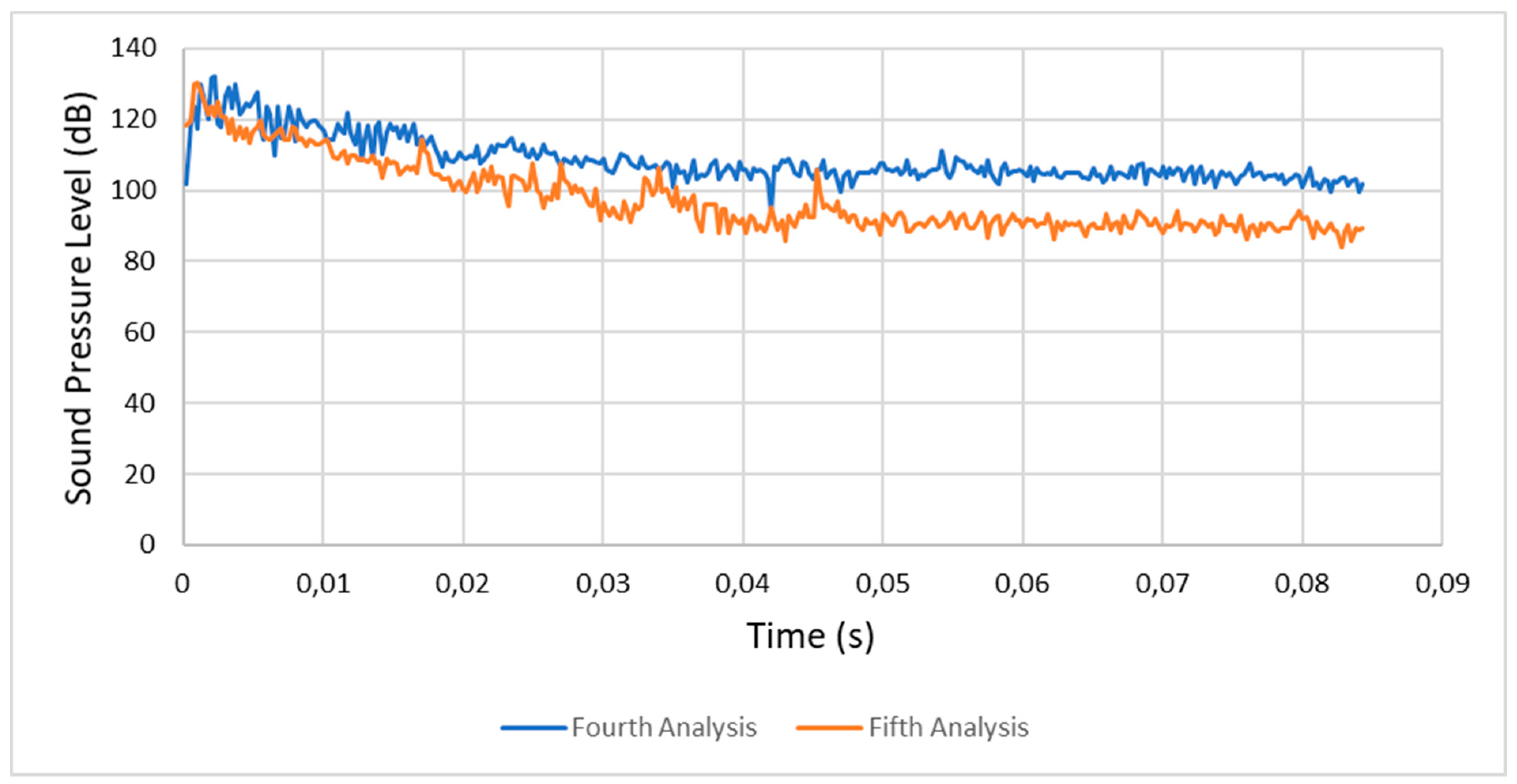
As we can see in the third and fourth analyses, the ductile iron spur gears had lower von Mises stress and lower contact pressure values, in agreement with comments regarding gear materials and ductile iron properties. Therefore, the sound excitation was lower as well.
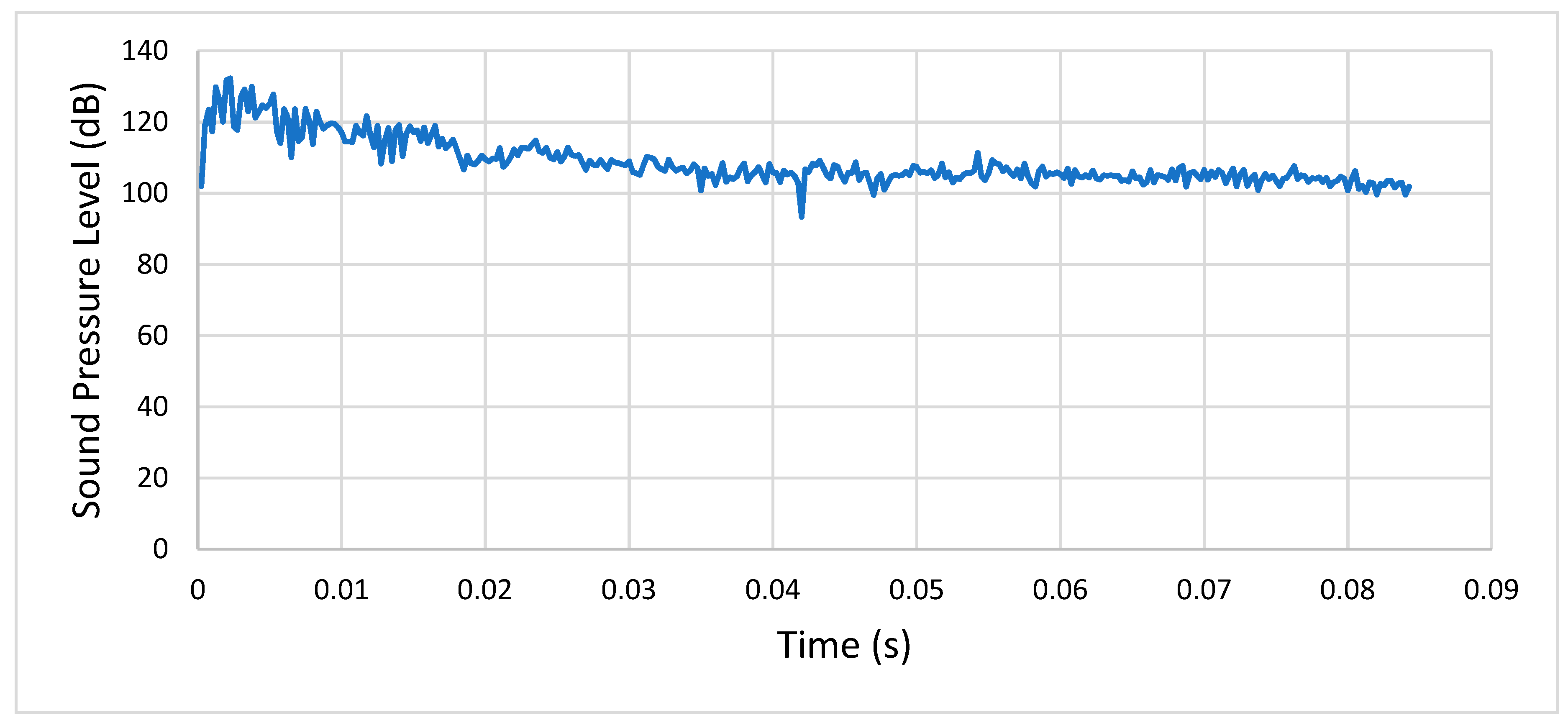
Fifth Analysis (Condition E) versus First Analysis (Condition A)
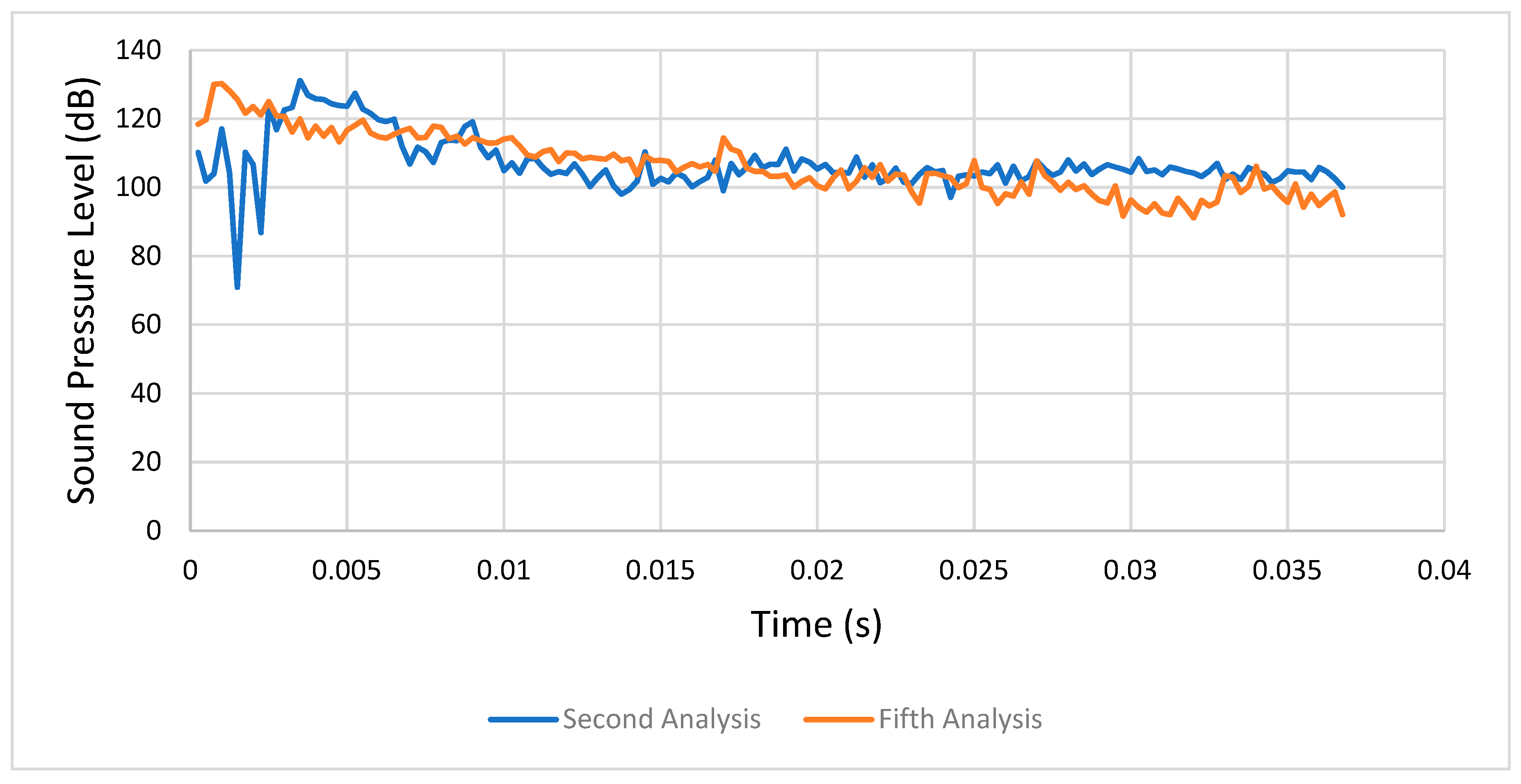
The fifth analysis showed that lubricated friction made the stress decrease together with the contact pressure, leading to agreement that the oil coating reduced the sound excitation of the gears.
First Two Analyses (Conditions A and B) versus Third and Fourth (Conditions C and D) Analyses
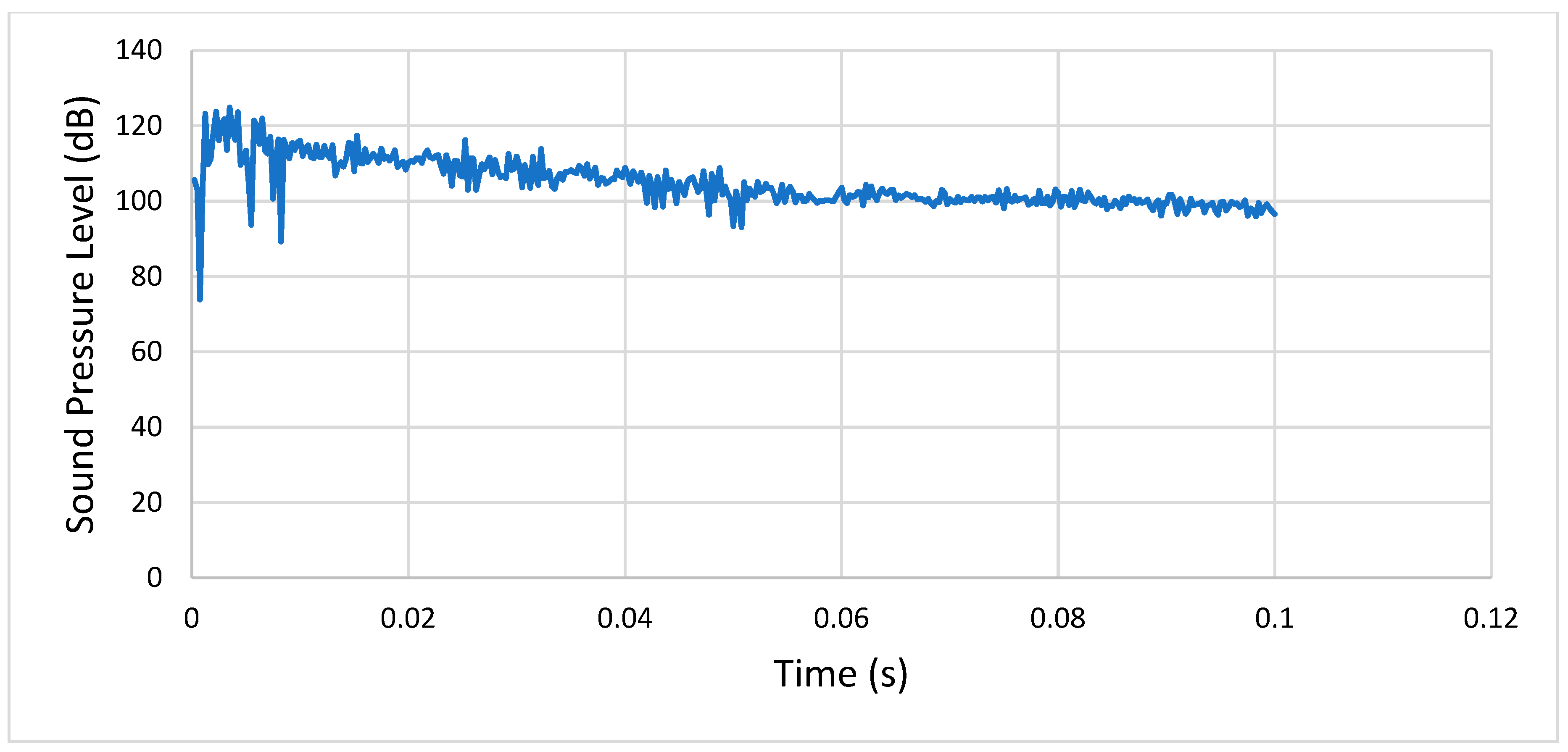
3.2. Difference Static and Dynamic Analyses
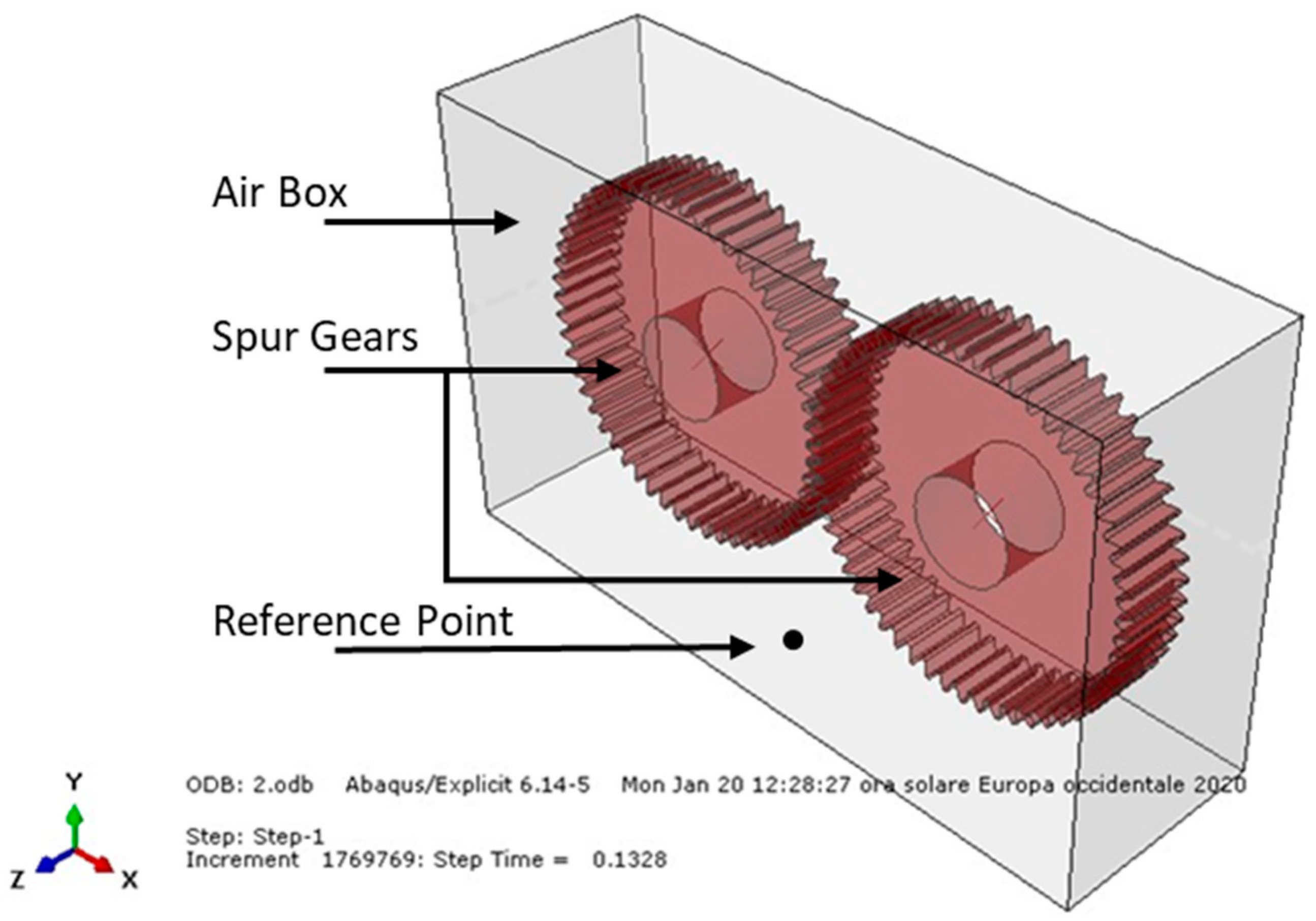
3.3. Coupled Eulerian–Lagrangian (CEL) Analysis of a Spur Gear Pair
“EULERIAN BOUNDARY, OUTFLOW = NON REFLECTING”.
4. Discussion
4.1. Comparisons
4.1.1. First Analysis (Condition 1) versus Second Analysis (Condition 2)
4.1.2. Third Analysis (Condition 3) versus Fourth Analysis (Condition 4)
4.1.3. Fourth Analysis (Condition 4) versus Fifth Analysis (Condition 5)
4.1.4. Second Analysis (Condition 2) versus Fifth Analysis (Condition 5)
4.1.5. Final Remarks
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wittbrodt, M.J.; Pechersky, M.J. A Hydrodynamic Analysis of Fluid Flow Between Meshing Spur Gear Teeth. J. Mech. Trans. Autom. 1989, 111, 395–401. [Google Scholar]
- Sosnovskiy, L.A.; Sherbakov, S.S. On the Development of Mechanothermodynamics as a New Branch of Physics. Entropy 2019, 21, 1188. [Google Scholar]
- Basaran, C. Entropy Based Fatigue, Fracture, Failure Prediction and Structural Health Monitoring. Entropy 2020, 22, 1178. [Google Scholar]
- Kondepudi, D. Modern Thermodynamics. From Heat Engines to Dissipative Structures; Kondepudi, D., Prigogine, I., Eds.; John Wiley & Sons: New York, NY, USA, 1998; p. 510. [Google Scholar]
- Mase, G. Theory and Problems of Continuum Mechanics; McGraw-Hill: New York, NY, USA, 1970; p. 221. [Google Scholar]
- Sedov, L.I. A Course in Continuum Mechanics; Wolters–Noordho: Groningen, The Netherlands, 1971; p. 242. [Google Scholar]
- Young, C.; Subbarayan, G. Maximum Entropy Models for Fatigue Damage in Metals with Application to Low-Cycle Fatigue of Aluminum 2024-T351. Entropy 2019, 21, 967. [Google Scholar]
- Yun, H.; Modarres, M. Measures of Entropy to Characterize Fatigue Damage in Metallic Materials. Entropy 2019, 21, 804. [Google Scholar]
- Wang, J.; Yao, Y. An Entropy-Based Failure Prediction Model for the Creep and Fatigue of Metallic Materials. Entropy 2019, 21, 1104. [Google Scholar]
- Glowacz, A. Recognition of acoustic signals of induction motor using FFT, SMOFS-10 and LSVM, Eksploatacja i Niezawodność. Maint. Reliab. 2015, 17, 569–574. [Google Scholar]
- Glowacz, A. Recognition of Acoustic Signals of Commutator Motors. Appl. Sci. 2018, 8, 2630. [Google Scholar]
- Armentani, E.; Sepe, R.; Parente, A.; Pirelli, M. Vibro-Acoustic Numerical Analysis for the Chain Cover of a Car Engine. Appl. Sci. 2017, 7, 610. [Google Scholar]
- Armentani, E.; Caputo, F.; Esposito, L.; Giannella, V.; Citarella, R. Multibody Simulation for the Vibration Analysis of a Turbocharged Diesel Engine. Appl. Sci. 2018, 8, 1192. [Google Scholar]
- Armentani, E.; Trapani, R.; Citarella, R.; Parente, A.; Pirelli, M. FEM-BEM Numerical Procedure for Insertion Loss Assessment of an Engine Beauty Cover. Open Mech. Eng. J. 2013, 7, 27–34. [Google Scholar]
- Ghosh, S.S.; Chakraborty, G. On optimal tooth profile modification for reduction of vibration and noise in spur gear pairs. Mech. Mach. Theory 2016, 105, 145–163. [Google Scholar]
- Axel Baumann, A.; Bertsche, B. Experimental study on transmission rattle noise behaviour with particular regard to lubricating oil. J. Sound Vib. 2015, 341, 195–205. [Google Scholar]
- Sharma, A.; Aggarwal, M.L.; Singh, L. Experimental investigation into the effect of noise and damping using composite spur gear. Mater. Today Proc. 2017, 4, 2777–2782. [Google Scholar]
- Sharma, R.B.; Parey, A.; Tandon, N. Modelling of acoustic emission generated in involute spur gear pair. J. Sound Vib. 2017, 393, 353–373. [Google Scholar]
- Kopsch, F. The cost of aircraft noise-Does it differ from road noise? A meta-analysis. J. Air Transp. Manag. 2016, 57, 138–142. [Google Scholar]
- Ducobu, F.; Filippi, E.; Arrazola, P.J.; Rivière, E.; Ortis de Zarate, G.; Madariaga, A. The CEL method as an alternative to the current modelling approaches for Ti6Al4V orthogonal cutting simulation. Procedia Cirp 2017, 58, 245–250. [Google Scholar]
- Chang, H.; Tang, H. Review and Comparison of Clock Jitter Noise Reduction Techniques for Lowpass Continuous-Time Delta-Sigma Modulators. J. Low Power Electron. Appl. 2017, 7, 22. [Google Scholar]
- Xiao, D.; Ding, J.; Li, X.; Huang, L. Gear Fault Diagnosis Based on Kurtosis Criterion VMD and SOM Neural Network. Appl. Sci. 2019, 9, 5424. [Google Scholar]
- Formato, G.; Romano, R.; Formato, A.; Sorvari, J.; Koiranen, T.; Pellegrino, A.; Villecco, F. Fluid–Structure Interaction Modeling Applied to Peristaltic Pump Flow Simulations. Machines 2019, 7, 50. [Google Scholar]
- Feng, Z.; Zhang, D.; Zuo, M.J. Planetary Gearbox Fault diagnosis via Joint Amplitude and Frequency Demodulation Analysis Based on Variational Mode Decomposition. Appl. Sci. 2017, 7, 775. [Google Scholar]
- Zhang, R.; Gu, X.; Gu, F.; Wang, T.; Ball, A.D. Gear Wear Process Monitoring Using a Sideband Estimator Based on Modulation Signal Bispectrum. Appl. Sci. 2017, 7, 274. [Google Scholar]
- Neubauer, P.; Bös, J.; Melz, T. Evaluation of the gear noise reduction potential of geometrically uneven inequidistant gears. J. Sound Vib. 2020, 473, 115234. [Google Scholar]
- Formato, A.; Guida, D.; Ianniello, D.; Villecco, F.; Lenza, T.L.; Pellegrino, A. Design of Delivery Valve for Hydraulic Pumps. Machines 2018, 6, 44. [Google Scholar]
- Huang, P.; Xu, L.; Luo, C.; Zhang, J.; Chi, F.; Zhang, Q.; Zhou, J. A Study on Noise Reduction of Gear Pumps of Wheel Loaders Based on the ICA Model. Int. J. Environ. Res. Public Health. 2019, 16, 999. [Google Scholar]
- Chen, Z.; Shao, Y. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack. Mech. Mach. Theory. 2013, 62, 63–74. [Google Scholar]
- Yuksel, C.; Kahraman, A. Dynamic tooth loads of planetary gear sets having tooth profile wear. Mech. Mach. Theory 2004, 39, 695–715. [Google Scholar]
- Liu, G.; Parker, R.G. Dynamic modeling and analysis of tooth profile modification for multimesh gear vibration. J. Mech. Design. 2008, 130, 121402. [Google Scholar]
- Sun, X.; Liu, H.; Song, W.; Villecco, F. Modeling of Eddy Current Welding of Rail: Three-Dimensional Simulation. Entropy 2020, 22, 947. [Google Scholar]
- Živković, M.; Dašić, P.; Predrag, P. Analysis of the Comparative Advantages of Gear Pumps Indicators. Lect. Notes Netw. Systems. 2020, 76, 158–164. [Google Scholar]
- Zhang, Y.; Sydorenko, I.; Tonkonogyi, V.; Bovnegra, L.; Dašić, P. Structural Analysis of Direct Passive Pressure Reducing Valves Using Modified Kinematic Graphs. Lect. Notes Netw. Syst. 2020, 128, 114–121. [Google Scholar]
- Zhang, Z.; Wu, Y.; Zhang, R.; Jiang, P.; Liu, G.; Ahmed, S.; Dong, Z. Novel Transformer Fault Identification Optimization Method Based on Mathematical Statistics. Mathematics 2019, 7, 288. [Google Scholar]
- Chen, Y.; Ishibashi, A. Investigation of noise and vibration of planetary gear drives. Gear Technol. 2006, 23, 48–55. [Google Scholar]
- Inapolat, M.; Kahraman, A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets. J. Sound Vib. 2009, 323, 667–696. [Google Scholar]
- Salvati, L.; d’Amore, M.; Fiorentino, A.; Pellegrino, A.; Sena, P.; Villecco, F. Development and Testing of a Methodology for the Assessment of Acceptability of LKA Systems. Machines 2020, 8, 47. [Google Scholar]
- Gill-Jeong, C. Numerical study on reducing the vibration of spur gear pairs with phasing. J. Sound Vib. 2010, 329, 3915–3927. [Google Scholar]
- Pappalardo, C.M.; Guida, D. An inverse dynamics approach based on the fundamental equations of constrained motion and on the theory of optimal control. In Proceedings of the 24th Conference of the Italian Association of Theoretical and Applied Mechanics (AIMETA 2019), Rome, Italy, 15–19 September 2019; pp. 336–352. [Google Scholar]
- Sicilia, M.; De Simone, M.C. Development of an Energy Recovery Device Based on the Dynamics of a Semi-trailer. In Proceedings of the 3rd International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, (DSMIE 2020), Kharkiv, Ukraine, 9–12 June 2020; pp. 74–84. [Google Scholar]
- Chen, X.; Hu, Q.; Zhu, C. Numerical Analysis on Load Sharing Characteristics of Multistage Face Gears in Planetary Transmission. Mech. Mach. Sci. 2020, 77, 63–83. [Google Scholar]
- Formato, A.; Ianniello, D.; Romano, R.; Pellegrino, A.; Villecco, F. Design and Development of a New Press for Grape Marc. Machines 2019, 7, 51. [Google Scholar]
- Wang, C.; Li, H.; Ou, J.; Hu, R.; Hu, S.; Liu, A. Identification of planetary gearbox weak compound fault based on parallel dual-parameter optimized resonance sparse decomposition and improved MOMEDA. Meas. J. Int. Meas. Confed. 2020, 165, 108079. [Google Scholar]
- De Simone, M.C.; Guida, D. Experimental investigation on structural vibrations by a new shaking table. In Proceedings of the 24th Conference of the Italian Association of Theoretical and Applied Mechanics, (AIMETA 2019), Rome, Italy, 15–19 September 2019; pp. 819–831. [Google Scholar]
- Cheng, L.I.; Jianzhong, L.I.; Song, M.U.; Youliang, S.U.; Tao, W.; Kai, J. Simulation analysis of the tooth modification about wind power gearbox based on Romax software. Mater. Sci. Eng. 2020, 788, 012005. [Google Scholar]
- Gäbel, G.; Millitzer, J.; Atzrodt, H.; Herold, S.; Mohr, A. Development and Implementation of a Multi-Channel Active Control System for the Reduction of Road Induced Vehicle Interior Noise. Actuators 2018, 7, 52. [Google Scholar]
- Naviglio, D.; Formato, A.; Scaglione, G.; Montesano, D.; Pellegrino, A.; Villecco, F.; Gallo, M. Study of the Grape Cryo-Maceration Process at Different Temperatures. Foods 2018, 7, 107. [Google Scholar]
- Manca, A.G.; Pappalardo, C.M. Topology optimization procedure of aircraft mechanical components based on computer-aided design, multibody dynamics, and finite element analysis. In Proceedings of the 3rd International Conference on Design, Simulation, Manufacturing: The Innovation Exchange (DSMIE 2020), Kharkiv, Ukraine, 9–12 June 2020; pp. 159–168. [Google Scholar]
- Lei, Y.; Hou, L.; Fu, Y.; Hu, J.; Chen, W. Research on vibration and noise reduction of electric bus gearbox based on multi-objective optimization. Appl. Acoust. 2020, 158, 107037. [Google Scholar]
- Tang, Z.P.; Chen, Z.X.; Sun, J.P.; Hu, Y.T.; Zhao, M. Noise prediction of traction gear in high-speed electric multiple unit. Int. J. Simul. Model. 2019, 18, 720–731. [Google Scholar]
- Formato, A.; Ianniello, D.; Pellegrino, A.; Villecco, F. Vibration-Based Experimental Identification of the Elastic Moduli Using Plate Specimens of the Olive Tree. Machines 2019, 7, 46. [Google Scholar]
- Kazaz, L.; Pfister, C.; Ziegler, P.; Eberhard, P. Transient gear contact simulations using a floating frame of reference approach and higher-order ansatz functions. Acta Mech. 2020, 231, 1337–1350. [Google Scholar]












| Parameters | Values |
|---|---|
| Number of teeth N | 55 |
| Module | 2.72 |
| Pitch circle | 150 mm |
| Dedendum circle | 142.50 mm |
| Addendum circle | 156 mm |
| Circular pitch | 6.5° |
| Pressure angle | 20° |
| Condition | Friction | Material Parameters | Lubricated Friction |
|---|---|---|---|
| A | NO | Steel | NO |
| B | μs = 0.74 μk = 0.57 dc = 0.2 | Steel | NO |
| C | NO | Ductile Iron | NO |
| D | μs = 1.1 μk = 0.15 dc = 0.2 | Ductile Iron | NO |
| E | NO | Steel | μs = 1.1 μk = 0.15 dc = 0.2 |
| Condition | Parameters | |||
|---|---|---|---|---|
| Friction | Material | Lubricated Friction | Rotational Speed (RPM) | |
| 1 | NO | Steel | NO | 500 |
| 2 | μs = 0.74 μk = 0.57 dc = 0.2 | Steel | NO | 500 |
| 3 | μs = 0.74 μk = 0.57 dc = 0.2 | Steel | NO | 1500 |
| 4 | μs = 0.74 μk = 0.57 dc = 0.2 | Steel | NO | 3000 |
| 5 | NO | Steel | μs = 0.11 μk = 0.05 dc = 0.2 | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liguori, A.; Armentani, E.; Bertocco, A.; Formato, A.; Pellegrino, A.; Villecco, F. Noise Reduction in Spur Gear Systems. Entropy 2020, 22, 1306. https://doi.org/10.3390/e22111306
Liguori A, Armentani E, Bertocco A, Formato A, Pellegrino A, Villecco F. Noise Reduction in Spur Gear Systems. Entropy. 2020; 22(11):1306. https://doi.org/10.3390/e22111306
Chicago/Turabian StyleLiguori, Aurelio, Enrico Armentani, Alcide Bertocco, Andrea Formato, Arcangelo Pellegrino, and Francesco Villecco. 2020. "Noise Reduction in Spur Gear Systems" Entropy 22, no. 11: 1306. https://doi.org/10.3390/e22111306
APA StyleLiguori, A., Armentani, E., Bertocco, A., Formato, A., Pellegrino, A., & Villecco, F. (2020). Noise Reduction in Spur Gear Systems. Entropy, 22(11), 1306. https://doi.org/10.3390/e22111306







