Complexity of Fracturing in Terms of Non-Extensive Statistical Physics: From Earthquake Faults to Arctic Sea Ice Fracturing
Abstract
1. Introduction
2. Fracturing Processes in Terms of Non-Extensive Statistical Physics
3. Applications to Fracturing: From Earthquake Faults to Sea Ice
3.1. Applications to Earthquake Fracturing
3.2. Application to Arctic Sea Ice Time Series
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cowie, P.A.; Sornette, D.; Vanneste, C. Multifractal scaling properties of growing fault population. Geophys. J. Int. 1995, 122, 457–469. [Google Scholar] [CrossRef]
- Scholz, C. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Keilis-Borok, V.I. The lithosphere of the earth as a nonlinear system with implications for earthquake prediction. Rev. Geophys. 1990, 28, 19–34. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41, 1019. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Michas, G.; Sammonds, P.; Vallianatos, F. Dynamic multifractality in earthquake time series: Insights from the Corinth rift, Greece. Pure Appl. Geophys. 2015, 172, 1909–1921. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Stochastic modeling of nonstationary earthquake time series with long-term clustering effects. Phys. Rev. E 2018, 98, 042107. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Scaling properties, multifractality and range of correlations in earthquake timeseries: Are earthquakes random? In Statistical Methods and Modeling of Seismogenesis; Limnios, N., Papadimitriou, E., Tsaklidis, G., Eds.; ISTE John Wiley: London, UK, 2020; in press. [Google Scholar]
- Utsu, T.; Ogata, Y.; Matsu’ura, R.S. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Sornette, D.; Werner, M.J. Statistical physics approaches to seismicity. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 7872–7891. [Google Scholar]
- Kawamura, H.; Hatano, T.; Kato, N.; Biswas, S.; Chakrabarti, B.K. Statistical physics of fracture, friction and earthquakes. Rev. Mod. Phys. 2012, 84, 839–884. [Google Scholar] [CrossRef]
- Sethna, J. Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Chelidze, T.; Vallianatos, F.; Telesca, L. Complexity of Seismic Time Series: Measurement and Application; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized statistical mechanics approaches to earthquakes and tectonics. Proc. R. Soc. A 2016, 472, 20160497. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Michas, G.; Papadakis, G. A description of seismicity based on non-extensive statistical physics: A review. In Earthquakes and Their Impact on Society; D’Amico, S., Ed.; Springer Natural Hazards: Heidelberg, Germany, 2016; pp. 1–42. [Google Scholar]
- Vallianatos, F.; Michas, G.; Papadakis, G. Nonextensive statistical seismology: An overview. In Complexity of Seismic Time Series; Chelidze, T., Vallianatos, F., Telesca, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 25–60. [Google Scholar]
- Weiss, J. Scaling of fracture and faulting of ice on earth. Surv. Geophys. 2003, 24, 185–227. [Google Scholar] [CrossRef]
- Weiss, J.; Marsan, D. Scale properties of sea ice deformation and fracturing. C. R. Phys. 2004, 5, 735–751. [Google Scholar] [CrossRef]
- Gell-Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; St. Martin’s Griffin: New York, NY, USA, 1994. [Google Scholar]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann-Gibbs statistics to Tsallis statistics. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Law for the distance between successive earthquakes. J. Geophys. Res. 2003, 108, 2113. [Google Scholar] [CrossRef]
- Vallianatos, F.; Kokinou, E.; Sammonds, P. Non-extensive statistical physics approach to fault population distribution. A case study from the Southern Hellenic Arc (Central Crete). Acta Geophys. 2011, 59, 770–784. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Statistical mechanics and scaling of fault populations with increasing strain in the Corinth Rift. Earth Planet. Sci. Lett. 2015, 431, 150–163. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. A non-extensive statistics of the fault-population at the Valles Marineris extensional province, Mars. Tectonophysics 2011, 509, 50–54. [Google Scholar] [CrossRef]
- Vallianatos, F. On the non-extensivity in Mars geological faults. EPL 2013, 102, 28006. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Posadas, A. Fragment-asperity interaction model for earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef]
- Silva, R.; França, G.S.; Vilar, C.S.; Alcaniz, J.S. Nonextensive models for earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L. Maximum likelihood estimation of the nonextensive parameters of the earthquake cumulative magnitude distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Telesca, L. Nonextensive analysis of seismic sequences. Physica A 2010, 389, 1911–1914. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-extensivity and long-range correlations in the earthquake activity at the West Corinth rift (Greece). Nonlinear Process. Geophys. 2013, 20, 713–724. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Evidence of nonextensive statistical physics behavior of the Hellenic subduction zone seismicity. Tectonophysics 2013, 608, 1037–1048. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Tzanis, A. Evidence of non-extensivity in the seismicity observed during the 2011–2012 unrest at the Santorini volcanic complex, Greece. Nat. Hazards Earth Syst. Sci. 2013, 13, 177–185. [Google Scholar] [CrossRef]
- Antonopoulos, C.G.; Michas, G.; Vallianatos, F.; Bountis, T. Evidence of q-exponential statistics in Greek seismicity. Physica A 2014, 409, 71–79. [Google Scholar] [CrossRef]
- Chochlaki, K.; Michas, G.; Vallianatos, F. Complexity of the Yellowstone Park volcanic field seismicity in terms of Tsallis entropy. Entropy 2018, 20, 721. [Google Scholar] [CrossRef]
- Telesca, L. A non-extensive approach in investigating the seismicity of L’ Aquila area (central Italy), struck by the 6 April 2009 earthquake (ML = 5.8). Terra Nova 2010, 22, 87–93. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-extensive and natural time analysis of seismicity before the Mw6.4, October 12, 2013 earthquake in the south west segment of the Hellenic arc. Physica A 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. A nonextensive statistical physics analysis of the 1995 Kobe, Japan earthquake. Pure Appl. Geophys. 2015, 172, 1923–1931. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Non-extensive statistical physics applied to heat flow and the earthquake frequency-magnitude distribution in Greece. Physica A 2016, 456, 135–144. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F. Non-extensive statistical physics analysis of earthquake magnitude sequences in North Aegean Trough, Greece. Acta Geophys. 2017, 65, 555–563. [Google Scholar] [CrossRef]
- Skordas, E.S.; Sarlis, N.V.; Varotsos, P.A. Precursory variations of Tsallis non-extensive statistical mechanics entropic index associated with the M9 Tohoku earthquake in 2011. Eur. Phys. J. Spec. Top. 2020, 229, 851–859. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Tsallis entropy index q and the complexity measure of seismicity in natural time under time reversal before the M9 Tohoku Earthquake in 2011. Entropy 2018, 20, 757. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time: Precursory Seismic Electric Signals, Earthquakes and Other Complex Time Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Caruso, F.; Pluchino, A.; Latora, V.; Vinciguerra, S.; Rapisarda, A. Analysis of self-organized criticality in the Olami-Feder-Christensen model and in real earthquakes. Phys. Rev. E 2007, 75, 055101. [Google Scholar] [CrossRef]
- Olami, Z.; Feder, H.J.S.; Christensen, K. Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes. Phys. Rev. Lett. 1992, 68, 1244. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Physica A 2005, 350, 588–596. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non- extensive statistical physics behaviour of fracture in triaxially deformed Etna basalt using acoustic emissions. EPL 2012, 97, 58002. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Sammonds, P. A non-extensive statistical physics view to the spatiotemporal properties of the June 1995, Aigion earthquake (M6.2) aftershock sequence (West Corinth rift, Greece). Acta Geophys. 2012, 60, 758–768. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Modelling earthquake diffusion as a continuous-time random walk with fractional kinetics: The case of the 2001 Agios Ioannis earthquake swarm (Corinth Rift). Geophys. J. Int. 2018, 215, 333–345. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Scaling properties and anomalous diffusion of the Florina micro-seismic activity: Fluid driven? Geomech. Energy Env. 2020, 24, 100155. [Google Scholar] [CrossRef]
- Darooneh, A.H.; Dadashinia, C. Analysis of the spatial and temporal distributions between successive earthquakes: Nonextensive statistical mechanics viewpoint. Physica A 2008, 387, 3647–3654. [Google Scholar] [CrossRef]
- Efstathiou, A.; Tzanis, A.; Vallianatos, F. Evidence of non extensivity in the evolution of seismicity along the San Andreas Fault, California, USA: An approach based on Tsallis statistical physics. Phys. Chem. Earth 2015, 85–86, 56–68. [Google Scholar] [CrossRef]
- Efstathiou, A.; Tzanis, A.; Vallianatos, F. On the nature and dynamics of the seismogenetic systems of North California, USA: An analysis based on Non-Extensive Statistical Physics. Phys. Earth Planet. Inter. 2017, 270, 46–72. [Google Scholar] [CrossRef]
- Chochlaki, K.; Vallianatos, F.; Michas, G. Global regionalized seismicity in view of Non-Extensive Statistical Physics. Physica A 2018, 493, 276–285. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Order parameter fluctuations of seismicity in natural time before and after mainshocks. EPL 2010, 91, 59001. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Livina, V.N.; Havlin, S.; Bunde, A. Memory in the occurrence of earthquakes. Phys. Rev. Lett. 2005, 95, 208501. [Google Scholar] [CrossRef]
- Queiroós, S.M.D. On the emergence of a generalised gamma distribution. Application to traded volume in financial markets. EPL 2005, 71, 339–345. [Google Scholar] [CrossRef][Green Version]
- McNutt, S.L.; Overland, J.E. Spatial hierarchy in Arctic sea ice dynamics. Tellus 2003, 554, 181–191. [Google Scholar] [CrossRef]
- Chmel, A.; Smirnov, V.; Shcherbakov, I. Hierarchy of non-extensive mechanical processes in fracturing sea ice. Acta Geophys. 2012, 60, 719–739. [Google Scholar] [CrossRef]
- Chmel, A.; Smirnov, V.N.; Astakhov, M.P. The Arctic sea-ice cover: Fractal space–time domain. Physica A 2005, 357, 556–564. [Google Scholar] [CrossRef]
- Zhang, J.; Rothrock, D.; Steele, M. Recent changes in arctic sea ice: The interplay between ice dynamics and thermodynamics. J. Clim. 2000, 13, 3099–3114. [Google Scholar] [CrossRef]
- Girard, L.; Weiss, J.; Molines, J.M.; Barnier, B.; Bouillon, S. Evaluation of high-resolution sea ice models on the basis of statistical and scaling properties of Arctic sea ice drift and deformation. J. Geophys. Res. 2009, 114, C08015. [Google Scholar] [CrossRef]
- Maykut, G.A. Large scale heat exchange and ice production in the central Arctic. J. Geophys. Res. 1982, 87, 7971–7984. [Google Scholar] [CrossRef]
- Marsan, D.; Stern, H.; Lindsay, R.; Weiss, J. Scale dependence and localization of the deformation of Arctic sea ice. Phys. Rev. Lett. 2004, 93, 178501. [Google Scholar] [CrossRef]
- Weiss, J. Intermittency of principal stress directions within Arctic sea ice. Phys. Rev. E 2008, 77, 056106. [Google Scholar] [CrossRef]
- Lewis, J.K.; Richter-Menge, J.A. Motion-induced stresses in pack ice. J. Geophys. Res. 1998, 103, 21831–21843. [Google Scholar] [CrossRef]
- Rampal, P.; Weiss, J.; Marsan, D. Positive trend in the mean speed and deformation rate of Arctic sea ice, 1979–2007. J. Geophys. Res. 2009, 114, C05013. [Google Scholar] [CrossRef]
- CEAREX Drift Group. CEAREX drift experiment. Eos Trans. AGU 1990, 71, 1115–1118. [Google Scholar] [CrossRef]
- Michas, G. Generalized Statistical Mechanics Description of Fault and Earthquake Populations in Corinth Rift (Greece). Ph.D. Thesis, University College London, London, UK, 2016. [Google Scholar]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics—An overview after 20 years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Tsallis, C. An introduction to nonadditive entropies and a thermostatistical approach to inanimate and living matter. Contemp. Phys. 2014, 55, 179–197. [Google Scholar] [CrossRef]
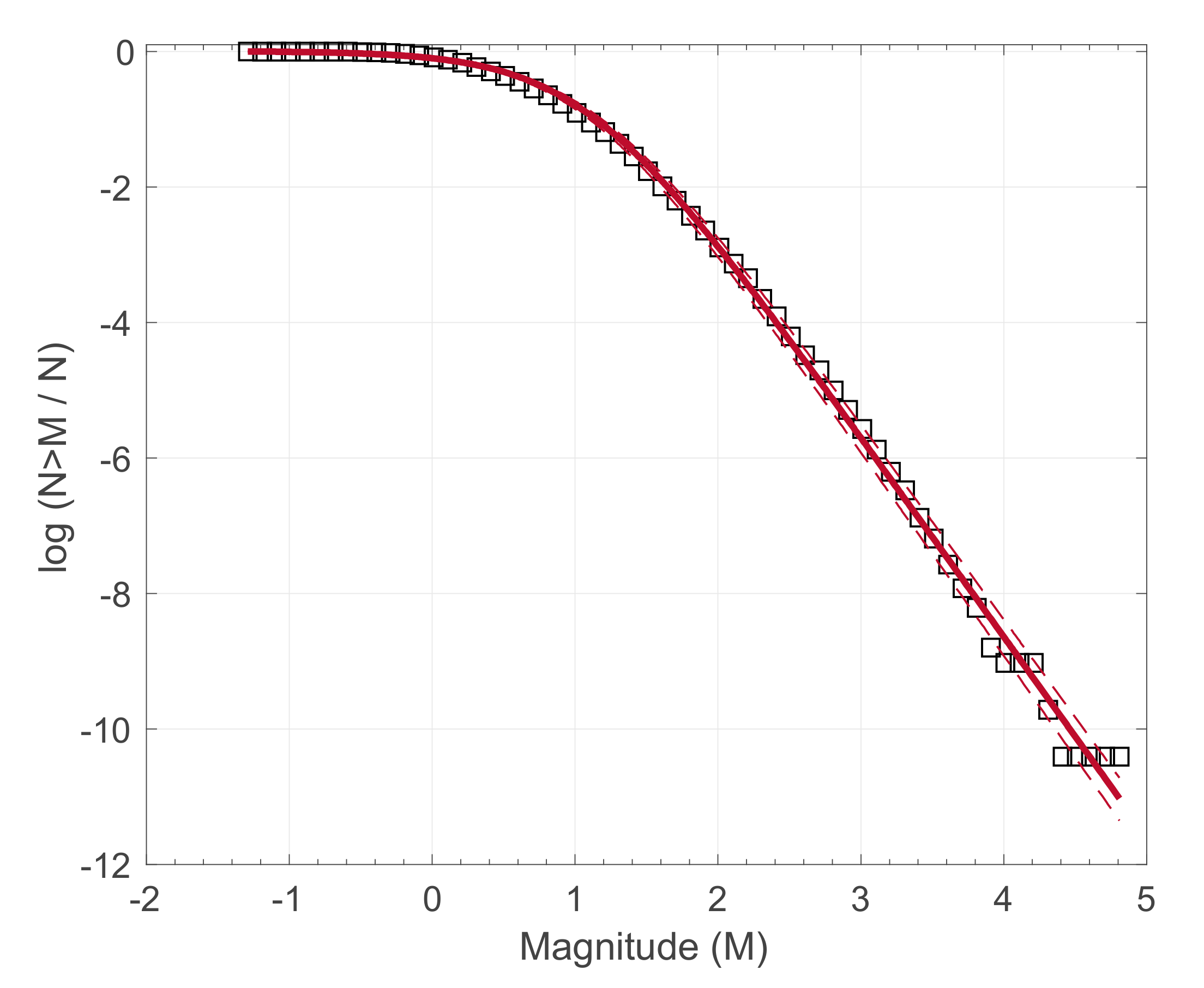
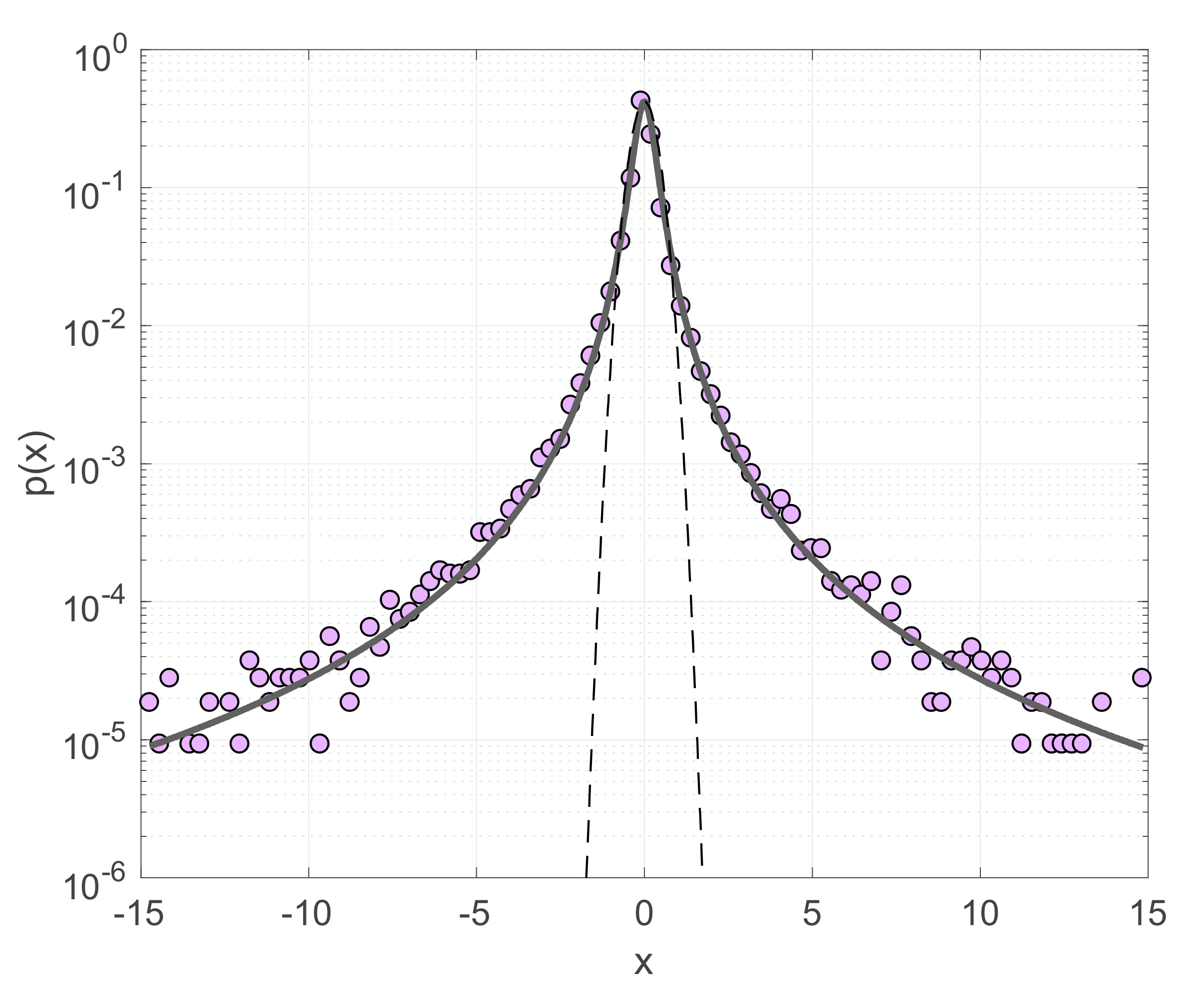
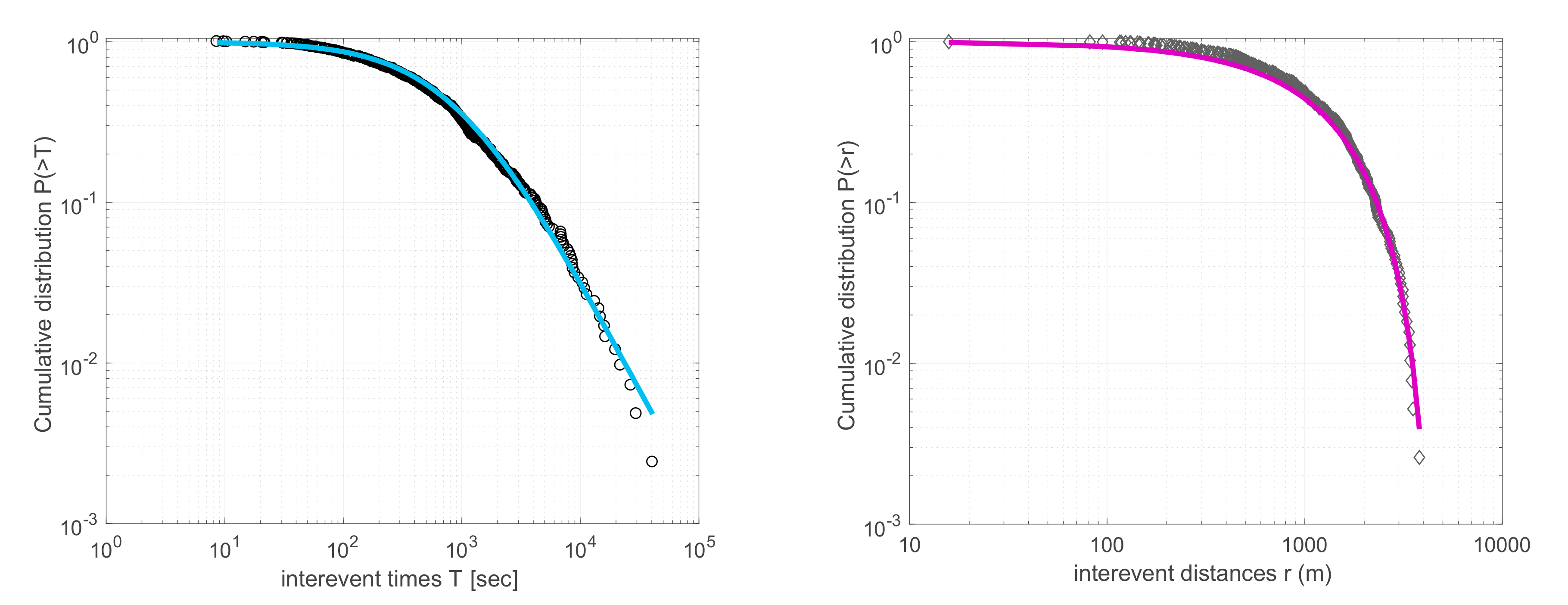
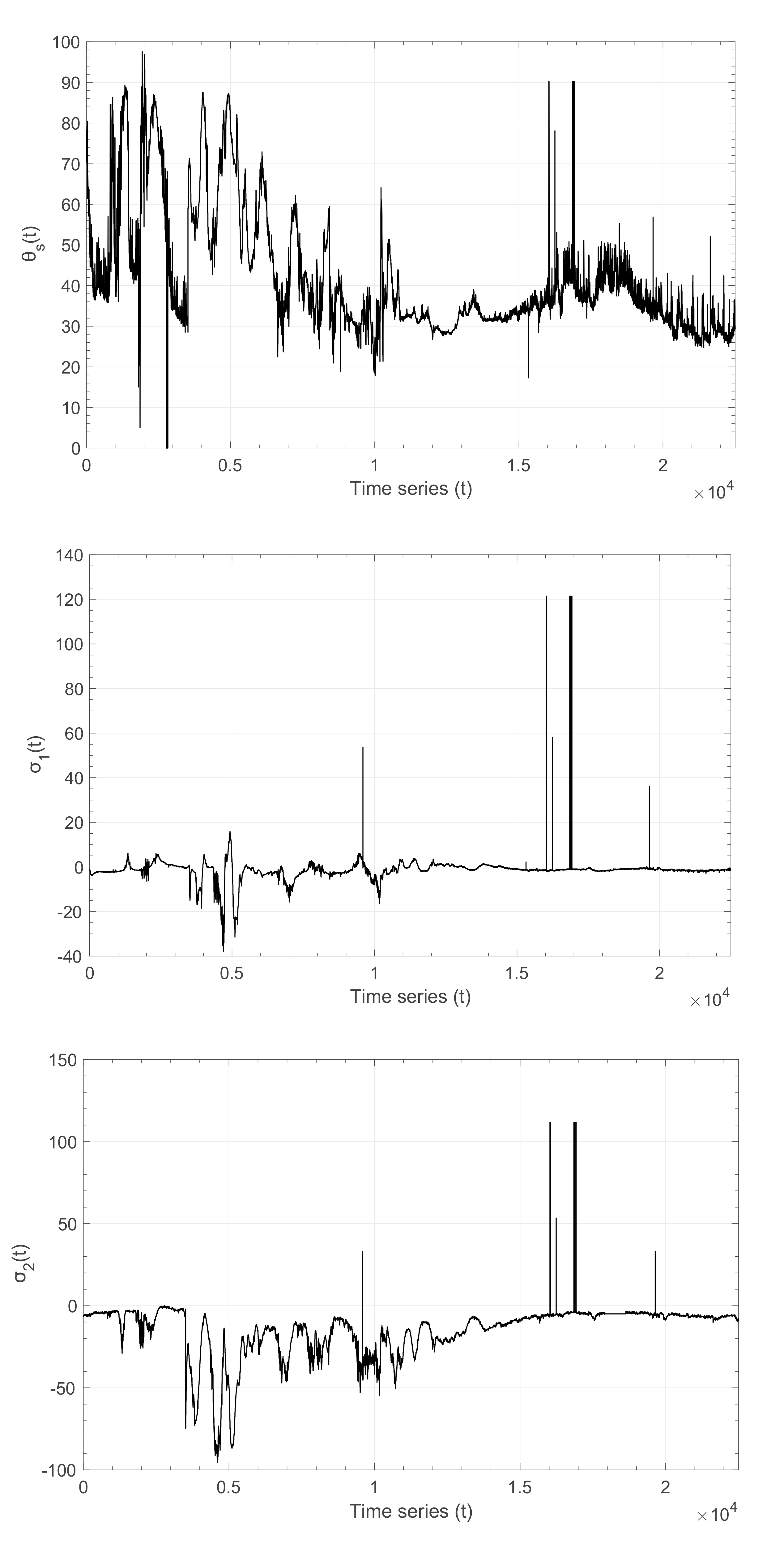

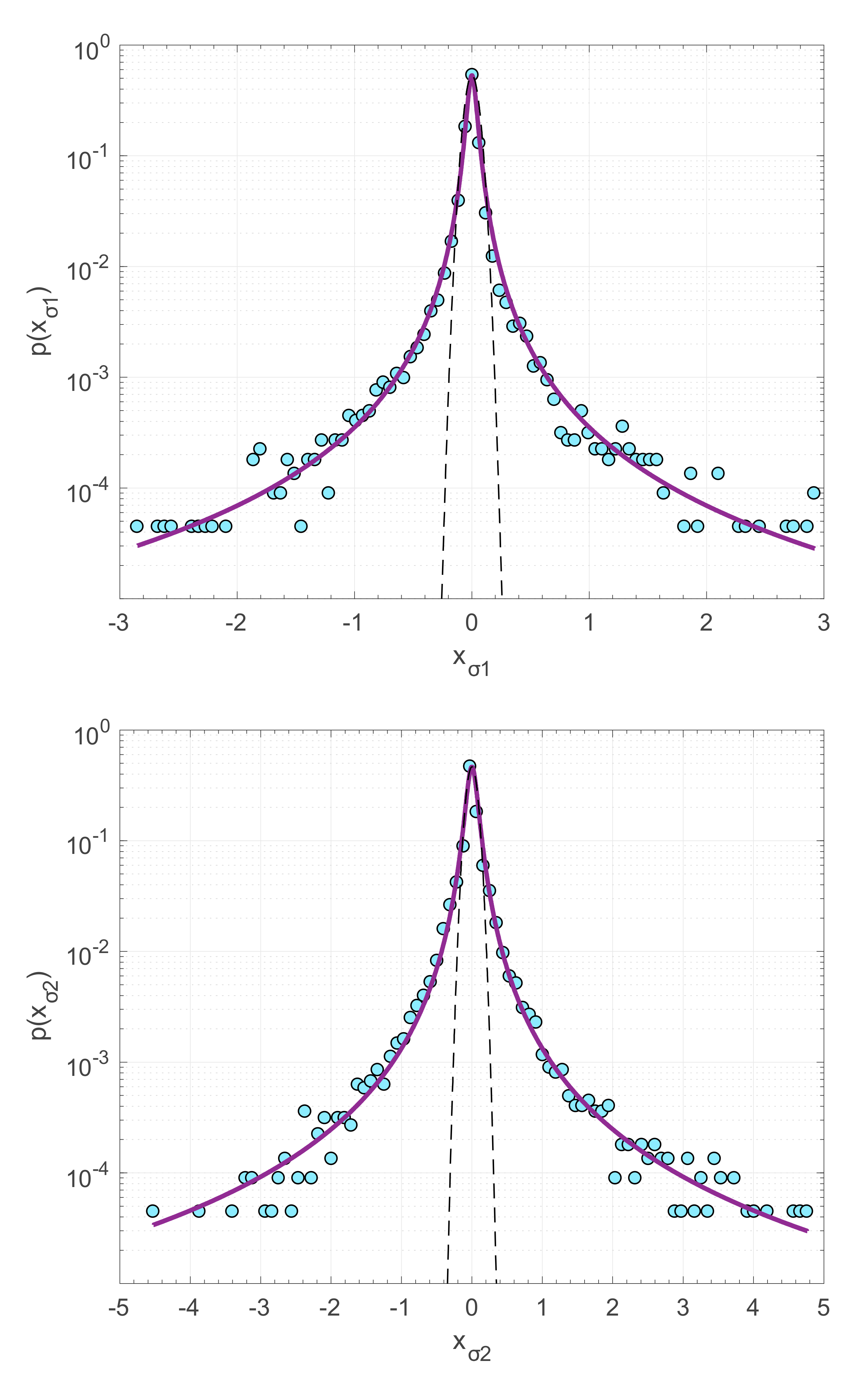
| Stress | q | δq | B | δB |
|---|---|---|---|---|
| σ1 | 1.85 | 0.04 | 0.0017 | 0.0002 |
| σ2 | 1.82 | 0.12 | 0.0068 | 0.0006 |
| θs | 1.74 | 0.03 | 0.078 | 0.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallianatos, F.; Michas, G. Complexity of Fracturing in Terms of Non-Extensive Statistical Physics: From Earthquake Faults to Arctic Sea Ice Fracturing. Entropy 2020, 22, 1194. https://doi.org/10.3390/e22111194
Vallianatos F, Michas G. Complexity of Fracturing in Terms of Non-Extensive Statistical Physics: From Earthquake Faults to Arctic Sea Ice Fracturing. Entropy. 2020; 22(11):1194. https://doi.org/10.3390/e22111194
Chicago/Turabian StyleVallianatos, Filippos, and Georgios Michas. 2020. "Complexity of Fracturing in Terms of Non-Extensive Statistical Physics: From Earthquake Faults to Arctic Sea Ice Fracturing" Entropy 22, no. 11: 1194. https://doi.org/10.3390/e22111194
APA StyleVallianatos, F., & Michas, G. (2020). Complexity of Fracturing in Terms of Non-Extensive Statistical Physics: From Earthquake Faults to Arctic Sea Ice Fracturing. Entropy, 22(11), 1194. https://doi.org/10.3390/e22111194






