Partial Classifier Chains with Feature Selection by Exploiting Label Correlation in Multi-Label Classification
Abstract
1. Introduction
- (1)
- First-order strategy: This divides the MLC problem into a number of independent binary classification problems. The prominent advantage is their conceptual simplicity and high efficiency even though the related classifiers might not acquire the optimal results because of ignoring the label couplings.
- (2)
- Second-order strategy: This considers pairwise relationships between labels. The resulting classifiers can achieve good levels of generalization performance since label couplings are exploited to some extent. However, they are only able to exploit label-coupling relationships to a limited extent. Many real-world applications go beyond these second-order assumptions.
- (3)
- High-order strategy: This tackles the MLC problem by considering high-order relationships between labels. This strategy is said to have stronger correlation-modeling capabilities than the other two strategies, and its corresponding classifiers to have a higher degree of time and space complexity.
- (1)
- A new construction method of chain mechanism that only considers the coupled labels (partial labels) and inserts them into the chain simultaneously, and thus improves the prediction performance;
- (2)
- A novel feature selection function that is integrated into the PCC-FS method by exploiting the coupling relationships between features and labels, thus reducing the number of redundant features and enhancing the classification performance;
- (3)
- Label couplings extracted from the MLC problem based on the theory of coupling learning, including intra-couplings within labels and inter-couplings between features and labels, which makes the exploration of label correlation more comprehensive.
2. Preliminaries
2.1. MLC Problem and CC Approach
| Algorithm 1. The training phase of the classifier chain (CC) algorithm |
| Input: Output: Steps
|
| Algorithm 2. The prediction phase of the CC algorithm |
| Input: , Output: predicted label sets of each instance in Steps
|
2.2. Feature Selection in the MLC Problem
2.3. Related Work of CC-Based Approaches
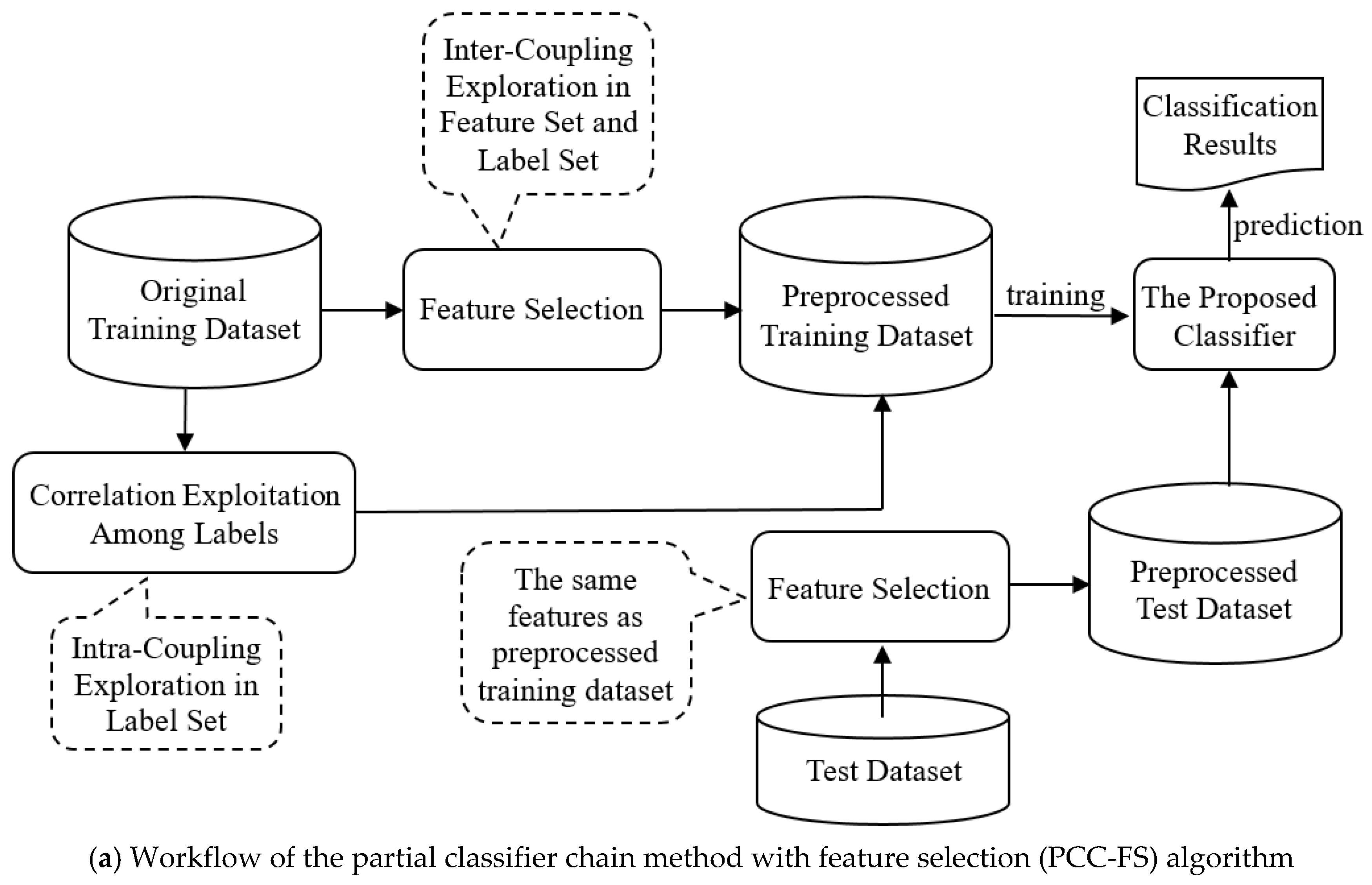
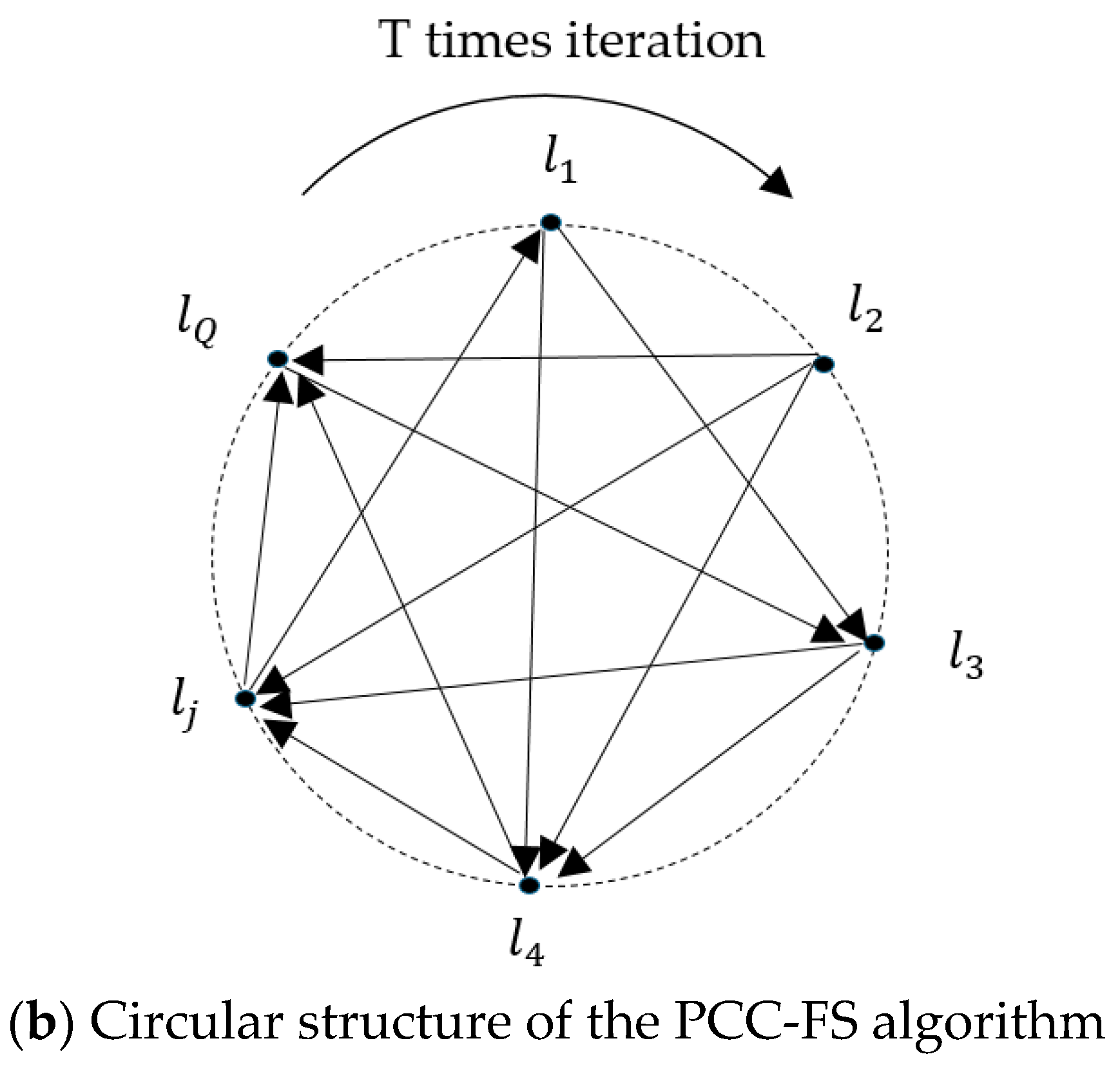
3. The Principle of the PCC-FS Algorithm
3.1. Overall Description of the PCC-FS Algorithm
- (1)
- In the feature selection stage, we explore the inter-couplings between each feature and label set. The features with low levels of inter-couplings would be cut off on the assumption that all the inter-couplings follow Gaussian-like distribution;
- (2)
- Intra-couplings among labels are extracted to provide the measurement used to select the relevant labels (partial labels) of each label. Irrelevant labels are not then able to hinder the classification performance;
- (3)
- After feature selection, as described in Figure 1b, the coupled labels of each label are inserted simultaneously into the chain, and label prediction is executed in an iterative process, thus avoiding the label ordering problem.
3.2. Feature Selection with Inter-Coupling Exploration
3.3. Intra-Coupling Exploration in Label Set
3.4. Label Prediction of the PCC-FS Algorithm
| Algorithm 3. The training phase of the PCC-FS algorithm |
| Input: original training data, iterative times T Output: binary classifiers Steps
|
| Algorithm 4. The prediction phase of the PCC-FS algorithm |
| Input: original test data, binary classifiers ; Output: predicted label sets for ; Steps
|
4. Experimental Results and Analysis
4.1. Experiment Environment and Datasets
4.2. Evaluation Criteria
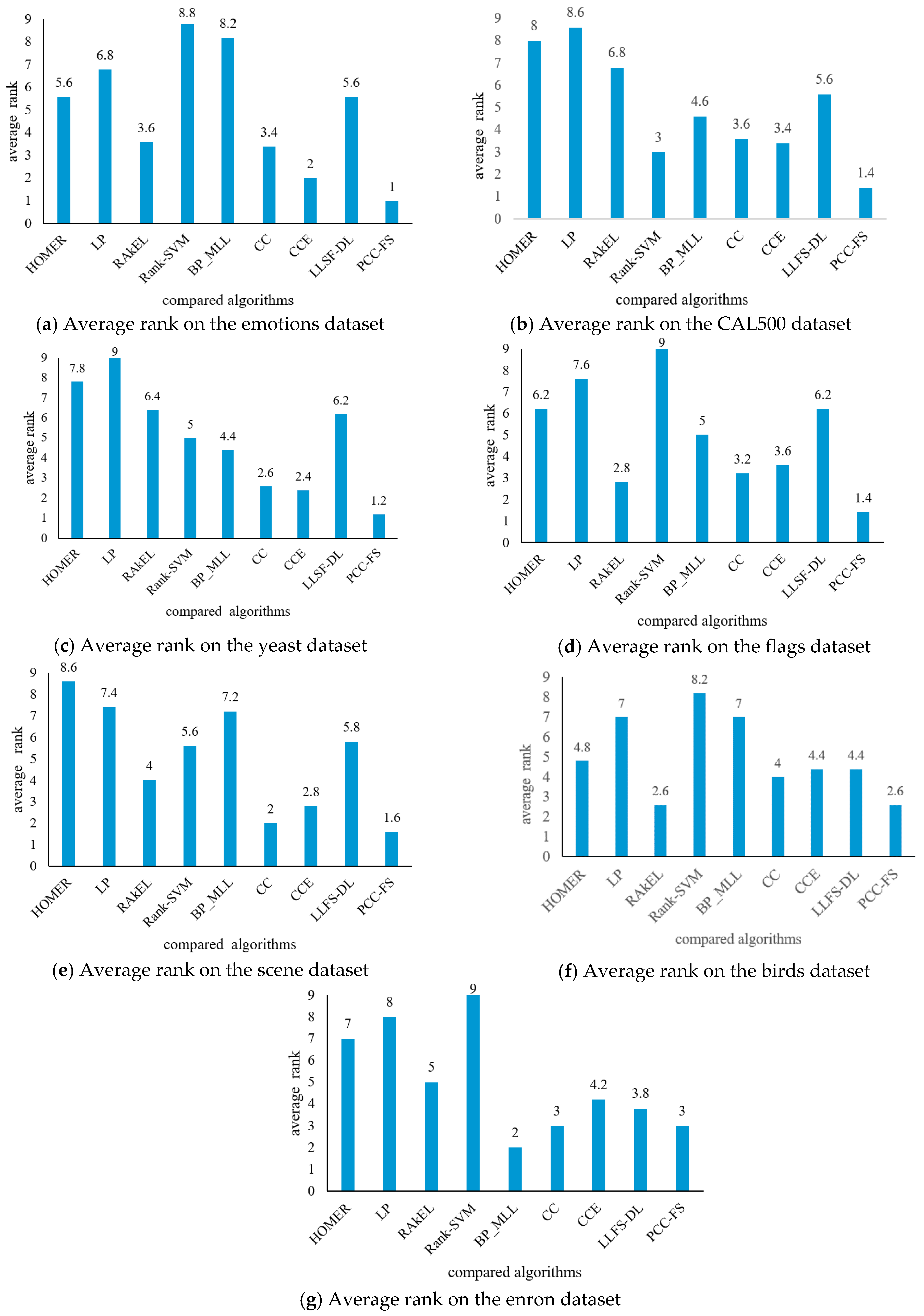
4.3. Experimental Results Analysis and Comparison
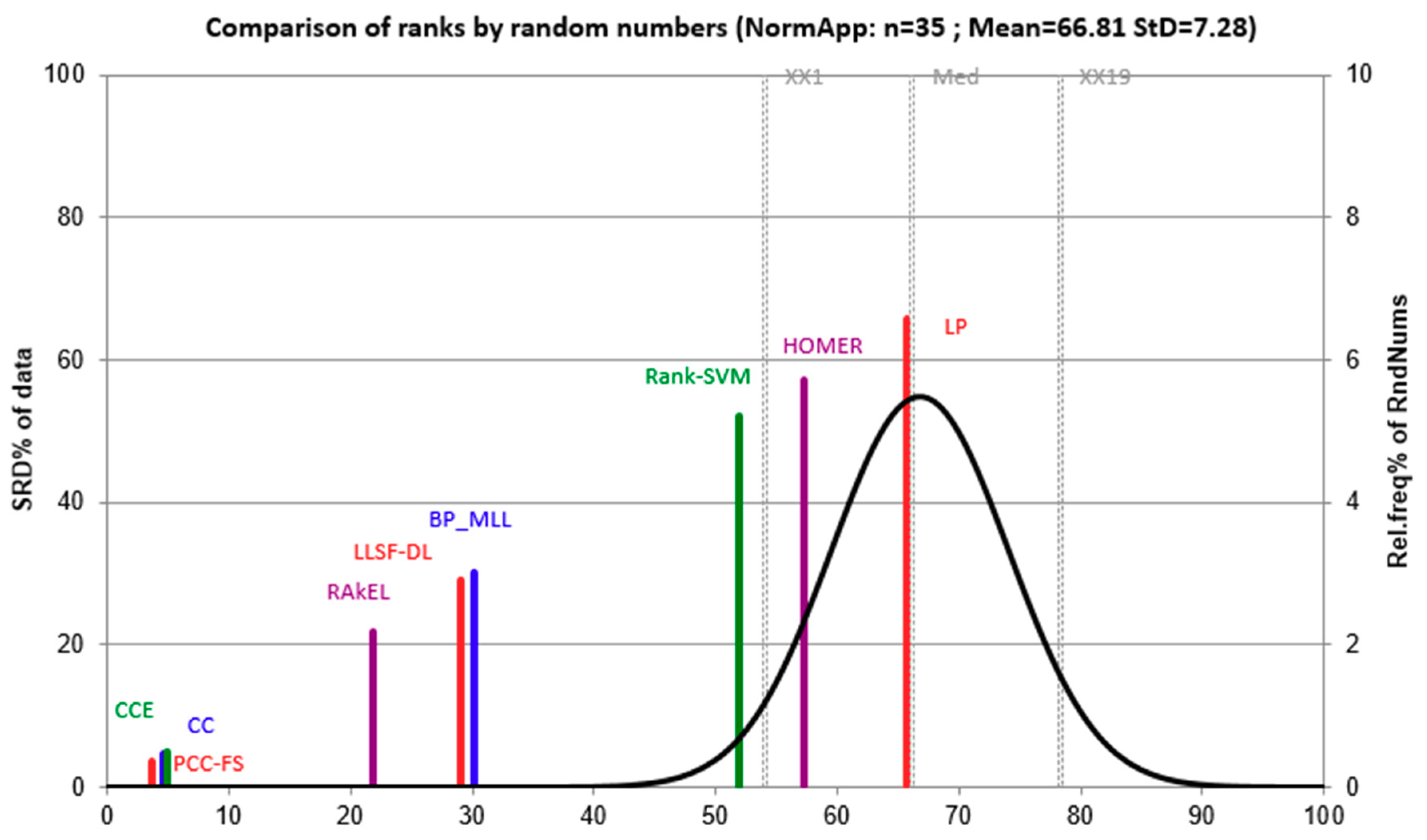
5. Conflicting Criteria for Algorithm Comparison and Statistical Test
5.1. Conflicting Criteria
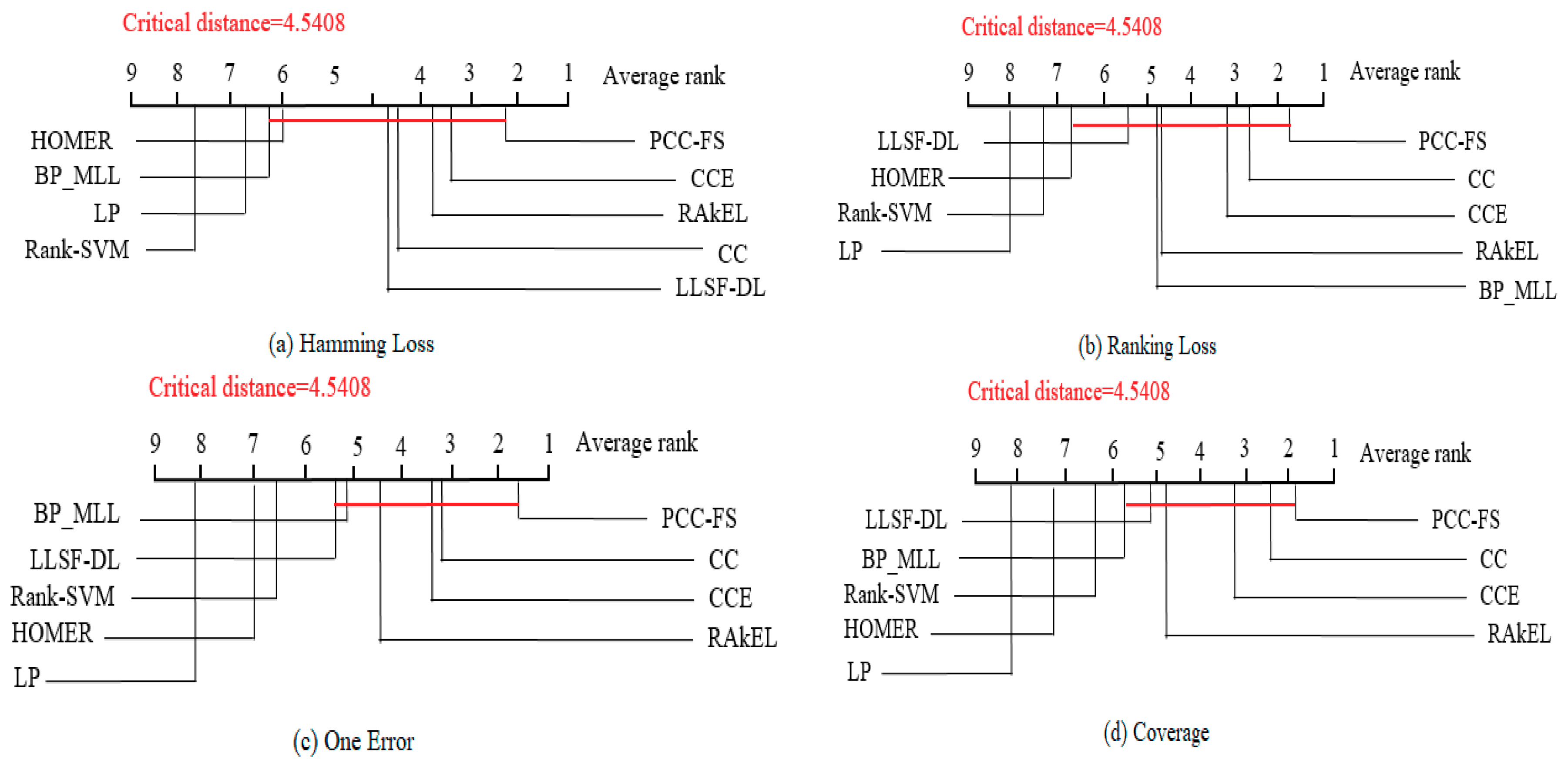
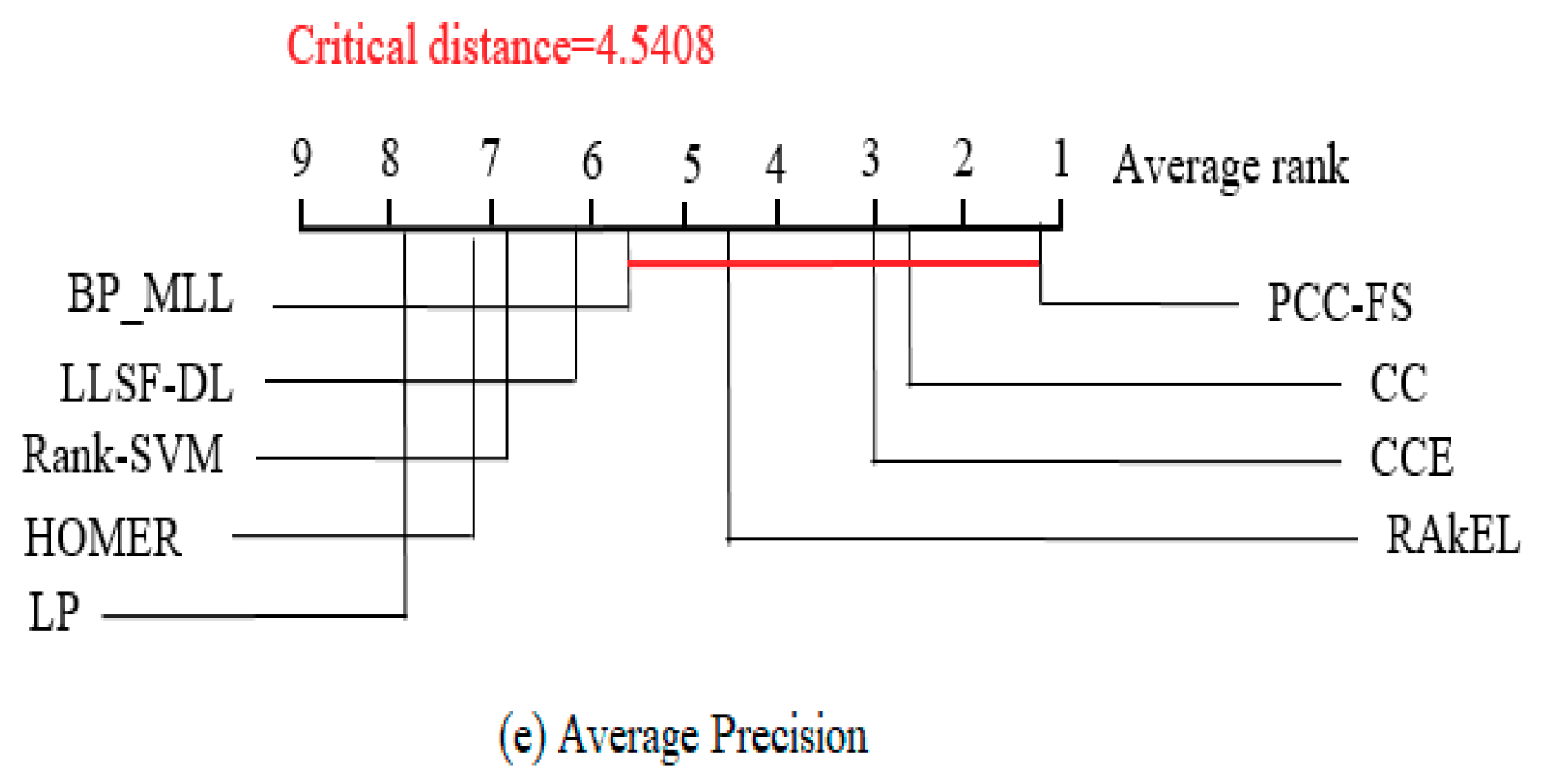
5.2. F-Test for All Algorithms
5.3. PCC-FS as Control Algorithm
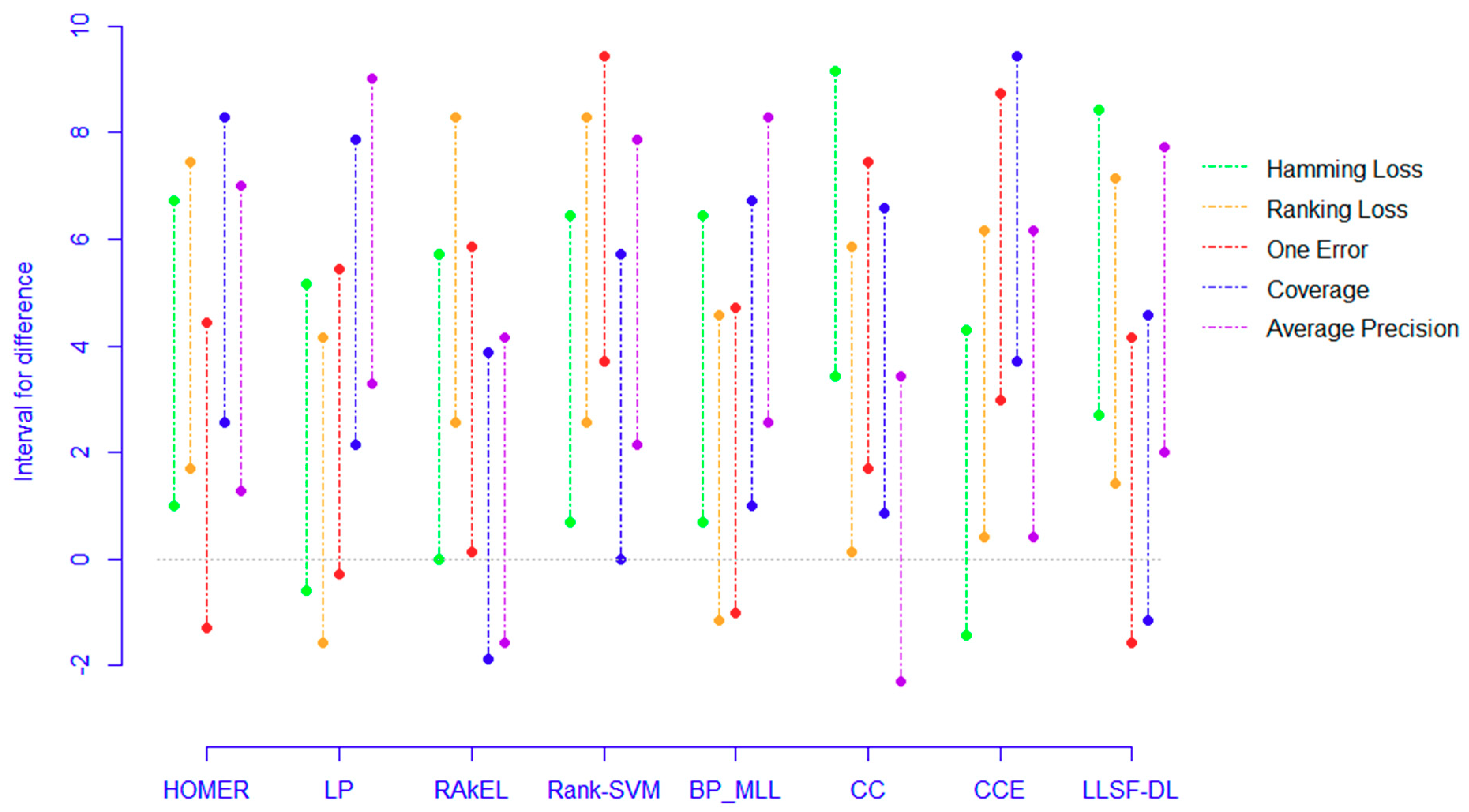
5.4. Confidence Intervals
5.5. Summaries
- (1)
- The proposed PCC-FS algorithm achieves the top average rank among nine algorithms across all five criteria, and the CC-based high-order algorithms (CC, CCE, PCC-FS) in general achieve better performance than the other algorithms. This is because these types of algorithms exploit the label couplings thoroughly.
- (2)
- Four out of five ranking differences for CC and CCE have shown positive intervals meaning that the probability of obtaining a higher rank for PCC-FS compared with CC or CCE is 80% for a given dataset even though they are comparable.
- (3)
- PCC-FS outperforms LP, HOMER, Rank-SVM, BP_MLL, and LLSF-DL because the ranking differences for them are significantly larger than the critical value across the five tested criteria. Corresponding confidence interval gives an overview of the quantified amount in ranking difference.
- (4)
- LP, HOMER, and Rank-SVM perform the worst on all of the five criteria because LP and HOMER transform MLC into one or more single label subproblems. Rank-SVM divides MLC into a series of pairwise classification problems and cannot be seen to describe label couplings very well.
- (5)
- RAkEL performs neutrally among the test algorithms.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schapire, R.E.; Singer, Y. BoosTexter: A Boosting-based System for Text Categorization. Mach. Learn. 2000, 39, 135–168. [Google Scholar] [CrossRef]
- Ñanculef, R.; Flaounas, I.; Cristianini, N. Efficient classification of multi-labeled text streams by clashing. Expert Syst. Appl. 2014, 41, 5431–5450. [Google Scholar] [CrossRef]
- Keikha, M.M.; Rahgozar, M.; Asadpour, M. Community aware random walk for network embedding. Knowl. Based Syst. 2018, 148, 47–54. [Google Scholar] [CrossRef]
- Vateekul, P.; Kubat, M.; Sarinnapakorn, K. Hierarchical multi-label classification with SVMs: A case study in gene function prediction. Intell. Data Anal. 2014, 18, 717–738. [Google Scholar] [CrossRef]
- Markatopoulou, F.; Mezaris, V.; Patras, I. Implicit and Explicit Concept Relations in Deep Neural Networks for Multi-Label Video/Image Annotation. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1631–1644. [Google Scholar] [CrossRef]
- Cetiner, M.; Akgul, Y.S. A Graphical Model Approach for Multi-Label Classification. In Information Sciences and Systems 2014, Proceedings of the 29th International Symposium on Computer and Information Sciences, Krakow, Poland, 27–28 October 2014; Czachórski, T., Gelenbe, E., Lent, R., Eds.; Springer: Cham, Switzerland, 2014; pp. 61–67. [Google Scholar]
- Zhang, M.-L.; Zhou, Z.-H. A Review on Multi-Label Learning Algorithms. IEEE Trans. Knowl. Data Eng. 2013, 26, 1819–1837. [Google Scholar] [CrossRef]
- Wang, C.; Dong, X.; Zhou, F.; Cao, L.; Chi, C.-H. Coupled Attribute Similarity Learning on Categorical Data. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 781–797. [Google Scholar] [CrossRef]
- Wang, C.; Cao, L.; Wang, M.; Li, J.; Wei, W.; Ou, Y. Coupled nominal similarity in unsupervised learning. In Proceedings of the 20th ACM international conference on Multimedia—MM’12, Glasgow, Scotland, 24 October 2011; Association for Computing Machinery; pp. 973–978. [Google Scholar]
- Wang, C.; Chi, C.-H.; She, Z.; Cao, L.; Stantic, B. Coupled Clustering Ensemble by Exploring Data Interdependence. ACM Trans. Knowl. Discov. Data 2018, 12, 1–38. [Google Scholar] [CrossRef]
- Pang, G.; Cao, L.; Chen, L.; Liu, H. Unsupervised Feature Selection for Outlier Detection by Modelling Hierarchical Value-Feature Couplings. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM); Institute of Electrical and Electronics Engineers, Barcelona, Spain, 12–15 December 2016; pp. 410–419. [Google Scholar]
- Cao, L.; Joachims, T.; Wang, C.; Gaussier, E.; Li, J.; Ou, Y.; Luo, D.; Zafarani, R.; Liu, H.; Xu, G.; et al. Behavior Informatics: A New Perspective. IEEE Intell. Syst. 2014, 29, 62–80. [Google Scholar] [CrossRef]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier Chains for Multi-label Classification. In Machine Learning and Knowledge Discovery in Databases; Buntine, W., Grobelnik, M., Mladenić, D., Shawe-Taylor, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 85, pp. 254–269. [Google Scholar]
- Senge, R.; Del Coz, J.J.; Hüllermeier, E. On the Problem of Error Propagation in Classifier Chains for Multi-label Classification. In Data Analysis, Machine Learning and Knowledge Discovery, Proceedings of the 36th Annual Conference of the German Classification Society, Hildesheim, Germany, 1–3 August 2012; Springer: Cham, Switzerland, 2013; pp. 163–170. [Google Scholar]
- Pereira, R.B.; Plastino, A.; Zadrozny, B.; Merschmann, L.H.C. Categorizing feature selection methods for multi-label classification. Artif. Intell. Rev. 2016, 49, 57–78. [Google Scholar] [CrossRef]
- Kashef, S.; Nezamabadi-Pour, H.; Nikpour, B. Multilabel feature selection: A comprehensive review and guiding experiments. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, 1–29. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Y. Streaming Feature Selection for Multi-Label Data with Dynamic Sliding Windows and Feature Repulsion Loss. Entropy 2019, 21, 1151. [Google Scholar] [CrossRef]
- Gustafsson, R. Ordering Classifier Chains Using Filter Model Feature Selection Techniques. Master’s Thesis, Blekinge Institute of Technology, Karlskrona, Sweden, 2017. [Google Scholar]
- Read, J.; Pfahringer, B.; Holmes, G.; Frank, E. Classifier chains for multi-label classification. Mach. Learn. 2011, 85, 333–359. [Google Scholar] [CrossRef]
- Chen, L.; Chen, D. A classifier chain method for multi-label learning based on kernel alignment. J. Nanjing Univ. Nat. Sci. 2018, 54, 725–732. [Google Scholar]
- Read, J.; Martino, L.; Luengo, D. Efficient Monte Carlo optimization for multi-label classifier chains. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3457–3461. [Google Scholar]
- Goncalves, E.C.; Plastino, A.; Freitas, A.A. A Genetic Algorithm for Optimizing the Label Ordering in Multi-label Classifier Chains. In Proceedings of the 2013 IEEE 25th International Conference on Tools with Artificial Intelligence, Herndon, VA, USA, 4–6 November 2013; pp. 469–476. [Google Scholar]
- Gonçalves, E.C.; Plastion, A.; Freitas, A.A. Simpler is Better: A Novel Genetic Algorithm to Induce Compact Multi-Label Chain Classifiers. In Proceedings of the 17th Genetic and Evolutionary Computation Conference (GECCO), Madrid, Spain, 11–15 July 2015; pp. 559–566. [Google Scholar]
- Li, N.; Pan, Z.; Zhou, X. Classifier Chain Algorithm Based on Multi-label Importance Rank. PR AI 2016, 29, 567–575. [Google Scholar]
- Sucar, E.; Bielza, C.; Morales, E.F.; Hernandez-Leal, P.; Zaragoza, J.H.; Larrañaga, P. Multi-label classification with Bayesian network-based chain classifiers. Pattern Recognit. Lett. 2014, 41, 14–22. [Google Scholar] [CrossRef]
- Zhang, Z.-D.; Wang, Z.-H.; Liu, H.-Y.; Sun, Y.-G. Ensemble multi-label classification algorithm based on tree-Bayesian network. Comput. Sci. 2018, 45, 189–195. [Google Scholar]
- Fu, B.; Wang, Z.H. A Multi-label classification method based on tree structure of label dependency. PR AI 2012, 25, 573–580. [Google Scholar]
- Lee, J.; Kim, H.; Kim, N.-R.; Lee, J.-H. An approach for multi-label classification by directed acyclic graph with label correlation maximization. Inf. Sci. 2016, 351, 101–114. [Google Scholar] [CrossRef]
- Varando, G.; Bielza, C.; Larrañaga, P. Decision functions for chain classifiers based on Bayesian networks for multi-label classification. Int. J. Approx. Reason. 2016, 68, 164–178. [Google Scholar] [CrossRef]
- Chen, B.; Li, W.; Zhang, Y.; Hu, J. Enhancing multi-label classification based on local label constraints and classifier chains. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1458–1463. [Google Scholar]
- Frey, B.J.; Dueck, D. Clustering by Passing Messages Between Data Points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Li, G.; Wang, S.; Zhang, W.; Huang, Q. Group sensitive Classifier Chains for multi-label classification. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Turin, Italy, 29 June–3 July 2015; pp. 1–6. [Google Scholar]
- Sun, L.; Kudo, M. Multi-label classification by polytree-augmented classifier chains with label-dependent features. Pattern Anal. Appl. 2018, 22, 1029–1049. [Google Scholar] [CrossRef]
- Kumar, A.; Vembu, S.; Menon, A.K.; Elkan, C. Learning and Inference in Probabilistic Classifier Chains with Beam Search. In Machine Learning and Knowledge Discovery in Databases; Flach, P.A., De Bie, T., Cristianini, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7523, pp. 665–680. [Google Scholar]
- Dembczyński, K.; Cheng, W.; Hüllermeier, E. Bayes optimal multilabel classification via probabilistic classifier chains. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 279–286. [Google Scholar]
- Read, J.; Martino, L.; Olmos, P.M.; Luengo, D. Scalable multi-output label prediction: From classifier chains to classifier trellises. Pattern Recognit. 2015, 48, 2096–2109. [Google Scholar] [CrossRef]
- Wang, S.B.; Li, Y.F. Classifier Circle Method for Multi-Label Learning. J. Softw. 2015, 26, 2811–2819. [Google Scholar]
- Jun, X.; Lu, Y.; Lei, Z.; Guolun, D. Conditional entropy based classifier chains for multi-label classification. Neurocomputing 2019, 335, 185–194. [Google Scholar] [CrossRef]
- Teisseyre, P. CCnet: Joint multi-label classification and feature selection using classifier chains and elastic net regularization. Neurocomputing 2017, 235, 98–111. [Google Scholar] [CrossRef]
- Teisseyre, P.; Zufferey, D.; Słomka, M. Cost-sensitive classifier chains: Selecting low-cost features in multi-label classification. Pattern Recognit. 2019, 86, 290–319. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Effective and Efficient Multilabel Classification in Domains with Large Number of Labels. In ECML/PKDD 2008 Workshop on Mining Multidimensional Data (MMD’08); Springer: Berlin/Heidelberg, Germany, 2008; pp. 30–44. [Google Scholar]
- Read, J.; Pfahringer, B.; Holmes, G. Multi-label Classification Using Ensembles of Pruned Sets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 995–1000. [Google Scholar]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Random k-Labelsets for Multilabel Classification. IEEE Trans. Knowl. Data Eng. 2010, 23, 1079–1089. [Google Scholar] [CrossRef]
- Elisseeff, A.; Weston, J. A kernel method for multi-labelled classification. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic (NIPS), Vancouver, BC, Canada, 3–8 December 2001; pp. 681–687. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. Multi-label neural networks with applications to functional genomics and text categorization. IEEE T. Knowl. Data En. 2006, 18, 1338–1351. [Google Scholar] [CrossRef]
- Huang, J.; Li, G.; Huang, Q.; Wu, X. Learning Label-Specific Features and Class-Dependent Labels for Multi-Label Classification. IEEE Trans. Knowl. Data Eng. 2016, 28, 3309–3323. [Google Scholar] [CrossRef]
- Héberger, K. Sum of ranking differences compares methods or models fairly. TrAC Trends Anal. Chem. 2010, 29, 101–109. [Google Scholar] [CrossRef]
- Kollár-Hunek, K.; Héberger, K. Method and model comparison by sum of ranking differences in cases of repeated observations (ties). Chemom. Intell. Lab. Syst. 2013, 127, 139–146. [Google Scholar] [CrossRef]
- Lourenço, J.M.; Lebensztajn, L. Post-Pareto Optimality Analysis with Sum of Ranking Differences. IEEE Trans. Magn. 2018, 54, 1–10. [Google Scholar] [CrossRef]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Rácz, A.; Bajusz, D.; Héberger, K. Multi-Level Comparison of Machine Learning Classifiers and Their Performance Metrics. Molecules 2019, 24, 2811. [Google Scholar] [CrossRef] [PubMed]
| Dataset | Instance Number | Label Number | Continuous Feature Number | Discrete Feature Number | Density | Field |
|---|---|---|---|---|---|---|
| emotions | 593 | 6 | 72 | 0 | 0.311 | Music |
| CAL500 | 502 | 174 | 68 | 0 | 0.150 | Music |
| yeast | 2417 | 14 | 103 | 0 | 0.303 | biology |
| flags | 194 | 7 | 10 | 9 | 0.485 | Image |
| scene | 2407 | 6 | 294 | 0 | 0.1790 | Image |
| birds | 645 | 19 | 258 | 2 | 0.053 | Audio |
| enron | 1702 | 53 | 0 | 1001 | 0.064 | Text |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.2525(5) | 0.3040(6) | 0.4032(5) | 2.5863(6) | 0.6897(6) |
| LP | 0.2808(6) | 0.3393(7) | 0.4605(7) | 2.6669(7) | 0.6643(7) |
| RAkEL | 0.2153(3) | 0.1891(4) | 0.3120(3) | 1.9464(4) | 0.7758(4) |
| Rank-SVM | 0.3713(9) | 0.4273(9) | 0.6154(9) | 3.0264(8) | 0.5714(9) |
| BP_MLL | 0.3519(8) | 0.4143(8) | 0.5868(8) | 3.0759(9) | 0.5732(8) |
| CC | 0.2171(4) | 0.1729(3) | 0.3124(4) | 1.8134(3) | 0.7852(3) |
| CCE | 0.2064(2) | 0.1646(2) | 0.2719(2) | 1.7699(2) | 0.8001(2) |
| LLSF-DL | 0.2893(7) | 0.2867(5) | 0.4273(6) | 2.3407(5) | 0.6936(5) |
| PCC-FS | 0.2008(1) | 0.1503(1) | 0.2550(1) | 1.7174(1) | 0.8130(1) |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.2104(8) | 0.4071(8) | 0.8565(8) | 169.3291(8) | 0.2609(8) |
| LP | 0.1993(7) | 0.6559(9) | 0.9880(9) | 171.1590(9) | 0.1164(9) |
| RAkEL | 0.1686(6) | 0.2870(7) | 0.3529(7) | 165.3036(7) | 0.4008(7) |
| Rank-SVM | 0.1376(2) | 0.1824(5) | 0.1156(2) | 129.2589(2) | 0.4986(4) |
| BP_MLL | 0.1480(5) | 0.1815(4) | 0.1186(3) | 130.084(6) | 0.4967(5) |
| CC | 0.1386(4) | 0.1814(3) | 0.1216(4) | 129.698(4) | 0.5025(3) |
| CCE | 0.1377(3) | 0.1781(2) | 0.1255(5) | 129.851(5) | 0.5094(2) |
| LLSF-DL | 0.2330(9) | 0.1985(6) | 0.3500(6) | 126.967(1) | 0.4463(6) |
| PCC-FS | 0.1370(1) | 0.1766(1) | 0.1155(1) | 129.616(3) | 0.5125(1) |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.2619(8) | 0.3287(8) | 0.2871(7) | 9.2457(8) | 0.6259(8) |
| LP | 0.2768(9) | 0.3977(9) | 0.5143(9) | 9.3607(9) | 0.5733(9) |
| RAkEL | 0.2270(6) | 0.2143(6) | 0.2946(8) | 7.5086(6) | 0.7144(6) |
| Rank-SVM | 0.2450(7) | 0.1928(5) | 0.2521(5) | 6.3554(3) | 0.7217(5) |
| BP_MLL | 0.2112(5) | 0.1761(4) | 0.2429(4) | 6.5101(5) | 0.7473(4) |
| CC | 0.1993(1) | 0.1699(3) | 0.2238(2) | 6.4200(4) | 0.7596(3) |
| CCE | 0.2015(3) | 0.1679(2) | 0.2284(3) | 6.3475(2) | 0.7645(2) |
| LLSF-DL | 0.2019(4) | 0.2585(7) | 0.2790(6) | 8.5881(7) | 0.7004(7) |
| PCC-FS | 0.2013(2) | 0.1665(1) | 0.2156(1) | 6.3335(1) | 0.7666(1) |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.2683(3) | 0.2895(7) | 0.3703(7) | 4.1221(7) | 0.7630(7) |
| LP | 0.2962(6) | 0.5011(8) | 0.5587(8) | 4.9495(8) | 0.6407(8) |
| RAkEL | 0.2428(1) | 0.2332(5) | 0.2255(3) | 3.7824(3) | 0.8118(2) |
| Rank-SVM | 0.5931(9) | 0.7052(9) | 0.7618(9) | 5.5303(9) | 0.4987(9) |
| BP_MLL | 0.3225(8) | 0.2226(3) | 0.2288(4) | 3.8734(5) | 0.8028(5) |
| CC | 0.2785(5) | 0.2136(2) | 0.2344(5) | 3.7400(1) | 0.8117(3) |
| CCE | 0.2749(4) | 0.2252(4) | 0.2283(2) | 3.8513(4) | 0.8032(4) |
| LLSF-DL | 0.2987(7) | 0.2786(6) | 0.2838(6) | 4.0921(6) | 0.7683(6) |
| PCC-FS | 0.2619(2) | 0.2068(1) | 0.2135(1) | 3.7492(2) | 0.8214(1) |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.1488(7) | 0.2345(9) | 0.4595(9) | 1.2685(9) | 0.6946(9) |
| LP | 0.1439(6) | 0.2121(8) | 0.3984(7) | 1.1550(8) | 0.7308(8) |
| RAkEL | 0.1014(4) | 0.0998(4) | 0.2672(4) | 0.5854(4) | 0.8378(4) |
| Rank-SVM | 0.1501(8) | 0.1039(5) | 0.2863(5) | 0.6266(5) | 0.8275(5) |
| BP_MLL | 0.1859(9) | 0.1383(6) | 0.4550(8) | 0.7725(6) | 0.7411(7) |
| CC | 0.1137(5) | 0.0801(1) | 0.2439(2) | 0.4844(1) | 0.8556(1) |
| CCE | 0.0949(2) | 0.0922(3) | 0.2447(3) | 0.5439(3) | 0.8495(3) |
| LLSF-DL | 0.0998(3) | 0.1898(7) | 0.3482(6) | 1.0536(7) | 0.7579(6) |
| PCC-FS | 0.0940(1) | 0.0872(2) | 0.2401(1) | 0.5193(2) | 0.8540(2) |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.0641(4) | 0.2076(3) | 0.8231(6) | 5.2117(6) | 0.3806(5) |
| LP | 0.0731(5) | 0.2733(7) | 0.9009(9) | 6.0743(8) | 0.2673(6) |
| RAkEL | 0.0502(1) | 0.1523 (1) | 0.6957(4) | 4.0188(4) | 0.5271(3) |
| Rank-SVM | 0.1080(9) | 0.5359(9) | 0.8273(7) | 6.2380(9) | 0.2421(7) |
| BP_MLL | 0.0587(3) | 0.4486(8) | 0.8637(8) | 5.2591(7) | 0.2023(9) |
| CC | 0.0923(8) | 0.2487(6) | 0.4959(2) | 3.3094(2) | 0.5311(2) |
| CCE | 0.0878(7) | 0.2521(5) | 0.5162(3) | 3.3771(3) | 0.5138(4) |
| LLSF-DL | 0.0536(2) | 0.1809(2) | 0.8229(5) | 4.2128(5) | 0.2239(8) |
| PCC-FS | 0.0827(6) | 0.2265(4) | 0.4457(1) | 3.1203(1) | 0.5646(1) |
| Algorithm | Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision |
|---|---|---|---|---|---|
| HOMER | 0.0606(7) | 0.2471(7) | 0.4918(7) | 28.0953(7) | 0.5067(7) |
| LP | 0.0707(8) | 0.5480(8) | 0.8144(8) | 39.5441(8) | 0.2246(8) |
| RAkEL | 0.0484(5) | 0.2011(6) | 0.2774(2) | 25.2163(6) | 0.6156(6) |
| Rank-SVM | 0.0737(9) | 0.6256(9) | 0.8854(9) | 45.4454(9) | 0.1471(9) |
| BP_MLL | 0.0553(6) | 0.0716(1) | 0.2679(1) | 11.2064(1) | 0.6847(1) |
| CC | 0.0481(4) | 0.0781(2) | 0.3099(4) | 11.8147(2) | 0.6817(3) |
| CCE | 0.0480(3) | 0.0809(4) | 0.3264(6) | 12.0097(4) | 0.6720(4) |
| LLSF-DL | 0.0454(1) | 0.1545(5) | 0.2954(3) | 20.9599(5) | 0.6408(5) |
| PCC-FS | 0.0474(2) | 0.0784(3) | 0.3152(5) | 11.8254(3) | 0.6832(2) |
| Evaluation Criteria | ||
|---|---|---|
| Hamming Loss | 4.2558 | 2.1382 |
| Ranking Loss | 8.9239 | |
| One-Error | 7.8679 | |
| Coverage | 9.6106 | |
| Average Precision | 13.6875 |
| Hamming Loss | Ranking Loss | One Error | Coverage | Average Precision | |
|---|---|---|---|---|---|
| HOMER | √ | √ | √ | √ | |
| LP | √ | √ | √ | √ | √ |
| RAkEL | |||||
| Rank-SVM | √ | √ | √ | √ | √ |
| BP_MLL | √ | ||||
| CC | |||||
| CCE | |||||
| LLSF-DL | √ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, T.; Wan, B.; Han, M. Partial Classifier Chains with Feature Selection by Exploiting Label Correlation in Multi-Label Classification. Entropy 2020, 22, 1143. https://doi.org/10.3390/e22101143
Wang Z, Wang T, Wan B, Han M. Partial Classifier Chains with Feature Selection by Exploiting Label Correlation in Multi-Label Classification. Entropy. 2020; 22(10):1143. https://doi.org/10.3390/e22101143
Chicago/Turabian StyleWang, Zhenwu, Tielin Wang, Benting Wan, and Mengjie Han. 2020. "Partial Classifier Chains with Feature Selection by Exploiting Label Correlation in Multi-Label Classification" Entropy 22, no. 10: 1143. https://doi.org/10.3390/e22101143
APA StyleWang, Z., Wang, T., Wan, B., & Han, M. (2020). Partial Classifier Chains with Feature Selection by Exploiting Label Correlation in Multi-Label Classification. Entropy, 22(10), 1143. https://doi.org/10.3390/e22101143







