Entropy Monotonicity and Superstable Cycles for the Quadratic Family Revisited
Abstract
1. Introduction
- (i)
- The monotonicity of the topological entropy for the family of quadratic maps;
- (ii)
- Some basic properties of the periodic orbits of its critical point (superstable cycles).
2. Mathematical Preliminaries
2.1. Multimodal Maps
2.2. Topological Entropy
2.3. Superstable Periodic Orbits
3. Application Case: Quadratic Maps
3.1. Root Branches
3.2. Smoothness Domains of the Root Branches
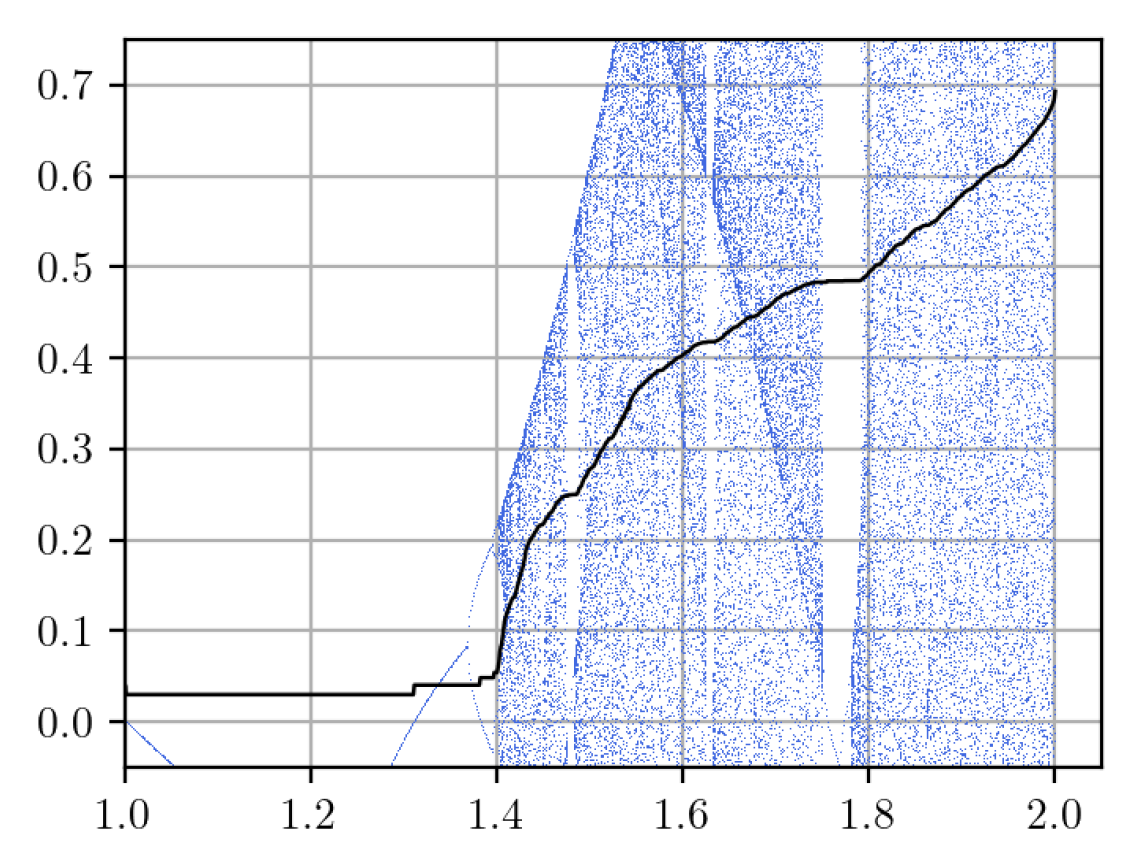
4. Application I: Monotonicity of the Topological Entropy
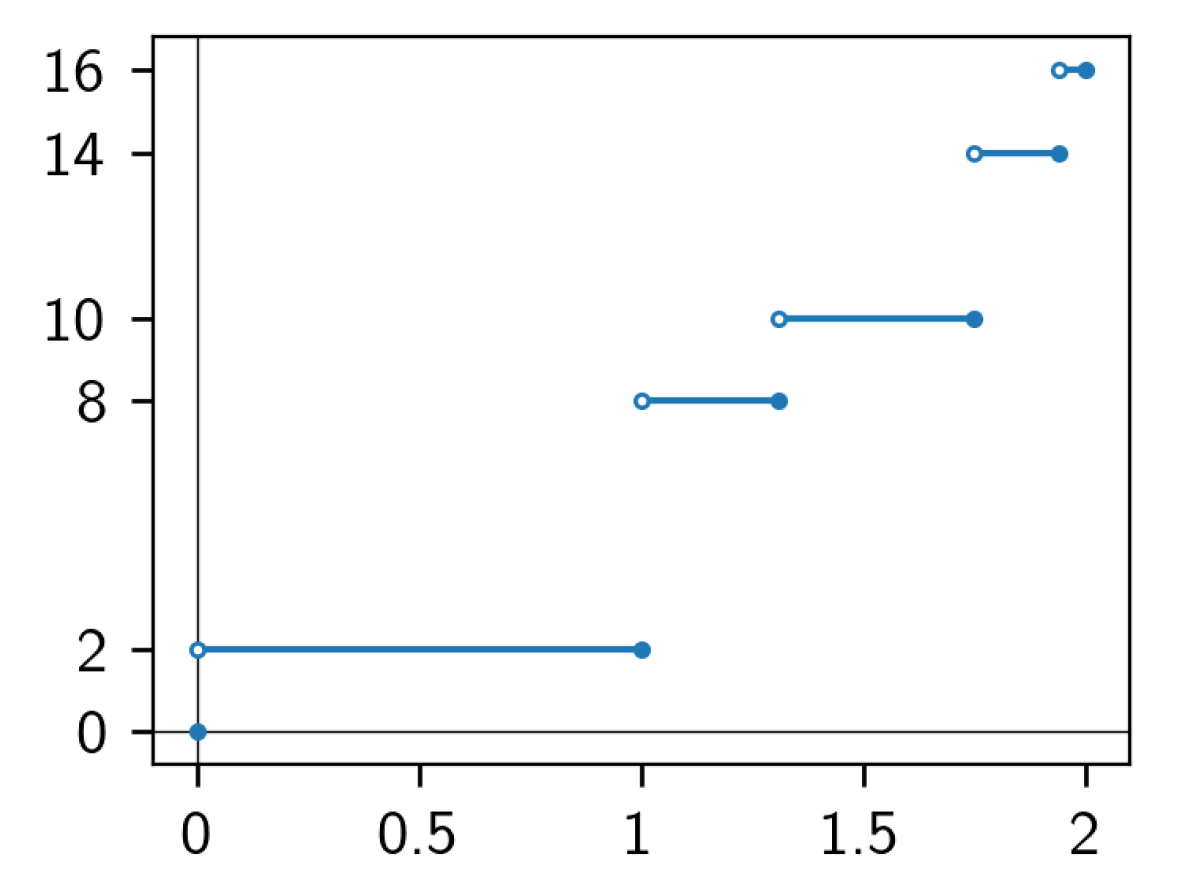
5. Application II: Superstable Period Orbits
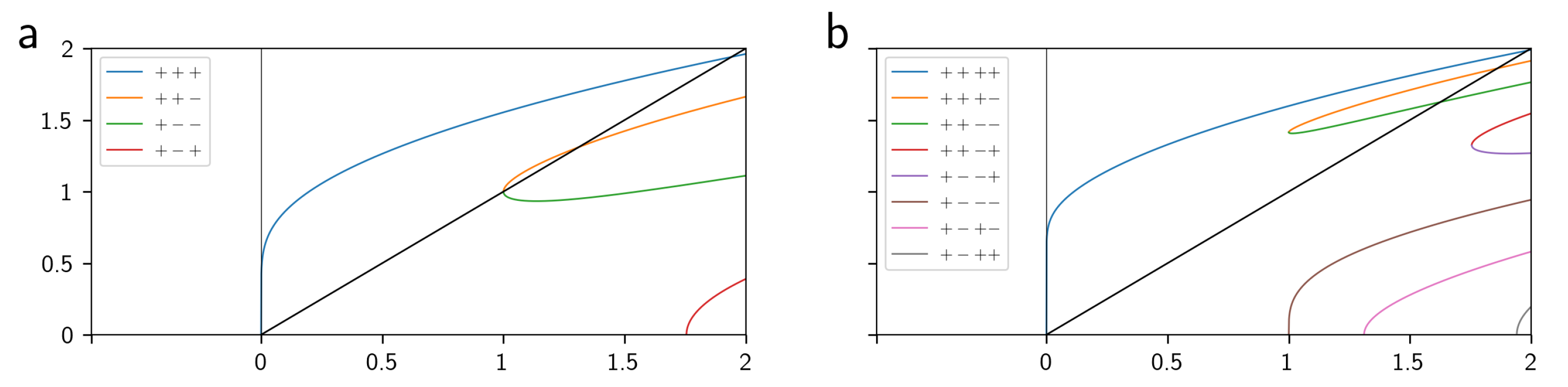
5.1. Symbolic Sequences
5.2. Dark Lines and the Misiurewicz Points
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Walters, P. An Introduction to Ergodic Theory; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1982. [Google Scholar]
- Bowen, R. Entropy for group endomorphisms and homogeneous spaces. Trans. Am. Math. Soc. 1971, 153, 401–414. [Google Scholar] [CrossRef]
- Milnor, J.; Thurston, W. On iterated maps of the interval. In Dynamical Systems; Lecture Notes in Mathematics; Alexander, J.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 465–563. [Google Scholar] [CrossRef]
- Dias de Deus, J.; Dilão, R.; Taborda Durate, J. Topological entropy and approaches to chaos in dynamics of the interval. Phys. Lett. A 1982, 90, 1–4. [Google Scholar] [CrossRef]
- Bandt, C.; Keller, G.; Pompe, B. Entropy of interval maps via permutations. Nonlinearity 2002, 15, 1595–1602. [Google Scholar] [CrossRef]
- Hirata, Y.; Mees, A.I. Estimating topological entropy via a symbolic data compression technique. Phys. Rev. E 2003, 67, 026205. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Dilão, R.; Giménez, A. Computing the Topological Entropy of Multimodal Maps via Min-Max Sequences. Entropy 2012, 14, 742–768. [Google Scholar] [CrossRef]
- Amigó, J.; Giménez, A. A Simplified Algorithm for the Topological Entropy of Multimodal Maps. Entropy 2014, 16, 627–644. [Google Scholar] [CrossRef]
- Amigó, J.M.; Giménez, A. Formulas for the topological entropy of multimodal maps based on min-max symbols. Discret. Contin. Dyn. Syst. B 2015, 20, 3415. [Google Scholar] [CrossRef]
- Milnor, J. Remarks on Iterated Cubic Maps. Exp. Math. 1992, 1, 5–24. [Google Scholar] [CrossRef]
- Douady, A.; Hubbard, J.H. Etude dynamique des polynomes complexes I, II; Universite de Paris-Sud, Dep. de Mathematique: Orsay, France, 1984. [Google Scholar]
- Douady, A. Topological Entropy of Unimodal Maps. In Real and Complex Dynamical Systems; Branner, B., Hjorth, P., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 65–87. [Google Scholar] [CrossRef]
- Tsujii, M. A simple proof for monotonicity of entropy in the quadratic family. Ergod. Theory Dyn. Syst. 2000, 20, 925–933. [Google Scholar] [CrossRef]
- Bruin, H.; van Strien, S. On the structure of isentropes of polynomial maps. Dyn. Syst. 2013, 28, 381–392. [Google Scholar] [CrossRef][Green Version]
- Bruin, H.; van Strien, S. Monotonicity of entropy for real multimodal maps. J. Am. Math. Soc. 2015, 28, 1–61. [Google Scholar] [CrossRef]
- Singer, D. Stable Orbits and Bifurcation of Maps of the Interval. SIAM J. Appl. Math. 1978, 35, 260–267. [Google Scholar] [CrossRef]
- Melo, W.D.; Strien, S.V. One-Dimensional Dynamics; Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge/A Series of Modern Surveys in Mathematics; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar] [CrossRef]
- Misiurewicz, M.; Szlenk, W. Entropy of piecewise monotone mappings. Studia Math. 1980, 67, 45–63. [Google Scholar] [CrossRef]
- Katok, A. Fifty years of entropy in dynamics: 1958–2007. J. Mod. Dyn. 2007, 1, 545–596. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K.; Unakafova, V.A. On entropy, entropy-like quantities, and applications. Discret. Contin. Dyn. Syst. B 2015, 20, 3301–3343. [Google Scholar] [CrossRef]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A Brief Review of Generalized Entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Alseda, L.; Llibre, J.; Misiurewicz, M. Combinatorial Dynamics and Entropy in Dimension One, 2nd ed.; World Scientific Publishing Company: Singapore, 2000. [Google Scholar]
- Cockram, N.; Rodrigues, A. A survey on the topological entropy of cubic polynomials. arXiv 2020, arXiv:2006.13795. [Google Scholar]
- Dilão, R.; Amigó, J. Computing the topological entropy of unimodal maps. Int. J. Bifurc. Chaos 2012, 22, 1250152. [Google Scholar] [CrossRef]
- Bruin, H. Non-monotonicity of entropy of interval maps. Phys. Lett. A 1995, 202, 359–362. [Google Scholar] [CrossRef]
- Polya, G.; Szegö, G. Problems and Theorems in Analysis I: Series. Integral Calculus. Theory of Functions; Classics in Mathematics; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Graczyk, J.; Swiatek, G. Generic Hyperbolicity in the Logistic Family. Ann. Math. 1997, 146, 1–52. [Google Scholar] [CrossRef]
- Lyubich, M. Dynamics of quadratic polynomials, I–II. Acta Math. 1997, 178, 185–297. [Google Scholar] [CrossRef]
- Hao, B.; Zheng, W.M. Applied Symbolic Dynamics and Chaos; World Scientific Publishing Co.: Singapore, 1998. [Google Scholar]
- Metropolis, N.; Stein, M.; Stein, P. On finite limit sets for transformations on the unit interval. J. Comb. Theory Ser. A 1973, 15, 25–44. [Google Scholar] [CrossRef]
- Misiurewicz, M.; Nitecki, Z. Combinatorial Patterns for Maps of the Interval; Number no. 456 in Memoirs of the American Mathematical Society; American Mathematical Soc.: Providence, RI, USA, 1991. [Google Scholar]
- Romera, M.; Pastor, G.; Montoya, F. Misiurewicz points in one-dimensional quadratic maps. Phys. A Stat. Mech. Its Appl. 1996, 232, 517–535. [Google Scholar] [CrossRef]
- Hutz, B.; Towsley, A. Misiurewicz points for polynomial mapsand transversality. N. Y. J. Math. 2015, 21, 297–319. [Google Scholar]
- Misiurewicz, M. Absolutely continuous measures for certain maps of an interval. Publications Mathématiques de l’IHÉS 1981, 53, 17–51. [Google Scholar] [CrossRef]
- Rychlik, M.; Sorets, E. Regularity and other properties of absolutely continuous invariant measures for the quadratic family. Commun. Math. Phys. 1992, 150, 217–236. [Google Scholar] [CrossRef]



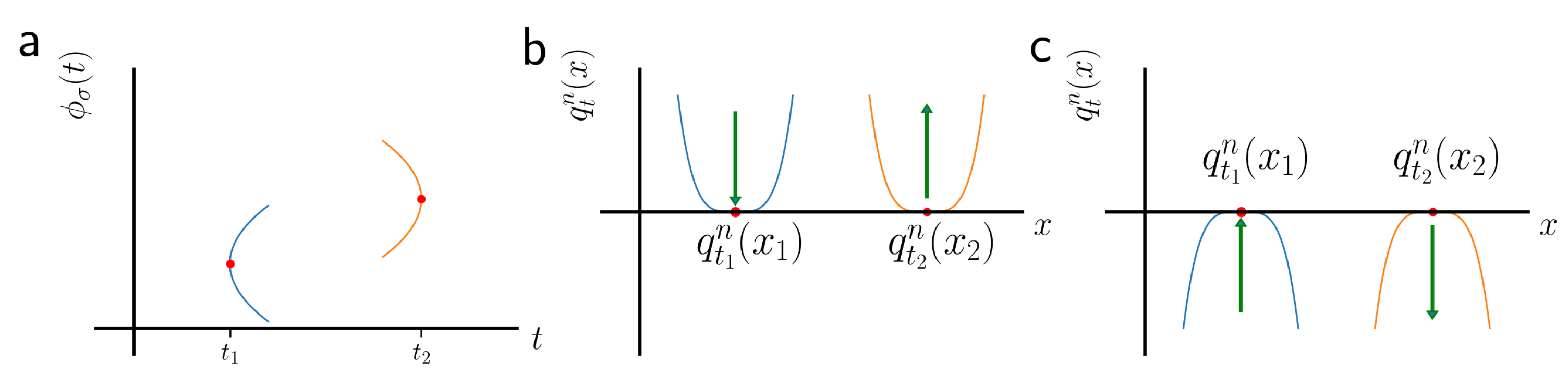
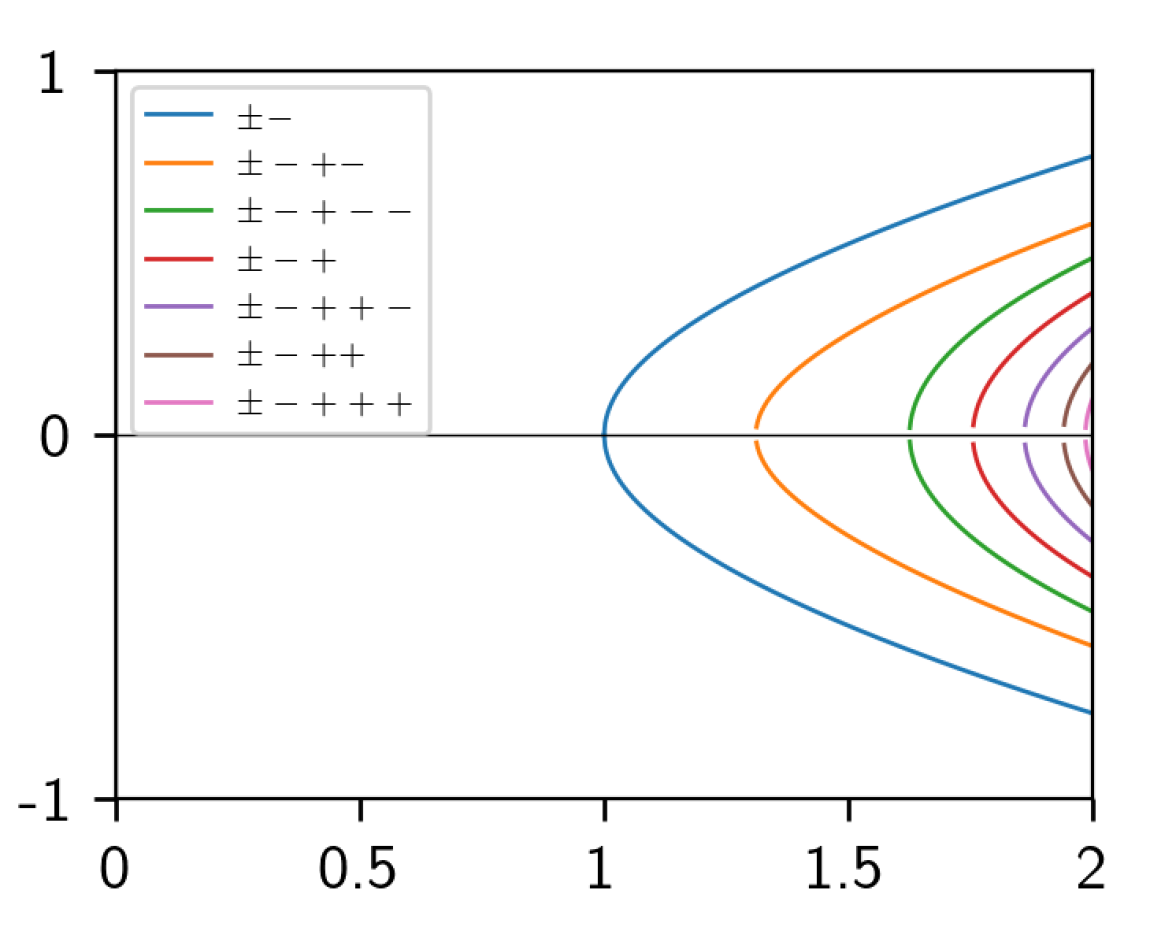

| Root Parabolas | |
|---|---|
| Period | Superstable Cycles |
|---|---|
| 1 | C |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
| Period | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # sup. cycles | 1 | 1 | 2 | 3 | 5 | 9 | 16 | 28 | 51 | 93 | 170 | 315 | 585 | 1091 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amigó, J.M.; Giménez, Á. Entropy Monotonicity and Superstable Cycles for the Quadratic Family Revisited. Entropy 2020, 22, 1136. https://doi.org/10.3390/e22101136
Amigó JM, Giménez Á. Entropy Monotonicity and Superstable Cycles for the Quadratic Family Revisited. Entropy. 2020; 22(10):1136. https://doi.org/10.3390/e22101136
Chicago/Turabian StyleAmigó, José M., and Ángel Giménez. 2020. "Entropy Monotonicity and Superstable Cycles for the Quadratic Family Revisited" Entropy 22, no. 10: 1136. https://doi.org/10.3390/e22101136
APA StyleAmigó, J. M., & Giménez, Á. (2020). Entropy Monotonicity and Superstable Cycles for the Quadratic Family Revisited. Entropy, 22(10), 1136. https://doi.org/10.3390/e22101136







