Cluster-Based Thermodynamics of Interacting Dice in a Lattice
Abstract
1. Introduction
2. Model
2.1. Modeling Concept
2.1.1. Sequential Lattice Construction as a Discrete Markov Chain
2.1.2. Set of Variables
2.2. Entropy of the System
2.3. Internal Energy of the System
2.4. Helmholtz Free Energy of the System
2.5. Constraints Applied to Minimize the Helmholtz Free Energy
2.5.1. Mathematical Constraints
2.5.2. Constraints Reflecting Lattice Isotropy
2.5.3. Constraints Derived from Cluster Construction
2.5.4. Model-Related Constraints
2.6. Resulting System of Equations
3. Results
3.1. Random Mixing
3.1.1. Pure-Component Systems
3.1.2. Two-Component Systems
3.2. Non-Random Mixing Considering Cooperative Effects
 , (b) ε
, (b) ε , and (c) ε
, and (c) ε . The energy of the whole system is then calculated by Equation (14).
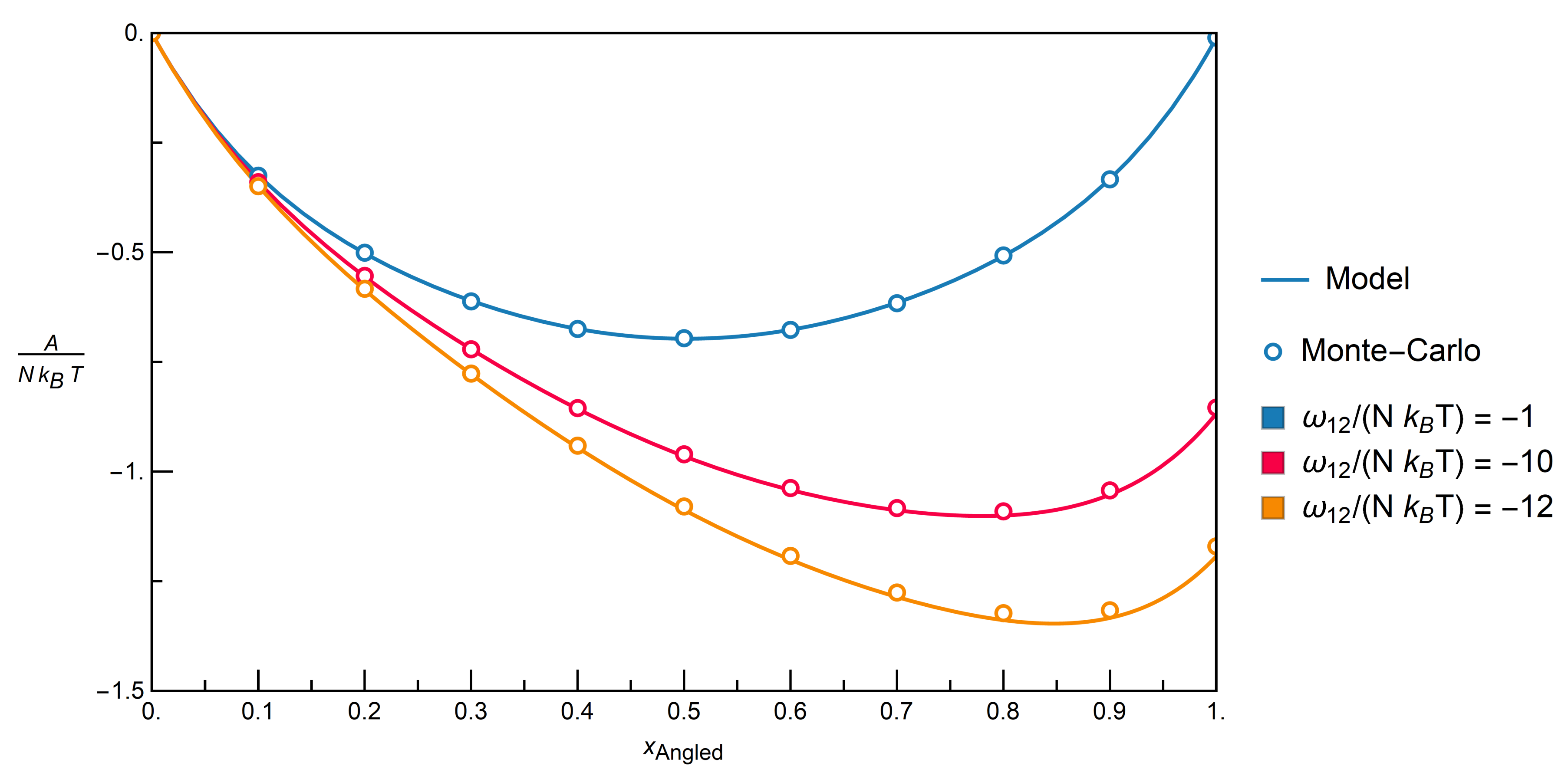
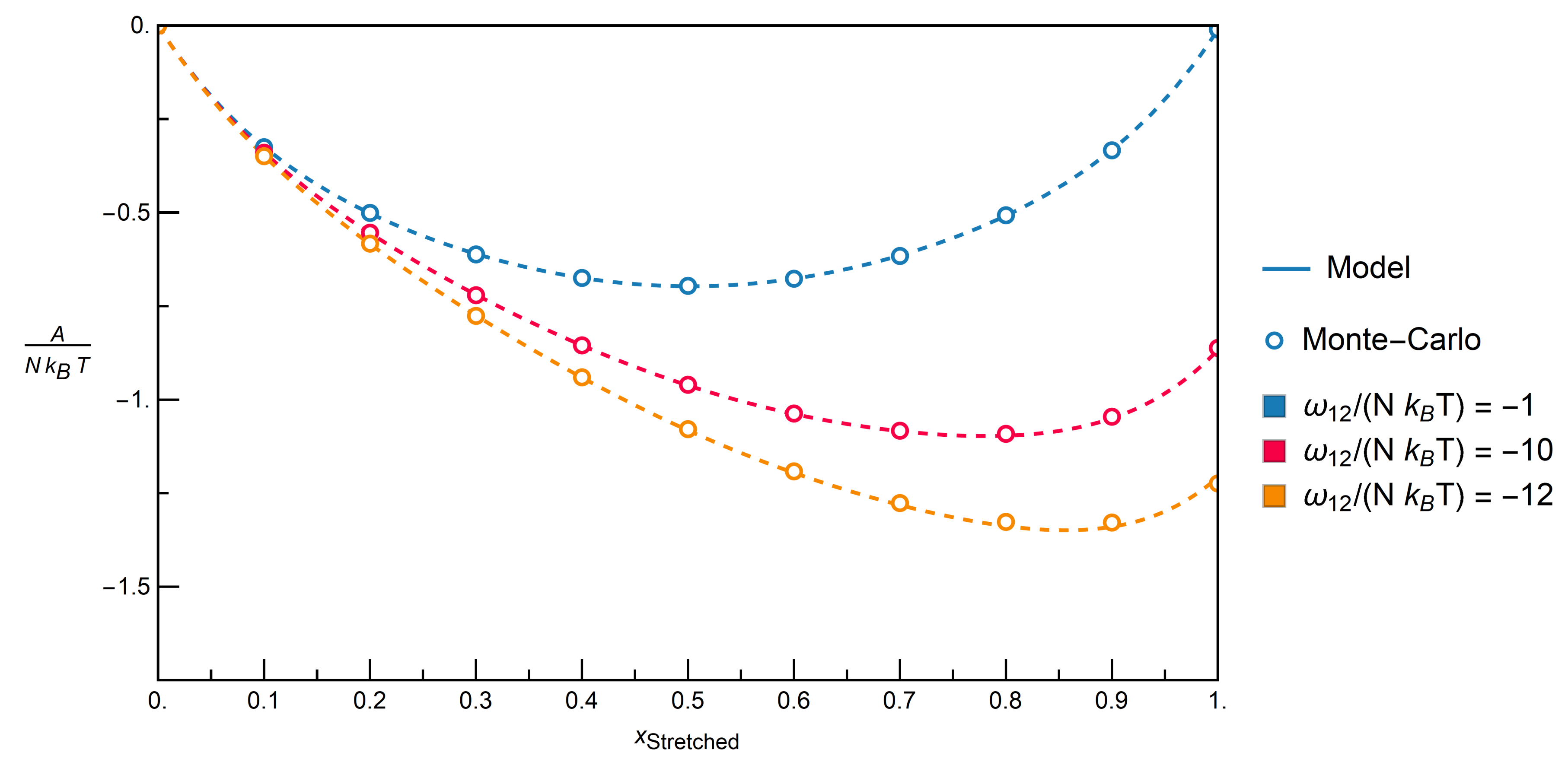
. The energy of the whole system is then calculated by Equation (14).3.2.1. Comparison with Monte-Carlo Simulations
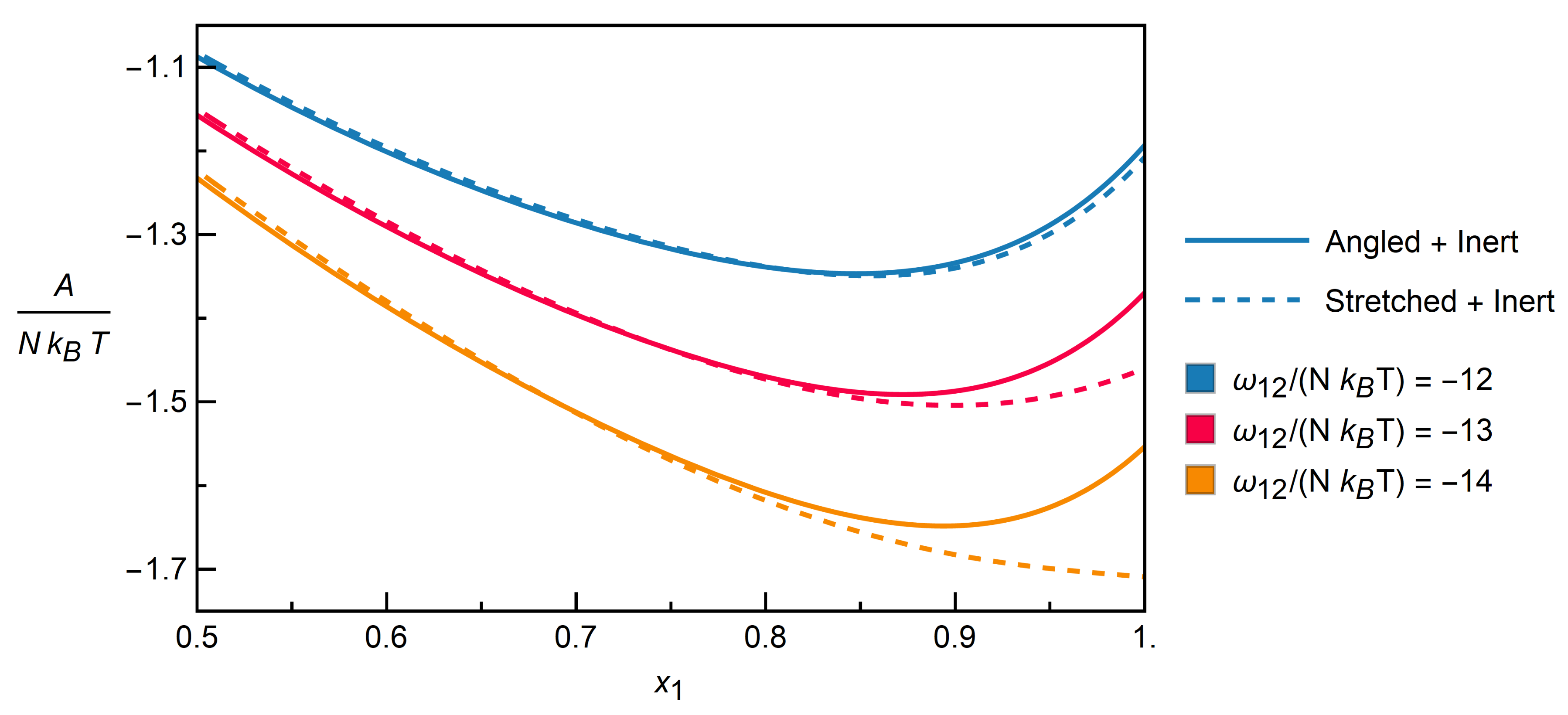
3.2.2. Mixtures of Angled + Inert Molecules
3.2.3. Mixtures of Stretched + Inert Molecules
3.2.4. Distinction between Isomers
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| bQCE | binary quantum cluster equilibrium theory |
| COSMO | conductor-like screening model |
| COSMO-RS | conductor-like screening model for real solvents |
| COSMOSPACE | COSMO surface-pair activity coefficient equation |
| CVM | cluster variation method |
| MCC | multiscale cell correlation method |
| MD | molecular dynamics |
| UNIFAC | universal quasichemical functional group activity coefficients |
| VSC | Vienna Scientific Cluster |
| Nomenclature in formulae: | |
| , , , | set of all possible states that the molecules at positions A, B, C, |
| and D in the cluster can reside in | |
| states of the molecules located at positions A, B, C, and D | |
| A | Helmholtz free energy |
| internal energy of a cluster | |
| excess Gibbs-energy | |
| Shannon information of the system | |
| Boltzmann’s constant | |
| numbers of possible state for each of the two probability distributions | |
| N | number of molecules |
| probability to find the three nearest neighbors for the central | |
| molecule in a particular state | |
| probability of an entire cluster to be in a particular state | |
| probabilities of inserting molecules of states , resp. | |
| d into an existing neighborhood of state a | |
| probability of inserting a molecule of state a into an existing neighborhood | |
| of states b, c, and d | |
| P | probability function |
| probability distributions | |
| probability of finding a system in state i | |
| thermodynamic entropy of an ensemble of clusters | |
| thermodynamic entropy of the system | |
| T | temperature |
| internal energy of an ensemble of clusters | |
| internal energy of the system | |
| V | volume |
| molecular fraction or molar fraction of component i | |
| random variables | |
| state i of the random variables Y, and Z | |
| interaction energy for the contact pair i-j | |
| interchange energy for the contact pair i-j |
References
- Guggenheim, E.A. Statistical thermodynamics of mixtures with zero energies of mixing. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1944, 183, 203–212. [Google Scholar]
- Guggenheim, E.A.; McGlashan, M.L. Statistical Mechanics of Regular Mixtures. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1951, 206, 335–353. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Mixtures; Oxford at the Clarendon Press: Oxford, UK, 1952. [Google Scholar]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Constantinescu, D.; Gmehling, J. Further Development of Modified UNIFAC (Dortmund): Revision and Extension 6. J. Chem. Eng. Data 2016, 61, 2738–2748. [Google Scholar] [CrossRef]
- Egner, K.; Gaube, J.; Pfennig, A. GEQUAC, an excess Gibbs energy model for simultaneous description of associating and non-associating liquid mixtures. Berichte Bunsenges. Phys. Chem. 1997, 101, 209–218. [Google Scholar] [CrossRef]
- Bronneberg, R.; Pfennig, A. MOQUAC, a new expression for the excess Gibbs energy based on molecular orientations. Fluid Phase Equil. 2013, 338, 67–77. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C. Refinement and parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F. COSMO-RS: A novel and efficient method for the a priori prediction of thermophysical data of liquids. Fluid Phase Equil. 2000, 172, 43–72. [Google Scholar] [CrossRef]
- Klamt, A. COSMO and COSMO-RS. In The Encyclopedia of Computational Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar] [CrossRef]
- Klamt, A.; Krooshof, G.J.P.; Taylor, R. COSMOSPACE: Alternative to conventional activity-coefficient models. AIChE J. 2002, 48, 2332–2349. [Google Scholar] [CrossRef]
- Sweere, A.J.M.; Fraaije, J.G.E.M. Force-field based quasi-chemical method for rapid evaluation of binary phase diagrams. J. Phys. Chem. B 2015, 119, 14200–14209. [Google Scholar] [CrossRef] [PubMed]
- Sweere, A.J.M.; Gracia, R.S.; Fraaije, J.G.E.M. Extensive accuracy test of the force-field-based quasichemical method PAC-MAC. J. Chem. Eng. Data 2016, 61, 3989–3997. [Google Scholar] [CrossRef]
- Sweere, A.J.; Fraaije, J.G. Prediction of polymer-solvent miscibility properties using the force field based quasi-chemical method PAC-MAC. Polymer 2016, 107, 147–153. [Google Scholar] [CrossRef]
- Sweere, A.J.M.; Fraaije, J.G.E.M. Accuracy test of the OPLS-AA force field for calculating free energies of mixing and comparison with PAC-MAC. J. Chem. Theory Comp. 2017, 13, 1911–1923. [Google Scholar] [CrossRef]
- Klamt, A. COSMO-RSC: Second-Order Quasi-Chemical Theory Recovering Local Surface Correlation Effects. J. Phys. Chem. A 2016, 120, 2049–2056. [Google Scholar] [CrossRef]
- Ingenmey, J.; Blasius, J.; Marchelli, G.; Riegel, A.; Kirchner, B. A Cluster Approach for Activity Coefficients: General Theory and Implementation. J. Chem. Eng. Data 2019, 64, 255–261. [Google Scholar] [CrossRef]
- Von Domaros, M.; Perlt, E.; Ingenmey, J.; Marchelli, G.; Kirchner, B. Peacemaker2: Making clusters talk about binary mixtures and neat liquids. SoftwareX 2018, 7, 356–359. [Google Scholar] [CrossRef]
- Von Domaros, M.; Jähnigen, S.; Friedrich, J.; Kirchner, B. Quantum cluster equilibrium model of N-methylformamide–water binary mixtures. J. Chem. Phys. 2016, 144, 064305. [Google Scholar] [CrossRef]
- Brüssel, M.; Perlt, E.; Lehmann, S.B.C.; von Domaros, M.; Kirchner, B. Binary systems from quantum cluster equilibrium theory. J. Chem. Phys. 2011, 135, 194113. [Google Scholar] [CrossRef]
- Kirchner, B.; Spickermann, C.; Lehmann, S.B.; Perlt, E.; Langner, J.; von Domaros, M.; Reuther, P.; Uhlig, F.; Kohagen, M.; Brüssel, M. What can clusters tell us about the bulk?: Peacemaker: Extended quantum cluster equilibrium calculations. Comput. Phys. Commun. 2011, 182, 1428–1446. [Google Scholar] [CrossRef]
- Kirchner, B. Cooperative versus dispersion effects: What is more important in an associated liquid such as water? J. Chem. Phys. 2005, 123, 204116. [Google Scholar] [CrossRef] [PubMed]
- Akkermans, R.L.C. Mesoscale model parameters from molecular cluster calculations. J. Chem. Phys. 2008, 128, 244904. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.; Andersen, H.C. Optimized Cluster Expansions for Classical Fluids. II. Theory of Molecular Liquids. J. Chem. Phys. 1972, 57, 1930–1937. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Curro, J.G. Integral equation theory of the structure and thermodynamics of polymer blends. J. Chem. Phys. 1989, 91, 5059–5081. [Google Scholar] [CrossRef]
- Bawendi, M.G.; Freed, K.F. Statistical mechanics of the packing of rods on a lattice: Cluster expansion for systematic corrections to mean field. J. Chem. Phys. 1986, 85, 3007–3022. [Google Scholar] [CrossRef]
- Dudowicz, J.; Freed, K.F. Effect of monomer structure and compressibility on the properties of multicomponent polymer blends and solutions: 1. Lattice cluster theory of compressible systems. Macromolecules 1991, 24, 5076–5095. [Google Scholar] [CrossRef]
- Kikuchi, R. A theory of cooperative phenomena. Phys. Rev. 1951, 81, 988–1003. [Google Scholar] [CrossRef]
- Kikuchi, R.; Brush, S.G. Improvement of the cluster-variation method. J. Chem. Phys. 1967, 47, 195–203. [Google Scholar] [CrossRef]
- Sanchez, J.M.; Ducastelle, F.; Gratias, D. Generalized cluster description of multicomponent systems. Phys. A Stat. Mech. Appl. 1984, 128, 334–350. [Google Scholar] [CrossRef]
- Kikuchi, R. Natural iteration method and boundary free energy. J. Chem. Phys. 1976, 65, 4545–4553. [Google Scholar] [CrossRef]
- Pelizzola, A. Cluster variation method in statistical physics and probabilistic graphical models. J. Phys. A Math. Gen. 2005, 38, R309–R339. [Google Scholar] [CrossRef]
- Gratias, D.; Sanchez, J.M.; De Fontaine, D. Application of group theory to the calculation of the configurational entropy in the cluster variation method. Phys. A Stat. Mech. Appl. 1982, 113, 315–337. [Google Scholar] [CrossRef]
- Pelizzola, A. Generalized belief propagation for the magnetization of the simple cubic Ising model. Nucl. Phys. B 2014, 880, 76–86. [Google Scholar] [CrossRef][Green Version]
- Vinograd, V.L.; Perchuk, L.L. Informational models for the configurational entropy of regular solid solutions: Flat lattices. J. Phys. Chem. 1996, 100, 15972–15985. [Google Scholar] [CrossRef]
- Vinograd, V.L.; Perchuk, L.L. Markov’s chains and the configurational thermodynamics of a solid solution. Vestn. Mosk. Univ. (Ser. Geol.) 1992, 3, 44–58, In Russian. [Google Scholar]
- Pfleger, M.; Wallek, T.; Pfennig, A. Constraints of compound systems: Prerequisites for thermodynamic modeling based on Shannon entropy. Entropy 2014, 16, 2990–3008. [Google Scholar] [CrossRef]
- Pfleger, M.; Wallek, T.; Pfennig, A. Discrete modeling: Thermodynamics based on shannon entropy and discrete states of molecules. Ind. Eng. Chem. Res. 2015, 54, 4643–4654. [Google Scholar] [CrossRef]
- Wallek, T.; Pfleger, M.; Pfennig, A. Discrete modeling of lattice systems: The concept of Shannon entropy applied to strongly interacting systems. Ind. Eng. Chem. Res. 2016, 55, 2483–2492. [Google Scholar] [CrossRef]
- Wallek, T.; Mayer, C.; Pfennig, A. Discrete Modeling Approach as a Basis of Excess Gibbs-Energy Models for Chemical Engineering Applications. Ind. Eng. Chem. Res. 2018, 57, 1294–1306. [Google Scholar] [CrossRef]
- Boltzmann, L. Lectures on Gas Theory; Brush, S.G., Translator; Dover Publications, Inc.: New York, NY, USA, 1964. [Google Scholar]
- Boltzmann, L. On Certain Questions of the Theory of Gases. Nature 1895, 51, 413–415. [Google Scholar] [CrossRef]
- Cercignani, C. Ludwig Boltzmann. The Man Who Trusted Atoms; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Boltzmann, L. Entropie und Wahrscheinlichkeit (1872–1905); Verlag Harri Deutsch: Thun, Switzerland; Frankfurt, Germany, 2000. [Google Scholar]
- Ben-Naim, A. Entropy Demystified; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2008. [Google Scholar]
- Ben-Naim, A. A Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2008. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Kapur, J.N.; Kesavan, H.K. Entropy Optimization Principles with Applications; Academic Press, Inc.: Cambridge, MA, USA, 1992. [Google Scholar]
- Münster, A. Classical Thermodynamics; Wiley-Interscience, Division of Wiley: Hoboken, NJ, USA, 1970. [Google Scholar]
- Jaynes, E.T. Where do we Stand on Maximum Entropy? In The Maximum Entropy Formalism; The MIT Press: Cambridge, MA, USA, 1978; pp. 15–118. [Google Scholar]
- Mehrotra, S. On the implementation of a primal-dual interior point method. SIAM J. Optim. 1992, 2, 575–601. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Maltezos, G. Simulation lokaler Zusammensetzungen. Master’s Thesis, RWTH Aachen University, Aachen, Germany, 1987. (In German). [Google Scholar]
- Ehlker, G.H. Entwicklung der Gruppenbeitragsmethode GEQUAC zur Thermodynamischen Beschreibung Ausgeprägt Nichtidealer Gemische. Ph.D. Thesis, RWTH Aachen, RWTH Aachen University, Aachen, Germany, 2001. (In German). [Google Scholar]
- König, L. Auswertung von Monte Carlo-Simulationen zur Validierung Thermodynamischer Modelle. Bachelor’s Thesis, Graz University of Technology, Graz, Austria, 2013. (In German). [Google Scholar]
- Zapf, F. Monte-Carlo Verfahren zur Diskretisierung von Gittersystemen. Bachelor’s Thesis, Graz University of Technology, Graz, Austria, 2015. (In German). [Google Scholar]

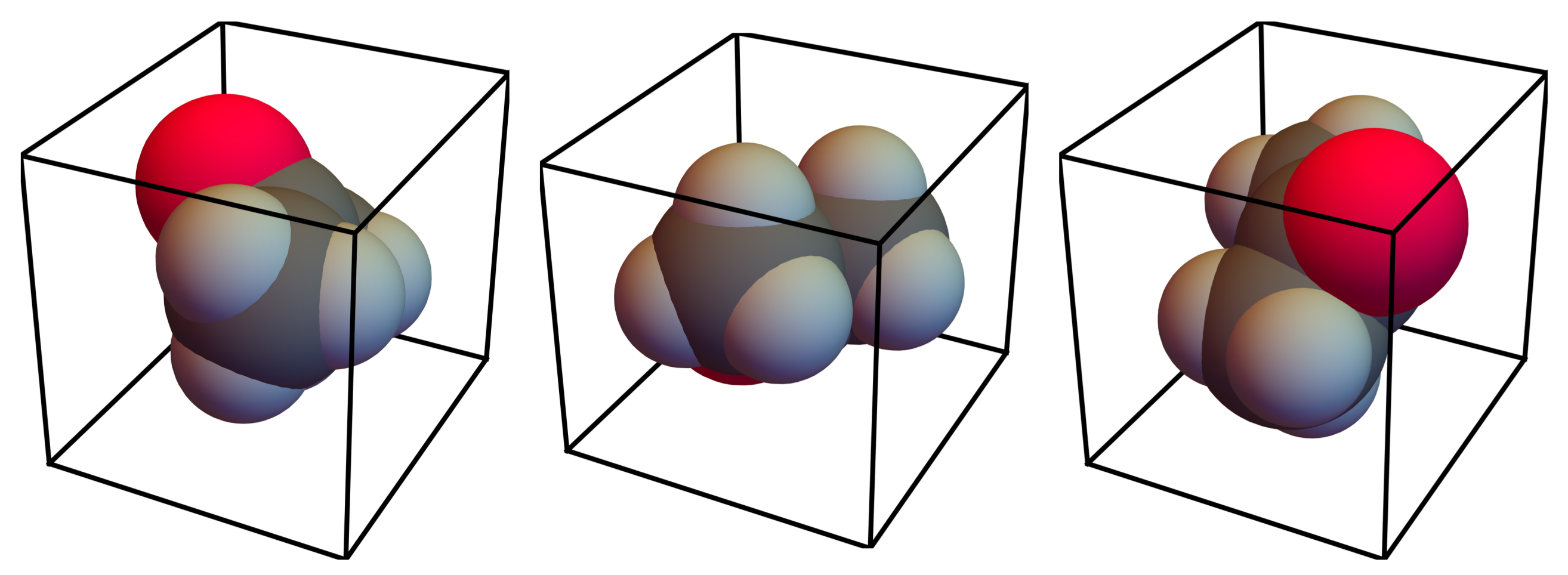


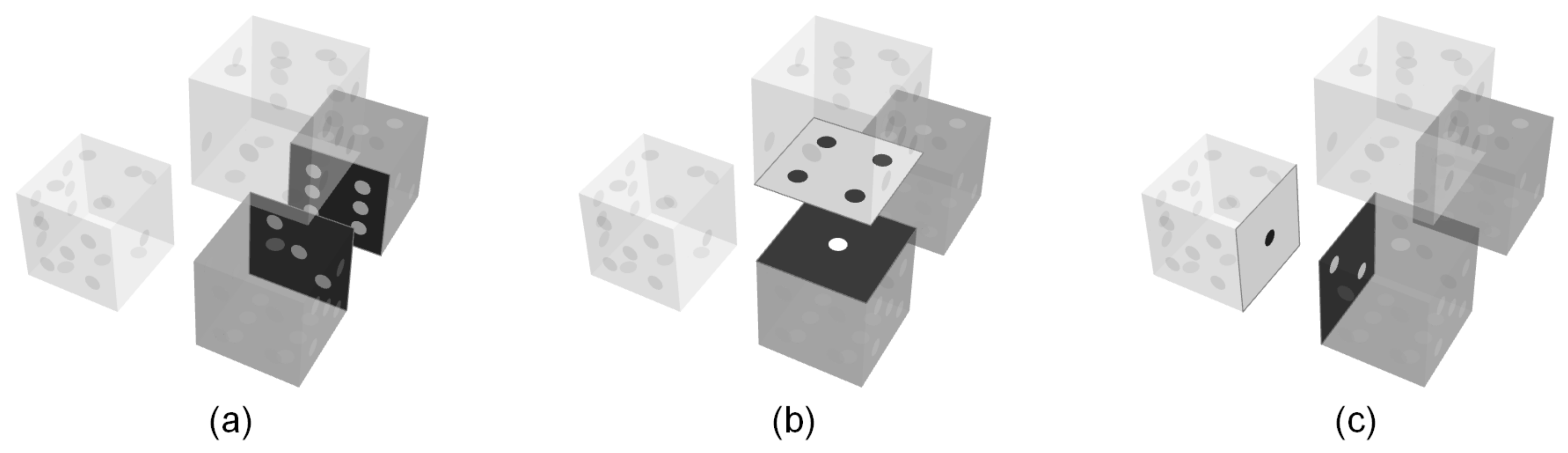
 , are assumed to have the same probability of occurrence; the model does not distinguish between these configurations.
, are assumed to have the same probability of occurrence; the model does not distinguish between these configurations.
 , are assumed to have the same probability of occurrence; the model does not distinguish between these configurations.
, are assumed to have the same probability of occurrence; the model does not distinguish between these configurations.
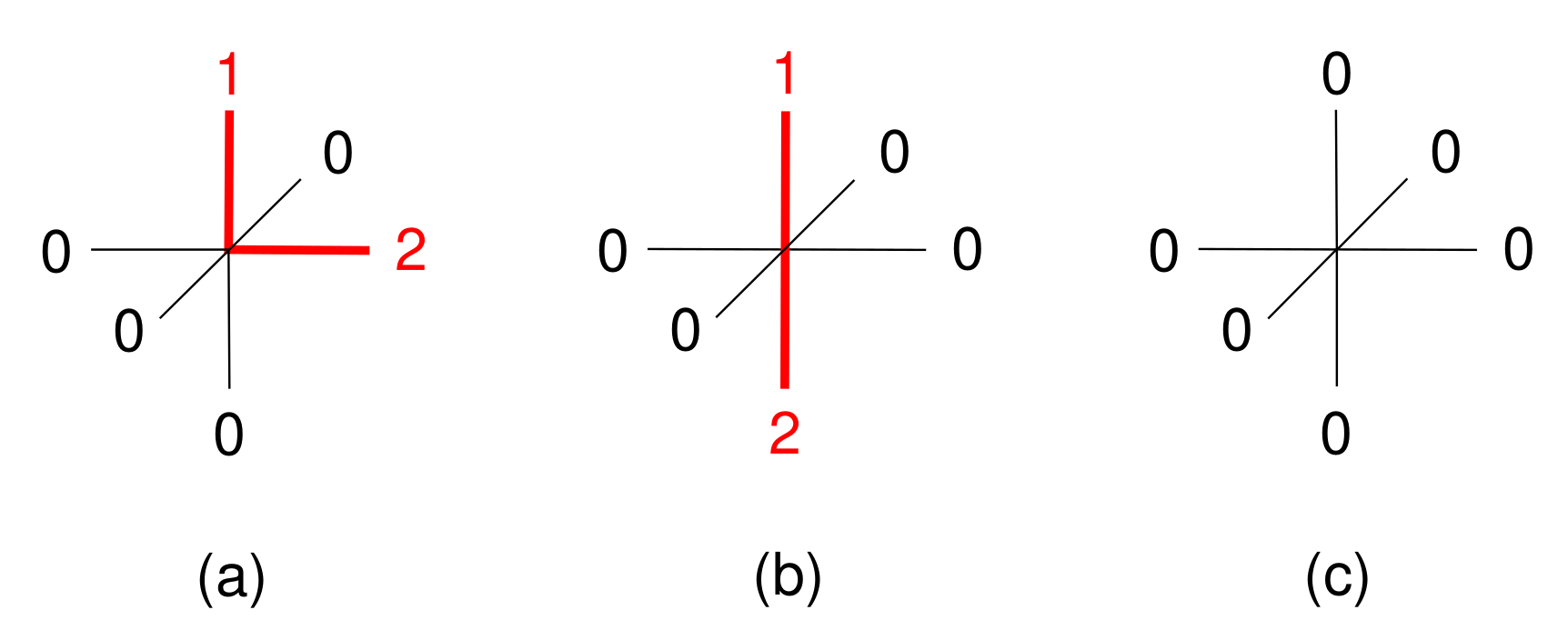
| Contact Pairs (i-j) | Interaction | |
|---|---|---|
| 1-1, 2-2 | 1200 | repulsion |
| 1-2, 2-1 | −1200 | attraction |
| 0-any, any-0 | 0 | inert |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayer, C.; Wallek, T. Cluster-Based Thermodynamics of Interacting Dice in a Lattice. Entropy 2020, 22, 1111. https://doi.org/10.3390/e22101111
Mayer C, Wallek T. Cluster-Based Thermodynamics of Interacting Dice in a Lattice. Entropy. 2020; 22(10):1111. https://doi.org/10.3390/e22101111
Chicago/Turabian StyleMayer, Christoph, and Thomas Wallek. 2020. "Cluster-Based Thermodynamics of Interacting Dice in a Lattice" Entropy 22, no. 10: 1111. https://doi.org/10.3390/e22101111
APA StyleMayer, C., & Wallek, T. (2020). Cluster-Based Thermodynamics of Interacting Dice in a Lattice. Entropy, 22(10), 1111. https://doi.org/10.3390/e22101111







