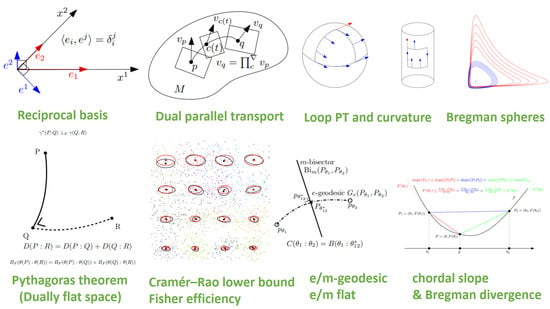
An Elementary Introduction to Information Geometry
Abstract
1. Introduction
1.1. Overview of Information Geometry
1.2. Rationale and Outline of the Survey
2. Prerequisite: Basics of Differential Geometry
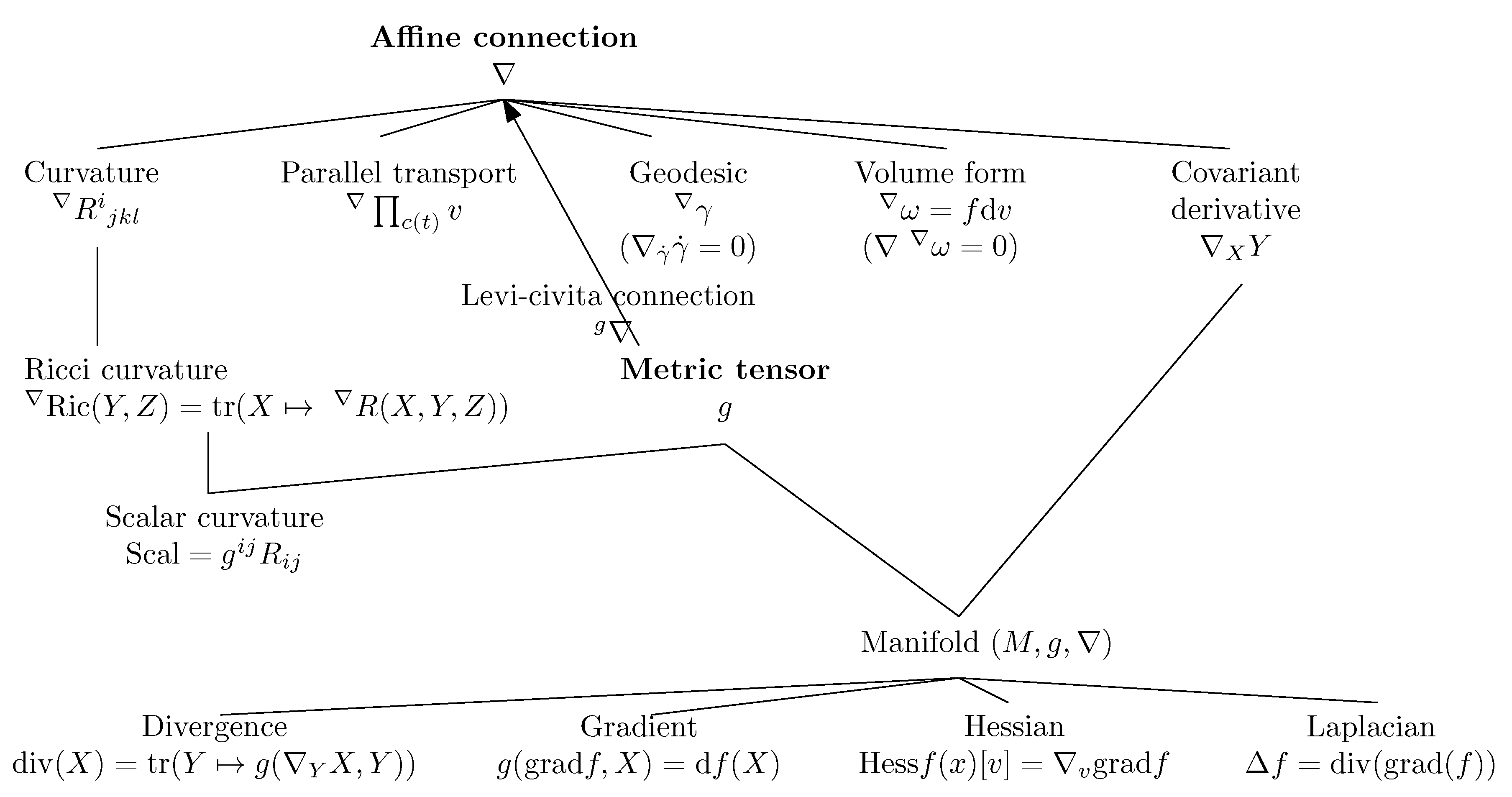
2.1. Overview of Differential Geometry: Manifold
- A metric tensor g, and
- An affine connection ∇.
- The covariant derivative operator which provides a way to calculate differentials of a vector field Y with respect to another vector field X: namely, the covariant derivative ,
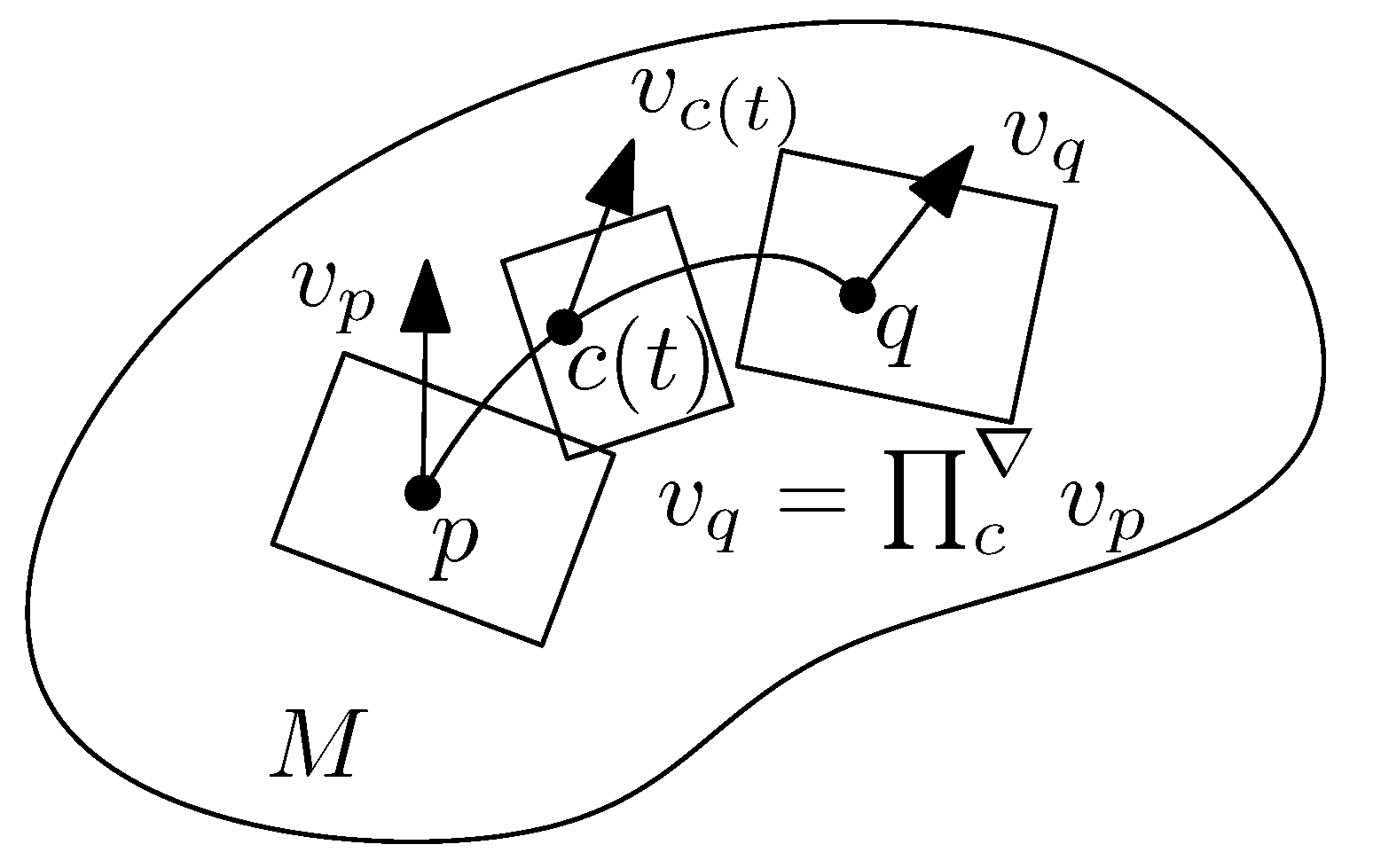
- The parallel transport which defines a way to transport vectors between tangent planes along any smooth curve c,
- The notion of ∇-geodesics which are defined as autoparallel curves, thus extending the ordinary notion of Euclidean straightness,
- The intrinsic curvature and torsion of the manifold.
2.2. Metric Tensor Fields g
2.3. Affine Connections ∇
2.3.1. Covariant Derivatives of Vector Fields
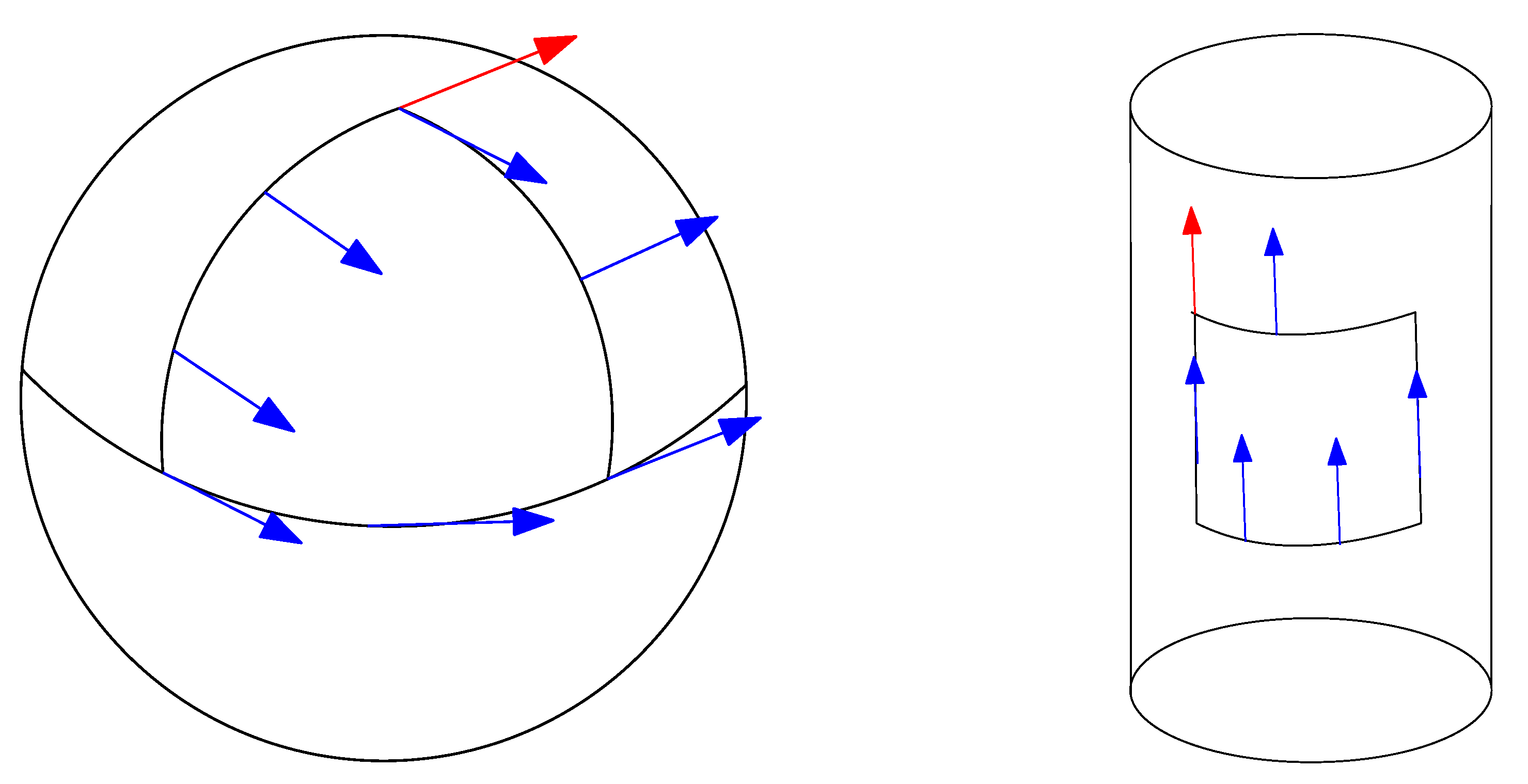
2.3.2. Parallel Transport along a Smooth Curve c
2.3.3. ∇-Geodesics : Autoparallel Curves
- Initial Value Problem (IVP): fix the conditions and for some vector .
- Boundary Value Problem (BVP): fix the geodesic extremities and .
2.3.4. Curvature and Torsion of a Manifold
2.4. The Fundamental Theorem of Riemannian Geometry: The Levi–Civita Metric Connection
2.5. Preview: Information Geometry versus Riemannian Geometry
3. Information Manifolds
3.1. Overview
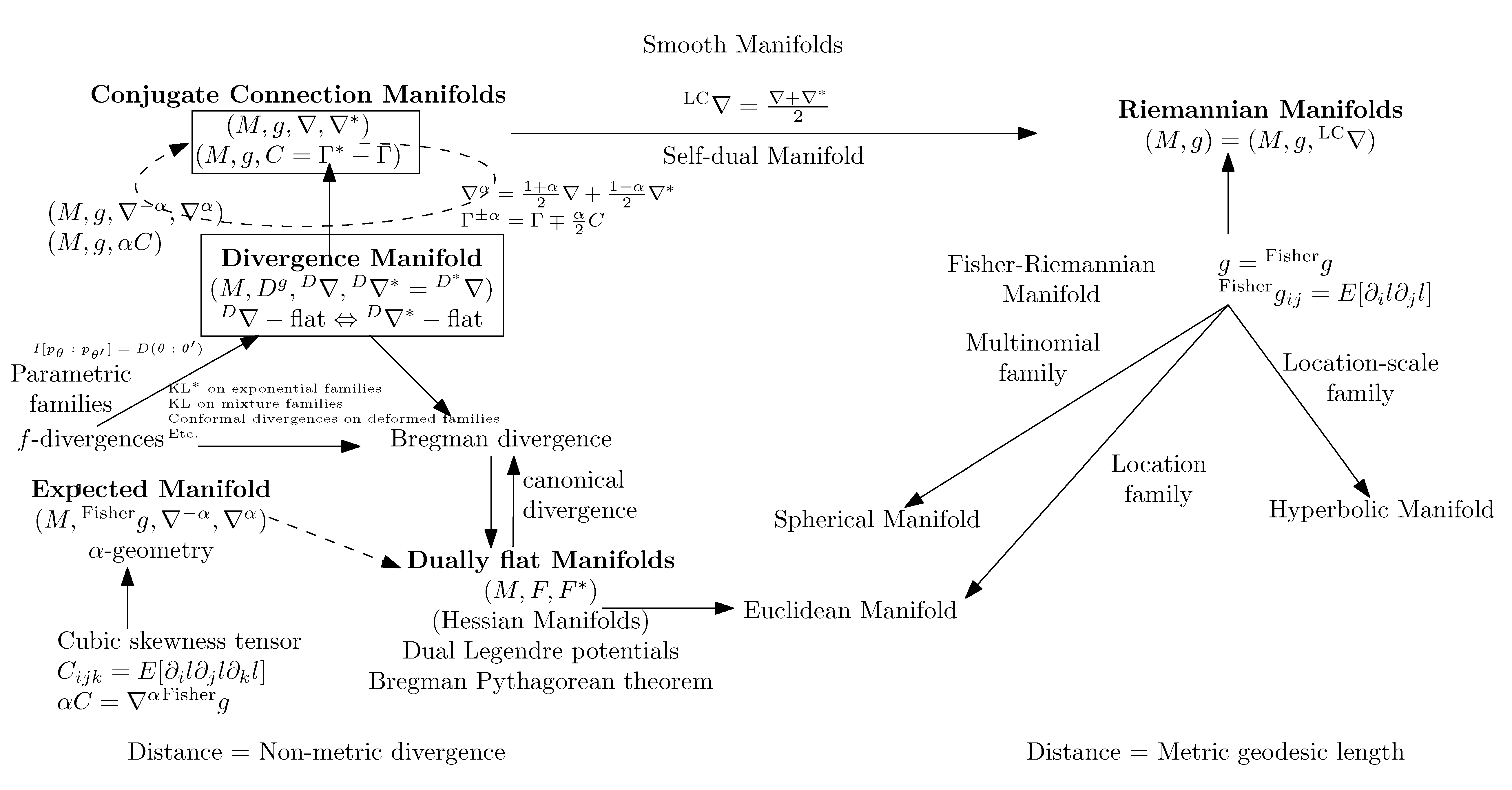
3.2. Conjugate Connection Manifolds:
3.3. Statistical Manifolds:
3.4. A Family of Conjugate Connection Manifolds
3.5. The Fundamental Theorem of Information Geometry: ∇ -Curved ⇔ -Curved
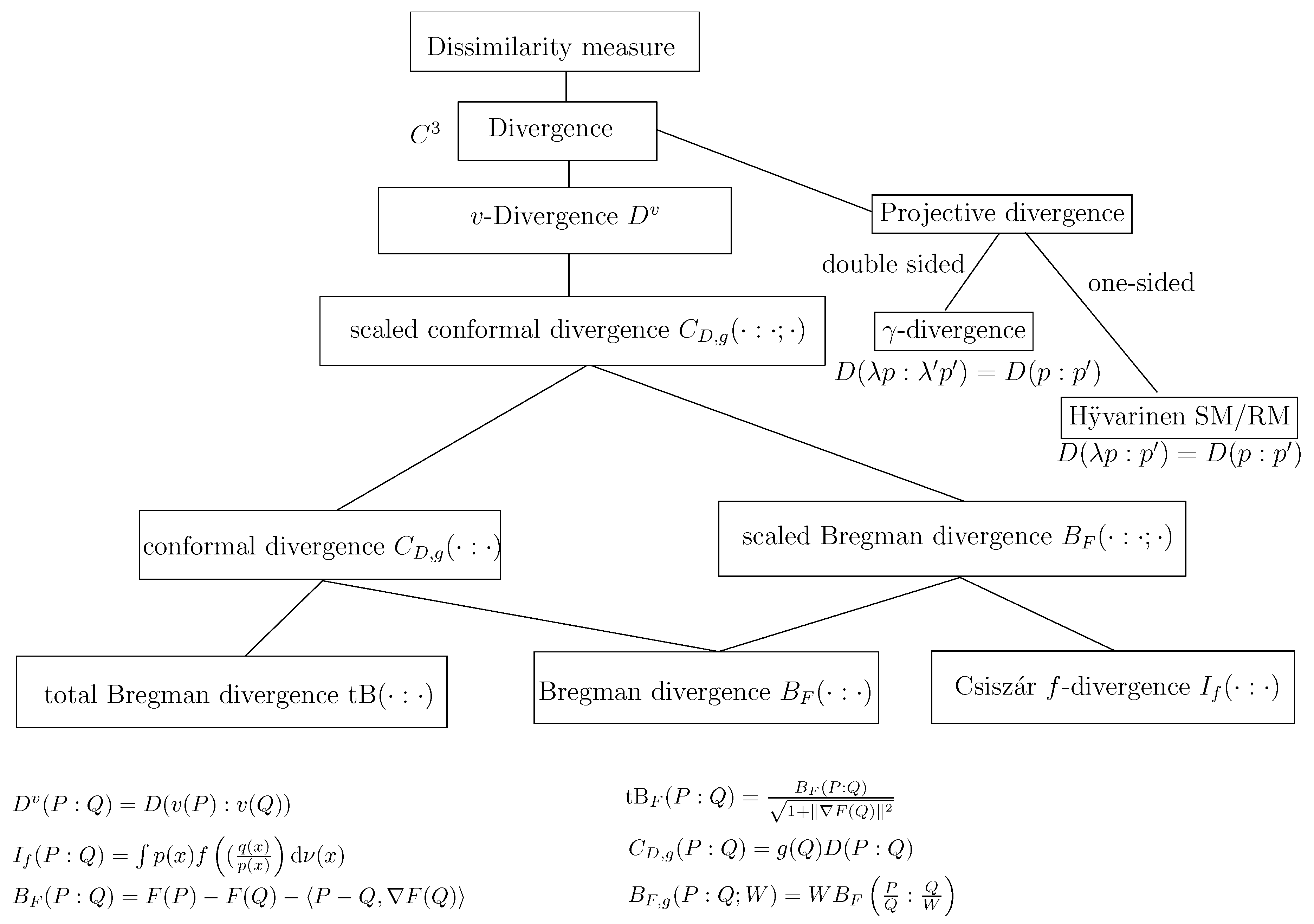
3.6. Conjugate Connections from Divergences:
- for all with equality holding iff (law of the indiscernibles),
- for all ,
- is positive-definite.
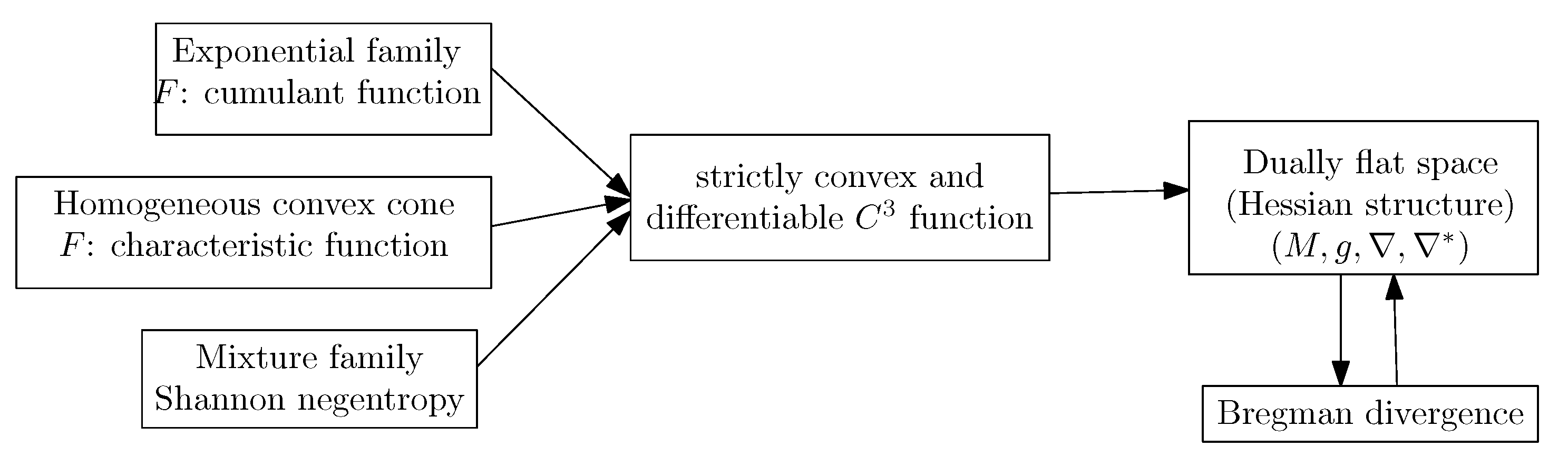
3.7. Dually Flat Manifolds (Bregman Geometry):
3.8. Hessian -Geometry: )
3.9. Expected -Manifolds of a Family of Parametric Probability Distributions:
3.10. Criteria for Statistical Invariance
- Which metric tensors g make sense in statistics?
- Which affine connections ∇ make sense in statistics?
- Which statistical divergences make sense in statistics (from which we can get the metric tensor and dual connections)?
- The family of -divergences:obtained for . The -divergences include:
- –
- The Kullback–Leibler when :for .
- –
- The reverse Kullback–Leibler :for .
- –
- The symmetric squared Hellinger divergence:for (corresponding to )
- –
- The Pearson and Neyman chi-squared divergences [62], etc.
- The Jensen–Shannon divergence:for .
- The Total Variationfor . The total variation distance is the only metric f-divergence (up to a scaling factor).
3.11. Fisher–Rao Expected Riemannian Manifolds:
- The Fisher–Riemannian manifold of the family of bivariate location-scale families amount to hyperbolic geometry (hyperbolic manifold).
- The Fisher–Riemannian manifold of the family of location families amount to Euclidean geometry (Euclidean manifold).
3.12. The Monotone -Embeddings and the Gauge Freedom of the Metric
3.13. Dually Flat Spaces and Canonical Bregman Divergences
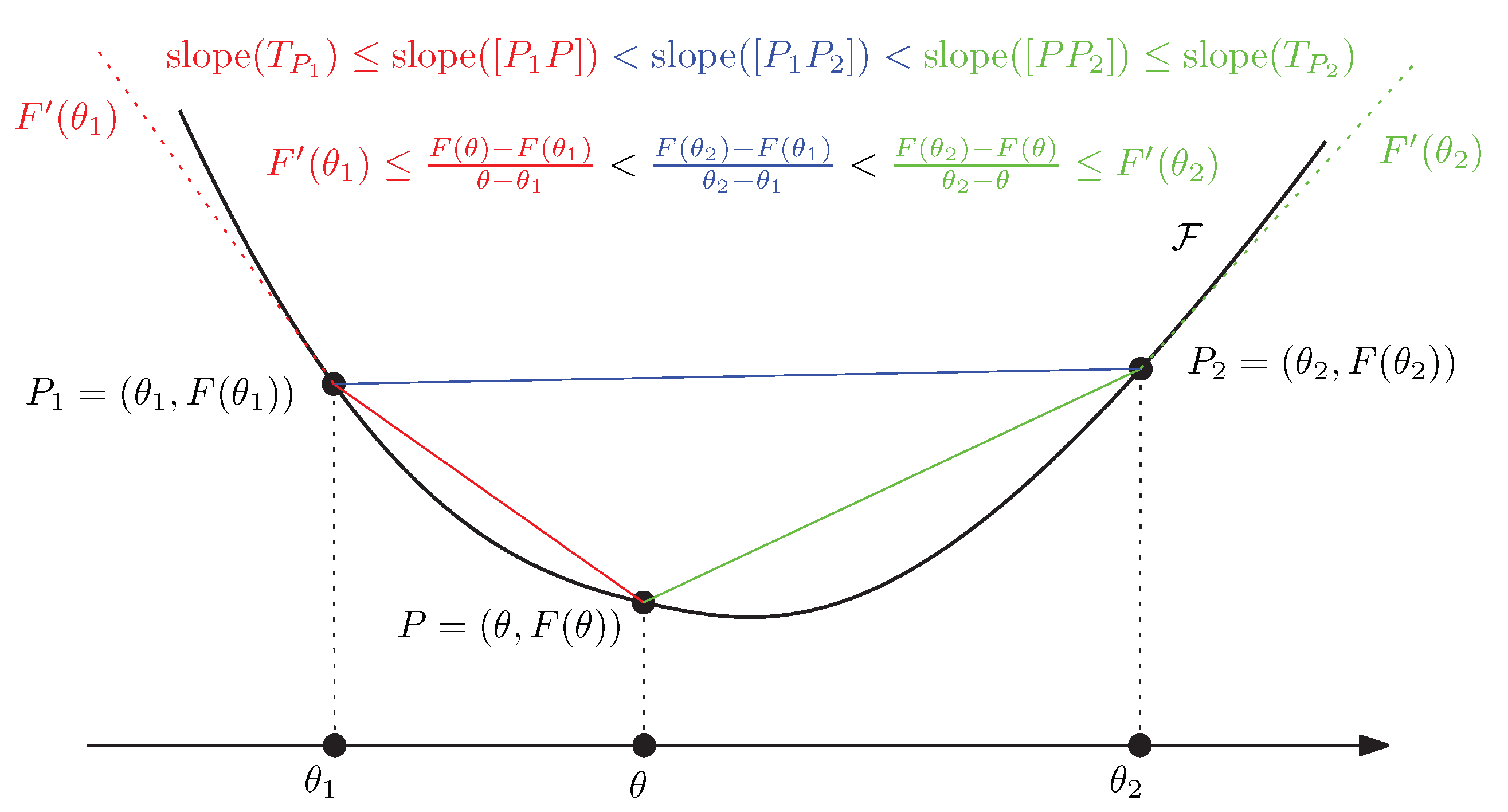
- Consider an exponential family of order D with densities defined according to a dominating measure :where the natural parameter and the sufficient statistic vector belong to . We have the integral-based Bregman generator:and the dual convex conjugatewhere denotes Shannon’s entropy.Let denotes the i-th coordinates of vector , and let us calculate the inner product of the Legendre–Fenchel divergence. We have . Using the linear property of the expectation , we find that . Moreover, we have . Thus we have:It follows that we getBy relaxing the exponential family densities and to be arbitrary densities and , we obtain the reverse KL divergence between and from the dually flat structure induced by the integral-based log-normalizer of an exponential family:Thus we have recovered the reverse Kullback–Leibler divergence from .The dual divergence is obtained by swapping the distribution parameter orders. We have:and .To summarize, the canonical Legendre–Fenchel divergence associated with the log-normalizer of an exponential family amounts to the statistical reverse Kullback–Leibler divergence between and (or the KL divergence between the swapped corresponding densities): . Notice that it is easy to check that [74,75]. Here, we took the opposite direction by constructing from .We may consider an auxiliary carrier term so that the densities write . Then the dual convex conjugate writes [76] as .Notice that since the Bregman generator is defined up to an affine term, we may consider the equivalent generator instead of the integral-based generator. This approach yields ways to build formula bypassing the explicit use of the log-normalizer for calculating various statistical distances [77].
- In this second example, we consider a mixture familywhere are linearly independent probability densities. The integral-based Bregman generator F is chosen as Shannon negentropy:We haveand the dual convex potential function isi.e., the cross-entropy between the density and the mixture . Let us calculate the inner product of the Legendre–Fenchel divergence as follows:That isThus it follows that we have the following statistical distance:Thus we have . By relaxing the mixture densities and to arbitrary densities and , we find that the dually flat geometry induced by the negentropy of densities of a mixture family induces a statistical distance which corresponds to the (forward) KL divergence. That is, we have recovered the statistical distance from . Note that in general the entropy of a mixture is not available in closed-form (because of the log sum term), except when the component distributions have pairwise disjoint supports. This latter case includes the case of Dirac distributions whose mixtures represent the categorical distributions.
- Base measure: where μ is the counting measure and represents an auxiliary measure carrier term for defining the base measure ν,
- Sufficient statistics: ,
- Natural parameter: ,
- Log-normalizer: since .
- Natural parameters: with with source parameter ,
- Sufficient statistics: ,
- Log-normalizer: ,
- Dual parameterization: , where denotes the digamma function.
4. Some Applications of Information Geometry
- Statistics: Asymptotic inference, Expectation-Maximization (EM and the novel information-geometric em), time series (AutoRegressive Moving Average model, ARMA) models,
- Signal processing: Principal Component Analysis (PCA), Independent Component Analysis (ICA), Non-negative Matrix Factorization (NMF),
- Mathematical programming: Barrier function of interior point methods,
- Game theory: Score functions.
4.1. Natural Gradient in Riemannian Space
4.1.1. The Vanilla Gradient Descent Method
4.1.2. Natural Gradient and Its Connection with the Riemannian Gradient
4.1.3. Natural Gradient in Dually Flat Spaces: Connections to Bregman Mirror Descent and Ordinary Gradient
4.1.4. An Application of the Natural Gradient: Natural Evolution Strategies (NESs)
4.2. Some Illustrating Applications of Dually Flat Manifolds
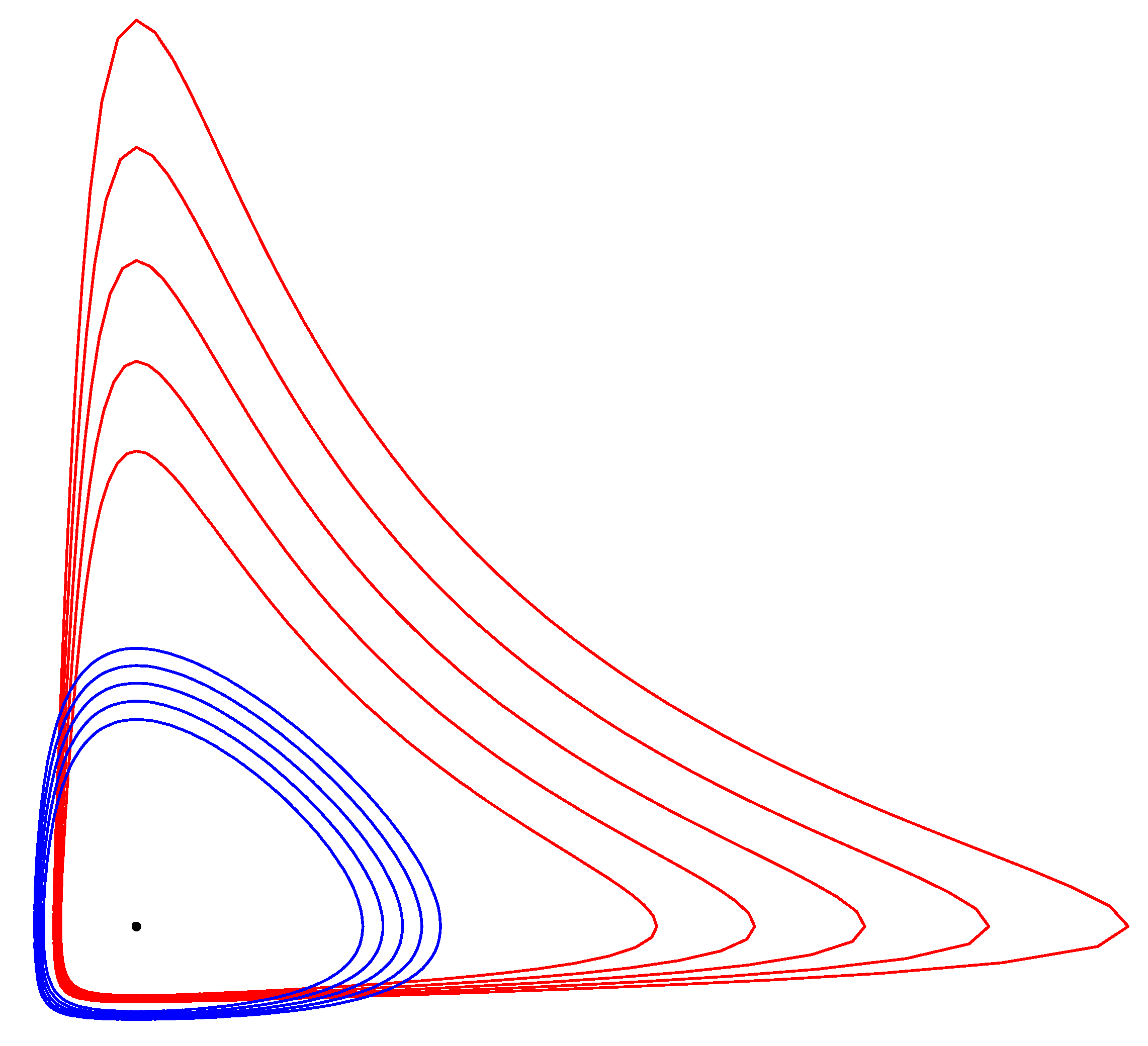
4.3. Hypothesis Testing in the Dually Flat Exponential Family Manifold
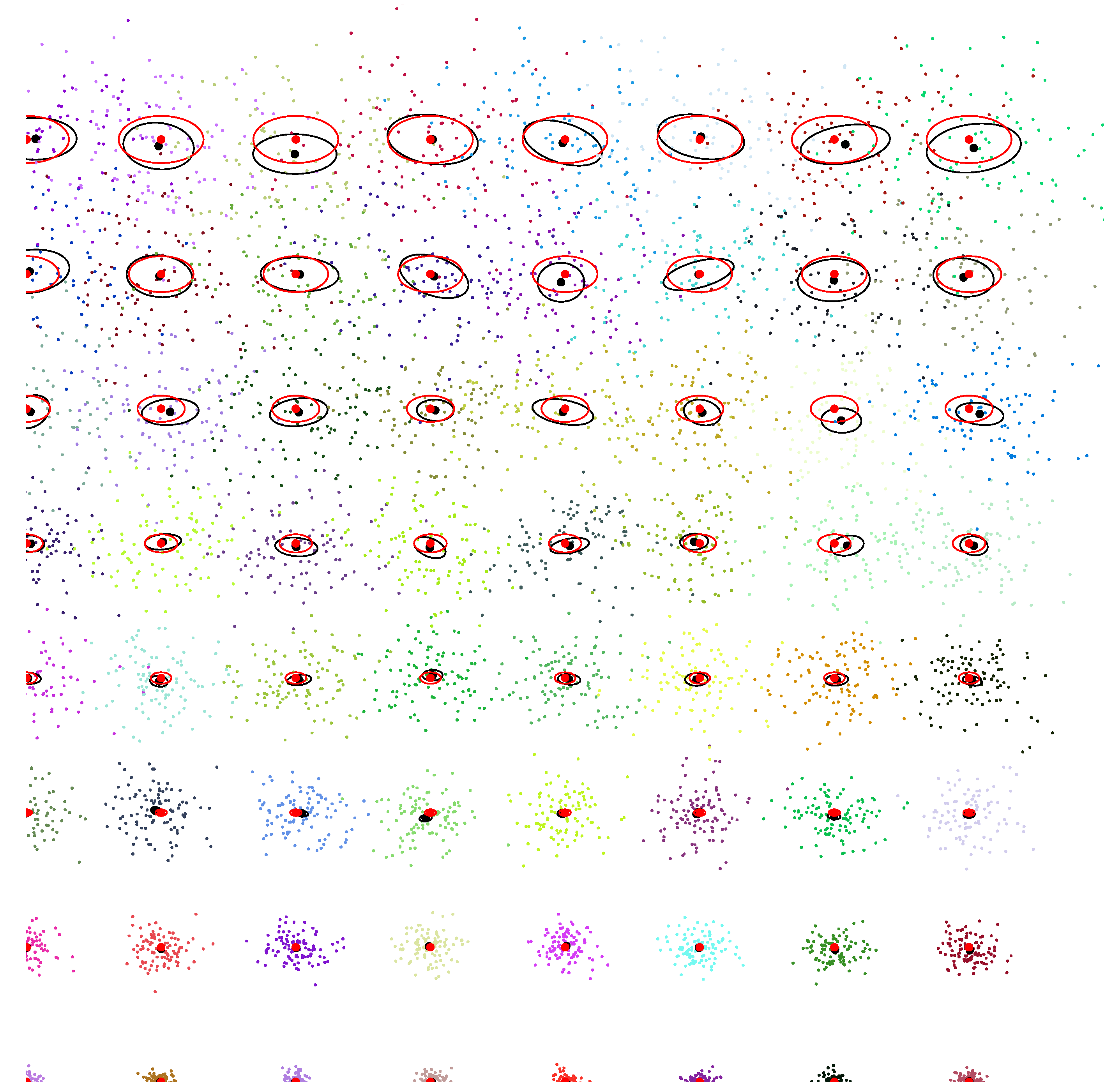
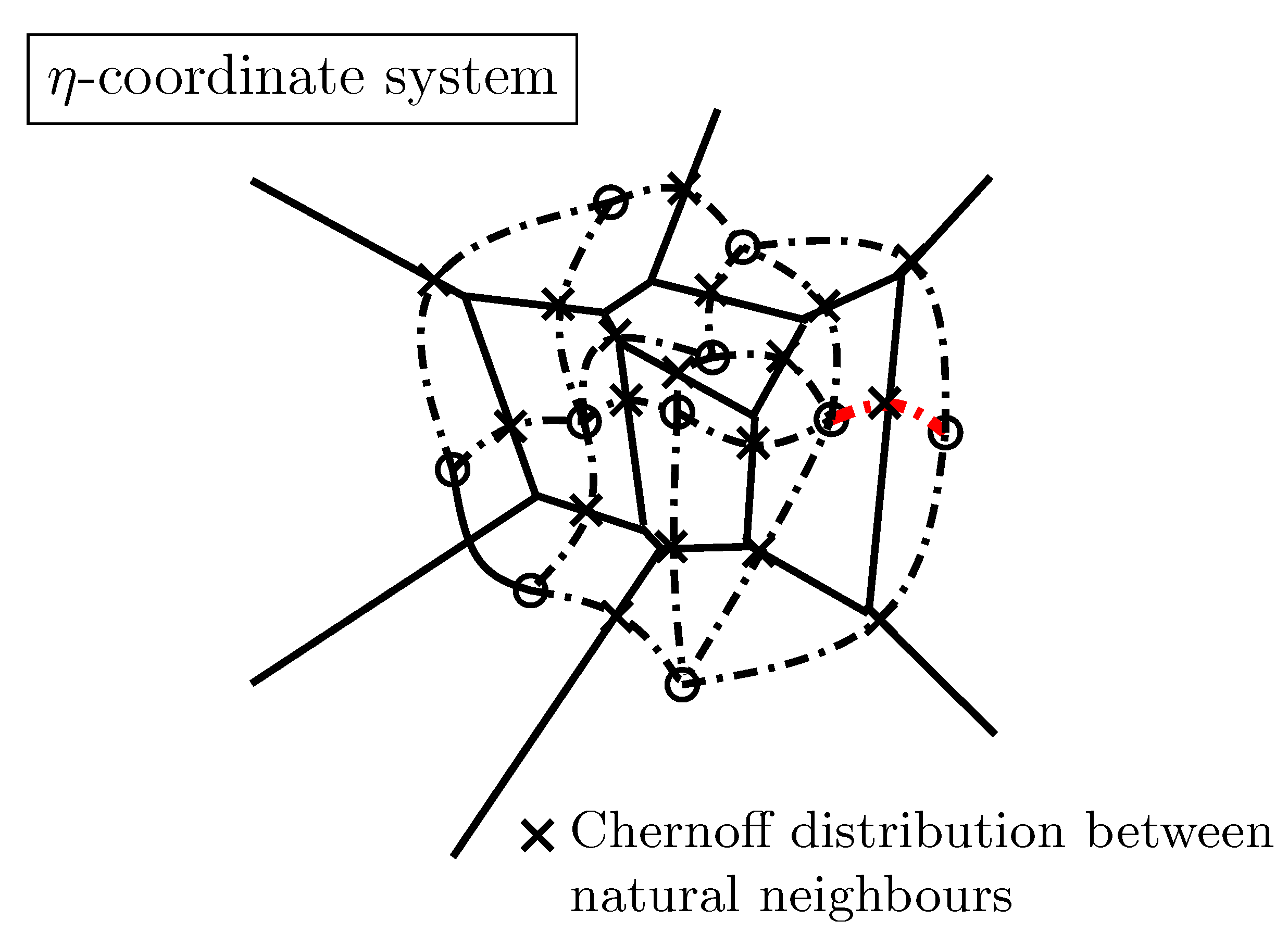
4.4. Clustering Mixtures in the Dually Flat Mixture Family Manifold
5. Conclusions: Summary, Historical Background, and Perspectives
5.1. Summary
5.2. A Brief Historical Review of Information Geometry
| Riemannian manifold | |
| Fisher–Riemannian (expected) Riemannian manifold | |
| Riemannian manifold with affine connection ∇ | |
| Chentsov’s manifold with affine exponential -connection | |
| Amari’s dualistic information manifold | |
| Amari’s (expected) information -manifold, -geometry | |
| Lauritzen’s statistical manifold [29] | |
| Eguchi’s conjugate connection manifold induced by divergence D | |
| Chentsov/Amari’s dually flat manifold induced by convex potential F |
5.3. Perspectives
Funding
Acknowledgments
Conflicts of Interest
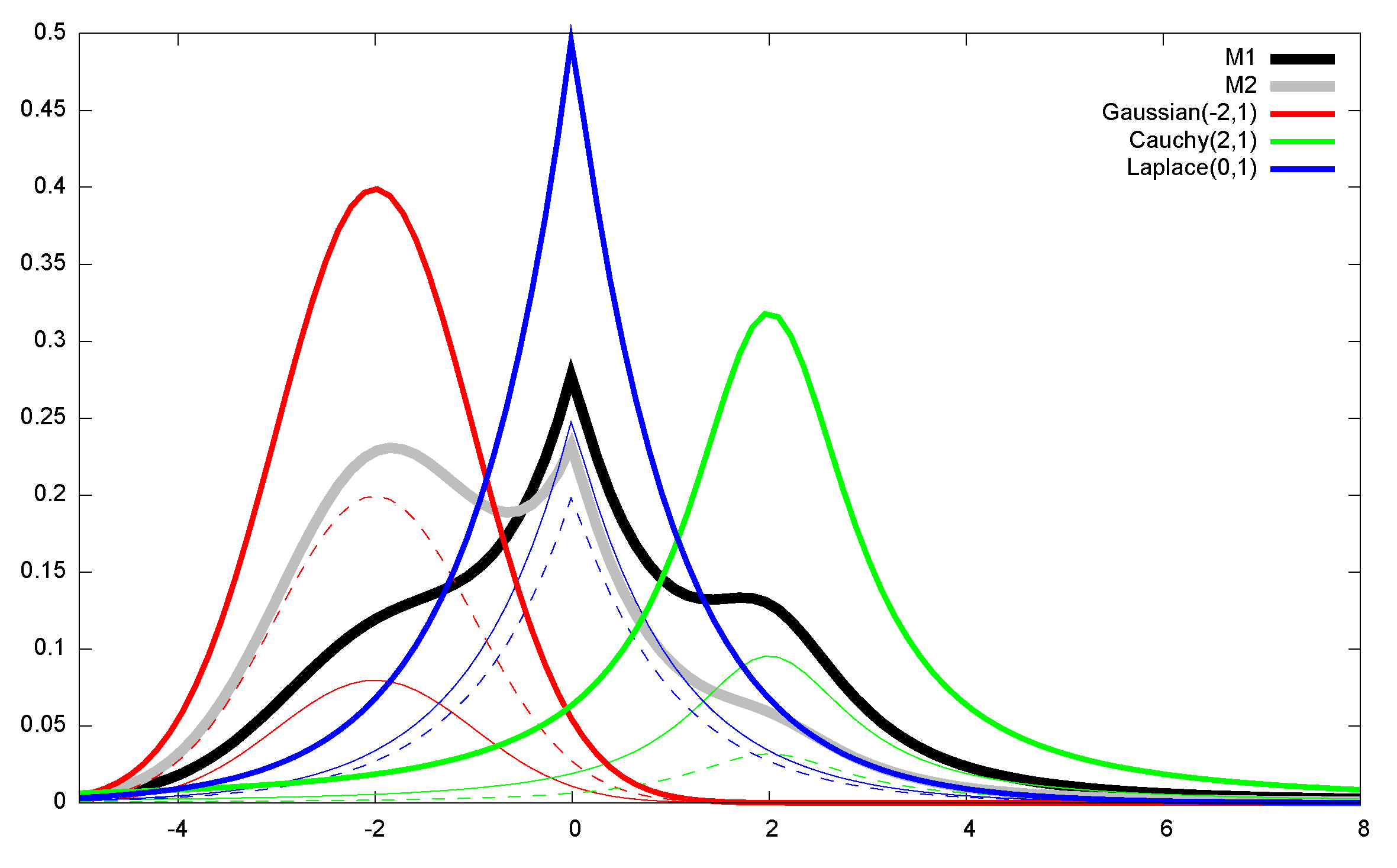
Appendix A. Monte Carlo Estimations of f-Divergences
Appendix B. The Multivariate Gaussian Family: An Exponential Family
Appendix C. Skew Jensen Divergences and Bregman Divergences
Notations
| inner product | |
| Mahalanobis distance , | |
| parameter divergence | |
| statistical divergence | |
| D, | Divergence and dual (reverse) divergence |
| Csiszár divergence | with |
| Bregman divergence | |
| Canonical divergence | |
| Bhattacharyya distance | |
| Jensen/Burbea-Rao divergence | |
| Chernoff information | |
| F, | Potential functions related by Legendre–Fenchel transformation |
| Riemannian distance | |
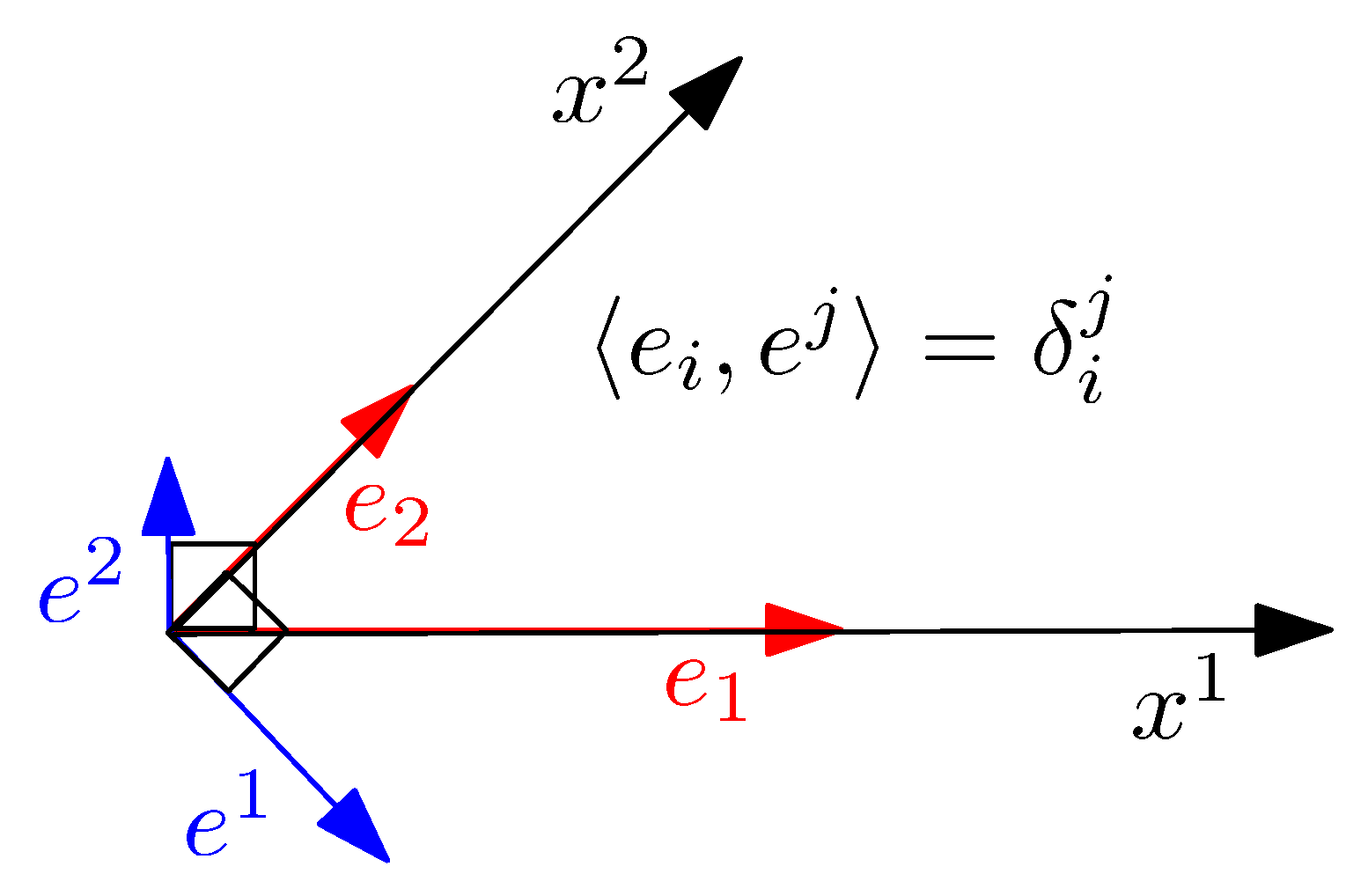
| B, | basis, reciprocal basis |
| natural basis | |
| covector basis (one-forms) | |
| contravariant components of vector v | |
| covariant components of vector v | |
| vector u is perpendicular to vector v () | |
| induced norm, length of a vector v | |
| M, S | Manifold, submanifold |
| tangent plane at p | |
| Tangent bundle | |
| space of smooth functions on M | |
| space of smooth vector fields on M | |
| direction derivative of f with respect to vector v | |
| Vector fields | |
| metric tensor (field) | |
| local coordinates x in a chat | |
| natural basis vector | |
| natural reciprocal basis vector | |
| ∇ | affine connection |
| covariant derivative | |
| parallel transport of vectors along a smooth curve c | |
| Parallel transport of along a smooth curve c | |
| , | geodesic, geodesic with respect to connection ∇ |
| Christoffel symbols of the first kind (functions) | |
| Christoffel symbols of the second kind (functions) | |
| R | Riemann–Christoffel curvature tensor |
| Lie bracket | |
| ∇-projection | |
| -projection | |
| C | Amari–Chentsov totally symmetric cubic 3-covariant tensor |
| parametric family of probability distributions | |
| exponential family, mixture family, probability simplex | |
| Fisher information matrix of family | |
| Fisher Information Matrix (FIM) for a parametric family | |
| Fisher information metric tensor field | |
| exponential connection | |
| mixture connection | |
| expected skewness tensor | |
| expected -connections | |
| ≡ | equivalence of geometric structures |
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Amari, S. Information Geometry and Its Applications; Applied Mathematical Sciences; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Kakihara, S.; Ohara, A.; Tsuchiya, T. Information Geometry and Interior-Point Algorithms in Semidefinite Programs and Symmetric Cone Programs. J. Optim. Theory Appl. 2013, 157, 749–780. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RL, USA, 2007. [Google Scholar]
- Peirce, C.S. Chance, Love, and Logic: Philosophical Essays; U of Nebraska Press: Lincoln, NE, USA, 1998. [Google Scholar]
- Schurz, G. Patterns of abduction. Synthese 2008, 164, 201–234. [Google Scholar] [CrossRef]
- Wald, A. Statistical decision functions. Ann. Math. Stat. 1949, 165–205. [Google Scholar] [CrossRef]
- Wald, A. Statistical Decision Functions; Wiley: Chichester, UK, 1950. [Google Scholar]
- Dabak, A.G. A Geometry for Detection Theory. Ph.D. Thesis, Rice University, Houston, TX, USA, 1993. [Google Scholar]
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces; Courier Dover Publications: New York, NY, USA, 2016. [Google Scholar]
- Amari, S.; Barndorff-Nielsen, O.E.; Kass, R.E.; Lauritzen, S.L.; Rao, C.R. Differential Geometry in Statistical Inference; Institute of Mathematical Statistics: Hayward, CA, USA, 1987. [Google Scholar]
- Dodson, C.T.J. (Ed.) Geometrization of Statistical Theory; ULDM Publications; University of Lancaster, Department of Mathematics: Bailrigg, UK, 1987. [Google Scholar]
- Murray, M.; Rice, J. Differential Geometry and Statistics; Number 48 in Monographs on Statistics and Applied Probability; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Kass, R.E.; Vos, P.W. Geometrical Foundations of Asymptotic Inference; Wiley-Interscience: New York, NY, USA, 1997. [Google Scholar]
- Arwini, K.A.; Dodson, C.T.J. Information Geometry: Near Randomness and Near Independance; Springer: Berlin, Germany, 2008. [Google Scholar]
- Calin, O.; Udriste, C. Geometric Modeling in Probability and Statistics; Mathematics and Statistics, Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Ay, N.; Jost, J.; Vân Lê, H.; Schwachhöfer, L. Information Geometry; Springer: Berlin, Germany, 2017; Volume 64. [Google Scholar]
- Corcuera, J.; Giummolè, F. A characterization of monotone and regular divergences. Ann. Inst. Stat. Math. 1998, 50, 433–450. [Google Scholar] [CrossRef]
- Mühlich, U. Fundamentals of Tensor Calculus for Engineers with a Primer on Smooth Manifolds; Springer: Berlin, Germany, 2017; Volume 230. [Google Scholar]
- Nielsen, F.; Nock, R. Hyperbolic Voronoi diagrams made easy. In Proceedings of the IEEE International Conference on Computational Science and Its Applications (ICCSA), Fukuoka, Japan, 23–26 March 2010; pp. 74–80. [Google Scholar]
- Whitney, H.; Eells, J.; Toledo, D. Collected Papers of Hassler Whitney; Nelson Thornes: London, UK, 1992. [Google Scholar]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Cartan, E.J. On Manifolds with an Affine Connection and the Theory of General Relativity; Bibliopolis; Humanities Pr: London, UK, 1986. [Google Scholar]
- Akivis, M.A.; Rosenfeld, B.A. Élie Cartan (1869–1951); American Mathematical Society: Cambridge, MA, USA, 2011; Volume 123. [Google Scholar]
- Wanas, M. Absolute parallelism geometry: Developments, applications and problems. arXiv 2002, arXiv:gr-qc/0209050. [Google Scholar]
- Bourguignon, J.P. Ricci curvature and measures. Jpn. J. Math. 2009, 4, 27–45. [Google Scholar] [CrossRef]
- Baez, J.C.; Wise, D.K. Teleparallel gravity as a higher gauge theory. Commun. Math. Phys. 2015, 333, 153–186. [Google Scholar] [CrossRef]
- Ashburner, J.; Friston, K.J. Diffeomorphic registration using geodesic shooting and Gauss-Newton optimisation. NeuroImage 2011, 55, 954–967. [Google Scholar] [CrossRef]
- Lauritzen, S.L. Statistical manifolds. Differ. Geom. Stat. Inference 1987, 10, 163–216. [Google Scholar]
- Vân Lê, H. Statistical manifolds are statistical models. J. Geom. 2006, 84, 83–93. [Google Scholar]
- Furuhata, H. Hypersurfaces in statistical manifolds. Differ. Geom. Its Appl. 2009, 27, 420–429. [Google Scholar] [CrossRef]
- Zhang, J. Divergence functions and geometric structures they induce on a manifold. In Geometric Theory of Information; Nielsen, F., Ed.; Springer: Berlin, Germany, 2014; pp. 1–30. [Google Scholar]
- Eguchi, S. Second order efficiency of minimum contrast estimators in a curved exponential family. Ann. Stat. 1983, 11, 793–803. [Google Scholar] [CrossRef]
- Eguchi, S. A differential geometric approach to statistical inference on the basis of contrast functionals. Hiroshima Math. J. 1985, 15, 341–391. [Google Scholar] [CrossRef]
- Hiriart-Urruty, J.B.; Lemaréchal, C. Fundamentals of Convex Analysis; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Crouzeix, J.P. A relationship between the second derivatives of a convex function and of its conjugate. Math. Program. 1977, 13, 364–365. [Google Scholar] [CrossRef]
- Ay, N.; Amari, S. A novel approach to canonical divergences within information geometry. Entropy 2015, 17, 8111–8129. [Google Scholar] [CrossRef]
- Nielsen, F. What is ... an information projection? Not. AMS 2018, 65, 321–324. [Google Scholar] [CrossRef]
- Kurose, T. On the divergences of 1-conformally flat statistical manifolds. Tohoku Math. J. Second Ser. 1994, 46, 427–433. [Google Scholar] [CrossRef]
- Boissonnat, J.D.; Nielsen, F.; Nock, R. Bregman Voronoi diagrams. Discret. Comput. Geom. 2010, 44, 281–307. [Google Scholar] [CrossRef]
- Nielsen, F.; Piro, P.; Barlaud, M. Bregman vantage point trees for efficient nearest neighbor queries. In Proceedings of the 2009 IEEE International Conference on Multimedia and Expo, New York, NY, USA, 28 June–3 July 2009; pp. 878–881. [Google Scholar]
- Nielsen, F.; Boissonnat, J.D.; Nock, R. Visualizing Bregman Voronoi diagrams. In Proceedings of the Twenty-Third Annual Symposium on Computational Geometry, Gyeongju, Korea, 6–8 June 2007; pp. 121–122. [Google Scholar]
- Nock, R.; Nielsen, F. Fitting the smallest enclosing Bregman ball. In Proceedings of the European Conference on Machine Learning, Porto, Portugal, 3–7 October 2005; Springer: Berlin, Germany, 2005; pp. 649–656. [Google Scholar]
- Nielsen, F.; Nock, R. On the smallest enclosing information disk. Inf. Process. Lett. 2008, 105, 93–97. [Google Scholar] [CrossRef]
- Fischer, K.; Gärtner, B.; Kutz, M. Fast smallest-enclosing-ball computation in high dimensions. In Proceedings of the European Symposium on Algorithms, Budapest, Hungary, 16–19 September 2003; Springer: Berlin, Germany, 2003; pp. 630–641. [Google Scholar]
- Della Pietra, S.; Della Pietra, V.; Lafferty, J. Inducing features of random fields. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 380–393. [Google Scholar] [CrossRef]
- Nielsen, F. On Voronoi Diagrams on the Information-Geometric Cauchy Manifolds. Entropy 2020, 22, 713. [Google Scholar] [CrossRef]
- Shima, H. The Geometry of Hessian Structures; World Scientific: New Jersey, NJ, USA, 2007. [Google Scholar]
- Zhang, J. Reference duality and representation duality in information geometry. AIP Conf. Proc. 2015, 1641, 130–146. [Google Scholar]
- Gomes-Gonçalves, E.; Gzyl, H.; Nielsen, F. Geometry and Fixed-Rate Quantization in Riemannian Metric Spaces Induced by Separable Bregman Divergences. In Proceedings of the 4th International Conference on Geometric Science of Information (GSI), Toulouse, France, 27–29 August 2019; Nielsen, F., Barbaresco, F., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2019; Volume 11712, pp. 351–358. [Google Scholar] [CrossRef]
- Nielsen, F. Cramér-Rao lower bound and information geometry. In Connected at Infinity II; Springer: Berlin, Germany, 2013; pp. 18–37. [Google Scholar]
- Nielsen, F.; Garcia, V. Statistical exponential families: A digest with flash cards. arXiv 2009, arXiv:0911.4863. [Google Scholar]
- Sato, Y.; Sugawa, K.; Kawaguchi, M. The geometrical structure of the parameter space of the two-dimensional normal distribution. Rep. Math. Phys. 1979, 16, 111–119. [Google Scholar] [CrossRef]
- Skovgaard, L.T. A Riemannian geometry of the multivariate normal model. Scand. J. Stat. 1984, 11, 211–223. [Google Scholar]
- Malagò, L.; Pistone, G. Information geometry of the Gaussian distribution in view of stochastic optimization. In Proceedings of the 2015 ACM Conference on Foundations of Genetic Algorithms XIII, Aberystwyth, UK, 17–20 January 2015; pp. 150–162. [Google Scholar]
- Nielsen, F.; Nock, R. On the geometry of mixtures of prescribed distributions. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2861–2865. [Google Scholar]
- Campbell, L.L. An extended Čencov characterization of the information metric. Proc. Am. Math. Soc. 1986, 98, 135–141. [Google Scholar]
- Vân Lê, H. The uniqueness of the Fisher metric as information metric. Ann. Inst. Stat. Math. 2017, 69, 879–896. [Google Scholar]
- Csiszár, I.; Shields, P.C. Information Theory and Statistics: A Tutorial; Foundations and Trends® in Communications and Information Theory; Now Publishers Inc.: Hanover, MA, USA, 2004; Volume 1, pp. 417–528. [Google Scholar]
- Jiao, J.; Courtade, T.A.; No, A.; Venkat, K.; Weissman, T. Information measures: The curious case of the binary alphabet. IEEE Trans. Inf. Theory 2014, 60, 7616–7626. [Google Scholar] [CrossRef]
- Qiao, Y.; Minematsu, N. A Study on Invariance of f-Divergence and Its Application to Speech Recognition. IEEE Trans. Signal Process. 2010, 58, 3884–3890. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. On the chi square and higher-order chi distances for approximating f-divergences. IEEE Signal Process. Lett. 2013, 21, 10–13. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observation. Stud. Sci. Math. Hung. 1967, 2, 229–318. [Google Scholar]
- Mitchell, A.F.S. Statistical manifolds of univariate elliptic distributions. Int. Stat. Rev. 1988, 56, 1–16. [Google Scholar] [CrossRef]
- Hotelling, H. Spaces of statistical parameters. Bull. Am. Math. Soc. (AMS) 1930, 36, 191. [Google Scholar]
- Rao, R.C. Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Komaki, F. Bayesian prediction based on a class of shrinkage priors for location-scale models. Ann. Inst. Stat. Math. 2007, 59, 135–146. [Google Scholar] [CrossRef]
- Stigler, S.M. The epic story of maximum likelihood. Stat. Sci. 2007, 22, 598–620. [Google Scholar] [CrossRef]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. In Breakthroughs in Statistics; Springer: Berlin, Germany, 1992; pp. 235–247. [Google Scholar]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. A 1946, 186, 453–461. [Google Scholar]
- Zhang, J. On monotone embedding in information geometry. Entropy 2015, 17, 4485–4499. [Google Scholar] [CrossRef]
- Naudts, J.; Zhang, J. Rho–tau embedding and gauge freedom in information geometry. Inf. Geom. 2018. [Google Scholar] [CrossRef]
- Nock, R.; Nielsen, F.; Amari, S. On Conformal Divergences and Their Population Minimizers. IEEE TIT 2016, 62, 527–538. [Google Scholar] [CrossRef]
- Azoury, K.S.; Warmuth, M.K. Relative loss bounds for on-line density estimation with the exponential family of distributions. Mach. Learn. 2001, 43, 211–246. [Google Scholar] [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Nielsen, F.; Nock, R. Entropies and cross-entropies of exponential families. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3621–3624. [Google Scholar]
- Nielsen, F.; Nock, R. Cumulant-free closed-form formulas for some common (dis)similarities between densities of an exponential family. Tech. Rep. 2020. [Google Scholar] [CrossRef]
- Amari, S. Differential geometry of a parametric family of invertible linear systems: Riemannian metric, dual affine connections, and divergence. Math. Syst. Theory 1987, 20, 53–82. [Google Scholar] [CrossRef]
- Schwander, O.; Nielsen, F. Fast learning of Gamma mixture models with k-MLE. In Proceedings of the International Workshop on Similarity-Based Pattern Recognition, York, UK, 3–5 July 2013; Springer: Berlin, Germany, 2013; pp. 235–249. [Google Scholar]
- Miura, K. An introduction to maximum likelihood estimation and information geometry. Interdiscip. Inf. Sci. 2011, 17, 155–174. [Google Scholar] [CrossRef]
- Reverter, F.; Oller, J.M. Computing the Rao distance for Gamma distributions. J. Comput. Appl. Math. 2003, 157, 155–167. [Google Scholar] [CrossRef]
- Pinele, J.; Strapasson, J.E.; Costa, S.I. The Fisher-Rao Distance between Multivariate Normal Distributions: Special Cases, Bounds and Applications. Entropy 2020, 22, 404. [Google Scholar] [CrossRef]
- Nielsen, F. Pattern learning and recognition on statistical manifolds: An information-geometric review. In Proceedings of the International Workshop on Similarity-Based Pattern Recognition, York, UK, 3–5 July 2013; Springer: Berlin, Germany, 2013; pp. 1–25. [Google Scholar]
- Sun, K.; Nielsen, F. Lightlike Neuromanifolds, Occam’s Razor and Deep Learning. arXiv 2019, arXiv:1905.11027. [Google Scholar]
- Sun, K.; Nielsen, F. Relative Fisher Information and Natural Gradient for Learning Large Modular Models. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 3289–3298. [Google Scholar]
- Amari, S. Natural gradient works efficiently in learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Cauchy, A. Methode générale pour la résolution des systèmes d’équations simultanées. C. R. l’Académie Sci. 1847, 25, 536–538. [Google Scholar]
- Curry, H.B. The method of steepest descent for non-linear minimization problems. Q. Appl. Math. 1944, 2, 258–261. [Google Scholar] [CrossRef]
- Bonnabel, S. Stochastic gradient descent on Riemannian manifolds. IEEE Trans. Autom. Control 2013, 58, 2217–2229. [Google Scholar] [CrossRef]
- Nielsen, F. On geodesic triangles with right angles in a dually flat space. arXiv 2019, arXiv:1910.03935. [Google Scholar]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Nielsen, F.; Hadjeres, G. Monte Carlo information-geometric structures. In Geometric Structures of Information; Springer: Berlin, Germany, 2019; pp. 69–103. [Google Scholar]
- Nielsen, F. Legendre Transformation and Information Geometry; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Raskutti, G.; Mukherjee, S. The information geometry of mirror descent. IEEE Trans. Inf. Theory 2015, 61, 1451–1457. [Google Scholar] [CrossRef]
- Bubeck, S. Convex Optimization: Algorithms and Complexity; Foundations and Trends® in Machine Learning: Hanover, MA, USA, 2015; Volume 8, pp. 231–357. [Google Scholar]
- Zhang, G.; Sun, S.; Duvenaud, D.; Grosse, R. Noisy natural gradient as variational inference. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5852–5861. [Google Scholar]
- Beyer, H.G.; Schwefel, H.P. Evolution strategies–A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Berny, A. Selection and reinforcement learning for combinatorial optimization. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; Springer: Berlin, Germany, 2000; pp. 601–610. [Google Scholar]
- Wierstra, D.; Schaul, T.; Glasmachers, T.; Sun, Y.; Peters, J.; Schmidhuber, J. Natural evolution strategies. J. Mach. Learn. Res. 2014, 15, 949–980. [Google Scholar]
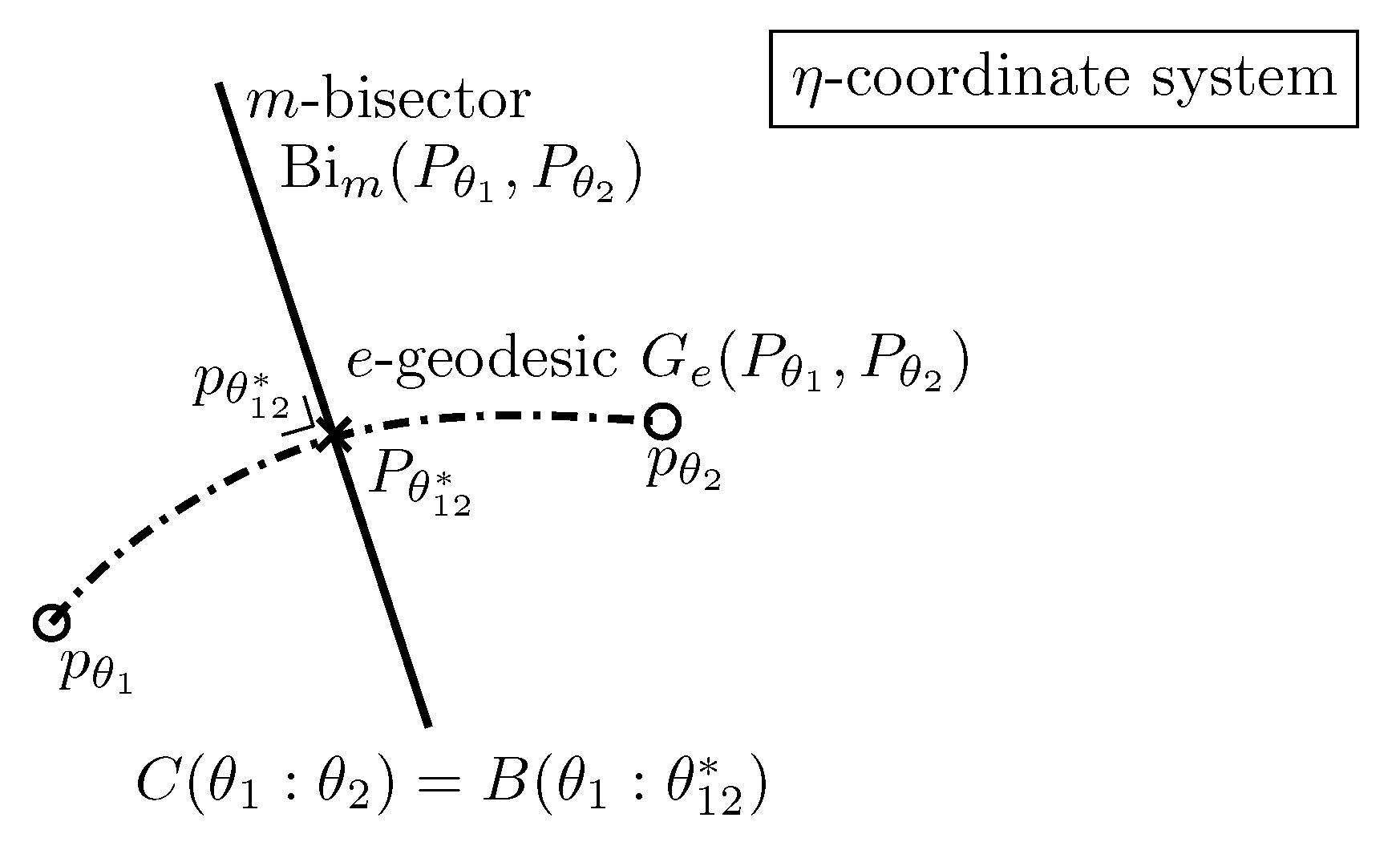
- Nielsen, F. An Information-Geometric Characterization of Chernoff Information. IEEE Sig. Proc. Lett. 2013, 20, 269–272. [Google Scholar] [CrossRef]
- Pham, G.; Boyer, R.; Nielsen, F. Computational Information Geometry for Binary Classification of High-Dimensional Random Tensors. Entropy 2018, 20, 203. [Google Scholar] [CrossRef]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Nielsen, F. Chernoff Information of Exponential Families. arXiv 2011, arXiv:1102.2684. [Google Scholar]
- Nielsen, F. Generalized Bhattacharyya and Chernoff upper bounds on Bayes error using quasi-arithmetic means. Pattern Recognit. Lett. 2014, 42, 25–34. [Google Scholar] [CrossRef][Green Version]
- Nielsen, F. Hypothesis Testing, Information Divergence and Computational Geometry. In Proceedings of the International Conference on Geometric Science of Information Geometric Science of Information (GSI), Paris, France, 28–30 August 2013; pp. 241–248. [Google Scholar]
- Nielsen, F.; Sun, K. Guaranteed Bounds on Information-Theoretic Measures of Univariate Mixtures Using Piecewise Log-Sum-Exp Inequalities. Entropy 2016, 18, 442. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Sided and symmetrized Bregman centroids. IEEE Trans. Inf. Theory 2009, 55, 2882–2904. [Google Scholar] [CrossRef]
- Nielsen, F.; Hadjeres, G. Monte Carlo Information Geometry: The dually flat case. arXiv 2018, arXiv:1803.07225. [Google Scholar]
- Ohara, A.; Tsuchiya, T. An Information Geometric Approach to Polynomial-Time Interior-Point Algorithms: Complexity Bound via Curvature Integral; Research Memorandum; The Institute of Statistical Mathematics: Tokyo, Japan, 2007; Volume 1055. [Google Scholar]
- Fuglede, B.; Topsøe, F. Jensen-Shannon divergence and Hilbert space embedding. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Chicago, IL, USA, 27 June–2 July 2004; p. 31. [Google Scholar]
- Vajda, I. On metric divergences of probability measures. Kybernetika 2009, 45, 885–900. [Google Scholar]
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin, Germany, 2008; Volume 338. [Google Scholar]
- Dowson, D.C.; Landau, B.V. The Fréchet distance between multivariate normal distributions. J. Multivar. Anal. 1982, 12, 450–455. [Google Scholar] [CrossRef]
- Takatsu, A. Wasserstein geometry of Gaussian measures. Osaka J. Math. 2011, 48, 1005–1026. [Google Scholar]
- Chentsov, N.N. Statistical Decision Rules and Optimal Inference; Monographs; American Mathematical Society: Providence, RI, USA, 1982. [Google Scholar]
- Amari, S. Differential-Geometrical Methods in Statistics; Lecture Notes on Statistics; Second Edition in 1990; Springer: New York, NY, USA, 1985; Volume 28. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Jouhou kika no Houhou; Iwanami Shoten: Tokyo, Japan, 1993. (In Japanese) [Google Scholar]
- Gibilisco, P.; Riccomagno, E.; Rogantin, M.P.; Wynn, H.P. (Eds.) Algebraic and Geometric Methods in Statistics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Srivastava, A.; Wu, W.; Kurtek, S.; Klassen, E.; Marron, J.S. Registration of Functional Data Using Fisher-Rao Metric. arXiv 2011, arXiv:1103.3817. [Google Scholar]
- Wei, S.W.; Liu, Y.X.; Mann, R.B. Ruppeiner geometry, phase transitions, and the microstructure of charged AdS black holes. Phys. Rev. D 2019, 100, 124033. [Google Scholar] [CrossRef]
- Quevedo, H. Geometrothermodynamics. J. Math. Phys. 2007, 48, 013506. [Google Scholar] [CrossRef]
- Amari, S. Theory of Information Spaces: A Differential Geometrical Foundation of Statistics; Post RAAG Reports; Tokyo, Japan, 1980; Available online: https://bsi-ni.brain.riken.jp/database/item/92 (accessed on 29 September 2020).
- Efron, B. Defining the curvature of a statistical problem (with applications to second order efficiency). Ann. Stat. 1975, 3, 1189–1242. [Google Scholar] [CrossRef]
- Nagaoka, H.; Amari, S. Differential Geometry of Smooth Families of Probability Distributions; Technical Report; METR 82-7; University of Tokyo: Tokyo, Japan, 1982. [Google Scholar]
- Croll, G.J. The Natural Philosophy of Kazuo Kondo. arXiv 2007, arXiv:0712.0641. [Google Scholar]
- Kawaguchi, M. An introduction to the theory of higher order spaces I. The theory of Kawaguchi spaces. RAAG Memoirs 1960, 3, 718–734. [Google Scholar]
- Barndorff-Nielsen, O.E.; Cox, D.R.; Reid, N. The role of differential geometry in statistical theory. Int. Stat. Rev. 1986, 54, 83–96. [Google Scholar] [CrossRef]
- Nomizu, K.; Katsumi, N.; Sasaki, T. Affine Differential Geometry: Geometry of Affine Immersions; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Norden, A.P. On Pairs of Conjugate Parallel Displacements in Multidimensional Spaces. In Doklady Akademii nauk SSSR; Kazan State University, Comptes rendus de l’Académie des Sciences de l’URSS: Kazan, Russia, 1945; Volume 49, pp. 1345–1347. [Google Scholar]
- Sen, R.N. On parallelism in Riemannian space I. Bull. Calcutta Math. Soc. 1944, 36, 102–107. [Google Scholar]
- Sen, R.N. On parallelism in Riemannian space II. Bull. Calcutta Math. Soc. 1944, 37, 153–159. [Google Scholar]
- Sen, R.N. On parallelism in Riemannian space III. Bull. Calcutta Math. Soc. 1946, 38, 161–167. [Google Scholar]
- Giné, E.; Nickl, R. Mathematical Foundations of Infinite-Dimensional Statistical Models; Cambridge University Press: Cambridge, UK, 2015; Volume 40. [Google Scholar]
- Amari, S. New Developments of Information Geometry; Jouhou Kikagaku no Shintenkai; Saiensu’sha: Tokyo, Japan, 2014. (In Japanese) [Google Scholar]
- Fujiwara, A. Foundations of Information Geometry; Jouhou Kikagaku no Kisou; Makino Shoten: Tokyo, Japan, 2015; p. 223. (In Japanese) [Google Scholar]
- Mitchell, A.F.S. The information matrix, skewness tensor and α-connections for the general multivariate elliptic distribution. Ann. Inst. Stat. Math. 1989, 41, 289–304. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, H.; Zhong, F. Information geometry of the power inverse Gaussian distribution. Appl. Sci. 2007, 9, 194–203. [Google Scholar]
- Peng, T.L.L.; Sun, H. The geometric structure of the inverse gamma distribution. Contrib. Algebra Geom. 2008, 49, 217–225. [Google Scholar]
- Zhong, F.; Sun, H.; Zhang, Z. The geometry of the Dirichlet manifold. J. Korean Math. Soc. 2008, 45, 859–870. [Google Scholar] [CrossRef]
- Peng, L.; Sun, H.; Jiu, L. The geometric structure of the Pareto distribution. Bol. Asoc. Mat. Venez. 2007, 14, 5–13. [Google Scholar]
- Pistone, G. Nonparametric information geometry. In Geometric Science of Information; Springer: Berlin, Germany, 2013; pp. 5–36. [Google Scholar]
- Hayashi, M. Quantum Information; Springer: Berlin, Germany, 2006. [Google Scholar]
- Pardo, M.d.C.; Vajda, I. About distances of discrete distributions satisfying the data processing theorem of information theory. IEEE Trans. Inf. Theory 1997, 43, 1288–1293. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Total Jensen divergences: Definition, properties and k-means++ clustering. arXiv 2013, arXiv:1309.7109. [Google Scholar]
- Nielsen, F.; Nock, R. Total Jensen divergences: Definition, properties and clustering. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2016–2020. [Google Scholar]
- Nielsen, F.; Nock, R. Patch Matching with Polynomial Exponential Families and Projective Divergences. In Proceedings of the International Conference on Similarity Search and Applications (SISAP), Tokyo, Japan, 24–26 October 2016; pp. 109–116. [Google Scholar]
- Nielsen, F.; Sun, K.; Marchand-Maillet, S. On Hölder Projective Divergences. Entropy 2017, 19, 122. [Google Scholar] [CrossRef]
- Nielsen, F.; Barbaresco, F. (Eds.) Geometric Science of Information; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2013; Volume 8085. [Google Scholar] [CrossRef]
- Nielsen, F.; Barbaresco, F. (Eds.) Geometric Science of Information; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2015; Volume 9389. [Google Scholar] [CrossRef]
- Nielsen, F.; Barbaresco, F. (Eds.) Geometric Science of Information; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2017; Volume 10589. [Google Scholar] [CrossRef]
- Nielsen, F. Geometric Structures of Information; Springer: Berlin, Germany, 2018. [Google Scholar]
- Nielsen, F. Geometric Theory of Information; Springer: Berlin, Germany, 2014. [Google Scholar]
- Ay, N.; Gibilisco, P.; Matús, F. Information Geometry and its Applications: On the Occasion of Shun-ichi Amari’s 80th Birthday, IGAIA IV Liblice, Czech Republic, 12–17 June 2016; Springer Proceedings in Mathematics & Statistics; Springer: Berlin, Germany, 2018; Volume 252. [Google Scholar]
- Keener, R.W. Theoretical Statistics: Topics for a Core Course; Springer: Berlin, Germany, 2011. [Google Scholar]
- Nielsen, F.; Sun, K. Guaranteed bounds on the Kullback–Leibler divergence of univariate mixtures. IEEE Signal Process. Lett. 2016, 23, 1543–1546. [Google Scholar] [CrossRef]
- Gordon, G.J. Approximate Solutions to Markov Decision Processes. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1999. [Google Scholar]
- Telgarsky, M.; Dasgupta, S. Agglomerative Bregman clustering. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012; Omnipress: Madison, WI, USA; pp. 1011–1018. [Google Scholar]
- Yoshizawa, S.; Tanabe, K. Dual differential geometry associated with Kullback–Leibler information on the Gaussian distributions and its 2-parameter deformations. SUT J. Math. 1999, 35, 113–137. [Google Scholar]
- Nielsen, F. On the Jensen–Shannon symmetrization of distances relying on abstract means. Entropy 2019, 21, 485. [Google Scholar] [CrossRef]
- Niculescu, C.; Persson, L.E. Convex Functions and Their Applications; Springer: Berlin, Germany, 2006. [Google Scholar]
- Nielsen, F.; Nock, R. The Bregman chord divergence. In Proceedings of the International Conference on Geometric Science of Information, Toulouse, France, 27–29 August 2019; Springer: Berlin, Germany; pp. 299–308. [Google Scholar]
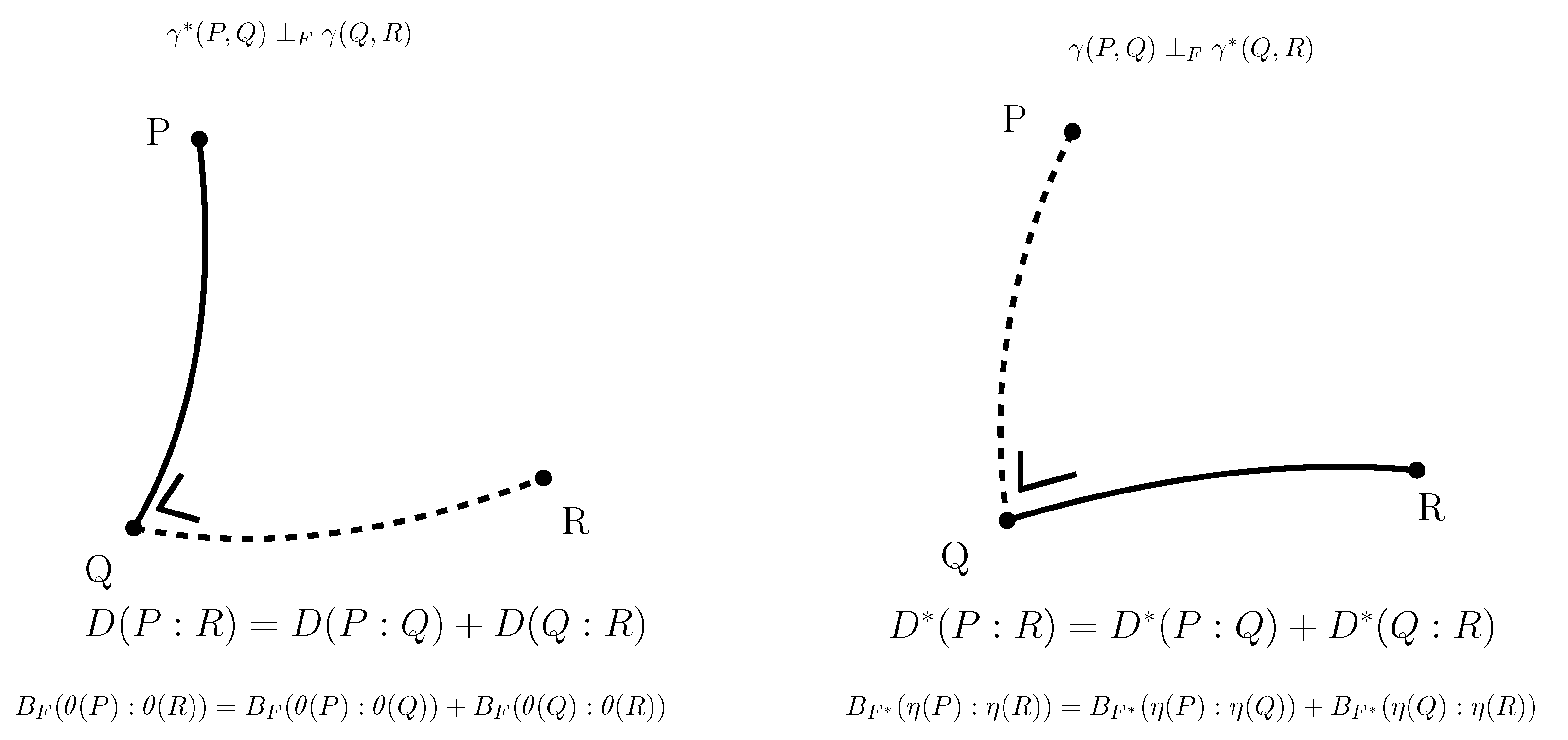

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, F. An Elementary Introduction to Information Geometry. Entropy 2020, 22, 1100. https://doi.org/10.3390/e22101100
Nielsen F. An Elementary Introduction to Information Geometry. Entropy. 2020; 22(10):1100. https://doi.org/10.3390/e22101100
Chicago/Turabian StyleNielsen, Frank. 2020. "An Elementary Introduction to Information Geometry" Entropy 22, no. 10: 1100. https://doi.org/10.3390/e22101100
APA StyleNielsen, F. (2020). An Elementary Introduction to Information Geometry. Entropy, 22(10), 1100. https://doi.org/10.3390/e22101100