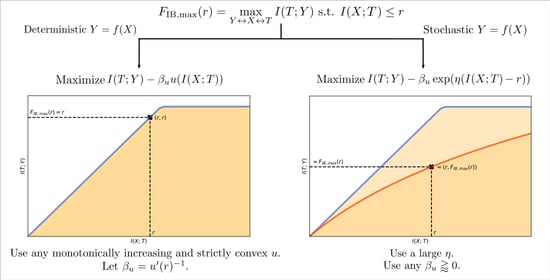
The Convex Information Bottleneck Lagrangian
Abstract
1. Introduction
- Supervised learning. In supervised learning, we are presented with a set of n pairs of input features and task outputs instances. We seek an approximation of the conditional probability distribution between the task outputs Y and the input features X. In classification tasks (i.e., when Y is a discrete random variable), the introduction of the variable T learned through the information bottleneck principle maintained the performance of standard algorithms based on the cross-entropy loss while providing with more adversarial attacks robustness and invariance to nuisances [2,3,4]. Moreover, by the nature of its definition the information bottleneck appears to be closely related with a trade-off between accuracy on the observable set and generalization to new, unseen instances (see Section 2).
- Clustering. In clustering, we are presented with a set of n pairs of instances of a random variable X and their attributes of interest Y. We seek groups of instances (or clusters T) such that the attributes of interest within the instances of each cluster are similar and the attributes of interest of the instances of different clusters are dissimilar. Therefore, the information bottleneck can be employed since it allows us to aim for attribute representative clusters (maximizing the similarity between instances within the clusters) and enforce a certain compression of the random variable X (ensuring a certain difference between instances of the different clusters). This has been successfully implemented, for instance, for gene expression analysis and word, document, stock pricing, or movie rating clustering [5,6,7].
- Image segmentation. In image segmentation, we want to partition an image into segments such that each pixel in a region shares some attributes. If we divide the image into very small regions X (e.g., each region is a pixel or a set of pixels defined by a grid), we can consider the problem of segmentation as that of clustering the regions X based on the region attributes Y. Hence, we can use the information bottleneck so that we seek region clusters T that are maximally informative about the attributes Y (e.g., the intensity histogram bins) and maintain a level of compression of the original regions X [8].
- Quantization. In quantization, we consider a random variable such that is a large or continuous set. Our objective is to map X into a variable such that is a smaller, countable set. If we fix the quantization set size to and aim at maximizing the information of the quantized variable with another random variable Y and restrict the mapping to be deterministic, then the problem is equivalent to the information bottleneck [9,10].
- Source coding. In source coding, we consider a data source which generates a signal , which is later perturbed by a channel that outputs X. We seek a coding scheme that generates a code from the output of the channel X which is as informative as possible about the original source signal Y and can be transmitted at a small rate . Therefore, this problem is equivalent to the the formulation of the information bottleneck [11].
- We introduce a general family of Lagrangians (the convex IB Lagrangians) which are able to explore the IB curve in any scenario for which the squared IB Lagrangian [21] is a particular case of. More importantly, the analysis made for deriving this family of Lagrangians can serve as inspiration for obtaining new Lagrangian families that solve other objective functions with intrinsic trade-offs such as the IB Lagrangian.
- We show that in deterministic scenarios (and other scenarios where the IB curve shape is known) one can use the convex IB Lagrangian to obtain a desired level of performance with a single optimization. That is, there is a one-to-one mapping between the Lagrange multiplier used for the optimization and the level of compression and informativeness obtained, and we provide the exact mapping. This eliminates the need for multiple optimizations to select a suitable representation.
- We introduce a particular case of the convex IB Lagrangians: the shifted exponential IB Lagrangian, which allows us to approximately obtain a specific compression level in any scenario. This way, we can approximately solve the initial constrained optimization problem from Equation (1) with a single optimization.
2. The IB in Supervised Learning
2.1. Supervised Learning Overview
2.2. Why Do We Use the IB?
3. The Information Bottleneck in Deterministic Scenarios
- 1.
- Any solution such that and solves for . That is, many different compression and performance levels can be achieved for .
- 2.
- Any solution such that and solves for . That is, many compression levels can be achieved with the same performance for .Note we use the supremum in this case since for we have that could be infinite and then the search set from Equation (1); i.e., is not compact anymore.
- 3.
- Any solutionsuch thatsolvesfor all. That is, many different β achieve the same compression and performance level.
4. The Convex IB Lagrangian
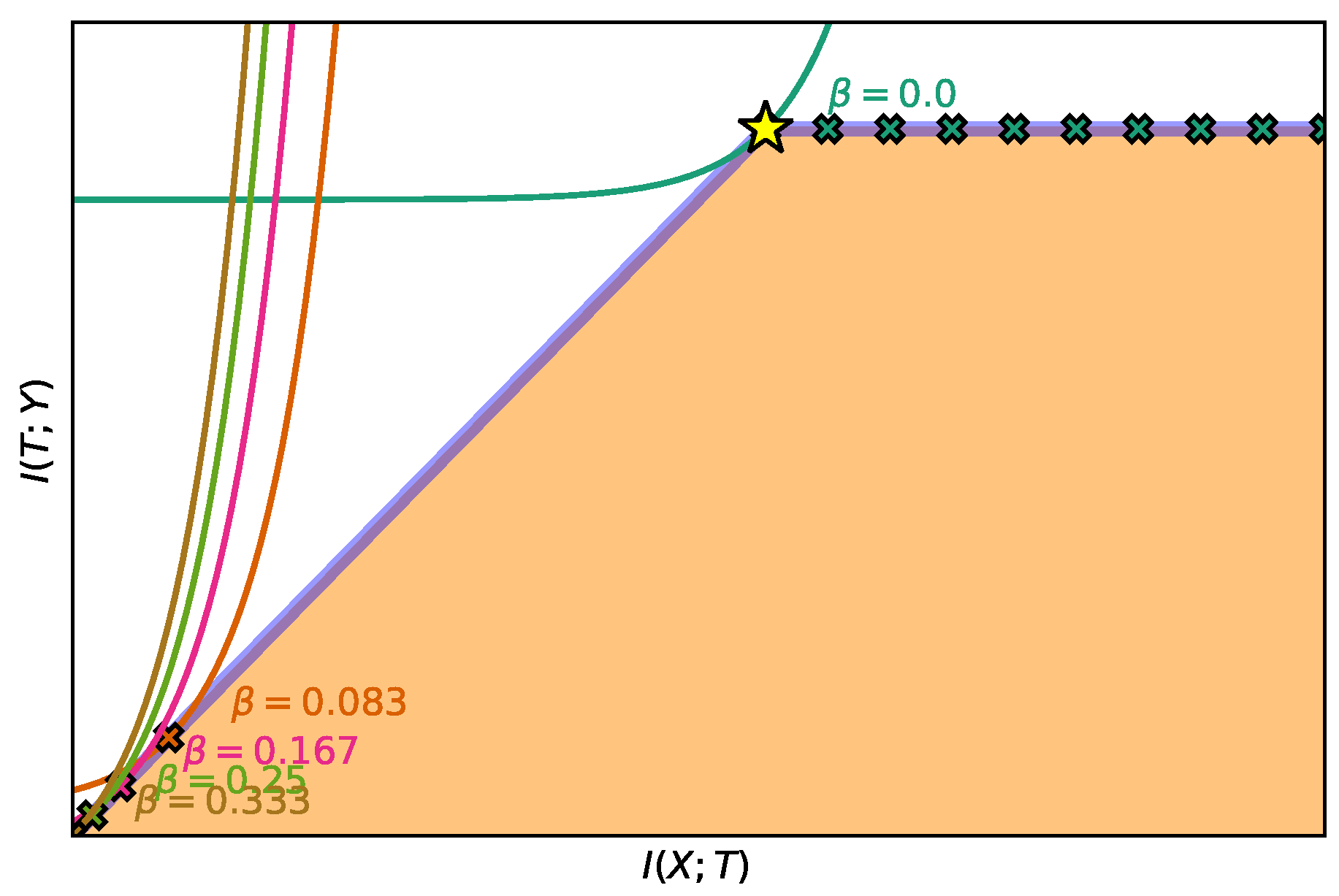
4.1. Exploring the IB Curve
4.2. Aiming for a Specific Compression Level
5. Experimental Support
- the power IB Lagrangians: , (Note when we have the squared IB functional from Kolchinsky et al. [21]).
- the exponential IB Lagrangians: , .
- the shifted exponential IB Lagrangians:
- In a deterministic or close to a deterministic setting (see -deterministic definition in Kolchinsky et al. [21]): Use the adequate for that performance using Proposition 3. Then if the performance is lower than desired, i.e., we are placed in the wrong performance plateau, gradually reduce the value of until reaching the previous performance plateau. Alternatively, exploit the value convergence phenomenon with, for instance, the shifted exponential IB Lagrangian.
- In a stochastic setting: exploit the value convergence phenomenon with, for instance, the shifted exponential IB Lagrangian. Alternatively, draw the IB curve with multiple values of on the range defined by Corollary 3 and select the representations that best fit their interests.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Alternative Proof of Theorem 1
- Proposition 2 states that the IB curve in the information plane follows the equation if . Then, since [1], we know in all these points. Therefore, for all points () such that are solutions of optimizing the IB Lagrangian.
- Similarly, Proposition 2 states that the IB curve follows the equation if . Then, since [1], we know in all points such that . We cannot ensure it at since for .
- Finally, in order to prove the last statement we will first prove that if achieves a solution, it is . Then, we will prove that if the solution exists, this can be yield by any . Hence, the solution is achieved and it is the only solution achievable.
- (a)
- Since the IB curve is concave we know is non-increasing in . We also know at the points in the IB curve where and at the points in the IB curve where . Hence, if we achieve a solution with , this solution is .
- (b)
- We can upper bound the IB Lagrangian bywhere the first and second inequalities use the DPI (Theorem 2.8.1 from Cover and Thomas [20]).Then, we can consider the point of the IB curve . Since the function is concave a tangent line to exists such that all other points in the curve lie below this line. Let be the slope of this curve (which we know it is from Tishby et al. [1]). Then,As we see, by the upper bound on the IB Lagrangian from Equation (A5), if the point exists, any can be the slope of the tangent line to that ensures concavity. □
Appendix C. Proof of Theorem 2
Appendix D. Proof of Proposition 3
Appendix E. Proof of Corollary 2
Appendix F. Proof of Corollary 3

Appendix G. Other Lagrangian Families
- We minimize the concave IB Lagrangian .
- We maximize the dual concave IB Lagrangian .
- We minimize the dual convex IB Lagrangian .
Appendix H. Experimental Setup Details and Further Experiments
Appendix H.1. Information Bottleneck Calculations
Appendix H.2. The Experiments
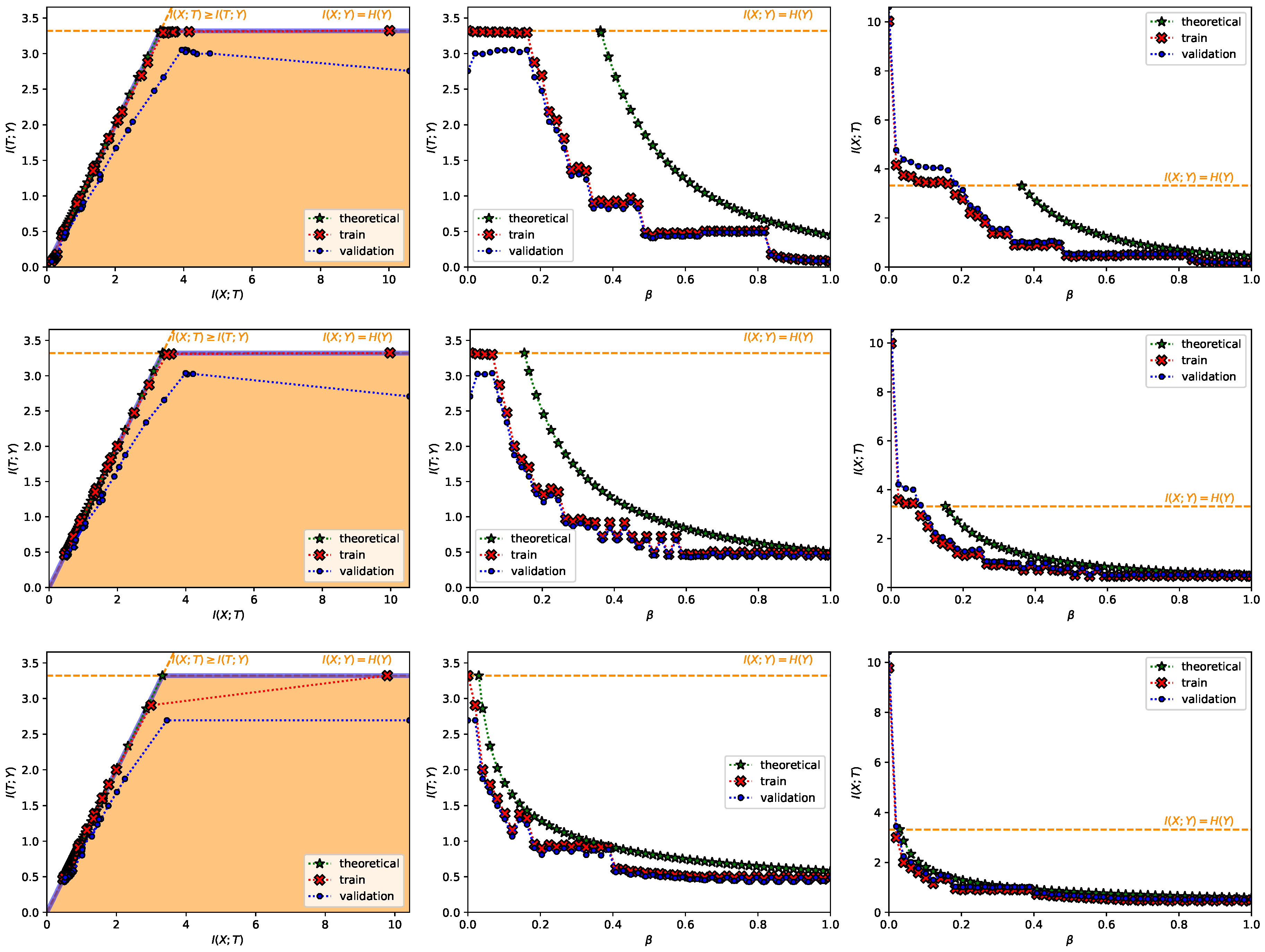
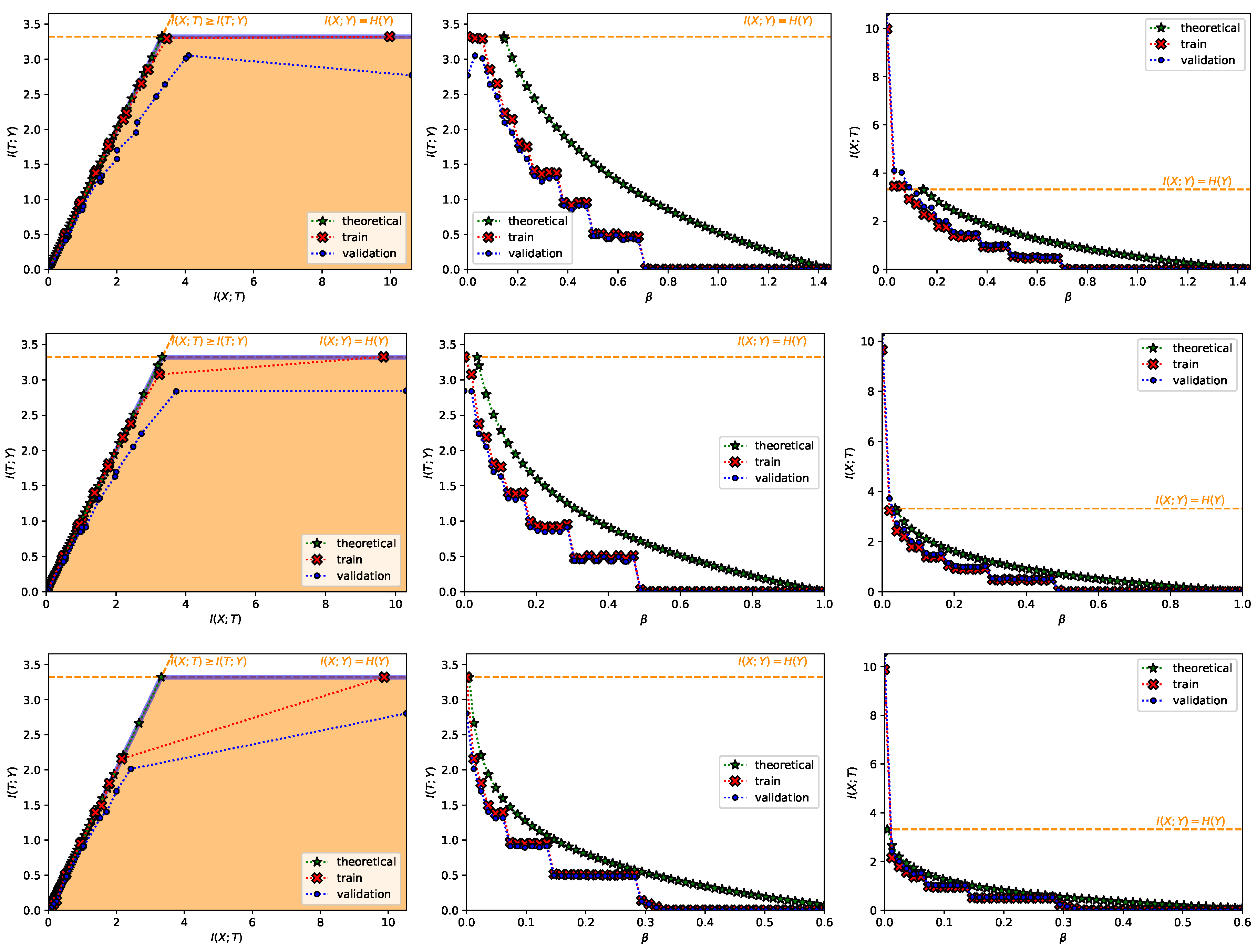
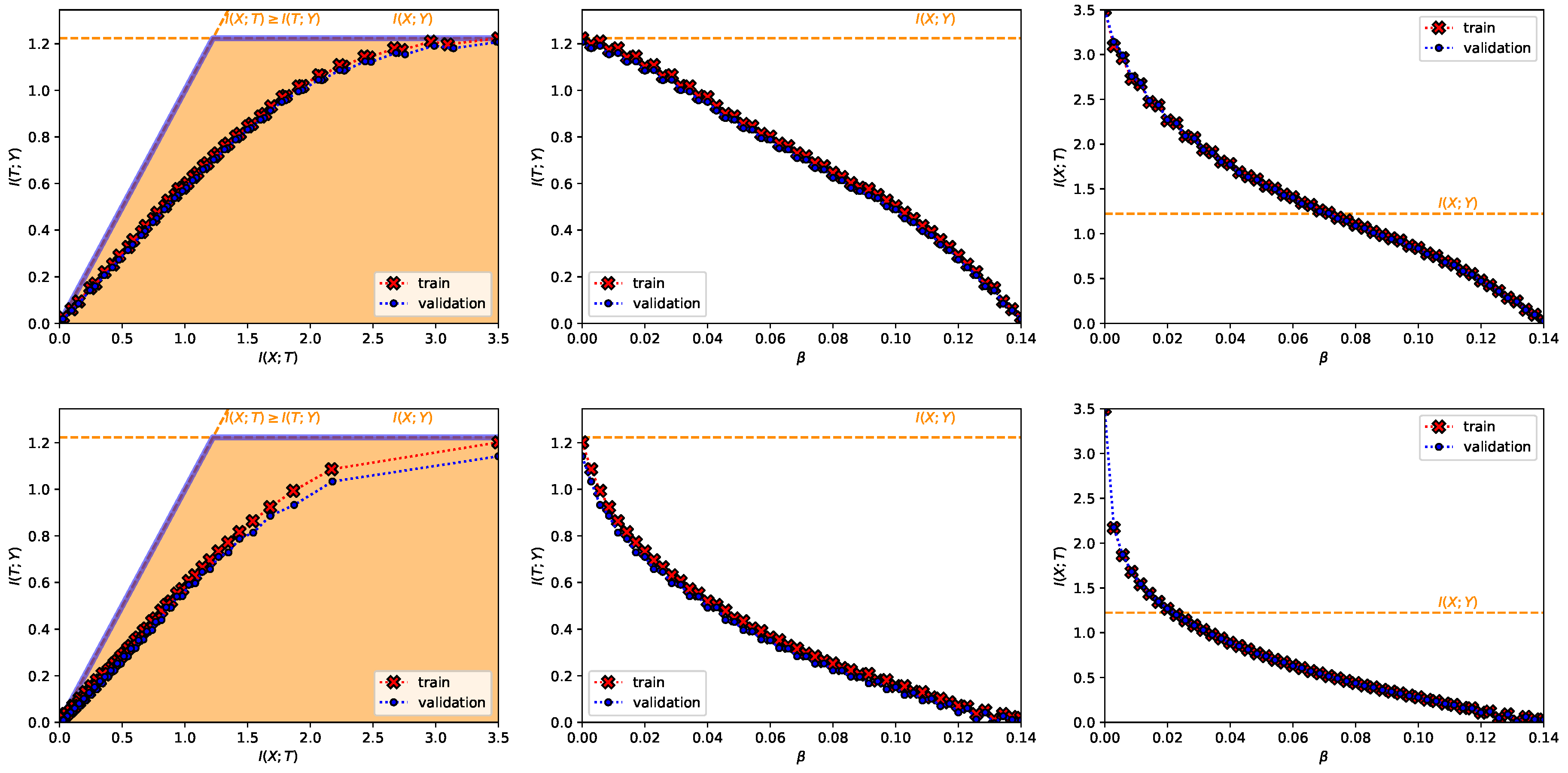
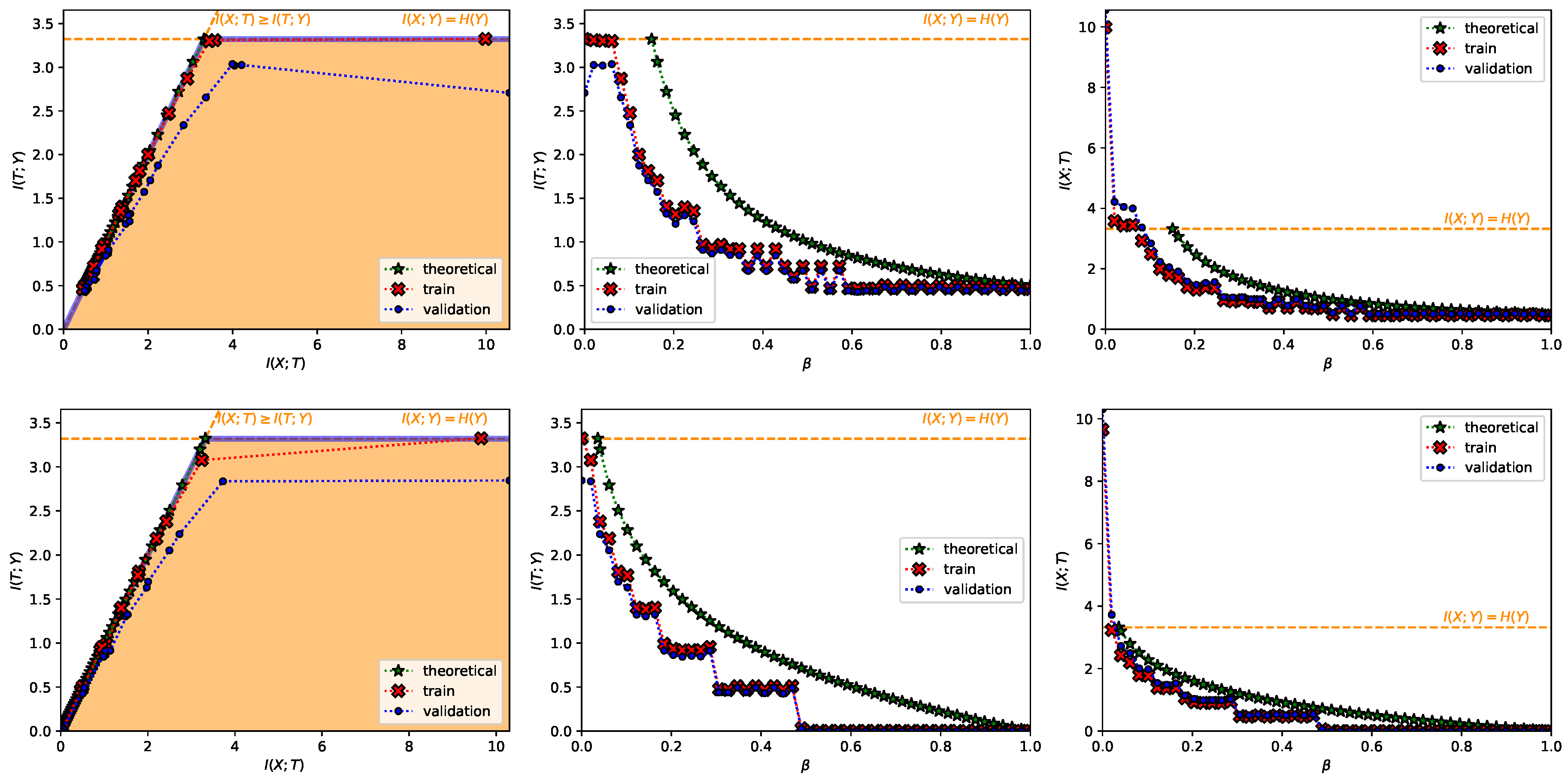
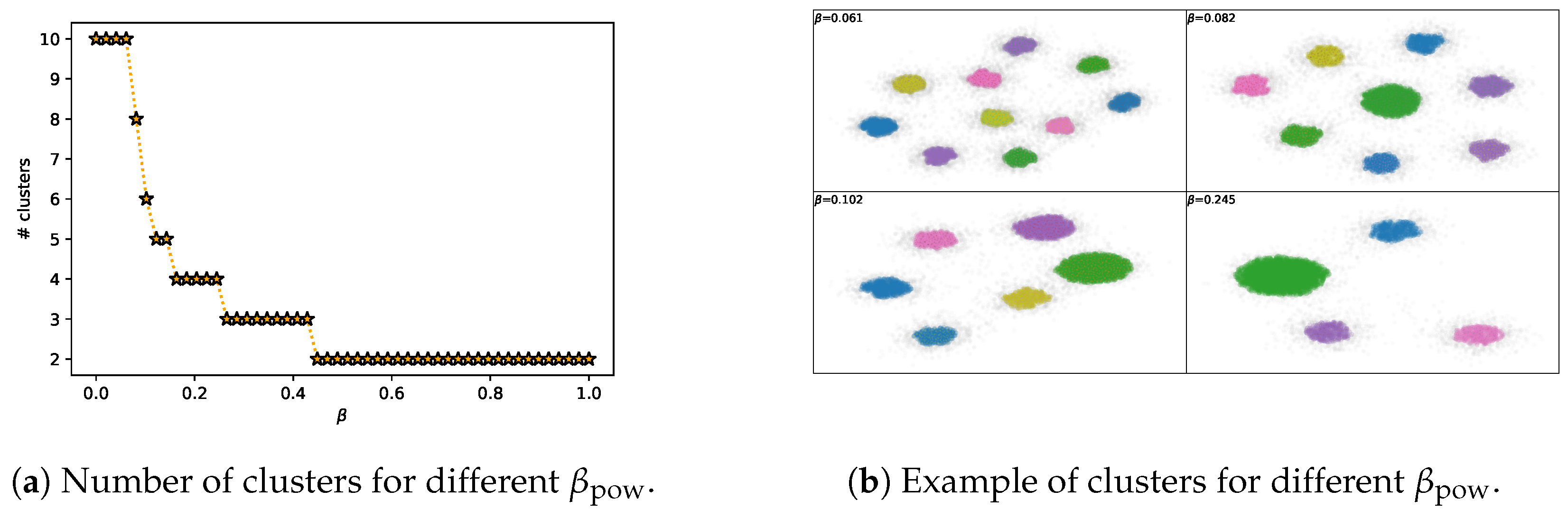
- A Classification Task on the MNIST Dataset [28] (Figure 1, Figure 2, Figure A2, Figure A3 and Figure A4 and top row from Figure 3). This dataset contains 60,000 training samples and 10,000 testing samples of hand-written digits. The samples are 28x28 pixels and are labeled from 0 to 9; i.e., and . The data is pre-processed so that the input has zero mean and unit variance. This is a deterministic setting, hence the experiment is designed to showcase how the convex IB Lagrangians allow us to explore the IB curve in a setting where the normal IB Lagrangian cannot and the relationship between the performance plateaus and the clusterization phenomena. Furthermore, it intends to showcase the behavior of the power and exponential Lagrangians with different parameters of and . Finally, it wants to demonstrate how the value convergence can be employed to approximately obtain a specific compression value. In this experiment, the encoder is a three fully-connected layer encoder with 800 ReLU units on the first two layers and two linear units on the last layer (), and the decoder is a fully-connected 800 ReLU unit layers followed by an output layer with 10 softmax units. The convex IB Lagrangian was calculated using the nonlinear-IB.In Figure A2 we show how the IB curve can be explored with different values of for the power IB Lagrangian and in Figure A3 for different values of and the exponential IB Lagrangian.Finally, in Figure A4 we show the clusterization for the same values of and as in Figure A2 and Figure A3. In this way the connection between the performance discontinuities and the clusterization is more evident. Furthermore, we can also observe how the exponential IB Lagrangian maintains better the theoretical performance than the power IB Lagrangian (see Appendix I for an explanation of why).
- A Classification Task on the Fashion-MNIST Dataset [49] (Figure A5). As MNSIT, this dataset contains 60,000 training and 10,000 testing samples of 28x28 pixel images labeled from 0 to 9 and constitutes a deterministic setting. The difference is that this dataset contains fashion products instead of hand-written digits and it represents a harder classification task [49]. The data is also pre-processed so that the input has zero mean and unit variance. For this experiment, the encoder is composed of a two-layer convolutional neural network (CNN) with 32 filters on the first layer and 128 filters on the second with kernels of size 5 and stride 2. This CNN is followed by two fully-connected layers of 128 linear units (). After the first convolution and the first fully-connected layer, a ReLU activation is employed. The decoder is a fully-connected 128 ReLU unit layer followed by an output layer with 10 softmax units. The convex IB Lagrangian was calculated using the nonlinear-IB. Therefore, this experiment intends to showcase how the convex IB Lagrangian can explore the IB curve for different neural network architectures and harder datasets.
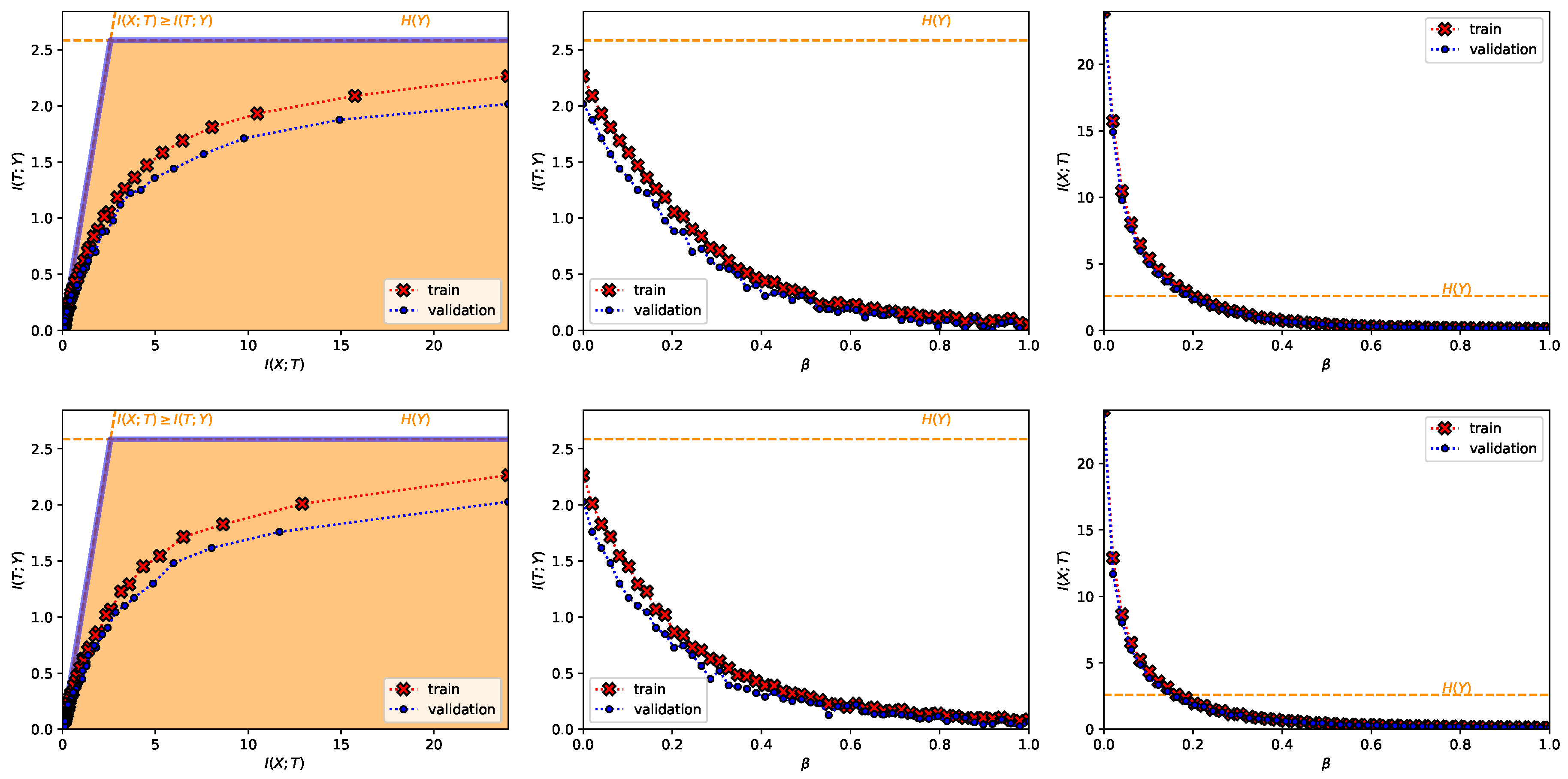
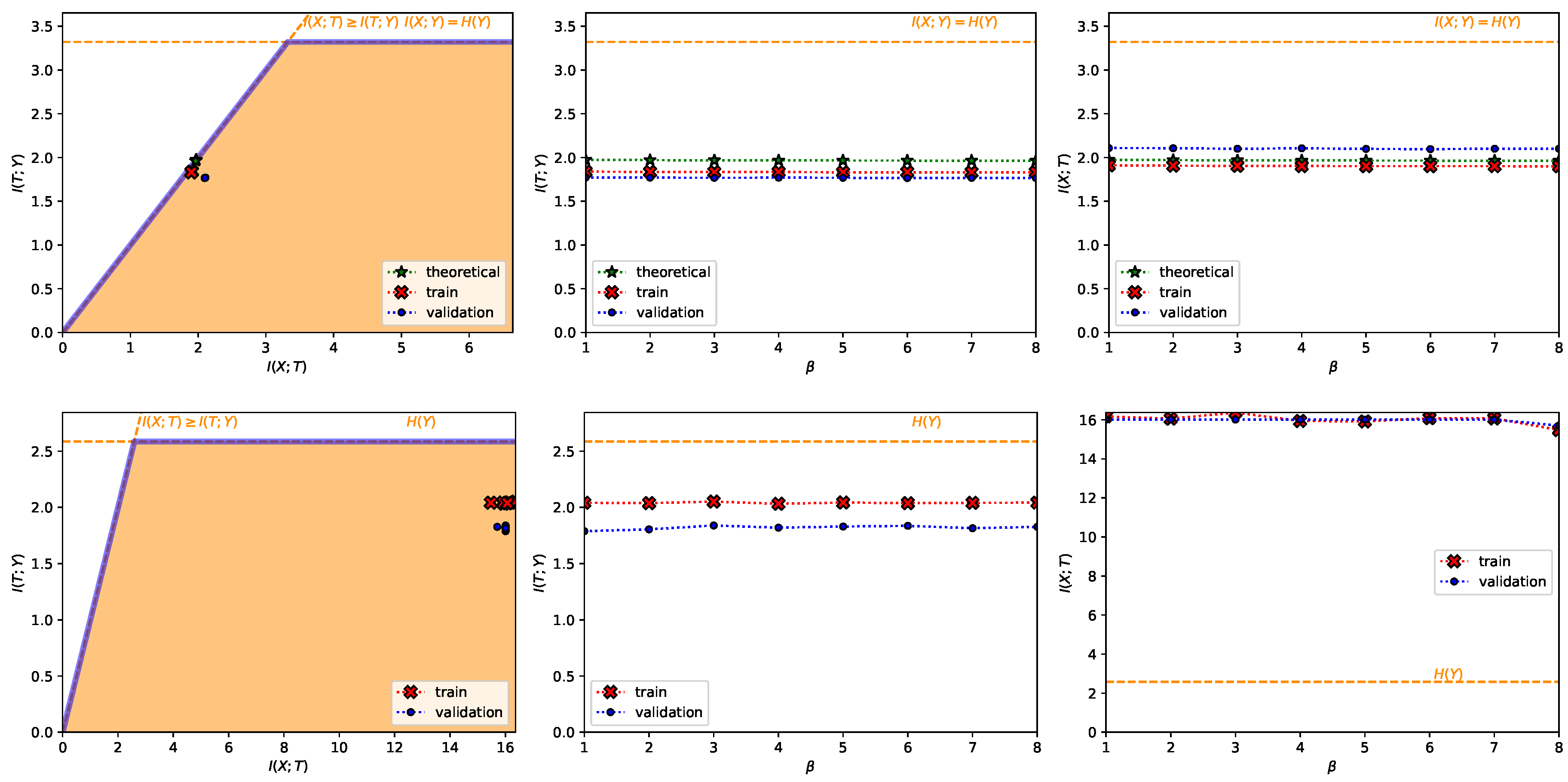
- A Regression Task on the California Housing Dataset [50] (Figure A6). This dataset contains 20,640 samples of 8 real number input variables like the longitude and latitude of the house (i.e., ) and a task output real variable representing the price of the house (i.e., ). We used the log-transformed house price as the target variable and dropped the 992 samples in which the house price was equal or greater than $ so that the output distribution was closer to a Gaussian as they did in [26]. The input variables were processed so that they had zero mean and unit variance and we randomly split the samples into a 70% training and 30% test dataset. As in [40], for regression tasks we approximate with the entropy of a Gaussian with variance and with the entropy of a Gaussian with variance equal to the mean-squared error (MSE). This leads to the estimate . The encoder is a three fully-connected layer encoder with 128 ReLU units on the first two layers and 2 linear units on the last layer (), and the decoder is a fully-connected 128 ReLU unit layers followed by an output layer with 1 linear unit. The convex IB Lagrangian was calculated using the nonlinear-IB. Hence, this experiment was designed to showcase the convex IB Lagrangian can explore the IB curve in stochastic scenarios for regression tasks.
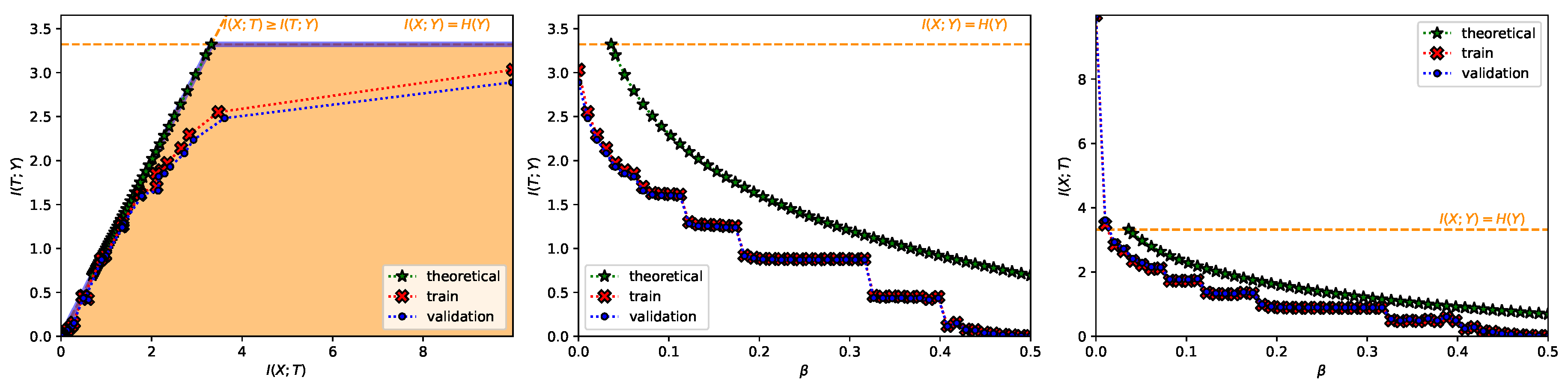
- A Classification Task on the TREC-6 Dataset [29] (Figure A7 and bottom row from Figure 3). This dataset is the six-class version of the TREC [51] dataset. It contains 5452 training and 500 test samples of text questions. Each question is labeled within six different semantic categories based on what the answer is; namely: Abbreviation, description and abstract concepts, entities, human beings, locations, and numeric values. This dataset does not constitute a deterministic setting since there are examples that could belong to more than one class and there are examples which are wrongly labeled (e.g., “What is a fear of parasites?” could belong both to the description and abstract concept category, however it is labeled into the entity category), and hence . Following Ben Trevett’s tutorial on Sentiment Analysis [52] the encoder is composed by a 6 billion token pre-trained 100-dimensional Glove word embedding [53], followed by a concatenation of three convolutions with kernel sizes 2–4 respectively, and finalized with a fully-connected 128 linear unit layer (). The decoder is a single fully-connected 6 softmax unit layer. The convex IB Lagrangian was calculated using the nonlinear-IB. Thus, this experiment intends to show an example where the classification task does not convey a deterministic scenario, that the convex IB Lagrangian can recover the IB curve in complex stochastic tasks with complex neural network architectures and that the value convergence can be employed to obtain a specific compression value even in stochastic settings where the IB curve is unknown.

Appendix I. Guidelines for Selecting A Proper Function in the Convex IB Lagrangian
Appendix I.1. Avoiding Value Convergence
- Power IB Lagrangian: and .
- Exponential IB Lagrangian: and .
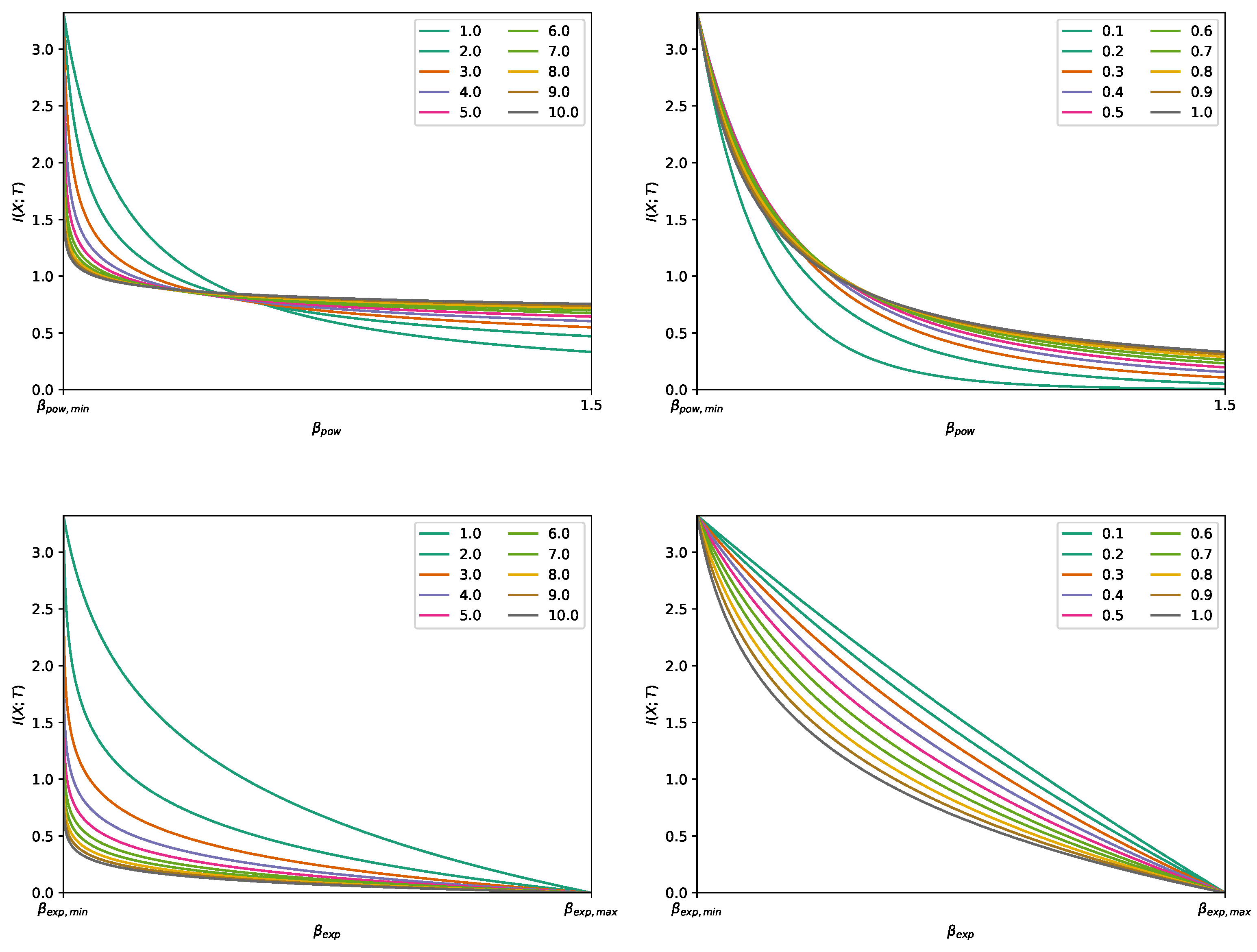
Appendix I.2. Aiming for Strong Convexity
Appendix I.3. Exploiting Value Convergence
References
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv 2000, arXiv:physics/0004057. [Google Scholar]
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep variational information bottleneck. arXiv 2016, arXiv:1612.00410. [Google Scholar]
- Peng, X.B.; Kanazawa, A.; Toyer, S.; Abbeel, P.; Levine, S. Variational Discriminator Bottleneck: Improving Imitation Learning, Inverse RL, and GANs by Constraining Information Flow. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Achille, A.; Soatto, S. Information dropout: Learning optimal representations through noisy computation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Slonim, N.; Tishby, N. Document clustering using word clusters via the information bottleneck method. In Proceedings of the 23rd annual international ACM SIGIR Conference on Research and Development in Information Retrieval, Athens, Greece, 24–28 July 2000. [Google Scholar]
- Slonim, N.; Tishby, N. Agglomerative information bottleneck. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Slonim, N.; Atwal, G.S.; Tkačik, G.; Bialek, W. Information-based clustering. Proc. Natl. Acad. Sci. USA 2005, 102, 18297–18302. [Google Scholar] [CrossRef] [PubMed]
- Teahan, W.J. Text classification and segmentation using minimum cross-entropy. In Content-Based Multimedia Information Access; LE CENTRE DE HAUTES ETUDES INTERNATIONALES D’INFORMATIQUE DOCUMENTAIRE: Paris, France, 2000; pp. 943–961. [Google Scholar]
- Strouse, D.; Schwab, D.J. The deterministic information bottleneck. Neur. Comput. 2017, 29, 1611–1630. [Google Scholar] [CrossRef]
- Nazer, B.; Ordentlich, O.; Polyanskiy, Y. Information-distilling quantizers. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 96–100. [Google Scholar]
- Hassanpour, S.; Wübben, D.; Dekorsy, A. On the equivalence of double maxima and KL-means for information bottleneck-based source coding. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Goyal, A.; Islam, R.; Strouse, D.; Ahmed, Z.; Botvinick, M.; Larochelle, H.; Levine, S.; Bengio, Y. Infobot: Transfer and exploration via the information bottleneck. arXiv 2019, arXiv:1901.10902. [Google Scholar]
- Yingjun, P.; Xinwen, H. Learning Representations in Reinforcement Learning:An Information Bottleneck Approach. arXiv 2019, arXiv:cs.LG/1911.05695. [Google Scholar]
- Sharma, A.; Gu, S.; Levine, S.; Kumar, V.; Hausman, K. Dynamics-Aware Unsupervised Skill Discovery. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Schulz, K.; Sixt, L.; Tombari, F.; Landgraf, T. Restricting the Flow: Information Bottlenecks for Attribution. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Li, X.L.; Eisner, J. Specializing Word Embeddings (for Parsing) by Information Bottleneck. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; pp. 2744–2754. [Google Scholar]
- Zaslavsky, N.; Kemp, C.; Regier, T.; Tishby, N. Efficient compression in color naming and its evolution. Proc. Natl. Acad. Sci. USA 2018, 115, 7937–7942. [Google Scholar] [CrossRef]
- Chalk, M.; Marre, O.; Tkačik, G. Toward a unified theory of efficient, predictive, and sparse coding. Proc. Natl. Acad. Sci. USA 2018, 115, 186–191. [Google Scholar] [CrossRef]
- Gilad-Bachrach, R.; Navot, A.; Tishby, N. An information theoretic tradeoff between complexity and accuracy. In Learning Theory and Kernel Machines; Springer: Berlin, Germany, 2003; pp. 595–609. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kolchinsky, A.; Tracey, B.D.; Van Kuyk, S. Caveats for information bottleneck in deterministic scenarios. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Courcoubetis, C. Pricing Communication Networks Economics, Technology and Modelling; Wiley Online Library: Hoboken, NJ, USA, 2003. [Google Scholar]
- Tishby, N.; Slonim, N. Data clustering by markovian relaxation and the information bottleneck method. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001; pp. 640–646. [Google Scholar]
- Slonim, N.; Friedman, N.; Tishby, N. Unsupervised document classification using sequential information maximization. In Proceedings of the 25th annual international ACM SIGIR Conference on Research and Development in Information Retrieval, Tampere, Finland, 11–15 August 2002. [Google Scholar]
- Chalk, M.; Marre, O.; Tkacik, G. Relevant sparse codes with variational information bottleneck. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; pp. 1957–1965. [Google Scholar]
- Kolchinsky, A.; Tracey, B.D.; Wolpert, D.H. Nonlinear information bottleneck. Entropy 2019, 21, 1181. [Google Scholar] [CrossRef]
- Wu, T.; Fischer, I.; Chuang, I.; Tegmark, M. Learnability for the Information Bottleneck. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. In Proceedings of the 1998 IEEE International Frequency Control Symposium, Pasadena, CA, USA, 27–29 May 1998. [Google Scholar]
- Li, X.; Roth, D. Learning question classifiers. In Proceedings of the 19th international conference on Computational linguistics—Volume 1; Association for Computational Linguistics: Stroudsburg, PA, USA, 2002; pp. 1–7. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the NIPS Autodiff Workshop, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer Science+ Business Media: Berlin, Germany, 2006. [Google Scholar]
- Xu, A.; Raginsky, M. Information-theoretic analysis of generalization capability of learning algorithms. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 2524–2533. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Shore, J.E.; Gray, R.M. Minimum cross-entropy pattern classification and cluster analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 1, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Shore, J.; Johnson, R. Properties of cross-entropy minimization. IEEE Trans. Pattern Anal. Mach. Intell. 1981, 27, 472–482. [Google Scholar] [CrossRef]
- Vera, M.; Piantanida, P.; Vega, L.R. The role of the information bottleneck in representation learning. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 1580–1584. [Google Scholar]
- Shamir, O.; Sabato, S.; Tishby, N. Learning and generalization with the information bottleneck. Theor. Comput. Sci. 2010, 411, 2696–2711. [Google Scholar] [CrossRef]
- Achille, A.; Soatto, S. Emergence of invariance and disentanglement in deep representations. J. Mach. Learn. Res 2018, 19, 1947–1980. [Google Scholar]
- Du Pin Calmon, F.; Polyanskiy, Y.; Wu, Y. Strong data processing inequalities for input constrained additive noise channels. IEEE Trans. Inf. Theory 2017, 64, 1879–1892. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Tracey, B. Estimating mixture entropy with pairwise distances. Entropy 2017, 19, 361. [Google Scholar] [CrossRef]
- Amjad, R.A.; Geiger, B.C. Learning representations for neural network-based classification using the information bottleneck principle. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 1. [Google Scholar] [CrossRef]
- Alemi, A.A.; Fischer, I.; Dillon, J.V. Uncertainty in the variational information bottleneck. arXiv 2018, arXiv:1807.00906. [Google Scholar]
- Wu, T.; Fischer, I. Phase Transitions for the Information Bottleneck in Representation Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Menlo Park, CA, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. TODS 2017, 42, 19. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Pace, R.K.; Barry, R. Sparse spatial autoregressions. Stat. Probab. Lett. 1997, 33, 291–297. [Google Scholar] [CrossRef]
- Voorhees, E.M.; Tice, D.M. Building a question answering test collection. In Proceedings of the 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Athens, Greece, 24–28 July 2000. [Google Scholar]
- Trevett, Ben. Tutorial on Sentiment Analysis: 5—Multi-class Sentiment Analysis. April 2019. Available online: https://github.com/bentrevett/pytorch-sentiment-analysis (accessed on 14 January 2020).
- Pennington, J.; Socher, R.; Manning, C. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez Gálvez, B.; Thobaben, R.; Skoglund, M. The Convex Information Bottleneck Lagrangian. Entropy 2020, 22, 98. https://doi.org/10.3390/e22010098
Rodríguez Gálvez B, Thobaben R, Skoglund M. The Convex Information Bottleneck Lagrangian. Entropy. 2020; 22(1):98. https://doi.org/10.3390/e22010098
Chicago/Turabian StyleRodríguez Gálvez, Borja, Ragnar Thobaben, and Mikael Skoglund. 2020. "The Convex Information Bottleneck Lagrangian" Entropy 22, no. 1: 98. https://doi.org/10.3390/e22010098
APA StyleRodríguez Gálvez, B., Thobaben, R., & Skoglund, M. (2020). The Convex Information Bottleneck Lagrangian. Entropy, 22(1), 98. https://doi.org/10.3390/e22010098