(Generalized) Maximum Cumulative Direct, Residual, and Paired Φ Entropy Approach
Abstract
1. Introduction
2. What does Maximizing Cumulative Direct, Residual, and Paired Shannon Entropies Mean?
3. Maximum Cumulative Entropy Distributions
3.1. General Class of Cumulative Entropies
3.2. General Results for Arbitrary Support
3.2.1. Maximum Cumulative Entropy Approach
3.2.2. Generalized Maximum Cumulative Entropy Approach
3.3. General Results for Non-Negative Support
3.3.1. Maximum Cumulative Entropy Approach
3.3.2. Generalized Maximum Cumulative Entropy Approach
4. Applications
5. Estimating the Entropy Generating Function
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Cumulative Paired Mielke(r) Entropy and the Symmetric Beta Distribution
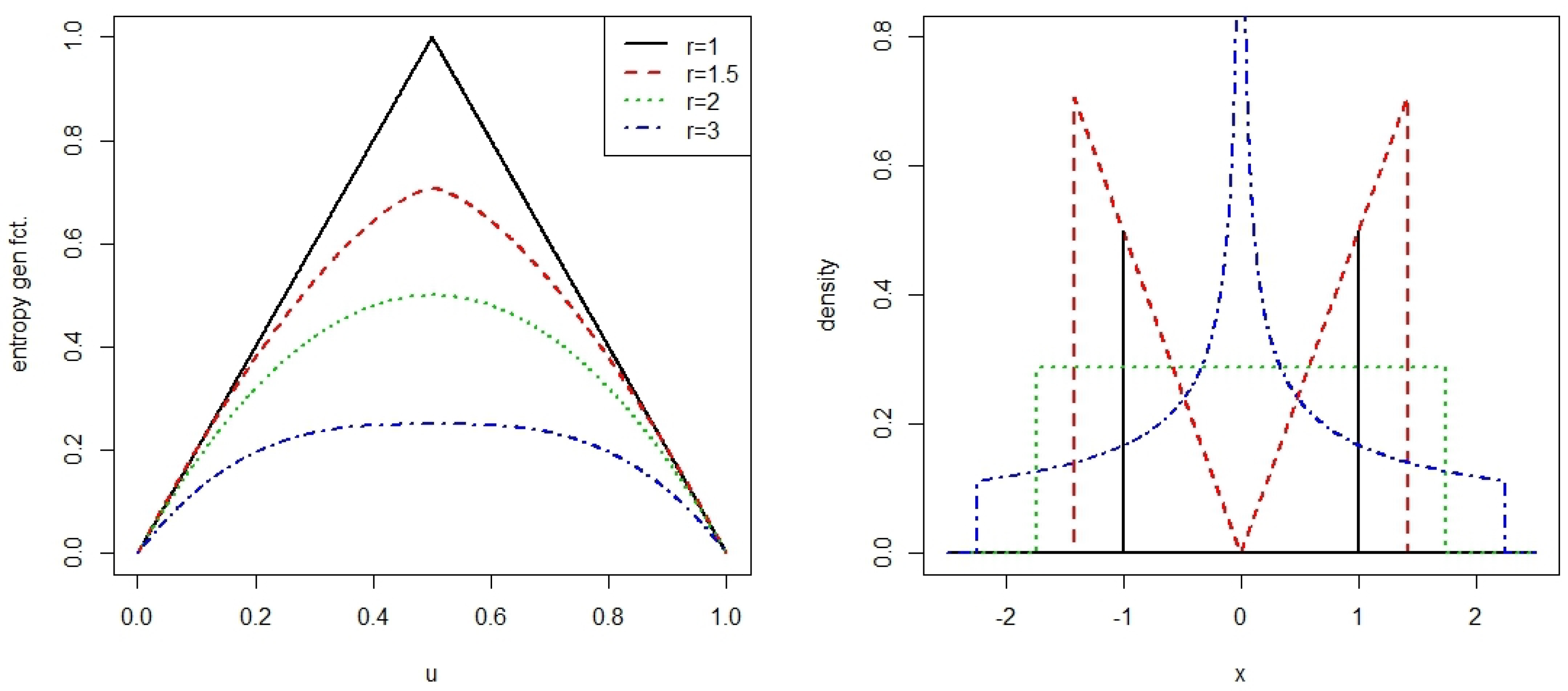
Appendix A.2. Cumulative Paired Shannon Entropy and the Generalized Logistic Distribution
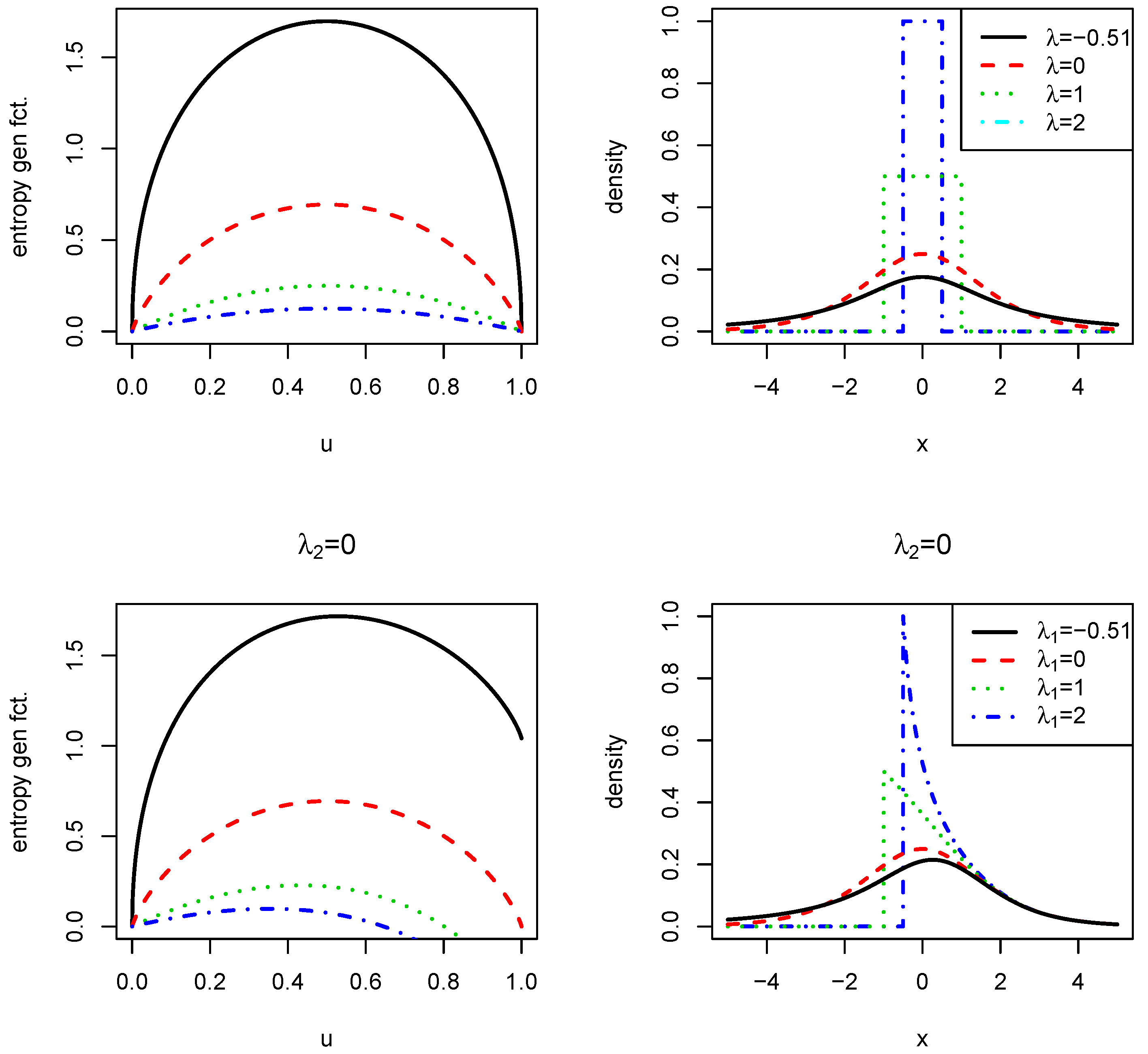
Appendix A.3. Asymmetric Entropy Generating Functions and ‘New’ Skewed Logistic and Tukey λ Distributions
| support | ||

Appendix A.4. Skewed Tukey λ Distribution and Entropy Generating Function Φ
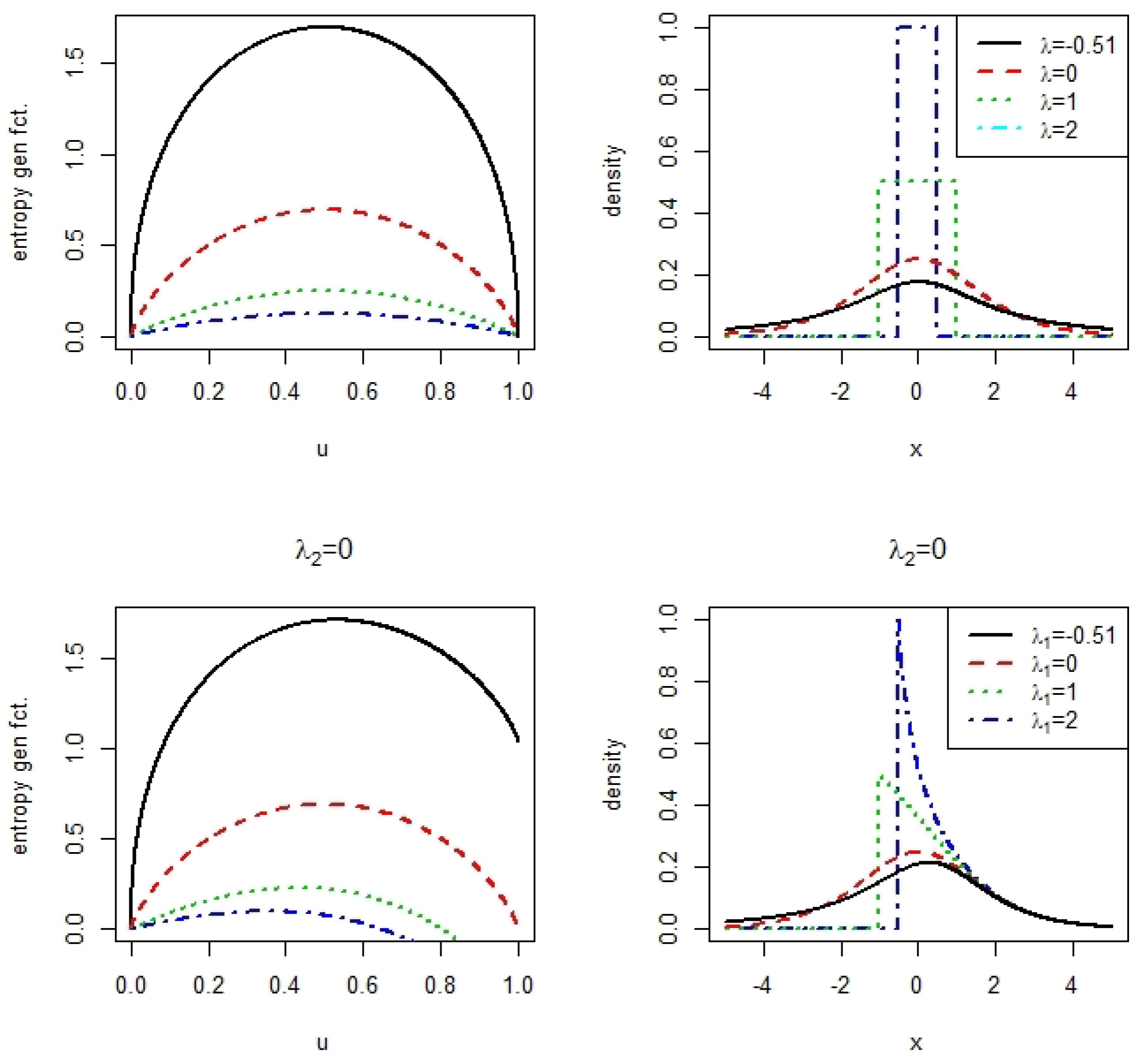
Appendix A.5. Fechner Approach of Skewness and Entropy Generating Function Φ

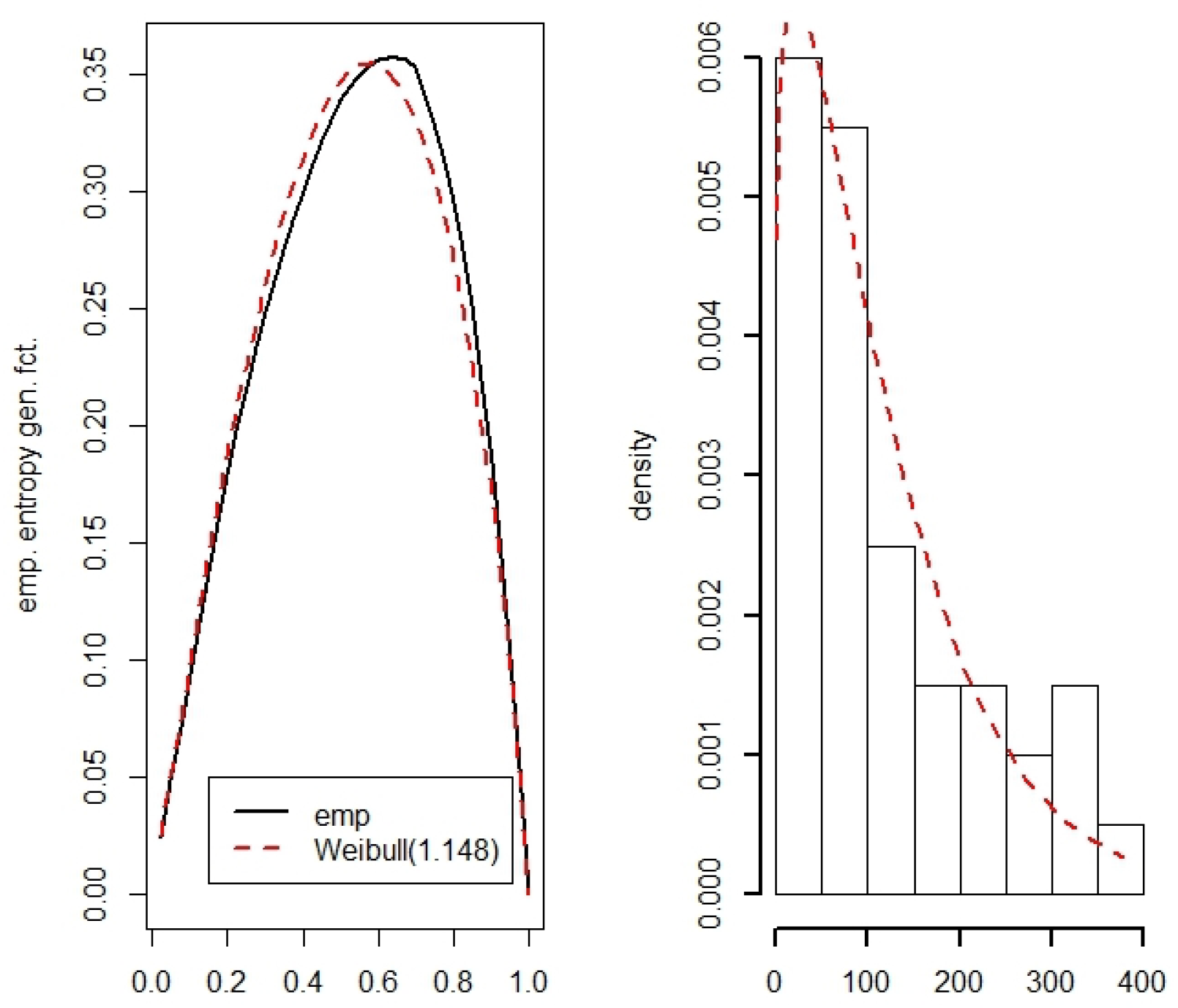
Appendix A.6. Cumulative Residual Shannon Entropy and the Weibull Distribution
Appendix A.7. Cumulative Residual Havrda & Charvát Entropy and the Extended Burr XII Distribution
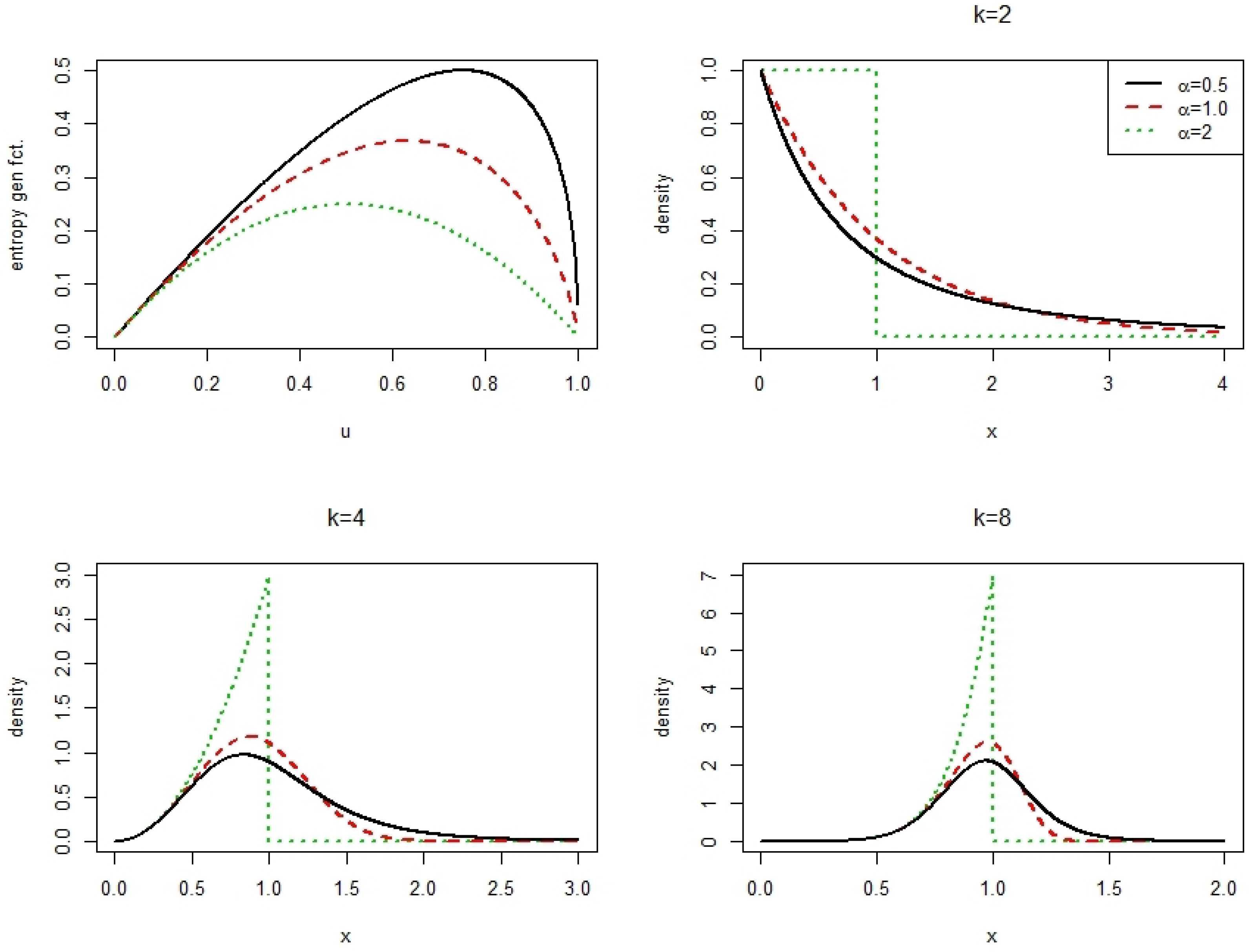
References
- Hosking, J.R.M. Distributions with maximum entropy subject to constraints on their L-moments or expected order statistics. J. Stat. Plan. Inference 2007, 137, 2870–2891. [Google Scholar] [CrossRef]
- Park, S.Y.; Bera, A.K. Maximum entropy autoregressive conditional heteroskedasticity model. J. Econom. 2008, 150, 219–230. [Google Scholar] [CrossRef]
- Schroeder, M.J. An alternative to entropy in the measurement of information. Entropy 2004, 6, 388–412. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Rao, M. More on a new concept of entropy and information. J. Theor. Probab. 2005, 18, 967–981. [Google Scholar] [CrossRef]
- Asadi, M.; Zohrevand, Y. On the dynamic cumulative residual entropy. J. Stat. Plan. Inference 2007, 137, 1931–1941. [Google Scholar] [CrossRef]
- Baratpour, S. Characterizations based on cumulative residual entropy of first-order statistics. Commun. Stat. Theory Methods 2010, 39, 3645–3651. [Google Scholar] [CrossRef]
- Baratpour, S.; Habibi, R.A. Testing goodness-of-fit for exponential distribution based on cumulative residual entropy. Commun. Stat. Theory Methods 2012, 39, 3645–3651. [Google Scholar] [CrossRef]
- Chamany, A.; Baratpour, S. A dynamic discrimination information based on cumulative residual entropy and its properties. Commun. Stat. Theory Methods 2014, 43, 1041–1049. [Google Scholar] [CrossRef]
- Drissi, N.; Chonavel, T.; Boucher, J.M. Generalized cumulative residual entropy distributions with unrestricted supports. Res. Lett. Signal Process. 2008, 11, 1–5. [Google Scholar] [CrossRef]
- Kumar, V.; Taneja, H.C. Some characterizations results on generalized cumulative residual entropy measures. Stat. Probab. Lett. 2011, 81, 1072–1077. [Google Scholar] [CrossRef]
- Minimol, S. On generalized dynamic cumulative past entropy measures. Commun. Stat. Theory Methods 2017, 46, 2816–2822. [Google Scholar] [CrossRef]
- Mirali, M.; Baratpur, S.; Fakoor, V. On weighted cumulative residual entropy. Commun. Stat. Theory Methods 2017, 46, 2857–2869. [Google Scholar] [CrossRef]
- Navarro, J.; del Aguila, Y.; Asadi, M. Some new results on the cumulative residual entropy. J. Stat. Plan. Inference 2010, 140, 310–322. [Google Scholar] [CrossRef]
- Navarro, J.; Psarrakos, G. Characterizations based on generalized cumulative residual entropy functions. Commun. Stat. Theory Methods 2017, 46, 1247–1260. [Google Scholar] [CrossRef]
- Psarrakos, G.; Navarro, J. Generalized cumulative residual entropy and record values. Metrika 2013, 76, 623–640. [Google Scholar] [CrossRef]
- Sankaran, P.G.; Sunoj, S.M. Quantile-based cumulative entropies. Commun. Stat. Theory Methods 2017, 46, 805–814. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. On cumulative entropies. J. Stat. Plan. Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy measure of fuzzy entropy. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Pal, N.R.; Bezdek, J.C. Measuring fuzzy uncertainty. IEEE Trans. Fuzzy Syst. 1994, 2, 107–118. [Google Scholar] [CrossRef]
- Li, P.; Liu, B. Entropy of credibility distributions for fuzzy variables. IEEE Trans. Fuzzy Syst. 2008, 16, 123–129. [Google Scholar]
- Chen, X.; Dai, W. Maximum entropy principle for uncertain variables. Int. J. Fuzzy Syst. 2011, 13, 232–236. [Google Scholar]
- Dai, W. Quadratic entropy of uncertain variables. Soft Comput. 2018, 22, 5699–5706. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory; Springer: New York, NY, USA, 2015. [Google Scholar]
- Havrda, J.; Charvát, F. Quantification method of classification processes. Concept of structural α-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Kapur, J.N. Measures of Information and their Applications; Wiley Eastern Limited: New Delhi, India, 1994. [Google Scholar]
- Rényi, A. On measures of entropy and information. Fourth Berkeley Symp. Math. Stat. Probab. 1961, 547–561. [Google Scholar]
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Csiszár, I. Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizität von Markoffschen Ketten. Magyar. Tud. Akad. Mat. Kut. Int. Kozl. 1963, 8, 85–108. [Google Scholar]
- Morimoto, T. Markov processes and the H-theorem. J. Phys. Soc. Jpn. 1963, 18, 328–331. [Google Scholar] [CrossRef]
- Liese, F.; Vajda, I. On divergences and information in statistics and information theory. IEEE Trans. Inf. Theory 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Cressie, N.A.; Pardo, L. Phi-divergence statistic. In Encyclopedia of Environmetrics; El-Shaarawi, A.H., Piegorsch, W.W., Eds.; John Wiley and Sons: New York, NY, USA, 2002; Volume 3, pp. 1551–1555. [Google Scholar]
- Zografos, K.; Nadarajah, S. Survival exponential entropies. IEEE Trans. Inf. Theory 2005, 51, 1239–1246. [Google Scholar] [CrossRef]
- Klein, I.; Mangold, B.; Doll, M. Cumulative paired ϕ entropies. Entropy 2016, 18, 248. [Google Scholar] [CrossRef]
- Burbea, J.; Rao, C.R. On the convexity of some divergence measures based on entropy functions. IEEE Trans. Inf. Theory 1982, 28, 489–495. [Google Scholar] [CrossRef]
- Kumar, V. Characterization results based on dynamic Tsallis cumulative residual entropy. Commun. Stat. Theory Methods 2017, 46, 8343–8354. [Google Scholar] [CrossRef]
- Rajesh, G.; Sunoj, S.M. Some properties of cumulative Tsallis entropy of order α. Stat. Pap. 2019, 60, 933–943. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann. Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Liu, B. A survey of entropy of fuzzy variables. J. Uncertain Syst. 2007, 1, 4–13. [Google Scholar]
- Verhoeff, J. Recreatieve Informatica. In Proceedings of the Speech on the Occasion of the 21th Dies Natalis of the Erasmus University Rotterdam, Rotterdam, The Netherlands, 9 November 1984. [Google Scholar]
- Di Crescenzo, A.; Longobardi, M. On cumulative entropies and lifetime estimation. In Methods and Models in Artificial and Natural Computation; Mira, J.M., Ferrández, J.M., Alvarez-Sachez, J.-P., Paz, F., Toledo, J., Eds.; IWINAC Part I, LNCS 5601; Springer: Berlin, Germany, 2009; pp. 132–141. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Kesavan, H.K.; Kapur, J.N. The generalized maximum entropy principle. IEEE Trans. Syst. Man Cybern. 1989, 19, 1042–1052. [Google Scholar] [CrossRef]
- Dai, W.; Chen, X. Entropy of function of uncertain variables. Math. Comput. Model. 2012, 55, 754–760. [Google Scholar] [CrossRef]
- De Sousa, A.M.C.; Tsallis, C. Student’s t abd r-distributions: Unified derivation from an entropic variational principle. Physica A 1997, 236, 52–57. [Google Scholar] [CrossRef]
- Kapur, J.N. Generalized Cauchy and Student’s distribution as maximum-entropy distributions. Proc. Natl. Acad. Sci. India 1988, 58, 235–246. [Google Scholar]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.T. Generalized Boltzmann factors and the maximum entropy principle: Entropies for complex systems. Physica A 2007, 380, 109–114. [Google Scholar] [CrossRef]
- Azzalini, A. A class of distributions which includes the Normal Ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Contreras-Reyes, J.E. Rényi entropy and complexity measure for skew-gaussian distributions and related families. Phys. A Stat. Mech. Appl. 2015, 433, 84–91. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. Maximum entropy principle in statistical inference: Case for non-Shannonian entropies. Phys. Rev. Lett. 2019, 122, 12601. [Google Scholar] [CrossRef]
- Ebanks, B.R. On measures of fuzziness and their representations. J. Math. Anal. Appl. 1983, 94, 24–37. [Google Scholar] [CrossRef]
- Schlittgen, R. Einführung in Die Statistik; Oldenbourg: München, Germany, 1996. [Google Scholar]
- van Staden, P.J. Modeling of Generalized Families of Probability Distributions in the Quantile Statistical Universe. Ph.D. Thesis, Department of Statistics, University of Pretoria, Pretoria, South Africa, 2013. [Google Scholar]
- Mielke, P.W., Jr. Asymptotic beavior of two-sample tests based on powers of ranks for detecting scale and location alternatives. J. Am. Stat. Assoc. 1972, 67, 850–854. [Google Scholar] [CrossRef]
- Mielke, P.W., Jr.; Johnson, E.S. Three-parameter kappa distribution maximum likelihood estimates and likelihood ratio tests. Mon. Weather Rev. 1973, 101, 701–707. [Google Scholar] [CrossRef]
- Ansari, A.R.; Bradley, R.A. Rank-sum tests for dispersion. Ann. Math. Stat. 1960, 31, 1147–1189. [Google Scholar] [CrossRef]
- Mood, A.M. On the asymptotic efficiency of certain nonparametric two-sample tests. Ann. Math. Stat. 1954, 25, 514–522. [Google Scholar] [CrossRef]
- Hosking, J.R.M. The Theory of Probability Weighted Moments; Research Report RC12210; IBM Research: Yorktown Heights, NY, USA, 1986. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Shabri, A.; Jemain, A.A. Fitting the generalized logistic distribution by LQ-Moments. Appl. Math. Sci. 2011, 5, 2663–2676. [Google Scholar]
- Morais, A.L.; Cordeiro, G.M. A Four-Parameter Generalized Logistic Distribution. 2010. Available online: http://www.ime.unicamp.br/sinape/sites/default/files/Lemos-Cordeiro.pdf (accessed on 11 January 2020).
- Nassar, M.M.; Elmasry, A. A study of the generalized logistic distributions. J. Egypt. Math. Soc. 2012, 20, 126–133. [Google Scholar] [CrossRef]
- Tripathi, Y.M.; Mahto, A.K.; Dey, S. Efficient estimation of the PDF and the CDF of a generalized logistic distribution. Ann. Data Sci. 2017, 4, 63–81. [Google Scholar] [CrossRef]
- van Staden, P.J.; King, R.A.R. The quantile-based skew logistic distribution. Stat. Probab. Lett. 2014, 96, 109–116. [Google Scholar] [CrossRef]
- Freimer, M.; Kollia, G.; Mudholkar, G.S.; Lin, C.T. A study of the generalized Tukey lambda family. Commun. Stat. Theory Methods 1988, 17, 3547–3567. [Google Scholar] [CrossRef]
- Chalabi, Y.; Scott, J.; Wuertz, D. Flexible Distribution Modeling with the Generalized Lambda Distribution. 2012. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/43333 (accessed on 11 January 2020).
- King, R.A.R.; MacGillivray, H.L. A starship estimation method for the generalized λ distributions. Aust. N. Z. J. Stat. 1999, 41, 353–374. [Google Scholar] [CrossRef]
- Su, S. Fitting single and mixture of generalized lambda distributions to data via discretized and maximum likelihood methods: GLDEX in R. J. Stat. Softw. 2007, 21, 1–17. [Google Scholar] [CrossRef]
- Su, S. GLDEX: Fitting Single and Mixture of Generalized Lambda Distribution (RS and FMKL) Using Discretized and Maximum Likelihood Methods. R Package Version 1.044. 2012. Available online: http://CRAN.R-project.org/package=GLDEX (accessed on 11 January 2020).
- van Staden, P.J.; Loots, M.T. Method of L moment estimation for the generalized lambda distribution. In Proceedings of the Third Annual Applied Statistics and Research Collaboration Research Conference, Callaghan, Australia, 7–8 December 2009. [Google Scholar]
- Fechner, G.T. Kollektivmaßlehre; Engelmann: Leipzig, Germany, 1897. [Google Scholar]
- Klein, I.; Fischer, M. Skewness by splitting the scale parameter. Commun. Stat. Theory Methods 2006, 35, 1159–1171. [Google Scholar] [CrossRef]
- van Zwet, W.R. Convex Transformations of Random Variables; Mathematical Centre Tracts No. 7; Mathematical Centre: Amsterdam, The Netherlands, 1964. [Google Scholar]
- Arellano-Valle, R.B.; Gomez, H.W.; Quintana, F.A. Statistical inference for a general class of asymmetric distributions. J. Stat. Plan. Inference 2005, 128, 427–443. [Google Scholar] [CrossRef]
- Fernandez, C.; Osiewalski, J.; Steel, M.F.J. Modelling and inference with ν-spherical distributions. J. Am. Stat. Assoc. 1995, 90, 1331–1340. [Google Scholar]
- Mudholkar, G.S.; Srivastava, D.K.; Kollia, G.D. A generalization of the Weibull distribution with applications to the analysis of survival data. J. Am. Stat. Assoc. 1996, 91, 1575–1583. [Google Scholar] [CrossRef]
- Burr, I.W. Cumulative frequency functions. Ann. Math. Stat. 1482, 13, 215–232. [Google Scholar] [CrossRef]
- Shao, Q. Notes on the maximum likelihood estimation for the three-parameter Burr XII distribution. Comput. Stat. Data Anal. 2004, 45, 675–687. [Google Scholar] [CrossRef]
- Ganora, D.; Liao, F. Hydrological applications of the Burr distribution: Practical method for parameter estimation. J. Hydrol. Eng. 2015, 20, 04015024. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Discussion of models for extremes using the extended three parameter Burr XII system with applications to the flood frequency analysis. Hydrol. Sci. J. 2006, 51, 1203–1204. [Google Scholar] [CrossRef]
- Shao, Q.; Wong, H.; Xia, J.; Ip, W. Models for extremes using the extended three-parameter Burr XII system with application to flood frequency analysis. Hydrol. Sci. J. 2004, 49, 685–702. [Google Scholar] [CrossRef]
- Usta, I. Different estimation methods for the parameters of the extended Burr XII distribution. J. Appl. Stat. 2013, 40, 397–414. [Google Scholar] [CrossRef]
| Max. | Max. | |||
|---|---|---|---|---|
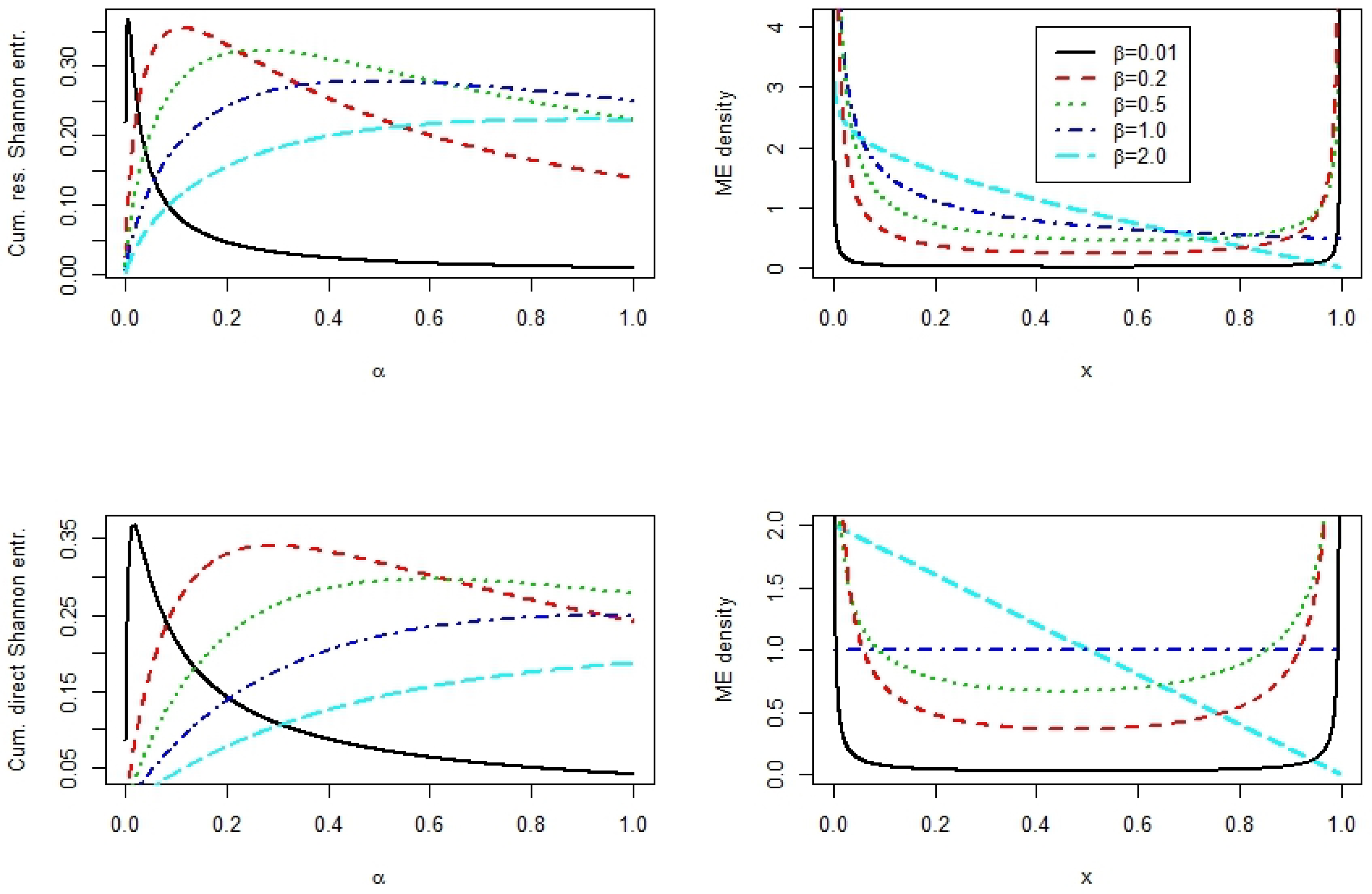
| 0.01 | 0.006 | 0.3678 | 0.017 | 0.3677 |
| 0.20 | 0.111 | 0.3543 | 0.290 | 0.3408 |
| 0.50 | 0.259 | 0.3222 | 0.595 | 0.2970 |
| 1.00 | 0.482 | 0.2778 | 1.000 | 0.2500 |
| 2.00 | 0.905 | 0.2226 | 1.000 | 0.1869 |
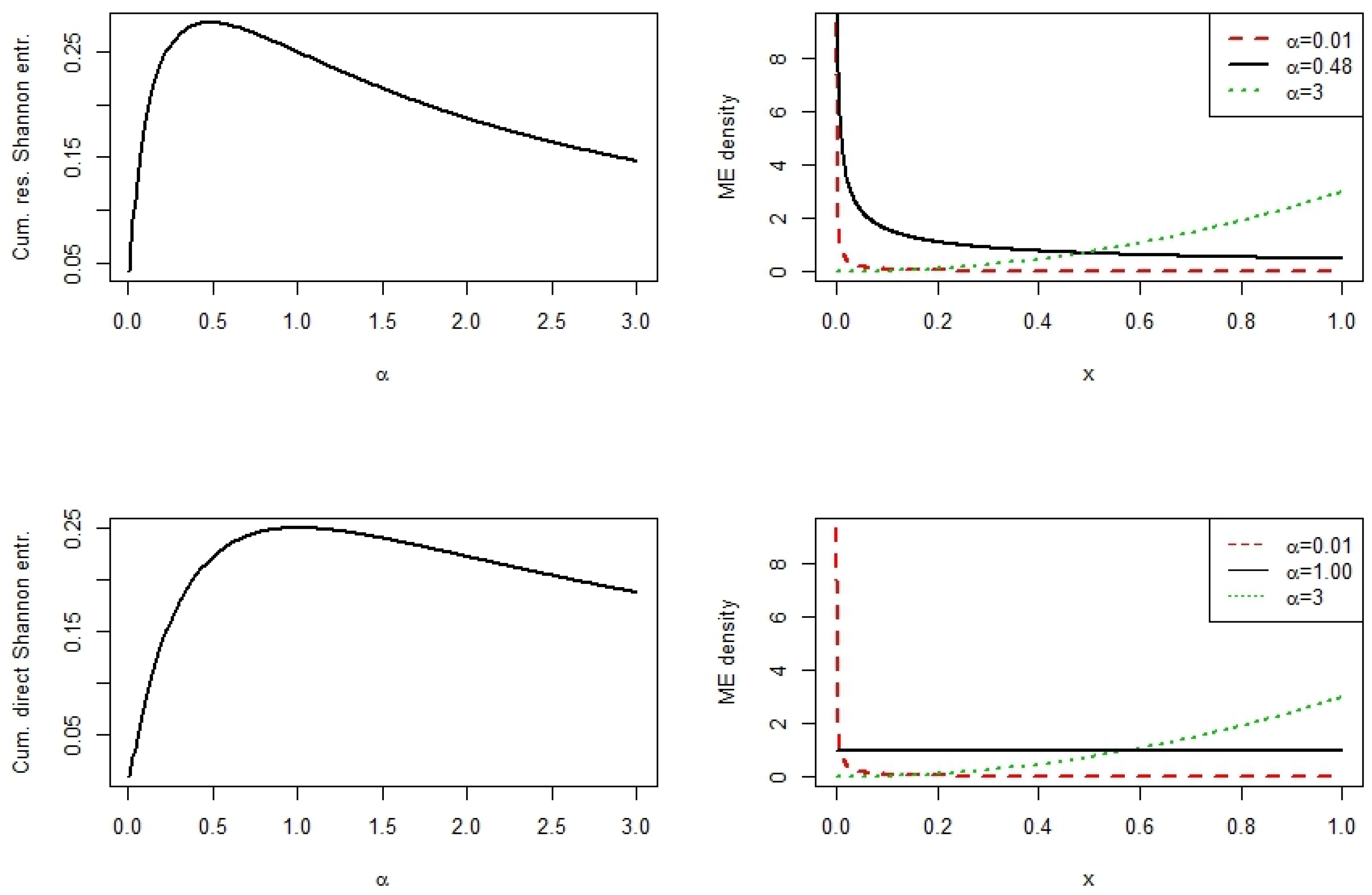
| 0.01 | 0.1836 | 0.0826 |
| 0.48 | 0.2779 | 0.2191 |
| 1.00 | 0.2500 | 0.2500 |
| 3.00 | 0.1464 | 0.1876 |
| No. | App. | ME distr. | ||
|---|---|---|---|---|
| Fixed mean and variance, without | ||||
| 1 | Shannon | logistic | ||
| 2 | Havrda-Charvát | Tukey | ||
| 3 | Appendix A.1 | Leik | bimodal | |
| 4 | Appendix A.1 | Gini | uniform | |
| 5 | Appendix A.1 | Mielke | symm. beta | |
| 6 | Appendix A.2 | Havrda-Charvát | general. logistic | |
| like | ||||
| 7 | Appendix A.3 | non-symm. | skewed logistic | |
| Shannon | ||||
| 8 | Appendix A.3 | non-symm. | skewed Tukey | |
| Havrda-Charvát | ||||
| 9 | Appendix A.4 | GMaxEnt | general. Tukey | |
| 10 | Appendix A.5 | GMaxEnt | skewed normal | |
| Fixed mean and k-th moment, with | ||||
| 11 | Appendix A.6 | Shannon | Weibull | |
| 12 | Appendix A.7 | Havrda-Charvát | ext. Burr XII | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klein, I.; Doll, M. (Generalized) Maximum Cumulative Direct, Residual, and Paired Φ Entropy Approach. Entropy 2020, 22, 91. https://doi.org/10.3390/e22010091
Klein I, Doll M. (Generalized) Maximum Cumulative Direct, Residual, and Paired Φ Entropy Approach. Entropy. 2020; 22(1):91. https://doi.org/10.3390/e22010091
Chicago/Turabian StyleKlein, Ingo, and Monika Doll. 2020. "(Generalized) Maximum Cumulative Direct, Residual, and Paired Φ Entropy Approach" Entropy 22, no. 1: 91. https://doi.org/10.3390/e22010091
APA StyleKlein, I., & Doll, M. (2020). (Generalized) Maximum Cumulative Direct, Residual, and Paired Φ Entropy Approach. Entropy, 22(1), 91. https://doi.org/10.3390/e22010091




