Modeling Bed Shear Stress Distribution in Rectangular Channels Using the Entropic Parameter
Abstract
1. Introduction
2. The Proposed Model
2.1. Definition of the Tsallis Entropy and Its Maximization
2.2. Reformulation of the Lagrange Multipliers
3. Experimental Data
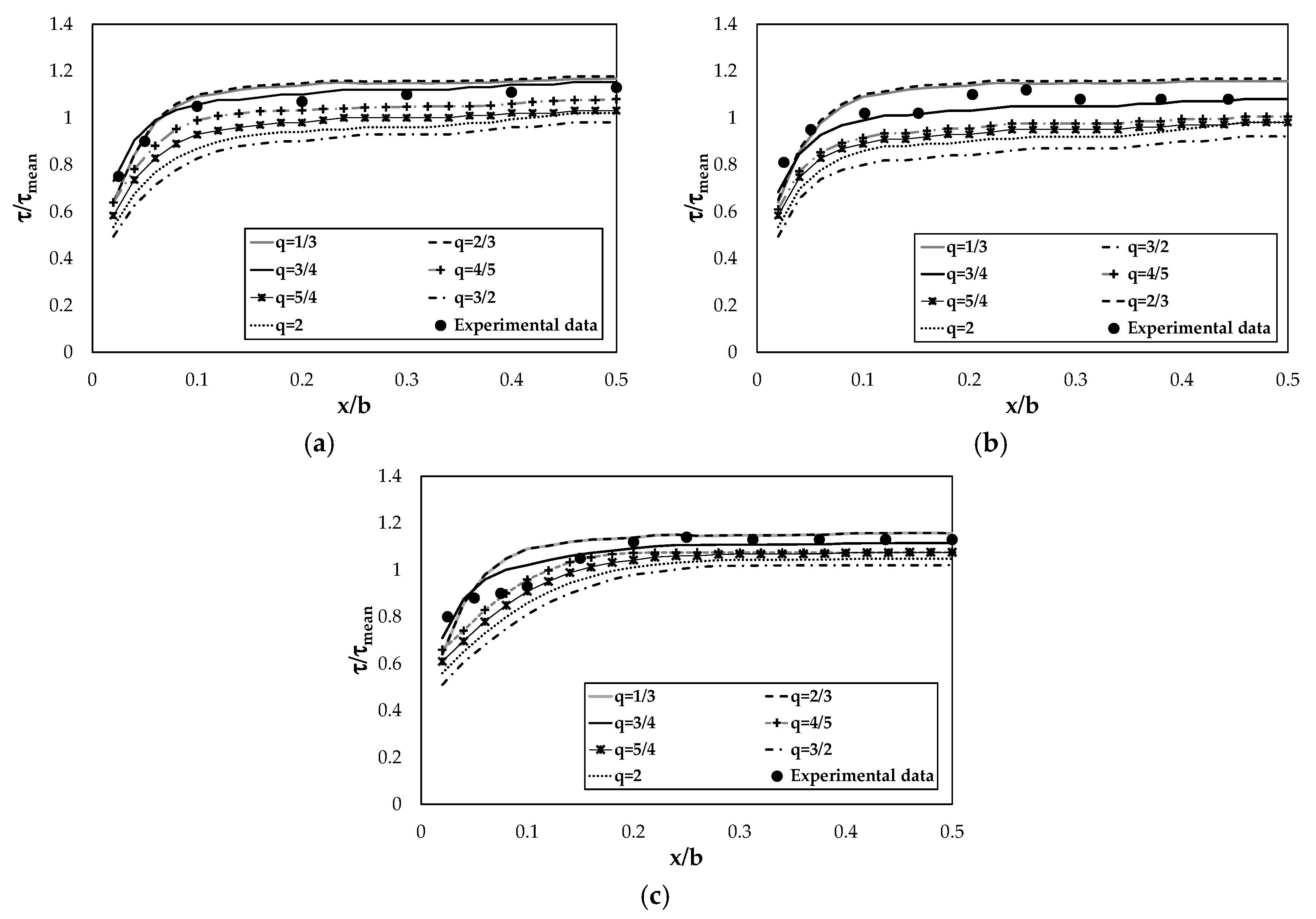
4. Discussion of Results
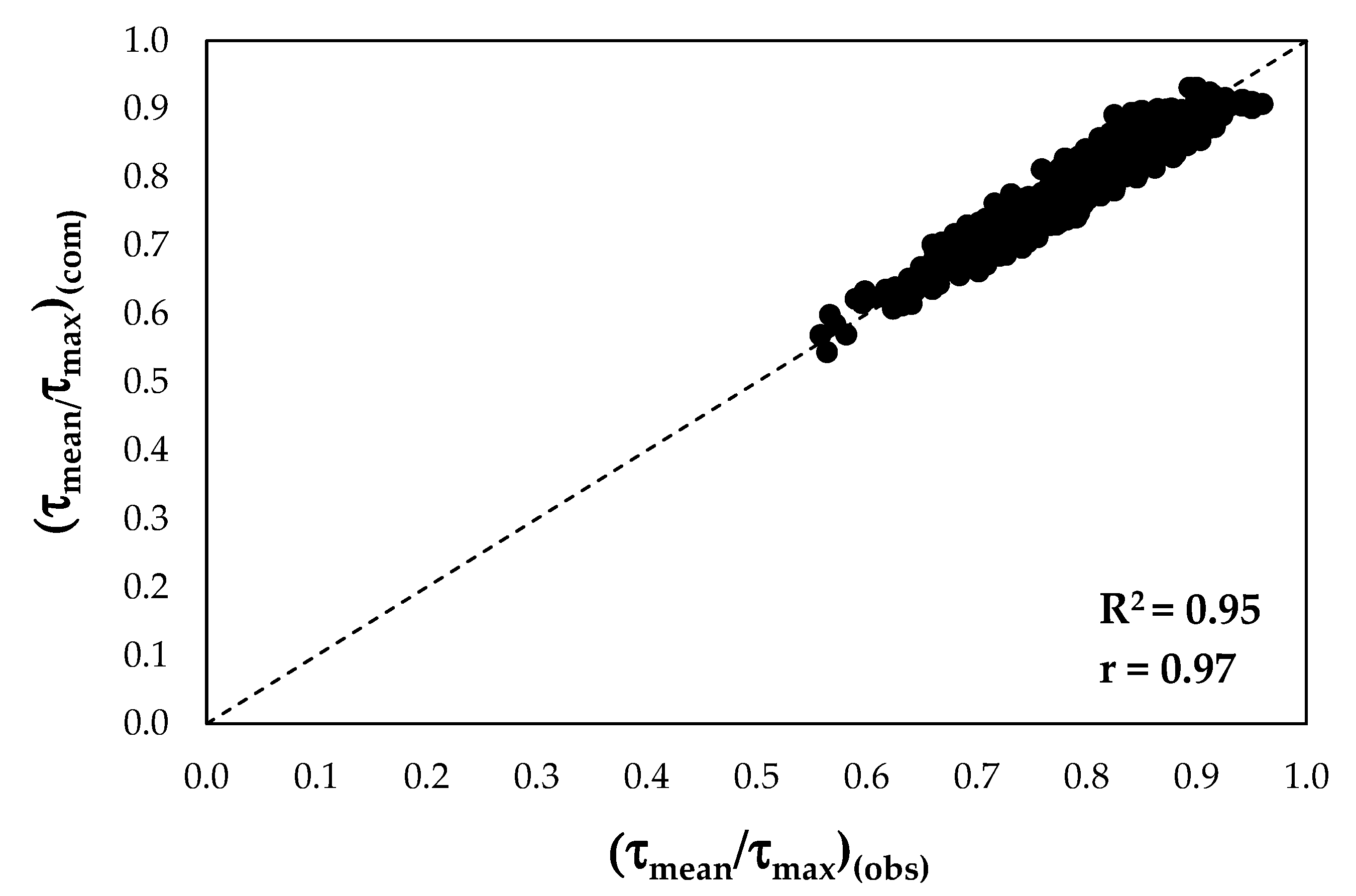
4.1. Validation of Proposed Model
4.2. Model Performance in Estimating Bed Shear Stress
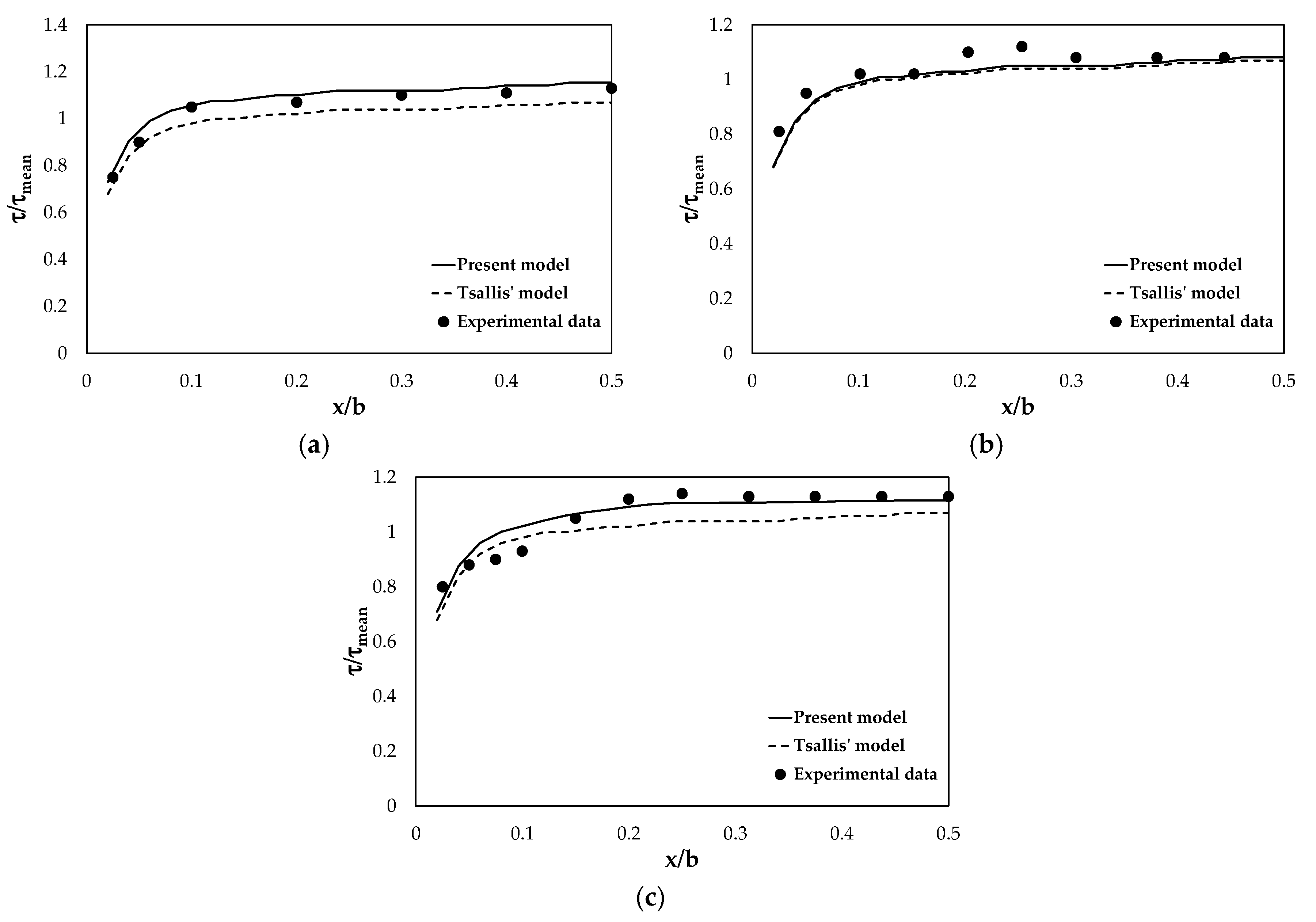
4.3. Simplified Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rhodes, D.G.; Knight, D.W. Distribution of shear force on the boundary of a smooth rectangular duct. J. Hydraul. Eng. 1994, 120, 787–807. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Chien, N.; Wan, Z.H. Mechanics of Sediment Transport; ASCE Press: New York, NY, USA, 1999. [Google Scholar]
- Khodashenas, S.R.; Paquier, A. River bed deformation calculated from boundary shear stress. J. Hydraul. Res. 2002, 40, 603–609. [Google Scholar]
- Moramarco, T.; Ammari, A.; Burnelli, A.; Mirauda, D.; Pascale, V. Entropy Theory Application for Flow Monitoring in Natural Channels. In Proceedings of the iEMSS 4th Biennial Meeting: International Congress on Environmental Modelling and Software (iEMSs 2008), Barcelona, Spain, 6–10 July 2008; pp. 430–437. [Google Scholar]
- Greco, M.; Mirauda, D.; Plantamura Volpe, A. Manning’s roughness through the entropy parameter for steady open channel flows in low submergence. Procedia Eng. 2014, 70, 773–780. [Google Scholar] [CrossRef]
- Mirauda, D.; Ostoich, M. Assessment of Pressure Sources and Water Body Resilience: An Integrated Approach for Action Planning in a Polluted River Basin. Int. J. Environ. Res. Public Health 2018, 15, 390. [Google Scholar] [CrossRef]
- Mirauda, D.; De Vincenzo, A.; Pannone, M. Simplified entropic model for the evaluation of suspended load concentration. Water 2018, 10, 378. [Google Scholar] [CrossRef]
- Choo, Y.M.; Yun, G.S.; Choo, T.H. A research on the estimation of coefficient roughness in open channel applying entropy concept. Environ. Earth Sci. 2018, 77, 624. [Google Scholar] [CrossRef]
- Mirauda, D.; De Vincenzo, A.; Pannone, M. Statistical characterization of flow field structure in evolving braided gravel beds. Spat. Stat. 2019, 34, 100268. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, J. Estimating the Bed-Load Layer Thickness in Open Channels by Tsallis Entropy. Entropy 2019, 21, 123. [Google Scholar] [CrossRef]
- Knight, D.W. Boundary shear in smooth and rough channels. J. Hydraul. Div. ASCE 1981, 107, 839–851. [Google Scholar]
- Yang, S.Q.; Lim, S.Y. Boundary shear stress distributions in trapezoidal channels. J. Hydraul. Res. 2005, 43, 98–102. [Google Scholar] [CrossRef]
- Bares, V.; Jirak, J.; Pollert, J. Bottom shear stress in unsteady sewer flow. Water Sci. Technol. 2006, 54, 93–100. [Google Scholar] [CrossRef]
- Knight, D.W.; Omran, M.; Tang, X. Modeling depth averaged velocity and boundary shear in trapezoidal channels with secondary flows. J. Hydraul. Eng. 2007, 133, 39–47. [Google Scholar] [CrossRef]
- Yang, S.Q. Depth-averaged shear stress and velocity in open-channel flows. J. Hydraul. Eng. 2010, 136, 952–958. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Farshi, F.; Chamani, M.R. Boundary shear stress in smooth trapezoidal open channel flows. J. Hydraul. Eng. 2013, 139, 205–212. [Google Scholar] [CrossRef]
- Martinez-Vazquez, P.; Sharifi, S. Modelling boundary shear stress distribution in open channels using a face recognition technique. J. Hydroinform. 2017, 19, 157–172. [Google Scholar] [CrossRef]
- Sheikh Khozani, Z.; Bonakdari, H.; Ebtehaj, I. An analysis of shear stress distribution in circular channels with sediment deposition based on Gene Expression Programming. Int. J. Sediment Res. 2017, 32, 575–584. [Google Scholar] [CrossRef]
- Milukow, H.A.; Binns, A.D.; Adamowski, J.; Bonakdari, H.; Gharabaghi, B. Estimation of the Darcy-Weisbach friction factor for ungauged streams using gene expression programming and extreme learning machines. J. Hydrol. 2019, 568, 311–321. [Google Scholar] [CrossRef]
- Bonakdari, H. Establishment of relationship between mean and maximum velocities in narrow sewers. J. Environ. Manag. 2012, 113, 474–480. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. One-dimensional velocity distribution in open channels using Tsallis entropy. J. Hydrol. Eng. 2013, 19, 290–298. [Google Scholar] [CrossRef]
- Greco, M.; Mirauda, D. An Entropy Based Velocity Profile for Steady Flows with Large-Scale Roughness. In Engineering Geology for Society and Territory, River Basins, Reservoir Sedimentation and Water Resources; Lollino, G., Arattano, M., Rinaldi, M., Giustolisi, O., Marechal, J.C., Grant, G.E., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 3, pp. 641–645. ISBN 978-3-319-09054-2. [Google Scholar]
- Greco, M.; Mirauda, D. Entropy parameter estimation in large-scale roughness open channel. J. Hydrol. Eng. 2015, 20, 04014047:1–04014047:6. [Google Scholar] [CrossRef]
- Farina, G.; Alvisi, S.; Franchini, M.; Corato, G.; Moramarco, T. Estimation of bathymetry (and discharge) in natural river cross-sections by using an entropy approach. J. Hydrol. 2015, 527, 20–29. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Mohammadian, A. A method based on the Tsallis entropy for characterizing threshold channel bank profiles. Phys. A Stat. Mech. Appl. 2019, 526, 121089. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K. One-dimensional velocity distribution in open channels using Renyi entropy. Stoch. Environ. Res. Risk Assess. 2017, 31, 949–959. [Google Scholar] [CrossRef]
- Kundu, S. Two-parameter Mittag-Leffler solution of space fractional advection-diffusion equation for sediment suspension in turbulent flows. J. Environ. Eng. 2018, 144, 06018005. [Google Scholar]
- Luo, H.; Singh, V.P.; Schmidt, A. Comparative study of 1D entropy-based and conventional deterministic velocity distribution equations for open channel flows. J. Hydrol. 2018, 563, 679–693. [Google Scholar] [CrossRef]
- Singh, V.P. Introduction to Tsallis Entropy Theory in Water Engineering; CRC Press: Boca Raton, FL, USA; Taylor and Francis: Boca Raton, FL, USA, 2016. [Google Scholar]
- Termini, D.; Moramarco, T. Dip phenomenon in high-curved turbulent flows and application of entropy theory. Water 2018, 10, 306. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, J.; Dou, J.; Peng, D. An Expression for Velocity Lag in Sediment-Laden Open-Channel Flows Based on Tsallis Entropy Together with the Principle of Maximum Entropy. Entropy 2019, 21, 522. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of entropy concept in open-channel flow study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Sterling, M.; Knight, D.W. An attempt at using the entropy approach to predict the transverse distribution of boundary shear stress in open channel flow. Stoch. Environ. Res. Risk Assess. 2002, 16, 127–142. [Google Scholar] [CrossRef]
- Sheikh, Z.; Bonakdari, H. Prediction of boundary shear stress in circular and trapezoidal channels with entropy concept. Urban Water J. 2015, 13, 629–636. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Bonakdari, H. Formulating the shear stress distribution in circular open channels based on the Renyi entropy. Phys. A Stat. Mech. Appl. 2018, 490, 114–126. [Google Scholar] [CrossRef]
- Bonakdari, H.; Sheikh, Z.; Tooshmalani, M. Comparison between Shannon and Tsallis entropies for prediction of shear stress distribution in open channels. Stoch. Environ. Res. Risk. Assess. 2015, 29, 1–11. [Google Scholar] [CrossRef]
- Bonakdari, H.; Tooshmalani, M.; Sheikh, Z. Predicting Shear Stress Distribution in Rectangular Channels Using Entropy Concept. Int. J. Eng. 2015, 28, 360–367. [Google Scholar]
- Kazemian-Kale-Kale, A.; Hossein Bonakdari, H.; Gholami, A.; Sheikh Khozani, Z.; Akhtari, A.A.; Gharabaghi, B. Uncertainty analysis of shear stress estimation in circular channels by Tsallis entropy. Physica A 2018, 510, 558–576. [Google Scholar] [CrossRef]
- Kazemian-Kale-Kale, A.; Bonakdari, H.; Gholami, A.; Gharabaghi, B. The uncertainty of the Shannon entropy model for shear stress distribution in circular channels. Int. J. Sediment Res. 2020, 35, 57–68. [Google Scholar] [CrossRef]
- Sheikh Khozani, Z.; Wan Mohtar, W.H.M. Investigation of New Tsallis-Based Equation to Predict Shear Stress Distribution in Circular and Trapezoidal Channels. Entropy 2019, 21, 1046. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell. Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Renyi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Kumbhakar, M.; Ghoshal, K. Two dimensional velocity distribution in open channels using Renyi entropy. Physica A 2016, 450, 546–559. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Derivation of Rouse equation for sediment concentration using Shannon entropy. Physica A 2017, 465, 494–499. [Google Scholar] [CrossRef]
- Ghoshal, K.; Kumbhakar, M.; Singh, V.P. Distribution of sediment concentration in debris flow using Rényi entropy. Phys. A Stat. Mech. Appl. 2019, 521, 267–281. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Misirli, F.; Gupta, H.V.; Sorooshian, S.; Thiemann, M. Bayesian recursive estimation of parameter and output uncertainty for watershed models. In Calibration of Watershed Models, Water Science Application, 1st ed.; Duan, Q.J., Gupta, H.V., Sorooshian, S., Rousseau, A.N., Turcotte, R., Eds.; AGU100: Washington, DC, USA, 2003; pp. 113–124. [Google Scholar]
- Corato, G.; Melone, F.; Moramarco, T.; Singh, V.P. Uncertainty analysis of flow velocity estimation by a simplified entropy model. Hydrol. Process. 2014, 28, 581–590. [Google Scholar] [CrossRef]
- Singh, V.P.; Luo, H. Entropy theory for distribution of one dimensional velocity in open channels. J. Hydrol. Eng. 2011, 16, 725–735. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.P. Entropy Theory for Two-Dimensional Velocity Distribution. J. Hydrol. Eng. 2011, 16, 303–315. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics: I. Phys. Rev. 1957, 106, 620–930. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics: II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E. On the rationale of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Mirauda, D.; Pannone, M.; De Vincenzo, A. An entropic model for the assessment of stream-wise velocity dip in wide open channels. Entropy 2018, 20, 69. [Google Scholar] [CrossRef]
- Guy, H.P.; Simons, D.B.; Richardson, E.V. Summary of Alluvial Channel Data from Flume Experiments, 1956–1961; Professional Paper; US Government Printing Office: Washington, DC, USA, 1966.
- Coleman, N.L. Effects of suspended sediment on the Open-Channel velocity distribution. Water Resour. Res. 1986, 22, 1377–1384. [Google Scholar] [CrossRef]
- Valiani, A. Nuove esperienze su correnti uniformi con trasporto di sedimenti in sospensione: La metodologia sperimentale ed alcuni risultati. In Seminario su Trasporto Solido ed Evoluzione Morfologica dei Corsi D’acqua; IRIS Università degli Studi di Ferrara: Ferrara, Italy, 1988. [Google Scholar]
- Lyn, D.A. Turbulence and Turbulent Transport in Sediment-Laden Open-Channel Flows. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1987. [Google Scholar]
- Tominaga, A.; Nezu, I.; Ezaki, K.; Nakagawa, H. Three-dimensional turbulent structure in straight open channel flows. J. Hydraul. Res. 1989, 27, 149–173. [Google Scholar] [CrossRef]
- Kironoto, B.; Graf, W.H. Turbulence characteristics in rough uniform open-channel flow. Proc. Inst. Civ. Eng. Water Marit. Energy 1994, 106, 333–344. [Google Scholar] [CrossRef]
- Graf, W.H.; Cellino, M. Suspension flows in open channels; experimental study. J. Hydraul. Res. 2002, 40, 435–447. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Demissie, M. 2004. Hydrologic modelling of the Iroquois River watershed using HSPF and SWAT. JAWRA 2007, 41, 343–360. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–890. [Google Scholar] [CrossRef]
- Mirauda, D.; Russo, M.G. Information Entropy Theory Applied to the Dip-Phenomenon Analysis in Open Channel Flows. Entropy 2019, 21, 554. [Google Scholar] [CrossRef]
- Xia, R. Relation between mean and maximum velocities in a natural river. J. Hydraul. Eng. 1997, 123, 720–723. [Google Scholar] [CrossRef]
- Chiu, C.L.; Said, C.A.A. Maximum and mean velocities and entropy in open-channel flow. J. Hydraul. Eng. 1995, 121, 26–35. [Google Scholar] [CrossRef]
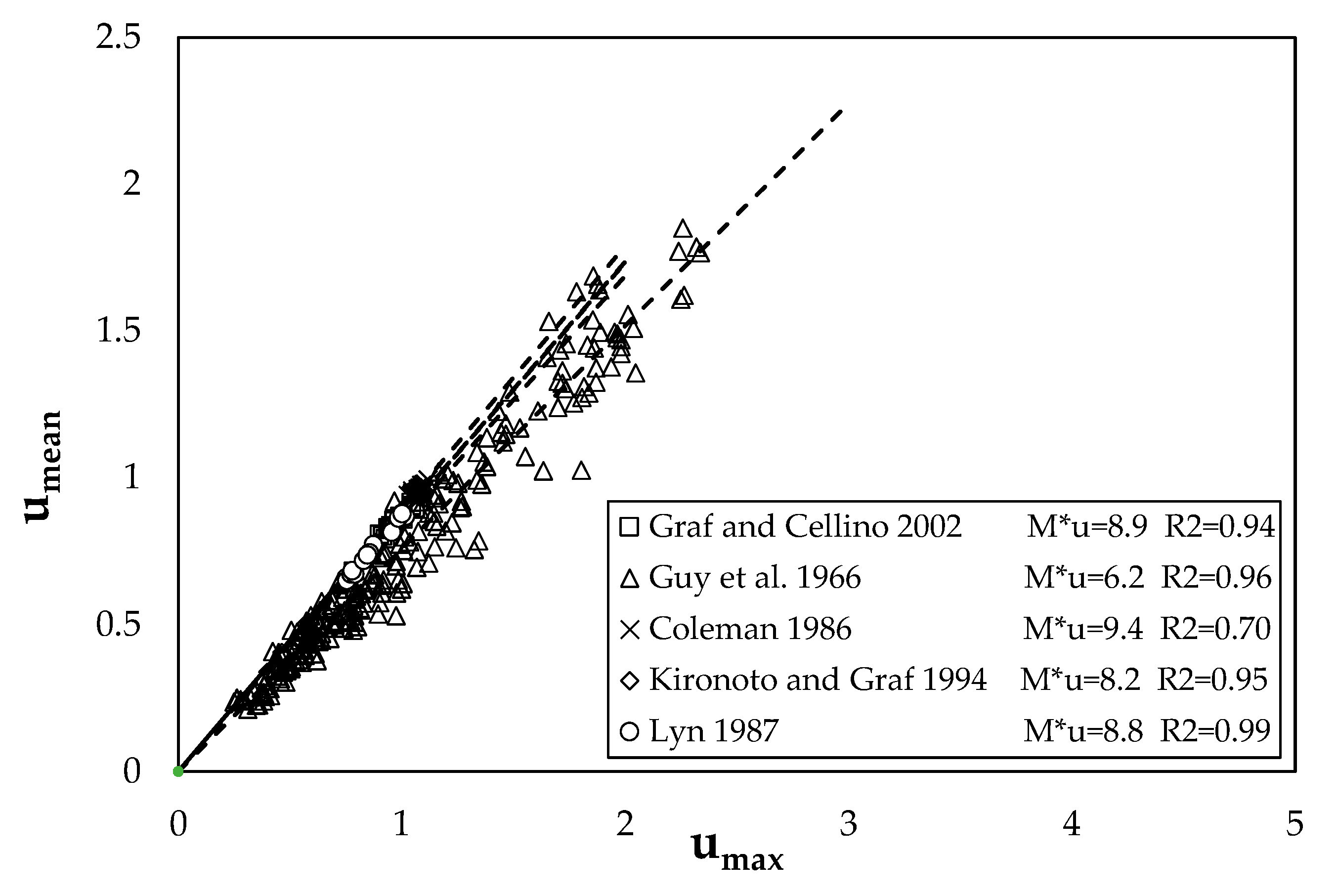
| Datasets | Q (m3/s) | Ar | umean (m/s) | umax (m/s) | τmean (N/m2) | τmax (N/m2) |
|---|---|---|---|---|---|---|
| Guy et al. (1966) | 0.05–0.64 | 7.00–29.00 | 0.21–1.85 | 0.25–2.34 | 0.12–14.91 | 0.15–16.60 |
| Coleman (1986) | 0.064 | 2.04–2.13 | 0.93–0.99 | 1.03–1.12 | 1.60–2.02 | 2.88–2.98 |
| Valiani (1988) | 0.023–0.024 | 3.63–3.83 | 0.63–0.66 | 0.69–0.74 | 0.69–0.88 | 0.72–0.96 |
| Lyn (1987) | 0.009–0.013 | 4.05–4.70 | 0.63–0.87 | 0.75–1.02 | 0.88–1.61 | 0.96–1.88 |
| Tominaga et al. (1989) | 0.008–0.015 | 2.01–8.00 | 0.19–0.40 | 0.23–0.46 | 0.08–0.70 | 0.11–0.78 |
| Kironoto and Graf (1994) | 0.022–0.081 | 2.07–6.90 | 0.34–0.50 | 0.40–0.58 | 0.21–0.82 | 0.48–1.53 |
| Graf and Cellino (2002) | 0.049–0.065 | 5.00 | 0.68–0.92 | 0.79–1.08 | 0.25–2.52 | 0.78–3.02 |
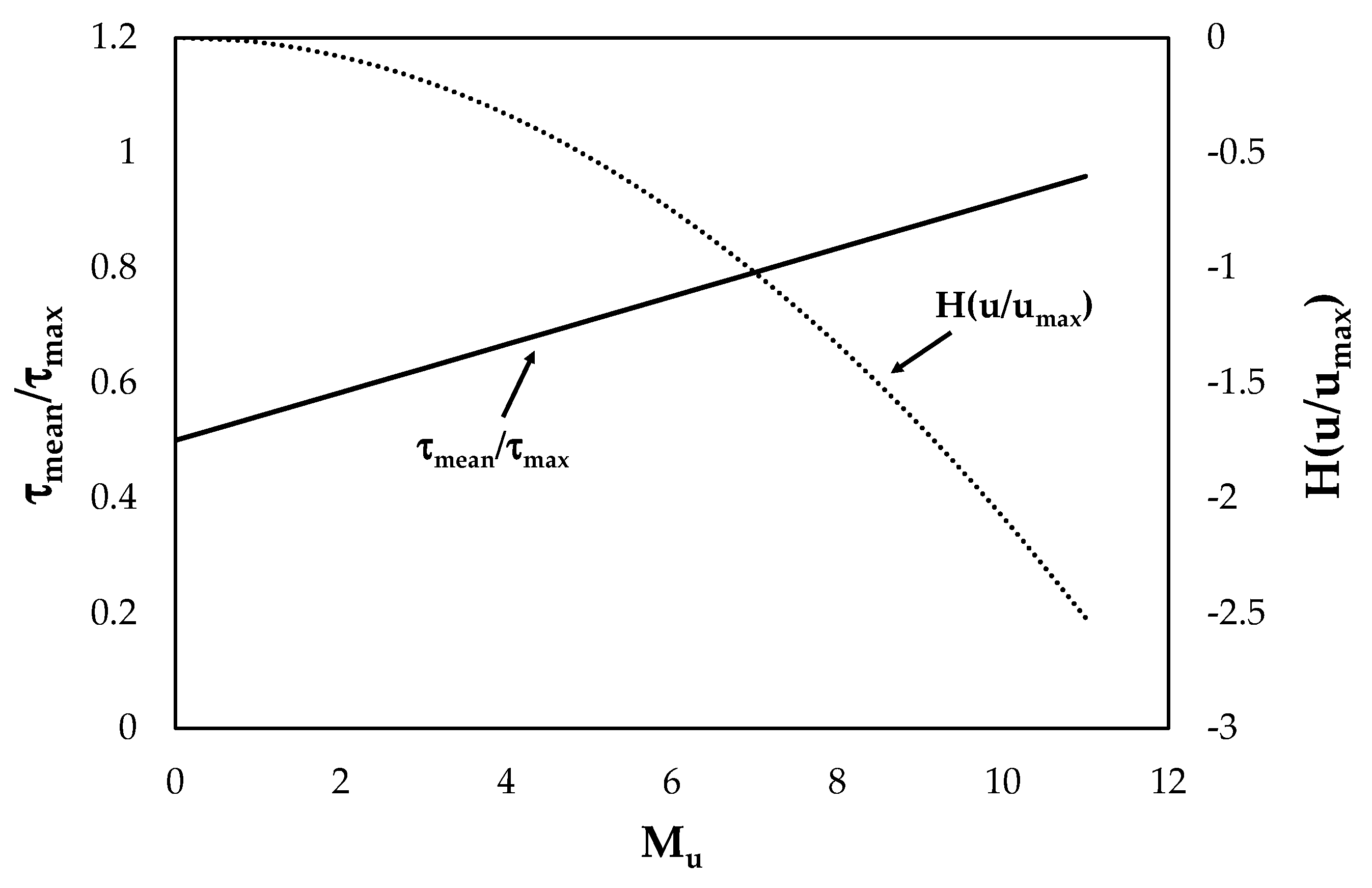
| Datasets | Mu | H (u/umax) | τmean/τmax |
|---|---|---|---|
| Guy et al. (1966) | 1.05–10.19 | −0.02–−2.16 | 0.56–0.93 |
| Coleman (1986) | 9.21–9.94 | −1.77–−2.06 | 0.84–0.95 |
| Valiani (1988) | 9.45–10.36 | −1.86–−2.24 | 0.89–0.96 |
| Lyn (1987) | 8.34–9.17 | −1.45–−1.75 | 0.81–0.92 |
| Tominaga et al. (1989) | 8.59–9.48 | −1.54–−1.87 | 0.82–0.92 |
| Kironoto and Graf (1994) | 7.51–9.14 | −1.17–−1.74 | 0.78–0.91 |
| Graf and Cellino (2002) | 8.23–9.45 | −1.41–−1.86 | 0.82–0.91 |
| Performance Rating | RSR | NSE | PBIAS |
|---|---|---|---|
| Very good | 0.00 ≤ RSR ≤ 0.50 | 0.75 < NSE ≤ 1.00 | PBIAS < ±10 |
| Good | 0.50 < RSR ≤ 0.60 | 0.65 < NSE ≤ 0.75 | ±10 ≤ PBIAS < ±15 |
| Satisfactory | 0.60 < RSR ≤ 0.70 | 0.50 < NSE ≤ 0.65 | ±15 ≤ PBIAS < ±25 |
| Unsatisfactory | RSR > 0.70 | NSE ≤ 0.50 | PBIAS ≥ ±25 |
| Index | Value |
|---|---|
| RMSE | 0.32 |
| MAE | 0.46 |
| RSR | 0.12 |
| NSE | 0.93 |
| PBIAS | 8.65 |
| Index | Value |
|---|---|
| R2 | 0.92 |
| r | 0.95 |
| RMSE | 0.35 |
| RSR | 0.13 |
| MAE | 0.60 |
| NSE | 0.87 |
| PBIAS | 11.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirauda, D.; Russo, M.G. Modeling Bed Shear Stress Distribution in Rectangular Channels Using the Entropic Parameter. Entropy 2020, 22, 87. https://doi.org/10.3390/e22010087
Mirauda D, Russo MG. Modeling Bed Shear Stress Distribution in Rectangular Channels Using the Entropic Parameter. Entropy. 2020; 22(1):87. https://doi.org/10.3390/e22010087
Chicago/Turabian StyleMirauda, Domenica, and Maria Grazia Russo. 2020. "Modeling Bed Shear Stress Distribution in Rectangular Channels Using the Entropic Parameter" Entropy 22, no. 1: 87. https://doi.org/10.3390/e22010087
APA StyleMirauda, D., & Russo, M. G. (2020). Modeling Bed Shear Stress Distribution in Rectangular Channels Using the Entropic Parameter. Entropy, 22(1), 87. https://doi.org/10.3390/e22010087






