Control of the Geometric Phase in Two Open Qubit–Cavity Systems Linked by a Waveguide
Abstract
1. Introduction
2. The Physical Model and Its Differential Equations
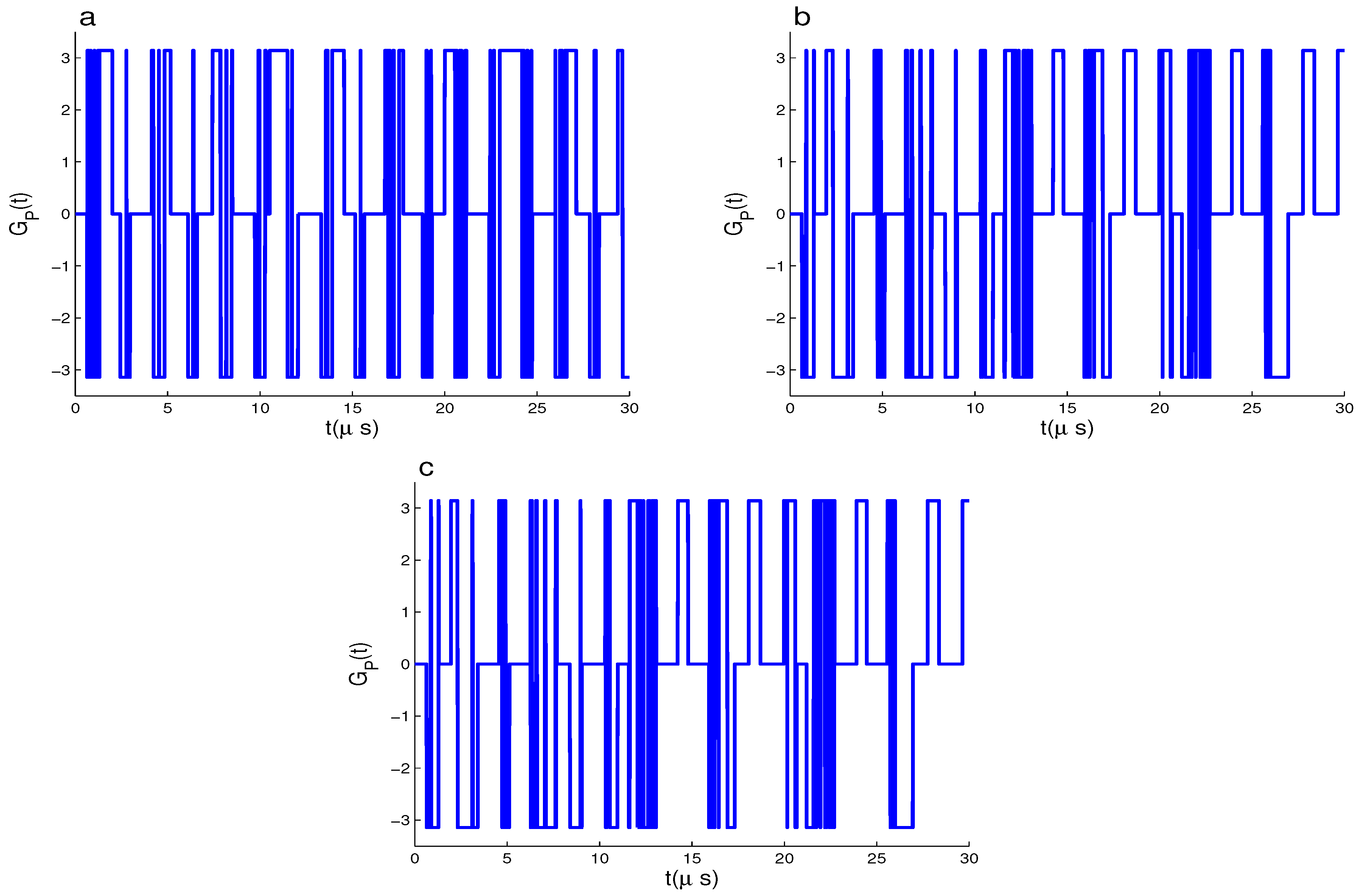
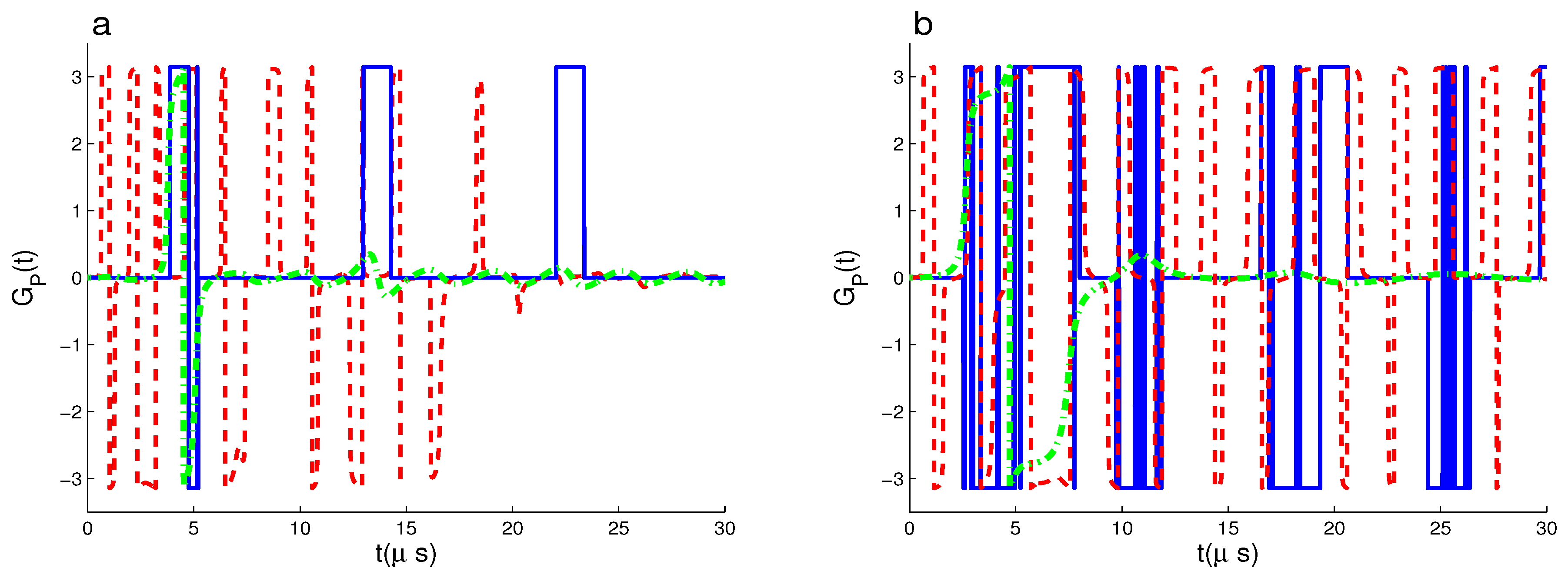
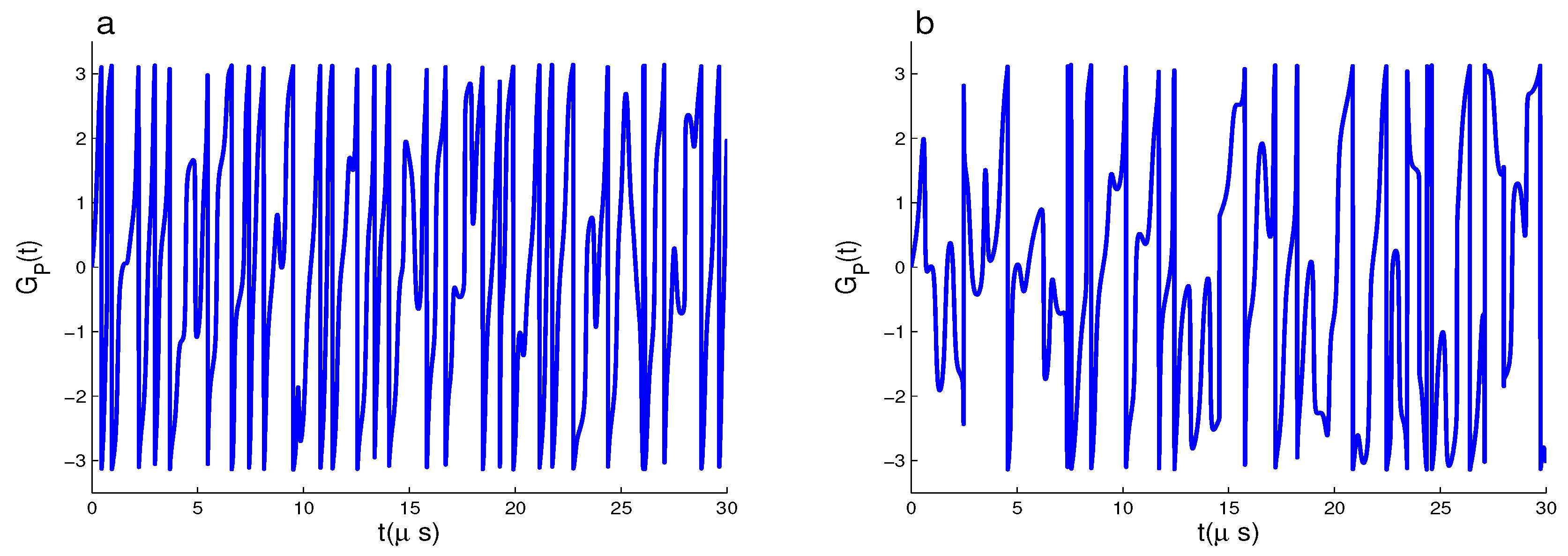
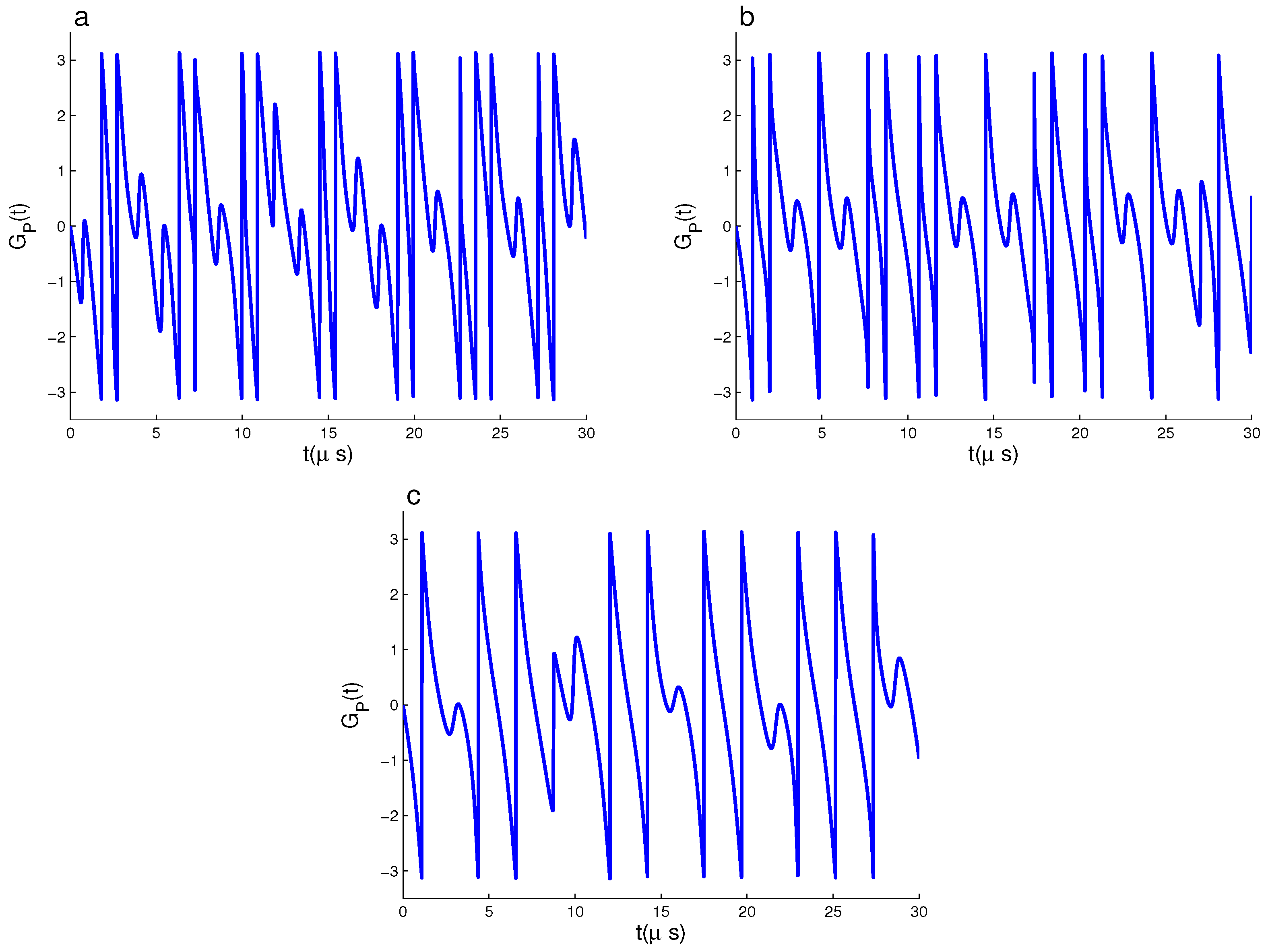
3. Geometric Phase and Its Computational Results
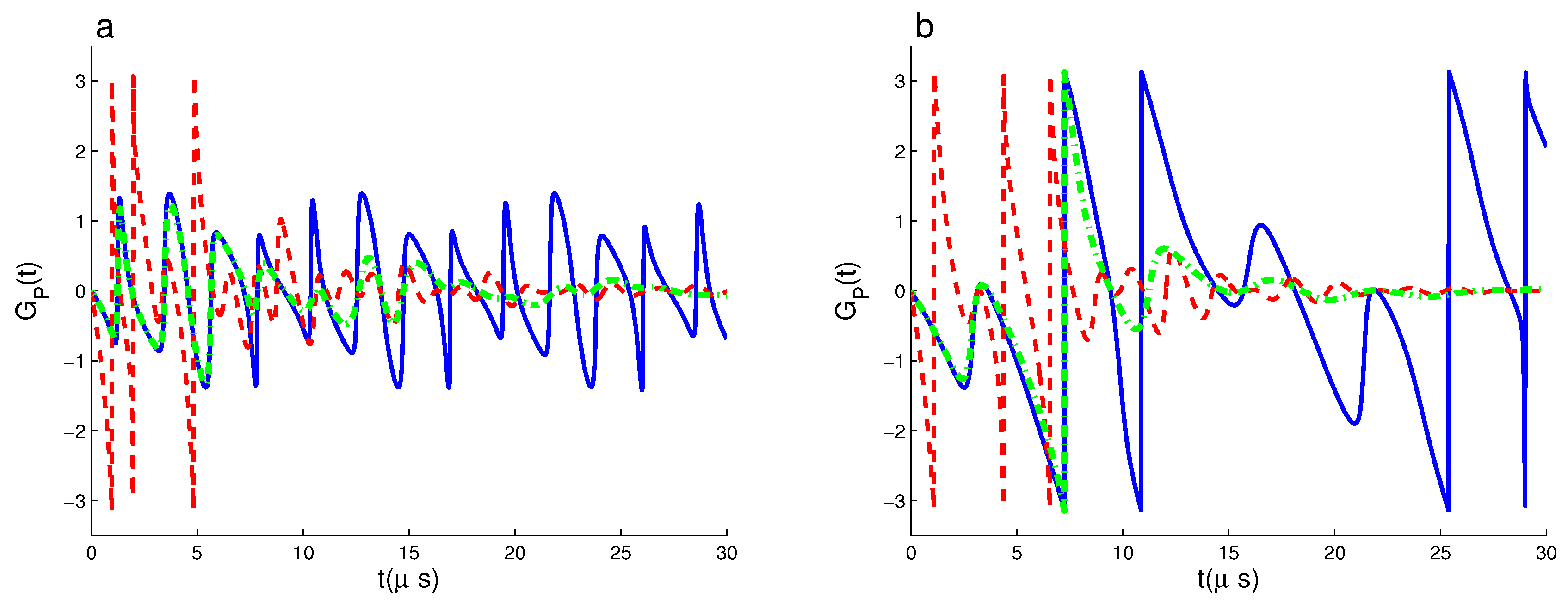
3.1. Dynamics of GP of
3.2. Dynamics of GP of
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Louisell, W.H. Quantum Statistical Properties of Radiation; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Milburn, G.J. Intrinsic decoherence in quantum mechanics. Phys. Rev. A 1991, 44, 5401. [Google Scholar] [CrossRef]
- Barnett, S.M.; Knight, P.L. Dissipation in a fundamental model of quantum optical resonance. Phys. Rev. A 1986, 33, 2444. [Google Scholar] [CrossRef]
- Puri, R.R.; Agarwal, G.S. Finite-Q cavity electrodynamics: Dynamical and statistical aspects. Phys. Rev. A 1987, 35, 3433. [Google Scholar] [CrossRef]
- Moya-Cessa, H. Decoherence in atomfield interactions: A treatment using superoperator techniques. Phys. Rep. 2006, 432, 1–41. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A. The effects of thermal photons on entanglement dynamics for a dispersive JaynesCummings model. Phys. Lett. A 2008, 372, 3699. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Hashem, M.; Eleuch, H. Enhancing the Generated Stable Correlation in a Dissipative System of Two Coupled Qubits inside a Coherent Cavity via Their Dipole-Dipole Interplay. Entropy 2019, 21, 672. [Google Scholar] [CrossRef]
- Jones, J.A.; Vedral, V.; Ekert, A.; Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 2000, 403, 869. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 1956, 44, 398–417. [Google Scholar] [CrossRef]
- Wagh, A.G.; Rakhecha, V.C.; Summhammer, J.; Badurek, G.; Weinfurter, H.; Allman, B.E.; Kaiser, H.; Hamacher, K.; Jacobson, D.L.; Werner, S.A. Experimental Separation of Geometric and Dynamical Phases Using Neutron Interferometry. Phys. Rev. Lett. 1997, 78, 755. [Google Scholar] [CrossRef]
- Wagh, A.G.; Rakhecha, V.C.; Fischer, P.; Ioffe, A. Neutron Interferometric Observation of Noncyclic Phase. Phys. Rev. Lett. 1998, 81, 1992. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. London A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Aharonov, Y.; Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 1987, 58, 1593. [Google Scholar] [CrossRef]
- Samuel, J.; Bhandari, R. General Setting for Berry’s Phase. Phys. Rev. Lett. 1988, 60, 2339. [Google Scholar] [CrossRef]
- Marzlin, K.-P.; Ghose, S.; Sanders, B.C. Geometric Phase Distributions for Open Quantum Systems. Phys. Rev. Lett. 2004, 93, 260402. [Google Scholar] [CrossRef]
- Duan, L.-M.; Cirac, J.I.; Zoller, P. Geometric Manipulation of Trapped Ions for Quantum Computation. Science 2001, 292, 1695–1697. [Google Scholar] [CrossRef]
- Recati, A.; Calarco, T.; Zanardi, P.; Cirac, J.I.; Zoller, P. Holonomic quantum computation with neutral atoms. Phys. Rev. A 2002, 66, 032309. [Google Scholar] [CrossRef]
- Liu, Y.-X.; Sun, C.P.; Nori, F. Scalable superconducting qubit circuits using dressed states. Phys. Rev. A 2006, 74, 052321. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Geometric phase in cavity QED containing a nonlinear optical medium and a quantum well. J. Mod. Opt. 2015, 62, 1630–1637. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Obada, A.-S.F. Asymptotic geometric phase and purity for phase qubit dispersively coupled to lossy LC circuit. Ann. Phys. 2011, 326, 2369–2376. [Google Scholar] [CrossRef]
- Bouchene, M.A.; Abdel-Aty, M.; Mandal, S. Sensitivity of the population and the Pancharatnam phase for a trapped ion with Stark shift. Phys. Rev. A 2010, 82, 023409. [Google Scholar] [CrossRef]
- Zbinden, H.; Gautier, J.; Gisin, N.; Huttner, B.; Muller, A.; Tittel, W. Interferometry with Faraday mirrors for quantum cryptography. Electron Lett. 1997, 33, 586–588. [Google Scholar] [CrossRef]
- Cirac, J.I.; Ekert, A.K.; Huelga, S.F.; Macchiavello, C. Distributed quantum computation over noisy channels. Phys. Rev. A 1999, 59, 4249. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Generation and robustness of bipartite non-classical correlations in two nonlinear microcavities coupled by an optical fiber. J. Opt. Soc. Am. B 2018, 35, 47–53. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A.; Homid, A.H. Implementing discrete quantum Fourier transform via superconducting qubits coupled to a superconducting cavity. J. Opt. Soc. Am. B 2013, 30, 1178–1185. [Google Scholar] [CrossRef]
- Obada, A.-S.F.; Hessian, H.A.; Mohamed, A.-B.A.; Homid, A.H. Efficient protocol of N-bit discrete quantum Fourier transform via transmon qubits coupled to a resonator. Quantum Information Process. 2014, 13, 475–489. [Google Scholar] [CrossRef]
- Haljan, P.C.; Brickman, K.-A.; Deslauriers, L.; Lee, P.J.; Monroe, C. Spin-Dependent Forces on Trapped Ions for Phase-Stable Quantum Gates and Entangled States of Spin and Motion. Phys. Rev. Lett. 2005, 94, 153602. [Google Scholar] [CrossRef]
- Van Enk, S.J.; Kimble, H.J.; Cirac, J.I.; Zoller, P. Quantum communication with dark photons. Phys. Rev. A 1999, 59, 2659. [Google Scholar] [CrossRef]
- Serafini, A.; Mancini, S.; Bose, S. Distributed Quantum Computation via Optical Fibers. Phys. Rev. Lett. 2006, 96, 010503. [Google Scholar] [CrossRef]
- Li, P.B.; Gu, Y.; Gong, Q.H.; Guo, G.C. Quantum-information transfer in a coupled resonator waveguide. Phys. Rev. A 2009, 79, 042339. [Google Scholar] [CrossRef]
- Vogell, B.; Vermersch, B.; Northup, T.E.; Lanyon, B.P.; Muschik, C.A. Deterministic quantum state transfer between remote qubits in cavities. Quantum Sci. Technol. 2017, 2, 045003. [Google Scholar] [CrossRef]
- Eleuch, H. Noise spectra of microcavity-emitting field in the linear regime. Eur. Phys. J. D 2008, 49, 391–395. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Quantum correlation control for two semiconductor microcavities connected by an optical fiber. Phys. Scr. 2017, 92, 065101. [Google Scholar] [CrossRef]
- Peters, N.A.; Altepeter, J.B.; Branning, D.; Jeffrey, E.R.; Wei, T.-C.; Kwiat, P.G. Maximally eentangled mixed states: Creation and concentration. Phys. Rev. Lett. 2004, 92, 133601. [Google Scholar] [CrossRef]
- Singh, H.; Dorai, K. Evolution of tripartite entangled states in a decohering environment and their experimental protection using dynamical decoupling. Phys. Rev. A 2018, 97, 022302. [Google Scholar] [CrossRef]
- Cunha, M.M.; Fonseca, A.; Silva, E.O. Tripartite entanglement: Foundations and applications. Universe 2019, 5, 209. [Google Scholar] [CrossRef]
- Uhlmann, A. Geometric phases and related structures. Rep. Math. Phys. 1995, 36, 461–481. [Google Scholar] [CrossRef]
- Tong, D.M.; Sjöqvist, E.; Kwek, L.C.; Oh, C.H. Kinematic approach to the mixed state geometric phase in nonunitary evolution. Phys. Rev. Lett. 2004, 93, 080405. [Google Scholar] [CrossRef]
- Dilley, J.; Nisbet-Jones, P.; Shore, B.W.; Kuhn, A. Single-photon absorption in coupled atom-cavity systems. Phys. Rev. A 2012, 85, 023834. [Google Scholar] [CrossRef]
- Shen, H.Z.; Qin, M.; Yi, X.X. Single-photon storing in coupled non-Markovian atom-cavity system. Phys. Rev. A 2013, 88, 033835. [Google Scholar] [CrossRef]
- Bhandari, D.R.; Samuel, J. Observation of topological phase by use of a laser interferometer. Phys. Rev. Lett. 1988, 60, 1211. [Google Scholar] [CrossRef]
- Loredo, J.C.; Ortíz, O.; Weingärtner, R.; De Zela, F. Measurement of Pancharatnam’s phase by robust interferometric and polarimetric methods. Phys. Rev. A 2009, 80, 012113. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tamate, S.; Nakanishi, T.; Sugiyama, K.; Kitano, M. Observation of Geometric Phases in Quantum Erasers. J. Phys. Soc. Jpn. 2011, 80, 034401. [Google Scholar] [CrossRef]
- Pellizzari, T. Quantum Networking with Optical Fibres. Phys. Rev. Lett. 1997, 79, 5242. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-B.A.; Masmali, I. Control of the Geometric Phase in Two Open Qubit–Cavity Systems Linked by a Waveguide. Entropy 2020, 22, 85. https://doi.org/10.3390/e22010085
Mohamed A-BA, Masmali I. Control of the Geometric Phase in Two Open Qubit–Cavity Systems Linked by a Waveguide. Entropy. 2020; 22(1):85. https://doi.org/10.3390/e22010085
Chicago/Turabian StyleMohamed, Abdel-Baset A., and Ibtisam Masmali. 2020. "Control of the Geometric Phase in Two Open Qubit–Cavity Systems Linked by a Waveguide" Entropy 22, no. 1: 85. https://doi.org/10.3390/e22010085
APA StyleMohamed, A.-B. A., & Masmali, I. (2020). Control of the Geometric Phase in Two Open Qubit–Cavity Systems Linked by a Waveguide. Entropy, 22(1), 85. https://doi.org/10.3390/e22010085



