Transverse Density Fluctuations around the Ground State Distribution of Counterions near One Charged Plate: Stochastic Density Functional View
Abstract
1. Introduction
2. Formal Background
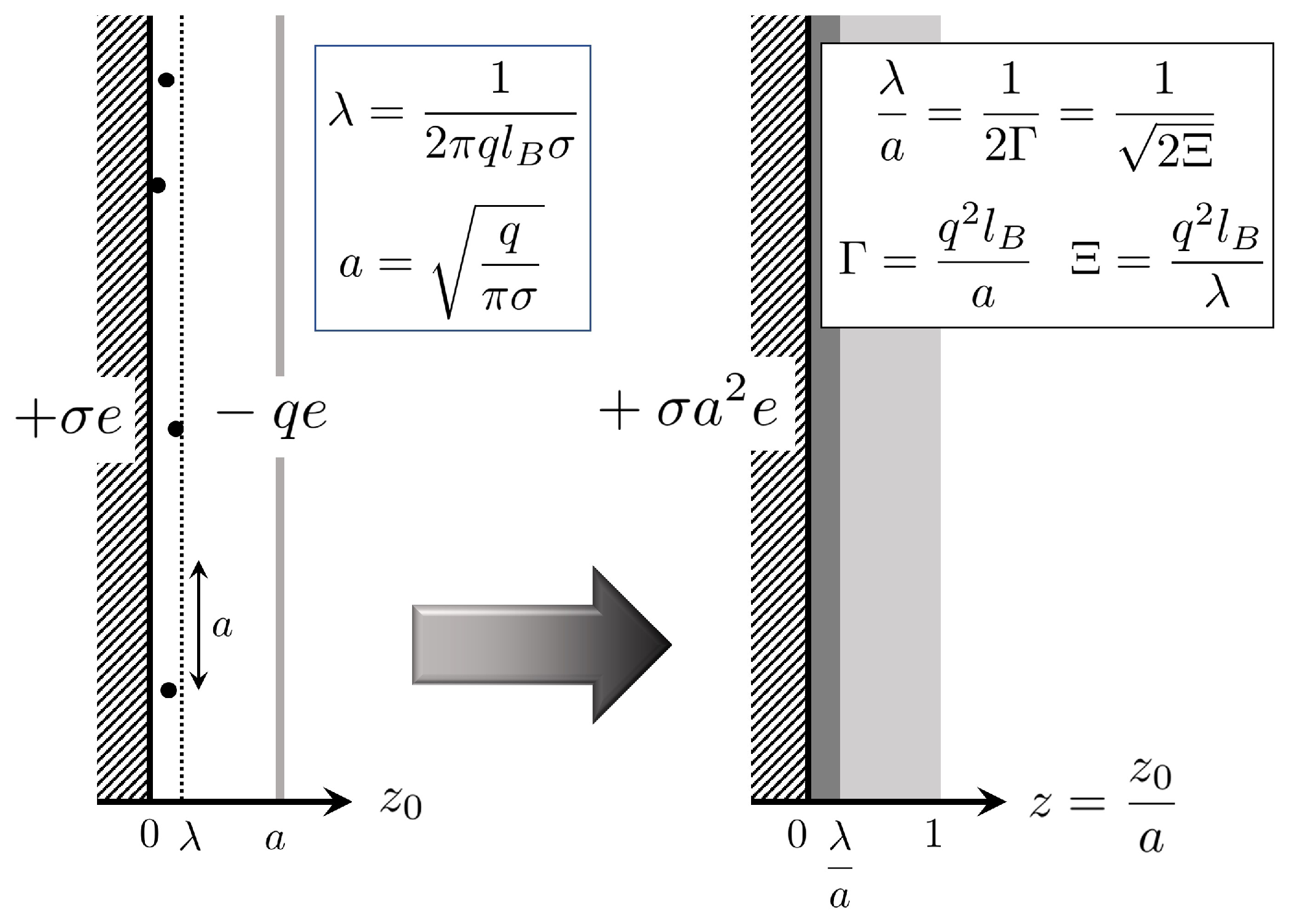
2.1. Ground State of Counterion System in the Strong Coupling Limit
2.2. Imposing a Given Density Distribution on the Grand Potential
2.3. Stochastic Density Dynamics Obeying the Dean–Kawasaki Equation
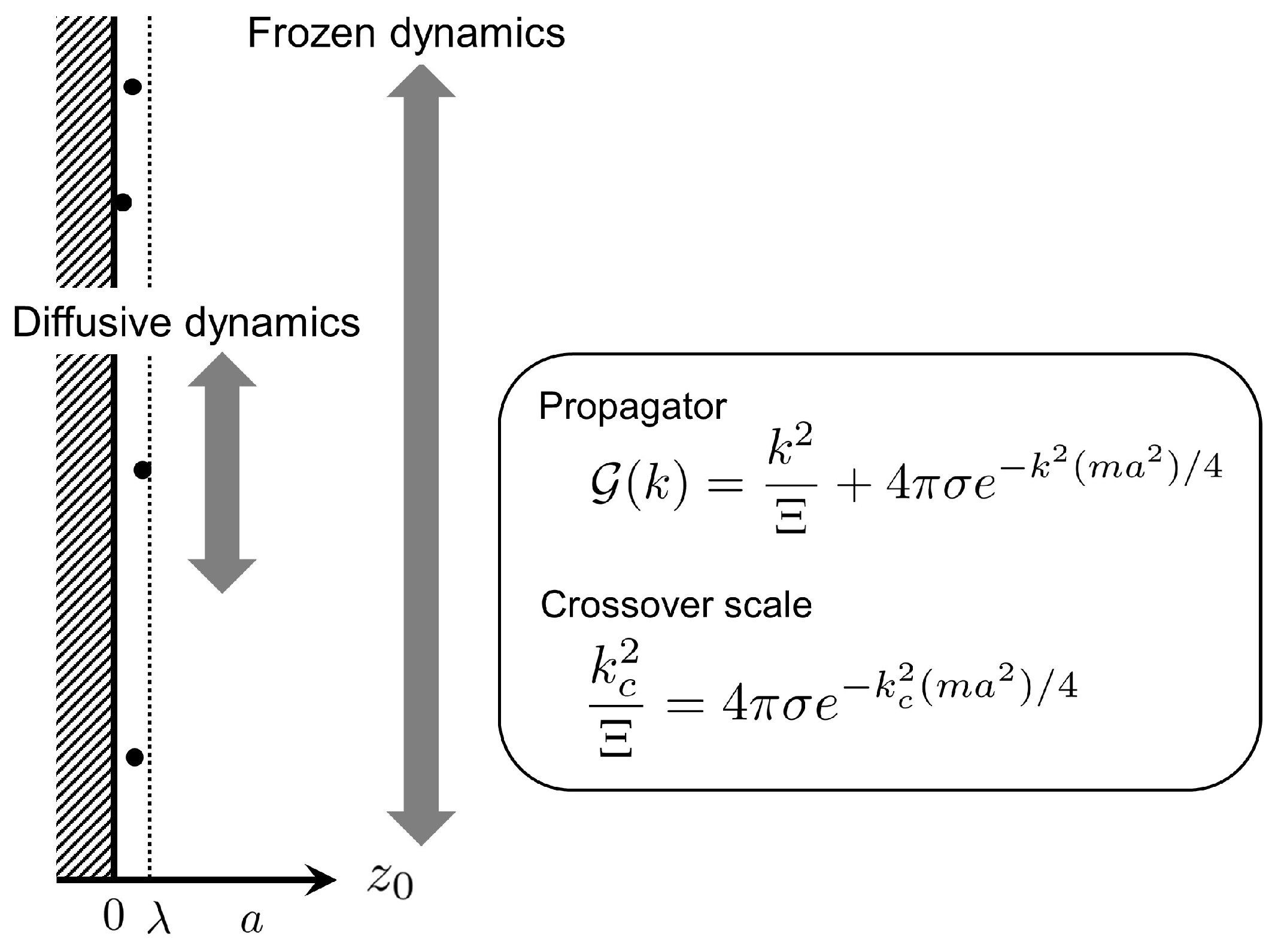
3. Stochastic Density Functional Equation for Fluctuations round the Ground State Distribution
3.1. Linearizing the Stochastic Dean–Kawasaki Equation (14)
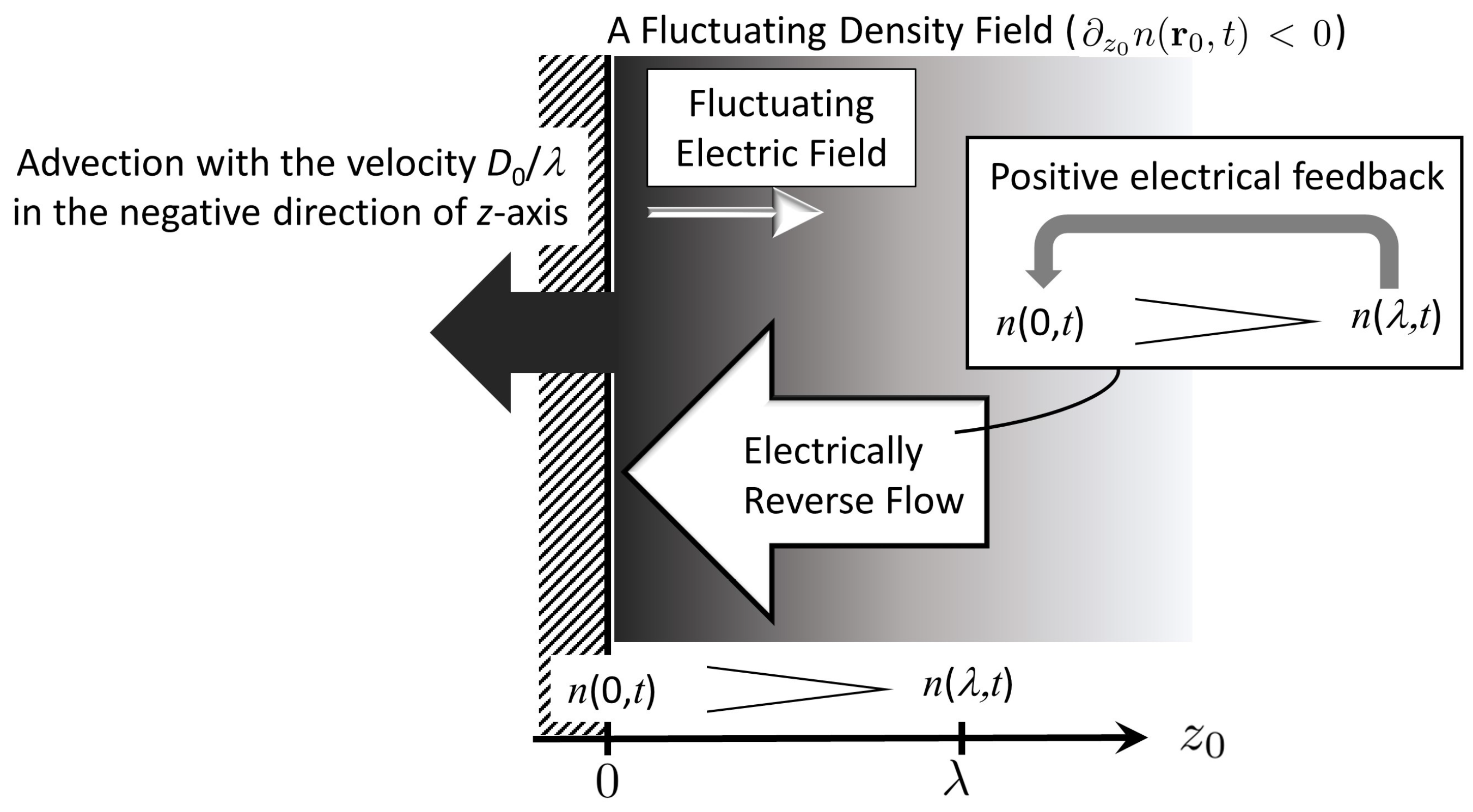
3.2. Implications of Longitudinal Contributions Given by Equation (33)
4. Density-Density Correlations Due to Transverse Dynamics Along the Plate Surface
5. Summary and Conclusions
Funding
Conflicts of Interest
Appendix A. Electrostatic Interaction Energies: General Forms When Rescaled by the Wigner–Seitz Radius a
Appendix B. The Grand Potential Ω[J] for a One-Plate System
Appendix C. A Remark on Equation (11)
Appendix D. Details of Equation (19)
References
- Israelachvili, J. Intermolecular and Surface Forces; Academic Press: London, UK, 2015. [Google Scholar]
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Prog. Phys. 2002, 65, 1577. [Google Scholar] [CrossRef]
- Baus, M.; Hansen, J.P. Statistical mechanics of simple Coulomb systems. Phys. Rep. 1980, 59, 1–94. [Google Scholar] [CrossRef]
- Morfill, G.E.; Ivlev, A.V. Complex plasmas: An interdisciplinary research field. Rev. Mod. Phys. 2009, 81, 1353. [Google Scholar] [CrossRef]
- Khrapak, S.A.; Khrapak, A.G. Internal energy of the elassical two-and three-dimensional one-component-plasma. Contrib. Plasm. Phys. 2016, 56, 270–280. [Google Scholar] [CrossRef]
- Netz, R.R. Electrostatistics of counter-ions at and between planar charged walls: From Poisson-Boltzmann to the strong-coupling theory. Eur. Phys. J. E 2001, 5, 557–574. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Nguyen, T.T.; Shklovskii, B.I. Colloquium: The physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002, 74, 329. [Google Scholar] [CrossRef]
- Naji, A.; Kanduč, M.; Forsman, J.; Podgornik, R. Perspective: Coulomb fluids-weak coupling, strong coupling, in between and beyond. J. Chem. Phys. 2013, 139, 150901. [Google Scholar] [CrossRef] [PubMed]
- Moreira, A.G.; Netz, R.R. Simulations of counterions at charged plates. Eur. Phys. J. E 2002, 8, 33–58. [Google Scholar] [CrossRef]
- Palaia, I.; Trulsson, M.; Šamaj, L.; Trizac, E. A correlation-hole approach to the electric double layer with counter-ions only. Mol. Phys. 2018, 116, 3134–3146. [Google Scholar] [CrossRef]
- Šamaj, L.; Trulsson, M.; Trizac, E. Strong-coupling theory of counterions between symmetrically charged walls: From crystal to fluid phases. Soft Matter 2018, 14, 4040–4052. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Tarazona, P. Dynamic density functional theory of fluids. J. Chem. Phys. 1999, 110, 8032–8044. [Google Scholar] [CrossRef]
- Dean, D.S. Langevin equation for the density of a system of interacting Langevin processes. J. Phys. A Math. Gen. 1996, 29, L613. [Google Scholar] [CrossRef]
- Frusawa, H.; Hayakawa, R. On the controversy over the stochastic density functional equations. J. Phys. A Math. Gen. 2000, 33, L155. [Google Scholar] [CrossRef]
- Archer, A.J.; Rauscher, M. Dynamical density functional theory for interacting Brownian particles: Stochastic or deterministic? J. Phys. A Math. Gen. 2004, 37, 9325. [Google Scholar] [CrossRef]
- Démery, V.; Bénichou, O.; Jacquin, H. Generalized Langevin equations for a driven tracer in dense soft colloids: Construction and applications. New J. Phys. 2014, 16, 053032. [Google Scholar] [CrossRef]
- Cornalba, F.; Shardlow, T.; Zimmer, J. A regularized Dean–Kawasaki model: Derivation and analysis. Siam J. Math. Anal. 2019, 51, 1137–1187. [Google Scholar] [CrossRef]
- Chavanis, P.H. Hamiltonian and Brownian systems with long-range interactions: V. stochastic kinetic equations and theory of fluctuations. Phys. A 2008, 387, 5716–5740. [Google Scholar] [CrossRef]
- Chavanis, P.H. Generalized stochastic Fokker-Planck equations. Entropy 2015, 17, 3205–3252. [Google Scholar] [CrossRef]
- Chavanis, P.H. The Generalized Stochastic Smoluchowski Equation. Entropy 2019, 21, 1006. [Google Scholar] [CrossRef]
- Frusawa, H. Stochastic dynamics and thermodynamics around a metastable state based on the linear Dean–Kawasaki equation. J. Phys. A Math. Theor. 2019, 52, 065003. [Google Scholar] [CrossRef]
- Démery, V.; Dean, D.S. The conductivity of strong electrolytes from stochastic density functional theory. J. Stat. Mech. Theory Exp. 2016, 2016, 023106. [Google Scholar] [CrossRef]
- Dean, D.S.; Lu, B.S.; Maggs, A.C.; Podgornik, R. Nonequilibrium Tuning of the Thermal Casimir Effect. Phys. Rev. Lett. 2016, 116, 240602. [Google Scholar] [CrossRef] [PubMed]
- Poncet, A.; Bénichou, O.; Démery, V.; Oshanin, G. Universal long ranged correlations in driven binary mixtures. Phys. Rev. Lett. 2017, 118, 118002. [Google Scholar] [CrossRef] [PubMed]
- Krüger, M.; Dean, D.S. A Gaussian theory for fluctuations in simple liquids. J. Chem. Phys. 2017, 146, 134507. [Google Scholar] [CrossRef]
- Krüger, M.; Solon, A.; Démery, V.; Rohwer, C.M.; Dean, D.S. Stresses in non-equilibrium fluids: Exact formulation and coarse-grained theory. J. Chem. Phys. 2018, 148, 084503. [Google Scholar] [CrossRef]
- Del Junco, C.; Tociu, L.; Vaikuntanathan, S. Energy dissipation and fluctuations in a driven liquid. Proc. Natl. Acad. Sci. USA 2018, 115, 3569–3574. [Google Scholar] [CrossRef]
- Evans, R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv. Phys. 1979, 28, 143–200. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic Press: London, UK, 2013. [Google Scholar]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. II. Modified Poisson-Nernst-Planck equations. Phys. Rev. E 2007, 75, 021503. [Google Scholar] [CrossRef]
- Ng, K.C. Hypernetted chain solutions for the classical one-component plasma up to Γ = 7000. J. Chem. Phys. 1974, 61, 2680–2689. [Google Scholar] [CrossRef]
- De Carvalho, R.L.; Evans, R.; Rosenfeld, Y. Decay of correlations in fluids: The one-component plasma from Debye-Hückel to the asymptotic-high-density limit. Phys. Rev. E 1999, 59, 1435. [Google Scholar] [CrossRef]
- Rodgers, J.M.; Weeks, J.D. Local molecular field theory for the treatment of electrostatics. J. Phys. Condens. Matter 2008, 20, 494206. [Google Scholar] [CrossRef][Green Version]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frusawa, H. Transverse Density Fluctuations around the Ground State Distribution of Counterions near One Charged Plate: Stochastic Density Functional View. Entropy 2020, 22, 34. https://doi.org/10.3390/e22010034
Frusawa H. Transverse Density Fluctuations around the Ground State Distribution of Counterions near One Charged Plate: Stochastic Density Functional View. Entropy. 2020; 22(1):34. https://doi.org/10.3390/e22010034
Chicago/Turabian StyleFrusawa, Hiroshi. 2020. "Transverse Density Fluctuations around the Ground State Distribution of Counterions near One Charged Plate: Stochastic Density Functional View" Entropy 22, no. 1: 34. https://doi.org/10.3390/e22010034
APA StyleFrusawa, H. (2020). Transverse Density Fluctuations around the Ground State Distribution of Counterions near One Charged Plate: Stochastic Density Functional View. Entropy, 22(1), 34. https://doi.org/10.3390/e22010034




