2.1. Background: Cluster States and Complex Networks
Ideal cluster states are built starting from a set of modes of light, which are placed in the zero-momentum eigenstate , i.e., infinitely squeezed vacuum states along the momentum quadrature p. Entangling gates are then applied between couples of modes i and j, according to a given configuration, which can be represented by a graph. A graph is defined by a set , where is the set of nodes (vertices) and are the edges. In the graphical representation of the cluster, the nodes represent different modes of light, while the edges between the nodes are the entanglement correlations given by the application of the gates. The graph is characterized by the adjacency matrix V whose elements are set to 1 when an entangling gate has been applied between the two nodes i and j, and 0, otherwise.
An ideal cluster state of
N modes with adjacency matrix
V is given by
Cluster states are characterized by a particular set of operators, called
nullifiers, that read
where
and
denote respectively the nullifier and the set of the nearest neighbours of the
i-th node. Cluster states are eigenstates of the nullifiers with zero eigenvalue, so, for an ideal cluster, the following condition holds:
. In addition, being Gaussian states, cluster states are fully described by mean values of quadratures and covariance matrices [
29]. By defining the vector
, cluster states are identified by mean values
and covariance matrix
with elements
.
As already said, in a realistic situation, CV cluster states are always imperfect, due to the impossibility of reaching an infinite amount of squeezing to obtain the zero momentum eigenstate. Approximated clusters, when used in measurement-based quantum computing protocols, at each step of the computation, introduce a certain amount of noise that can be quantified with the variance of the nullifiers of the cluster [
22]. Therefore, the smaller the value of
is for every node, the better the quality of cluster is.
Instead of acting with
gates on multimode squeezed vacuum states, as in the original formulation, cluster states can be implemented via linear optics transformations on the multimode squeezed vacuum state [
30,
31,
32]. This is the implementation that is pursued in experimental setups [
18,
19,
20,
21], as it is easier and less costly than the implementation of
, which requires online squeezing.
Linear optics manipulations are described by unitary transformations U on the creation and annihilation operators of the different light modes, so that the annihilation operator of the mode i is transformed as . This corresponds to orthogonal symplectic transformations S acting on the quadratures, which transform the covariance matrix as .
To implement a cluster with adjacency matrix
V, we can apply the following unitary operation:
where
is the identity matrix and
O is an arbitrary real orthogonal matrix. This orthogonal matrix provides supplementary
degrees of freedom that can be exploited to optimize given properties of the cluster [
25]. In particular, we can optimize given properties of the nullifiers via an analytical protocol [
33], with the aim, for example, of reducing their variances, hence improving the quality of the cluster.
In this work, we investigate, for the first time, clusters whose graphical representation
corresponds to three different models of complex networks [
1]: the Barabási–Albert [
34], the Erdős–Rényi [
35], and the Watts–Strogatz [
36]. These models have been developed in graph theory in order to reproduce the behaviors of complex systems. The Erdős–Rényi has been the first model considered for complex networks. It is based on random graph: given a fixed number of nodes
n, two nodes have the probability
to be connected by an edge. The model generates graphs with approximately
edges which are distributed randomly. Most nodes have a comparable node degree
k, defined as the number of edges of the given node.
Later, by looking at the degree distribution of many real-world networks, it has been clear that complex networks go beyond the random graph model, as many networks (like Internet or the WWW) are characterized by a power-law distribution of the degree. Thus, new models, such as the Barabási–Albert, have been developed in order to reproduce the structure of these networks, also known as scale-free networks. Barabási–Albert networks grow from a small number of nodes according to preferential attachment, i.e., the fact that new nodes attach preferentially to nodes that already have a high degree (high number of links). In the growth process, the parameter specifies the number of links coming with the new node. Hubs, i.e., heavily linked nodes, arise spontaneously in this model.
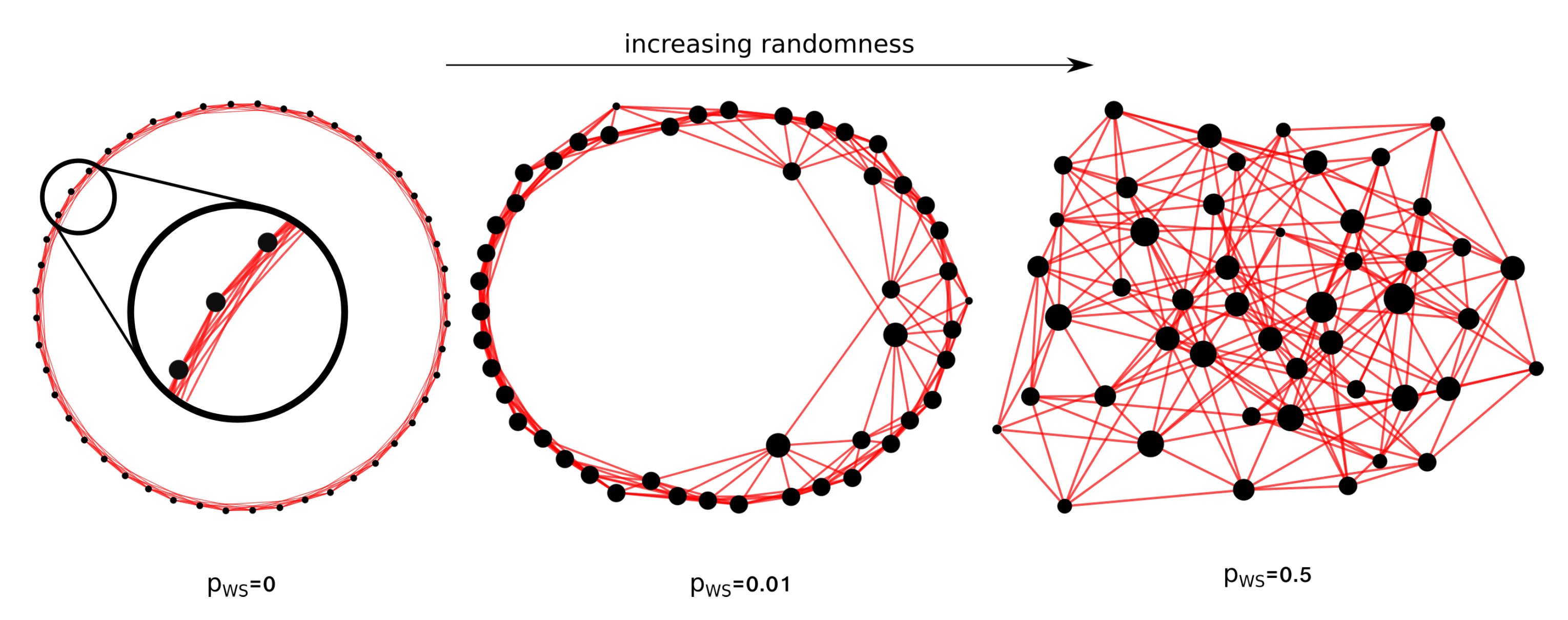
Watts–Strogatz networks lie between regular and random graphs and exhibit small-world properties typical of social networks. They are built from a regular network by rewiring its edges, to increase randomness. From a ring lattice with
n nodes and
k edges per node, which connect it to the closest neighbors, each edge is randomly rewired with probability
. The rewiring parameter
spans from 0, the regular graph, to 1, which corresponds to a totally random graph, as shown in
Figure 1. Even if we are going to study graphs with a small number of nodes compared to the ones for which these models have been developed, we can assess a different behavior for the corresponding graph states in the three classes.
In the following, we will see how, starting from a given set of modes with finite squeezing values, we can optimize the quality of the clusters corresponding to these complex networks models and how the result of the optimization depends on the parameters of the analyzed model.
2.2. Improving the Overall Quality of a Complex Cluster
We test here cluster states with the structure of the three models defined above: Barabási–Albert (BA), Erdős–Rényi (ER), and Watts–Strogatz (WS), with different characterizing parameters
,
, and
. In
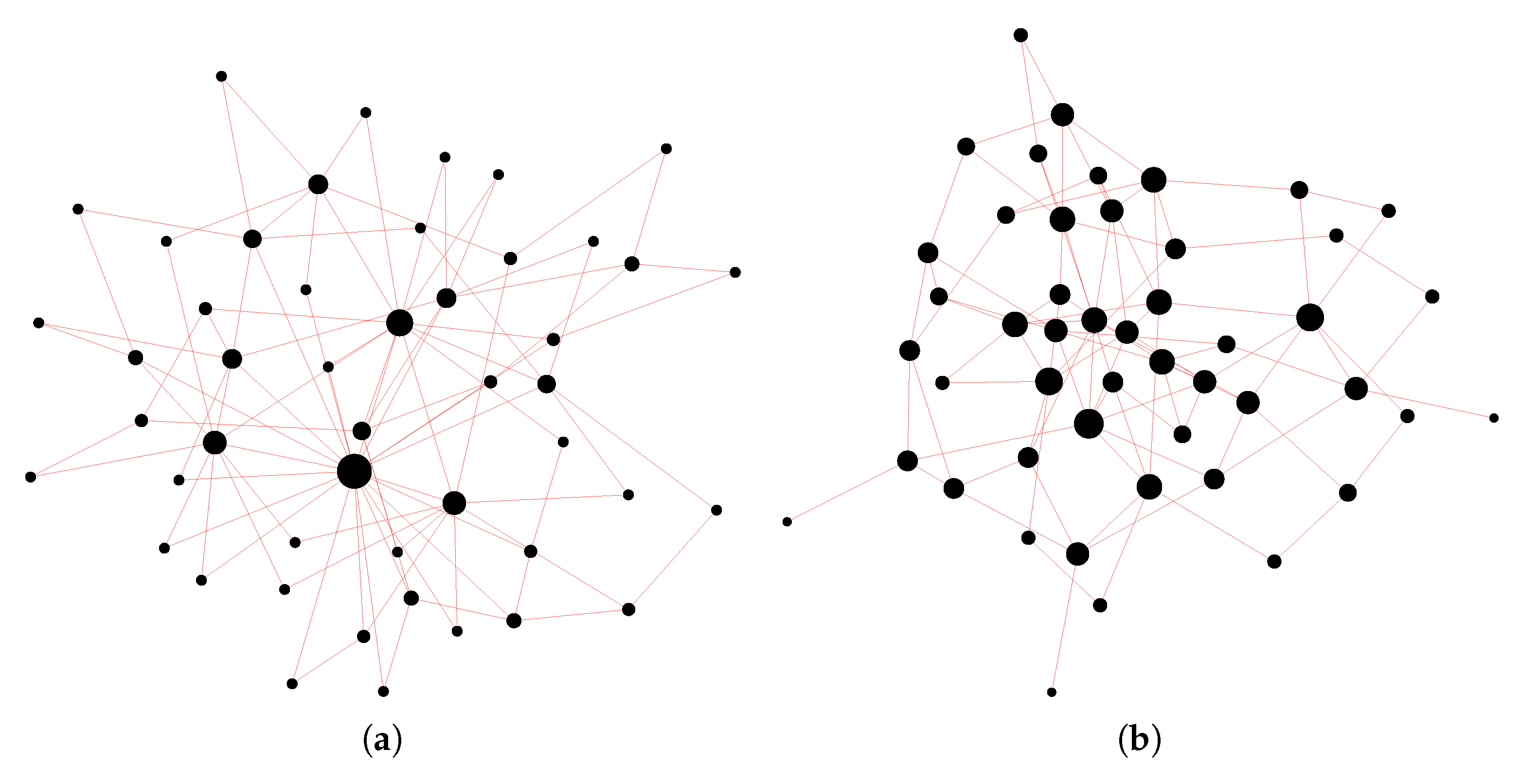
Figure 2, the difference between a scale-free network and a random network with a comparable average degree is shown. As we see in
Figure 2a, the Barabási–Albert network exhibits highly connected nodes (
hubs) that are absent in the Erdős–Rényi model (
Figure 2b).
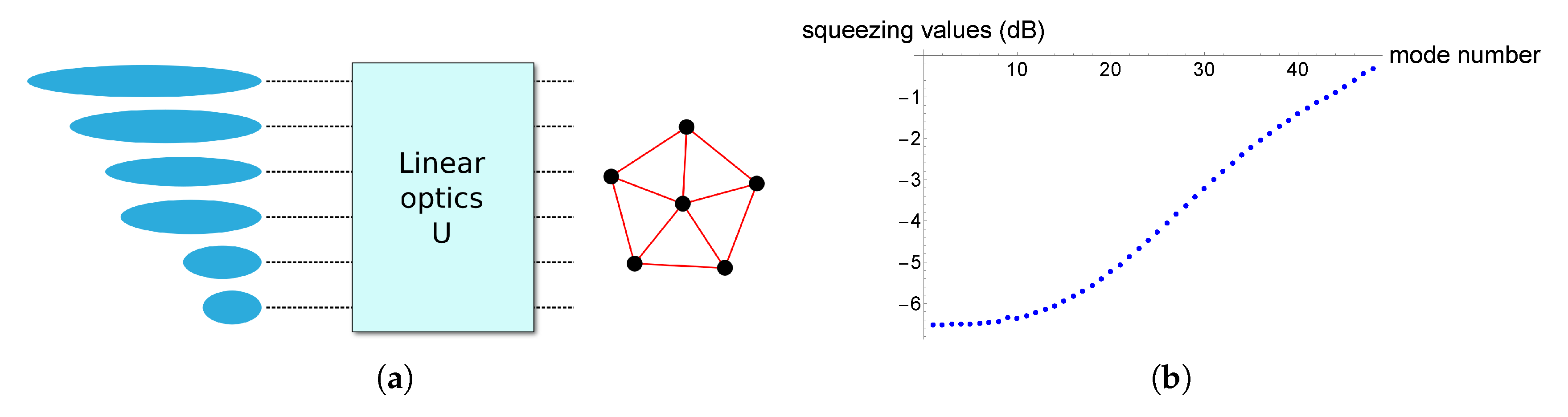
We consider at first the implementation of 48-mode complex clusters. As explained above, the clusters are implemented from a 48-mode squeezed vacuum via the application of the linear optics unitary of Equation (
3) corresponding to the graphical shape we want to reach [
25]. The scheme is presented in
Figure 3a. In order to pursue realistic implementations, we consider the list of squeezing values presented in
Figure 3b, which corresponds to a series of faithful values that can be obtained via the Schmidt decomposition of parametric process Hamiltonian of the experiment described in [
20,
37]. In this work, the input squeezing values for the implementation of the cluster are fixed: this is because our interest lies in understanding what is the best we can do when, like in a realistic situation, we are provided with a given set of squeezed input states. We stress that this scheme, as well as the associated results, is different to the one dealing with the canonical decomposition of [
22].
The obtained clusters are optimized, acting on the parameters of the arbitrary orthogonal matrix
O of Equation (
3), by minimizing the fitness function
, where
denotes the
i-th nullifier normalized with the vacuum noise.
As BA, ER, and WS are statistical models for graph families, we implement
graphs for each model with a given set of parameters. We define the average quality of a single graph
j as
and the average quality for a set of graphs as
, as follows:
where
identifies variance of the
i-th nullifier of the
j-th graph. We will indicate as
the standard deviation of the
values. This way, we can average out the fluctuations due to the randomness of the complex shape.
As we can see from
Table 1, the implementation of quantum complex networks following the Barabási–Albert model or the Erdős–Rényi model shows that the quality of the cluster increases when the average number of edges per node, the average degree
, increases. The average degree
can be raised by increasing the parameters
and
, for the BA and the ER models, respectively. The results clearly show that the quality of the cluster
increases with these parameters, until the limiting case of the fully connected graph (
for the Barabási–Albert model and
for the Erdős–Rényi model) is reached.
The Watts–Strogatz cluster confirms that the quality of the cluster increases for a larger value of
, as we can see by comparing
Table 2a,b, but it also shows a peculiar behavior that depends on
. As already said,
is a rewiring parameter that can be varied from 0 to 1 in order to tune the randomness of the graph without changing the average degree, as the number of edges is not changed by the rewiring. From the
Table 2, it is clear that the quality of the cluster is reduced when
approaches 1, so that regular graphs states are optimized better than random graphs.
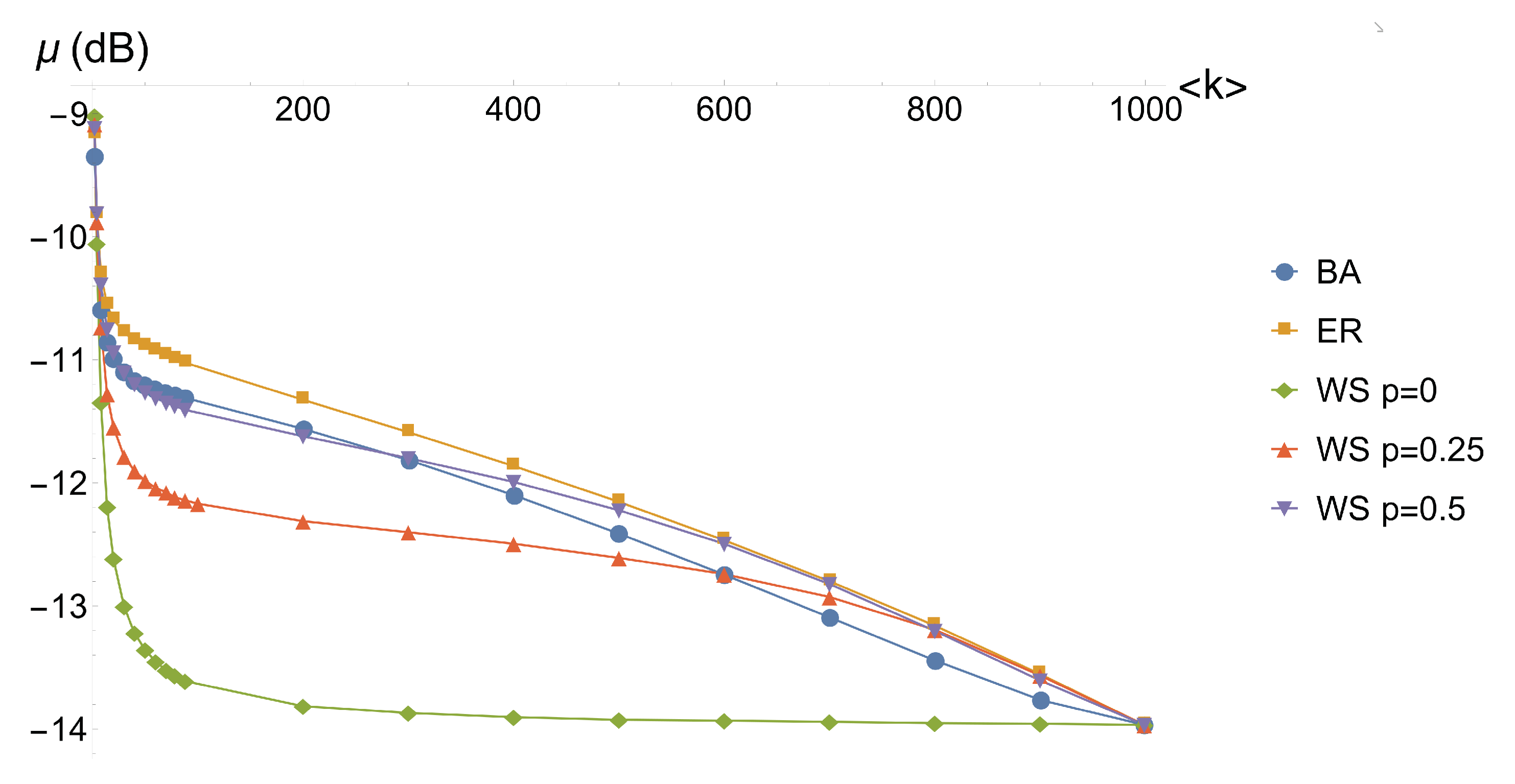
The results we obtained on the 48-node graphs we analyzed show a dependence between the quality of the optimization and the topology of the graph and in particular its dependence on the average degree
. In order to reduce the influence of the finite size in the network models we have been using, we repeat the procedure for larger networks. We optimize the mean value
of nullifiers squeezing (Equation (
4)) of a set of 10 complex graphs of 1000 nodes for a certain complex network model with given parameters. The optimization is reiterated by varying the average degree
and by varying the model. The initial list of 1000 squeezing values is obtained from a pseudorandom number generator that created uniformly distributed random numbers in the range
. The results are reported in
Figure 4.
The data show that the regular cluster (Watts–Strogatz model with ) converges very fast to its optimal overall quality. Indeed, as we expected from the 48-node cluster analysis, we see that, for a fixed , increasing the regularity, via the parameter, results in a better quality of the optimized cluster and in a faster convergence, as we can see comparing the curves for the Watts–Strogatz model with , and . On the other hand, the difference among the Barabási–Albert, Erdős–Rényi and Watts–Strogatz complex graphs is less significant. Nevertheless, the convergence of the Watts–Strogatz follows a different behavior, being closer to the Barabási–Albert for lower and converging to the behavior of the Erdős–Rényi for larger . The Erdős–Rényi is found to be the one with the worst overall quality, differing only slightly from the Barabási–Albert behavior.
2.3. Concentrating the Squeezing
The overall quality is the quantity to optimize if we want to use the cluster in MBQC protocols. On the contrary, if we want to use just two nodes to perform a quantum teleportation protocol, the best we can do is to concentrate the entanglement correlations in the two nodes: this corresponds to concentrating the squeezing on the nullifiers of the two chosen nodes.
Given a set of squeezing values for the input state we use the protocol to concentrate the squeezing on the nullifiers of two nodes and , using the fitness function , where and are two given modes. We set if and otherwise. We see that the squeezing of the nullifiers is indeed concentrated on the two desired nodes, by reaching (and never exceeding) the highest squeezing values provided on the set of input states.
In this case, we will indicate as
the mean of the nodes of the graph
j that are not concerned with the teleportation protocol and with
the mean of the
values as follows:
where
identifies variance of the
i-th nullifier of the
j-th graph.
denotes the mean of the set of values
, where
and
are two given nodes on which we chose to perform the teleportation.
As an example, in
Table 3, we show that, for a 48-node Barabási–Albert model, the squeezing on the two selected nodes
and
indeed take the highest value provided on the input list of
Figure 3b. The same results hold for the Erdős–Rényi model and the Watts–Strogatz model.
2.4. Creating a Quantum Channel between Nodes by Manipulating Existing Networks
In the previous section, we have seen how to optimize the generation of complex clusters when we have multimode squeezed vacuum modes and we perform linear optics transformations. As already said, several experimental setups demonstrated the ability to deterministically generate large clusters following this approach; therefore, they can be used to generate the complex clusters presented above. The generated cluster can then be distributed among different parties, i.e., different optical modes corresponding to different nodes of the network can be sent to different players, which can eventually use the entanglement correlations between the shared nodes for quantum communication protocols. According to the given task, it may be necessary to reshape the entanglement correlations among the set of nodes. We consider here the simplest case: the protocol wants to establish a maximally entangled state between two arbitrary nodes of a network in order to use it for quantum teleportation. The two-nodes entangled state is a two mode-squeezed state also called EPR, as it is the approximation of the entangled state used by Einstein, Poldolsky, and Rosen in their famous paper in 1935 [
38].
The task of generating an entanglement link between chosen nodes corresponds to what is called quantum routing. As already said, the procedure we follow is well suited to CV entangled networks as it is relatively easy to deterministically generate the resources and then reshape them, while in the DV case the generation of optical entangled networks is costly and not deterministic so that the best procedure consists in routing the right entanglement connections at the beginning.
In the following, we reshape the resource by allowing only for the easiest operations that preserve the number of nodes, i.e., passive linear optics transformations. Quadrature measurements for cluster state reshaping are also an option, but this would imply the removal of the measured node and subsequently the owner of said mode could be cut off from the communication network. For this reason, we will concentrate on linear optics operations, and we will leave open the possibility, in future works, of adding measurements if no other option is possible. These can be global, when they operate on all the nodes at the same time, or local, when they act on a subset of nodes.
The case of a global transformation is somewhat trivial as, if we are provided with a cluster A implemented with a linear optics transformation acting on a set of squeezed input states, it is always possible to find the transformation that leads us to the cluster B. This transformation is simply , where is the linear optics transformation that we should perform on the same set of input states to build the cluster B.
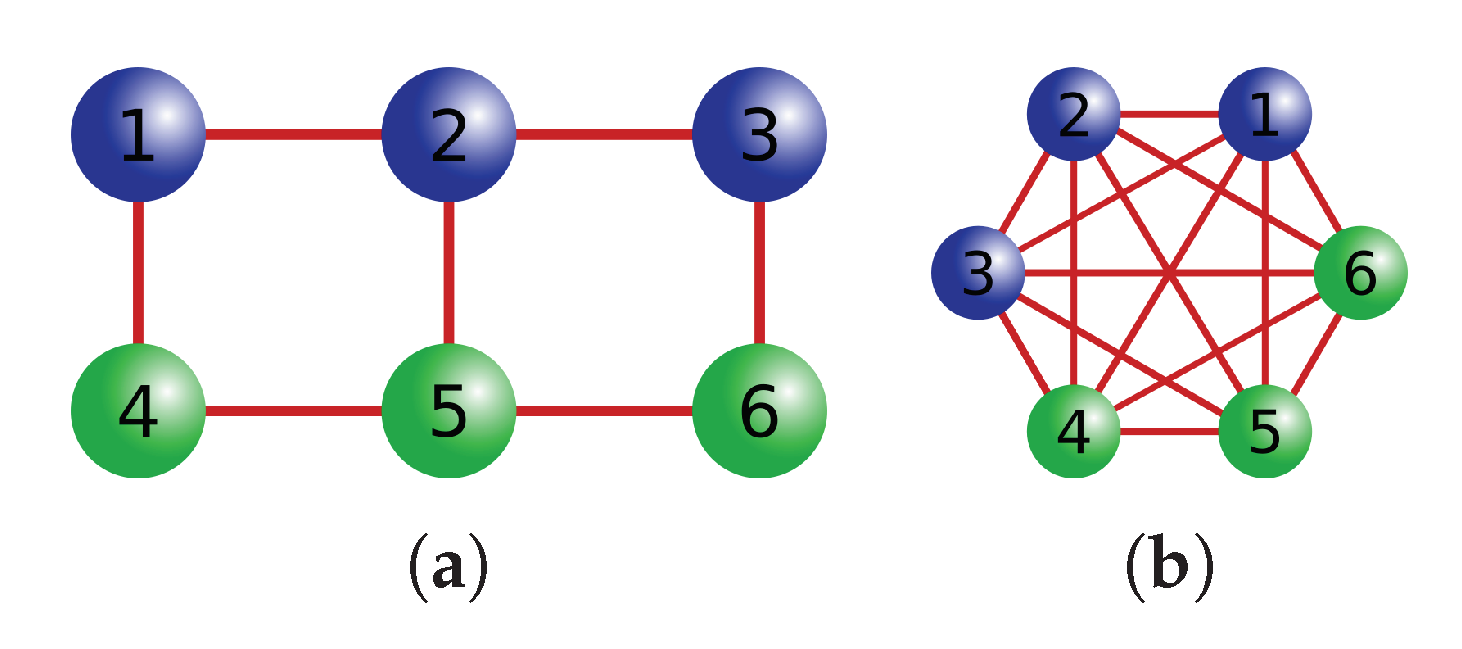
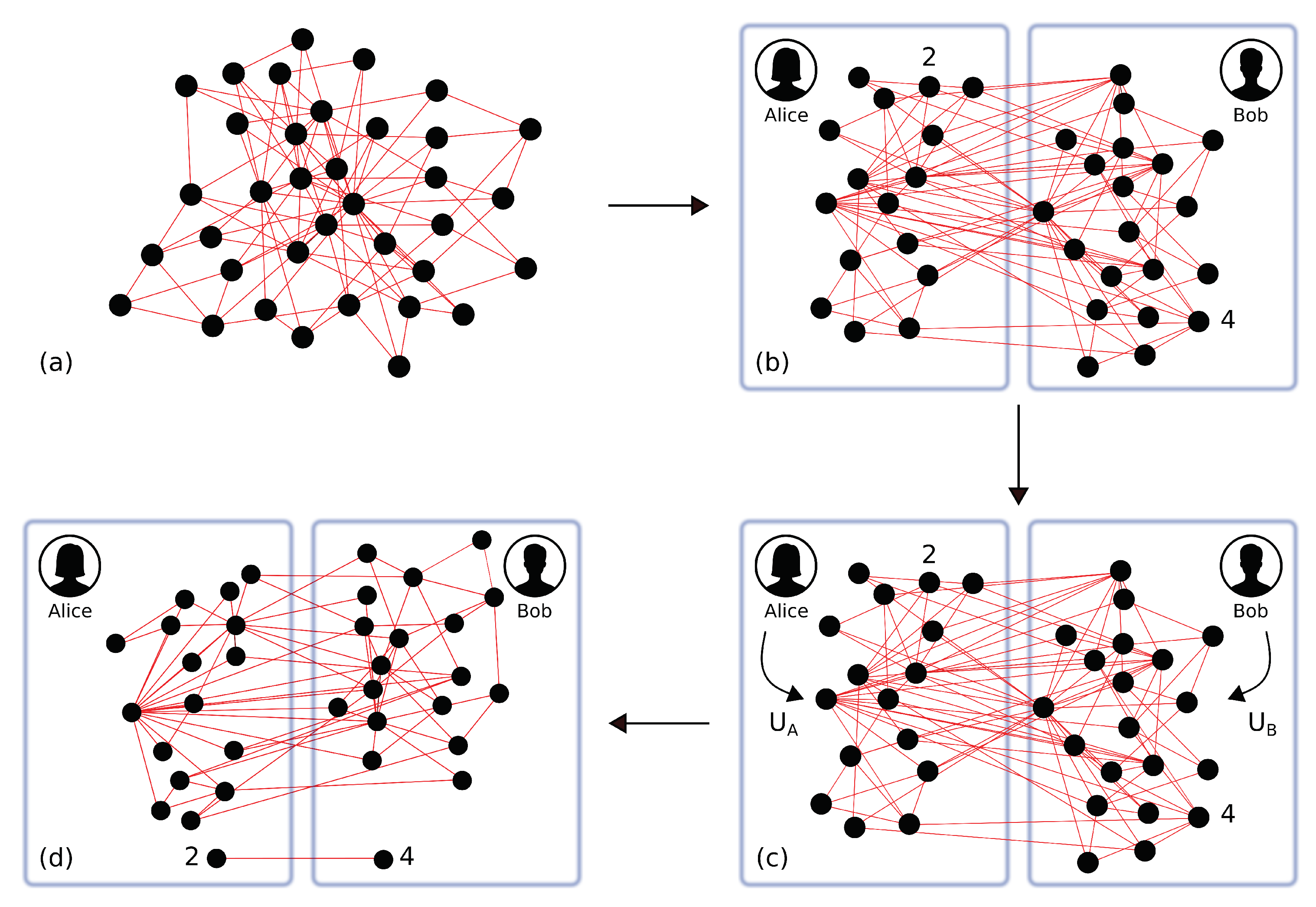
We now consider a more interesting scenario: the modes of the cluster are distributed to two spatially separated parties, such that each party is allowed to perform local linear optics transformations only on its set of nodes, as shown in
Figure 5. We then want to check which cluster shapes can be reconfigured in order to get a teleportation channel between two arbitrary nodes. A solution to this problem has already been found if we allow for more general symplectic transformations and weighted graphs [
39].
Let us say that
n and
p are the number of nodes of party A (Alice) and B (Bob), respectively. We want to act with a linear optics transformation
locally on the
n modes and with a linear optics transformation
locally on the
p modes. The transformation acting on the whole set of quadratures of the modes then reads
where
and
are two unitary matrices parametrized respectively by
and
parameters [
40]. A method for the generation of numerically random unitary matrices is presented in [
41]. If we define
as the covariance matrix of the cluster we are given and
as the covariance matrix of the cluster we obtain after the transformation,
holds, where
S is defined in Equation (
6). Our goal is to find the two matrices
and
, whose real and imaginary parts define
S, such that
is of the desired form. In our case, we want
to be such that, for two given nodes, we get an EPR channel. In this case, it is hard to find an analytical solution to the problem, so we use a Derandomized Evolution Strategy (DES) algorithm to explore the parameter space [
42].
If
and
are the nodes out of which we want to obtain an EPR channel, we can define
as the reduced
matrix obtained by selecting only the rows of
we want to set as a quantum channel. We thus define the
matrix
as the matrix with null entries except for
where the subscript “channel” has been omitted for simplicity and where
and
are numerical values that we fix according to the squeezing we want to attain on the modes of the quantum channel. This squeezing cannot exceed the squeezing of the input states of the cluster. For simplicity, we worked with an equal value of squeezing of –10 dB, both for the input squeezed states used to implement the cluster and for the squeezing chosen for the quantum channel. We will search for the minimal value of the function
where
indicates the Frobenius norm.
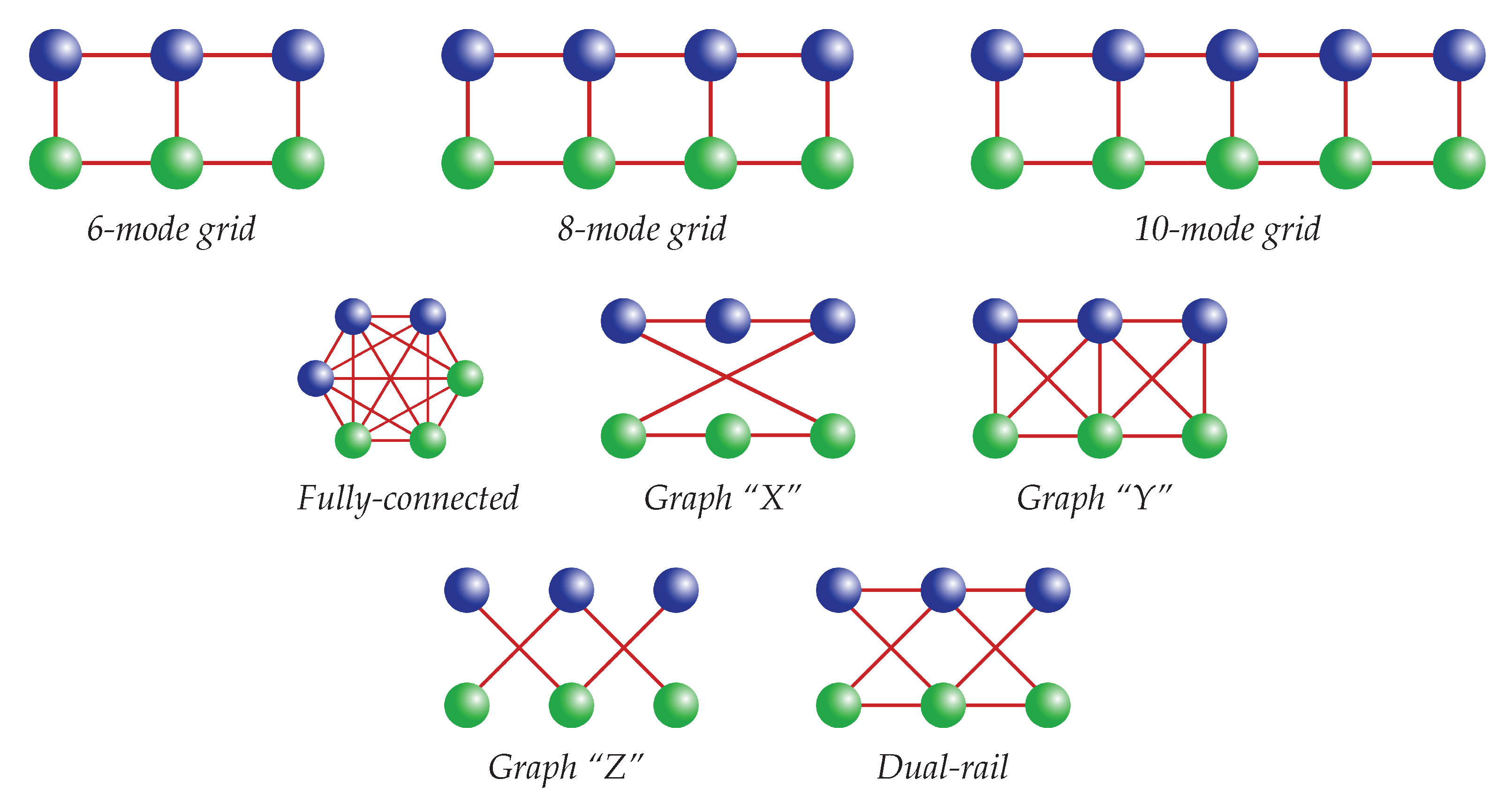
In
Table 4, we show preliminary results on different graphs with a restricted number of nodes, shown in
Figure 6. For the 6-mode and 10-mode “grid” graphs and the graphs “X” and “Y”, a result can be found for the creation of a quantum channel between Alice and Bob. For these structures, however, it was not possible to find a solution for the creation of a quantum channel between nodes of the same team. The opposite stands for the fully-connected cluster, for which it was possible to create a channel between nodes of the same team but not between nodes of different teams. Lastly, for the graph “Z”, which represents two 3-mode cluster states distributed to the two parties, for the dual-rail and for the 8-mode “grid” graph, no solution was found. As an example, the results of the fully-connected graph and of the 6-mode “grid” graph of
Figure 6 are shown in
Appendix A.