Determining the Bulk Parameters of Plasma Electrons from Pitch-Angle Distribution Measurements
Abstract
1. Introduction
2. Methods
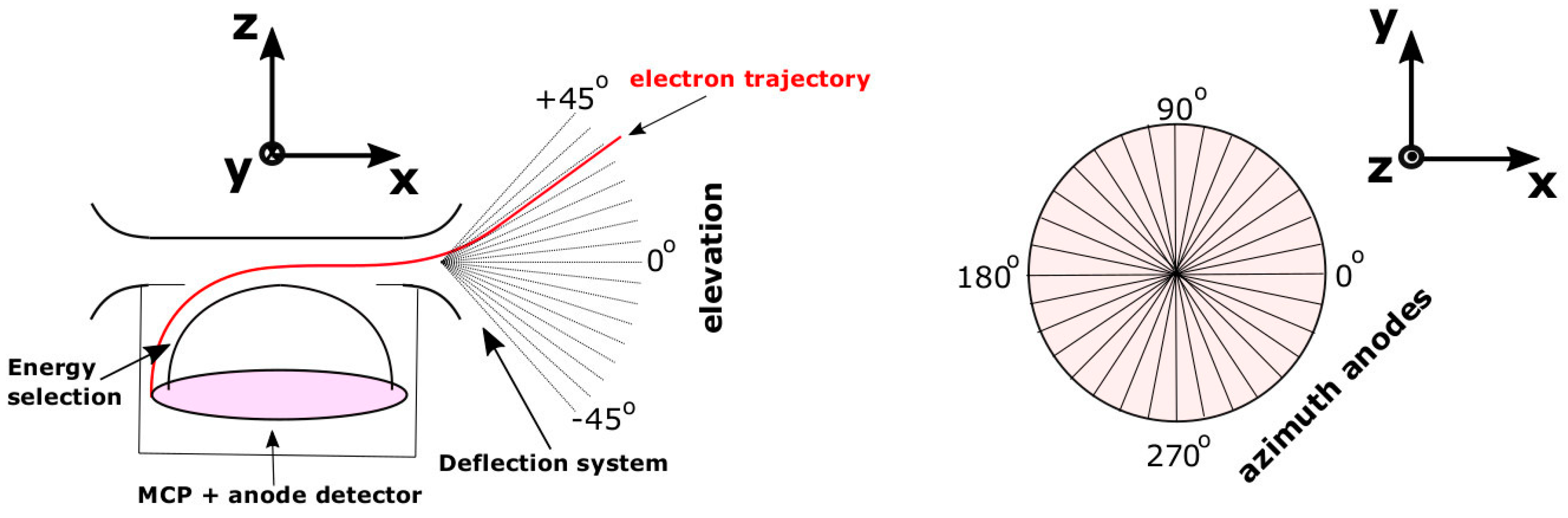
2.1. Instrument Model
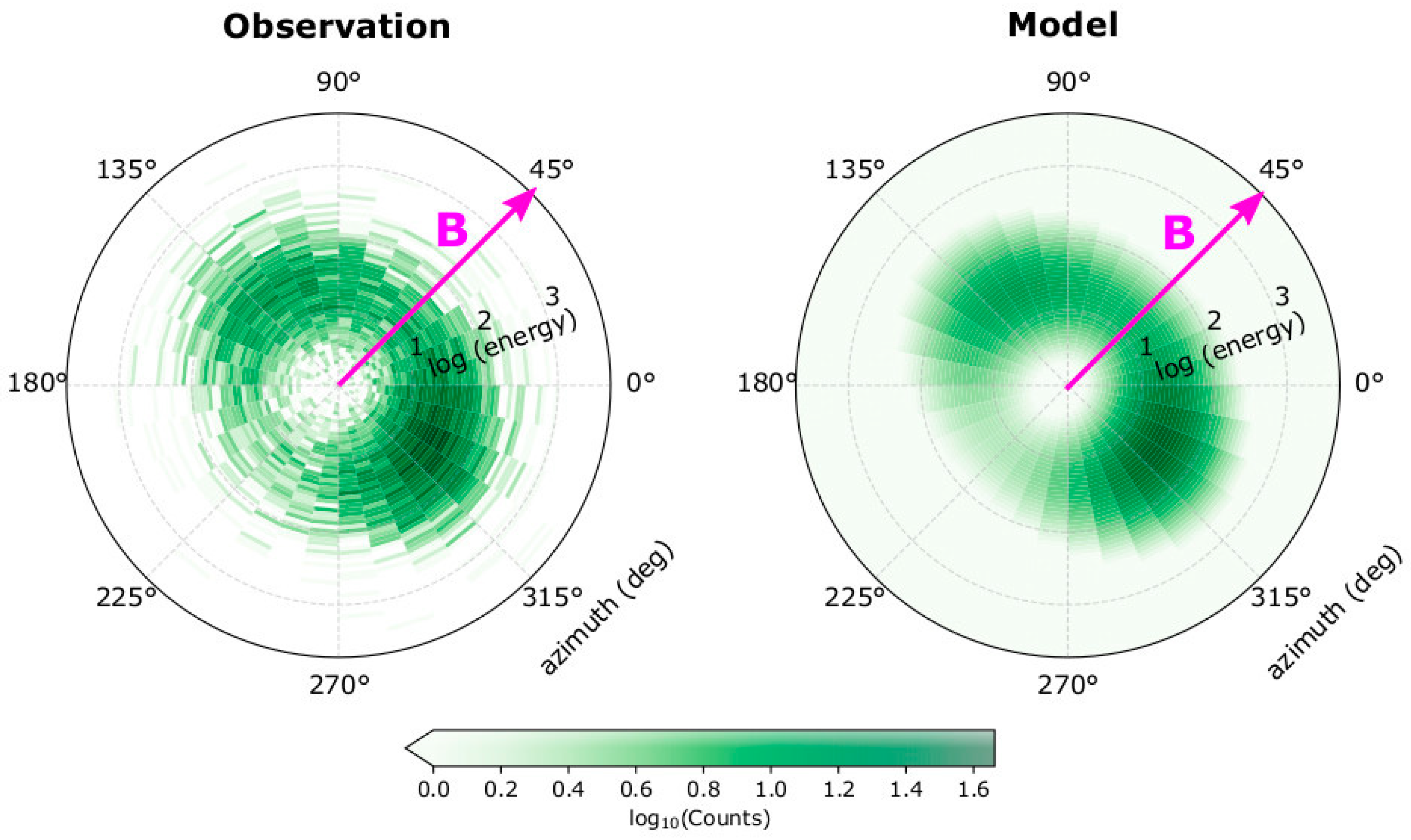
2.2. Synthetic Dataset
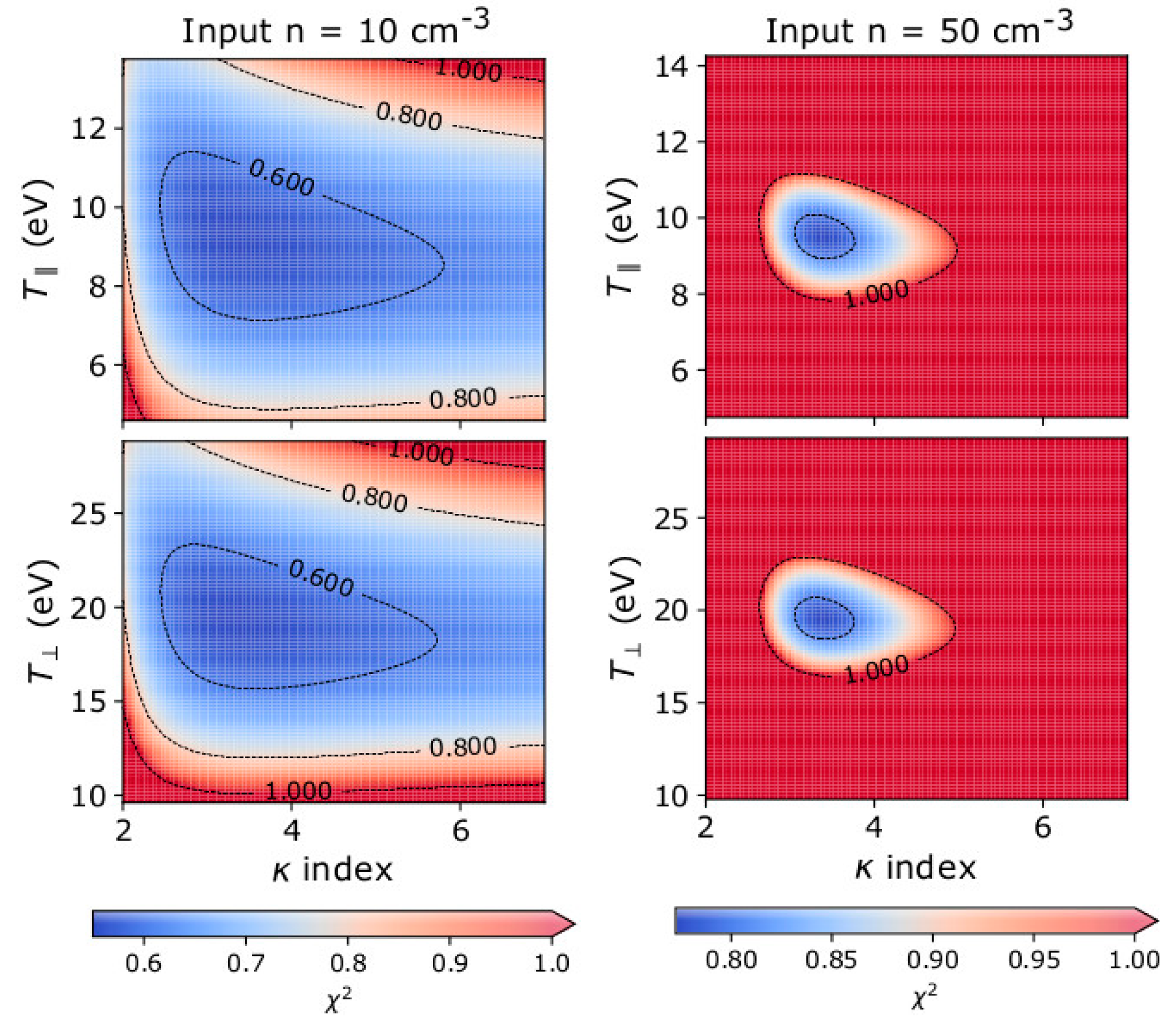
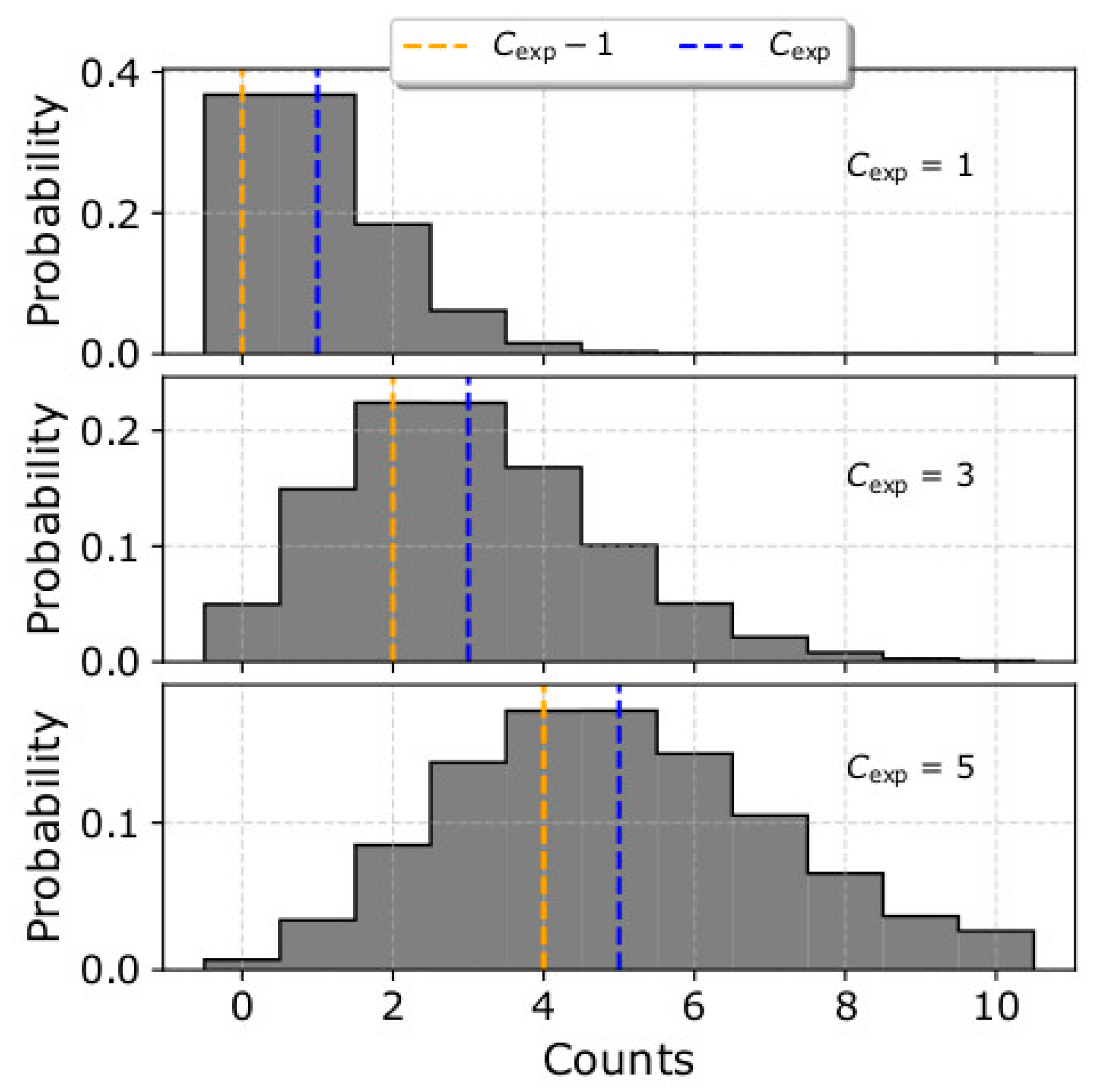
3. Results
4. Discussion
5. Conclusions
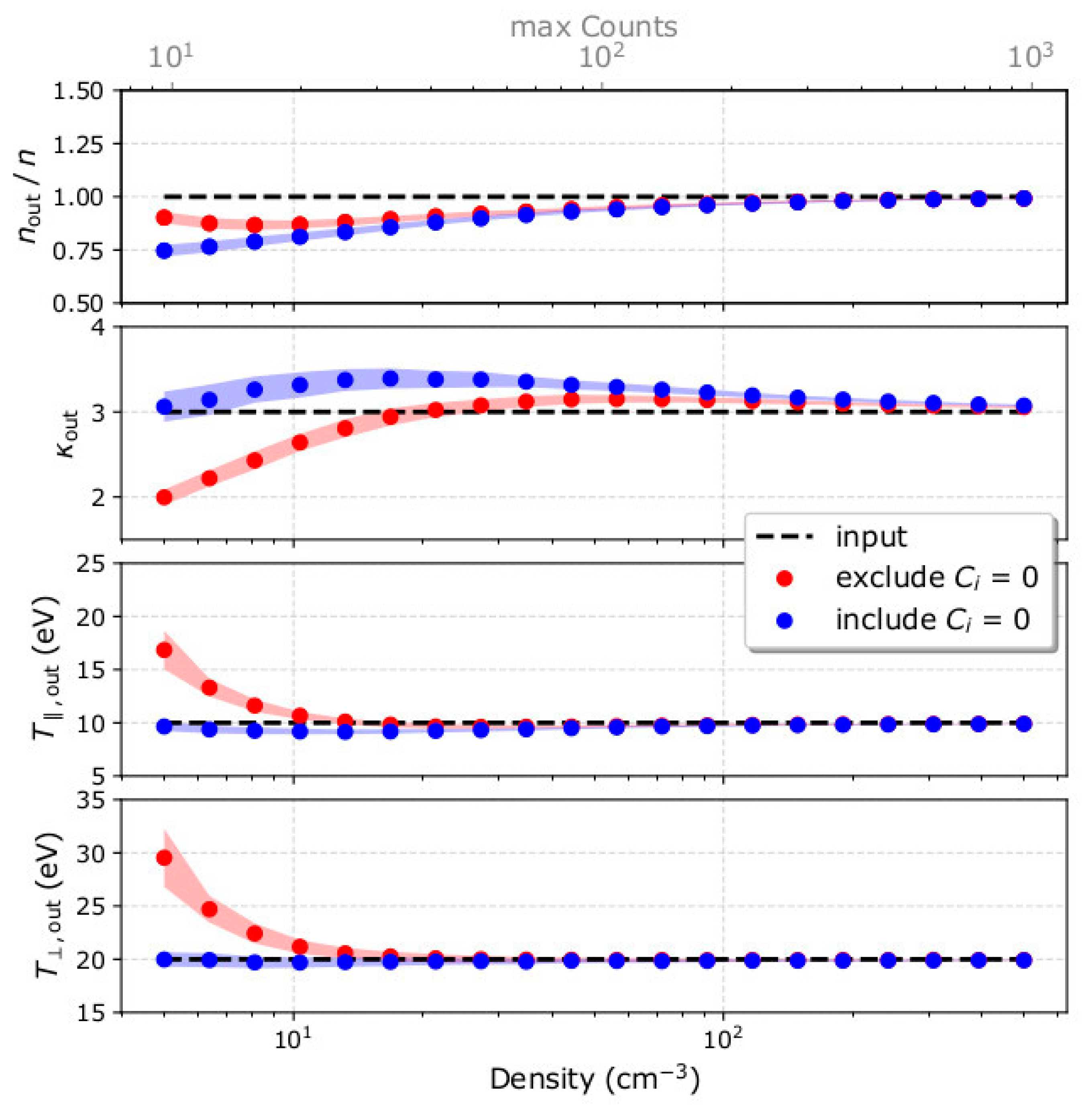
- The fit analysis of plasma measurements with relatively high flux (Cmax > 30) estimates the plasma temperature and kappa index more accurately if it excludes measurement points with Ci = 0. The corresponding analysis of measurements with low particle flux (Cmax < 30) estimates the temperature and kappa index more accurately if it includes measurement points with Ci = 0. Although Ci = 0 is a measurement with a large uncertainty, it contains information that becomes useful when the overall signal is weak.
- Examination of the fit convergence indicates that the determination of the plasma temperature and the determination of the kappa index are interdependent. As expected, the uncertainty of the derived parameters decreases with increasing particle flux.
- The plasma density is underestimated when the particle flux is low (Cmax < 100). We show that the misestimation is due to the asymmetry of the Poisson distribution and the assigned uncertainties to the data points.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shizgal, B.D. Suprathermal particle distributions in space physics: Kappa distributions and entropy. Astrophys. Space Sci. 2007, 312, 227–237. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsalis statistical mechanics in space plasmas. J. Geophys. Res. 2009, 114, A11105. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Understanding kappa distributions: A toolbox for space science and astrophysics. Space Sci. Rev. 2013, 175, 183–214. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M. Kappa distributions: Theory and applications in space plasmas. Sol. Phys. 2010, 267, 153–174. [Google Scholar] [CrossRef]
- Livadiotis, G. Introduction to special section on origins and properties of kappa distributions: Statistical Background and properties of kappa distributions in space plasmas. J. Geophys. Res. 2015, 120, 1607–1619. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distributions: Theory and Applications in Plasmas; Elsavier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Maksimovic, M.; Pierrard, V.; Riley, P. Ulysses electron distributions fitted with kappa functions. Geophys. Res. Lett. 1997, 24, 1151–1154. [Google Scholar] [CrossRef]
- Maksimovic, M.; Zouganelis, I.; Chaufray, J.Y.; Issautier, K.; Scime, E.E.; Littleton, J.E.; Marsch, E.; McComas, D.J.; Salem, C.; Lin, R.P.; et al. Radial evolution of the electron distribution functions in the fast solar wind between 0.3 and 1.5 AU. J. Geophys. Res. 2005, 110, A09104. [Google Scholar] [CrossRef]
- Pierrard, V.; Maksimovic, M.; Lemaire, J. Electron velocity distribution functions from the solar wind to the corona. J. Geophys. Res. 1999, 104, 17021–17032. [Google Scholar] [CrossRef]
- Zouganelis, I.; Maksimovic, M.; Meyer-Vernet, N.; Lamy, H.; Issautier, K. A transonic collisionless model of the solar wind. Astrophys. J. 2004, 606, 542–554. [Google Scholar] [CrossRef]
- Livadiotis, G. Using kappa distributions to identify the potential energy. J. Geophys. Res. 2018, 123, 1050–1060. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G. Long-term correlations of polytropic indices with kappa distributions in solar wind plasma near 1 au. Astrophys. J. 2019, 884, 52. [Google Scholar] [CrossRef]
- Mauk, B.H.; Mitchell, D.G.; McEntire, R.W.; Paranicas, C.P.; Roelof, E.C.; Williams, D.J.; Krimigis, S.M.; Lagg, A. Energetic ion characteristics and neutral gas interactions in Jupiter’s magnetosphere. J. Geophys. Res. 2004, 109, A09S12. [Google Scholar] [CrossRef]
- Dialynas, K.; Krimigis, S.M.; Mitchell, D.G.; Hamilton, D.C.; Krupp, N.; Brandt, P.C. Energetic ion spectral characteristics in the Saturnian magnetosphere using Cassini/MIMI measurements. J. Geophys. Res. 2009, 114, A01212. [Google Scholar] [CrossRef]
- Ogasawara, K.; Angelopoulos, V.; Dayeh, M.A.; Fuselier, S.A.; Livadiotis, G.; McComas, D.J.; McFadden, J.P. Characterizing the dayside magnetosheath using energetic neutral atoms: IBEX and THEMIS observations. J. Geophys. Res. 2013, 118, 3126–3137. [Google Scholar] [CrossRef]
- Broiles, T.W.; Livadiotis, G.; Burch, J.L.; Chae, K.; Clark, G.; Cravens, T.E.; Davidson, R.; Frahm, R.A.; Fuselier, S.A.; Goldstein, R.; et al. Characterizing cometary electrons with kappa distributions. J. Geophys. Res. 2016, 121, 7407–7422. [Google Scholar] [CrossRef]
- Decker, R.B.; Krimigis, S.M. Voyager observations of low-energy ions during solar cycle 23. Adv. Space Res. 2003, 32, 597–602. [Google Scholar] [CrossRef]
- Zank, G.P.; Heerikhuisen, J.; Pogorelov, N.V.; Burrows, R.; McComas, D. Microstructure of the heliospheric termination shock: Implications for energetic neutral atom observations. Astrophys. J. 2010, 708, 1092–1106. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Dayeh, M.A.; Funsten, H.O.; Schwadron, N.A. First Sky map of the inner heliosheath temperature using IBEX spectra. Astrophys. J. 2011, 734, 1. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Randol, B.M.; Funsten, H.O.; Möbius, E.S.; Schwadron, N.A.; Dayeh, M.A.; Zank, G.P.; Frisch, P.C. Pick-up ion distributions and their influence on energetic neutral atom spectral curvature. Astrophys. J. 2012, 751, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Schwadron, N.A.; Funsten, H.O.; Fuselier, S.A. Pressure of the proton plasma in the inner heliosheath. Astrophys. J. 2013, 762, 134. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. The influence of pick-up ions on space plasma distributions. Astrophys. J. 2011, 738, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Non-equilibrium thermodynamic processes: Space plasmas and the inner heliosheath. Astrophys. J. 2012, 749, 11. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G. Misestimation of temperature when applying Maxwellian distributions to space plasmas described by kappa distributions. Astrophys. Space Sci. 2016, 361, 359. [Google Scholar] [CrossRef]
- Johnstone, A.D.; Alsop, C.; Burge, S.; Carter, P.J.; Coates, A.J.; Coker, A.J.; Fazakerley, A.N.; Grande, M.; Gowen, R.A.; Gurgiolo, C.; et al. PEACE: A plasma electron and current experiment. Space Sci. Rev. 1997, 79, 351–398. [Google Scholar] [CrossRef]
- Owen, C.J.; Bruno, R.; Livi, S.; Louarn, P.; Al Janabi, K.; Allegrini, F.; Amoros, C.; Baruah, R.; Barthe, A.; Berthomier, M.; et al. The Solar Orbiter Analyser (SWA) Suite. Astron. Astrophys. 2020. submitted. [Google Scholar]
- Horbury, T.S.; O’Brien, H.; Carrasco Blazquez, I.; Bendyk, M.; Brown, P.; Hudson, R.; Evans, V.; Carr, C.M.; Beek, T.J.; Bhattacharya, S.; et al. The Solar Orbiter Magnetometer. Astron. Astrophys. 2020. submitted. [Google Scholar]
- Vaivads, A.; Retinò, A.; Soucek, J.; Khotyaintsev, Y.V.; Valentini, F.; Escoubet, C.P.; Alexandrova, O.; André, M.; Bale, S.D.; Balikhin, M.; et al. Turbulence heating ObserveR-satellite mission proposal. J. Plasma Phys. 2016, 82, 905820501. [Google Scholar] [CrossRef]
- Cara, A.; Lavraud, B.; Fedorov, A.; De Keyser, J.; DeMarco, R.; Federica Marucci, M.; Valentini, F.; Servidio, S.; Bruno, R. Electrostatic analyzer design for solar wind proton measurements with high temporal, energy, and angular resolutions. J. Geophys. Res. 2017, 122, 1439–1450. [Google Scholar] [CrossRef]
- Nicolaou, G.; McComas, D.J.; Bagenal, F.; Elliott, H.A. Properties of plasma ions in the distant Jovian magnetosheath using Solar Wind Around Pluto data on New Horizons. J. Geophys. Res. 2014, 119, 3463–3479. [Google Scholar] [CrossRef]
- Nicolaou, G.; McComas, D.J.; Bagenal, F.; Elliott, H.A.; Ebert, R.W. Jupiter’s deep magnetotail boundary layer. Planet. Space Sci. 2015, 111, 116–125. [Google Scholar] [CrossRef]
- Nicolaou, G.; McComas, D.J.; Bagenal, F.; Elliott, H.A.; Wilson, R.J. Plasma Properties in the deep jovian magnetotail. Planet. Space Sci. 2015, 119, 222–232. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G.; Owen, C.J.; Verscharen, D.; Wicks, R.T. Determining the kappa distributions of space plasmas from observations in a limited energy range. Astrophys. J. 2018, 864, 3. [Google Scholar] [CrossRef]
- Nicolaou, G.; Verscharen, D.; Wicks, R.T.; Owen, C.J. The impact of turbulent solar wind fluctuations on Solar Orbiter plasma proton measurements. Astrophys. J. 2019, 886, 101. [Google Scholar] [CrossRef]
- Wilson, R.J.; Bagenal, F.; Persoon, A.M. Survey of thermal ions in Saturn’s magnetosphere utilizing a forward model. J. Geophys. Res. 2017, 122, 7256–7278. [Google Scholar] [CrossRef]
- Kim, T.K.; Ebert, R.W.; Valek, P.W.; Allegrini, F.; McComas, D.J.; Bagenal, F.; Chae, K.; Livadiotis, G.; Loeffler, C.E.; Pollock, C.; et al. Method to derive ion properties from Juno JADE including abundance estimates for O+ and S2+. J. Geophys. Res. 2019. accepted article. [Google Scholar] [CrossRef]
- Wilson, R.J. Error analysis for numerical estimates of space plasma parameters. Earth Space Sci. 2015, 2, 201–222. [Google Scholar] [CrossRef]
- Ebert, R.W.; Allegrini, F.; Fuselier, S.A.; Nicolaou, G.; Bedworth, P.; Sinton, S.; Trattner, K.J. Angular scattering of 1–50 keV ions through graphene and thin carbon foils: Potential applications for space plasma instrumentation. Rev. Sci. Instrum. 2014, 85, 033302. [Google Scholar] [CrossRef]
- Allegrini, F.; Ebert, R.W.; Nicolaou, G.; Grubbs, G. Semi-empirical relationships for the energy loss and straggling of 1-50 keV hydrogen ions passing through thin carbon foils. Nuclear Instrum. Methods Phys. Res. Sect. B 2015, 359, 115–119. [Google Scholar] [CrossRef]

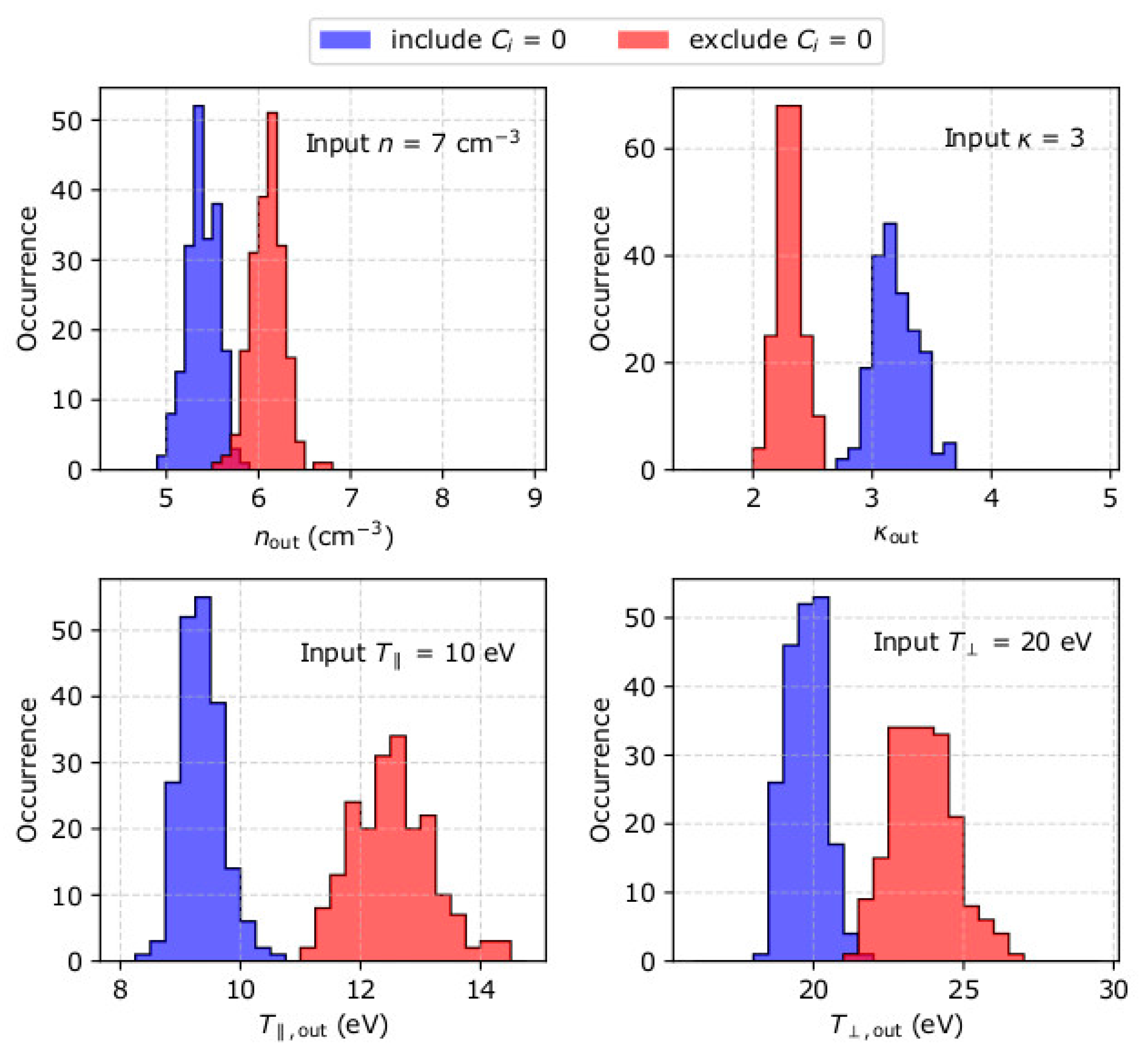

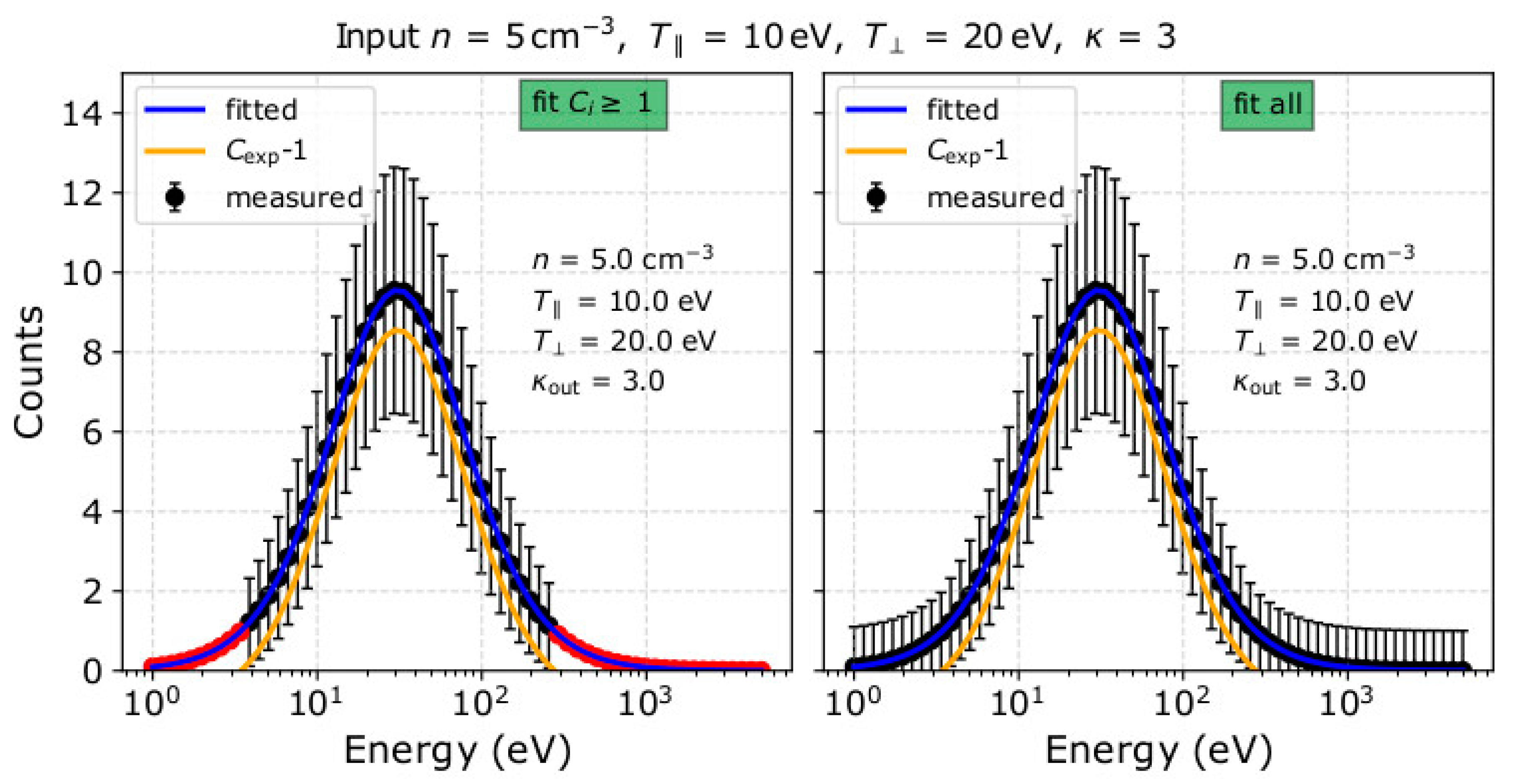
| Parameter | Input | Fit Including Ci = 0 Points | Fit Excluding Ci = 0 Points |
|---|---|---|---|
| n (cm−3) | 7 | 5.4 ± 0.2 | 6.1 ± 0.2 |
| κ | 3 | 3.2 ± 0.2 | 2.3 ± 0.1 |
| (eV) | 10 | 9.4 ± 0.3 | 12.5 ± 0.7 |
| (eV) | 20 | 19.8 ± 0.6 | 23.7 ± 1.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolaou, G.; Wicks, R.; Livadiotis, G.; Verscharen, D.; Owen, C.; Kataria, D. Determining the Bulk Parameters of Plasma Electrons from Pitch-Angle Distribution Measurements. Entropy 2020, 22, 103. https://doi.org/10.3390/e22010103
Nicolaou G, Wicks R, Livadiotis G, Verscharen D, Owen C, Kataria D. Determining the Bulk Parameters of Plasma Electrons from Pitch-Angle Distribution Measurements. Entropy. 2020; 22(1):103. https://doi.org/10.3390/e22010103
Chicago/Turabian StyleNicolaou, Georgios, Robert Wicks, George Livadiotis, Daniel Verscharen, Christopher Owen, and Dhiren Kataria. 2020. "Determining the Bulk Parameters of Plasma Electrons from Pitch-Angle Distribution Measurements" Entropy 22, no. 1: 103. https://doi.org/10.3390/e22010103
APA StyleNicolaou, G., Wicks, R., Livadiotis, G., Verscharen, D., Owen, C., & Kataria, D. (2020). Determining the Bulk Parameters of Plasma Electrons from Pitch-Angle Distribution Measurements. Entropy, 22(1), 103. https://doi.org/10.3390/e22010103






