Statistical Complexity Analysis of Turing Machine tapes with Fixed Algorithmic Complexity Using the Best-Order Markov Model
Abstract
1. Introduction
1.1. Turing Machines
1.2. Data Complexity
2. Methods
2.1. Turing Machines Configuration
- the machines start with a blank tape (all set to zero, “0”);
- the machines do not have an internal condition to halt ();
- the halting is performed by a external condition representing a certain number of iterations that is set equal to every single machine; and
- the TMs are restricted to read only one tape character at a time and perform three types of movement on the tape, namely move one cell to the left, move one cell to the right, or stay on the same position.
2.2. Search Approaches
2.3. Statistical Complexity
| Algorithm 1: Determine the NC of a generated TM tape. |
 |
2.4. Normal and Dynamic Complexity Profiles
2.5. Increasing the Statistical Complexity of TM’s Tape
- Method I aims to increase statistical complexity by optimizing the impact of the rules on the TM’s statistical complexity (aggregation of key rules).
- Method II aims to globally increase statistical complexity by iteratively changing the TM’s rules.
2.5.1. Method I
2.5.2. Method II
| Algorithm 2: Method II: Pseudo-code algorithm. |
 |
3. Assessment
4. Results
4.1. Statistical Complexity Patterns of Turing Machines
4.2. Normal and Dynamic Complexity Profiles
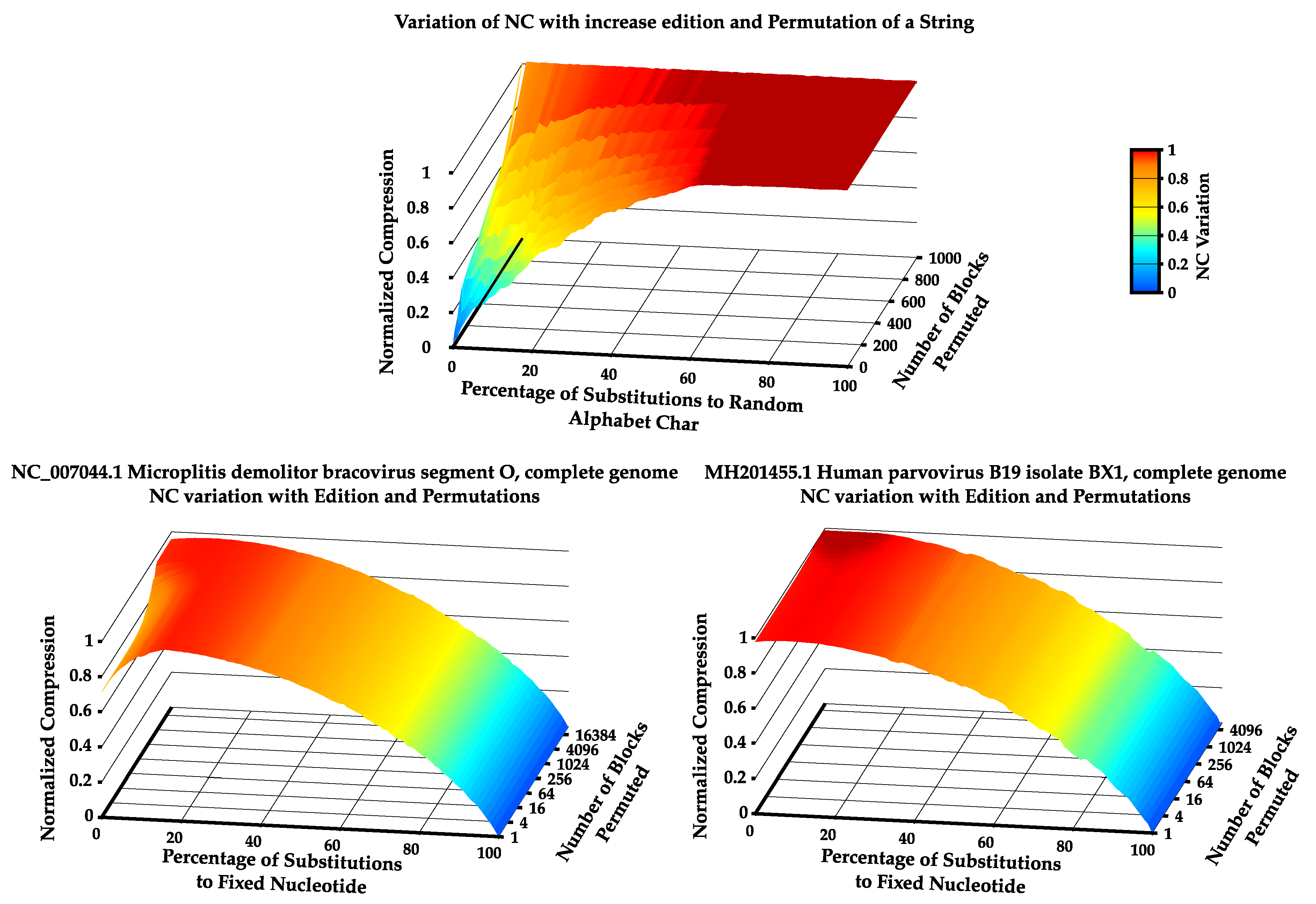
4.3. Comparison between NC and BDM
4.4. Increase Statistical Complexity of Turing Machines Tapes
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AID | Algorithmic Information Dynamics |
| AIT | Algorithmic Information Theory |
| BR | Bits Required |
| BDM | Block Decomposition Method |
| CTM | Coding Theorem Method |
| MML | Minimum Message Length |
| MDL | Minimum Description Length |
| NC | Normalized Compression |
| TNTM | Total Number of Turing Machines |
| TM | Turing Machine |
| US | Universal Levin Search |
Appendix A. Auxiliary Algorithms and Methods
Appendix A.1. Mapping Rule Matrix to ID
| Algorithm A1: Mapping a Turing machine rule matrix M to a unique identifier , in order to traverse through all TMs. |
| 1; 2; 3forcMdo 4 | ; 5 end 6 return ; |
Appendix A.2. Method I
| Algorithm A2: Method I: Pseudo-code algorithm. |
 |
Appendix B. Statistical Complexity Patterns of Turing Machines
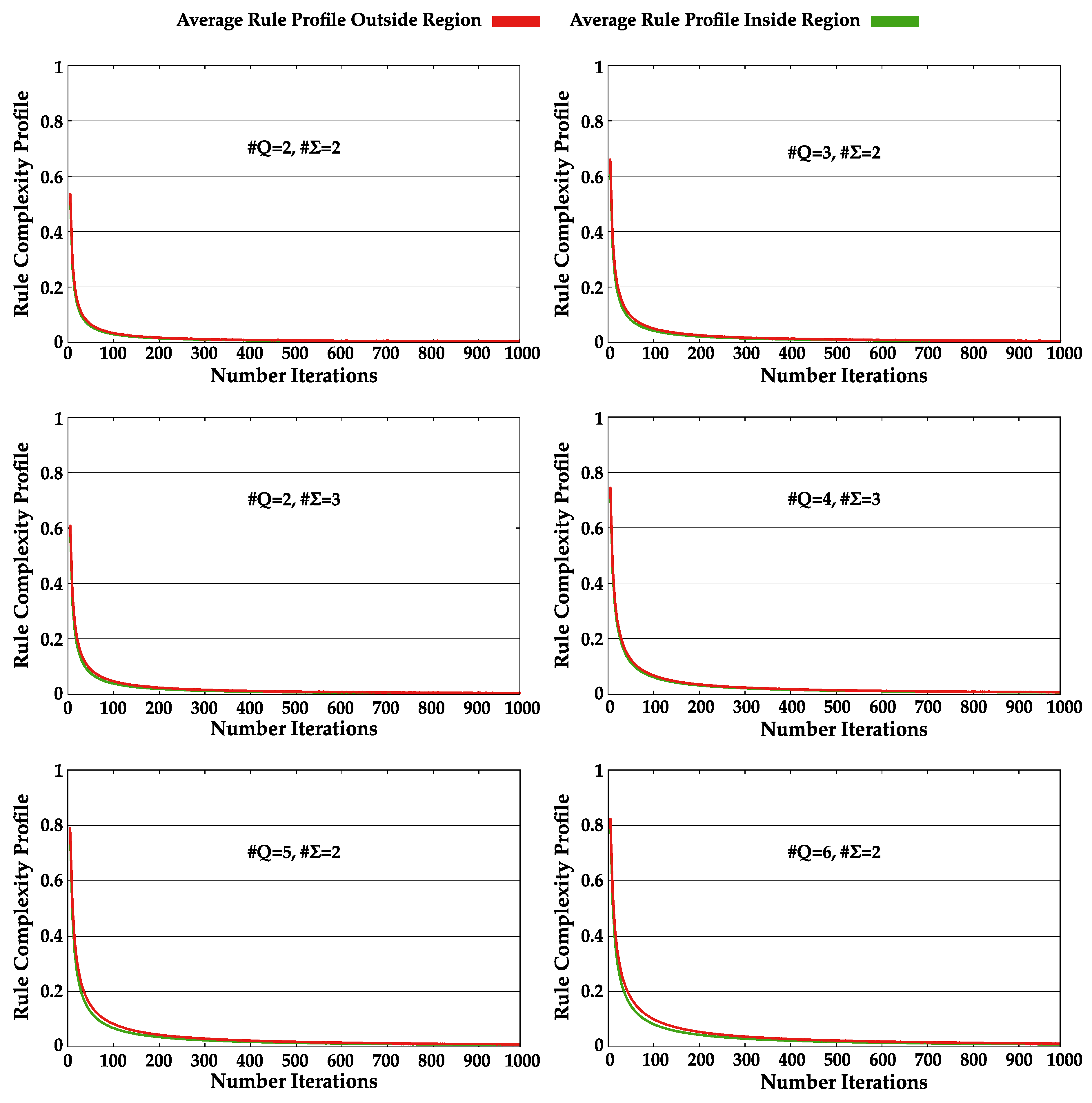
Appendix C. Comparison between BDM and NC
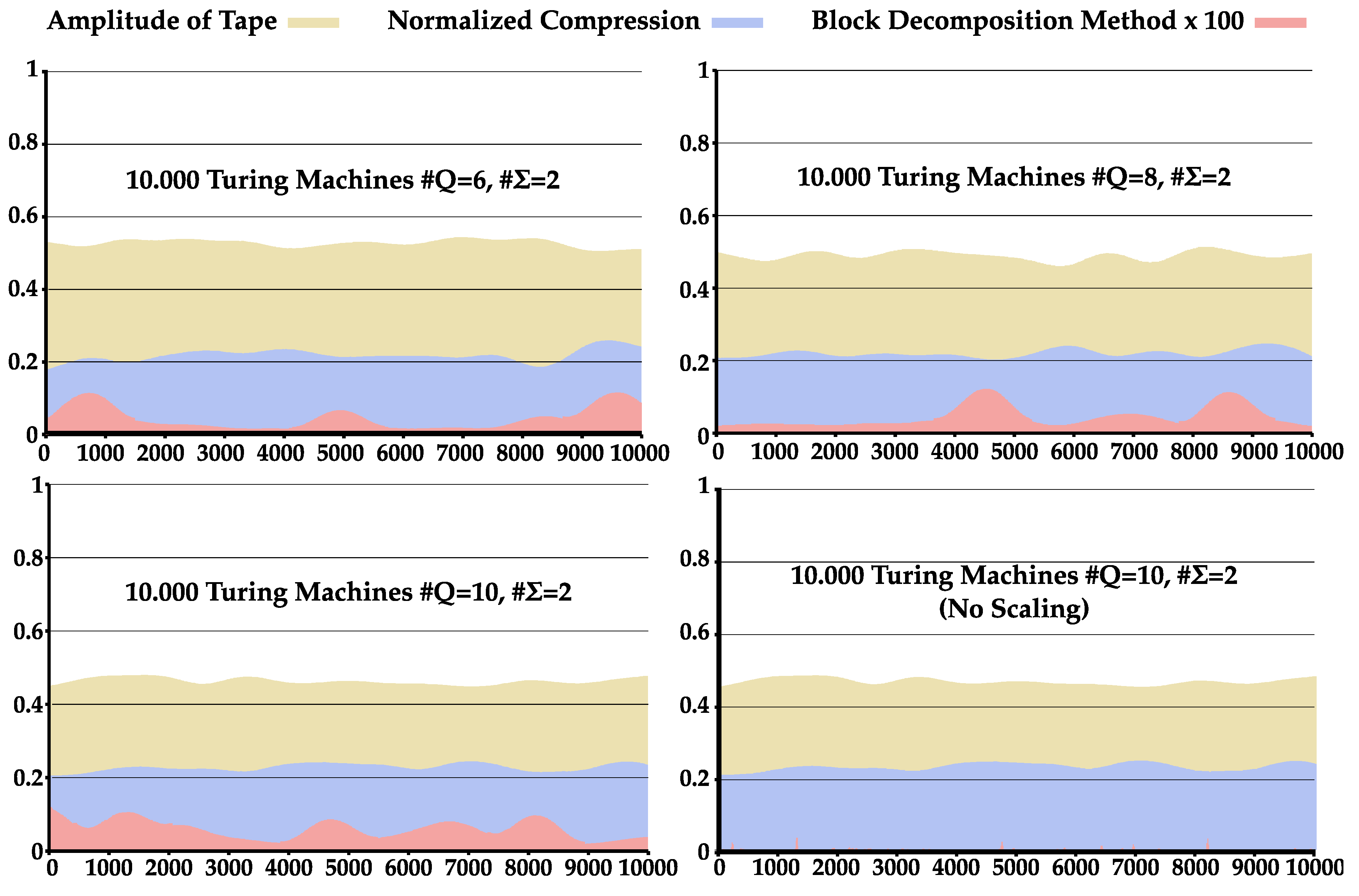
References
- Sacks, D. Letter Perfect: The Marvelous History of Our Alphabet from A to Z; Broadway Books: Portland, OR, USA, 2004; p. 395. [Google Scholar]
- Drucker, J. The Alphabetic Labyrinth: The Letters in History and Imagination; Thames and Hudson: London, UK, 1995; p. 320. [Google Scholar]
- Copeland, B.J. The Modern History of Computing. Available online: https://plato.stanford.edu/entries/computing-history/ (accessed on 13 January 2020).
- Newman, M.H.A. General principles of the design of all-purpose computing machines. Proc. R. Soc. Lond. 1948, 195, 271–274. [Google Scholar]
- Turing, A.M. On Computable Numbers, with an Application to the Entscheidungsproblem. Proc. R. Soc. Lond. 1936, s2-42, 230–265. [Google Scholar] [CrossRef]
- Goldin, D.; Wegner, P. The Church-Turing Thesis: Breaking the Myth; New Computational Paradigms; Cooper, S.B., Löwe, B., Torenvliet, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 152–168. [Google Scholar]
- Minsky, M.L. Computation: Finite and Infinite Machines; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1967. [Google Scholar]
- Boolos, G.S.; Burgess, J.P.; Jeffrey, R.C. Computability and Logic; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Nyquist, H. Certain Factors Affecting Telegraph Speed. Bell Syst. Tech. J. 1924, 3, 324–346. [Google Scholar] [CrossRef]
- Hartley, R.V.L. Transmission of Information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Anderson, J.B.; Johnnesson, R. Understanding Information Transmission; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar]
- Solomonoff, R.J. A Preliminary Report on a General Theory of Inductive Inference; United States Air Force, Office of Scientific Research: Montgomery, OH, USA, 1960. [Google Scholar]
- Solomonoff, R.J. A formal theory of inductive inference. Part I. Inf. Control 1964, 7, 1–22. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part II. Inf. Control 1964, 7, 224–254. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three Approaches to the Quantitative Definition of Information. Prob. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences. J. ACM (JACM) 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Chaitin, G.J. A theory of program size formally identical to information theory. J. ACM (JACM) 1975, 22, 329–340. [Google Scholar] [CrossRef]
- Bennett, C.H. On random and hard-to-describe numbers. Randomness Complex. Leibniz Chaitin 2007, 3–12. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the difficulty of computations. IEEE Trans. Inf. Theory 1970, 16, 5–9. [Google Scholar] [CrossRef]
- Chaitin, G.J. Incompleteness theorems for random reals. Adv. Appl. Math. 1987, 8, 119–146. [Google Scholar] [CrossRef]
- Chaitin, G.J.; Arslanov, A.; Calude, C. Program-Size Complexity Computes the Halting Problem; Technical Report; Department of Computer Science, The University of Auckland: Auckland, New Zealand, 1995. [Google Scholar]
- Hammer, D.; Romashchenko, A.; Shen, A.; Vereshchagin, N. Inequalities for Shannon Entropy and Kolmogorov Complexity. J. Comput. Syst. Sci. Int. 2000, 60, 442–464. [Google Scholar] [CrossRef]
- Henriques, T.; Gonçalves, H.; Antunes, L.; Matias, M.; Bernardes, J.; Costa-Santos, C. Entropy and compression: Two measures of complexity. J. Eval. Clin. Pract. 2013, 19, 1101–1106. [Google Scholar] [CrossRef] [PubMed]
- Levin, L.A. Laws of information conservation (nongrowth) and aspects of the foundation of probability theory. Problemy Peredachi Informatsii 1974, 10, 30–35. [Google Scholar]
- Gács, P. On the symmetry of algorithmic information. Dokl. Akad. Nauk SSSR 1974, 218, 1265–1267. [Google Scholar]
- Blum, M. A machine-independent theory of the complexity of recursive functions. J. ACM (JACM) 1967, 14, 322–336. [Google Scholar] [CrossRef]
- Burgin, M. Generalized Kolmogorov complexity and duality in theory of computations. Not. Russ. Acad. Sci. 1982, 25, 19–23. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: Berlin/Heidelberger, Germany, 2008. [Google Scholar]
- Wallace, C.S.; Boulton, D.M. An information measure for classification. Comput. J. 1968, 11, 185–194. [Google Scholar] [CrossRef]
- Vitanyi, P.M.B.; Li, M. Minimum description length induction, Bayesianism, and Kolmogorov complexity. IEEE Trans. Inf. Theory 2000, 46, 446–464. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Bennett, C.H. Logical Depth and Physical Complexity. In The Universal Turing Machine, a Half-Century Survey; Oxford University Press: Oxford, UK, 1995; pp. 207–235. [Google Scholar]
- Martin-Löf, P. The definition of random sequences. Inf. Control 1966, 9, 602–619. [Google Scholar] [CrossRef]
- Von Mises, R. Grundlagen der wahrscheinlichkeitsrechnung. Math. Z. 1919, 5, 52–99. [Google Scholar] [CrossRef]
- Schnorr, C.P. A unified approach to the definition of random sequences. Math. Syst. Theory 1971, 5, 246–258. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.A.; Tegnér, J. Low-algorithmic-complexity entropy-deceiving graphs. Phys. Rev. E 2017, 96, 012308. [Google Scholar] [CrossRef] [PubMed]
- Zenil, H.; Hernández-Orozco, S.; Kiani, N.A.; Soler-Toscano, F.; Rueda-Toicen, A.; Tegnér, J. A Decomposition Method for Global Evaluation of Shannon Entropy and Local Estimations of Algorithmic Complexity. Entropy 2018, 20, 605. [Google Scholar] [CrossRef]
- Bloem, P.; Mota, F.; de Rooij, S.; Antunes, L.; Adriaans, P. A safe approximation for Kolmogorov complexity. Algorithmic Learn. Theory 2014, 8776, 336–350. [Google Scholar]
- Zenil, H.; Badillo, L.; Hernández-Orozco, S.; Hernández-Quiroz, F. Coding-theorem like behaviour and emergence of the universal distribution from resource-bounded algorithmic probability. Int. J. Parallel Emerg. Distrib. Syst. 2018, 34, 1–20. [Google Scholar] [CrossRef]
- Pratas, D.; Pinho, A.J.; Ferreira, P.J.S.G. Efficient compression of genomic sequences. In Proceedings of the 2016 Data Compression Conference (DCC), Snowbird, UT, USA, 30 March–1 April 2016. [Google Scholar]
- Levin, L.A. Universal sequential search problems. Problemy Peredachi Informatsii 1973, 9, 115–116. [Google Scholar]
- Levin, L.A. Randomness conservation inequalities, information and independence in mathematical theories. Inf. Control 1984, 61, 15–37. [Google Scholar] [CrossRef]
- Hutter, M. The fastest and shortest algorithm for all well-defined problems. Int. J. Found. Comput. Sci. 2002, 13, 431–443. [Google Scholar] [CrossRef]
- Hutter, M. Universal Artificial Intelligence: Sequential Decisions Based on Algorithmic Probability; Springer Science & Business Media: Berlin/Heidelberger, Germany, 2004. [Google Scholar]
- Soler-Toscano, F.; Zenil, H.; Delahaye, J.P.; Gauvrit, N. Calculating Kolmogorov Complexity from the Output Frequency Distributions of Small Turing Machines. PLoS ONE 2014, 9, e96223. [Google Scholar] [CrossRef]
- Zenil, H.; Soler-Toscano, F.; Dingle, K.; Louis, A.A. Correlation of automorphism group size and topological properties with program-size complexity evaluations of graphs and complex networks. Physica A 2014, 404, 341–358. [Google Scholar] [CrossRef]
- Kempe, V.; Gauvrit, N.; Forsyth, D. Structure emerges faster during cultural transmission in children than in adults. Cognition 2015, 136, 247–254. [Google Scholar] [CrossRef]
- Zenil, H.; Soler-Toscano, F.; Delahaye, J.P.; Gauvrit, N. Two-dimensional Kolmogorov complexity and an empirical validation of the coding theorem method by compressibility. PeerJ Comput. Sci. 2015, 1, e23. [Google Scholar] [CrossRef]
- Motwani, R.; Raghavan, P. Randomized Algorithms; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gill, J. Computational complexity of probabilistic Turing machines. SIAM J. Comput. 1977, 6, 675–695. [Google Scholar] [CrossRef]
- Pratas, D.; Pinho, A.J. On the approximation of the Kolmogorov complexity for DNA sequences. Pattern Recognit. Image Anal. 2017, 10255, 259–266. [Google Scholar]
- Pinho, A.J.; Ferreira, P.J.S.G.; Neves, A.J.R.; Bastos, C.A.C. On the Representability of Complete Genomes by Multiple Competing Finite-Context (Markov) Models. PLoS ONE 2011, 6, e21588. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.; Tegnér, J. Algorithmic Information Dynamics of Emergent, Persistent, and Colliding Particles in the Game of Life. In From Parallel to Emergent Computing; Adamatzky, A., Ed.; Taylor & Francis/CRC Press: Boca Raton, FL, USA, 2019; pp. 367–383. [Google Scholar]
- Pratas, D.; Hosseini, M.; Pinho, A.J. Substitutional tolerant Markov models for relative compression of DNA sequences. In Proceedings of the 11th International Conference on Practical Applications of Computational Biology & Bioinformatics, Porto, Portugal, 21–23 June 2017; pp. 265–272. [Google Scholar]
- Pinho, A.J.; Neves, A.J.R.; Ferreira, P.J.S.G. Inverted-repeats-aware finite-context models for DNA coding. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitanyi, P.M.B. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Cilibrasi, R.; Vitanyi, P.M.B. Clustering by compression. IEEE Trans. Inf. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Gödel, K. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik 1931, 38, 173–198. [Google Scholar] [CrossRef]
- Russell, B. Principles of Mathematics; Routledge: London, UK, 2009. [Google Scholar]
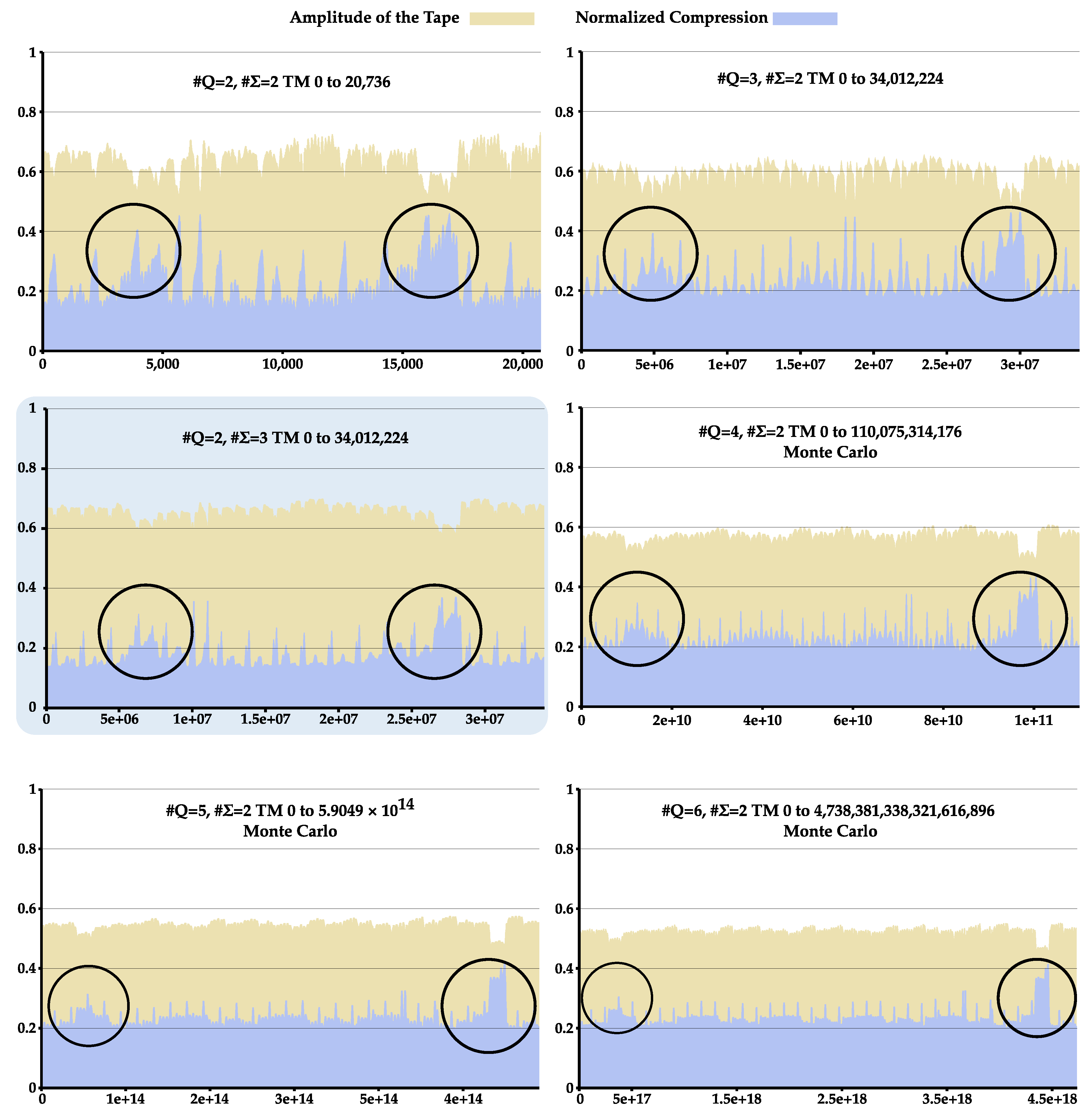
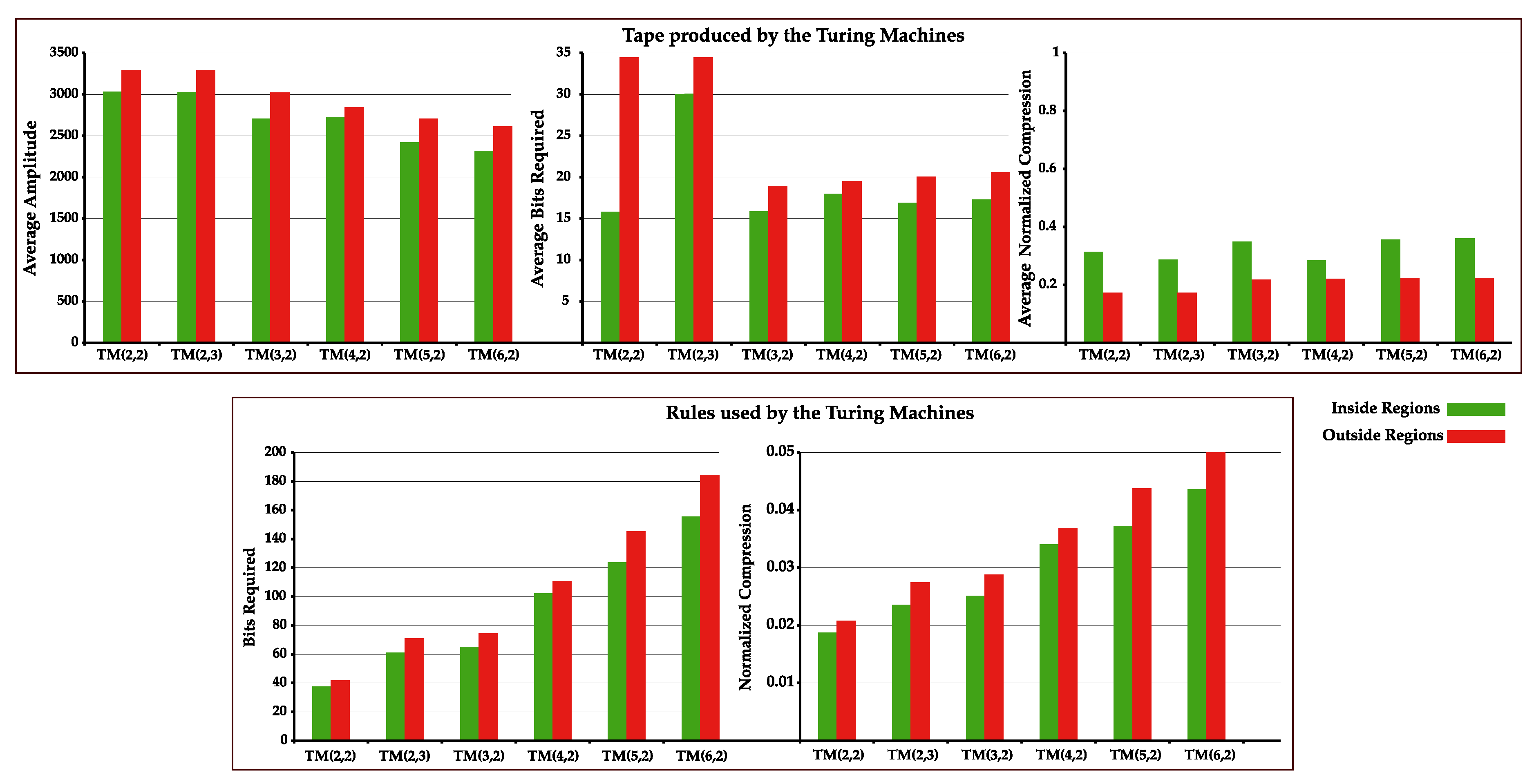
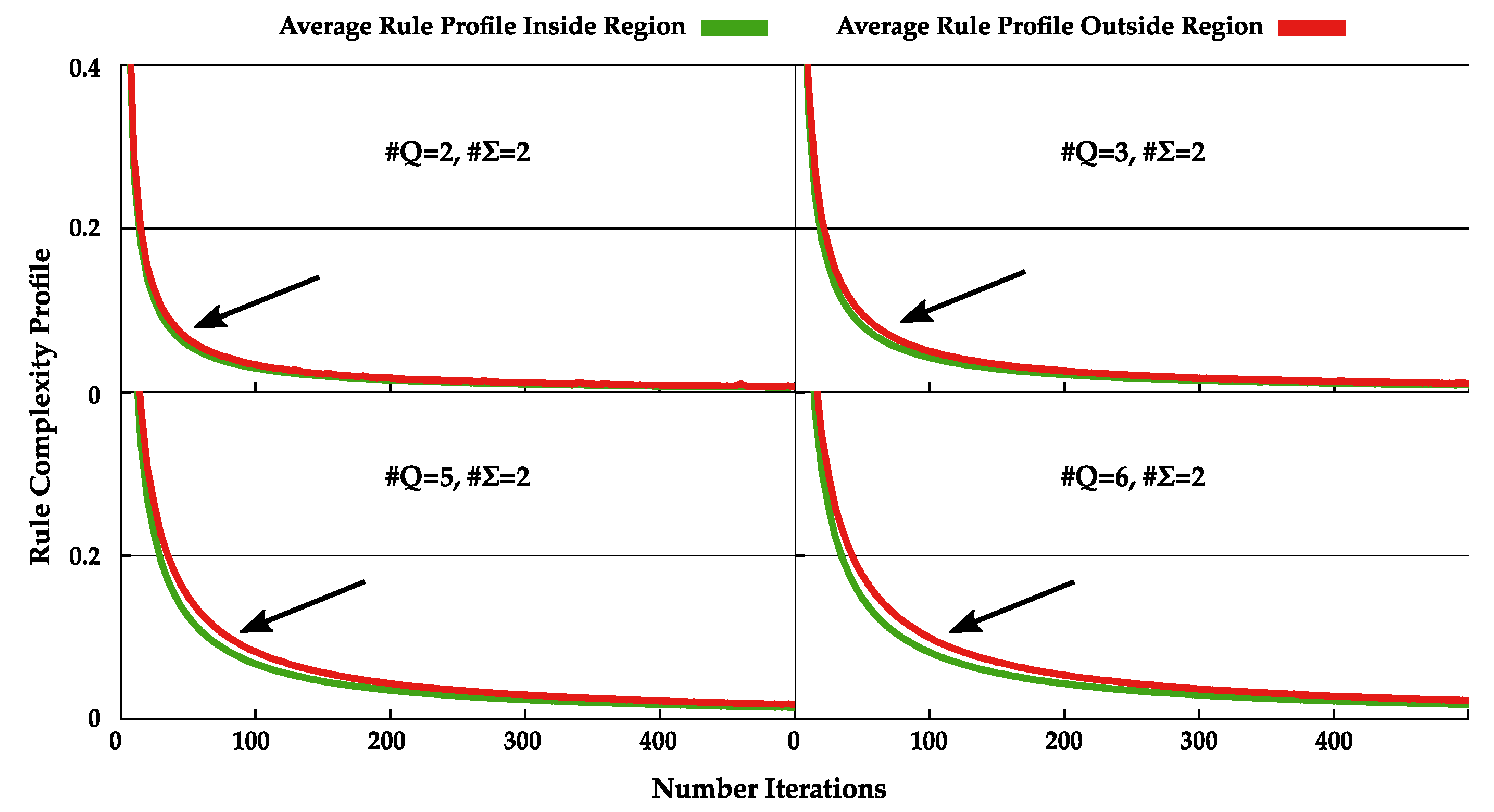
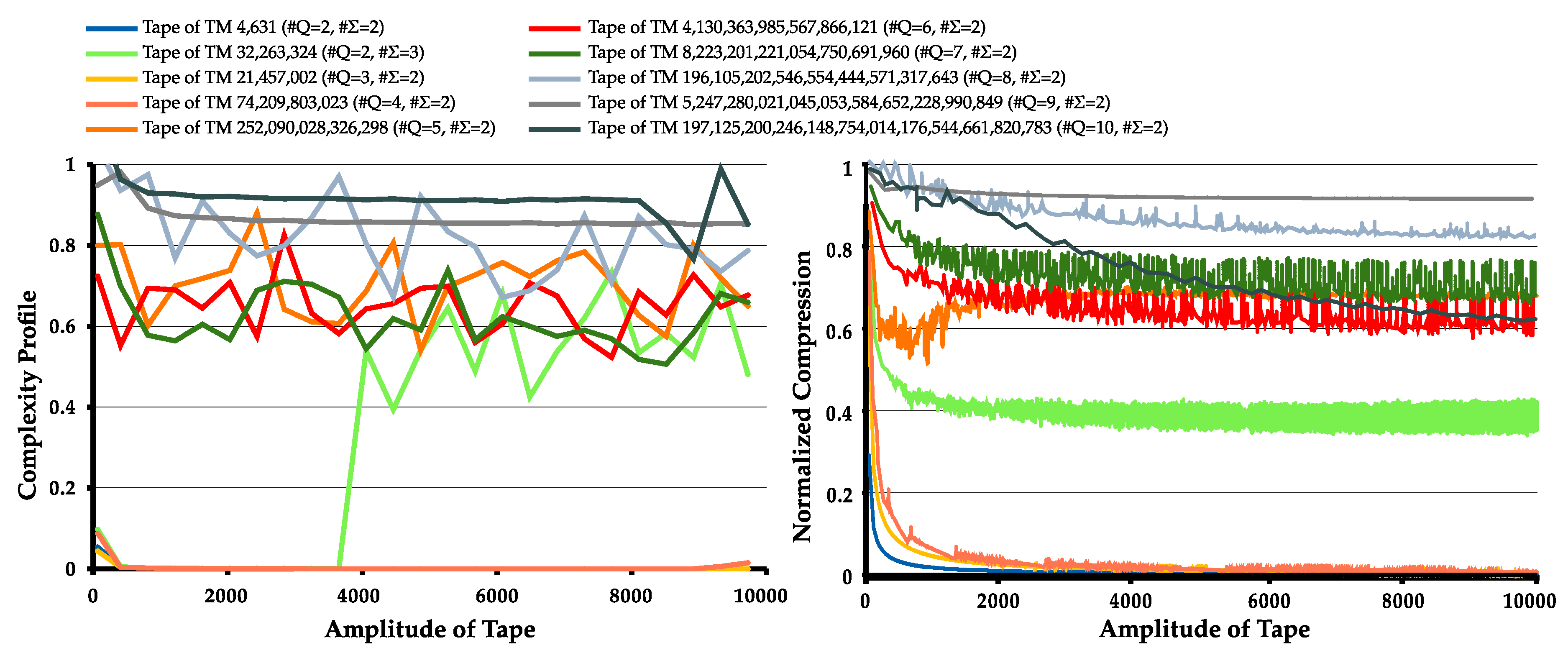
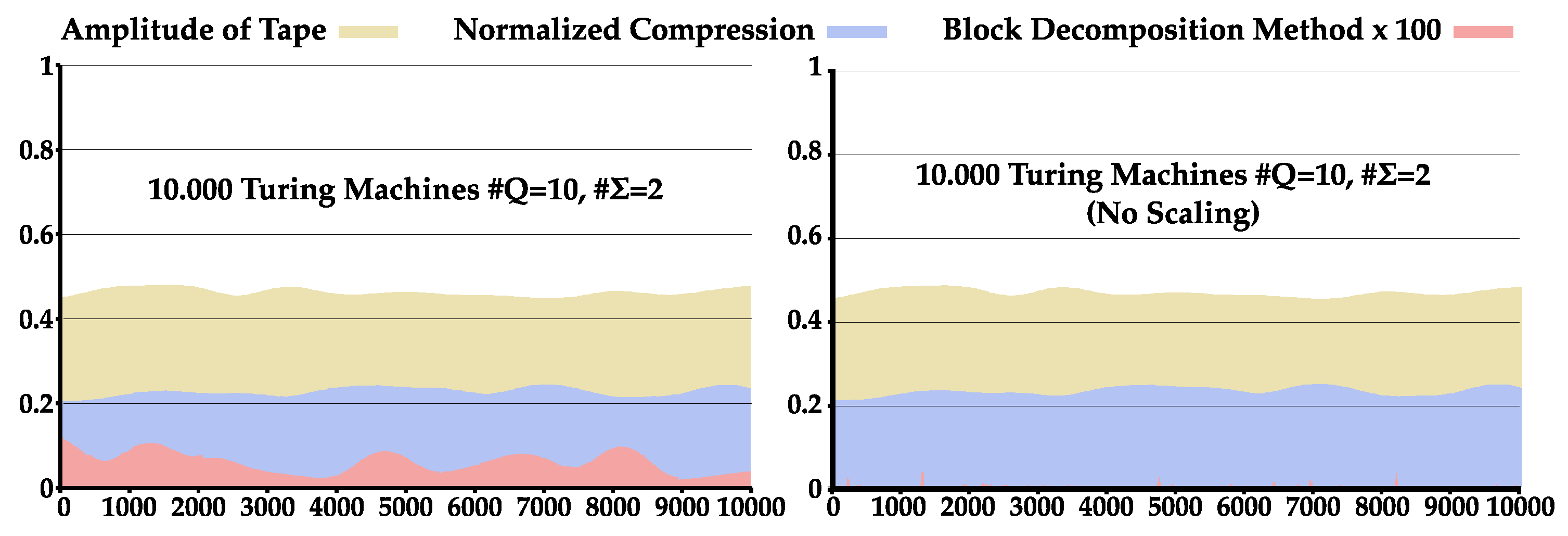
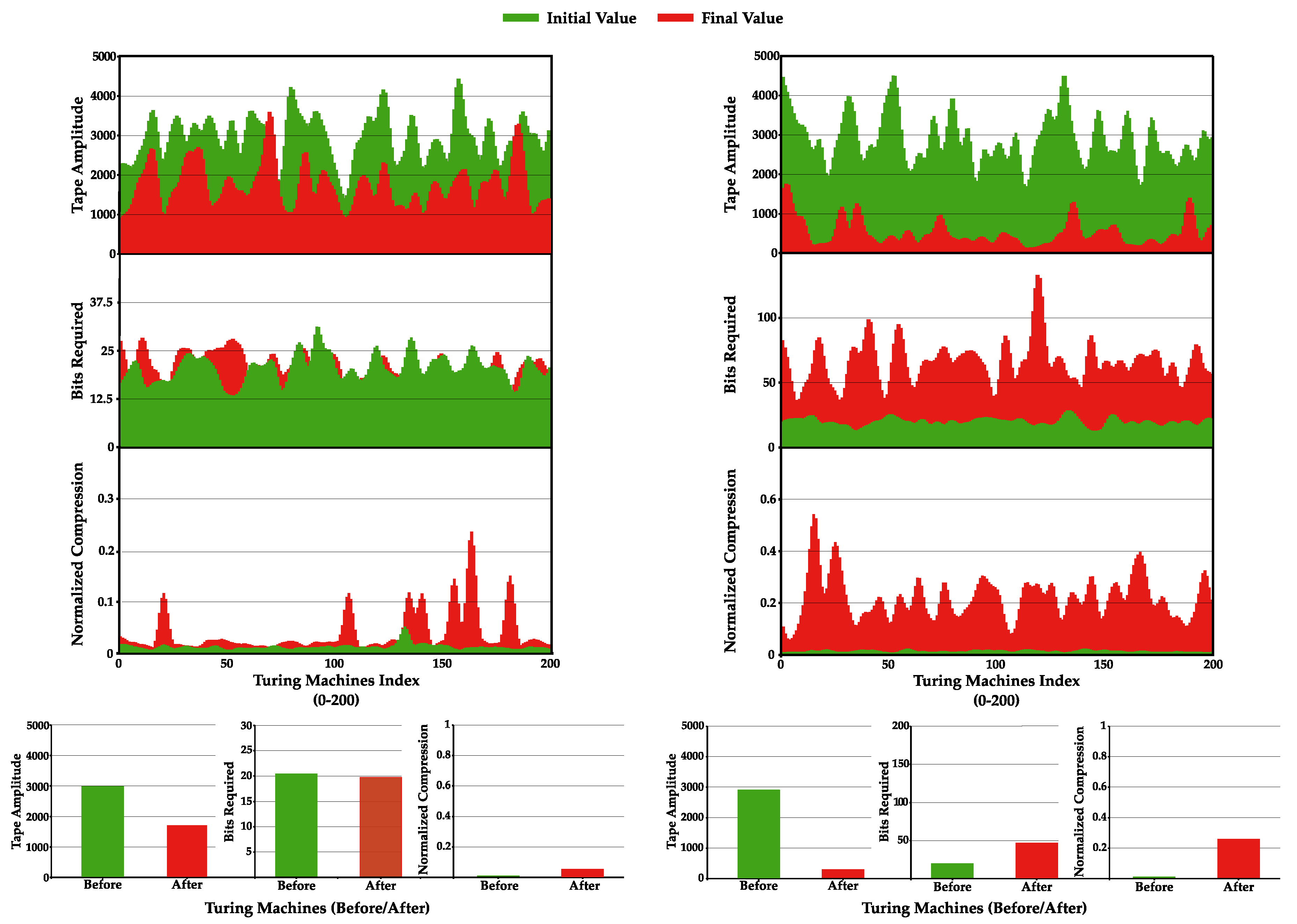

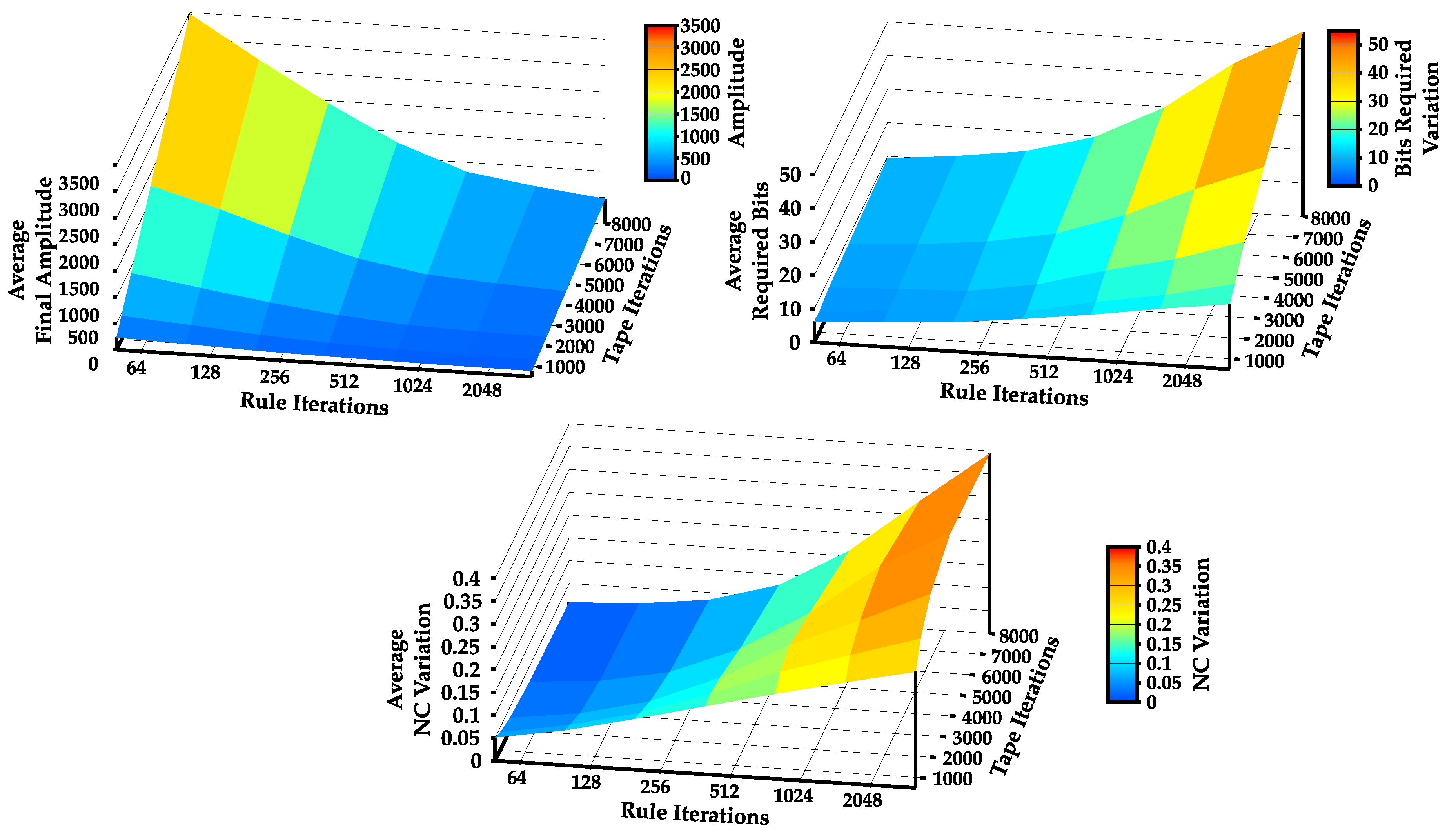
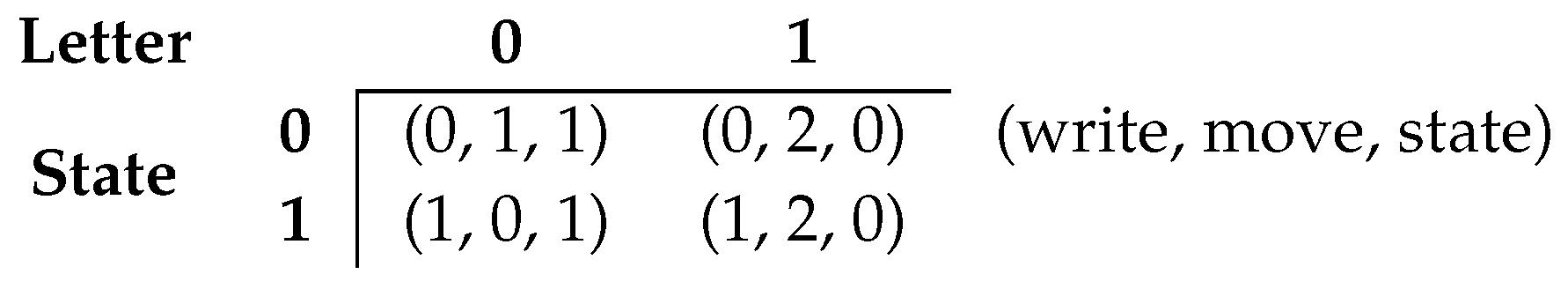
| # | #Q | TM No. | Search Approach | Mean Amp ± std | Mean NC ± std |
|---|---|---|---|---|---|
| 2 | 2 | 20,736 | Sequential | 32,055 ± 20,836 | 0.22724 ± 0.42095 |
| 2 | 3 | 34,012,224 | Sequential | 29,745 ± 20,609 | 0.22808 ± 0.42330 |
| 3 | 2 | 34,012,224 | Sequential | 32,603 ± 19,923 | 0.17887 ± 0.38230 |
| 2 | 4 | 34,000,000 | Monte Carlo | 28,146 ± 20,348 | 0.22753 ± 0.42403 |
| 2 | 5 | 34,000,000 | Monte Carlo | 26,932 ± 20,092 | 0.22643 ± 0.42403 |
| 2 | 6 | 50,000,000 | Monte Carlo | 25,963 ± 19,856 | 0.22512 ± 0.42363 |
| 2 | 7 | 50,000,000 | Monte Carlo | 25,164 ± 19,636 | 0.22356 ± 0.42285 |
| 2 | 8 | 30,000,000 | Monte Carlo | 24,477 ± 19,433 | 0.22219 ± 0.42215 |
| 2 | 9 | 30,000,000 | Monte Carlo | 23,882 ± 19,245 | 0.22079 ± 0.42134 |
| 2 | 10 | 30,000,000 | Monte Carlo | 23,357 ± 19,068 | 0.21933 ± 0.42039 |
| # | #Q | TM No. | Mean Amp ± std | Mean BDM ± std | Mean NC ± std |
|---|---|---|---|---|---|
| 2 | 6 | 10,000 | 26,359.6 ± 19,821 | 0.00042801 ± 0.011328 | 0.21631 ± 0.41753 |
| 2 | 8 | 10,000 | 24,471.8 ± 19,353 | 0.00045401 ± 0.010250 | 0.21975 ± 0.42054 |
| 2 | 10 | 10,000 | 23,123 ± 19,157 | 0.00060360 ± 0.012539 | 0.22696 ± 0.42404 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, J.M.; Pinho, E.; Matos, S.; Pratas, D. Statistical Complexity Analysis of Turing Machine tapes with Fixed Algorithmic Complexity Using the Best-Order Markov Model. Entropy 2020, 22, 105. https://doi.org/10.3390/e22010105
Silva JM, Pinho E, Matos S, Pratas D. Statistical Complexity Analysis of Turing Machine tapes with Fixed Algorithmic Complexity Using the Best-Order Markov Model. Entropy. 2020; 22(1):105. https://doi.org/10.3390/e22010105
Chicago/Turabian StyleSilva, Jorge M., Eduardo Pinho, Sérgio Matos, and Diogo Pratas. 2020. "Statistical Complexity Analysis of Turing Machine tapes with Fixed Algorithmic Complexity Using the Best-Order Markov Model" Entropy 22, no. 1: 105. https://doi.org/10.3390/e22010105
APA StyleSilva, J. M., Pinho, E., Matos, S., & Pratas, D. (2020). Statistical Complexity Analysis of Turing Machine tapes with Fixed Algorithmic Complexity Using the Best-Order Markov Model. Entropy, 22(1), 105. https://doi.org/10.3390/e22010105





