Parameter Optimization Based BPNN of Atmosphere Continuous-Variable Quantum Key Distribution
Abstract
1. Introduction
2. Transmittance and Security Analysis
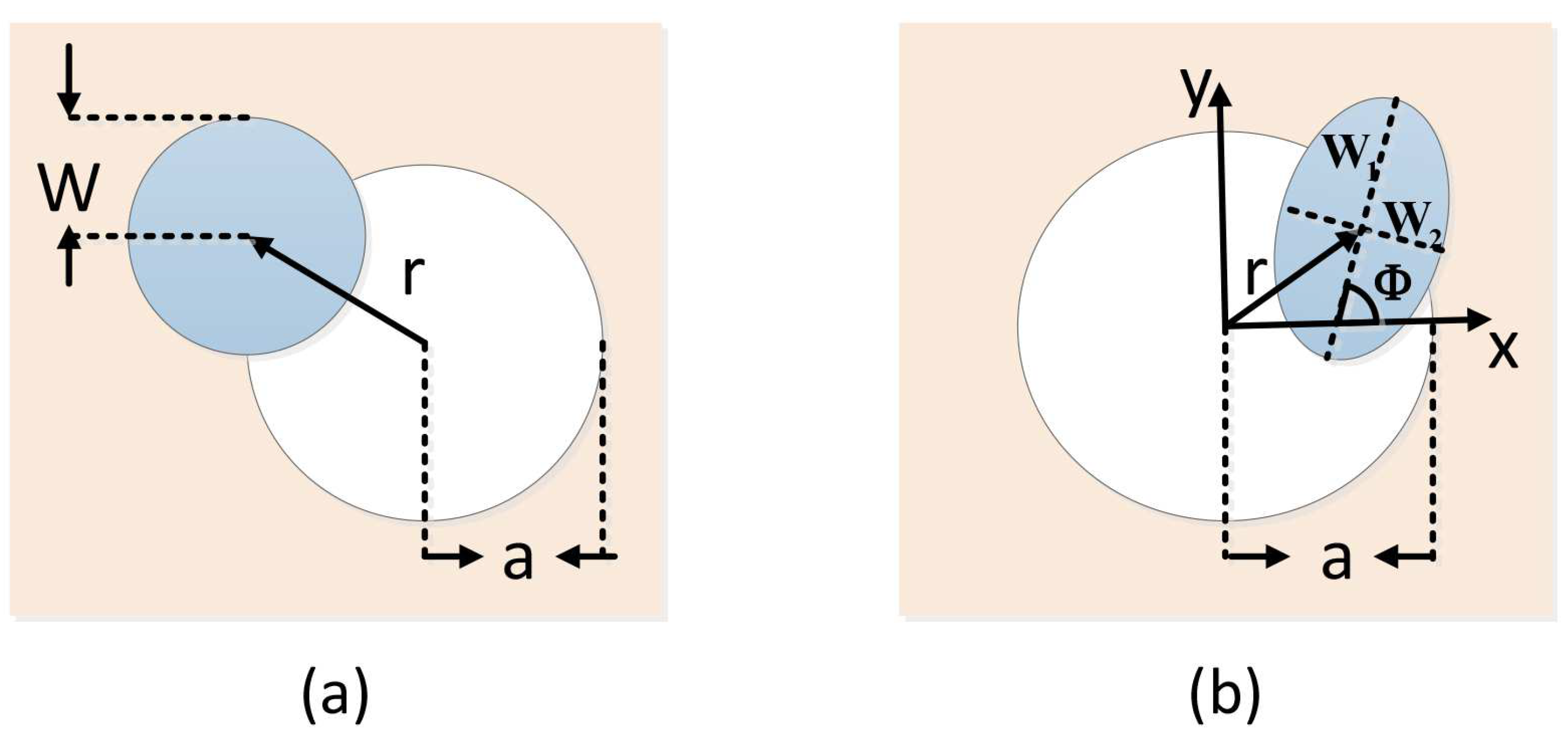
2.1. Transmittance Analysis
2.2. Secret Key Rate in the Atmosphere Turbulence Channel
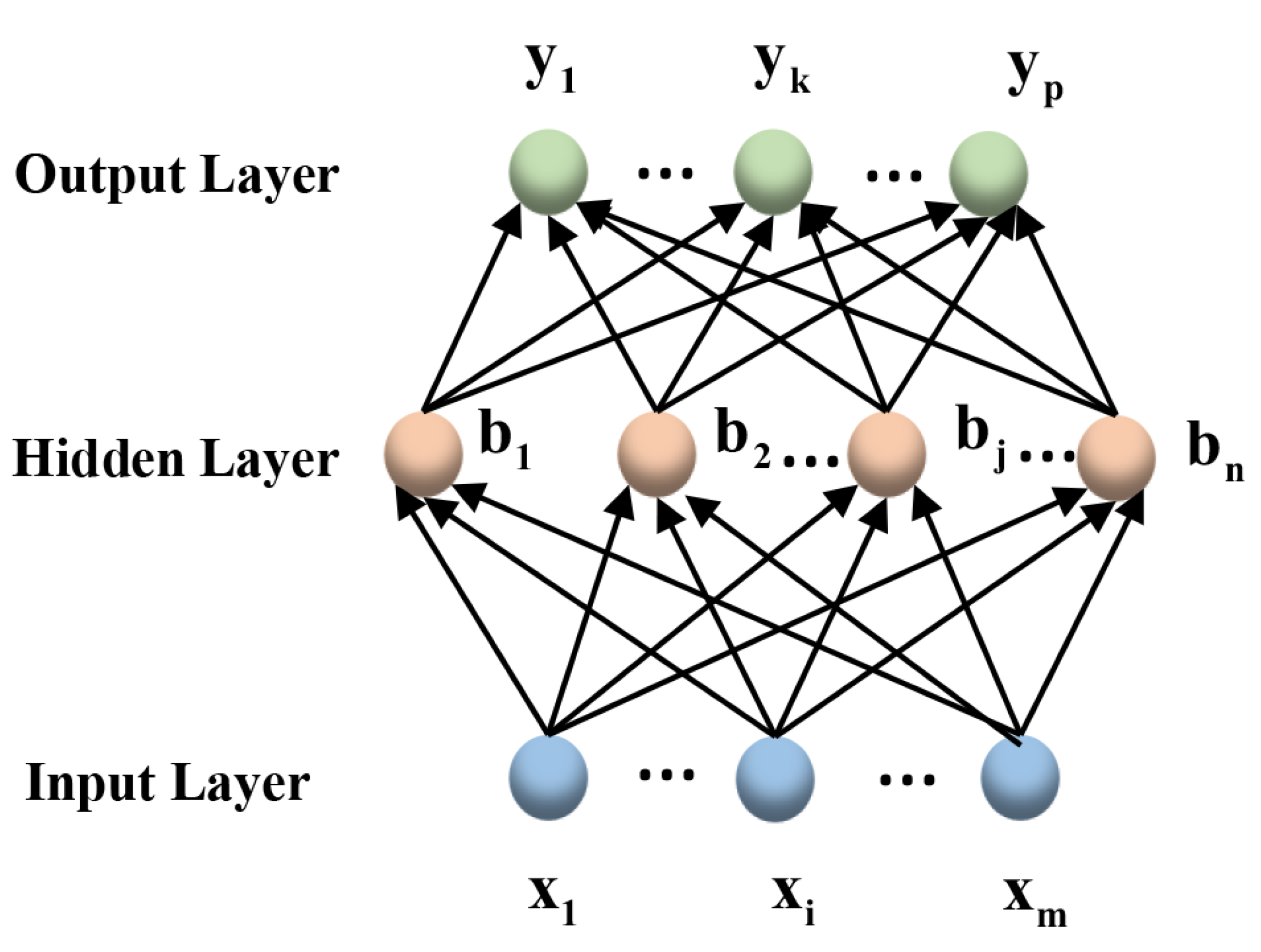
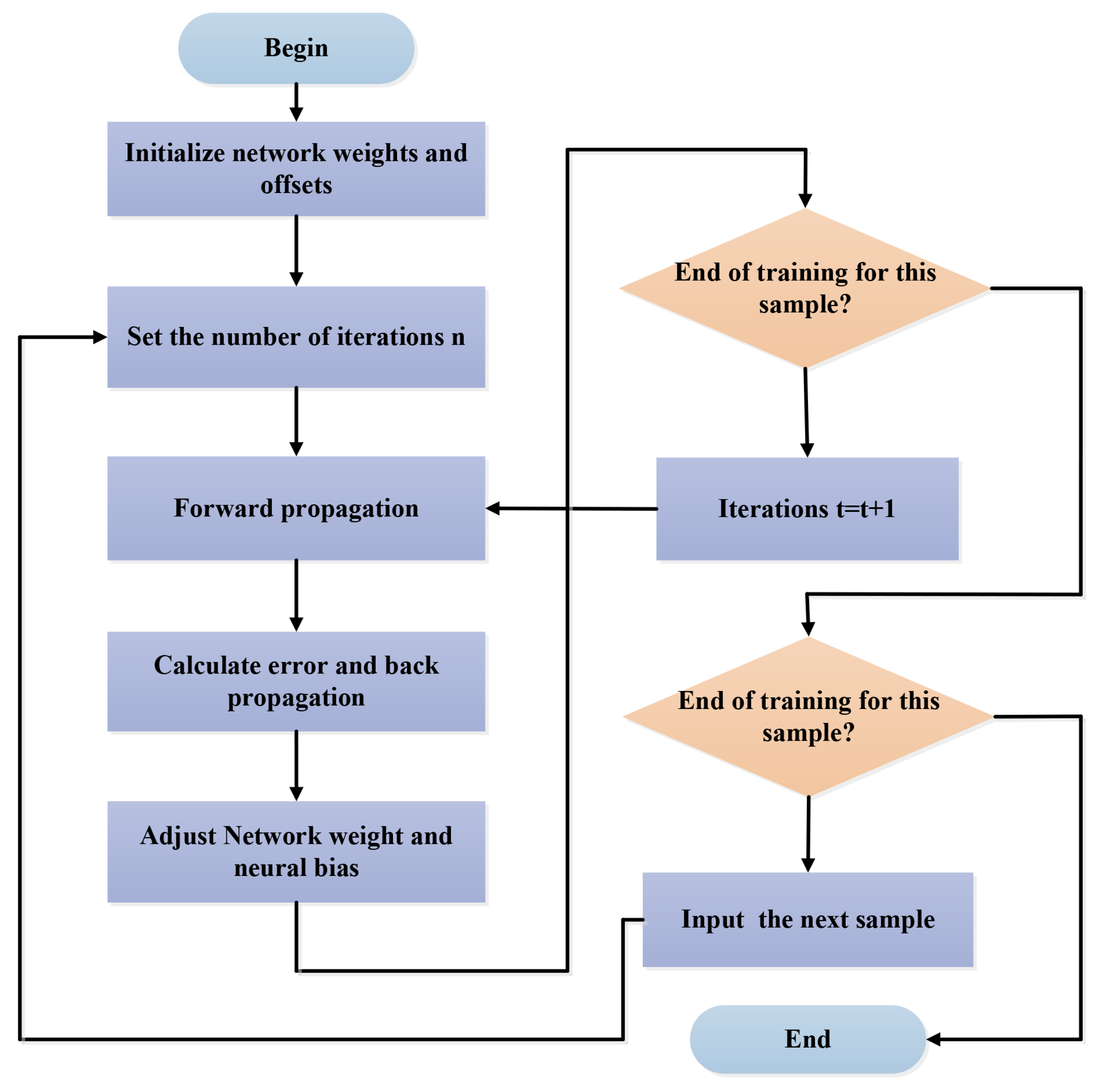
3. BPNN-Based CVQKD Scheme
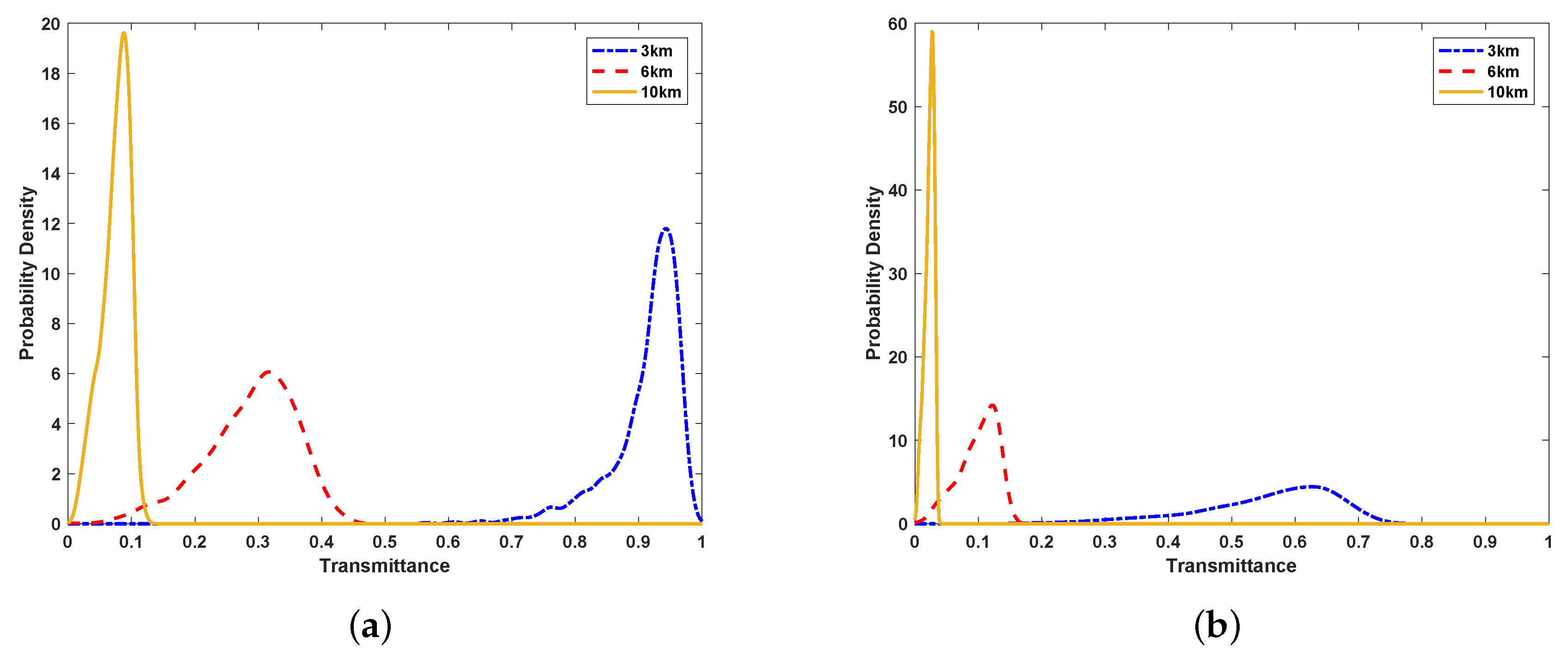
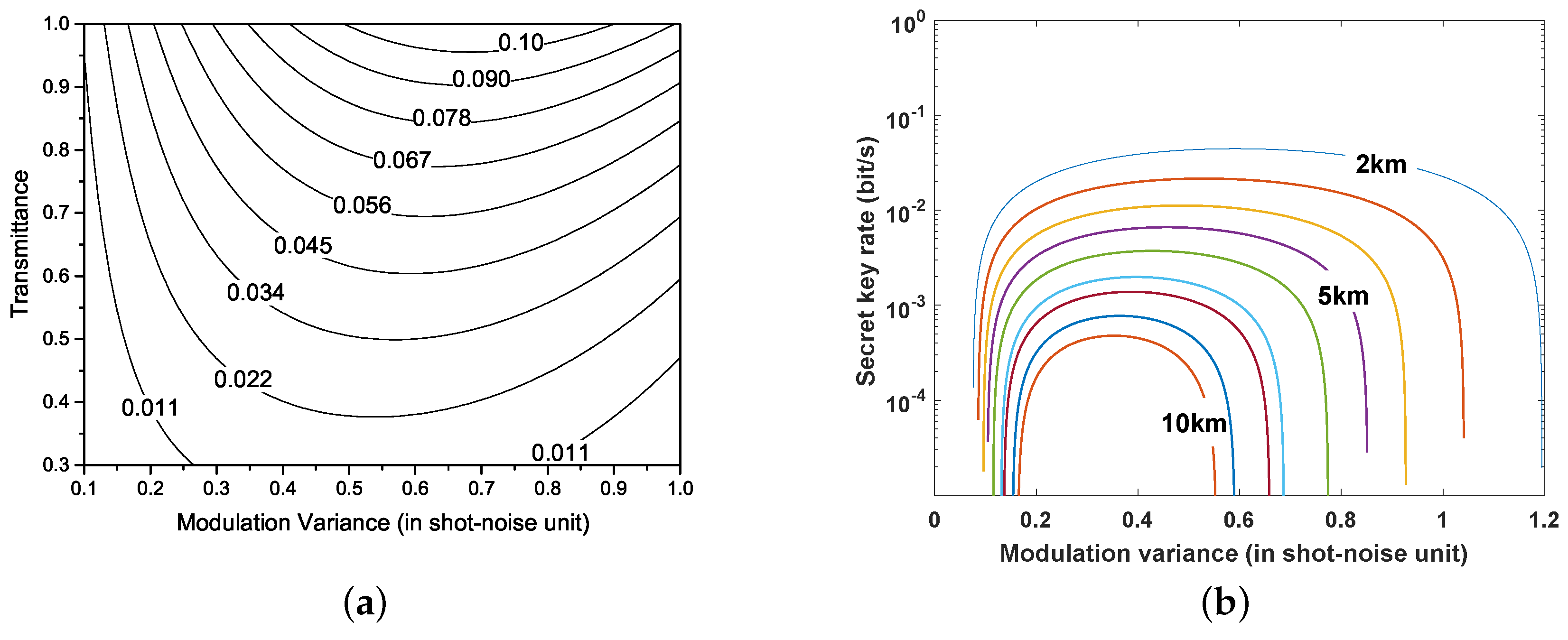
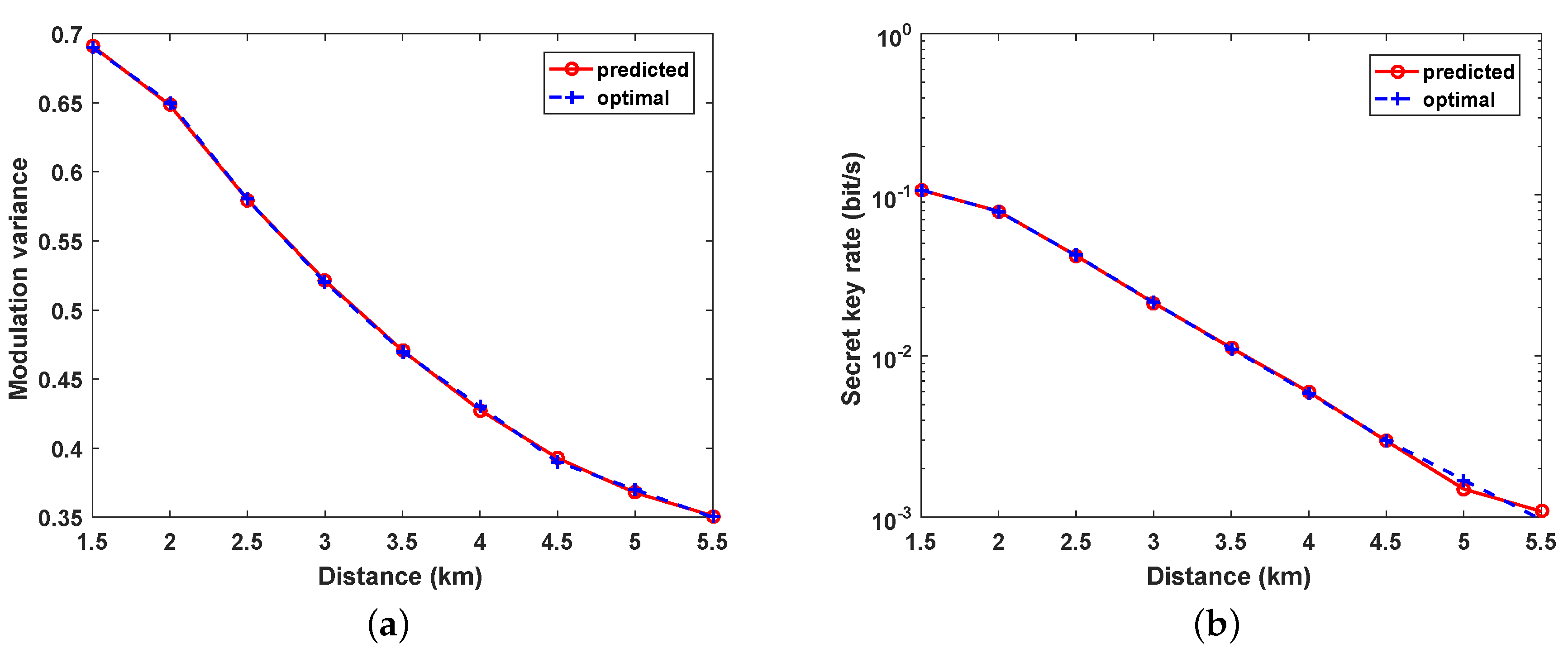
4. Performance Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Atmospheric Transmittance Analysis

Appendix B. Secret Key Rate
Appendix C. Back-Propagation Neural Network
| Parameter | Definition |
|---|---|
| Threshold of the k-th neuron in output layer | |
| Threshold of the j-th neuron in hidder layer | |
| The weight between the i-th node in the input layer and the j-th node in the hidden layer | |
| The weight between the j-th node in the hidden layer and the k-th node in the output layer | |
| The input value that the j-th neuron received in the hidden layer | |
| The input value that the k-th neuron received in the output layer | |
| Activation function. | |
| Learning rate |
References
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, C.T.; Shapiro, J.H. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2011, 55, 298. [Google Scholar]
- Pirandola, S.; Mancini, S.; Lloyd, S.; Braunstein, S.L. Continuous variable quantum cryptography using two-way quantum communication. Nat. Phys. 2006, 5, 726–730. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.K.; Zeng, G.H. Supplementary Material for: Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 2015, 6, 19201. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Pomerene, A.; Starbuck, A.L.; Lentine, A.L.; Long, C.M.; Derose, C.T.; Trotter, D.C. Silicon photonic transceiver circuit for high-speed polarization-based discrete variable quantum key distribution. Opt. Express 2017, 25, 12282–12294. [Google Scholar]
- Huang, P.; He, G.Q.; Fang, J.; Zeng, G.H. Performance improvement of continuous-variable quantum key distribution via photon subtraction. Phys. Rev. A 2013, 87, 530–537. [Google Scholar] [CrossRef]
- Fang, J.; Huang, P.; Zeng, G.H. Multichannel parallel continuous-variable quantum key distribution with Gaussian modulation. Phys. Rev. A 2014, 89, 022315. [Google Scholar] [CrossRef]
- Liao, Q.; Guo, Y.; Huang, D.; Huang, P.; Zeng, G.H. Long-distance continuous-variable quantum key distribution using non-Gaussian state-discrimination detection. New J. Phys. 2017, 20, 023015. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Y.; Huang, D. Kalman filter-based phase estimation of continuous-variable quantum key distribution without sending local oscillator. Phys. Let. A 2019, 383, 2394–2399. [Google Scholar] [CrossRef]
- Tunick, A.; Moore, T.; Deacon, K.; Meyers, R. Quantum Communications and Quantum Imaging VIII. Int. Soc. Opt. Photonics 2010, 7815, 781512. [Google Scholar]
- Fedrizzi, A.; Ursin, R.; Herbst, T.; Nespoli, M.; Prevedel, R.; Scheisl, T.; Tiefenbacher, F.; Jennewein, T.; Zeilinger, A. High-fidelity transmission of entanglement over a high-loss free-space channel. Nat. Phys. 2009, 5, 389–392. [Google Scholar] [CrossRef]
- Liao, S.K.; Yong, H.L.; Liu, C.; Shentu, G.L.; Li, D.D.; Lin, J.; Dai, H.; Zhao, S.Q.; Li, B.; Guan, J.Y.; et al. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photonics 2017, 11, 509–513. [Google Scholar] [CrossRef]
- Ursin, R.; Tiefenbacher, F.; Schmitt-Manderbach, T.; Weier, H.; Scheidl, T.; Lindenthal, M.; Blauensteiner, B.; Jennewein, T.; Perdigues, J.; Trojek, P.; et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 2007, 3, 481–486. [Google Scholar] [CrossRef]
- Scheidl, T.; Ursin, R.; Fedrizzi, A.; Ramelow, S.; Ma, X.S.; Herbst, T.; Prevedel, R.; Ratschbacher, L.; Kofler, J.; Jennewein, T.; et al. Feasibility of 300 km Quantum Key Distribution with Entangled States. New J. Phys. 2009, 11, 085002. [Google Scholar] [CrossRef]
- Capraro, I.; Tomaello, A.; Dall’Arche, A.; Gerlin, F.; Ursin, R.; Vallone, G.; Villoresi, P. Impact of turbulence in long range quantum and classical communications. Phys. Rev. Lett. 2012, 109, 200502. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Ren, J.G.; Lu, H.; Cao, Y.; Yong, H.L.; Wu, Y.P.; Liu, C.; Liao, S.K.; Zhou, F.; Jiang, Y.; et al. Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature (London) 2012, 488, 185–188. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.S.; Herbst, T.; Scheidl, T.; Wang, D.; Kropatschek, S.; Naylor, W.; Wittmann, B.; Mech, A.; Kofler, J.; Anisimova, E.; et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature (London) 2012, 489, 269–273. [Google Scholar] [CrossRef] [PubMed]
- Peuntinger, C.; Heim, B.; Müller, C.R.; Gabriel, C.; Marquardt, C.; Leuchs, G. Distribution of Squeezed States through an Atmospheric Channel. Phys. Rev. Lett. 2014, 113, 060502. [Google Scholar] [CrossRef]
- Liao, S.K.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef]
- Miao, E.L.; Han, Z.F.; Gong, S.S.; Zhang, T.; Diao, D.S.; Guo, G.C. Background noise of satellite-to-ground quantum key distribution. New J. Phys. 2005, 7, 215. [Google Scholar]
- Heim, B.; Peuntinger, C.; Wittmann, C.; Marquardt, C.; Leuchs, G. Free Space Quantum Communication using Continuous Polarization Variables. In Applications of Lasers for Sensing & Free Space Communications; Optical Society of America: Washington, DC, USA, 2011. [Google Scholar]
- Vasylyev, D.Y.; Semenov, A.A.; Vogel, W. Toward Global Quantum Communication: BeamWandering Preserves Nonclassicality. Phys. Rev. Lett. 2012, 108, 220501. [Google Scholar] [CrossRef]
- Vasylyev, D.; Semenov, A.A.; Vogel, W. Atmospheric quantum channels with weak and strong turbulence. Phys. Rev. Lett. 2016, 117, 090501. [Google Scholar] [CrossRef] [PubMed]
- Vasylyev, D.; Semenov, A.A.; Vogel, W. Free-space quantum links under diverse weather conditions. Phys. Rev. A 2017, 96, 043856. [Google Scholar] [CrossRef]
- Wang, W.; Xu, F.; Lo, H.-K. Enabling a scalable high-rate measurement-device-independent quantum key distribution network. arXiv 2018, arXiv:1807.03466. [Google Scholar]
- Xu, F.; Xu, H.; Lo, H.-K. Protocol choice and parameter optimization in decoy-state measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052333. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Harrington, P. Machine Learning in Action; Manning Co.: New York, NY, USA, 2012. [Google Scholar]
- Zibar, D.; Winther, O.; Franceschi, N.; Borkowski, R.; Caballero, A.; Arlunno, V.; Schmidt, M.N.; Gonzales, N.G.; Mao, B.; Ye, Y.; et al. Nonlinear impairment compensation using expectation maximization for dispersion managed and unmanaged PDM 16-QAM transmission. Opt. Express 2012, 20, B181–B196. [Google Scholar] [CrossRef]
- Jarajreh, M.A.; Giacoumidis, E.; Aldaya, I.; Le, S.T.; Tsokanos, A.; Ghassemlooy, Z.; Doran, N.J. Artificial Neural Network Nonlinear Equalizer for Coherent Optical OFDM. Photonics Technol. Lett. 2015, 27, 387–390. [Google Scholar] [CrossRef]
- Zibar, D.; Piels, M.; Jones, R.; Schäeffer, C.G. Machine learning techniques in optical communication. J. Lightwave Technol. 2016, 34, 1442–1452. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Li, Z.; Song, C.; Fu, M.; Li, J.; Chen, X. System impairment compensation in coherent optical communications by using a bio-inspired detector based on artificial neural network and genetic algorithm. Opt. Commun. 2017, 399, 1–12. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, M.; Luo, P.F.; Ghassemlooy, Z.; Wang, D.S.; Tang, X.Y.; Han, D.H. SVM detection for superposed pulse amplitude modulation in visible light communications. In Proceedings of the 2016 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Prague, Czech Republic, 20–22 July 2016; pp. 1–5. [Google Scholar]
- Liu, W.; Huang, P.; Peng, J.; Fan, J.; Zeng, G. Integrating machine learning to achieve an automatic parameter prediction for practical continuous-variable quantum key distribution. Phys. Rev. A 2018, 97, 022316. [Google Scholar] [CrossRef]
- Li, J.W.; Guo, Y.; Wang, X.D.; Xie, C.L.; Zhang, L.; Huang, D. Discrete-modulated continuous variable quantum key distribution with a machine-learning-based detector. Opt. Eng. 2018, 57, 066109. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, P.; Guo, Y.; Zhang, L.; Huang, D. Blind modulation format identification based on machine learning algorithm for continuous variable quantum key distribution. J. Opt. Soc. Am. B 2019, 36, 51–58. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W.; Wei, K.; Fang, X.-T.; Li, L.; Liu, N.-L.; Liang, H.; Zhang, S.-J.; Zhang, W.; Li, H.; et al. Experimental demonstration of high-rate measurement-device-independent quantum key distribution over asymmetric channels. arXiv 2018, arXiv:1808.08584. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.Y.; Yin, Z.Q.; Wang, C.; Cui, C.H.; Teng, J.; Wang, S.; Chen, W.; Huang, W.; Xu, B.J.; Guo, G.C.; et al. Parameter optimization and real-time calibration of a measurement-device-independent quantum key distribution network based on a back propagation artificial neural network. J. Opt. Soc. Am. B 2019, 36, 92–98. [Google Scholar] [CrossRef]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Fante, R.L. Electromagnetic beam propagation in turbulent media. Proc. IEEE 1975, 63, 1669–1692. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, C.; Wei, H. Laser Beam Propagation and Applications through the Atmosphere and Sea Water; National Defense Industry Press: Beijing, China, 2015. [Google Scholar]
- Zunino, L.; Gulich, D.; Funes, G.; Perez, D.G. Turbulence-induced persistence in laser beam wandering. Opt. Lett. 2015, 40, 3145–3148. [Google Scholar] [CrossRef] [PubMed]
- Berman, G.P.; Chumak, A.A.; Gorshkov, V.N. Beam wandering in the atmosphere: The effect of partial coherence. Phys. Rev. E 2007, 76, 056606. [Google Scholar] [CrossRef]
- Jakeman, E.; Ridley, K.D. A Review of Modeling Fluctuations in Scattered Waves. Waves Random Complex Media 2007, 17, 405. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Usenko, V.C.; Heim, B.; Peuntinger, C.; Wittmann, C.; Marquardt, C.; Leuchs, G.; Filip, R. Entanglement of Gaussian states and the applicability to quantum key distribution over fading channels. New J. Phys. 2012, 14, 093048. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Unconditional Security Proof of Long-Distance Continuous-Variable Quantum Key Distribution with Discrete Modulation. Phys. Rev. Lett. 2009, 102, 180504. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zou, H.X.; Tian, L.; Chen, P.X.; Yuan, J.M. Experimental study on discretely modulated continuous-variable quantum key distribution. Phys. Rev. A 2010, 82, 022317. [Google Scholar] [CrossRef]
- Wang, S.Y.; Huang, P.; Wang, T.; Zeng, G.H. Atmospheric effects on continuous-variable quantum key distribution. New J. Phys. 2018, 20, 083037. [Google Scholar] [CrossRef]

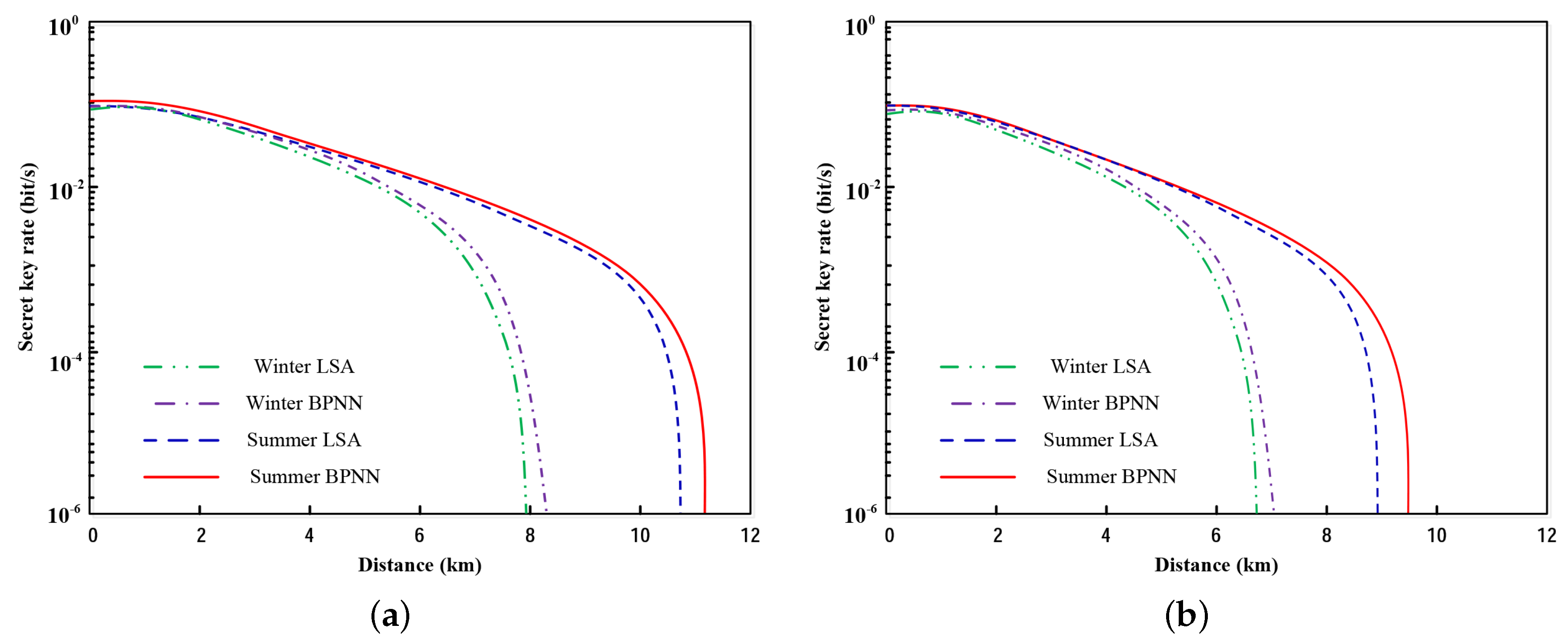
| Spring | Summer | Autumn | Winter | |
|---|---|---|---|---|
| 2.03 | 2.12 | 5.56 | 7.46 |
| Method | L | K | ||||
|---|---|---|---|---|---|---|
| Optimized | 2 km | 2.3269 | 0.8597 | 0.70 | 0.2550 | |
| BPNN | 2 km | 2.3269 | 0.8597 | 0.6975 | 0.2556 | |
| Optimized | 4 km | 8.2922 | 0.3859 | 0.1160 | 0.0388 | |
| BPNN | 4 km | 8.2922 | 0.3859 | 0.1161 | 0.0391 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Guo, Y.; Huang, D. Parameter Optimization Based BPNN of Atmosphere Continuous-Variable Quantum Key Distribution. Entropy 2019, 21, 908. https://doi.org/10.3390/e21090908
Su Y, Guo Y, Huang D. Parameter Optimization Based BPNN of Atmosphere Continuous-Variable Quantum Key Distribution. Entropy. 2019; 21(9):908. https://doi.org/10.3390/e21090908
Chicago/Turabian StyleSu, Yu, Ying Guo, and Duan Huang. 2019. "Parameter Optimization Based BPNN of Atmosphere Continuous-Variable Quantum Key Distribution" Entropy 21, no. 9: 908. https://doi.org/10.3390/e21090908
APA StyleSu, Y., Guo, Y., & Huang, D. (2019). Parameter Optimization Based BPNN of Atmosphere Continuous-Variable Quantum Key Distribution. Entropy, 21(9), 908. https://doi.org/10.3390/e21090908






