On NACK-Based rDWS Algorithm for Network Coded Broadcast
Abstract
1. Introduction
1.1. Motivation
1.2. Contributions and Organization of the Paper
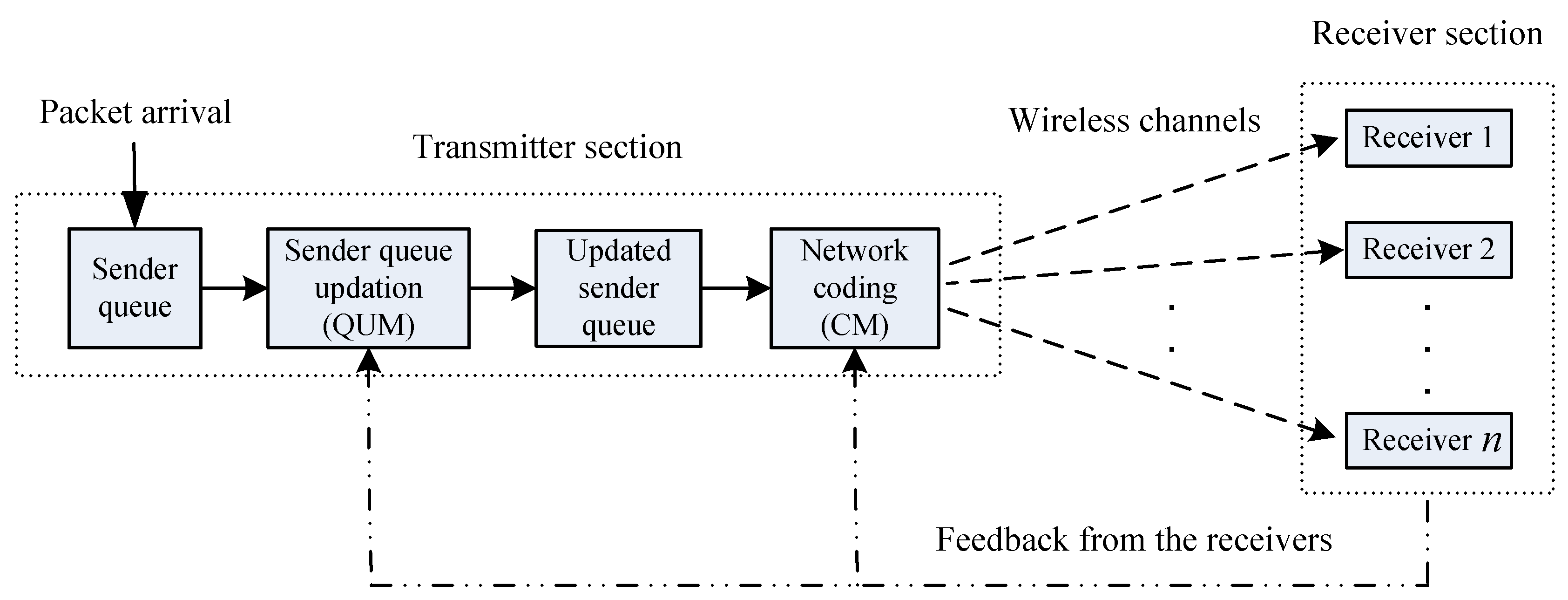
2. System Model
Definitions
- Packet index: Following in-order packet delivery (i.e., the packets are delivered in the same order they arrive at the SQ), the ith packet which arrives at the SQ is said to have index i.
- Coefficient vector of a coded packet: The vector corresponding to a network coded packet or coded combination which consists of the coefficient of the raw packets which are involved in that combination.
- Knowledge space of a node: The vector space at a node which is the span of the coefficient vectors of the available packets at that node.
- Innovative packet: A network coded packet is innovative to a receiver if the corresponding coefficient vector does not belong to the receiver’s knowledge space. An innovative packet will always increase the dimension of a receiver’s knowledge space upon successful reception.
- Hearing a packet: A receiver has heard of a packet if it has received a linear combination involving .
- Seeing a packet: A receiver has seen a packet if it can compute a linear combination of the form ( and for each k) based on the combinations it has received up to a slot.
- Witness of a seen packet: Linear combination of the form, ( and for each k), is the witness for receiver j of seeing which is denoted by .
3. Existing DWS Technique and the Proposed rDWS Technique
3.1. The Coding Module
3.1.1. DWS Case
| Algorithm 1 DWS Algorithm (The Coding Module) |
|
Minimum Field Size Requirement
3.1.2. rDWS Case
| Algorithm 2 rDWS Algorithm (The Coding Module) |
|
Minimum Field Size Requirement
3.1.3. Remarks
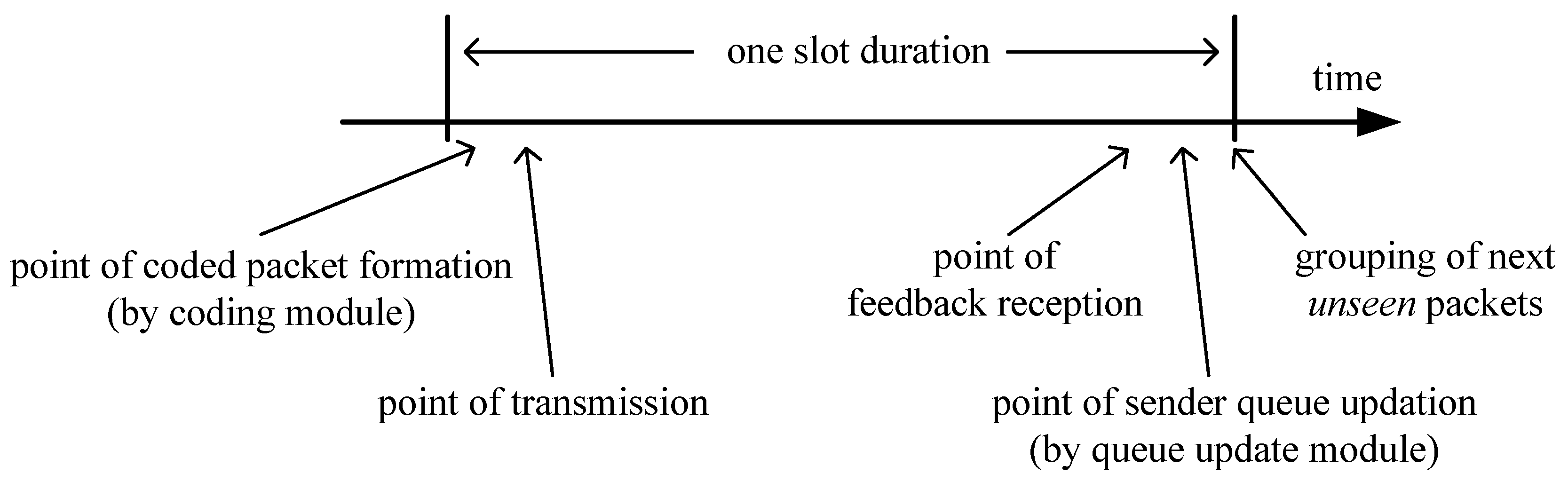
3.2. The Queue Update Module
3.2.1. DWS Case
| Algorithm 3 DWS Algorithm (The Queue Update Module) |
|
3.2.2. rDWS Case
| Algorithm 4 NACK generation at receiver j |
|
| Algorithm 5 rDWS Algorithm (The Queue Update Module) |
|
3.2.3. Remarks
4. Throughput Efficiency Analysis of rDWS Technique
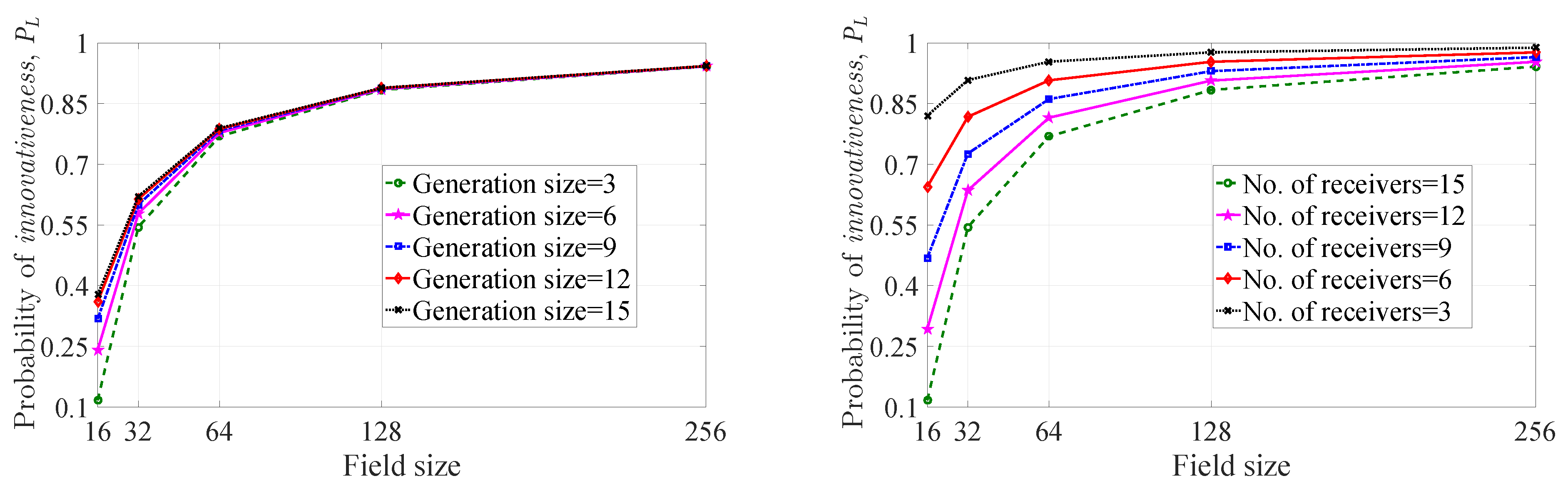
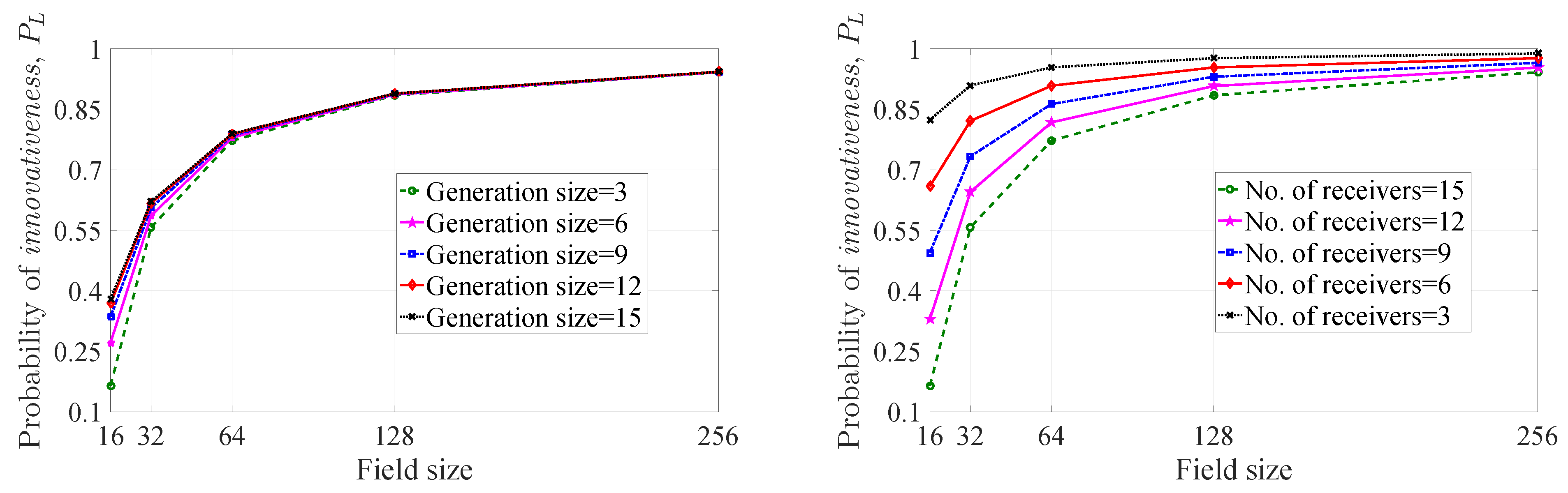
4.1. Probability of Innovativeness of a Picked-up Coefficient
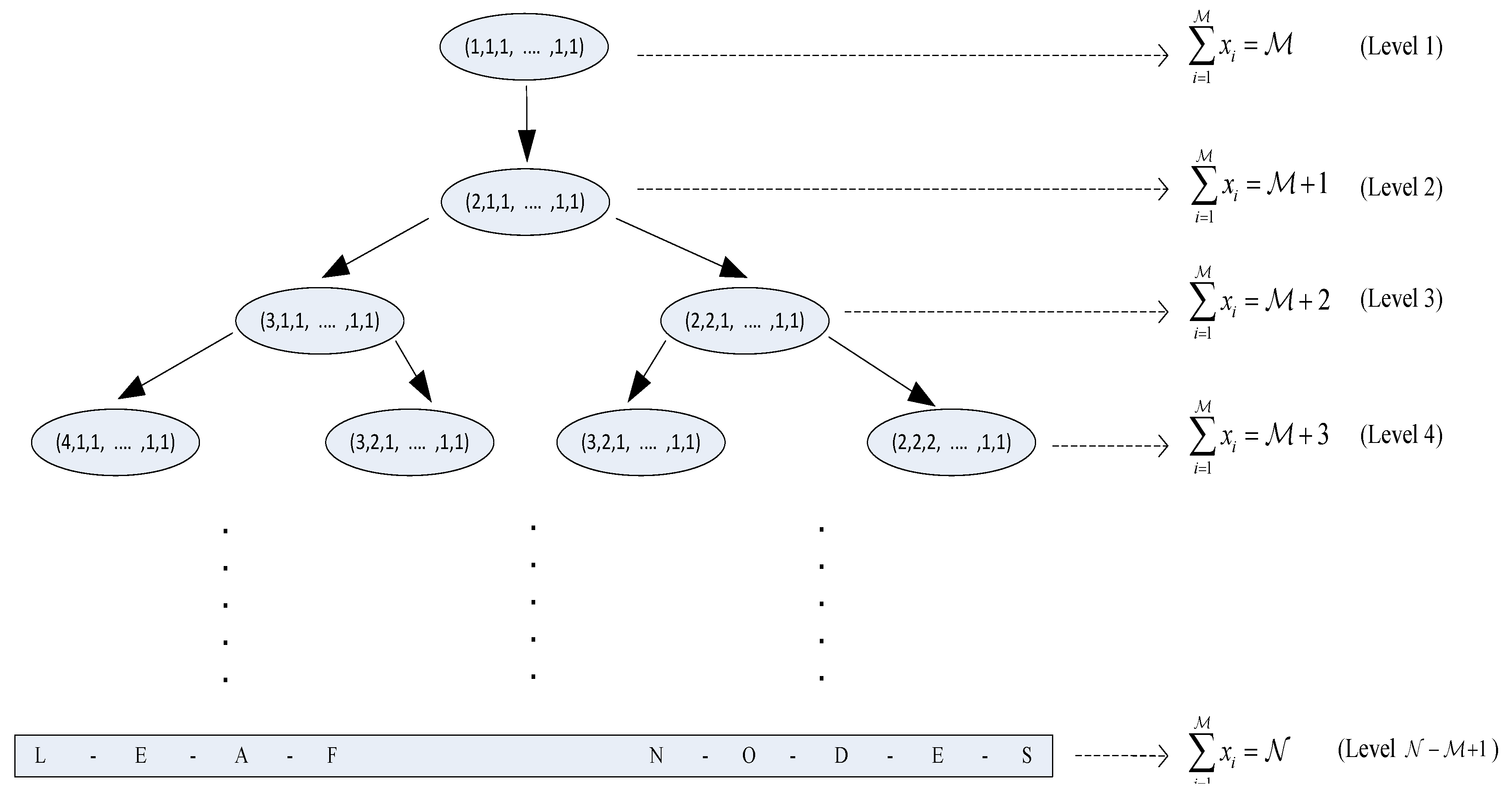
4.1.1. Integer Partitions of and
Probability of Occurrence of a Partition of
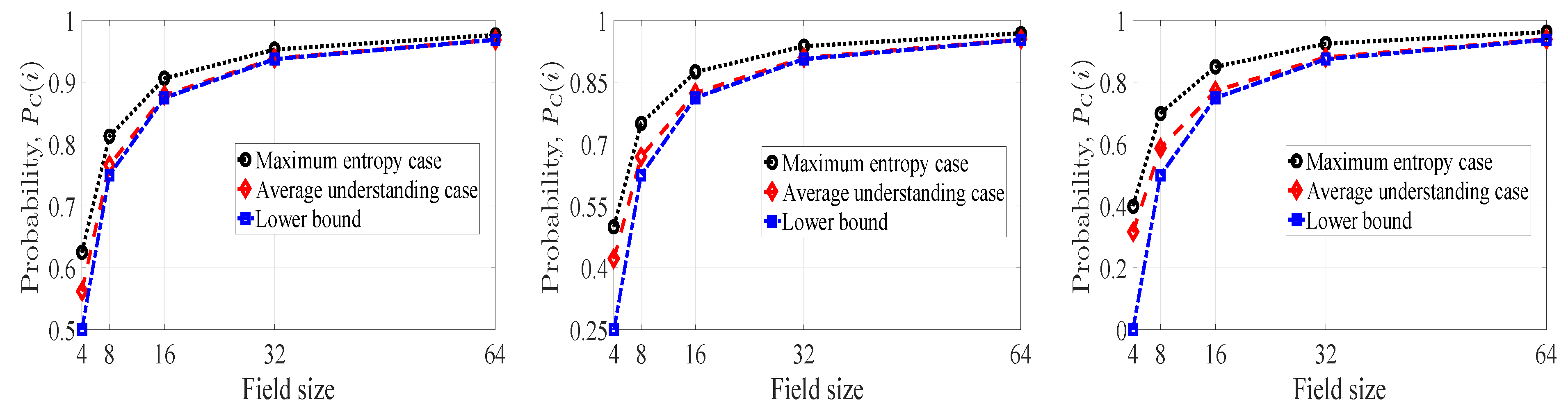
4.1.2. Maximum Entropy of and
4.1.3. Average Understanding of Innovativeness and
4.1.4. Lower Bound on
4.2. Probability of Innovativeness of a Linear Combination
4.2.1. Special Cases
Analysis of and the Minimum Value
A Practical Consideration and the Minimum Value of
5. Performance Evaluation of rDWS Scheme in Terms of Dropping and Decoding Statistics
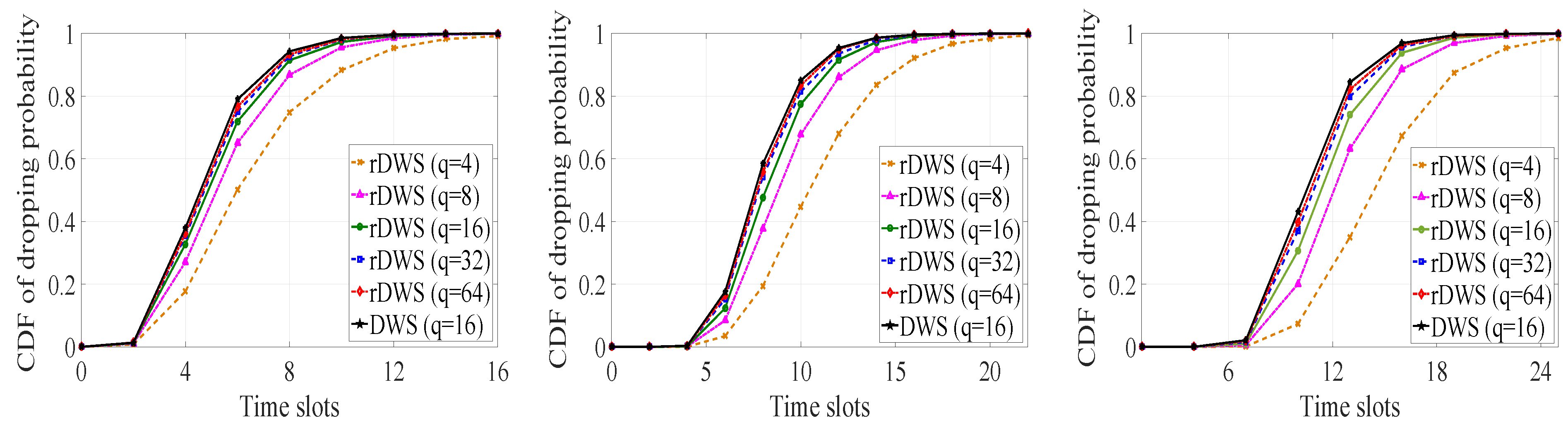
5.1. Packet Dropping Statistics
5.1.1. Cumulative Dropping Probability
5.1.2. Average Dropping Time for the Last Packet of a Generation
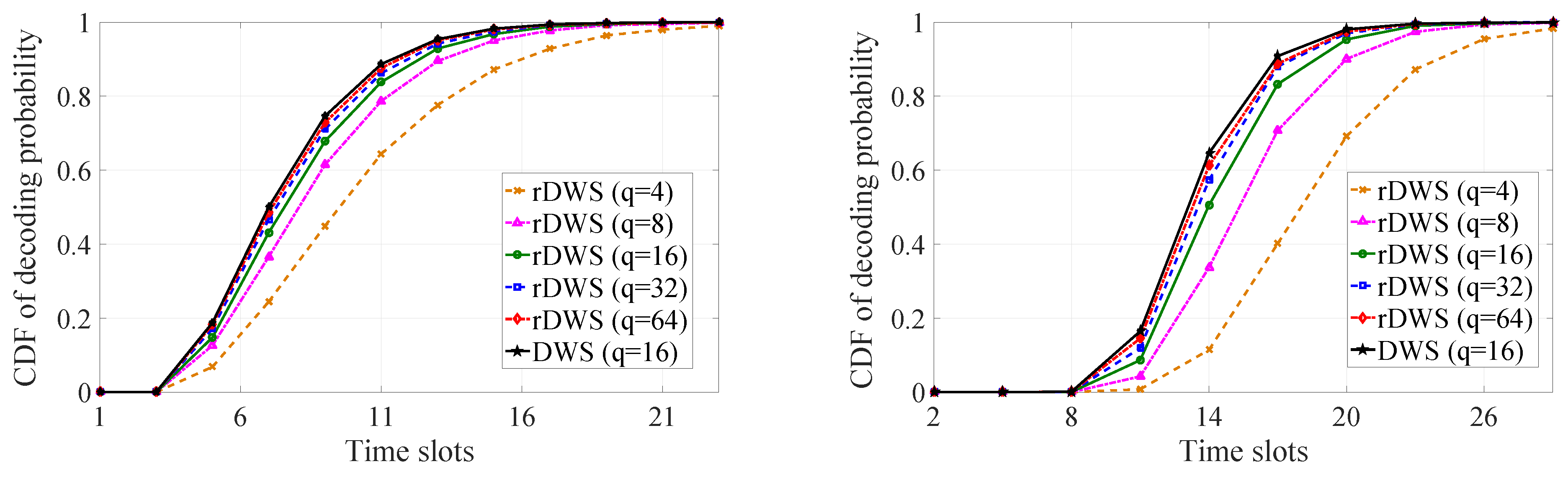
5.2. Generation Decoding Statistics
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LNC | Linear network coding |
| RLNC | Random linear network coding |
| DLNC | Deterministic linear network coding |
| IDNC | Instantly decodable network coding |
| SQ | Sender queue |
| DWD | Drop when decoded |
| DWS | Drop when seen |
| rDWS | Randomized drop when seen |
| QUM | Queue update module |
| CM | Coding module |
References
- Luby, M. LT codes. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Providence, RI, USA, 21–23 October 2002; pp. 271–280. [Google Scholar] [CrossRef]
- Shokrollahi, A. Raptor codes. IEEE Trans. Inf. Theory 2006, 52, 2551–2567. [Google Scholar] [CrossRef]
- Pakzad, P.; Fragouli, C.; Shokrollahi, A. Coding schemes for line networks. In Proceedings of the International Symposium on Information Theory, Adelaide, Australia, 4–9 September 2005; pp. 1853–1857. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N.; Li, S.R.; Yeung, R.W. Network information flow. IEEE Trans. Inf. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Fragouli, C.; Le Boudec, J.Y.; Widmer, J. Network coding: An instant primer. ACM SIGCOMM Comput. Commun. Rev. 2006, 36, 63–68. [Google Scholar] [CrossRef]
- Li, S.R.; Yeung, R.W.; Ning, C. Linear network coding. IEEE Trans. Inf. Theory 2003, 49, 371–381. [Google Scholar] [CrossRef]
- Ho, T.; Medard, M.; Koetter, R.; Karger, D.R.; Effros, M.; Shi, J.; Leong, B. A Random Linear Network Coding Approach to Multicast. IEEE Trans. Inf. Theory 2006, 52, 4413–4430. [Google Scholar] [CrossRef]
- Ho, T.; Leong, B.; Medard, M.; Koetter, R.; Chang, Y.-H.; Effros, M. On the utility of network coding in dynamic environments. In Proceedings of the International Workshop on Wireless Ad-Hoc Networks, Oulu, Finland, 31 May–1 June 2004; pp. 196–200. [Google Scholar] [CrossRef]
- Widmer, J.; Le Boudec, J.Y. Network coding for efficient communication in extreme networks. In Proceedings of the 2005 ACM SIGCOMM workshop on Delay-tolerant networking, Philadelphia, PA, USA, 26 August 2005; pp. 284–291. [Google Scholar]
- Lucani, D.E.; Stojanovic, M.; Medard, M. Random Linear Network Coding For Time Division Duplexing: When To Stop Talking And Start Listening. In Proceedings of the IEEE INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1800–1808. [Google Scholar] [CrossRef]
- Joshi, G.; Liu, Y.; Soljanin, E. On the Delay-Storage Trade-Off in Content Download from Coded Distributed Storage Systems. IEEE J. Sel. Areas Commun. 2014, 32, 989–997. [Google Scholar] [CrossRef]
- Sipos, M.; Gahm, J.; Venkat, N.; Oran, D. Erasure Coded Storage on a Changing Network: The Untold Story. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Gkantsidis, C.; Rodriguez, P.R. Network coding for large scale content distribution. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; Volume 4, pp. 2235–2245. [Google Scholar] [CrossRef]
- Cai, N.; Yeung, R.W. Secure network coding. In Proceedings of the IEEE International Symposium on Information Theory, Lausanne, Switzerland, 30 June–5 July 2002; p. 323. [Google Scholar] [CrossRef]
- Ambadi, N. Multicast Networks Solvable over Every Finite Field. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 236–240. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Fragouli, C. Vector network coding algorithms. In Proceedings of the IEEE International Symposium on Information Theory, Austin, TX, USA, 12–18 June 2010; pp. 2408–2412. [Google Scholar] [CrossRef]
- Das, N.; Rai, B.K. Linear Network Coding: Effects of Varying the Message Dimension on the Set of Characteristics. arXiv 2019, arXiv:1901.04820. [Google Scholar]
- Ebrahimi, J.; Fragouli, C. Algebraic Algorithms for Vector Network Coding. IEEE Trans. Inf. Theory 2011, 57, 996–1007. [Google Scholar] [CrossRef]
- Koetter, R.; Medard, M. An algebraic approach to network coding. IEEE/ACM Trans. Netw. 2003, 11, 782–795. [Google Scholar] [CrossRef]
- Jaggi, S.; Sanders, P.; Chou, P.A.; Effros, M.; Egner, S.; Jain, K.; Tolhuizen, L.M.G.M. Polynomial time algorithms for multicast network code construction. IEEE Trans. Inf. Theory 2005, 51, 1973–1982. [Google Scholar] [CrossRef]
- Fragouli, C.; Soljanin, E. Information flow decomposition for network coding. IEEE Trans. Inf. Theory 2006, 52, 829–848. [Google Scholar] [CrossRef]
- Médard, M.; Effros, M.; Karger, D.; Ho, T. On coding for non-multicast networks. In Proceedings of the Annual Allerton Conference on Communication Control and Computing, Monticello, IL, USA, 23–25 September 1998; Volume 41, pp. 21–29. [Google Scholar]
- Das, N.; Rai, B.K. On the Message Dimensions of Vector Linearly Solvable Networks. IEEE Commun. Lett. 2016, 20, 1701–1704. [Google Scholar] [CrossRef]
- Sun, Q.T.; Yang, X.; Long, K.; Yin, X.; Li, Z. On Vector Linear Solvability of Multicast Networks. IEEE Trans. Commun. 2016, 64, 5096–5107. [Google Scholar] [CrossRef]
- Etzion, T.; Wachter-Zeh, A. Vector Network Coding Based on Subspace Codes Outperforms Scalar Linear Network Coding. IEEE Trans. Inf. Theory 2018, 64, 2460–2473. [Google Scholar] [CrossRef]
- Sun, Q.T.; Yin, X.; Li, Z.; Long, K. Multicast Network Coding and Field Sizes. IEEE Trans. Inf. Theory 2015, 61, 6182–6191. [Google Scholar] [CrossRef]
- Chou, P.A.; Wu, Y.; Jain, K. Practical network coding. In Proceedings of the Annual Allerton Conference on Communication Control and Computing, Monticello, IL, USA, 23–25 September 1998; Volume 41, pp. 40–49. [Google Scholar]
- Li, Y.; Soljanin, E.; Spasojevic, P. Effects of the Generation Size and Overlap on Throughput and Complexity in Randomized Linear Network Coding. IEEE Trans. Inf. Theory 2011, 57, 1111–1123. [Google Scholar] [CrossRef]
- Thibault, J.; Yousefi, S.; Chan, W. Throughput Performance of Generation-Based Network Coding. In Proceedings of the 10th Canadian Workshop on Information Theory (CWIT), Edmonton, AL, Canada, 6–8 June 2007; pp. 89–92. [Google Scholar] [CrossRef]
- Trullols-Cruces, O.; Barcelo-Ordinas, J.M.; Fiore, M. Exact Decoding Probability Under Random Linear Network Coding. IEEE Commun. Lett. 2011, 15, 67–69. [Google Scholar] [CrossRef]
- Larsson, P. Multicast Multiuser ARQ. In Proceedings of the IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 30 March–3 April 2008; pp. 1985–1990. [Google Scholar] [CrossRef]
- Qureshi, J.; Foh, C.H.; Cai, J. Optimal solution for the index coding problem using network coding over GF(2). In Proceedings of the 9th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Seoul, Korea, 18–21 June 2012; pp. 209–217. [Google Scholar] [CrossRef]
- Lucani, D.E.; Pedersen, M.V.; Ruano, D.; Sørensen, C.W.; Fitzek, F.H.P.; Heide, J.; Geil, O.; Nguyen, V.; Reisslein, M. Fulcrum: Flexible Network Coding for Heterogeneous Devices. IEEE Access 2018, 6, 77890–77910. [Google Scholar] [CrossRef]
- Skevakis, E.; Lambadaris, I. Decoding and file transfer delay balancing in network coding broadcast. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Lucani, D.E.; Medard, M.; Stojanovic, M. On Coding for Delay—Network Coding for Time-Division Duplexing. IEEE Trans. Inf. Theory 2012, 58, 2330–2348. [Google Scholar] [CrossRef]
- Sagduyu, Y.E.; Georgiadis, L.; Tassiulas, L.; Ephremides, A. Capacity and Stable Throughput Regions for the Broadcast Erasure Channel With Feedback: An Unusual Union. IEEE Trans. Inf. Theory 2013, 59, 2841–2862. [Google Scholar] [CrossRef]
- Cocco, G.; de Cola, T.; Berioli, M. Performance analysis of queueing systems with systematic packet-level coding. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 4524–4529. [Google Scholar] [CrossRef]
- Chatzigeorgiou, I.; Tassi, A. Decoding Delay Performance of Random Linear Network Coding for Broadcast. IEEE Trans. Veh. Technol. 2017, 66, 7050–7060. [Google Scholar] [CrossRef]
- Aljohani, A.J.; Ng, S.X.; Hanzo, L. Distributed Source Coding and Its Applications in Relaying-Based Transmission. IEEE Access 2016, 4, 1940–1970. [Google Scholar] [CrossRef]
- Giacaglia, G.; Shi, X.; Kim, M.; Lucani, D.E.; Médard, M. Systematic network coding with the aid of a full-duplex relay. In Proceedings of the IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 3312–3317. [Google Scholar] [CrossRef]
- Wunderlich, S.; Gabriel, F.; Pandi, S.; Fitzek, F.H.P.; Reisslein, M. Caterpillar RLNC (CRLNC): A Practical Finite Sliding Window RLNC Approach. IEEE Access 2017, 5, 20183–20197. [Google Scholar] [CrossRef]
- Pandi, S.; Gabriel, F.; Cabrera, J.A.; Wunderlich, S.; Reisslein, M.; Fitzek, F.H.P. PACE: Redundancy Engineering in RLNC for Low-Latency Communication. IEEE Access 2017, 5, 20477–20493. [Google Scholar] [CrossRef]
- Sundararajan, J.K.; Shah, D.; Médard, M.; Sadeghi, P. Feedback-Based Online Network Coding. IEEE Trans. Inf. Theory 2017, 63, 6628–6649. [Google Scholar] [CrossRef]
- Chi, K.; Jiang, X.; Horiguchi, S. Network coding-based reliable multicast in wireless networks. Comput. Netw. 2010, 54, 1823–1836. [Google Scholar] [CrossRef]
- Fragouli, C.; Lun, D.; Medard, M.; Pakzad, P. On Feedback for Network Coding. In Proceedings of the 41st Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 14–16 March 2007; pp. 248–252. [Google Scholar] [CrossRef]
- Keller, L.; Drinea, E.; Fragouli, C. Online Broadcasting with Network Coding. In Proceedings of the Fourth Workshop on Network Coding, Theory and Applications, Hong Kong, China, 3–4 January 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Sundararajan, J.K.; Shah, D.; Medard, M. ARQ for network coding. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1651–1655. [Google Scholar] [CrossRef]
- Lucani, D.E.; Medard, M.; Stojanovic, M. Online Network Coding for Time-Division Duplexing. In Proceedings of the IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Fu, A.; Sadeghi, P.; Médard, M. Delivery delay analysis of network coded wireless broadcast schemes. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Paris, France, 1 April 2012; pp. 2236–2241. [Google Scholar] [CrossRef]
- Barros, J.; Costa, R.A.; Munaretto, D.; Widmer, J. Effective Delay Control in Online Network Coding. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 208–216. [Google Scholar] [CrossRef]
- Karim, M.S.; Sadeghi, P. Decoding delay reduction in broadcast erasure channels with memory for network coding. In Proceedings of the IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications—(PIMRC), Sydney, Australia, 9–12 September 2012; pp. 60–65. [Google Scholar] [CrossRef]
- Sadeghi, P.; Traskov, D.; Koetter, R. Adaptive network coding for broadcast channels. In Proceedings of the Workshop on Network Coding, Theory, and Applications, Lausanne, Switzerland, 15–16 June 2009; pp. 80–85. [Google Scholar] [CrossRef]
- Sundararajan, J.K.; Sadeghi, P.; Medard, M. A feedback-based adaptive broadcast coding scheme for reducing in-order delivery delay. In Proceedings of the Workshop on Network Coding, Theory, and Applications, Lausanne, Switzerland, 15–16 June 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Fu, A.; Sadeghi, P.; Médard, M. Dynamic Rate Adaptation for Improved Throughput and Delay in Wireless Network Coded Broadcast. IEEE/ACM Trans. Netw. 2014, 22, 1715–1728. [Google Scholar] [CrossRef]
- Wu, F.; Sun, Y.; Chen, L.; Xu, J.; Srinivasan, K.; Shroff, N.B. High Throughput Low Delay Wireless Multicast via Multi-Channel Moving Window Codes. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018; pp. 2267–2275. [Google Scholar] [CrossRef]
- Garrido, P.; Leith, D.; Aguero, R. Joint scheduling and coding over lossy paths with delayed feedback. arXiv 2018, arXiv:1804.04921. [Google Scholar]
- Wu, F.; Sun, Y.; Yang, Y.; Srinivasan, K.; Shroff, N.B. Constant-Delay and Constant-Feedback Moving Window Network Coding for Wireless Multicast: Design and Asymptotic Analysis. IEEE J. Sel. Areas Commun. 2015, 33, 127–140. [Google Scholar] [CrossRef]
- Ho, T.; Viswanathan, H. Dynamic Algorithms for Multicast With Intra-Session Network Coding. IEEE Trans. Inf. Theory 2009, 55, 797–815. [Google Scholar] [CrossRef]
- Eryilmaz, A.; Lun, D.S. Control for inter-session network coding. In Proceedings of the 3rd Workshop on Network Coding, Theory & Applications, Citeseer, San Diego, CA, USA, 29 January 2007; pp. 1–9. [Google Scholar]
- Sundararajan, J.K.; Shah, D.; Medard, M. Online network coding for optimal throughput and delay—The three-receiver case. In Proceedings of the International Symposium on Information Theory and Its Applications, Auckland, New Zealand, 7–10 December 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Giri, S.; Roy, R. Packet Dropping and Decoding Statistics for Linear Network Coded Broadcast with Feedback. In Proceedings of the IEEE 43rd Conference on Local Computer Networks Workshops (LCN Workshops), Chicago, IL, USA, 1–4 October 2018; pp. 70–77. [Google Scholar] [CrossRef]
- Andrews, G.E.; Eriksson, K. Integer Partitions; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Li, D.; Sun, X. Nonlinear Integer Programming; Springer Science & Business Media: Berlin, Germany, 2006; Volume 84. [Google Scholar]
- Lucani, D.E. Composite Extension Fields for (Network) Coding: Designs and Opportunities. In Proceedings of the Network Coding and Designs (Final Conference of COST Action IC1104), Dubrovnik, Croatia, 4–8 April 2016. [Google Scholar]


| Form of | Partition of | No. of Parts | No. of Good Choices for | Probability of Innovativeness |
|---|---|---|---|---|
| 1 + 1 + 1 + 1 | 4 | |||
| 1 + 1 + 2 | 3 | |||
| 2 + 2 | 2 | |||
| 1 + 3 | 2 | |||
| 4 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giri, S.; Roy, R. On NACK-Based rDWS Algorithm for Network Coded Broadcast. Entropy 2019, 21, 905. https://doi.org/10.3390/e21090905
Giri S, Roy R. On NACK-Based rDWS Algorithm for Network Coded Broadcast. Entropy. 2019; 21(9):905. https://doi.org/10.3390/e21090905
Chicago/Turabian StyleGiri, Sovanjyoti, and Rajarshi Roy. 2019. "On NACK-Based rDWS Algorithm for Network Coded Broadcast" Entropy 21, no. 9: 905. https://doi.org/10.3390/e21090905
APA StyleGiri, S., & Roy, R. (2019). On NACK-Based rDWS Algorithm for Network Coded Broadcast. Entropy, 21(9), 905. https://doi.org/10.3390/e21090905





