Universality and Exact Finite-Size Corrections for Spanning Trees on Cobweb and Fan Networks
Abstract
1. Introduction
2. Spanning Tree on Networks
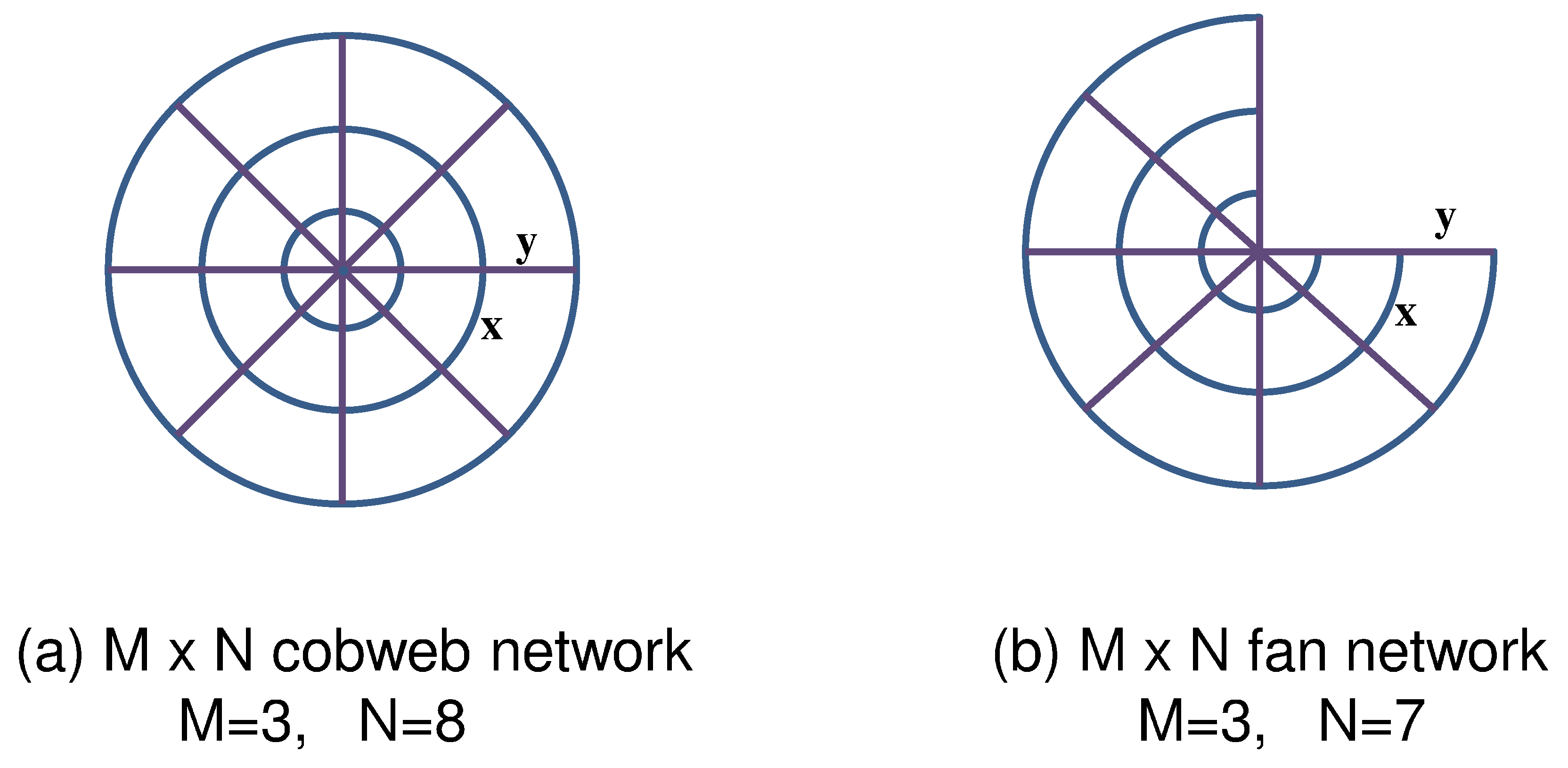
2.1. Spanning Tree on the Cobweb Network
2.2. Spanning Tree on the Fan Network
3. Asymptotic Expansion of Free Energy
3.1. Asymptotic Expansion of Free Energy of the Spanning Tree on the Cobweb Network
3.2. Asymptotic Expansion of Free Energy of the Spanning Tree on the Fan Network
4. Spanning Tree on Infinitely Long Strips
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Asymptotic Expansion of and
References
- Kirchhoff, G. Ueber die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Vertheilung galvanischer Ströme geführt wird. Ann. Phys. Chem. 1847, 72, 497–508. [Google Scholar] [CrossRef]
- Burton, R.; Pemantle, R. Local characteristics, entropy and limit theorems for spanning trees and domino tilings via transfer-impedances. Ann. Probab. 1993, 21, 1329–1371. [Google Scholar] [CrossRef]
- Lyons, R. Asymptotic enumeration of spanning trees. Combin. Probab. Comput. 2005, 14, 491–522. [Google Scholar] [CrossRef]
- Wu, F.Y. Number of spanning trees on a lattice. J. Phys. A 1977, 10, L113. [Google Scholar] [CrossRef]
- Jayakumar, R.; Thulasiraman, K.; Swamy, M. MOD-CHAR: An implementation of char’s spanning tree enumeration algorithm and its complexity analysis. IEEE Trans. Circuits Syst. 1989, 36, 219–228. [Google Scholar] [CrossRef][Green Version]
- Noh, J.D.; Rieger, H. Random walks on complex networks. Phys. Rev. Lett. 2004, 92, 118701. [Google Scholar] [CrossRef]
- Dhar, D.; Dhar, A. Distribution of sizes of erased loops for loop-erased random walks. Phys. Rev. E 1997, 55, R2093. [Google Scholar] [CrossRef]
- Wu, F.Y. The potts model. Rev. Mod. Phys. 1982, 54, 235. [Google Scholar] [CrossRef]
- Jacobsen, L.; Salas, J.; Sokal, A.D. Spanning forests and the q-state Potts model in the limit q → 0. J. Stat. Phys. 2005, 119, 1153–1281. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef]
- Wu, B.Y.; Chao, K.M. Spanning Trees and Optimization Problems; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Tzeng, W.J.; Wu, F.Y. Spanning trees on hypercubic lattices and nonorientable surfaces. Appl. Math. Lett. 2000, 13, 19–25. [Google Scholar] [CrossRef]
- Shrock, R.; Wu, F.Y. Spanning trees on graphs and lattices in d dimensions. J. Phys. A 2000, 33, 3881. [Google Scholar] [CrossRef]
- Izmailian, N.S.; Kenna, R.; Wu, F.Y. The two-point resistance of a resistor network: A new formulation and application to the cobweb network. J. Phys. A: Math. Theor. 2014, 47, 035003. [Google Scholar] [CrossRef]
- Izmailian, N.S.; Kenna, R. The two-point resistance of fan networks. Chin. J. Phys. 2015, 53, 040703. [Google Scholar]
- Chang, S.C.; Chen, L.C.; Yang, W.S. Spanning trees on the Sierpinski gasket. J. Stat. Phys. 2007, 126, 649–667. [Google Scholar] [CrossRef]
- Temperley, H.N.V. Combinatorics. In London Math. Soc. Lecture Note Series; McDonough, T.P., Mavron, V.C., Eds.; Cambridge University Press: Cambridge, UK, 1974; Volume 13, pp. 202–204. [Google Scholar]
- Fisher, M.; Barber, M.N. Scaling theory for finite-size effects in the critical region. Phys. Rev. Lett. 1972, 28, 1516. [Google Scholar] [CrossRef]
- Privman, V. (Ed.) Finite-size Scaling and Numerical Simulation of Statistical Systems; World Scientific: Singapore, 1990. [Google Scholar]
- Hu, C.K. Historical review on analytic, Monte Carlo, and renormalization group approaches to critical phenomena of some lattice Models. Chin. J. Phys. 2014, 52, 1–76. [Google Scholar]
- Vernier, E.; Jacobsen, J.L. Corner free energies and boundary effects for Ising, Potts and fully packed loop models on the square and triangular lattices. J. Phys. A 2012, 45, 045003. [Google Scholar] [CrossRef]
- Baxter, R.J. The bulk, surface and corner free energies of the square lattice Ising model. J. Phys. A 2016, 50, 014001. [Google Scholar] [CrossRef][Green Version]
- Kawata, S.; Sun, H.B.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697. [Google Scholar] [CrossRef]
- Puntes, V.F.; Krishnan, K.M.; Alivisatos, A.P. Colloidal nanocrystal shape and size control: The case of cobalt. Science 2001, 291, 2115–2117. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Rioux, R.M.; Erdonmez, C.K.; Hughes, S.; Somorjai, G.A.; Alivisatos, A.P. Formation of hollow nanocrystals through the nanoscale Kirkendall effect. Science 2004, 304, 711–714. [Google Scholar] [CrossRef] [PubMed]
- Ivashkevich, E.; Izmailian, N.S.; Hu, C.K. Kronecker’s double series and exact asymptotic expansions for free models of statistical mechanics on torus. J. Phys. A Math. Gen. 2002, 35, 5543. [Google Scholar] [CrossRef]
- Izmailian, N.S.; Oganesyan, K.; Hu, C.K. Exact finite-size corrections of the free energy for the square lattice dimer model under different boundary conditions. Phys. Rev. E 2003, 67, 066114. [Google Scholar] [CrossRef] [PubMed]
- Izmailian, N.; Kenna, R.; Guo, W.; Wu, X. Exact finite-size corrections and corner free energies for the c=-2 universality class. Nucl. Phys. B 2014, 884, 157–171. [Google Scholar] [CrossRef]
- Izmailian, N.S.; Kenna, R. Exact finite-size corrections for the spanning-tree model under different boundary conditions. Phys. Rev. E 2015, 91, 022129. [Google Scholar] [CrossRef]
- Privman, V.; Fisher, M.E. Universal critical amplitudes in finite-size scaling. Phys. Rev. B 1984, 30, 322. [Google Scholar] [CrossRef]
- Cardy, J.L.; Peschel, I. Finite-size dependence of the free energy in two-dimensional critical systems. Nucl. Phys. B 1988, 300, 377–392. [Google Scholar] [CrossRef]
- Blöte, H.W.J.; Cardy, J.L.; Nightingale, M.P. Conformal invariance, the central charge, and universal finite-size amplitudes at criticality. Phys. Rev. Lett. 1986, 56, 742. [Google Scholar]
- Affleck, I. Universal Term in the Free Energy at a Critical Point and the Conformal Anomaly. Phys. Rev. Lett. 1986, 56, 746–748. [Google Scholar] [CrossRef]
- Kleban, P.; Vassileva, I. Free energy of rectangular domains at criticality. J. Phys. A 1991, 24, 3407. [Google Scholar] [CrossRef]
- Wu, X.; Izmailian, N.; Guo, W. Finite-size behavior of the critical Ising model on a rectangle with free boundaries. Phys. Rev. E 2012, 86, 041149. [Google Scholar] [CrossRef] [PubMed]
- Ferdinand, A.E.; Fisher, M.E. Bounded and inhomogeneous Ising models. I. Specific-heat anomaly of a finite lattice. Phys. Rev. 1969, 185, 832. [Google Scholar] [CrossRef]
- Ferdinand, A.E. Statistical mechanics of dimers on a quadratic lattice. J. Math. Phys. 1967, 8, 2332–2339. [Google Scholar] [CrossRef]
- Di Francesco, P.; Mathieu, P.; Sénégal, D. Conformal Field Theory; Springer: New York, NY, USA, 1997. [Google Scholar]
- Wu, X.; Izmailian, N.; Guo, W. Shape-dependent finite-size effect of the critical two-dimensional Ising model on a triangular lattice. Phys. Rev. E 2013, 87, 022124. [Google Scholar] [CrossRef] [PubMed]
- Imamura, Y.; Isono, H.; Matsuo, Y. Boundary states in the open string channel and CFT near a corner. Prog. Theor. Phys. 2006, 115, 979–1002. [Google Scholar] [CrossRef]
- Bondesan, R.; Dubail, J.; Jacobsen, J.L.; Saleur, H. Conformal boundary state for the rectangular geometry. Nucl. Phys. B 2012, 862, 553–575. [Google Scholar] [CrossRef]
- Bondesan, R.; Jacobsen, J.L.; Saleur, H. Rectangular amplitudes, conformal blocks, and applications to loop models. Nucl. Phys. B 2013, 867, 913–949. [Google Scholar] [CrossRef]
- Wu, X.; Izmailyan, N. Critical two-dimensional Ising model with free, fixed ferromagnetic, fixed antiferromagnetic, and double antiferromagnetic boundaries. Phys. Rev. E 2015, 91, 012102. [Google Scholar] [CrossRef]
- Lu, W.T.; Wu, F.Y. Partition function zeroes of a self-dual Ising model. Physica A 1998, 258, 157–170. [Google Scholar] [CrossRef]
- Izmailian, N.S.; Oganesyan, K.B.; Wu, M.C.; Hu, C.K. Finite-size corrections and scaling for the triangular lattice dimer model with periodic boundary conditions. Phys. Rev. E 2006, 73, 016128. [Google Scholar] [CrossRef] [PubMed]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Privman, V. Universal size dependence of the free energy of finite systems near criticality. Phys. Rev. B 1988, 38, 9261. [Google Scholar] [CrossRef] [PubMed]
- Cardy, J.L. Effect of boundary conditions on the operator content of two-dimensional conformally invariant theories. Nucl. Phys. B 1986, 275, 200–218. [Google Scholar] [CrossRef]
- Korn, A.G.; Korn, T.M. Mathematical Handbook; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Weil, A. Elliptic Functions According to Eisenshtein and Kronecker; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1976. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izmailian, N.; Kenna, R. Universality and Exact Finite-Size Corrections for Spanning Trees on Cobweb and Fan Networks. Entropy 2019, 21, 895. https://doi.org/10.3390/e21090895
Izmailian N, Kenna R. Universality and Exact Finite-Size Corrections for Spanning Trees on Cobweb and Fan Networks. Entropy. 2019; 21(9):895. https://doi.org/10.3390/e21090895
Chicago/Turabian StyleIzmailian, Nickolay, and Ralph Kenna. 2019. "Universality and Exact Finite-Size Corrections for Spanning Trees on Cobweb and Fan Networks" Entropy 21, no. 9: 895. https://doi.org/10.3390/e21090895
APA StyleIzmailian, N., & Kenna, R. (2019). Universality and Exact Finite-Size Corrections for Spanning Trees on Cobweb and Fan Networks. Entropy, 21(9), 895. https://doi.org/10.3390/e21090895





