1. Introduction
In a biomedical context, a signal describes a physiological state of a biological system that is part of a biological organism under investigation. The interpretation of those signals is not always trivial, due to either their nature, or the underlying physiological system that generates the signal. For this reason, feature extracting methods have been developed in order to uniquely identify different signal characteristics [
1].
Traditional feature extracting methods can be mainly divided into two large categories; one originating from time-domain analysis and one from frequency-domain analysis [
2]. Examples in the first category include autoregressive modelling (AR), cepstrum analysis and linear predictive modelling (LPC) while the second includes Fourier transform (FT) and Hilbert transform. A third category can be the combination of these two; in this way the advantages of both are combined or limitations are cancelled out. An example in this category is the wavelet transform (WT).
The study of non-linear dynamical analysis falls under the category of time-domain analysis and is well-suited to the analysis of biomedical signals as a result of the complex dynamics contained therein. Among the different non-linear analysis methods, entropy algorithms have found many applications in the context of biomedical signal analysis [
3]. Nevertheless, in many cases these entropy algorithms are applied to the analysis of signals without an a priori, thorough understanding of what they measure.
Entropy methods have showed great potential in the analysis of electroencephalogram (EEG) signals—recordings of the electrical activity of the human brain. This is mostly due to the high complexity of the human brain and the non-linear interactions between the neurons, which translates into a signal whose dynamics might be characterised in more detail using entropy algorithms. Research in this area could help characterise in more detail the EEG signals in, for example, epilepsy, Alzheimer’s disease (AD), other forms of dementia, Parkinson’s disease (PD), and different kinds of sleep disorders, which that could help us obtain a greater understanding of these pathological conditions and, eventually, be use them for early diagnosis.
Over the years many different entropy algorithms have been introduced in the literature, all of them relying on the idea of detecting chaotic or regular behaviour in the biomedical signals. Two large families of those, which are covered in our study, are the algorithms based on Shannon’s entropy and those based on embedding. Permutation entropy (PEn) and modified permutation entropy (MPEn) belong to the former group, while sample entropy (SEn), quadratic sample entropy (QSEn) and fuzzy entropy (FEn) belong to the latter family.
PEn was first introduced by Bandt and Pompe [
4]. It is based on calculating Shannon’s entropy of fixed length partitions of the signal, which are grouped in bins based on the frequency of appearance of their permutation pattern. Several studies using PEn have focused on classifying epileptic and healthy EEG data. Cao et al. [
5] studied three patients with epileptic events by recording intracranial EEGs and by using PEn to detect any dynamic change. They found that PEn drops suddenly when a seizure occurs and then immediately starts to increase gradually until it reaches the normal values again. Nicolaou and Georgiou [
6] trained a support vector machine (SVM) algorithm with PEn features extracted from healthy and epileptic EEG data, and succeeded in predicting between the two with a classification accuracy of over 90%. Staniek and Lehnertz [
7] studied 15 subjects diagnosed with epilepsy by using EEG data and combining PEn and Transfer Entropy. Their study proved the potential of identifying the epileptogenic area without even recording an actual epileptic event.
More recently, modified permutation entropy (MPEn) has been introduced as a modified version of PEn in which the presence of equal signal values is handled differently [
8]. It has been used to distinguish between young and elderly heart rate variability (HRV) signals, and between signals of subjects with severe congestive heart failure. Compared to PEn, it has been found to improve greatly, the ability to distinguish between signals in cases when the occurrence of equal values is an intrinsic property of the signal (i.e., the HRV signal) or when the digitisation resolution is low. In addition, MPEn has been used to distinguish between simulated EEG signals of normal and epileptiform types created using a single neural mass model [
9]. Comparative statistical results suggested the better performance of MPEn compared to the conventional PEn algorithm.
A third approach for quantifying the complexity of a time series is SEn, which is a modified improvement of approximate entropy (ApEn) and was introduced by Richman and Moorman [
10]. The authors, in this seminal study, performed tests on cardiovascular data, including heart rate and chest volume, and pointed to the increased statistical consistency of SEn on such data. Continuing on cardiovascular physiology applications, Alcaraz and Rieta [
11] performed a wide study with SEn for the non-invasive analysis of atrial fibrillation (AF), in which they used typical surface electrocardiography data and presented robustness in detecting spontaneous AF termination, and variations of onset and rhythm maintenance, suggesting a useful tool for the non-linear quantification of cardiac dynamics in general. Moreover, Zhang and Zhou [
12] proposed a novel technique for discriminating the onset of surface electromyography (EMG) activity from random background spikes or noise using an implementation of SEn and proved an effective reduction of latency time compared to other methods, with promising applications to any application involving EMG and muscle activity.
Despite its wide use, SEn is now often combined or replaced with QSEn. This method was introduced by Lake [
13] as an improvement that is less dependent on its input parameters, as it includes a normalisation with respect to them. QSEn was applied to normal and AF cardiac rhythm signals to demonstrate the algorithm’s improvements over SEn [
13]. After its introduction, it has also been applied to short biomedical signals, such as the blood pressure signal recorded using ambulatory blood pressure monitoring. Statistical results in the study revealed the ability of QSEn to distinguish between control and pathological groups while SEn and ApEn could not [
14]. Relatively short signals have also been successfully characterised using QSEn for the classification of AD based on EEG recordings [
15]. QSEn has shown a statistically significant increase in regularity of AD patients’ EEG signals in complete concordance with SEn and ApEn but for a greater range of input parameters, while the optimal parameter values have been found to be outside of the other algorithms’ ranges. Finally, QSEn has been recently used to distinguish between sleep stages (quiet and active sleep) based on the HRV of newborn infants [
16], and also to classify between calm and negative stress based on EEG recordings with results showing great potential [
17].
The modification of the original SEn algorithm has also led to the introduction of another entropy measure, which is now widely known as fuzzy entropy (FEn). This recent embedding type of entropy differs in the way it calculates the similarity degree of signals and could be considered as a more analytical, accurate, and consistent (i.e., under different settings) version of SEn [
18]. FEn has been applied in EEG studies of AD, in which it has shown greater robustness to noise, better distinguishing ability between AD and control signals, and better classification accuracy compared to SEn and ApEn [
3,
19]. In addition, its suitability even for short biomedical signals and outperformance of SEn and ApEn has been demonstrated by successfully tracking qualitative changes in surface EMG signals during different motion tasks, during muscle fatigue, and during a 45-day head-down bed-rest experiment in simulated microgravity [
20,
21,
22]. Finally, FEn has also recently shown its potential in biometrics applications according to a study on EEG-based person authentication. The authors have shown that using FEn as a feature results in classification accuracy greater than 87.3%, while only two frontal electrodes are required. The study was heavily based on the algorithm’s robustness to noise and sensitivity to different levels of signal randomness which eventually aid in the reduction of electrodes and the improvement of classification rates simultaneously [
23].
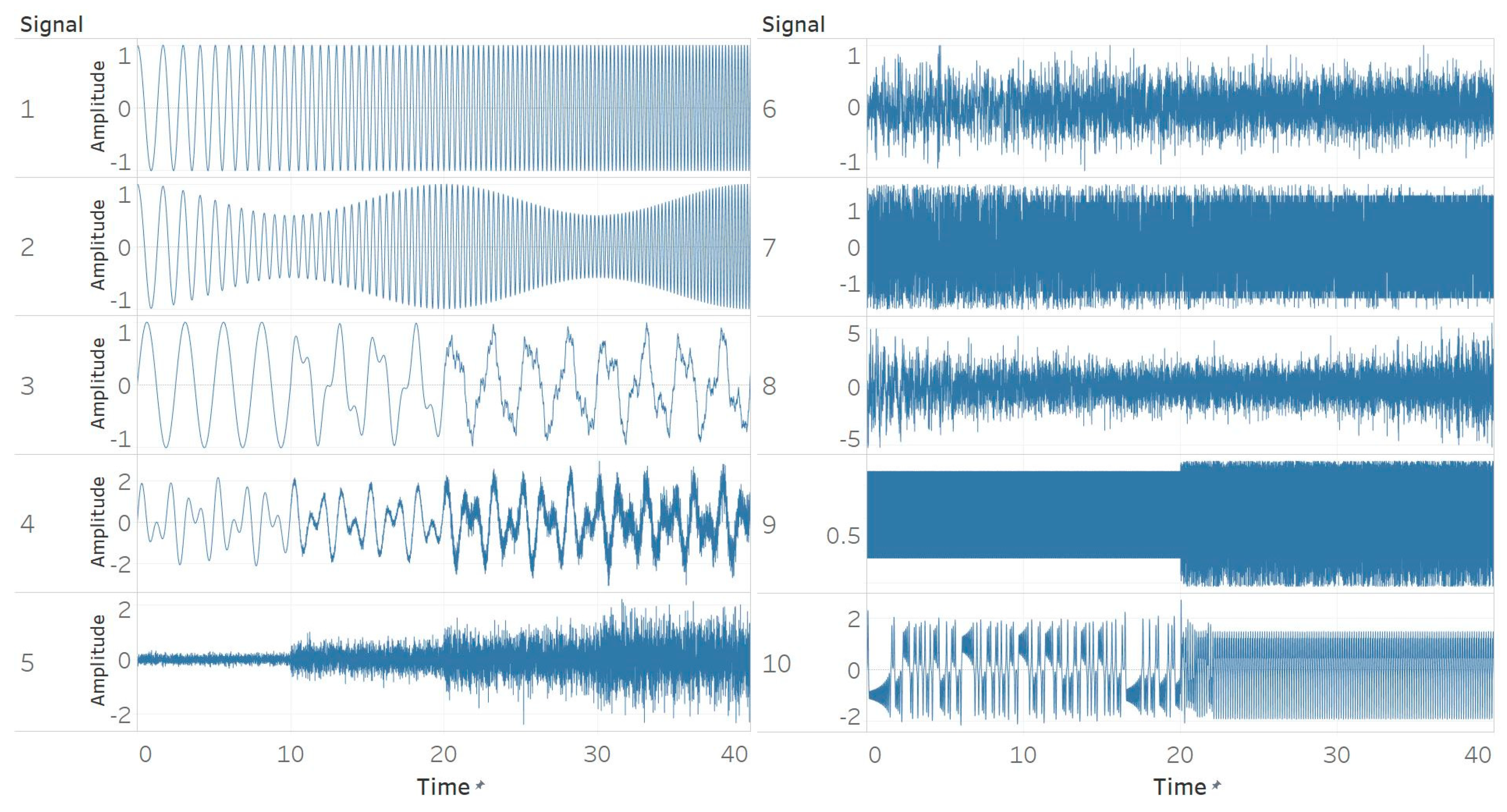
In spite of all the previous work done with these entropy metrics, it is necessary to understand them in greater detail, in particular the relationship of entropy to relevant signal processing concepts. To that end, we created different synthetic signals with different signal characteristics that are widely encountered in signal analysis, particularly in the biomedical context, and analysed them with the five entropy algorithms aforementioned. This was done to reveal the relationship of the different entropy algorithms with those signal characteristics and the ability of each of the algorithm to detect changes in the properties of the signals. Subsequently, and to test the possible usefulness of these entropy algorithms in the classification of biomedical signals in a clinical context, we applied the algorithms to the analysis of two different epileptic EEG data sets. The first EEG data set contained two groups of data: One with surface EEG segments recorded from healthy control subjects with eyes open or closed, and one with intracranial epileptic EEG segments recorded during ictal or interictal periods and at different brain locations. The second EEG data set contained interictal segments corresponding to focal or non-focal channels. We hypothesised that it would be possible to observe statistically significant differences in the means of populations belonging to different classes of signals by means of the entropy algorithms. Finally, we also attempted to predict the class to which the EEG signals belonged to using their entropy measures as features. In this way, a thorough theoretical and practical comparison of the five entropy algorithms is provided.
The structure of the paper is as follows.
Section 2 contains a detailed description of the entropy algorithms to be tested, the synthetic signals created to that aim, and the EEG data used to evaluate the possible clinical usefulness of the different entropy metrics. Exhaustive results are presented in
Section 3, which is followed by the discussion and, finally, the conclusions extracted from our study.
4. Discussion
In this study, the performance of five entropy algorithms in characterising biomedical signals was analysed. Before applying them to real signals, a thorough analysis of ten synthetic signals was carried out with each entropy algorithm. The signals were chosen in accordance with the relevant literature in order to have a common point of reference and to lay the ground for possible comparisons between non-linear analysis methods.
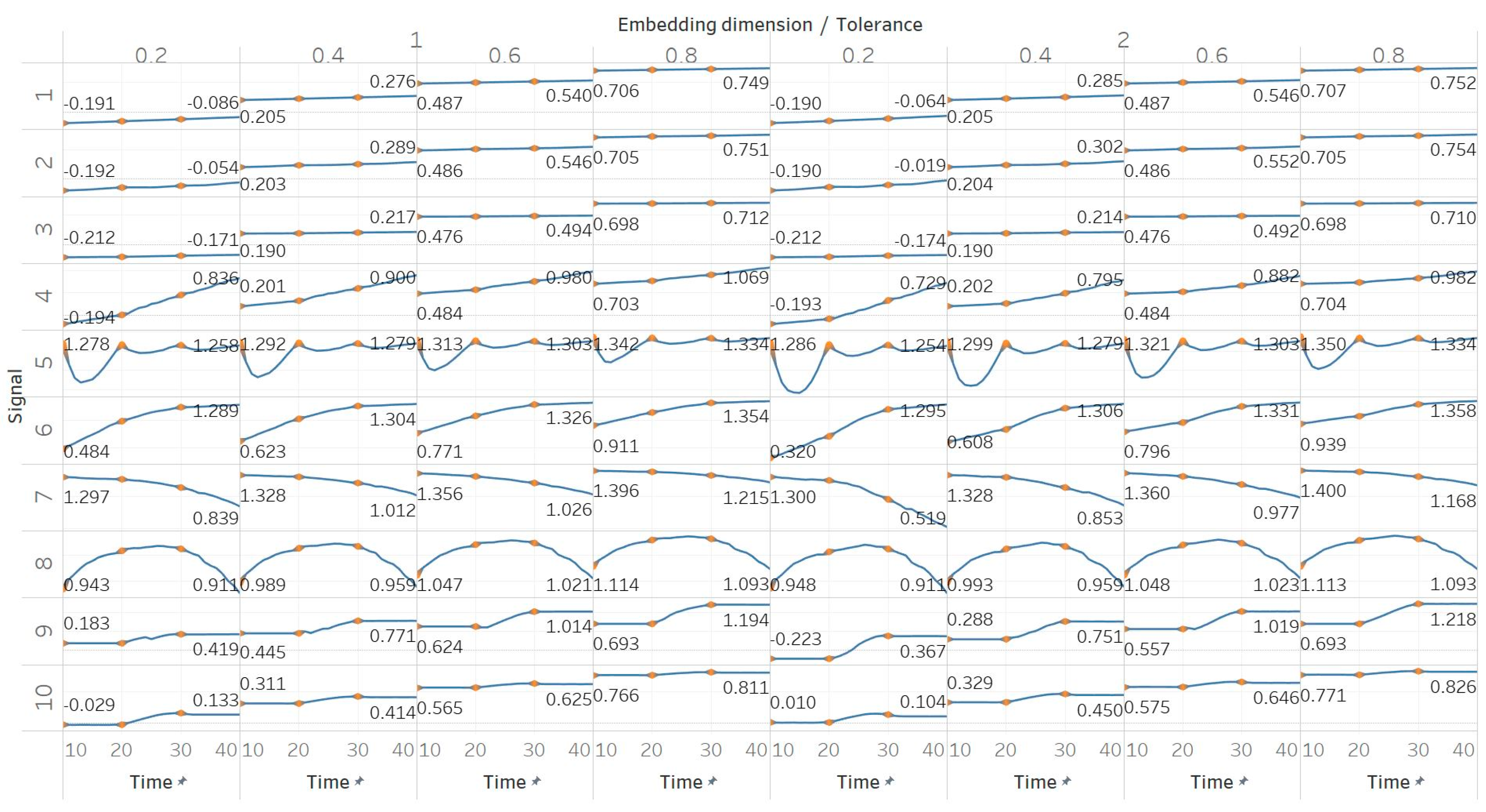
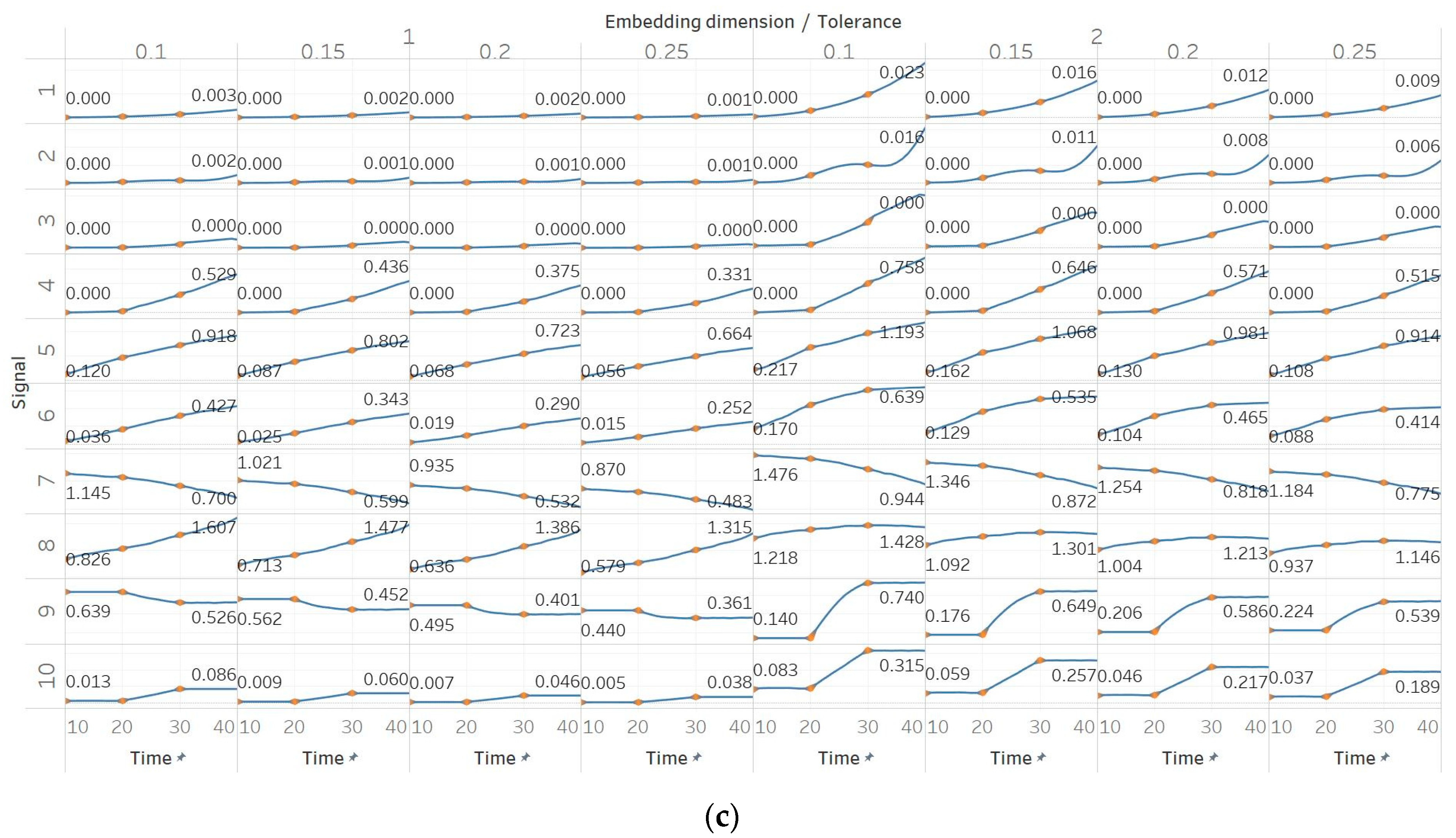
Through the synthetic signal analysis, we observed the main signal characteristics that affect the calculated entropy value of each algorithm. Interestingly, we observed almost complete consistency between the different algorithms, as all ten signals produced the same types and shapes of curves. In addition, the curves maintained their shapes for all variations of input parameters, and therefore, no absolute conclusion can be extracted on the optimal parameter values for any algorithm. In general, all five entropy algorithms are linearly affected by the increase of a single harmonic’s frequency, exponentially affected by the increase in the number of harmonics, linearly affected by WGN noise in high signal-to-noise ratio environments, and logarithmically affected by the increase in noise bandwidth during an AR process. In addition, they are all able to successfully detect a transition from randomness to orderliness in a MIX process, from periodicity to chaos in a logistic map and from chaos to periodicity in a Lorenz system. The highest entropy is observed when a signal is characterised by randomness, while entropy values for chaotic behaviour and periodicity can surpass each other depending on the level of regularity contained in their particular realisation. Permutation entropy algorithms (PEn and MPEn) are significantly faster to compute than entropies of the embedding family (SEn, QSEn, and FEn). The latter appear to be more accurate with noisy or complex signals with subtle transitions between different states. Although no absolute conclusion can be extracted for the optimal entropy algorithm based on the synthetic signals analysis alone, FEn seems to have increased sensitivity in signal changes while it also offers more possibilities for parameter fine-tuning. Nevertheless, all of the entropy algorithms but FEn had the same saturated response against a WGN signal, suggesting that FEn might be unique in being more affected by changes in the power of WGN (
Figure 6).
These observations are consistent with the relevant literature, in which similar synthetic signals were analysed using Lempel–Ziv complexity (LZC), ApEn, auto-mutual information rate of decrease (AMIRD) and SEn [
28,
32,
33,
34]. However, although LZC produced similar results to our study, it failed to detect changes in a signal with an increasing number of harmonics, unlike the entropy algorithms analysed herein. Moreover, the study with AMIRD provided identical results for the AR and MIX process signals, while it could only detect changes in a Lorenz system in the window that contained both chaotic and periodic behaviour, similar to results obtained using SEn of
m = 2 (
Figure 4).
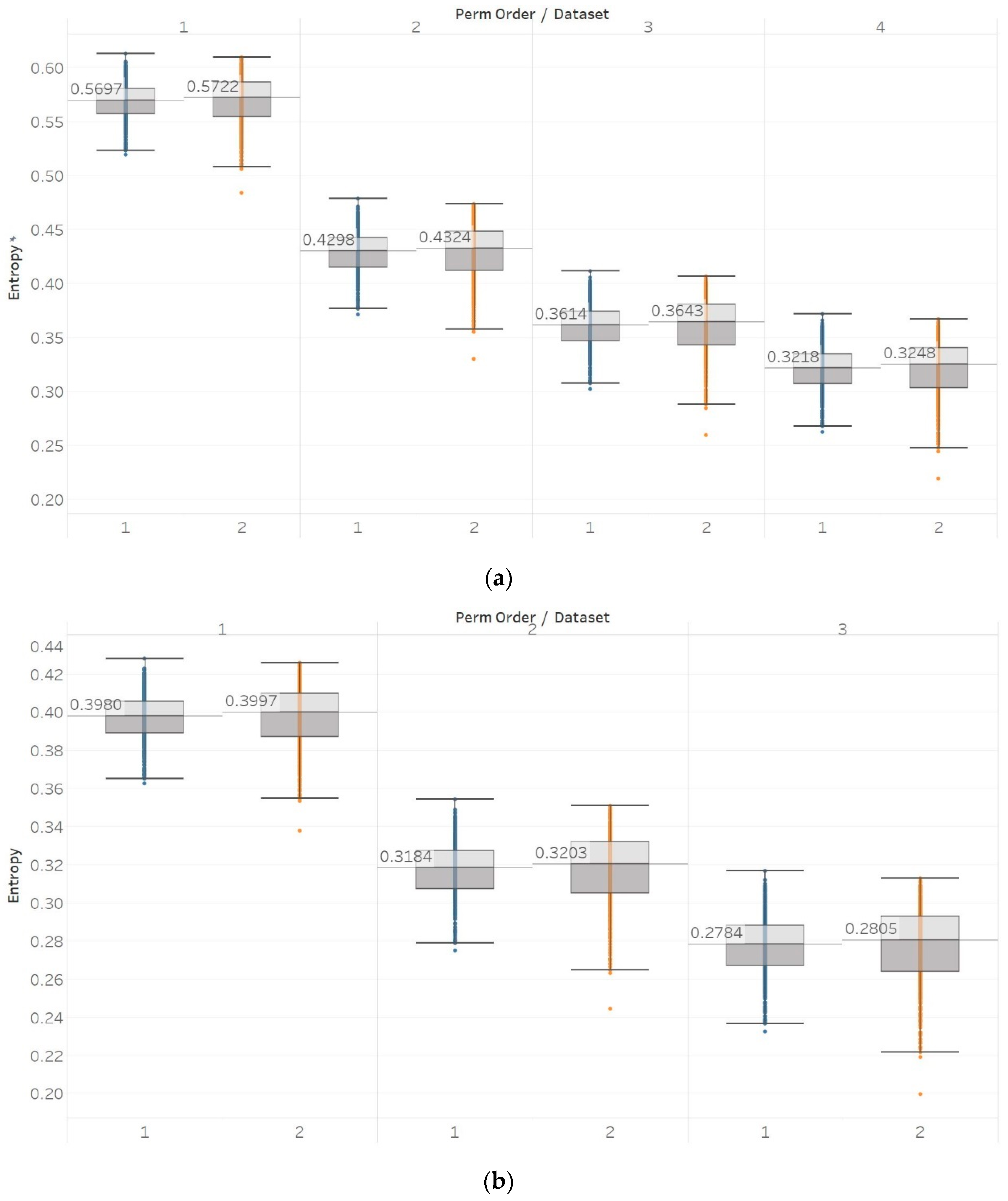
Through the application of entropy algorithms to real biomedical signals, we attempted to use their sensitivity to changes in signal complexity to distinguish between different classes of signals. EEG signals from two different epilepsy studies were used, due to the reported changes in signal complexity associated with epileptic activity [
29,
30]. In healthy subjects, we observed significant differences between surface EEG recordings that were made with eyes open or closed for all permutation entropy (PEn and MPEn) algorithm combinations and for most of the embedding entropy (SEn, QSEn, and FEn) algorithms. However, the former showed a decrease in entropy in closed-eyes EEG while the latter showed mostly the opposite. Permutation entropy algorithms are in line with the literature in which closed eyes are associated with the appearance of alpha brain rhythms, which are characterised by regularity [
6]. On the contrary, though, another study that has compared the results of a Shannon-based entropy algorithm (namely Distribution Entropy) to FEn shows opposite results to what we have for both algorithm families [
31]. Nevertheless, it is worth noting that distribution entropy is not the same as PEn or MPEn. Furthermore, the approach used in [
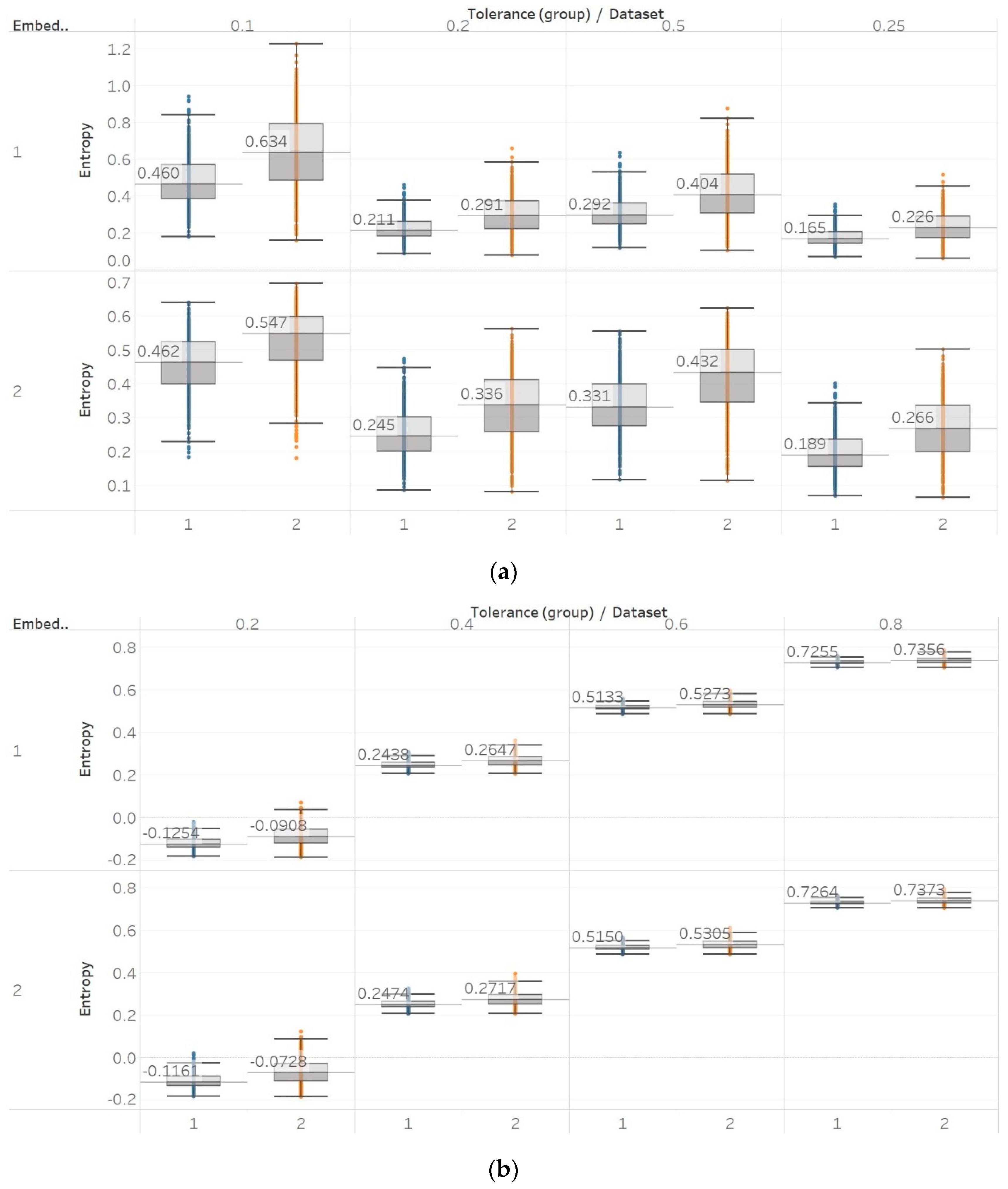
31] is quite different to the one we have used in our study, as windows of different length were used to compute entropy (in our study the entropy of the whole signal was calculated instead), intracranial recordings from different groups in the data sets were combined to perform a comparison between ictal and interictal EEGs (we kept them separate in our study), and different types of EEGs were compared in the classification between the healthy (surface EEG) and epileptic (intracranial EEG) groups. In our study, for recordings made from the epileptogenic zone of the brain, the opposite hemisphere and during seizures, significant differences were mostly detected between the seizure and non-seizure recordings, while the differences between the brain zones during interictal periods were always significant for permutation entropy algorithms and never significant for embedding algorithms. At the same time, permutation entropy algorithms returned lower entropy values from the seizure EEG segments, followed by the epileptogenic zone, while embedding entropy algorithms returned mostly the opposite (apart from SEn of
m = 2,
Figure 9). For permutation entropy algorithms, results are in complete accordance with the literature [
6,
35,
36]. In all these studies, PEn was used to either classify either between healthy and epileptic, or between ictal and interictal EEG segments and was found to decrease during ictal compared to interictal segments. On the other hand, results from SEn, QSEn, and FEn are less consistent across the literature. FEn analysis using the same data set has been found to produce higher entropy in seizure signals, followed by the epileptogenic zone and then by the opposite hemisphere signals [
37]. SEn analysis from the same study has been found to produce higher entropy in the epileptogenic signals, followed by the seizure signals, and finally the ones from the opposite hemisphere. Additionally, studies that used other entropy or complexity measures, such as ApEn, LZC, and Spectral Entropy, have also reported increased values during seizures compared to interictal EEG segments [
38,
39]. All these are similar to what we have reported (
Figure 9,
Figure 10 and
Figure 11). On the other hand, a different study [
40] using the first EEG data set (i.e., the one originally published in [
29]) reports increased SEn in ictal versus interictal signals. Nevertheless, there are several differences between our study and [
40], as the latter focused on the analysis of shorter 5 s epochs extracted from the original EEG recordings, combined signals from the opposite hemisphere and the epileptogenic zone into a single interictal data set, and extended the set of input parameters used in the calculation of SEn beyond the ranges originally recommended by Richman and Moorman [
10] and used in our study. Moreover, another study using the intracranial EEG data set from [
29] and the whole signal length supports the claims of reduced SEn (calculated with
m = 0.2 and
r = 0.2) in recordings containing ictal activity when compared to epochs with interictal EEG activity [
41].
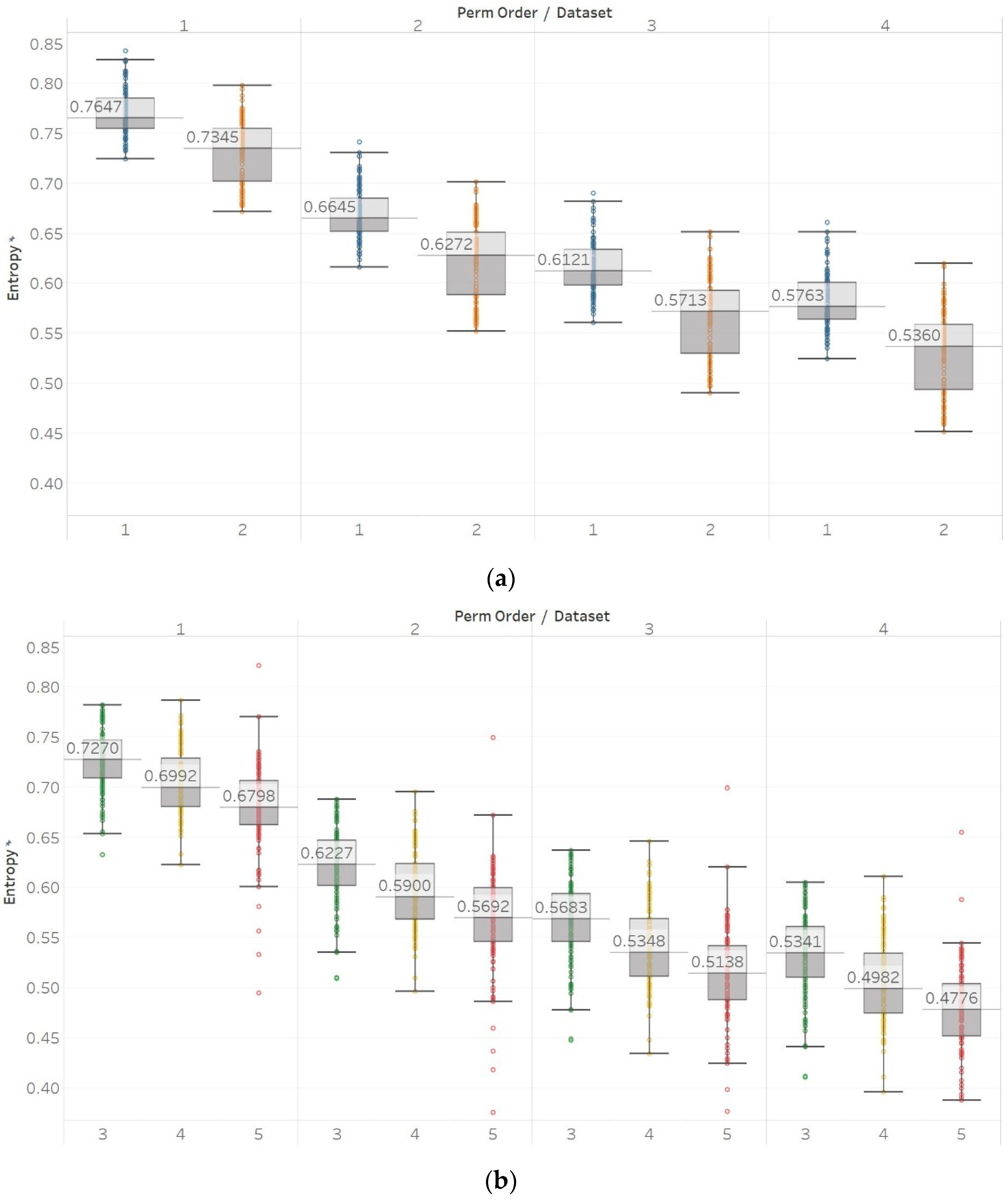
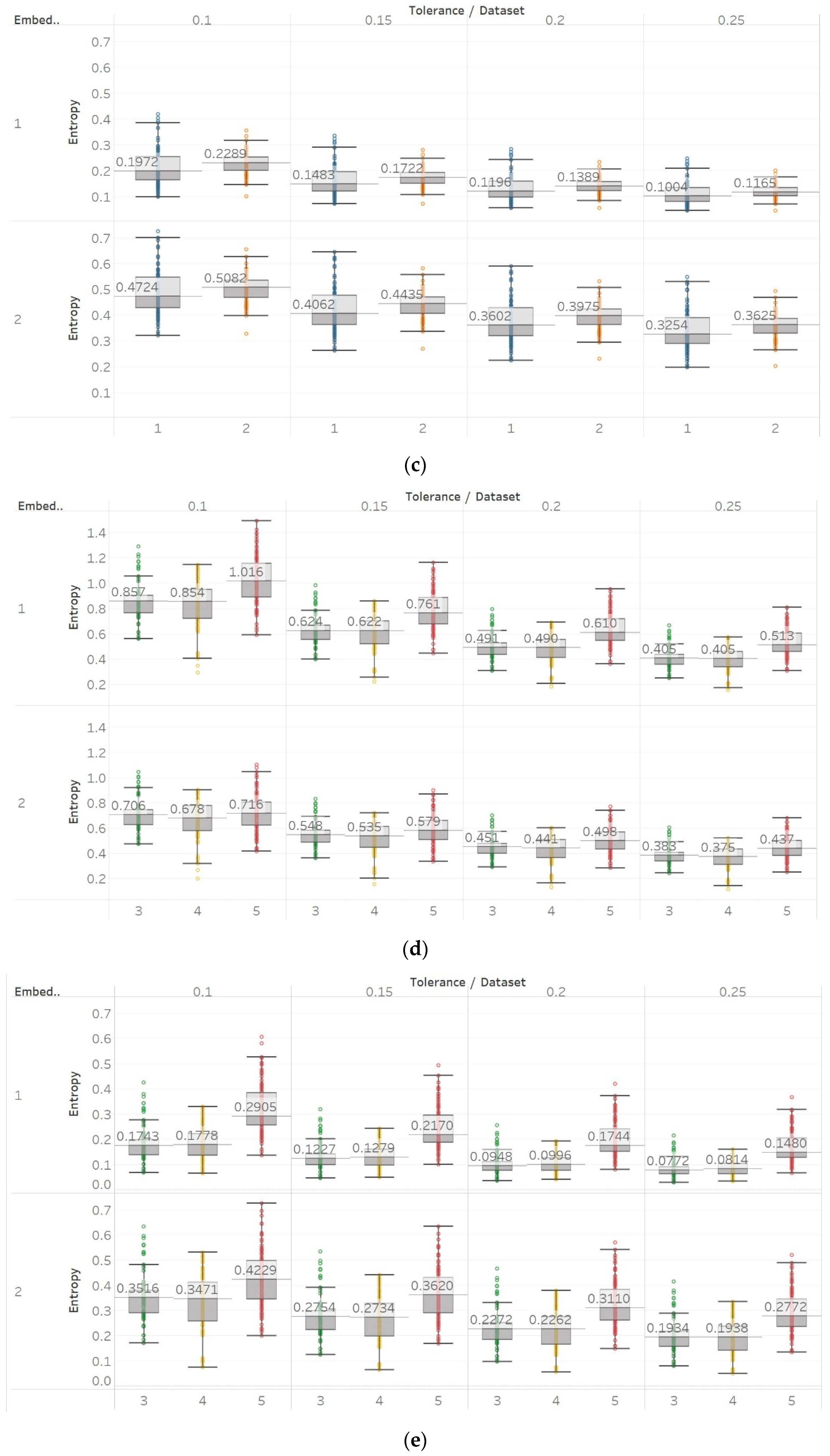
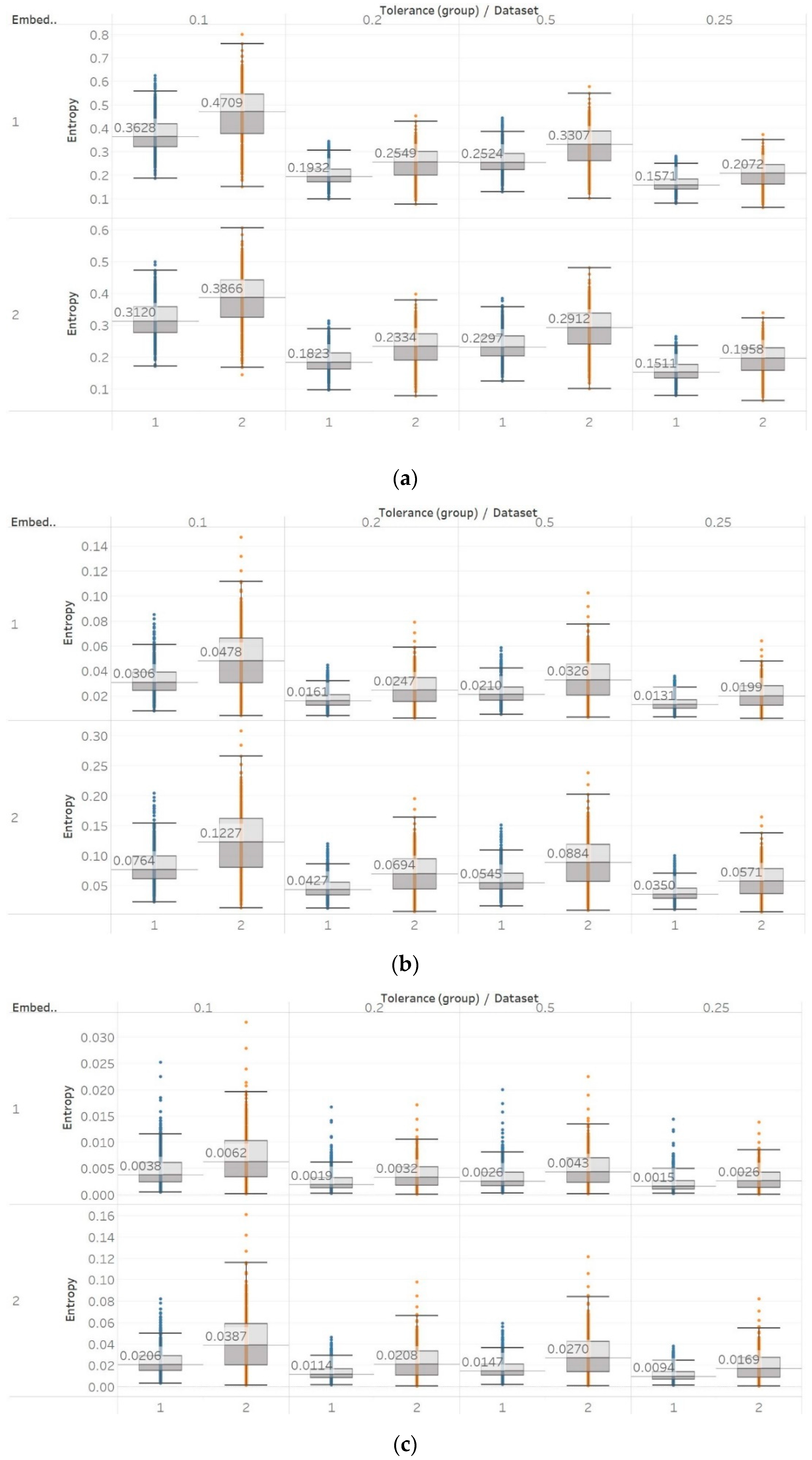
To further investigate these observations, we used the second epilepsy data set, which included intracranial EEG recordings from epilepsy patients during interictal periods from focal and non-focal channels. In contrast with previous findings, permutation entropy algorithms in this case failed completely to detect any difference between focal and non-focal signals, while most embedding algorithms showed a statistically significant increase in entropy in non-focal signals (
Figure 12,
Figure 13 and
Figure 14). This observation is also consistent with the literature where SEn and FEn have shown the same results on the same data set [
42].
As a result, permutation entropy algorithms performed well in differentiating between signal classes in all tests except for the focal and non-focal signals. On the other hand, embedding algorithms performed well in all statistical tests except for the insignificant differences between epileptogenic and opposite hemisphere data sets, but their results in the first epilepsy database were inconsistent and dependent on input parameter combinations. Combining these conclusions with results from the literature, permutation entropy algorithms seem to have the advantage of significantly faster computation time and consistency, but they are not as sensitive (proven by failing to detect differences between focal and non-focal signals from the second data set). On the other hand, embedding entropy algorithms have increased sensitivity (proven by the differentiation between focal and non-focal signals) while also potentially having greater potential with correct tuning of their input parameters. However, this tuning is not trivial and might result in different results than expected. In terms of classification tasks, permutation entropy algorithms performed better in classifying data in the first data set (reached the maximum accuracy of 73.5%) while embedding algorithms performed better in the second data set (reached the maximum accuracy of 63%). Nonetheless, it is worth noting that using only one entropy algorithm as a feature generally yields low classification accuracies. These accuracies were equal to 73.5% for the classification between eyes-open and eyes-closed surface EEGs in healthy controls (obtained using PEn with n = 5); 63% for the classification between intracranial EEGs from epileptic patients recorded at the epileptogenic area, the opposite hemisphere and during seizures (obtained using FEn with n = 3, m = 1, and r = 0.2); and 63% for the classification between focal and non-focal intracranial EEGs (obtained using FEn with n = 1, m = 1, and r = 0.1). Increasing the number of features from one to five can increase the maximum possible accuracy significantly. This accuracy reached 94% for the first classification task using all algorithms except PEn (MPEn with n = 5; SEn with m = 2 and r = 0.15; QSEn with m = 1 and r = 0.8; FEn with n = 3, m = 1, and r = 0.1), 87% for the second classification task using all algorithms except MPEn (PEn with n = 4; SEn with m = 2 and r = 0.25; FEn with n = 3, m = 2, and r = 0.2), and 75.5% for the third classification task using all five entropy algorithms (PEn with n = 5; MPEn with n = 4; SEn with m = 2 and r = 0.15; QSEn with m = 2 and r = 0.25; FEn with n = 1, m = 1, and r = 0.15). It is worth noting than in all cases, the combination of results obtained with entropy algorithms from both families (i.e., based on Shannon’s entropy and based on embedding) clearly outperformed the results obtained by using methods from each family separately.
Our study has some limitations that should be highlighted. Firstly, although many synthetic signals were used to characterise the different entropy algorithms, there is scope to evaluate them with other synthetic data. This would provide additional and potentially valuable information about the way entropy algorithms characterise signals. In addition to that, the performance of other entropy algorithms (spectral entropy, wavelet entropy, etc.) could be analysed as well. In this way, we could find more common or uncommon responses between different entropy algorithms to synthetic and biomedical signals. Another limitation would be the classification techniques used and the extensiveness of the study as a whole. Our approach was limited to a pilot study, while trying to extend the theoretical analysis with a more practical approach and to provide a baseline for potential further studies. Finally, but equally importantly, the limited number of patients and EEG signals available and the limited number of signals used as part of the second epilepsy study, along with any potential bias of the data sets, should also be highlighted as a limitation.