Abstract
Currently, chaos-based cryptosystems are being proposed in the literature to provide confidentiality for digital images, since the diffusion effect in the Advance Encryption Standard (AES) algorithm is weak. Security is the most important challenge to assess in cryptosystems according to the National Institute of Standard and Technology (NIST), then cost and performance, and finally algorithm and implementation. Recent chaos-based image encryption algorithms present basic security analysis, which could make them insecure for some applications. In this paper, we suggest an integral analysis framework related to comprehensive security analysis, cost and performance, and the algorithm and implementation for chaos-based image cryptosystems. The proposed guideline based on 20 analysis points can assist new cryptographic designers to present an integral analysis of new algorithms. Future comparisons of new schemes can be more consistent in terms of security and efficiency. In addition, we present aspects regarding digital chaos implementation, chaos validation, and key definition to improve the security of the overall cryptosystem. The suggested guideline does not guarantee security, and it does not intend to limit the liberty to implement new analysis. However, it provides for the first time in the literature a solid basis about integral analysis for chaos-based image cryptosystems as an effective approach to improve security.
1. Introduction
Information security in modern digital systems and telecommunication networks has been one of the major concerns during the last few decades with an increasing research area in cryptography to provide confidentiality and protect secrets from eavesdroppers, intruders, adversaries, or enemies by using cryptosystems. Transmitting or storing confidential images over insecure channels can have a high risk. Thus, such information must be protected prior to sending or storing, e.g., clinical images or radiological photos (for diagnosis or consultation) in telemedicine, personal identifiers such face, iris, or fingerprint images (for control access systems) in biometric systems, or satellite maps in military are some potential applications for image encryption. Basically, an encryption algorithm will map the plain text (recognizable message) to encrypted text (unrecognizable message) with some specific key, and a decryption algorithm will map the encrypted text to plain text with the corresponding specific key. Cryptosystems can be performed by hand methods, machine methods, or software based on Shannon’s model. In cryptanalysis, several kinds of attacks can be implemented to break a cryptosystem such as side-channel attack, physical attack, invasive attack, radio frequency attack, impersonation attack, chosen/known plain text attack, differential attack, exhaustive search attack, among others. For example, a physical attack in cryptographic implementations includes all kind of attacks related to physical means against encryption devices, e.g., a microcontroller-based cryptosystem or a smart card [1].
In modern cryptography, asymmetric-key and symmetric-key are the most common methods of conventional cryptosystems. Asymmetric-key schemes use a pair of keys, i.e., private key and public key, such as Rivest, Shamir, and Adleman (RSA), which is an encryption algorithm for data confidentiality with a common key length between 1024 and 2048 bits [2]; or Elliptic-curve Diffie–Hellman (ECDH), which is an anonymous key agreement protocol to establish a shared secret key over an insecure channel that can be used in a symmetric-key encryption scheme [3]. These kinds of methods are based on intractable mathematical problems, i.e., problems that can be resolved in theory, but in practice take too long for their solution (e.g., factoring a number into primes, integer factorization, or discrete logarithm). In symmetric-key cryptosystems, the same key is used for encryption and decryption, which is considered secret, and it must be shared between parties securely. In addition, there are block ciphers and stream ciphers. Block cipher encrypts plain data in fixed-length groups of bits such as the Advanced Encryption Standard (AES), the Triple Data Encryption Standard (3DES), or the International Data Encryption Algorithm (IDEA). Stream cipher encrypts plain data bit-by-bit with a pseudorandom keystream such as Rivest Cipher 4 (RC4), Rabbit, HC-128/256, Salsa 20/12, and Trivium, among others. These schemes are based on an iterated process or a series of linked mathematical operations, i.e., the Feistel network and the substitution-permutation network (SPN), where several rounds of substitution boxes (S-boxes) and permutation boxes (P-boxes) are implemented with exclusive-or (XOR) or bitwise rotation. In addition, key lengths of 128, 192, or 256 bits are used [4]. According to the National Institute of Standard and Technology (NIST), a key of 15360-bit in the RSA algorithm is equivalent in strength to a 256-bit one in the AES algorithm [5]. Although asymmetric-key schemes use two keys to increase the security of the cryptosystem, symmetric-key schemes are typically faster and less expensive to implement. In this sense, symmetric-key cryptography is typically used for data encryption, and asymmetric-key cryptography is used for digital signatures or secure-key exchange protocols. Because the diffusion effect in the AES algorithm is weak, conventional symmetric-key cryptosystems as AES are not suitable to encrypt digital images securely and efficiently.
In the last years of the Twenty Century, the scientific community found an interesting research area related to chaos-based cryptography (non-conventional cryptography), since chaotic systems present properties such as extreme sensibility to initial conditions and control parameters, ergodicity, mixing data, non-linearity, random-like behavior, aperiodic dynamics, and determinism, which are strongly related to cryptographic properties such as complexity in the source system, pseudorandomness, and an excellent substitution-permutation process to provide security and efficiency in chaos-based image cryptosystems. Analog and digital chaos-based cryptosystems have been proposed in the literature. The analog implementation was first proposed in the 1990s, which is based on chaotic synchronization techniques first proposed by Pecora and Carroll in 1990 [6] and analog circuits (hardware-based key) to transmit analogical or digital information (such as digital images) by using techniques such as chaos modulation and chaos masking proposed by Oppenheim et al. [7], or chaos spreading spectrum proposed by Cuomo et al. [8]. Based on such techniques, analog chaos-based cryptosystems have been proposed in the literature; see, e.g., [9,10,11,12].
On the other hand, Fridrich proposed the permutation-diffusion architecture for digital chaos-based image encryption in 1998 [13]. Based on Fridrich’s scheme, digital chaos-based cryptosystems or hyperchaos-based cryptosystems have been proposed based on computer simulation and the symmetric-key method, e.g., gray-scale image encryption [14,15,16], RGB color image encryption [17,18,19,20], H.264 video encryption [21], text encryption [22], biometric encryption [23], and biosignal encryption [24].
Recent chaos-based image cryptosystems (2015–2019) present “basic” security analysis (i.e., key space, key sensitivity, plain text sensitivity, graphic histogram, graphic correlation, correlation coefficient, and information entropy) or partial security analysis and speed performance (for encryption/decryption); see, e.g., [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Table 1 summarizes the security analysis of recent chaos-based image cryptosystems. NIST considers security as the most important criteria in a cryptographic evaluation, following the cost, algorithm, and finally, implementation [44,45]. Recent chaos-based image cryptosystems or hyperchaos-based cryptosystems do not present a comprehensive security analysis according to Table 1, which could make them unreliable and insecure for some applications (e.g., telemedicine, biometrics systems, or in military affairs). Even analysis about cost end performance and the algorithm and implementation are not considered in detail. Such differences in security terms between recent chaos-based algorithms are due to the lack of frameworks or guidelines for security analysis, which is the main motivation of this paper.

Table 1.
Security analysis presented in recent chaos-based image cryptosystems, where √ means “presented” and - means “not presented”.
Security analysis is a testing technique to determine if a cryptosystem protects the information adequately, and it must include analysis against all known attacks efficiently, since excellent performance and implementation advantages of a broken cryptosystem are irrelevant. Therefore, every chaos-based cryptosystem must provide enough information regarding their security and efficiency.
Few efforts to establish the cryptographic requirements for chaos-based cryptography have been proposed in the literature. In 2006, Álvarez and Li proposed some basic cryptographic requirements for chaos-based cryptosystems with the aim of assisting designers to present their work in a more systematic and rigorous way; several recommendations based on 17 suggested rules (related to implementation, key management, and security analysis) were proposed for analog chaos-based secure communications [46]. In 2018, Özkaynak proposed a roadmap for the security analysis of new chaos-based image cryptosystems, since many proposals that only used the unified averaged changed intensity (UACI) and the number of changing pixel rate (NPCR) tests to evaluate security with respect to differential attacks have been observed to be weak; in addition, a checklist and design guide were proposed to make more robust analyses, which is based on 12 steps [47]. The checklist of Özkaynak has been implemented in recent chaos-based image cryptosystem to complement the discussion of the proposed scheme in [40]. In the same year, Preishuber et al. showed that computational effort and security benefits are highly questionable for chaos-based image cryptosystems in comparison with conventional algorithms; even they demonstrated that statistical tests used to assess the security of chaos-based encryption schemes are insufficient metrics for security analysis. They pointed out that further methodologies for the security assessment for chaos-based encryption schemes need to be entirely reconsidered [48].
In this paper, we present a suggested integral analysis framework based on a comprehensive security analysis, cost and performance analysis, and algorithm and implementation details, with the aim to establish a basis in security analysis for chaos-based image cryptosystems. The proposed guideline based on 20 analysis points can assist cryptographic designers to present a common study about an integral security analysis of their new cryptosystems with the aim to show exhaustive information about security, reliability, integrity, protection of secrets, easy of use, speed, and acceptable costs. If the authors consider this guideline, future comparisons of new proposals can be more consistent in terms of security and efficiency, which can help to develop more secure and efficient encryption algorithms. The suggested framework is based on a literature review, new analysis (such as histogram uniformity, graphic autocorrelation, and floating frequency), and the evaluation criteria of NIST for cryptosystems (security, cost and performance, and the algorithm and implementation). We use the chaos-based RGB image encryption algorithm [25] to determine the results of the suggested framework. Furthermore, we present aspects regarding digital chaos implementation, chaos validation, and key definition with the aim to improve the overall security of new cryptosystems. Designers are invited to follow the recommendations of this work, but without limiting their liberty, new analysis, and their own creativity to establish the security of their new cryptosystems.
The rest of the paper is organized as follows. In Section 2, digital chaos aspects are presented to improve the overall cryptosystem security. The suggested framework related to a comprehensive security analysis is given in Section 3. The cost and performance analysis are shown in Section 4. In Section 5, the algorithm and implementation details of chaos-based digital cryptosystems are presented. Finally, the conclusions are mentioned in Section 6.
2. Digital Chaos
Cryptosystems based on digital chaos have attracted more attention than its analog version, since discrete chaotic systems or chaotic maps present advantages related to security, performance, flexibility, and cost. In 2003, Li proposed some basic suggestions to design fast and low-cost digital chaotic ciphers: choosing the simplest chaotic map to achieve better performance, using the minimum iterations in chaotic maps, avoiding use of multiple chaotic maps in software implementations, using fixed-point arithmetic as much as possible, avoiding chaotic maps with floating-point arithmetic requirements, and adopting a parallel mechanism in hardware implementations [49].
Digital chaos implementation implies finite numbers either with floating-point arithmetic, fixed-point arithmetic, or other arithmetic at a reasonable digital word size. Chaos degradation occurs principally for continuous chaotic systems, when a numerical solution such as Euler or Runge–Kutta (RK4) is applied. On the other hand, chaotic maps are discrete by nature. Nevertheless, a chaotic sequence can fall into a short chaotic cycle when it is realized in a low digital word size. It is known that fixed-point arithmetic requires low-power, low-cost, simpler, and smaller hardware than floating-point arithmetic for a reasonable word size in signal processing. However, the floating-point has a larger dynamic range and can represent numbers of the real world. Therefore, the floating-point reduces the risk of overflow, quantization errors, and the need for scaling. For example, when a chaos-based cryptosystem is implemented in MATLAB, the format long is used for a 64-bit word size in fixed-point arithmetic, whereas format long E is for a 64-bit word size in floating-point.
In the last two decades, designers have been implementing cryptosystems based on one-dimensional chaotic maps such as the logistic map or piecewise linear chaotic maps and with two-dimensional chaotic maps such as the 2D logistic map, Hénon map, Arnold’s cat map, the Duffing map, the Ikeda map, the standard map, the Tinkerbell map, and the Baker map.
2.1. Chaos Validation
The sequences used for the encryption process must be validated chaotically to produce cryptograms with good statistical properties. The initial conditions and control parameter of chaotic maps are considered as the secret key. Therefore, control parameters must be defined adequately to avoid non-chaotic regimes. For example, the logistic map produces chaos when the control parameter is between 3.57 and four. Nevertheless, there are some values where the dynamics become periodic. A robust numerical validation of the chaotic sequence must be presented such as the Lyapunov exponent [50] or the recent 0–1 Gottwald–Melbourne test [51]. A positive Lyapunov exponent indicates chaos, and a value close to one in the Gottwald–Melbourne test indicates chaos.
In some cases, the control parameter can be adjusted to guarantee chaos. For example, if the control parameter of the logistic map starts with 3.9 and a double precision (64 bits) floating-point format is adopted, then we can manipulate 14 digits (but reducing the complexity from to , approximately), but it produces always chaotic sequences (strong keys). We suggest to complement this with some numerical validation by using several tests with several secret keys selected randomly to provide robustness.
2.2. Key Definition
Recent chaos-based digital cryptosystems reported in the literature are based on fixed-point or floating-point arithmetic with double precision. Therefore, 15 decimal digits of initial conditions and control parameters are defined as the secret key, which make it complicated to implement in real applications. For example, Niyat et al. in 2017 [33] defined the secret key with 135 decimal digits based on six initial conditions and three control parameters. In this sense, there are recent cryptosystems (see, e.g., [27,28,30,32]). In some cryptosystems, the secret key is defined with a stream of hexadecimal numbers, which can be more practical for implementation and sharing between parties. The initial conditions and control parameters are determined from this secret key by using some mathematical process; see, e.g., [25,31,52]. We suggest including some efficient algorithm to implement practical keys with bits such as used in conventional cryptography. For example, the one-dimensional logistic map is described as follows:
where is the discrete state with initial condition and control parameter to produce chaotic sequences. If this chaotic map is implemented by using IEEE 754 double floating-point arithmetic (until 15 decimals) and all decimals are considered, the maximum complexity for state x is and for control parameter a is . A practical key could be the hexadecimal format such as used in conventional cryptography. In this case, we can define a secret key H with 26 hexadecimal digits, and an algorithm determines the value for x and a of the logistic map. An example of this process can be defined as follows:
- Calculate constants and .
- Assign constants to the initial condition and control parameter with and .
The key space and key sensitivity must be reviewed carefully when this kind of process is included in a cryptosystem (see Section 3.1).
2.3. Encryption Algorithm
The substitution-permutation network has been adopted in most chaos-based encryption algorithms proposed in the literature, with one or several rounds of each process to increase security. The main idea is to change the value of each plain element and change its position according to chaotic sequences to produce cryptograms that are statistically efficient.
On the other hand, cryptanalysis has been applied in chaos-based image cryptosystems by using the powerful chose/known plain image attacks [53,54,55]. The chaotic keystream for encryption could be derived from both the secret key and the plain image to provide robustness against this kind of attack. Nevertheless, if an error occurs in the transmitted cryptogram, than it could be impossible to decrypt such a cryptogram. Some recent chaos-based digital cryptosystems do not considered this important fact. In addition, it provides higher sensitivity against plain images. Recently, some advances over the algorithm design have been addressed to resist the chosen/known plain image attack, where the plain image is included for the chaotic keystream used in the encryption process [25,36], adding random values to the plain image before encryption [52], or by using the SHA256 algorithm (hash function) for the plain image [16,56], but the receiver must have the same hash value for each different image encryption; it could be included in the cryptogram, but if it is damaged during transmission, the receiver cannot retrieve the original image; or the sender could securely exchange it with the receiver each time a different plain image is encrypted.
3. Security Analysis
In this section, we present several statistical security analyses that can be applied over chaos-based image cryptosystems. The presented security analysis is based on a literature review, and we propose three new statistical analyses such as histogram uniformity, graphic autocorrelation, and floating frequency. Table 1 shows us that most authors included basic tests such as key size, sensitivity of the secret key and plain image, information entropy, histograms, and correlation. In some cases, other analyses are considered such as encryption quality, noise, and occlusion. Such differences make it difficult for a robust comparison among cryptosystems in terms of security or efficiency.
Consider an RGB color plain image of pixels, where M is the rows, N is the columns, and three is the color component with dimension for red, green, and blue. A gray-scale plain image of pixels has a bit depth of eight bits, whereas the color image has 24 bits (eight bits for each component). Therefore, a color plain image of has a bulk data of 196.608 KB (which can vary according to the image format). The results of the proposed framework are based on the chaos-based RBG encryption algorithm proposed in [25].
First at all, a chaos-based image encryption algorithm must produce encrypted image E visually without clear information. In Figure 1, the gray-scaleLena plain image of pixels and the RGB color Landscape plain image of pixels are shown with their corresponding encrypted images, which do not present clear information for human eyes.

Figure 1.
Plain images and their corresponding encrypted images: (a) Lena plain image, (b) Lena encrypted image, (c) Landscape plain image, and (d) Landscape encrypted image.
3.1. Point 1: Key Space
The key is defined as a bit string that determines how the algorithm will map the plain image P to encrypted image E. It is considered highly important from a security point of view, since all about the cryptosystem is know by the adversary except the key (Kerckhoffs’ principle). The most obvious attack over the cryptosystem is the exhaustive search attack or brute-force attack, where each possible key is used until the cryptosystem is broken. In addition, adversaries have access to latest technology including supercomputers. The key space is designed to be large enough to resit this kind of attack considering the actual technology, e.g., the fastest supercomputer today (Summit) is capable of 200 PFLOPS ( floating-point operation per second) or 200,000 trillion calculations per second. The key space must be more than 100 bits according to Álvarez and Li [46]. This key size requires years (Equation (2)) to break a cryptosystem with the above supercomputer and assuming 1000 FLOPS per checking,
Most of the chaos-based digital cryptosystems implemented in MATLAB use the IEEE Standard for Floating-Point Arithmetic (IEEE 754) for floating-point computation in 64 bits (double precision) to represent real numbers of chaotic states with the aim of avoiding digital degradation and providing a huge key space. Note that not always all 64 bits (1 bit for the sign, 11 bits for the exponent, and 52 bits for the significant precision) are used for each variable of chaotic maps (i.e., chaotic states or control parameters). Therefore, the cryptographic designer must take care about the range of these values to estimate the key space. For example, the well-known 2D Hénon map is defined by:
where b and c are the two control parameters and and are the two initial conditions. The dynamics of the map in Equation (3) is chaotic when , , , and . The sign and integer section of the IEEE 754 format (12 bits) cannot be considered as part of the key space, since it does not vary enough in this case. Nevertheless, the decimal part (significant precision) can vary with thousands of possibilities. If control parameters start with and , then b and c will have a complexity of (approximate) instead of , since just 14 of the 15 decimals can change their value. Therefore, the key space by using the Hénon map (Equation (3)) in this case is about , i.e., a key of 200 bits. These bits can be divided by four to have 50 hexadecimal numbers, and an effective algebraic process must be developed to determine all initial conditions and control parameters of the chaotic map.
In the encryption design, all the key space must produce chaotic behavior (i.e., strong keys) and avoid using weak keys (i.e., some secret key that produces non-chaotic dynamics). In some chaotic maps, the bifurcation diagram presents periodic windows combined with chaotic dynamics. In this sense, designers must avoid such values that generate periodic behavior. One method to determine if all the key spaces are strong is that the bifurcation diagram for each control parameter could be presented or calculating the Lyapunov exponent to validate chaos.
3.2. Point 2: Plain Image Sensitivity
In this subsection, the plain image sensitivity is determined by means of the next process. Two similar plain images and are encrypted by using the same secret key K to determine the difference between the resulting cryptograms and . The plain image sensitivity level is based on two tests: (net pixel change rate) and (unified average changing intensity). The determines how many pixels are different between and (in percentage), whereas the determines the intensity difference average. The and of an eight-bit gray-scale image of pixels are calculated using Equation (4) and Equation (6), respectively.
These quantities have been used to determine the robustness against differential analysis of several chaos-based image cryptography systems, but recent research points out that such quantities are not enough to be used as a security tool for differential attacks. Özkaynak in [58] proposed a comprehensive security road map to complement this problem, which is recommended to be considered for chaos-based image encryption designs.
3.3. Point 3: Graphic Histogram
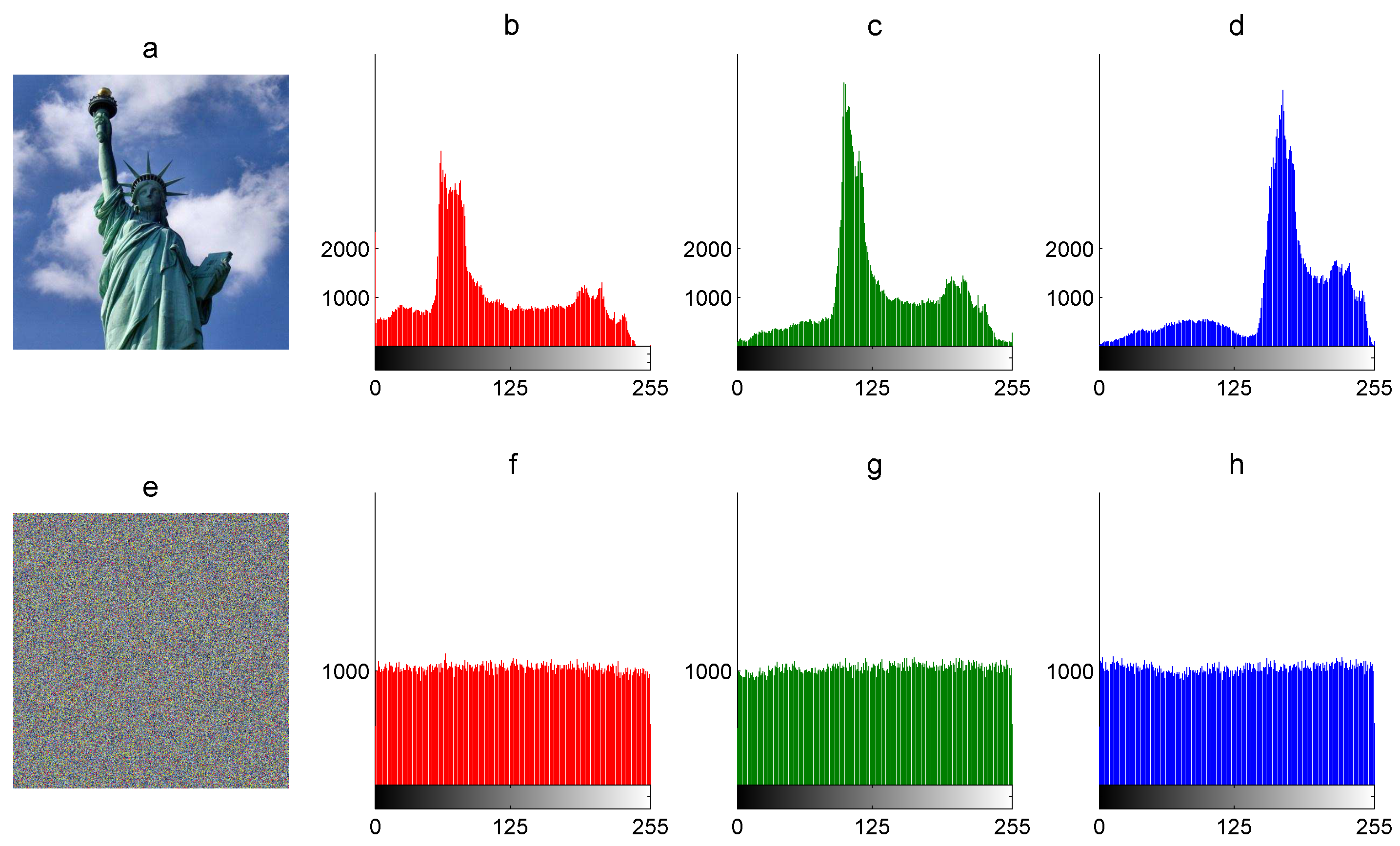
The graphic histogram of an image is the visual inspection of statistical data and the tone of the image. It shows the frequency of pixel intensity values of the image graphically. The horizontal axis of the graphic represents the intensity variations, whereas the vertical axis represents the frequency of some particular intensity. The graphic histogram of the encrypted image must present similar frequencies for each pixel intensity value (uniform distribution) to avoid the leaking of statistical information related to the plain image and resist statistical attacks. For example, Figure 2 shows the graphic histograms for each R, B, and G component of The Statue of Liberty plain image P and the graphic histograms of the corresponding encrypted image E.
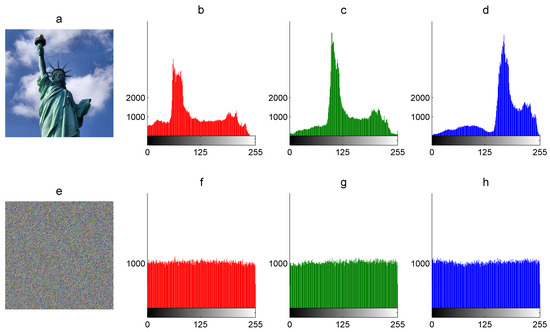
Figure 2.
Graphic histograms: (a) color plain image P, (b) R-component of P, (c) G-component of P, (d) B-component of P, (e) encrypted image E, (f) R-component of E, (g) G-component of E, and (h) B-component of E.
3.4. Point 4: Histogram Statistics
The variance and standard deviation are metrics of dispersion implemented to support the results of visual inspection in graphic histograms. They measure how much the elements of a set of data vary with respect to each other around the mean. Two datasets may have the same average value (mean), but the variations can be drastically different.
The variance calculates the average difference between each of the values with respect to their central point (mean ). This average is calculated by squaring each of the differences and calculating its mean again. The squaring process is used to eliminate the negative signs and to increase the variance of dispersed (non-uniform) datasets. On the other hand, the more uniform is the graphic histogram, the lower is the histogram variance, which is determined with the following expression:
where:
x is the frequency for each intensity value from 0–255 of the histogram, is the histogram variance, and is the mean of the histogram, i.e., it will be 256 for a image size or 1024 for a image size.
The standard deviation allow us to know the arithmetic average of fluctuations of the dataset with respect to the mean. It is determined with the square root of the histogram variance as follows:
where is the standard deviation of the histogram. In Table 2, the histogram variance and its standard deviation are presented for plain and encrypted images. For example, the histogram variance of plain images is much higher than its corresponding encrypted images, which means the non-uniform dataset and uniform dataset, respectively. In addition, the average more-less pixel fluctuation around the mean (1024) in the R component of The Statue of Liberty color plain image is 803 (see Figure 2b–d), whereas the corresponding encrypted component presents just 60 (see Figure 2f–g).

Table 2.
Histogram statistics with the variance and standard deviation of plain and encrypted images.
3.5. Point 5: Histogram Uniformity
An ideal uniform histogram of an encrypted image must have the same pixel frequency for all 256 intensity values. In this case, the histogram variance will be zero with a standard deviation of zero. The histogram uniformity percentage (HUP) is introduced to determine the intensity values falling between the acceptable range, which is defined as follows:
where:
where is the acceptable range, is the mean, and is the standard deviation. For example, the HUP of the gray scale Lena encrypted image and B component of The Statue of Liberty encrypted image are 85.54% and 85.93%, respectively.
3.6. Point 6: Graphic Correlation
The pixel values of any plain image at any position have neighbors (horizontally, vertically, or diagonally) with pixel values that are highly similar, i.e., all plain images are strongly correlated. This natural property implies designing efficient cryptosystems to produce non-correlated encrypted images and reduce the risk of statistical attack.
The graphic correlation is a visual inspection of the pixel’s correlation of the image, where the horizontal axis represents the intensity value of the pixel and the vertical axis represents the neighbor pixel value, either horizontal, vertical, diagonal, or random. The expected graphic correlation of the plain image must present a strong pattern over a line at 45 degrees; the more close to this line, the more correlated is the tested image. In the encrypted image, the expected graphic correlation must present points over all the plane since most of the neighbors of any pixel have different intensity values with respect to that pixel.
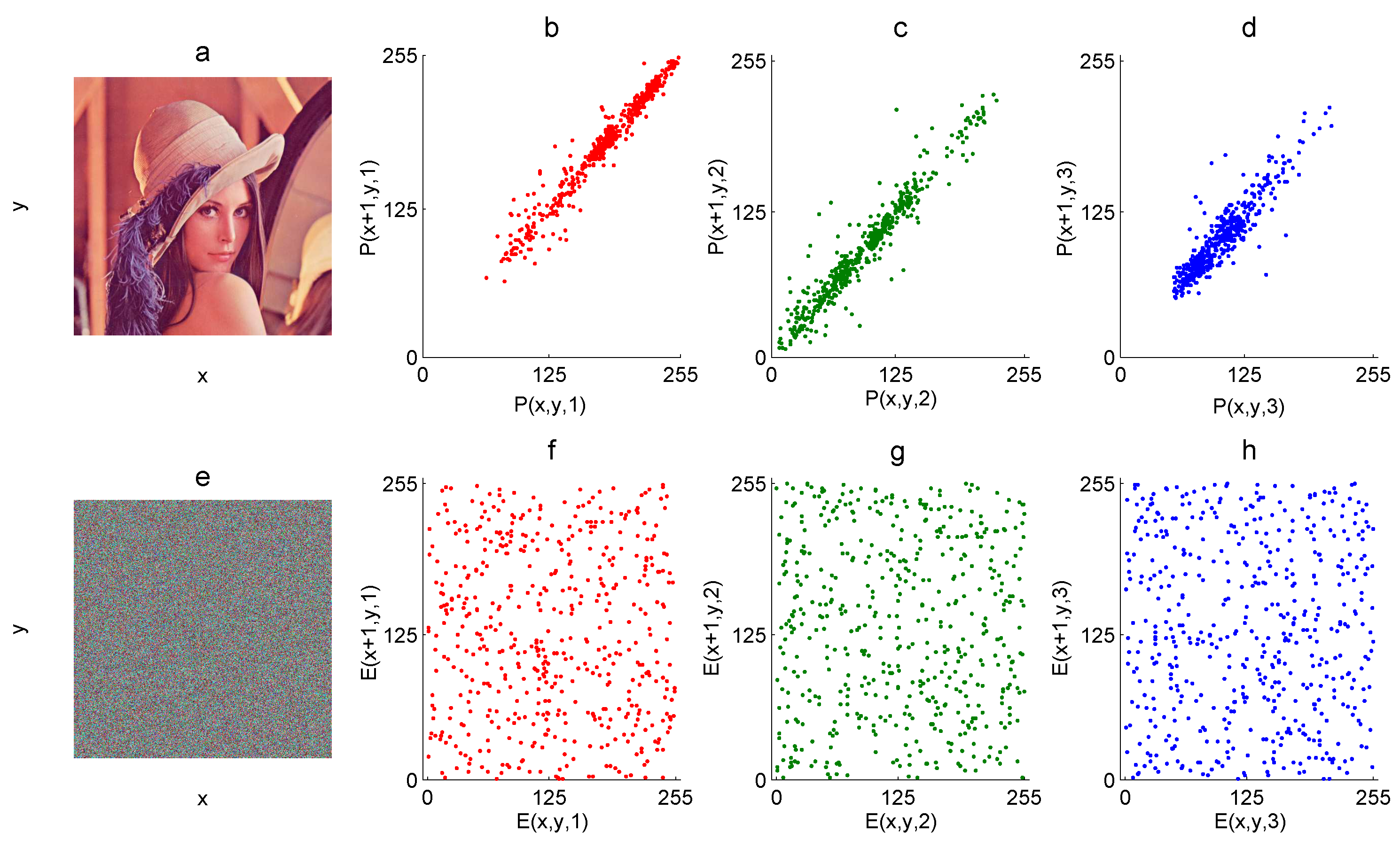
In Figure 3b–d, the graphic correlation (horizontal) of 5000 random pixels of the Lena color plain image is presented for each R, G, and B component, whereas the graphic correlation of the corresponding encrypted components is shown in Figure 3f–h.
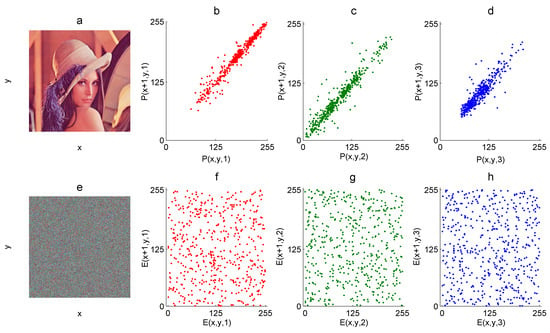
Figure 3.
Graphic horizontal correlation: (a) RGB plain image P, (b) R-component of P, (c) G-component of P, (d) B-component P, (e) RGB encrypted image E, (f) R-component of E, (g) G-component of E, and (h) B-component of E.
3.7. Point 7: Correlation Coefficient
The Pearson correlation coefficient (PCC) is the metric implemented to support the visual inspection of the graphic correlation. In statistics, PCC measures the grade of the linear relationship between two quantitative variables by the numeric index, which varies between [−1,1]. When it is −1, there is a perfect inverse relationship, whereas when it is one, there is a perfect direct relationship. Just when PCC is zero, neither tested variables has a linear relationship (null correlation).
Therefore, plain images do not need to present PCC close to one since they are highly correlated. On the other hand, encrypted images must present PCC close to zero to resist statistical attacks. The PCC of an image can be measured as follows:
where x and y are two variables defined by some pixel values and their neighbor pixel values, N is the number of pixel pairs, and is the PCC. For example, 5000 random pixels of the Lena color plain image P (Figure 3a) are defined as x, and its corresponding horizontal neighbor pixels are defined as y. In this case, for the R-component of P, for the G-component of P, and for the B-component of P. On the other hand, the PCC for the corresponding encrypted image E is for the R-component of E, for the G-component of E, and for the B-component of E.
3.8. Point 8: Key Sensitivity
The encryption algorithm must be highly sensitive against the lowest change of the secret key to make all the key space efficient. The encryption and decryption process must show this important characteristic. In the encryption process, the same plain image P is encrypted two times with two similar secret keys ( and ), and the corresponding cryptograms ( and ) must be very different between them and visually unrecognizable.
This test must be performed over the smallest change at the initial condition, or the control parameter of chaotic map, or at any variable that determines the chaotic keystream used in the encryption process. For example, if the Hénon map (Equation (3)) is adopted with the IEEE 754 standard for double floating-point arithmetic, the secret key is defined with two states and two control parameters, but just one of them is lightly modified, e.g., (part of ) and (part of ).
Figure 4 shows the corresponding cryptograms ( and ) with their graphic histograms and graphic correlations. The statistics of and are as follows, respectively: 127 and 128 for image mean , 443.50 and 414.92 for histogram variance , 21 and 20 for histogram standard deviation , and 0.06642 and 0.01271 for the correlation coefficient . The NPCR and UACI tests were used to determine the difference between both and cryptograms. In this case, the NPCR was 99.6093% and the UACI was 33.0435%. This visual and numerical results verified the sensitivity of secret keys in the encryption process. In addition, the statistical results were similar in both cryptograms.
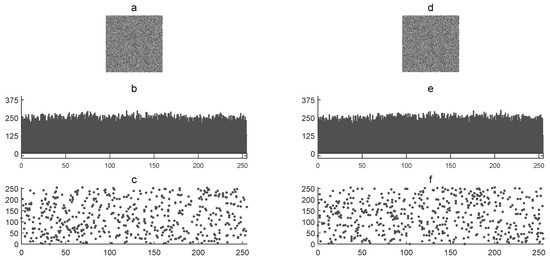
Figure 4.
Key sensitivity analysis: (a) cryptogram , (b) graphic histogram of , (c) graphic horizontal correlation of , (d) cryptogram , (e) graphic histogram of , and (f) graphic horizontal correlation of .
In the decryption process, just the correct secret key must retrieve the plain image, whereas decryption with highly similar secret keys to the correct one must produce a similar result as encryption cryptograms both visually and statistically.
3.9. Point 9: Graphic Autocorrelation
The graphic autocorrelation of the 2D image compares all possible pixel pairs and expresses the probability that both pixels will have similar values as a function of the distance and direction of separation. Mathematically, the autocorrelation of an image i is the convolution of a function with itself, which can be calculated by:
where is the autocorrelation function, is the image intensity at position , “∗” represents the convolution, and a and b represent the distance from the corresponding x and y position. Equation (13) is almost never used due the required high computational complexity. Autocorrelation can be calculated efficiently via fast Fourier transform by using the Wiener–Khinchin theorem described as follows:
where is the power spectrum of the image i and F is the Fourier transform. This theorem states that the Fourier transform of the autocorrelation of image i is equal to the inverse Fourier transform of . can be calculated by squaring the magnitude of the Fourier transform of image i, which is equivalent to multiplying the Fourier transform by its conjugate. Therefore, the autocorrelation of image i is determined by:
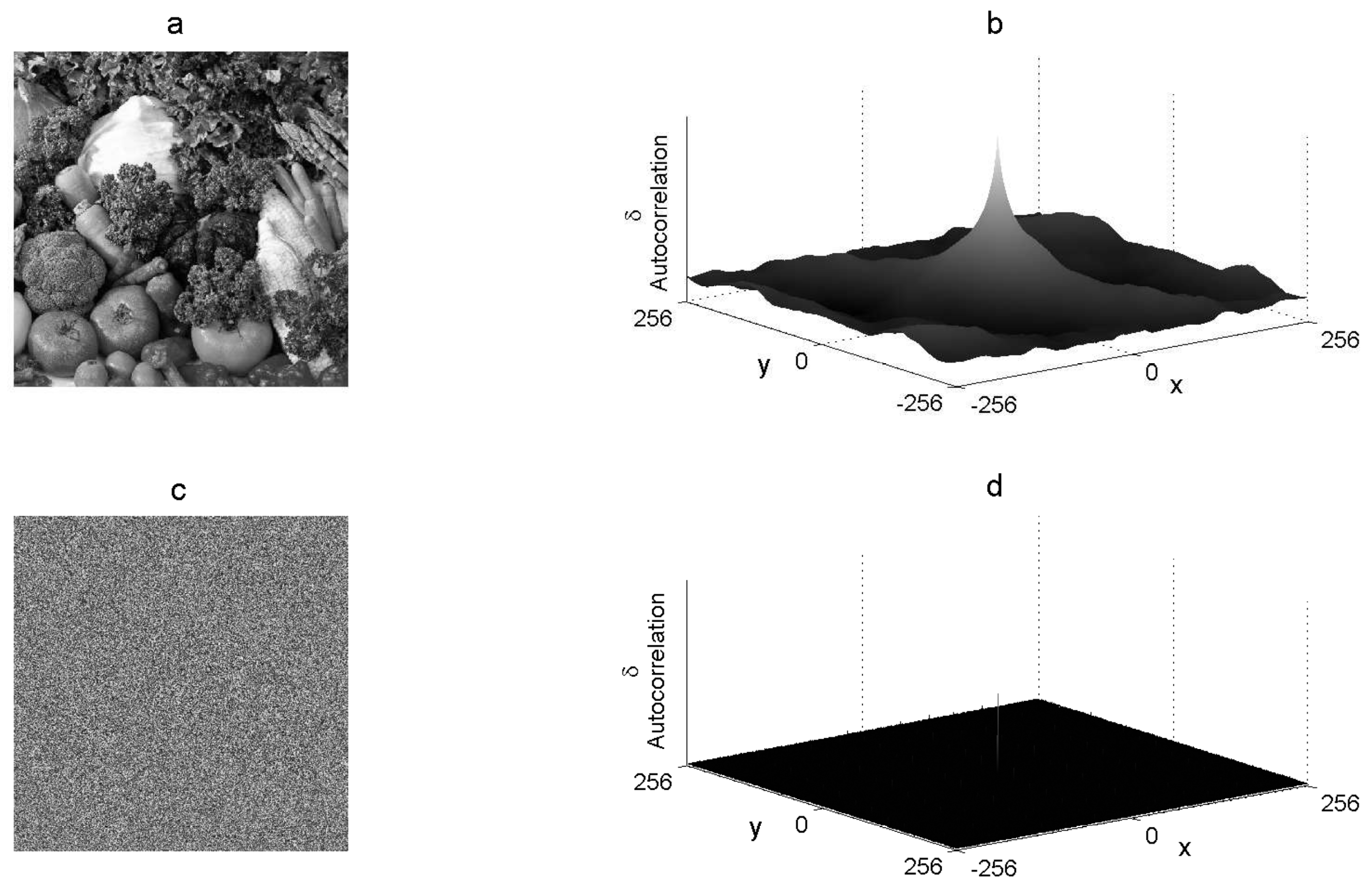
where is the inverse Fourier transform and is the conjugated Fourier transform. The graphic autocorrelation of the plain image must present waves and a cone in the center of the graphic space, whereas an encrypted image must present a flat and uniform graphic autocorrelation. Figure 5 shows the graphic autocorrelation of both the Vegetables gray-scale plain image and its corresponding encrypted image.
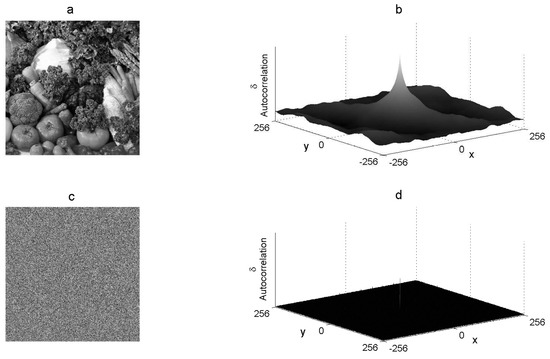
Figure 5.
Autocorrelation graphics: (a) plain image P, (b) autocorrelation of P, (c) cryptogram E, and (d) autocorrelation of E .
3.10. Point 10: Information Entropy
Information entropy is a mathematical property that determines the randomness, unpredictability, or complexity of a message. If encryption process does not produce enough disorder at the output, the cryptosystem can be the subject of entropy attack. An encrypted image E with possible combinations will have maximum entropy of ideally. Therefore, the maximum information entropy of any gray-scale image or any RGB component image is eight. The entropy of a message m can be calculated as follows:
where N is the number of bits of message m, are all possible values, represents the probability of , represents the base two logarithm, and the entropy is expressed in bits. In Table 3, the entropy results of both The Statue of Liberty RGB plain image and its corresponding encrypted image are presented. Therefore, the entropy value close to eight in encrypted image means a highly unpredictable message; hence, the encryption algorithm can resist entropy attack.

Table 3.
Information entropy of the plain and encrypted image.
3.11. Point 11: Encryption Quality
In this section, measuring techniques are used to verify the image encryption quantitatively such as mean-squared error (MSE), peak signal-to-noise ratio (PSNR), and structural similarity index (SSIM). The MSE is a parameter to measure the difference between two images, which is described as follows:
where is the size of the image, P is the plain image, and E is the encrypted image. The higher value of MSE represents better encryption quality. This MSE analysis is a useful test for a color RGB plain image and encrypted RGB color image with pixel values in the range of [0–255]. The PSNR (expressed in logarithmic scale and decibels) determines the ratio between the maximum possible power of a signal and the power of distorting noise that affects the quality of its representation. It is calculated by next equation:
The MSE of efficient cryptograms is high. Therefore, the PSNR of encrypted images with high quality is expected to be low, less than 10 dB.
On the other hand, the SSIM determines the similarity between two images with a more consistent technique than MSE, i.e., a burred image is perceived as a bad quality image, which is consistent with SSIM, but not with MSE. SSIM considers the mean, standard deviation, and cross-correlation in both plain image P and encrypted image E. It is calculated with the following expression:
where:
and:
and:
where is the mean of the plain image, is the mean of the encrypted image, is the standard deviation of the plain image, is the standard deviation of encrypted image, is the cross-correlation of the plain and encrypted image, and . and are used for stability, where L is the dynamic range of the pixel values (for gray-scale images, L = 255) with and . The SSIM is one for identical images, whereas it is close to zero for images structurally different between them.
Table 4 presents the results of the encryption quality of three color cryptograms from different plain images. The cryptogram with large values of MSE, PSNR lower than 10 dB, and SSIM close to zero means an efficient pseudorandom cryptogram and structurally different compared with the corresponding plain image.

Table 4.
Quality metrics’ analysis.
3.12. Point 12: Decryption Error
In image chaos-based cryptosystems, the recovered image is supposed to be identical to the plain image, which is required in sensitive applications such as telemedicine, biometrics, military, and others. In some recent schemes in the literature, designers implement techniques to enhance the security such as random pixel insertion in the plain image or save some specific data in the encrypted image before sending it over the insecure channel. Therefore, the recovered image is not the same as the original plain image, and this error must be determined quantitatively. The decryption error is defined as follows:
and:
where P is the original plain image, D is the recovered or decrypted image, and is the error in percentage. An ideal chaos-based image cryptosystem must present an error of zero, i.e., the recovered image must be identical to the original plain image.
3.13. Point 13: Floating Frequency
The floating frequency analysis determines the uniformity of the encryption process for all the rows and columns of the image and the capacity of encryption to produce uniform random data for all sections of the plain image. This powerful analysis can show weak encryption sections in a cryptogram. The analysis is performed over windows of 256 elements based on the rows and columns of an image. The analysis consists of determining how many elements are different in each window. We introduce a rows’ and columns’ floating frequency of a gray-scale image, which is determined as follows:
- Select windows of 256 elements for each row and each column of the image.
- Determine how many different elements are in each window.
- Define the row floating frequency (RFF) and column floating frequency (CFF) with the corresponding frequencies of each window.
- Determine the mean and plot for both RFF and CFF.
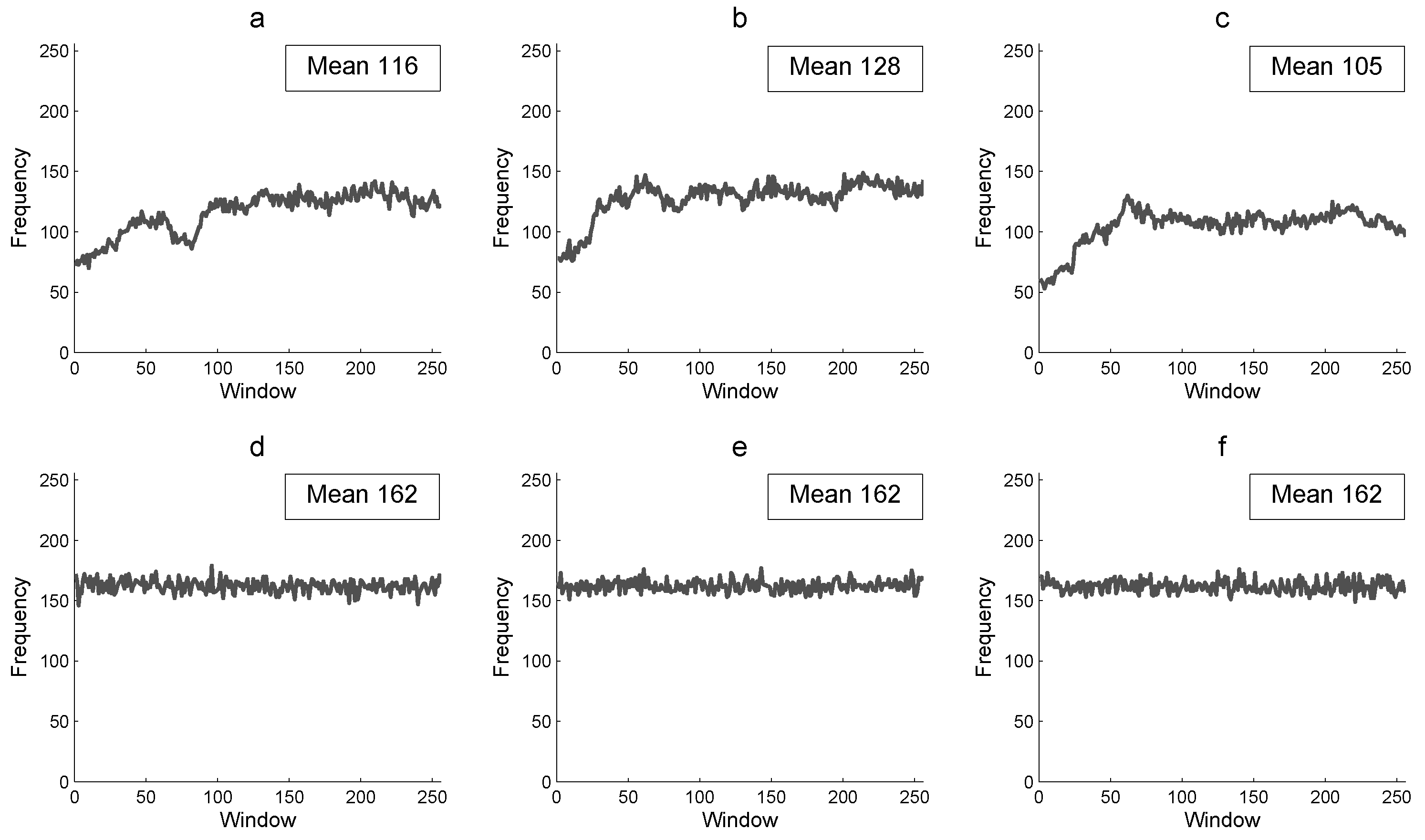
Figure 6 presents the CFF of the Lena color plain image P and of its corresponding encrypted image E. Figure 6a–c shows the floating frequency for each column from 1–256 of the Lena plain image, which is expected to be low and without uniformity (i.e., there are many repetitive pixels). Nevertheless, in Figure 6d–f, the floating frequency of the corresponding encrypted image shows that there are more pixels with different intensity in each column, which is desirable in the encrypted image with a mean of 162 different pixels of 256, (i.e., there are 63% different pixels for each column of 256 pixels). A greater percentage of CFF in the encrypted image is more efficient for the image encryption algorithm to produce a random cryptogram at column scale.
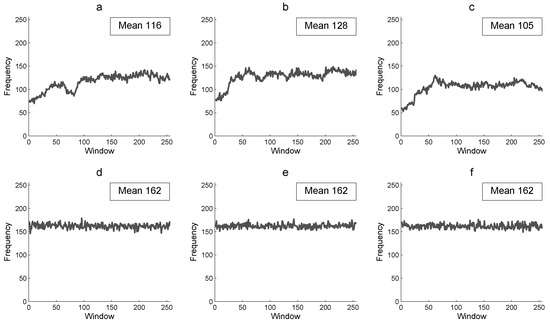
Figure 6.
Column floating frequency and its mean: (a) R-component of P, (b) G-component of P, (c) B-component P, (d) R-component of E, (e) G-component of E, and (f) B-component of E.
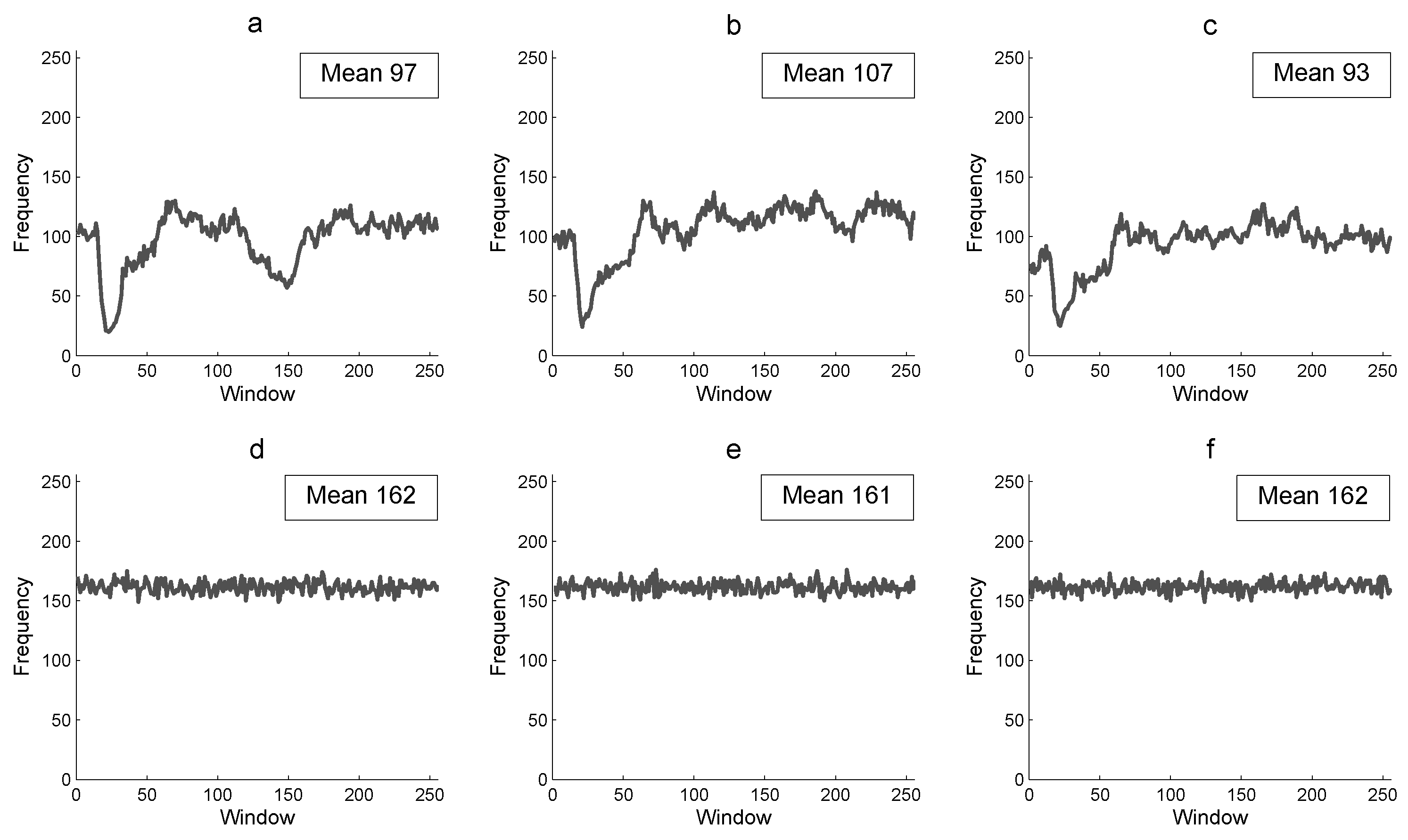
Figure 7 presents the RFF of the Lena color plain image P and of its corresponding encrypted image E. The results in RFF for the plain image are low with a mean of 97, 107, and 93 for the red, green, and blue component, respectively (Figure 7a–c). Furthermore, it shows non uniform data as expected. Figure 7c–f shows the RFF for the corresponding encrypted image, with a mean of 162, 161, and 162 different pixel values for each row of 256 pixels (similar results as CFF). A greater percentage of RFF in the encrypted image is more efficient for the image encryption algorithm to produce a random cryptogram at row scale.
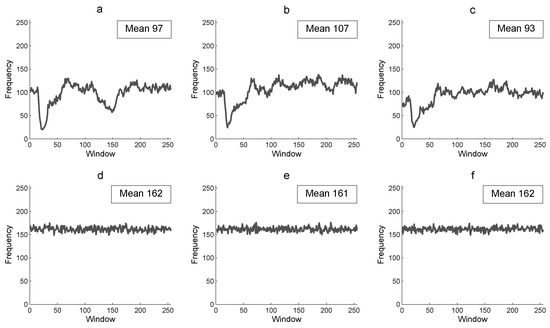
Figure 7.
Row floating frequency and its mean: (a) R-component of P, (b) G-component of P, (c) B-component P, (d) R-component of E, (e) G-component of E, and (f) B-component of E.
The floating frequency is very useful to determine the capacity of the encryption algorithm to produce uniform random data for all the plain image data, i.e., the higher the floating frequency and uniformity, the higher the security and capacity of the encryption method. If floating frequency presents lower peaks in some sections, it means weak encryption in some part of the cryptogram, i.e., low capacity of the encryption process. Finally, the floating frequency test can be applied to images of pixels by dividing it in four subsections of pixels.
3.14. Point 14: Noise Robustness
The encrypted image can be alterable either by noise attack or noise jamming in the transmission channel, which can make it difficult to recover the plain image. Thus, the robustness against noise must be evaluated over chaos-based image cryptosystems. The encryption process of recent algorithms gives some advantages against noise since most of them are based on the substitution-permutation network, uniform chaos, and one-per-one pixel encryption. Considering such principles and the bulk data of images, the original plain image can still be reconstructed with high visual quality.
In noise analysis, the cryptogram is spread with salt and pepper noise with different densities by using the “imnoise” function of MATLAB. The percentage of affected pixels can be determined as follows:
where is the selected density of salt and pepper noise.
The decryption process is performed by using the correct secret key and cryptograms affected by noise. Figure 8 shows the cryptograms of the Baboon color plain image with 1%, 5%, 20%, and 50% of noise and the corresponding recovered image. The original plain image can still be recovered visually with details. The decryption error between the plain image and the recovered images is 0.95%, 4.98%, 19.92%, and 49.88% on average for the three components. Therefore, the encryption algorithm is robust against noise.
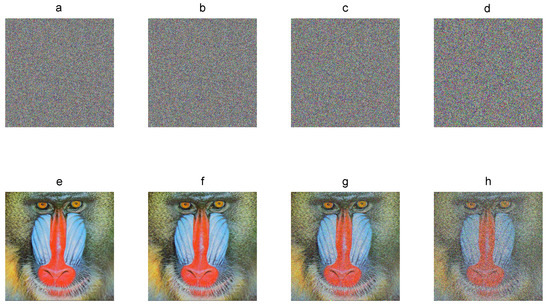
Figure 8.
Noise robustness: (a–d) Baboon cryptograms with 1%, 5%, 20%, and 50% of noise added; (e–f) corresponding recovered images.
3.15. Point 15: Occlusion Robustness
The encrypted image can lose information by an occlusion attack or by transmitting over network and storage, which can make it difficult to recover the plain image. In this sense, occlusion robustness must evaluate the capacity of recovering the original image against lost data. In occlusion analysis, the encrypted image is alterable with several pixels defined as zero. For example, Figure 9 shows the recovered Vegetables color plain images from the corresponding cryptograms with 10%, 25%, and 50% of occlusion. The original plain image can still be recovered visually with enough details. The decryption error between the plain image and recovered images is 10.3%, 25.53%, and 50.01% on average for each component. Therefore, the encryption algorithm is robust against occlusion.

Figure 9.
Occlusion robustness: (a–d) Vegetables cryptograms with 10%, 25%, and 50% of lost pixels; (e–f) corresponding recovered images.
4. Cost and Performance
The cost and performance of image chaos-based cryptosystems must be provided in detail, since they are the next important point to evaluate after security. Cryptographic designers and cryptanalysts could decrease the performance of some highly secure cryptosystems if it is at a high cost. Therefore, the cryptosystem must provide enough security with a reasonable cost and performance. Memory requirements, computational efficiency, and speed analysis are some constraints that must be evaluated.
Most of the chaos-based image cryptography proposed in the literature is based on the symmetric-key, since it is faster than asymmetric-key cryptography. In addition, most of them are based on MATLAB (software) implementations with C code due the fast prototype design and practical environment for testing. Others are implemented with Java code for professional applications to achieve better speed in encryption. On the other hand, the cost and performance of chaos-based image cryptosystems based on hardware implementations such as in field programmable gate array (FPGAs) and application-specific integrated circuits (ASICs) are currently an interesting research area due to the wide applications, where large volumes of secure data need to be processed (such as in biometrics, telemedicine, military, pay TV, SSL accelerators, etc.), and due to the benefits in space and cost with high performance security in an embedded system. Therefore, other requirements must be determined such as power consumption or occupied logical elements (slices, LUTs, DSP blocks, etc.) for hardware applications.
4.1. Point 16: Memory Requirements
Chaos-based image cryptosystems require considerable memory space in both the hard drive or FLASH memory and RAM memory due to the bulk data of images and real variables for chaos implementation. When countermeasures are added to increase security and chaos uniformity, the memory requirements are more demanding.
In digital encryption/decryption algorithms, RAM is required for the secret key, plain image, encrypted image, chaotic vectors, and any other temporal variable. The encryption algorithm code size requires some mega-bytes (MB) in the hard drive on a personal computer or in FLASH memory for an embedded system. For example, the color image encryption algorithm proposed in [25] was implemented in MATLAB with 16.38 MB in the hard drive memory according to the computer’s properties. If the color plain image of a size is encrypted, the required RAM memory is 1.68 MB approximately, according to the function “whos” of MATLAB (see Table 5).

Table 5.
RAM memory requirements.
4.2. Point 17: Algorithm Efficiency
The encryption algorithm is a step-by-step procedure written by some language, and its efficiency is highly important in terms of complexity and execution speed. The complexity is asymptotically estimated with big-O notation as a function that depends on the input size n, e.g., . The complexity of a series of sentences of an algorithm is of the order of the sum of the individual complexities, and some practical rules are considered, e.g.,: input-output simple sentences and If sentences are of order , the for cycle is order for k iterations independent of the input n or for n iterations; the for double nested cycle is of order for n iterations for each cycle; the iterative cycles with divisive-multiplicative sentences are of order for n iterations; and in the for cycle with n iterations is of order .
The computational cost of most chaos-based image encryption algorithms depends on the substitution-permutation network process, where both of them can be approximated with order , where M and N are the size of the input image in pixels. This is for the two for cycles double nested with M and N iterations, respectively. For example, the encryption algorithm proposed in [25] can be approximated to a computational complexity of due to the encryption process in Equation (12).
4.3. Point 18: Speed Analysis
The speed analysis can be presented in both encryption and decryption process in seconds, encryption throughput () in bytes per seconds, and number of needed cycles to encrypt one byte (). Basic details of implementation must be provided such as the operating system, CPU with the main frequency, RAM memory size, compiler, and programming language, since speed is dependent on these characteristics.
In Table 6, the speed analysis of the encryption algorithm proposed in [25] is presented for several plain RGB color image sizes. The algorithm was implemented in MATLAB software, where a laptop with Intel(R) Core(TM) i3-5005U CPU 2 GHz, 8 GB RAM, and Windows 10 64-bit operation system were used. The speed in seconds was determined with the tic and toc MATLAB functions; the bytes per second or encryption throughput () were calculated by dividing the image size (in bytes) between time encryption (in seconds); and the number of needed cycles to encrypt one byte () was obtained by dividing the main clock frequency (in Hertz) between (in bytes per second). The results showed the best performance for plain images close to pixels, since the throughput was about 10.58 MB/s and there was less in encryption. In addition, the time encryption was compared with the conventional symmetric-key AES-128 in ECB (Electronic Code Book) mode, but without considering the vector construction process (plain text/encrypted text byte-vector with a length multiple of 16) of all plain pixels before AES encryption and the recovered image construction process after AES decryption. The AES-128 ECB mode encryption/decryption high-level MATLAB functions were download from the MathWorks file exchange database (mathworks.com).

Table 6.
Speed analysis for RGB image encryption and the AES-128 ECB algorithm.
5. Algorithm and Implementation
Chaos-based image cryptosystems must meet another important aspect related to reliability, integrity, flexibility, simplicity, and ease of implementation since there are several types and formats of images and several kinds of digital platforms. The most-used bitmap image formats are BMP, GIF, JPG, TIF, and PNG. However, it is convenient to use a format that does not imply loss of information (e.g., JPG) for the encrypted image since the decryption process could not be successfully. High processing platforms such as FPGA or ASIC can be used for cryptosystem implementation at the hardware level for low-cost embedded system applications of high-definition image encryption (HD), audio encryption, and video encryption. On the other hand, high-performance microcontrollers are interesting for the software level to medium quality image encryption applications at low cost. Finally, the PC is the platform most widely implemented for image encryption algorithms based on MATLAB programming.
5.1. Point 19: Flexibility
Flexibility is related to the capacity of the algorithm to endure minor modifications according to the requirements. Encryption algorithms with greater flexibility are preferable since they will meet the needs of more users (assuming good overall security and performance). For example, the 3DES structure does not support any modifications (i.e., its flexibility is null), and RC6 has a variable key length until 2048 bits with a multiple of 32 bits (secret key flexibility). Examples of flexibility may include (but are not limited to) the following:
- The algorithm can be parallelized to achieve higher performance.
- The algorithm can be implemented securely and efficiently on a wide variety of platforms.
- The cryptosystem can be used with different secret key lengths.
- The cryptosystem can be used with different plain image formats.
- The algorithm can support any image size.
- The algorithm can support gray-scale images or RGB color images.
- The algorithm can be incorporated into existing protocols and applications, requiring as few changes as possible.
5.2. Point 20: Simplicity
The simplicity is related to the relative algorithm design simplicity to analyze and implement efficiently such as using less arithmetic operations, using simple substitution-permutation processes, including GUI (graphical user interface) with intuitive symbols and easy operation, or including GUIDE (Graphical User Interface Development Environment) by using MATLAB, among others. It is one of the most important factors in selecting cryptographic algorithms, e.g., the Rijndael algorithm was less secure than its rivals in the AES competition, but it was selected as the AES winner due to its simplicity [45]. In this sense, chaos-based image encryption algorithms must provide detail about their flexibility and simplicity.
6. Conclusions
Chaos-based image cryptography is currently a world-wide research topic with hundreds of papers that have been published in the last few years. The lack of security frameworks for chaos-based image cryptosystems make each author present different tests about security over the proposed algorithms. Even some algorithms have been broken in the last few years. In this sense, security guidelines are required to make chaos-based image cryptography more consistent and promising.
The suggested guideline in this paper does not intend to limit the liberty of cryptographic designers to implement new analysis, and it does not guarantee security. However, if cryptographic designers consider this framework based on 20 points, an integral analysis about the comprehensive security analysis, cost and performance, and algorithm and implementation of new chaos-based image cryptosystems can be presented more consistently in terms of security and efficiency. Consequently, future chaos-based image encryption algorithms can be compared rigorously in terms of security and efficiency capabilities. Cryptographic designers could present just the results about security in their works (e.g., in a Table) pointing out to each of the 20 points suggested in this paper without describing all details about each test.
The guideline can be adapted for other kinds of plain text in chaos-based cryptosystems, e.g., alphanumeric text, biometrics, biosignals in telemedicine, or pseudo-random number generators. Future detailed frameworks related to chaos-based image cryptanalysis could be presented to design algorithms robust against powerful attacks (for example, chosen-known plain image attack).
Author Contributions
Conceptualization, M.A.M.-E. and M.O.M.-C.; methodology, M.A.M.-E. and C.C.-H.; software, M.A.M.-E. and M.O.M.-C.; validation, M.A.M.-E., M.O.M.-C., R.M.L.-G., and C.C.-H.; formal analysis, M.A.M.-E. and R.M.L.-G.; investigation, M.A.M.-E.; writing, original draft preparation, M.A.M.-E. and M.O.M.-C.; writing, review and editing, R.M.L.-G. and C.C.-H.; supervision, C.C.-H.; funding acquisition, C.C.-H.
Funding
This work was supported by the CONACYT, Mexico, under Research Grant 166654 (A1-S-31628).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van Tilborg, H.C.A.; Jajodia, S. Encyclopedia of Cryptography and Security, 2nd ed.; Springer US: New York, NY, USA, 2011; p. 1416. [Google Scholar]
- Rivest, R.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 10, 120–126. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography, 1st ed.; Springer: New York, NY, USA, 2004; p. 312. [Google Scholar]
- Menezes, A.J.; van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography, 1st ed.; CRC Press: Boca Raton, FL, USA, 1997; p. 810. [Google Scholar]
- Barker, E. Recommendation for Key Management Part 1: General. In NIST Special Publication 800-57; NIST Special Publication: Maryland, MD, USA, 2016; Volume 800, pp. 1–160. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Lett. A 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Oppenheim, A.V.; Wornell, G.W.; Isabelle, S.H.; Cuomo, K.M. Signal processing in the context of chaotic signals. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992, 4th ed.; IEEE: New York, NY, USA; pp. 117–120.
- Cuomo, K.M.; Oppenheim, A.V.; Isabelle, S.H. Spread Spectrum Modulation and Signal Masking Using Synchronized Chaotic Systems; Technical Report for MIT Research Laboratory of Electronics: Cambridge, MA, USA, February 1992; p. 44. [Google Scholar]
- Cruz-Hernández, C.; Romero-Haros, N.R. Communicating via synchronized time-delay Chua’s circuits. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 645–659. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; López-Gutiérrez, R.M.; Aguilar-Bustos, A.Y.; Posadas-Castillo, C. Communicating encrypted information based on synchronized hyperchaotic maps. Int. J. Nonlin. Sci. Num. 2010, 11, 337–349. [Google Scholar] [CrossRef]
- Cardoza-Avendaño, L.; López-Gutiérrez, R.M.; Cruz-Hernández, C.; Spirine, V.; Chávez-Pérez, R.A.; Arellano-Delgado, A. Encrypted audio transmission via synchronized chaotic Nd:YAG lasers. Revista Mexicana de Física 2012, 58, 472–480. [Google Scholar]
- Arellano-Delgado, A.; López-Gutiérrez, R.M.; Cruz-Hernández, C.; Posadas-Castillo, C.; Cardoza-Avendaño, L.; Serrano-Guerrero, H. Experimental network synchronization via plastic optical fiber. Opt. Fiber Technol. 2012, 19, 93–108. [Google Scholar] [CrossRef]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurcat. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn. 2010, 62, 615–621. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Chen, H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt. Laser Eng. 2017, 90, 238–246. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Li, L.; Zhu, X. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dyn. 2018, 94, 1–15. [Google Scholar]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Wua, X.; Kana, H.; Kurths, J. A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl. Soft Compt. 2015, 37, 24–39. [Google Scholar] [CrossRef]
- Abundiz-Pérez, F.; Cruz-Hernández, C.; Murillo-Escobar, M.A.; López-Gutiérrez, R.M.; Arellano-Delgado, A. A fingerprint image encryption scheme based on hyperchaotic Rössler Map. Math. Prob. Eng. 2016, 2016, 1–15. [Google Scholar] [CrossRef]
- Chen, H.; Tanougast, C.; Liu, Z.; Hao, B. Securing color image by using hyperchaotic system in gyrator transform domains. Opt. Quant. Electron. 2016, 48, 1–13. [Google Scholar] [CrossRef]
- Peng, F.; Zhu, X.W.; Long, M. An ROI privacy protection scheme for H.264 video based on FMO and chaos. IEEE T. Inf. Foren. Sec. 2013, 8, 1688–1699. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M. Implementation of an improved chaotic encryption algorithm for real-time embedded systems by using a 32-bit microcontroller. Microprocess. Microsyst. 2016, 45, 297–309. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M. A robust embedded biometric authentication system based on fingerprint and chaotic encryption. Expert Syst. Appl. 2015, 42, 8198–8211. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cardoza-Avendaño, L.; López-Gutiérrez, R.M.; Cruz-Hernández, C. A double chaotic layer encryption algorithm for clinical signals in telemedicine. J. Med. Syst. 2017, 41, 1–17. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M.; Acosta Del Campo, O.R. A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015, 109, 119–131. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Belghith, S. A novel image encryption scheme based on substitution-permutation network and chaos. 3D Research 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Diaconu, A.V. Circular inter–intra pixels bit-level permutation and chaos-based image encryption. Inform. Sci. 2016, 355, 314–327. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system. Inform. Sci. 2016, 349, 137–153. [Google Scholar] [CrossRef]
- Assad, S.E.; Farajallah, M. A new chaos-based image encryption system. Signal Process-Image 2016, 41, 144–157. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü.; Kaçar, S.; Pehlivan, I.; Zengin, A. Secure image encryption algorithm design using a novel chaos based S-Box. Chaos Solit. Fract. 2017, 95, 92–101. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. An image encryption algorithm based on compound homogeneous hyper-chaotic system. Nonlinear Dyn. 2017, 89, 61–79. [Google Scholar] [CrossRef]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Laser Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Laser Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Sun, X. Chaos-based fast colour image encryption scheme with true random number keys from environmental noise. IET Image. Process. 2017, 11, 324–332. [Google Scholar] [CrossRef]
- Yuan, H.M.; Liu, Y.; Lin, T.; Hu, T.; Gong, L.H. A new parallel image cryptosystem based on 5D hyper-chaotic system. Signal Process-Image 2017, 52, 87–96. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, G.Y.; Zhu, M.; Chen, Z.; Lei, W.M. A new chaos-based color image encryption scheme with an efficient substitution keystream generation strategy. Secur. Commun. Netw. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. 2018, 149, 148–161. [Google Scholar] [CrossRef]
- Li, S.; Ding, W.; Yin, B.; Zhang, T.; Ma, Y. A Novel Delay Linear Coupling Logistics Map Model for Color Image Encryption. Entropy 2018, 20, 463. [Google Scholar] [CrossRef]
- Diab, H. An efficient chaotic image cryptosystem based on simultaneous permutation and diffusion operations. IEEE Access 2018, 6, 42227–42244. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Huang, X.; Mei, Q. An efficient pixel-level chaotic image encryption algorithm. Nonlinear Dyn. 2018, 94, 1–12. [Google Scholar] [CrossRef]
- Cai, S.; Huang, L.; Chen, X.; Xiong, X. A symmetric plaintext-related color image encryption system based on bit permutation. Entropy 2019, 20, 282. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, Z.; Yu, H. A symmetric image encryption algorithm based on a coupled logistic–bernoulli map and cellular automata diffusion strategy. Entropy 2019, 21, 504. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Zuo, Z. Chaos-based image encryption algorithm with orbit perturbation and dynamic state variable selection mechanisms. Opt. Laser Eng. 2019, 115, 197–207. [Google Scholar] [CrossRef]
- Chang, S.; Perlner, R.; Burr, W.E.; Turan, M.S.; Kelsey, J.M.; Paul, S.; Bassham, L.E. Third-round report of the SHA-3 cryptographic Hash algorithm competition. NISTIR 7886 2012, 1–84. Available online: https://nvlpubs.nist.gov/nistpubs/ir/2012/NIST.IR.7896.pdf (accessed on 11 August 2019).
- Nechvatal, J.; Barker, E.; Bassham, L.; Burr, W.; Dworkin, M.; Foti, J.; Roback, E. Report on the Development of the Advanced Encryption Standard (AES). J. Res. Natl. Inst. Stand. Technol. 2001, 106, 511. [Google Scholar] [CrossRef]
- Álvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Özkaynak, F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn. 2018, 92, 305–313. [Google Scholar] [CrossRef]
- Preishuber, M.; Hütter, T.; Katzenbeisser, S.; Uhl, A. Depreciating motivation and empirical security analysis of chaos-based image and video encryption. IEEE T. Inf. Foren. Sec. 2018, 13, 2137–2150. [Google Scholar] [CrossRef]
- Li, S. Analyses and New Designs of Digital Chaotic Ciphers. Ph.D. Thesis, School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an, China, April 2003. Available online: https://core.ac.uk/download/pdf/30340300.pdf (accessed on 11 August 2019).
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. The 0-1 Test for Chaos: A Review. In Chaos Detection and Predictability; Skokos, C., Gottwald, G.A., Laskar, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 221–247. [Google Scholar]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Info. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Chen, L.; Ma, B.; Zhao, X.; Wang, S. Differential cryptanalysis of a novel image encryption algorithm based on chaos and Line map. Nonlinear Dyn. 2016, 87, 1797–1807. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, D.; Chen, X.; Huang, H. Cryptanalysis and enhancements of image encryption using combination of the 1D chaotic map. Signal Process. 2018, 144, 444–452. [Google Scholar] [CrossRef]
- Zhu, C.; Sun, K. Cryptanalyzing and improving a novel color image encryption algorithm using RT-enhanced chaotic Tent maps. IEEE Access 2018, 6, 18759–18770. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C.; Wang, W. A New Image Encryption Algorithm Based on Chaos and Secure Hash SHA-256. Entropy 2018, 20, 716. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. J. Sel. Areas Telecommun. 2012, 1, 31–38. [Google Scholar]
- Özkaynak, F. Role of NPCR and UACI tests in security problems of chaos based image encryption algorithms and possible solution proposals. In IEEE International Conference on Computer Science and Engineering (UBMK), Antalya, Turkey, 5-8 October 2017; IEEE: New York, NY, USA; pp. 1–4.
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).