Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States
Abstract
Entropy is the most important quantity in the physics of heat.Charles Kittel [1]
John von Neumann mentioned that ‘nobody knows what entropy really is’.Jürn W. P. Schmelzer, Timur V. Tropin [2]
1. Introduction
2. Clausius Entropy
3. Boltzmann Entropy
4. Pauling Entropy
5. Shannon Entropy
- (i)
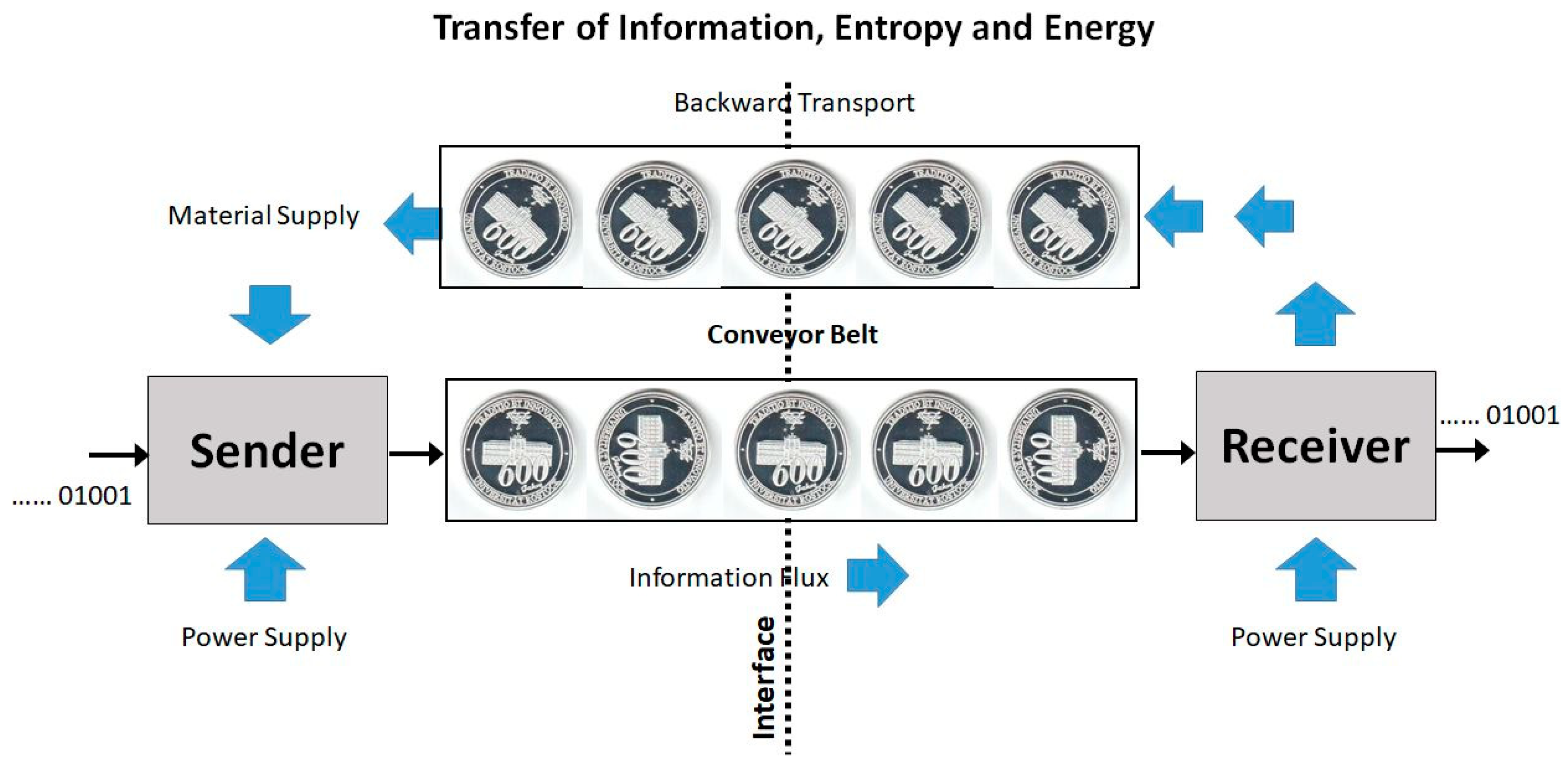
- Across the interface, there is no net energy flux sustained by the conveyor belt. Each coin is carried back and forth with the same internal energy and the same potential energy in the gravity field.
- (ii)
- Across the interface, there is no net Clausius entropy flux sustained by the conveyor belt. Each coin is carried back and forth with the same Clausius entropy, which is additive to form the Clausius entropy of the message.
- (iii)
- Across the interface, there is no net single-coin Boltzmann entropy flux sustained by the conveyor belt. Each coin separately is carried back and forth with the same Boltzmann entropy, despite its actual orientation. The super-additive Boltzmann entropy of the sequence of coins applies to both transport directions independently of the actually transferred message.
- (iv)
- Across the interface, there is no net single-coin Pauling entropy flux sustained by the conveyor belt. Each coin separately is carried back and forth with the same Pauling entropy, despite its actual orientation. Also the Pauling entropy of the set of coins does not depend on their actual individual turning angles.
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A: On the History of the 3rd Law of Thermodynamics
Beim Nullpunkt der absoluten Temperatur besitzt die Entropie eines jeden chemisch homogenen festen oder flüssigen Körpers den Wert Null.
At the zero point of the absolute temperature, the entropy of any chemically homogeneous solid or liquid body possesses the value of zero.
Appendix B: On the History of the Zero-Point Entropy

Appendix C

References
- Kittel, C. Physik der Wärme; Akademische Verlagsgesellschaft Geest & Portig: Leipzig, Germany, 1973. [Google Scholar]
- Schmelzer, J.W.P.; Tropin, T.V. Glass Transition, Crystallization of Glass-Forming Melts, and Entropy. Entropy 2018, 20, 103. [Google Scholar] [CrossRef]
- Grambow, K. Die Rostocker Sieben; Hinstorff: Rostock, Germany, 2000. [Google Scholar]
- Einstein, A. Beiträge zur Quantentheorie. Verh. Dtsch. Phys. Ges. 1914, 16, 820–828. [Google Scholar]
- Gutzow, I.; Schmelzer, J. The Vitreous State; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Schmelzer, J.W.P.; Gutzow, I.S.; Mazurin, O.V.; Priven, A.I.; Todorova, S.V.; Petroff, B.P. Glasses and the Third Law of Thermodynamics. In Glasses and the Glass Transition; Wiley: Hoboken, NJ, USA, 2011; pp. 357–378. [Google Scholar]
- Gutzow, I.; Schmelzer, J. The Vitreous State, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Planck, M. Vorlesungen über die Theorie der Wärmestrahlung; Johann Ambrosius Barth: Leipzig, Germany, 1906. [Google Scholar]
- Planck, M. Vorlesungen über Thermodynamik, 3; Auflage, Verlag von Veit und Comp.: Leipzig, Germany, 1911. [Google Scholar]
- Nernst, W. Ueber die Berechnung chemischer Gleichgewichte aus thermischen Messungen. Nachrichten der Königlichen Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse 1906, 1906, 1–40. [Google Scholar]
- Pauling, L. The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. J. Am. Chem. Soc. 1935, 57, 2680–2684. [Google Scholar] [CrossRef]
- Gujrati, P.D. Hierarchy of Relaxation Times and Residual Entropy: A Nonequilibrium Approach. Entropy 2018, 20, 149. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Falkenhagen, H.; Ebeling, W. Theorie der Elektrolyte; S. Hirzel: Leipzig, Germany, 1971. [Google Scholar]
- Subarew, D.N. Statistische Thermodynamik des Nichtgleichgewichts; Akademie-Verlag: Berlin, Germany, 1976. [Google Scholar]
- Ebeling, W.; Feistel, R. Physik der Selbstorganisation und Evolution; Akademie-Verlag: Berlin, Germany, 1982. [Google Scholar]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North Holland Publishing Company: Amsterdam, The Netherlands; Dover Publications: New York, NY, USA, 1984. [Google Scholar]
- Feistel, R. Thermodynamic properties of seawater, ice and humid air: TEOS-10, before and beyond. Ocean Sci. 2018, 14, 471–502. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Feistel, R. Self-organisation of symbolic information. Eur. Phys. J. Special Top. 2017, 226, 207–228. [Google Scholar] [CrossRef]
- Hahn, H. Geometrical Aspects of the Pseudo Steady State Hypothesis in Enzyme Reactions. In Lecture Notes in Biomathematics; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 1974; Volume 4, pp. 528–545. [Google Scholar]
- Haken, H. Synergetics: An Introduction; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1978. [Google Scholar]
- Feistel, R.; Ebeling, W. Physics of Self-Organization and Evolution; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Handle, P.H.; Sciortino, F.; Giovambattista, N. Glass polymorphism in TIP4P/2005 water: A description based on the potential energy landscape formalism. J. Chem. Phys. 2019, 150, 244506. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Thermodynamics; North Holland: Amsterdam, The Netherlands, 1949. [Google Scholar]
- Schmelzer, J.W.P.; Tropin, T.V. Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy”’ by Zanotto and Mauro. Entropy 2018, 20, 704. [Google Scholar] [CrossRef]
- Feistel, R.; Ebeling, W. Entropy and the Self-Organization of Information and Value. Entropy 2016, 18, 193. [Google Scholar] [CrossRef]
- Feistel, R. Emergence of Symbolic Information by the Ritualisation Transition. In Information Studies and the Quest for Transdisciplinarity; Burgin, M., Hofkirchner, W., Eds.; World Scientific Pub Co Pte Lt.: Singapore, 2017; pp. 115–164. [Google Scholar]
- Burgin, M.; Feistel, R. Structural and Symbolic Information in the Context of the General Theory of Information. Information 2017, 8, 139. [Google Scholar] [CrossRef]
- Darwin, C. The Origin of Species by Means of Natural Selection or the Preservation of Favored Races in the Struggle for Life. Reprinted from the Sixth London Edition, with Additions and Corrections; Hurst and Company Publishers: New York, NY, USA, 1911. [Google Scholar]
- Pattee, H.H. The physics of symbols: Bridging the epistemic cut. Biosystems 2001, 60, 5–21. [Google Scholar] [CrossRef]
- Clausius, R. Die mechanische Wärmetheorie. Zweite umgearbeitete und vervollständigte Auflage des unter dem Titel “Abhandlungen über die mechanische Wärmetheorie” erschienenen Buches; Friedrich Vieweg und Sohn: Braunschweig, Germany, 1876. [Google Scholar]
- Fermi, E. Thermodynamics; Prentice-Hall: Upper Saddle River, NJ, USA, 1937. [Google Scholar]
- Feistel, R.; Wagner, W. Sublimation pressure and sublimation enthalpy of H2O ice Ih between 0 and 273.16 K. Geochim. et Cosmochim. Acta 2007, 71, 36–45. [Google Scholar] [CrossRef]
- Feistel, R. Thermodynamic Properties of Seawater. In (UNESCO-EOLSS Joint Committee, ed.): Encyclopedia of Life Support Systems (EOLSS); Eolss Publishers: Oxford, UK, 2011. [Google Scholar]
- Feistel, R. A Gibbs function for seawater thermodynamics for −6 to 80 °C and salinity up to 120 g kg−1. Deep Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 1639–1671. [Google Scholar] [CrossRef]
- Maxwell, J.C. Theory of Heat; Longmans, Green & Co.: London, UK; New York, NY, USA, 1888. [Google Scholar]
- Feistel, R.; Wright, D.G.; Kretzschmar, H.-J.; Hagen, E.; Herrmann, S.; Span, R. Thermodynamic properties of sea air. Ocean Sci. 2010, 6, 91–141. [Google Scholar] [CrossRef]
- Simon, F. On the Third Law of Thermodynamics. Physica 1937, IV, 1089–1096. [Google Scholar] [CrossRef]
- Ebeling, W. On the relation between various entropy concepts and the valoric interpretation. Phys. A Stat. Mech. Its Appl. 1992, 182, 108–120. [Google Scholar] [CrossRef]
- Boltzmann, L. Vorlesung über Gastheorie, 1; Wiener Sitzungsberichte: Wien, Austria, 1896. [Google Scholar]
- Planck, M. Theorie der Wärmestrahlung, 6. Auflage; Johann Ambrosius Barth: Leipzig, Germany, 1966. [Google Scholar]
- Boltzmann, L. On the Relationship between the Second Main Theorem of Mechanical Heat Theory and the Probability Calculation with Respect to the Results about the Heat Equilibrium; Sitzb. d. Kaiserlichen Akademie der Wissenschaften, Mathematisch-Naturwissen. Cl: Wien, Austria, 1877; LXXVI, Abt II; pp. 373–435. [Google Scholar]
- Jensen, J.L.W.V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
- Alberti, P.M.; Uhlmann, A. Dissipative Motion in State Spaces; BSB B. G. Teubner Verlagsgesellschaft: Leipzig, Germany, 1981. [Google Scholar]
- Lieb, E.H.; Yngvason, J. The physics and mathematics of the second law of thermodynamics. Phys. Rep. 1999, 310, 1–96. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Statistische Physik; Akademie-Verlag: Berlin, Germany, 1966. [Google Scholar]
- Schrödinger, E. Statistical Thermodynamics; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Klimontovich, Y.L. Statisticheskaya fizika (Statistical Physics); Nauka: Moscow, Russia, 1982. [Google Scholar]
- Brillouin, L. Negentropy Principle of Information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Ebeling, W.; Feistel, R. About Self-organization of Information and Synergetics. In Complexity and Synergetics; Müller, S.C., Plath, P.J., Radons, G., Fuchs, A., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 3–8. [Google Scholar]
- Klimontovich, Y.L. Turbulent Motion. The Structure of Chaos; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 1991; pp. 329–371. [Google Scholar]
- Schöpf, H.-G. Rudolf Clausius. Ein Versuch, ihn zu verstehen. Ann. Phys. 1984, 496, 185–207. [Google Scholar] [CrossRef]
- Gibbs, J.W. A Method of Graphical Representation of the Thermodynamic Properties of Substances by Means of Surfaces. Trans. Conn. Acad. Arts Sci. 1873, 2, 382–404. [Google Scholar]
- Gujrati, P.D. On Equivalence of Nonequilibrium Thermodynamic and Statistical Entropies. Entropy 2015, 17, 710–754. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Hydrodynamik; Akademie-Verlag: Berlin, Germany, 1974. [Google Scholar]
- Ebeling, W.; Feistel, R. Theory of Selforganization: The Role of Entropy, Information and Value. J. Nonequilibrium Thermodyn. 1992, 17, 303–332. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Charles Scribner’s Sons: New York, NY, USA; Edward Arnold: London, UK, 1902. [Google Scholar]
- Ishioka, S.; Fuchikami, N. Thermodynamics of computing: Entropy of nonergodic systems. Chaos Interdiscip. J. Nonlinear Sci. 2001, 11, 734–746. [Google Scholar] [CrossRef]
- Goldstein, M. On the reality of the residual entropies of glasses and disordered crystals: Counting microstates, calculating fluctuations, and comparing averages. J. Chem. Phys. 2001, 134, 124502. [Google Scholar] [CrossRef]
- Ufflink, J. Compendium of the Foundations of Classical Statistical Physics; Universiteit Utrecht: Utrecht, The Netherlands, 2006. [Google Scholar]
- Berthier, L.; Ozawa, M.; Scalliet, C. Configurational entropy of glass-forming liquids. J. Chem. Phys. 2019, 150, 160902. [Google Scholar] [CrossRef]
- Ben-Naim, A. Entropy, Shannon’s Measure of Information and Boltzmann’s H-Theorem. Entropy 2017, 19, 48. [Google Scholar] [CrossRef]
- Petz, D. Entropy, von Neumann and the von Neumann Entropy. In John von Neumann and the Foundation of Quantum Physics; Redei, M., Stöltzner, M., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2001; pp. 83–96. [Google Scholar]
- Obukhov, S.P. Self-organized criticality: Goldstone modes and their interactions. Phys. Rev. Lett. 1990, 65, 1395–1398. [Google Scholar] [CrossRef]
- Pruessner, G. Self-Organised Criticality; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Strehlow, P. Die Kapitulation der Entropie. 100 Jahre III. Hauptsatz der Thermodynamik. Phys. J. 2005, 4, 45–51. [Google Scholar]
- Helmholtz, H.V. Die Thermodynamik chemischer Vorgänge (Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, abgedruckt in Wissenschaftl). Abhandlungen 1882, Bd. I, 22–39. [Google Scholar]
- Kluge, G.; Neugebauer, G. Grundlagen der Thermodynamik; Deutscher Verlag der Wissenschaften: Berlin, Germany, 1976. [Google Scholar]
- Planck, M. Über neuere thermodynamische Theorien. (Nernstsches Wärmetheorem und Quantenhypothese.). Phys. Z. 1912, XIII, 165–175. [Google Scholar]
- Marquet, P. The Third Law of Thermodynamics or an Absolute Definition for Entropy. Part 1: The Origin and Applications in Thermodynamics. 2019. Available online: https://www.researchgate.net/publication/332726165_The_third_law_of_thermodynamics_or_an_absolute_definition_for_Entropy_Part_1_the_origin_and_applications_in_thermodynamics (accessed on 23 July 2019).
- Pauling, L.; Pauling, P. Chemistry; Freeman & Co.: San Francisco, CA, USA, 1975. [Google Scholar]
- Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef]
- Feistel, R.; Wagner, W. A Comprehensive Gibbs Thermodynamic Potential of Ice. In Proceedings of the 14th International Conference on the Properties of Water and Steam, Kyoto, Japan, 30 August–3 September 2004; pp. 751–756. [Google Scholar] [CrossRef]
- Feistel, R.; Wagner, W. A Comprehensive Gibbs Potential of Ice Ih. In Nucleation Theory and Applications; Schmelzer, J.W.P., Ed.; JINR: Dubna, Russia, 2005; pp. 120–145. [Google Scholar]
- Feistel, R.; Wagner, W. High-pressure thermodynamic Gibbs functions of ice and sea ice. J. Mar. Res. 2005, 63, 95–139. [Google Scholar] [CrossRef]
- Feistel, R. A New Equation of State for H2O Ice Ih. J. Phys. Chem. Ref. Data 2006, 35, 1021. [Google Scholar] [CrossRef]
- Grüneisen, E. Über den Einfluß von Temperatur und Druck auf Ausdehnungskoeffizient und spezifische Wärme der Metalle. Ann. Phys. 1910, 338, 65–78. [Google Scholar] [CrossRef]
- Giauque, W.F.; Ashley, M.F. Molecular Rotation in Ice at 10°K. Free Energy of Formation and Entropy of Water. Phys. Rev. 1933, 43, 81–82. [Google Scholar] [CrossRef]
- Gordon, A.R. The Calculation of Thermodynamic Quantities from Spectroscopic Data for Polyatomic Molecules; the Free Energy, Entropy and Heat Capacity of Steam. J. Chem. Phys. 1934, 2, 65. [Google Scholar] [CrossRef]
- Cox, J.D.; Wagman, D.D.; Medvedev, V.A. CODATA Key Values for Thermodynamics; Hemisphere Publishing Corp.: Washington, DC, USA, 1989. [Google Scholar]
- Giauque, W.F.; Stout, J.W. The Entropy of Water and the Third Law of Thermodynamics. The Heat Capacity of Ice from 15 to 273°K. J. Am. Chem. Soc. 1936, 58, 1144–1150. [Google Scholar] [CrossRef]
- Fletcher, N.H. The Chemical Physics of Ice; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Nagle, J.F. Lattice statistics of hydrogen-bonded crystals. I. The residual entropy of ice. J. Math. Phys. 1966, 7, 1484–1491. [Google Scholar] [CrossRef]
- Haida, O.; Matsuo, T.; Suga, H.; Seki, S. Calorimetric study of the glassy state X. Enthalpy relaxation at the glass-transition temperature of hexagonal ice. J. Chem. Thermodyn. 1974, 6, 815–825. [Google Scholar] [CrossRef]
- Petrenko, V.F.; Whitworth, R.W. Physics of Ice; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Penny, A.H. A theoretical determination of the elastic constants of ice. Math. Proc. Camb. Philos. Soc. 1948, 44, 423. [Google Scholar] [CrossRef]
- Schulson, E.M. The structure and mechanical behavior of ice. Memb. J. Min. Met. Mat. Soc. 1999, 51, 21–27. [Google Scholar] [CrossRef]
- Bjerrum, N. Structure and Properties of Ice. Science 1952, 115, 385–390. [Google Scholar] [CrossRef]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Johari, G.P. Study of the low-temperature “transition” in ice Ih by thermally stimulated depolarization measurements. J. Chem. Phys. 1975, 62, 4213. [Google Scholar] [CrossRef]
- Kuo, J.-L.; Hirsch, T.K.; Knight, C.; Ojamäe, L.; Klein, M.L.; Singer, S. Hydrogen-Bond Topology and the Ice VII/VIII and Ice Ih/XI Proton-Ordering Phase Transitions. Phys. Rev. Lett. 2005, 94, 135701. [Google Scholar]
- Lamb, D.; Verlinde, J. Physics and Chemistry of Clouds; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Pelkowski, J.; Frisius, T. The Theoretician’s Clouds—Heavier or Lighter than Air? On Densities in Atmospheric Thermodynamics. J. Atmos. Sci. 2011, 68, 2430–2437. [Google Scholar] [CrossRef]
- Randall, D. Atmosphere, Clouds, and Climate; Princeton University Press: Princeton, NJ, USA; Oxford, UK, 2012. [Google Scholar]
- Feistel, R.; Wielgosz, R.; Bell, S.A.; Camões, M.F.; Cooper, J.R.; Dexter, P.; Dickson, A.G.; Fisicaro, P.; Harvey, A.H.; Heinonen, M.; et al. Metrological challenges for measurements of key climatological observables: Oceanic salinity and pH, and atmospheric humidity. Part 1: Overview. Metrologia 2016, 53, R1–R32. [Google Scholar] [CrossRef]
- Ostwald, W. Über die vermeintliche Isomerie des roten und gelben Quecksilberoxyds und die Oberflächenspannung fester Körper. Z. Phys. Chem. 1900, 34, 495–503. [Google Scholar] [CrossRef]
- Schmelzer, J. Zur Kinetik des Keimwachstums in Lösungen. Z. Phys. Chem. 1985, 266, 1057–1070. [Google Scholar] [CrossRef]
- Schmelzer, J. Zur Kinetik des Wachstums von Tropfen in der Gasphase. Z. Phys. Chem. 1985, 266, 1121–1134. [Google Scholar] [CrossRef]
- Mahnke, R.; Feistel, R. The Kinetics of Ostwald Ripening as a Competitive Growth in a Selforganizing System. Rostocker Phys. Manuskr. 1985, 8, 54–59. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Ulbricht, H. Thermodynamics of finite systems and the kinetics of first-order phase transitions. J. Colloid Interface Sci. 1987, 117, 325–338. [Google Scholar] [CrossRef]
- Thomson, W. On the equilibrium of vapour at a curved surface of liquid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1871, 42, 448–452. [Google Scholar] [CrossRef]
- Pelkowski, J. On the Clausius-Duhem Inequality and Maximum Entropy Production in a Simple Radiating System. Entropy 2014, 16, 2291–2308. [Google Scholar] [CrossRef]
- Gassmann, A.; Herzog, H.-J. How is local material entropy production represented in a numerical model? Q. J. R. Meteorol. Soc. 2015, 141, 854–869. [Google Scholar] [CrossRef]
- Sobac, B.; Brutin, D. Heat and Mass Transfer. Pure Diffusion. In Droplet Wetting and Evaporation: From Pure to Complex Fluids; Brutin, D., Ed.; Academic Press: London, UK; San Diego, CA, USA; Waltham, MA, USA; Oxford, UK, 2015; pp. 103–114. [Google Scholar]
- Jakubczyk, D.; Kolwas, M.; Derkachov, G.; Kolwas, K.; Zientara, M. Evaporation of Micro-Droplets: The “Radius-Square-Law” Revisited. Acta Phys. Pol. A 2012, 122, 709–716. [Google Scholar] [CrossRef]
- Schmelzer, J.; Ulbricht, H.; Schmelzer, J.W.P. Kinetics of first-order phase transitions in adiabatic systems. J. Colloid Interface Sci. 1989, 128, 104–114. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; (Rostock University, Rostock, MV, Germany). Personal communication, 2019.
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]



© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feistel, R. Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States. Entropy 2019, 21, 799. https://doi.org/10.3390/e21080799
Feistel R. Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States. Entropy. 2019; 21(8):799. https://doi.org/10.3390/e21080799
Chicago/Turabian StyleFeistel, Rainer. 2019. "Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States" Entropy 21, no. 8: 799. https://doi.org/10.3390/e21080799
APA StyleFeistel, R. (2019). Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States. Entropy, 21(8), 799. https://doi.org/10.3390/e21080799