1. Introduction
Clustering is one of the oldest machine-learning fields, where the objective is, given data points, to group them into clusters according to some measure. Many clustering methods have been proposed for a long while [
1], and been applied to real-world problems [
2].
The best known classical methods are k-means [
3] and Gaussian Mixture Model (GMM) clustering [
4]. Though those methods are computationally efficient, they can only model convex shapes and are thus applicable in limited cases. The kernel k-means [
5], kernel GMM clustering [
6] and Spectral Clustering (SC) [
7] can capture more complicated shapes than k-means and GMM but are difficult to scale up to large datasets. In recent years, due to technological progress, we can acquire many types of data such as images, texts, and genomes in large numbers. Thus, the demand of advanced efficient clustering methods grows even stronger [
8].
Thanks to the development of deep neural networks, we can now handle large datasets with complicated shapes [
9]. Consequently, the studies of clustering using deep neural networks has been proposed. One major direction in the studies is to combine deep AutoEncoders (AE) [
10] with classical clustering methods. This AE is used to obtain a clustering friendly low dimensional representation. Another major direction is directly grouping a given unlabeled dataset into the clusters in the original input space by employing a deep neural network to model the distribution of cluster labels.
With both directions, there exist popular methods. We summarize their applicable data domain and well performing condition in
Table 1. For examples, CatGAN (Categorical Generative Adversarial Networks) learns discriminative neural network classifiers that maximize mutual information between the input data points and the cluster labels, while enforcing the robustness of the classifiers to data points produced by adversarial generative models. Since maximizing mutual information implicitly encourages the cluster-balance distribution of the model to be uniform, CatGAN performs well under the condition of the uniform cluster balance. JULE (Joint Unsupervised LEarning) learns a clustering friendly low dimensional representation for image datasets by using a convolutional neural network [
11]. The assigned cluster labels and low dimensional representation are jointly optimized by updating a
similarity matrix of the representations, where
n is the number of data points. Thus,
memory space must be secured to conduct the method.
As we can see in
Table 1, most of their key conditions are not always realistic since the details of given unlabeled datasets are unknown and their size is large in typical machine-learning scenarios. On the other hand, SpectralNet does not require key condition. It only requires the following two fundamental assumptions: the smoothness and manifold assumptions [
18]. Please note that the other methods in
Table 1 also require the two assumptions. As for the weakness of SpectralNet, it is not robust against outliers. In the learning process, it learns the pairwise similarities over all data points. Therefore, the existence of outliers disturbs the method learning the similarities precisely, and thus returns inaccurate clustering results.
In this paper, we propose a deep clustering method named Spectral Embedded Deep Clustering (SEDC). Given an unlabeled dataset and the number of clusters, SEDC directly groups the dataset into the given number clusters in the input space. Our statistical model is the conditional discrete probability distribution, which is defined by a fully connected deep neural network. SEDC does not require key condition except the smoothness and manifold assumptions, and it can be applied to various data domains. Moreover, throughout our numerical experiments, we observed that our method was more robust against outliers than SpectralNet.
The procedure of SEDC is composed of two stages. In the first stage, we conduct SC only on the unlabeled data points selected from high-density region by using the geodesic metric to estimate the cluster labels. This special type of SC is named as Selective Geodesic Spectral Clustering (SGSC), which we propose for assisting SEDC as well. Thereafter, we conduct semi-supervised learning to train the model by using the estimated cluster labels and the remaining unlabeled data points. Please note that in this semi-supervised learning, we treat the estimated cluster labels of the selected unlabeled data points as the given true cluster labels. At last, by using the trained model, we obtain the estimated cluster labels of all given unlabeled data points.
In the remainder of this paper, we introduce related works in
Section 2. We then introduce our proposed method in
Section 3. We demonstrate the efficiency of our method with numerical experiments in
Section 4. Finally, in
Section 5, we conclude the paper with the discussion on future works.
3. Proposed Method
As we already mentioned in the end of
Section 1 and the beginning of
Section 2.2, given an unlabeled dataset
(
) and the number of clusters
C, our proposed deep clustering named SEDC groups
into
C clusters. Since this grouping is achieved by obtaining the estimated cluster labels of
, our goal can be replaced by estimating the cluster labels up to permutation of labels. In SEDC, the estimated cluster label of each
is defined by
, where
is the trained set of parameters. The training scheme of the classifier
is as follows: we firstly only estimate the cluster labels of selected unlabeled data points by using only
(this part is done by SGSC algorithm.), and then conduct semi-supervised learning to train the classifier. Regarding with this semi-supervised learning, we use the estimated cluster labels of selected unlabeled data points and the remaining unlabeled data points, which are treated as the given true cluster labels and unlabeled data points respectively.
In this section, we first introduce SGSC. Thereafter, we present our main method SEDC.
3.1. Selective Geodesic Spectral Clustering
Using SGSC, the clustering problem is converted into a semi-supervised learning problem as shown below. In SGSC, firstly some unlabeled data points are selected from high-density regions in the original dataset. Then, the SC is used to the selected unlabeled data points with the geodesic metric. As a result, we obtain cluster labels on the selected points. Since the points are picked up from the high-density regions, the locations of selected points are stable and robust against outliers [
31]. The geodesic metric is approximated by the graph shortest path distances on the graph. The reason to employ the geodesic metric is that the metric is known to be useful to capture the structure of the data manifolds especially when the number of given data points is large [
32]. Here, the number of selected data points is a hyperparameter in SGSC. Suppose that the hyperparameters are tuned appropriately, Then, the set of the selected data points with their estimated cluster labels can roughly approximate the manifolds represented by the full original dataset even when the dataset has complicated manifolds inluding outliers.
Throughout numerical experiments on five datasets in later section, the following two are confirmed. Firstly, the estimation accuracy of cluster labels with selected points by SGSC can stay high. Then, secondly, due to the highly accurate estimation by SGSC, it can help the clustering by SEDC to be successful on several types of datasets on average.
We will refer to the selected data points as hub data points. Let be the set of hub data points. The hub dataset H is formally defined below.
Definition 1. Let be the given unlabeled dataset. On the graph , let be the set of adjacent nodes of . For a natural number h, the hub set H is defined as the collection of nodes that ranked in the top-h cardinality of in .
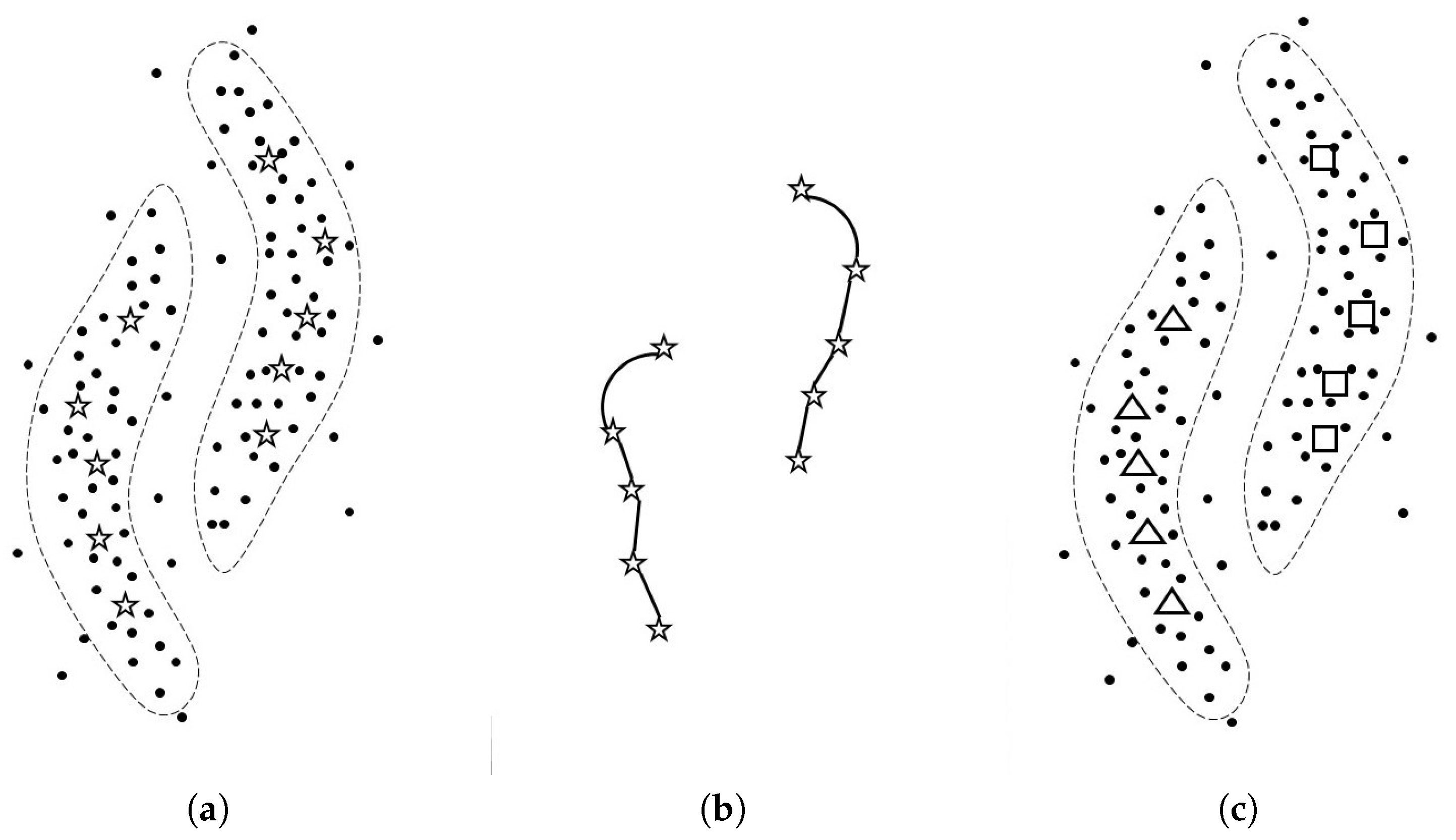
Algorithm 1 and
Figure 1 show the pseudo code of SGSC and the mechanism of SGSC, respectively. The detail of this algorithm is explained below.
| Algorithm 1: |
Input: Unlabeled dataset . Number of neighbors . Number of hub data points h. Number of clusters C. Output: The estimated conditional discrete probability distributions with hub data points, .
- 1:
Construct the undirected graph , where the edge set E is defined by -NN with the Euclidean distance. - 2:
Build the hub dataset H on graph such that . Denote the element of H by (). - 3:
Define the geodesic metric as the shortest path distance on the graph . - 4:
Define and as the two outputs of , where the weight is defined by . Then, compute the conditional cluster probability with each hub data point in H as follows:
where is a small positive number and is i-th row of . - 5:
Let and be and matrix, respectively. The i-th row of is defined by .
|
Line 1: Given an unlabeled dataset , the undirected graph is constructed in the -nearest neighbor (-NN) manner with the Euclidean metric. is used not only for defining the hub set H but also for approximating the geodesic distance on the manifolds shaped by . We consider as a hyperparameter.
Line 2: Given the number of hub points h and , the algorithm defines the hub set H based on Definition 1. Outliers can be excluded from H by setting h appropriately. In this algorithm, h is considered to be a hyperparameter.
Line 3: The geodesic distance is determined from the Euclidean distances on the undirected edges of
. In Line 4, we need to compute the geodesic distances between the data points of
H. Efficient algorithms are available for this purpose [
32,
33].
Line 4: Given the number of clusters
C, we estimate the conditional discrete probability distribution
for each
, where
y is the cluster label ranging
. The estimated
is denoted as
. This estimation relies on conducting SC with
metric only on
H. The definition of the weight
w in this SC follows Equation (
1). The key to succeed the estimation is to employ the combination of a different number of neighbors
from
and the geodesic metric
to a SC. Typically, given data points that are dense in the input space, the combination of a small number of neighbors and the Euclidean metric makes a SC perform well. However, we consider
H, which is sparse in the input space. Therefore, we employ the combination. We consider
as a hyperparameter as well. Following [
34], we compute
by using the outputs
and
of
. Please note that
can be considered to be the probability that
belongs to the cluster
j, where
is the low dimensional representation of
according to the property of SC [
23]. As for
, we set
to it.
Remark 2. Though we say we estimate the “cluster labels” of hub data points by SGSC, it actually outputs the estimated conditional probability distributions with hub data points. The reason is that throughout our preliminary experiments, we observed that employing of line 5 made SEDC perform better than employing the one-hot vector. This one-hot vector, for instance, can be defined by using the estimated cluster labels which is one of the outputs of .
3.2. Spectral Embedded Deep Clustering
SEDC is a deep clustering method for clustering. Given an unlabeled dataset
and the number of clusters
C, it groups
into
C clusters. As mentioned in the beginning of this section, this method employs the conditional discrete probability distribution
as the statistical model, which is defined by a fully connected deep neural network. By using the trained model, we obtain the estimated cluster label of each
. This method does not require an additional condition except two fundamental assumptions: the smoothness and manifold assumptions. Therefore, among the methods of
Table 1, only SpectralNet is comparable to SEDC in this point. In addition, our method can be applied to various data domains once the raw data is transformed to the feature vector. Furthermore, empirically speaking, the performance of SEDC can be robust against outliers due to the robustness of SGSC against them. The pseudo code of SEDC is shown in Algorithm 2. The explanation is below.
The procedure of SEDC is composed of two stages. In the first stage, we estimate the conditional discrete probability distributions with hub data points. In the second stage, by treating as the given true distributions of hub data points, we conduct semi-supervised learning where and the remaining unlabeled data points are used, to train the statistical model . After this training, SEDC returns the estimated cluster labels of each by , where is the trained set of parameters and . The estimated cluster labels of is denoted by . Note that the estimated cluster labels of hub data points might be updated at the end of SEDC procedure.
In the second stage, we conduct semi-supervised learning to train the statistical model
using
. Recall that the model
is defined by the deep neural network whose last layer is soft-max function. The number of neurons of the first and last layer are the dimension of feature vector
D and the number of clusters
C, respectively. In this semi-supervised learning, we minimize the following loss with respect to
:
where
and
are hyperparameters that range over positive numbers. In Equation (
8), the first and second terms express VAT loss of Equation (
4) and the pseudo empirical loss with estimated cluster probabilities of hub data points, respectively. The third term is the conditional Shannon entropy [
30] averaged over
, and it is defined as follows:
| Algorithm 2: |
Input: Unlabeled dataset . Number of neighbors . Number of hub data points h. Number of clusters C. Regularization parameters . Output: The estimated cluster labels of , .
- 1:
Obtain the matrix of estimated conditional discrete probability distributions with hub data points by computing of Algorithm 1. Denote i-th row of by , which means the estimated cluster label probability distribution of hub data point . The index i ranges . - 2:
Let be a statistical model, which is the cluster label probability distribution with given data point . The cluster label ranges . Define the objective of Equation ( 8) by using , and given . Then, minimize the objective with in stochastic gradient descent fashion. Denote the optimized parameter by . - 3:
Obtain the estimated cluster labels of all data points in by using the trained classifier . Denote by . Then, for all data point index i, compute by
|
We use the Adam optimizer [
35] for the minimization. After minimizing Equation (
8), we estimate the labels of
by using the trained parameter
. Let
denote the estimated cluster labels of
. The labels are computed as follows:
.
As mentioned in
Section 2.2, the minimization of the VAT loss encourages
to follow the smoothness assumption. In addition, that of entropy loss helps the model to follow the cluster assumption [
18]. The cluster assumption says that true decision boundary is not located in regions of the input space that are densely populated with data points. The entropy loss is commonly used in many studies [
15,
26,
36,
37]. Please note that the entropy loss is defined only by using the unlabeled data points, like VAT loss. With regard to the pseudo empirical loss, we can consider other candidates such as the cross entropy. The reason we chose the KL-divergence is that we observed that the KL-divergence made SEDC perform better than other candidates in our preliminary experiments.
3.3. Computational and Space Complexity of SEDC
The procedure of SEDC is composed of two stages. The first stage (line 1 of Algorithm 2) is conducting SGSC algorithm. The second stage (line 2 of Algorithm 2) is training the model by optimizing Equation (
8). Therefore, total computational complexity of SEDC is the summation of the total computational complexity of SGSC and the complexity consumed in the mini-batch training. In the following, we analyze the computational complexity consumed in each line of Algorithm 1: see this summary in
Table 2. Suppose that
. In line 1 of the algorithm, we consume
to construct
-NN graph [
38], where
D is the dimension of feature vector. Then, in the line 2, we consume
because we sort the nodes of the graph in descending order of degree for defining the hub set
H. Then, in the line 3, we consume
for computing the graph shortest path distances between the data points in
H: see algorithm 1 of [
32]. Thereafter, in the line 4, we consume
for solving the eigenvector problem of the Laplacian matrix.
As for the memory complexity, since the dominant factors are to save -NN graph and the model, SEDC needs where is the set of parameters in a deep neural network.
Remark 3. For most of deep clustering methods relying on k-NN graph construction, the dominant factor with their total computational complexity is k-NN graph construction, i.e., we need . However, according to [39,40], by constructing the approximated k-NN graph, we only need for the construction. 5. Conclusions and Future Work
In this paper, we propose a deep clustering method named SEDC. Given an unlabeled dataset and the number of clusters, the method groups the dataset into the given number clusters. Regarding its advantages, it does not require an additional condition except two fundamental assumptions: smoothness and manifolds assumptions. In this point, only SpectralNet of
Table 1 is comparable. In addition, SEDC also can be applied to various data domains since it does not have preferred data domains, as long as raw data is transformed to feature vectors. Furthermore, the performance of SEDC can be robust against existence of outliers unlike SpectralNet. According to these advantages, our proposed method can be expected to averagely perform better than previous deep clustering methods. As a result, this expectation is empirically confirmed by conducting numerical experiments on five commonly used datasets: see
Table 7. Therefore, we think our method can be a competitive candidate for users in some practical clustering scenarios where prior knowledge of the given unlabeled dataset is limited.
However, there are two main drawbacks. On the one hand, since the method needs hyperparameter tuning, if we do not have appropriate labeled source domains to learn them from and transfer, then it may fail. On the other hand, since the method requires the number of clusters, it does not work for datasets where nothing is known on the number of clusters such as genome datasets.
Finally, we discuss about our two future works. The first one is to invent a more noise-robust semi-supervised learning framework and then apply it to SEDC instead of Equation (
8). Since some of the estimated cluster labels by SGSC are not perfectly accurate, we need to invent such the framework to stabilize the performance of SEDC. The second one is to modify our method for handling structured data, i.e., graph data or sequential data.