Causality Detection Methods Applied to the Investigation of Malaria Epidemics
Abstract
1. Introduction
2. Methods
2.1. Kernel Granger Causality (KGC)
2.2. Transfer Entropy (TE)
2.3. Recurrence Plots (RP)
2.4. Causal Decomposition (CD)
2.5. Complex Networks (CN)
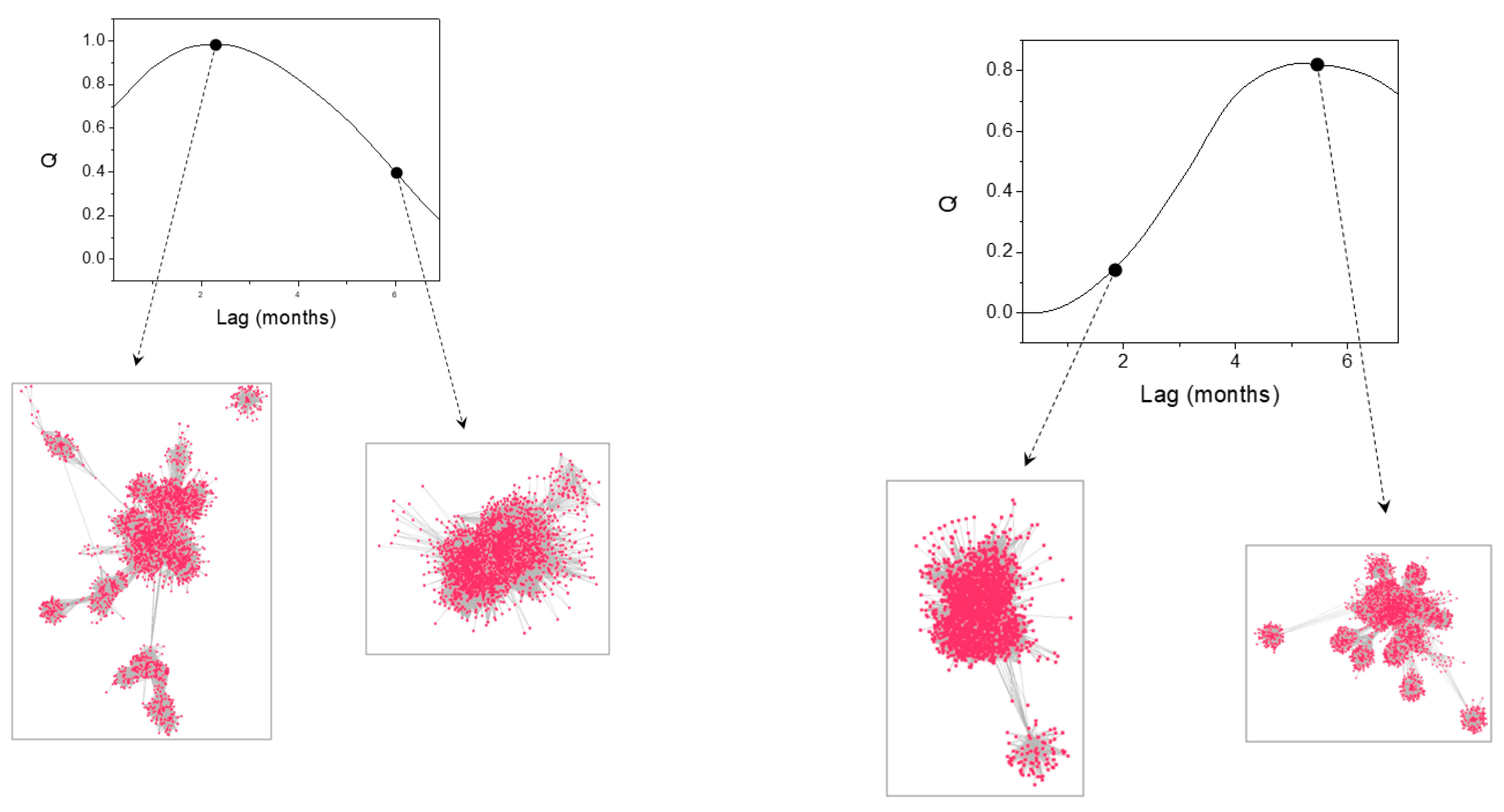
3. Results and Discussion
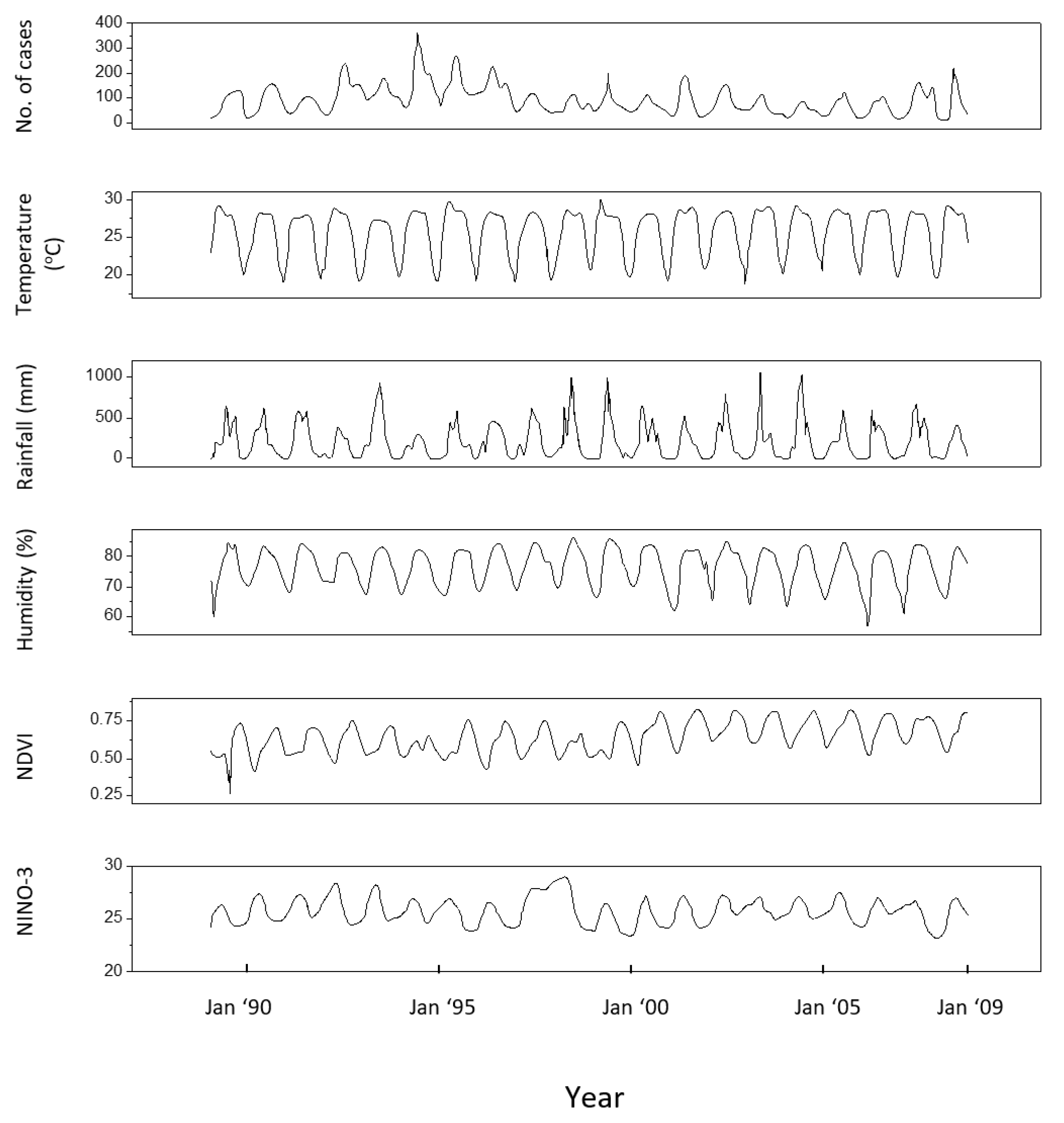
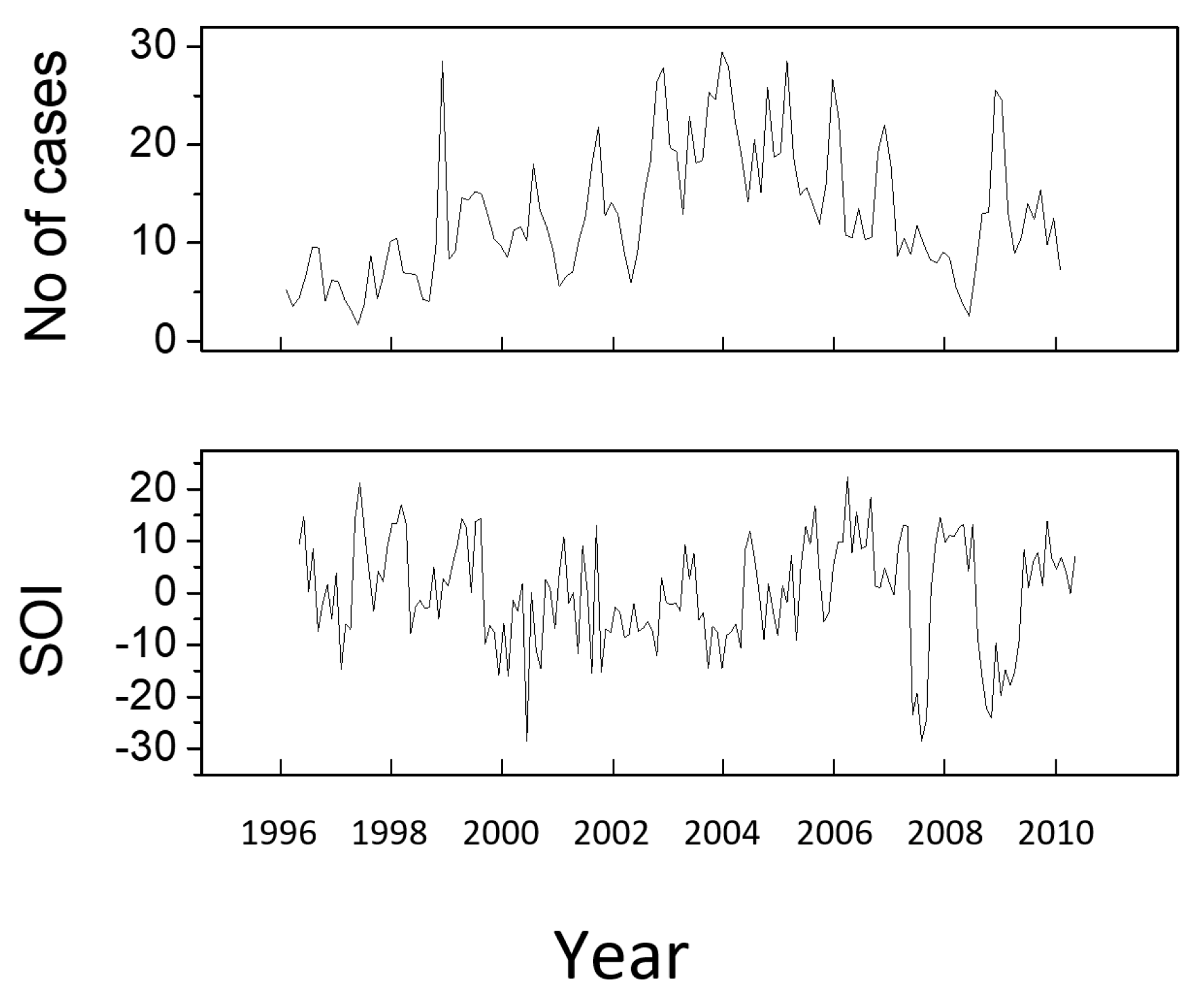
3.1. Malaria Data
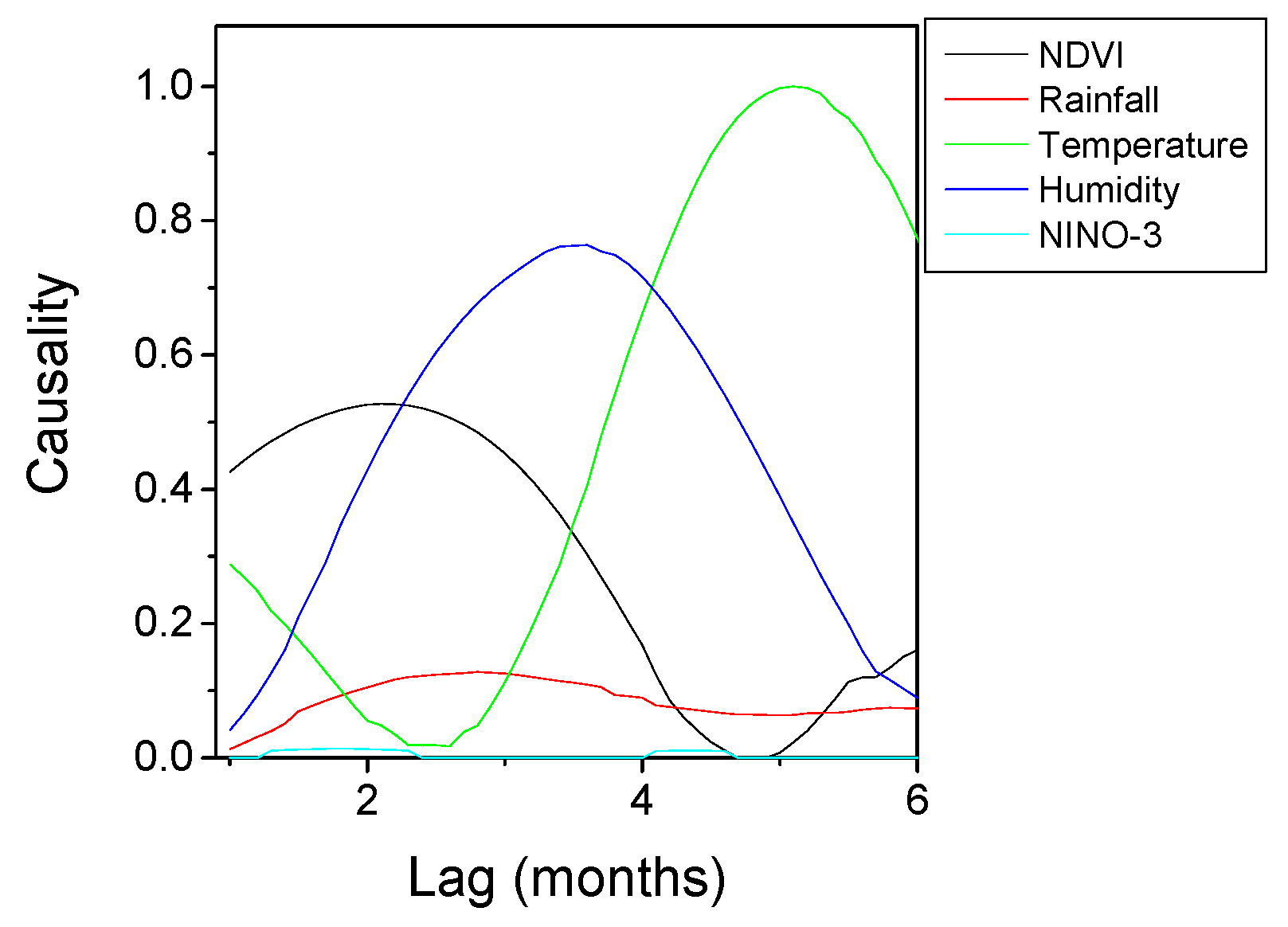
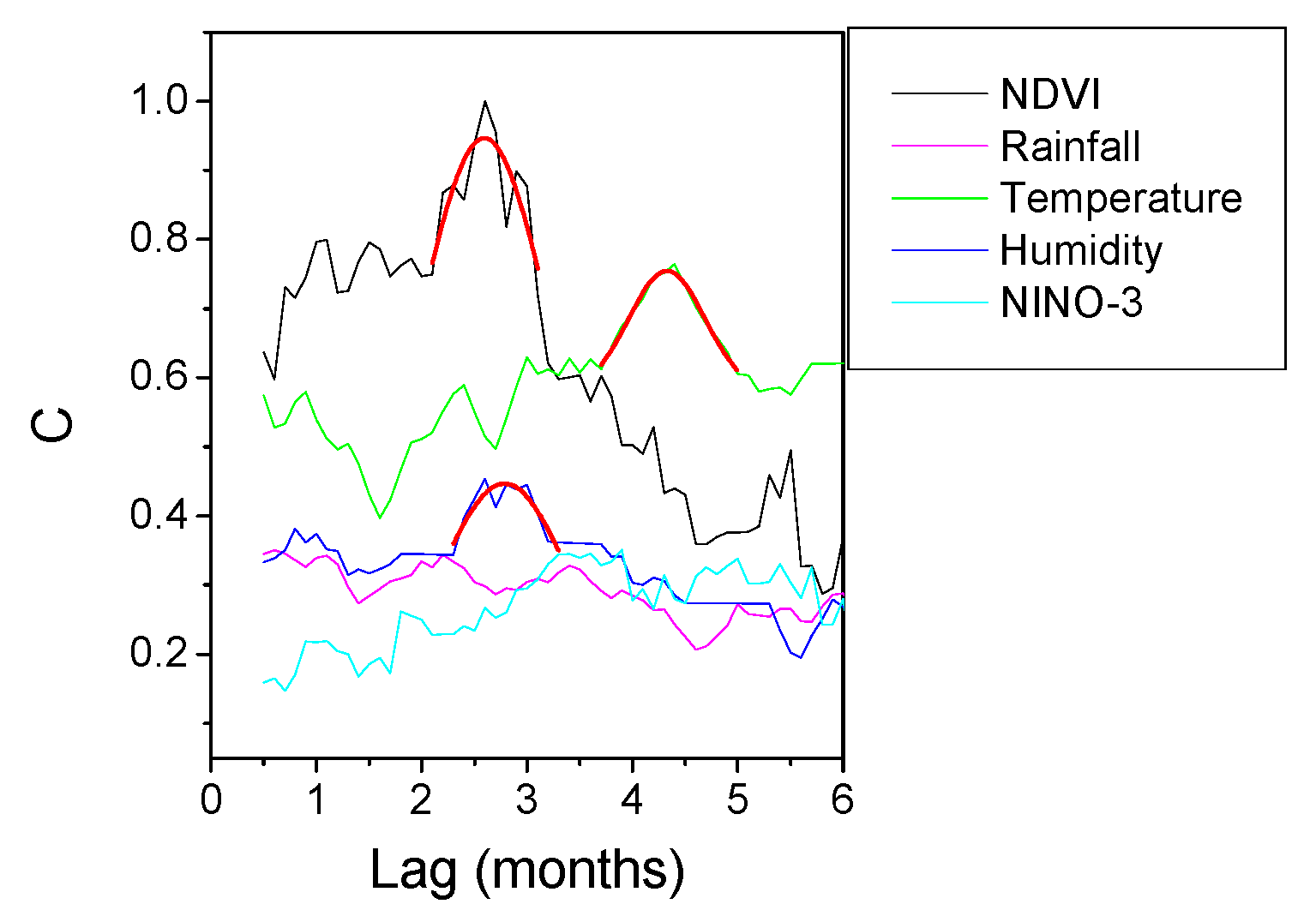
3.2. Data Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- World Health Organization (WHO) and WHO Global Malaria Programme. Available online: http://www.who.int/malaria/about_us/en/index.html, (accessed on 19 March 2019).
- Lindsay, S.W.; Martens, W.J. Malaria in the African highlands: past, present and future. Bull. WHO 1998, 76, 33–45. [Google Scholar] [PubMed]
- Lafferty, K.D. The ecology of climate change and infectious diseases. Ecology 2009, 90, 888–900. [Google Scholar] [CrossRef] [PubMed]
- Pascual, M.; Bouma, M.J. Do rising temperatures matter. Ecology 2009, 90, 906–912. [Google Scholar] [CrossRef] [PubMed]
- Field, C.B.; Barros, V.R.; Dokken, D.J.; Mach, K.J.; Mastrandrea, M.D.; Bilir, T.E.; Chatterjee, M.; Ebi, K.L.; Estrada, Y.O.; Genova, R.C.; et al. (Eds.) Climate change 2014: Impacts, adaptation, and vulnerability. Part A: global and sectoral aspects. Contribution of working group II to the fifth assessment report of the intergovernmental panel on climate change. In IPCC (2014) Summary for Policymakers; Cambridge University Press: Cambridge, UK, 2014; pp. 1–32. [Google Scholar]
- Carter, R.; Mendis, K.N. Evolutionary and historical aspects of the burden of malaria. Clin. Microbiol. Rev. 2002, 15, 564–594. [Google Scholar] [CrossRef] [PubMed]
- Eikenberry, S.E.; Gumel, A.B. Mathematical modeling of climate change and malaria transmission dynamics: A historical review. J. Math. Biol. 2018, 77, 857–933. [Google Scholar] [CrossRef] [PubMed]
- Haque, U.; Hashizume, M.; Glass, G.E.; Dewan, A.M.; Overgaard, H.J.; Yamamoto, T. The Role of Climate Variability in the Spread of Malaria in Bangladeshi Highlands. PLoS ONE 2010, 5, e14341. [Google Scholar] [CrossRef] [PubMed]
- Hanf, M.; Adenis, A.; Nacher, M.; Carme, B. The role of El Niño southern oscillation (ENSO) on variations of monthly Plasmodium falciparum malaria cases at the cayenne general hospital, 1996–2009, French Guiana. Malar. J. 2011, 10, 100. [Google Scholar] [CrossRef] [PubMed]
- Sadoine, M.L.; Smargiassi, A.; Ridde, V.; Tusting, L.S.; Zinszer, K. The associations between malaria, interventions, and the environment: A systematic review and meta-analysis. Malar. J. 2018, 17, 73. [Google Scholar] [CrossRef] [PubMed]
- Mabaso, M.L.H.; Ndlovu, N.C. Critical review of research literature on climate-driven malaria epidemics in sub-Saharan Africa. Public Health 2012, 126, 909–919. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Yang, L.; Ou, C.-Q.; Li, L.; Zhuang, Y.; Yang, J.; Zhou, Y.-X.; Qian, J.; Chen, P.-Y.; Liu, Q.-Y. Malaria incidence from 2005–2013 and its associations with meteorological factors in Guangdong, China. Malar. J. 2015, 14, 116. [Google Scholar] [CrossRef] [PubMed]
- Akpalu, W.; Codjoe, S.N.A. Economic Analysis of Climate Variability Impact on Malaria Prevalence: The Case of Ghana. Sustainability 2013, 5, 4362–4378. [Google Scholar] [CrossRef]
- Hwang, S.-M.; Yoon, S.-J.; Jung, Y.-M.; Kwon, G.-Y.; Jo, S.-N.; Jang, E.-J.; Kwon, M.-O. Assessing the impact of meteorological factors on malaria patients in demilitarized zones in Republic of Korea. Infect. Dis. Poverty 2016, 5, 20. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel Method for Nonlinear Granger Causality. Phys. Rev. Lett. 2008, 200, 144103. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel-Granger Causality and the Analysis of Dynamical Networks. Phys. Rev. E 2008, 77, 056215. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E 2011, 83, 051112. [Google Scholar] [CrossRef] [PubMed]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plot of dynamical systems. Europhys. Lett. 1987, 5, 973–977. [Google Scholar] [CrossRef]
- Yang, A.C.; Peng, C.-K.; Huang, N.E. Causal decomposition in the mutual causation system. Nat. Commun. 2018, 9, 3378. [Google Scholar] [CrossRef]
- Craciunescu, T.; Murari, A.; Gelfusa, M. Improving Entropy Estimates of Complex Network Topology for the Characterization of Coupling in Dynamical Systems. Entropy 2018, 20, 891. [Google Scholar] [CrossRef]
- Wiener, N. The Theory of Prediction; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Information domain approach to the investigation of cardio-vascular, cardiopulmonary and vasculo-pulmonary causal couplings. Front. Physiol. 2011, 2, 80. [Google Scholar] [CrossRef] [PubMed]
- Small, M. Applied Nonlinear Time Series Analysis: Applications in Physics, Physiology and Finance; World Scientific: Singapore, 2005. [Google Scholar]
- Porta, A.; Baselli, G.; Liberati, D.; Montano, N.; Cogliati, C.; Gnecchi-Ruscone, T.; Malliani, A.; Cerutti, S. Measuring regularity by means of a corrected conditional entropy in sympathetic outflow. Biol. Cybern. 1998, 78, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Craciunescu, T.; Murari, A. Geodesic distance on Gaussian Manifolds for the robust identification of chaotic systems. Nonlinear Dyn. 2016, 86, 677–693. [Google Scholar] [CrossRef]
- Mindlin, G.M.; Gilmore, R. Topological analysis and synthesis of chaotic time series. Phys. D 1992, 58, 229–242. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L., Jr. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403. [Google Scholar] [CrossRef] [PubMed]
- Thiel, M.; Romano, M.C.; Kurths, J. How much information is contained in a recurrence plot? Phys. Lett. A 2004, 330, 343–349. [Google Scholar] [CrossRef]
- Donner, R.V.; Zou, Y.; Donges, J.F.; Marwan, N.; Kurths, J. Recurrence networks—a novel paradigm for nonlinear time series analysis. New J. Phys. 2010, 12, 033025. [Google Scholar] [CrossRef]
- Marwan, N. A historical review of recurrence plots. Eur. Phys. J. Spec. Top. 2008, 164, 3–12. [Google Scholar] [CrossRef]
- Romano, M.C.; Thiel, M.; Kurths, J.; Grebogi, C. Estimation of the direction of the coupling by conditional probabilities of recurrence. Phys. Rev. E 2007, 76, 036211. [Google Scholar] [CrossRef] [PubMed]
- Mocenni, C.; Facchini, A.; Vicino, A. Comparison of recurrence quantification methods for the analysis of temporal and spatial chaos. Math. Comput. Model. 2011, 53, 1535–1545. [Google Scholar] [CrossRef]
- Murari, A.; Craciunescu, T.; Peluso, E.; Lerche, E.; Gelfusa, M.; Contributors, J. On efficiency and interpretation of sawteeth pacing with on-axis ICRH modulation in JET. Nucl. Fusion 2017, 57, 126057. [Google Scholar] [CrossRef]
- Murari, A.; Craciunescu, T.; Peluso, E.; Gelfusa, M.; Contributors, J. Detection of causal relations in time series affected by noise in tokamaks using geodesic distance on gaussian manifolds. Entropy 2017, 19, 569. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C.-K. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted data analysis method. Adv. Adapt. Data Anal. 2008, 1, 1–41. [Google Scholar] [CrossRef]
- Hahn, S.L. Hilbert transforms. In The Transforms and Applications Handbook; Poularikas, A.D., Ed.; Chemical Rubber Company: Boca Raton, FL, USA, 1996; Chapter 7. [Google Scholar]
- Mehraban, S.; Shirazi, A.H.; Zamani, M.; Jafari, G.R. Coupling between time series: A network view. EPL 2016, 103, 50011. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nun, J.C. From time series to complex networks: The visibility graph. PNAS 2008, 105, 4972–4975. [Google Scholar] [CrossRef]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E. Querying and Mining of Time Series Data: Experimental Comparison of Representations and Distance Measures. Proc. VLDB Endow. 2008, 1, 1542–1552. [Google Scholar] [CrossRef]
- Iglesias, F.; Kastner, W. Analysis of Similarity Measures in Times Series Clustering for the Discovery of Building Energy Patterns. Energies 2013, 6, 579–597. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Senra Filho, A.C.S.; Fazan, V.P.S.; Felipe, J.C.; Murta Junior, L.O. Two-dimensional sample entropy: Assessing image texture through irregularity. Biomed. Phys. Eng. Express 2016, 2, 045002. [Google Scholar] [CrossRef]
- Rak, R.; Kwapień, J.; Oświęcimka, P.; Zięba, P.; Drożdż, S. Universal features of mountain ridge networks on Earth. J. Complex Netw. 2019, cnz017, 1–21. [Google Scholar]
- NOAA ESRL Physical Sciences Division Data. Available online: https://www.esrl.noaa.gov/psd/data/gridded/index.html (accessed on 10 July 2019).
- S.O.I. (Southern Oscillation Index) Archives. Available online: http://www.bom.gov.au/climate/glossary/soi.shtml (accessed on 10 July 2019).
- Shannon, P.; Markiel, A.; Ozier, O.; Baliga, N.S.; Wang, J.T.; Ramage, D.; Amin, N.; Schwikowski, B.; Ideker, T. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003, 13, 2498–2504. [Google Scholar] [CrossRef] [PubMed]
- Coufal, D.; Jakubík, J.; Jajcay, N.; Hlinka, J.; Krakovská, A.; Paluš, M. Detection of coupling delay: A problem not yet solved. Chaos 2017, 27, 083109. [Google Scholar] [CrossRef]
- Krakovská, A.; Jakubík, J.; Chvosteková, M.; Coufal, D.; Jajcay, N.; Paluš, M. Comparison of six methods for the detection of causality in a bivariate time series. Phys. Rev. E 2018, 97, 042207. [Google Scholar] [CrossRef]

| Method | |||||
|---|---|---|---|---|---|
| Parameter | Kernel Granger Causality | Transfer Entropy | Recurrence Plots | Causal Decomposition | Complex Networks |
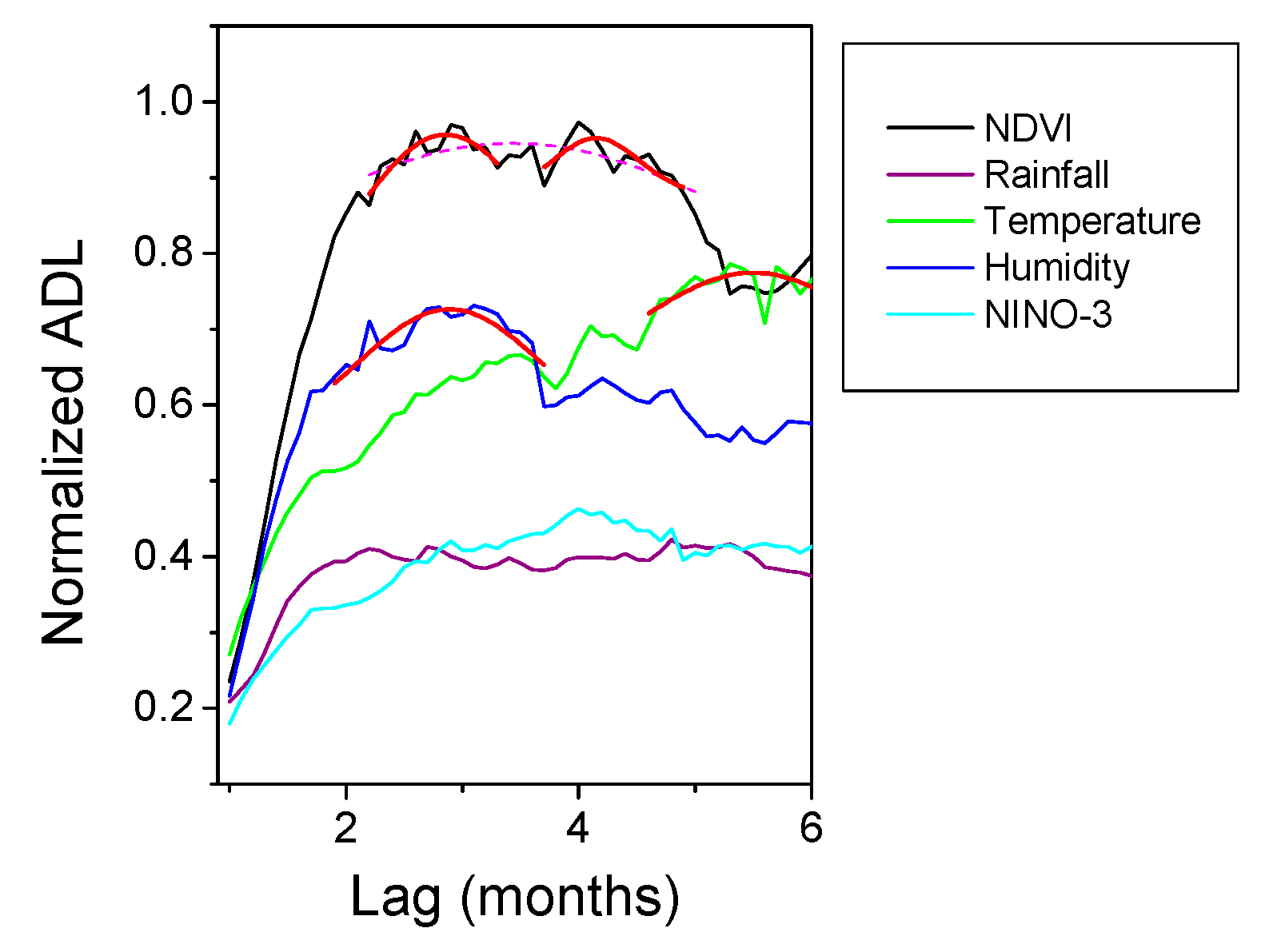
| NDVI | 2.2 | 2.6 | 2.8, 4.2 | [1.7–2.5] | 2.3 |
| Rainfall | - | - | - | - | - |
| Temperature | 5.1 | 4.4 | 5.5 | [4.8–5.5] | 5.4 |
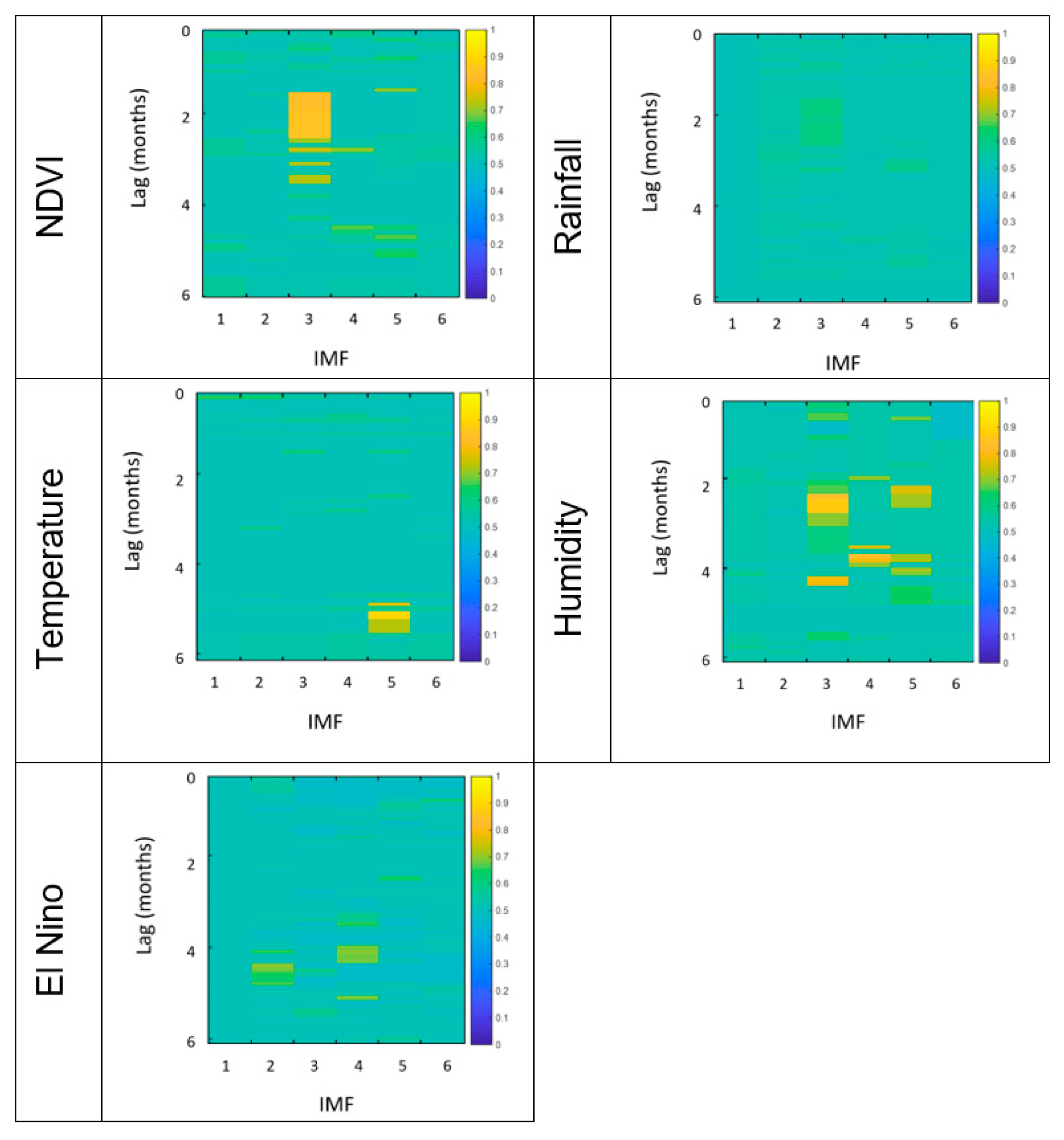
| Humidity | 3.4 | 2.8 | 2.9 | [2.1–2.7] [3.8–4.2] | 3.6 |
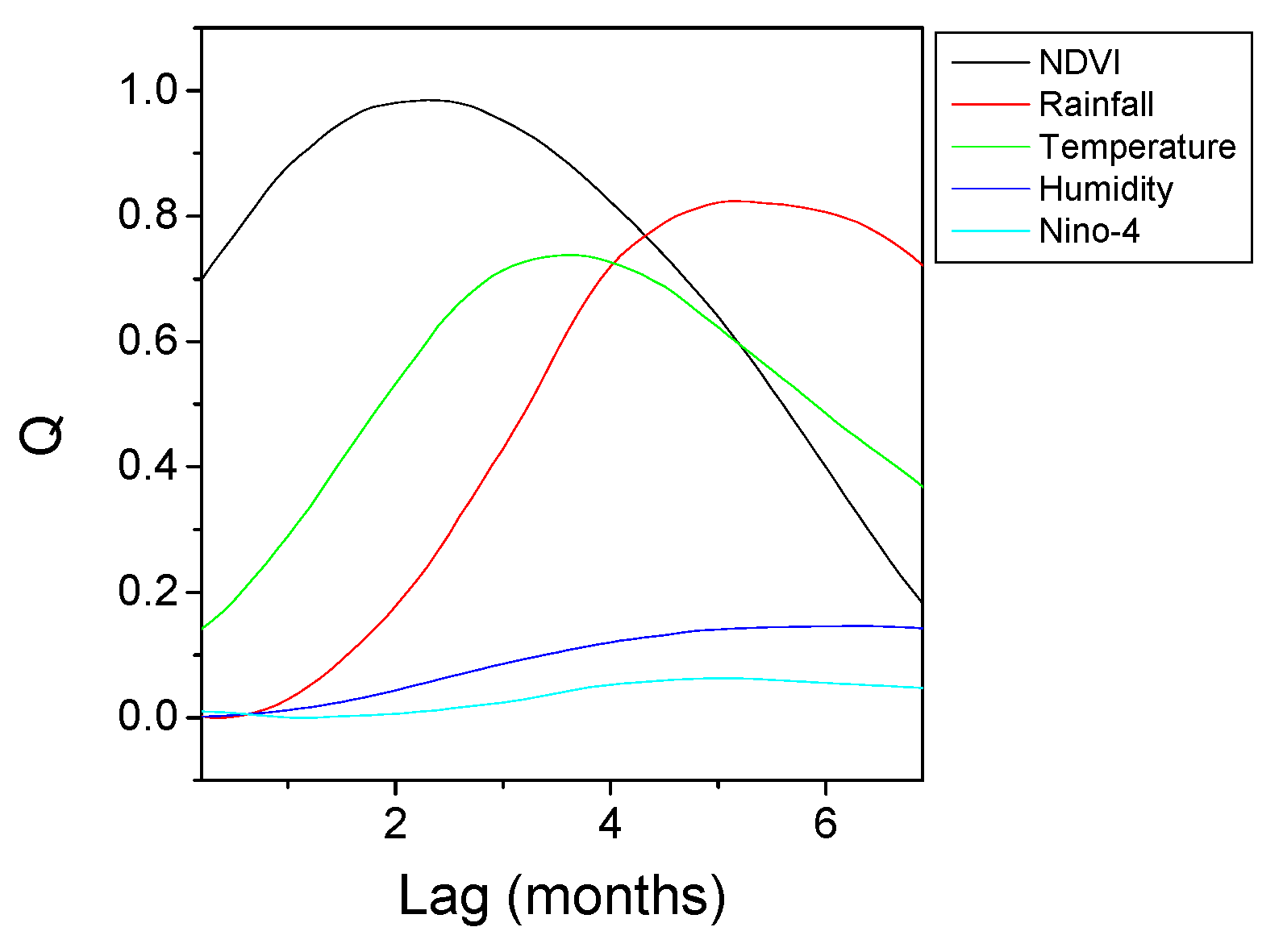
| NINO-3 | - | - | - | [4.0–4.4] | - |
| Method | |||||
|---|---|---|---|---|---|
| Parameter | Kernel Granger Causality | Transfer Entropy | Recurrence Plots | Causal Decomposition | Complex Networks |
| NDVI | 3 | 1 | 1 | 1 | 1 |
| Temperature | 1 | 2 | 2 | 2 | 2 |
| Humidity | 2 | 3 | 3 | 3 | 3 |
| Method | LAG (Months) |
|---|---|
| Kernel Granger causality | 3.35 |
| Transfer Entropy | 3.06 |
| Recurrence plots | 3.18 |
| Causal decomposition | [3.1–3.3] |
| Complex networks | 2.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Craciunescu, T.; Murari, A.; Gelfusa, M. Causality Detection Methods Applied to the Investigation of Malaria Epidemics. Entropy 2019, 21, 784. https://doi.org/10.3390/e21080784
Craciunescu T, Murari A, Gelfusa M. Causality Detection Methods Applied to the Investigation of Malaria Epidemics. Entropy. 2019; 21(8):784. https://doi.org/10.3390/e21080784
Chicago/Turabian StyleCraciunescu, Teddy, Andrea Murari, and Michela Gelfusa. 2019. "Causality Detection Methods Applied to the Investigation of Malaria Epidemics" Entropy 21, no. 8: 784. https://doi.org/10.3390/e21080784
APA StyleCraciunescu, T., Murari, A., & Gelfusa, M. (2019). Causality Detection Methods Applied to the Investigation of Malaria Epidemics. Entropy, 21(8), 784. https://doi.org/10.3390/e21080784







