Secure Service Composition with Quantitative Information Flow Evaluation in Mobile Computing Environments
Abstract
1. Introduction
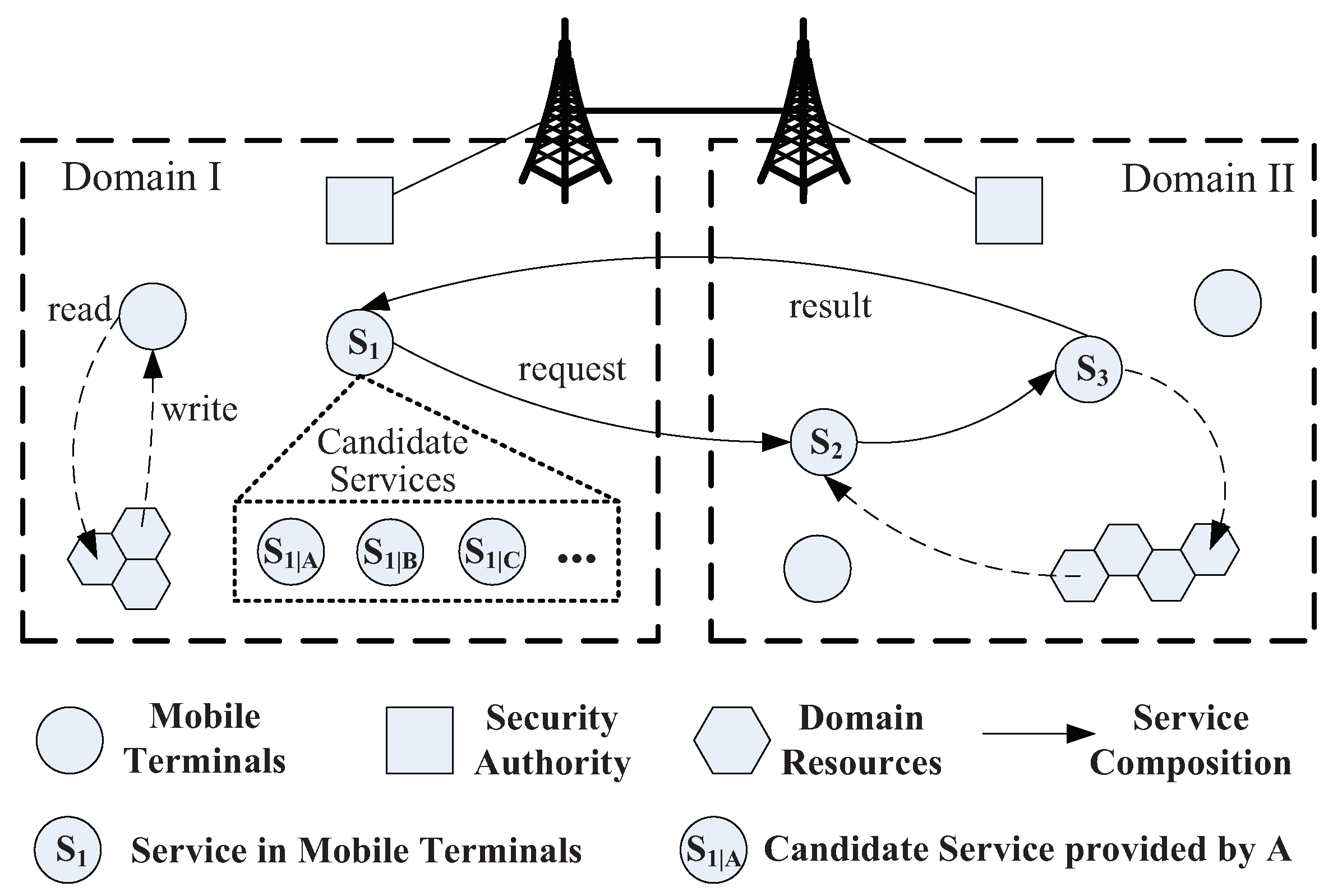
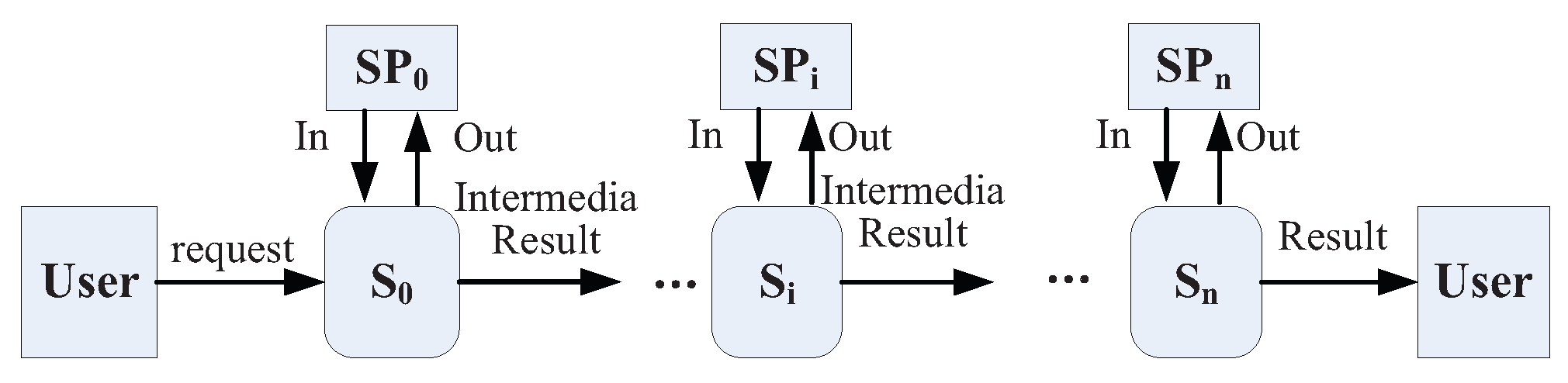
2. Mobile Service System
2.1. System Model
2.2. Threat Model
3. Quantitative Information Flow Model for Service Composition in a Mobile Computing Environment
3.1. Quantitative Information Flow Model Based on Information Theory
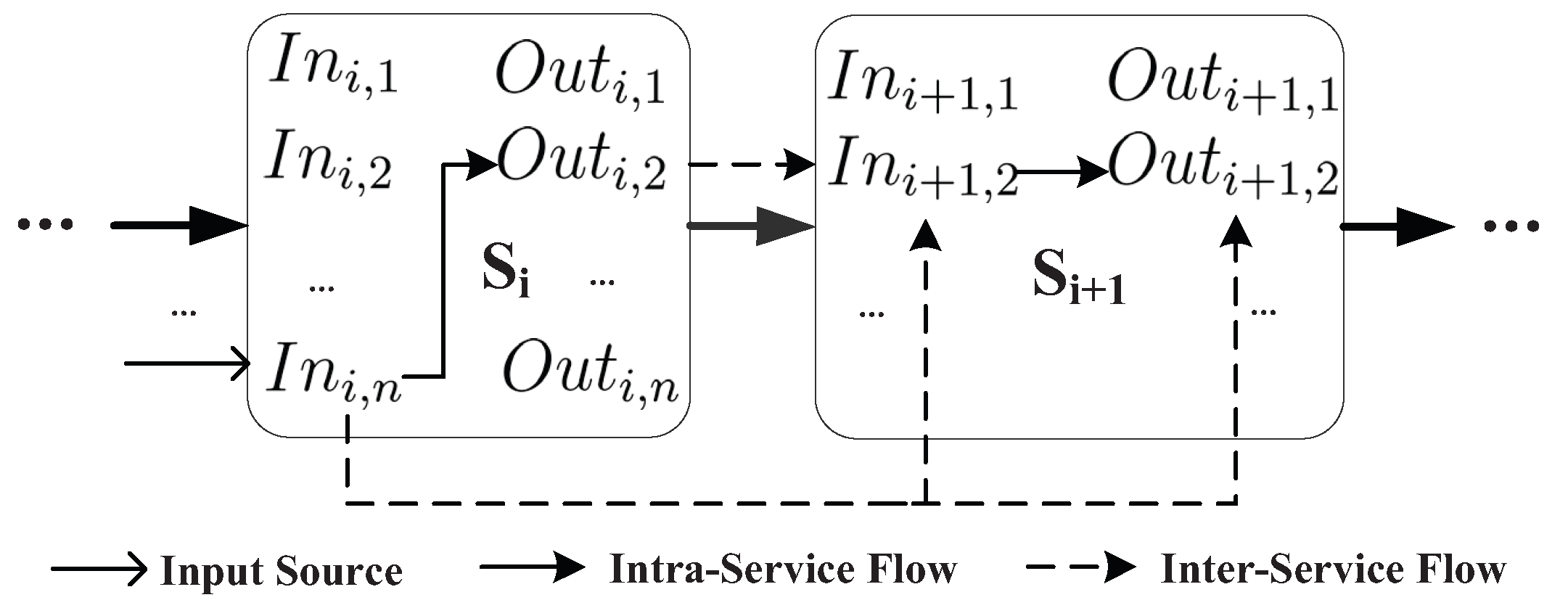
3.2. Quantifying the Information Flow in Service Components
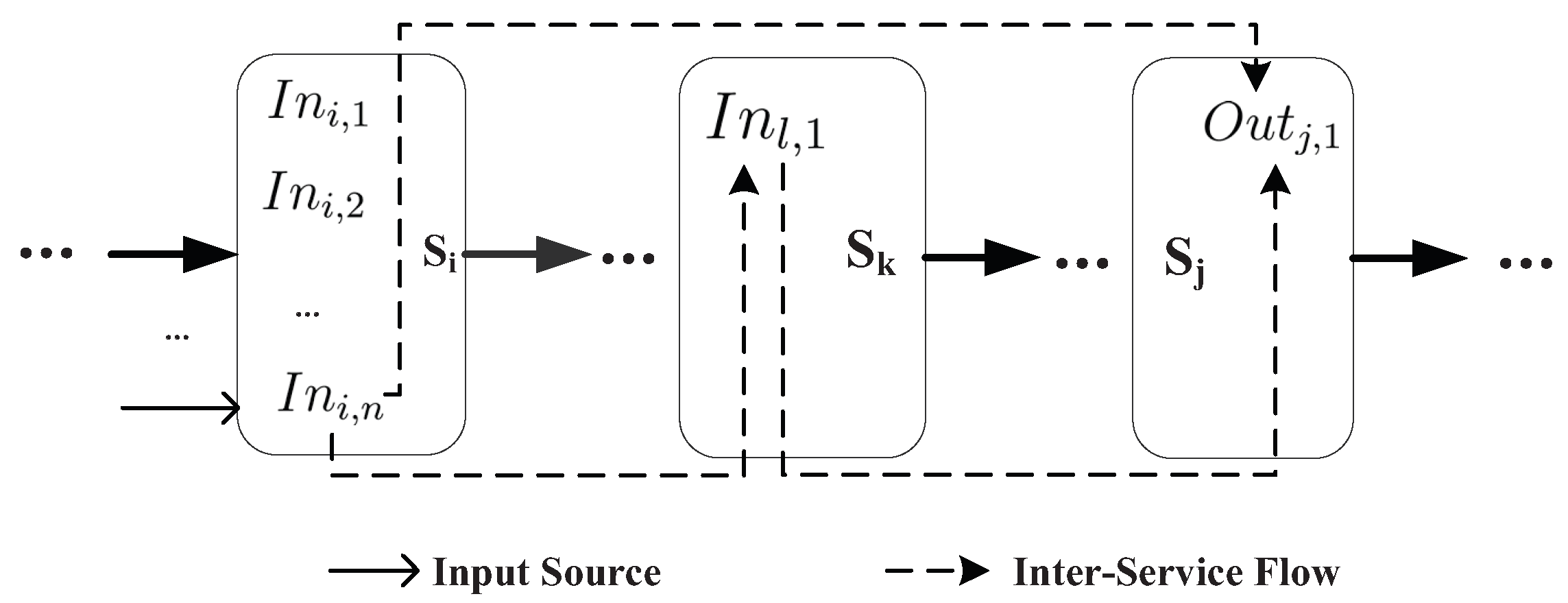
3.3. Quantifying the Information Flow in the Service Chain
4. Distributed Quantitative Information Flow Evaluation for Service Composition in a Mobile Computing Environment
4.1. Intra-Service Evaluation
| public static intCompare(inthin, int lin){ |
| int hout, lout; |
| hout=hin; |
| lout=−1; |
| if(hin>lin) |
| lout=0; |
| else |
| lout=1; |
| } |
| Algorithm 1 |
| Input:, K |
| Output:True or False, . |
|
4.2. Inter-Service Evaluation
| Algorithm 2 |
| Input:, K, , |
| Output: True or False, , . |
|
4.3. Distributed Quantitative Information Flow Evaluation Algorithm for the Service Composition in Mobile Computing Environments
| Algorithm 3 |
| Input:, K |
| Output: |
|
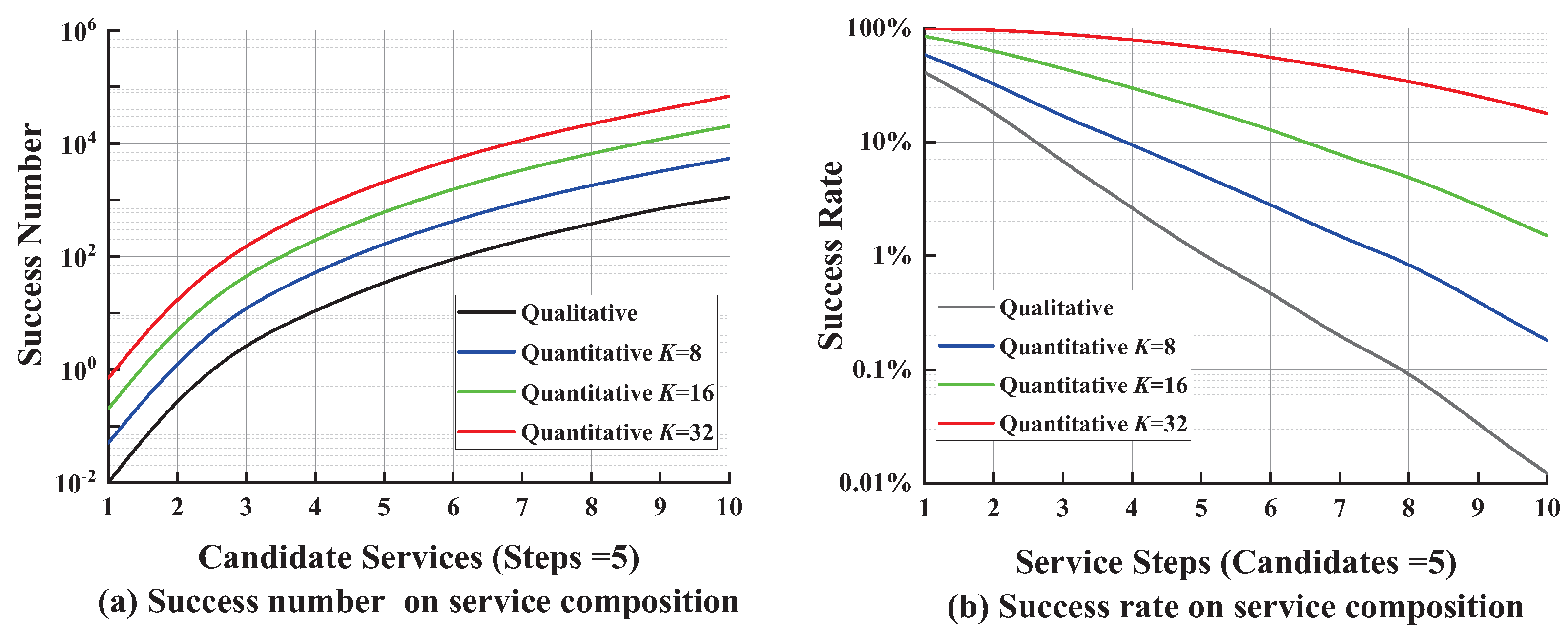
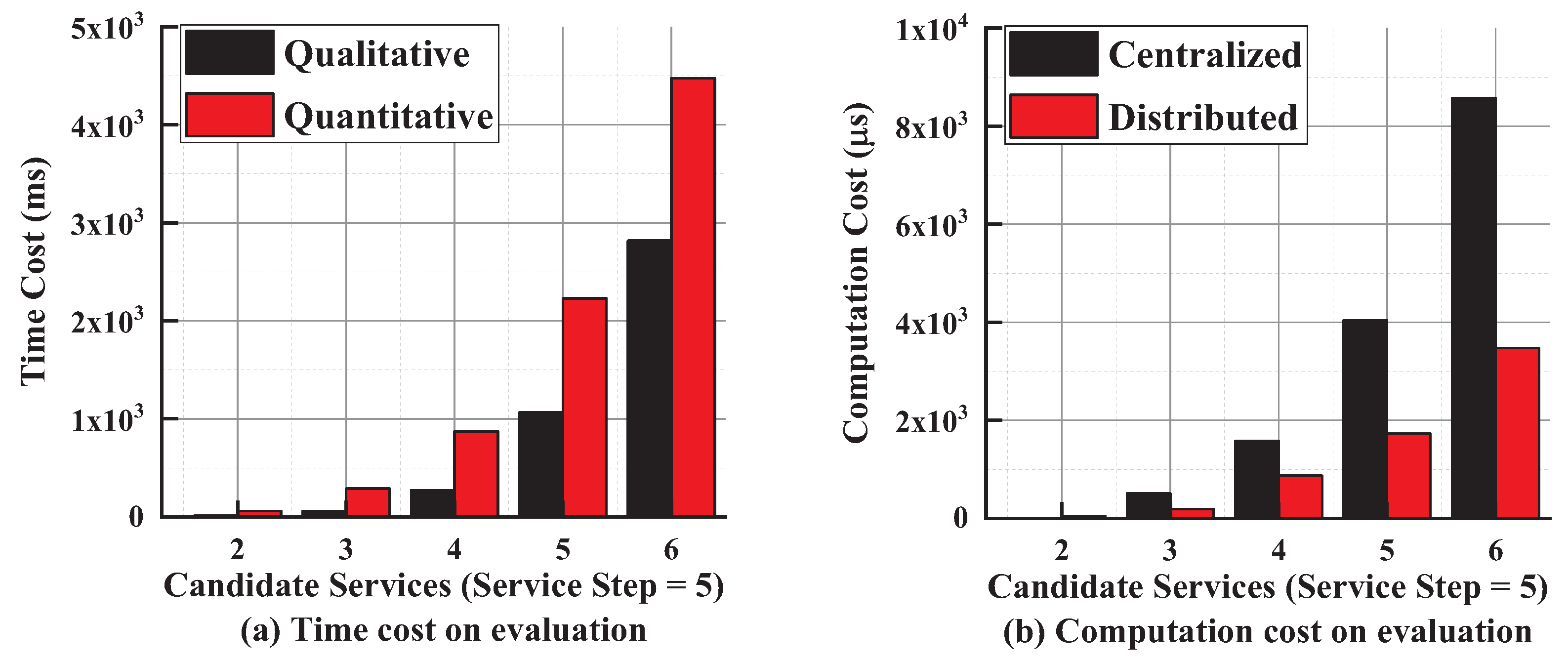
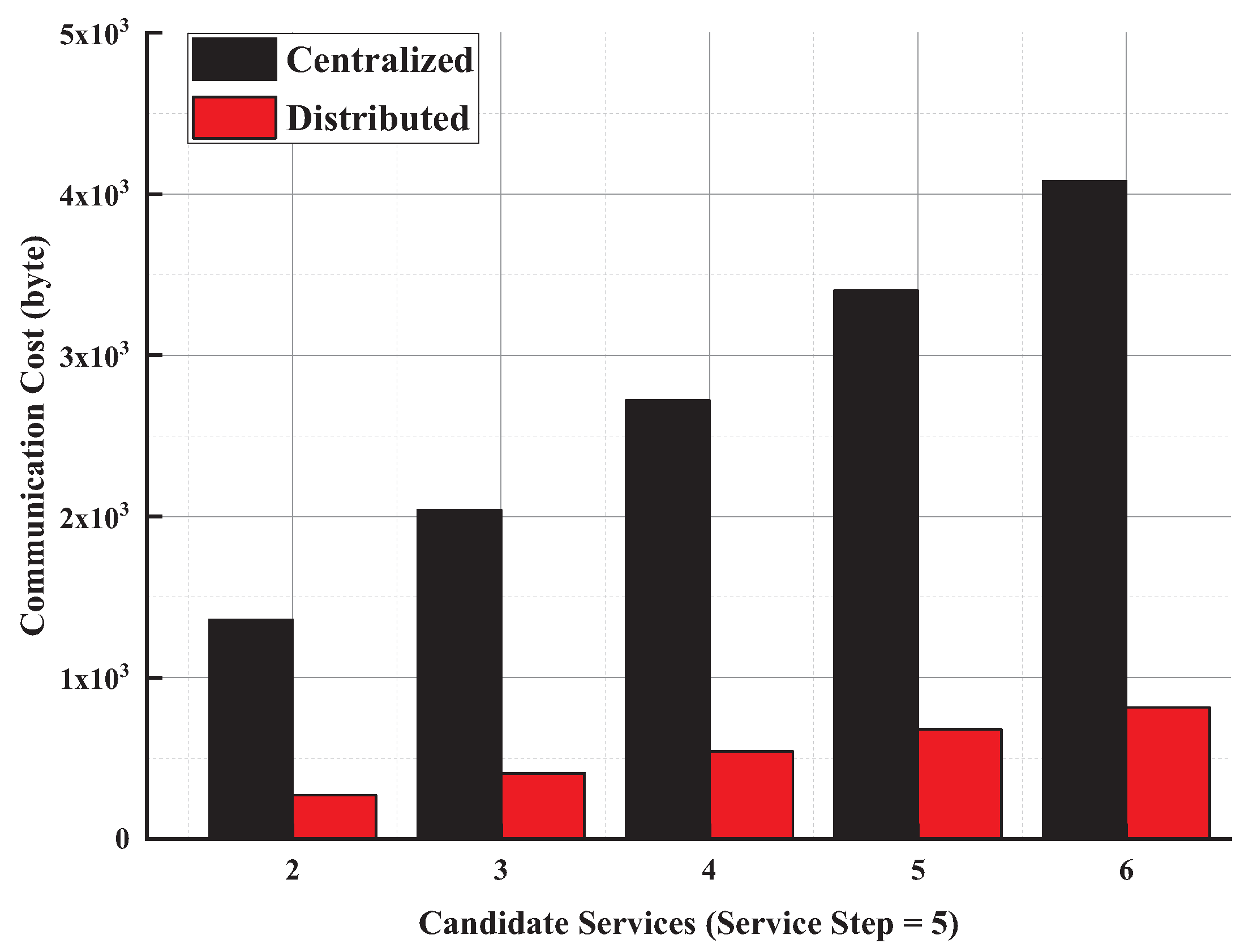
5. Experiments and Evaluations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Lemma 2
References
- Agiwal, M.; Roy, A.; Saxena, N. Next, Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Beshley, H.; Kyryk, M.; Beshley, M.; Panchenko, O. Method of Information Flows Engineering and Resource Distribution in 4G/5G Heterogeneous Network for M2M Service Provisioning. In Proceedings of the 2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Lviv, Ukraine, 20–21 September 2018; pp. 229–233. [Google Scholar] [CrossRef]
- Ngoc, N.C.H.; Lin, D.; Nakaguchi, T.; Ishida, T. QoS-Aware Service Composition in Mobile Environments. In Proceedings of the 2014 IEEE 7th International Conference on Service-Oriented Computing and Applications, Matsue, Japan, 17–19 November 2014; pp. 97–104. [Google Scholar] [CrossRef]
- Ridhawi, Y.A.; Karmouch, A. Decentralized Plan-Free Semantic-Based Service Composition in Mobile Networks. IEEE Trans. Serv. Comput. 2015, 8, 17–31. [Google Scholar] [CrossRef]
- Palade, A.; Clarke, S. Stigmergy-Based QoS Optimisation for Flexible Service Composition in Mobile Communities. In Proceedings of the 2018 IEEE World Congress on Services (SERVICES), San Francisco, CA, USA, 2–7 July 2018; pp. 27–28. [Google Scholar] [CrossRef]
- Deng, S.; Huang, L.; Taheri, J.; Yin, J.; Zhou, M.; Zomaya, A.Y. Mobility-Aware Service Composition in Mobile Communities. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 555–568. [Google Scholar] [CrossRef]
- Xi, N.; Ma, J.; Sun, C.; Zhang, T. Decentralized Information Flow Verification Framework for the Service Chain Composition in Mobile Computing Environments. In Proceedings of the 2013 IEEE 20th International Conference on Web Services, Santa Clara, CA, USA, 27 June–2 July 2013; pp. 563–570. [Google Scholar] [CrossRef]
- Bertino, E.; Squicciarini, A.C.; Mevi, D. A fine-grained access control model for web services. In Proceedings of the IEEE International Conference on Services Computing (SCC 2004), Shanghai, China, 15–18 September 2004; pp. 33–40. [Google Scholar]
- Bhatti, R.; Bertino, E.; Ghafoor, A. A trust-based context-aware access control model for web-services. Distrib. Parallel Databases 2005, 18, 83–105. [Google Scholar] [CrossRef]
- Hutter, D.; Volkamer, M. Information Flow Control to Secure Dynamic Web Service Composition; SPC; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3934, pp. 196–210. [Google Scholar]
- Nakajima, S. Model-Checking of Safety and Security Aspects in Web Service Flows; ICWE; Springer: Munich, Germany, 2004; Volume 3140, pp. 488–501. [Google Scholar]
- Rossi, S. Model Checking Adaptive Multilevel Service Compositions; FACS; Springer: Guimaraes, Portugal, 2010; pp. 106–124. [Google Scholar]
- She, W.; Yen, I.L.; Thuraisingham, B.; Huang, S.Y. Rule-Based Run-Time Information Flow Control in Service Cloud. In Proceedings of the 2011 IEEE International Conference on Web Services, Washington, DC, USA, 4–9 July 2011; pp. 524–531. [Google Scholar] [CrossRef]
- She, W.; Yen, I.L.; Thuraisingham, B.; Bertino, E. Security-aware service composition with fine-grained information flow control. Serv. Comput. IEEE Trans. 2013, 6, 330–343. [Google Scholar] [CrossRef]
- Schwartz, E.J.; Avgerinos, T.; Brumley, D. All You Ever Wanted to Know about Dynamic Taint Analysis and Forward Symbolic Execution (but Might Have Been Afraid to Ask). In Proceedings of the 2010 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 16–19 May 2010; pp. 317–331. [Google Scholar] [CrossRef]
- Schuette, J.; Brost, G.S. LUCON: Data Flow Control for Message-Based IoT Systems. In Proceedings of the 2018 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/12th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 289–299. [Google Scholar] [CrossRef]
- Denning, D.E. A Lattice Model of Secure Information Flow. Commun. ACM 1976, 19, 236–243. [Google Scholar] [CrossRef]
- Smith, G. Recent Developments in Quantitative Information Flow (Invited Tutorial). In Proceedings of the 2015 30th Annual ACM/IEEE Symposium on Logic in Computer Science, Kyoto, Japan, 6–10 July 2015; pp. 23–31. [Google Scholar] [CrossRef]
- Clark, D.; Hunt, S.; Malacaria, P. Quantitative Information Flow, Relations and Polymorphic Types. J. Log. Comput. 2005, 15, 181–199. [Google Scholar] [CrossRef]
- Clark, D.; Hunt, S.; Malacaria, P. A static analysis for quantifying information flow in a simple imperative language. J. Comput. Secur. 2007, 15, 321–371. [Google Scholar] [CrossRef]
- Backes, M.; Kopf, B.; Rybalchenko, A. Automatic Discovery and Quantification of Information Leaks. In Proceedings of the 2009 30th IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 17–20 May 2009; IEEE Computer Society: Washington, DC, USA, 2009; pp. 141–153. [Google Scholar] [CrossRef]
- Smith, D.M.; Smith, G. Tight Bounds on Information Leakage from Repeated Independent Runs. In Proceedings of the 2017 IEEE 30th Computer Security Foundations Symposium (CSF), Santa Barbara, CA, USA, 21–25 August 2017; pp. 318–327. [Google Scholar] [CrossRef]
- Zhou, B.; Shi, Q.; Yang, P. A Survey on Quantitative Evaluation of Web Service Security. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 715–721. [Google Scholar] [CrossRef]
- Clark, D.; Hunt, S.; Malacaria, P. Quantitative Analysis of the Leakage of Confidential Data. Electron. Notes Theor. Comput. Sci. 2002, 59, 238–251. [Google Scholar] [CrossRef]
- Xi, N.; Sun, C.; Ma, J.; Shen, Y. Secure service composition with information flow control in service clouds. Future Gener. Comput. Syst. 2015, 49, 142–148. [Google Scholar] [CrossRef]
- Ferrante, J.; Ottenstein, K.J.; Warren, J.D. The Program Dependence Graph and Its Use in Optimization. ACM Trans. Program. Lang. Syst. 1987, 9, 319–349. [Google Scholar] [CrossRef]
- Snelting, G.; Robschink, T.; Krinke, J. Efficient Path Conditions in Dependence Graphs for Software Safety Analysis. ACM Trans. Softw. Eng. Methodol. 2006, 15, 410–457. [Google Scholar] [CrossRef]
| Approach | Mode | Service Composition | |
|---|---|---|---|
| Our Approach | Quantitative | Distributed | √ |
| She et al. [13,14] | Qualitative | Centralized | √ |
| Xi et al. [25] | Qualitative | Distributed | √ |
| Clark et al. [20,24] | Quantitative | Centralized | × |
| Smith et al. [22] | Quantitative | Centralized | × |
| Mobile Environment | |
| Network Type | WLAN |
| Network Speed | 150 Mbps |
| Mobile Mode | random walk |
| Mobile Devices | Huawei nova 3 |
| Device’s CPU and RAM | 2.8 GHz, 6 G |
| Mobile Device’s Operation System | Android 9.0 |
| Data Set | |
| Service Step | 1–10 |
| Candidate Number | 1–10 |
| Security Level | H, L |
| High Level Input and Output | 2, 2 |
| Low Level Input and Output | 2, 2 |
| Flows between Input and Output | randomly generated |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, N.; Lv, J.; Sun, C.; Ma, J. Secure Service Composition with Quantitative Information Flow Evaluation in Mobile Computing Environments. Entropy 2019, 21, 753. https://doi.org/10.3390/e21080753
Xi N, Lv J, Sun C, Ma J. Secure Service Composition with Quantitative Information Flow Evaluation in Mobile Computing Environments. Entropy. 2019; 21(8):753. https://doi.org/10.3390/e21080753
Chicago/Turabian StyleXi, Ning, Jing Lv, Cong Sun, and Jianfeng Ma. 2019. "Secure Service Composition with Quantitative Information Flow Evaluation in Mobile Computing Environments" Entropy 21, no. 8: 753. https://doi.org/10.3390/e21080753
APA StyleXi, N., Lv, J., Sun, C., & Ma, J. (2019). Secure Service Composition with Quantitative Information Flow Evaluation in Mobile Computing Environments. Entropy, 21(8), 753. https://doi.org/10.3390/e21080753





