A Self-Adaptive Discrete PSO Algorithm with Heterogeneous Parameter Values for Dynamic TSP
Abstract
:1. Introduction
1.1. Self-Adaptivity
1.2. Contributions
- We propose a method for automatically setting the values of four crucial DPSO parameters. This method is based on discrete probability distributions defined to diversify the behaviors of the particles in the heterogeneous DPSO. The aim of this diversification is to improve the convergence of the algorithm.
- We perform an analysis of the convergence of the proposed algorithm based on computational experiments conducted on a set of DTSP instances of varying sizes. We discuss the relationships between the values of the DPSO parameters and their effect on particle movement through the problem’s solution search space.
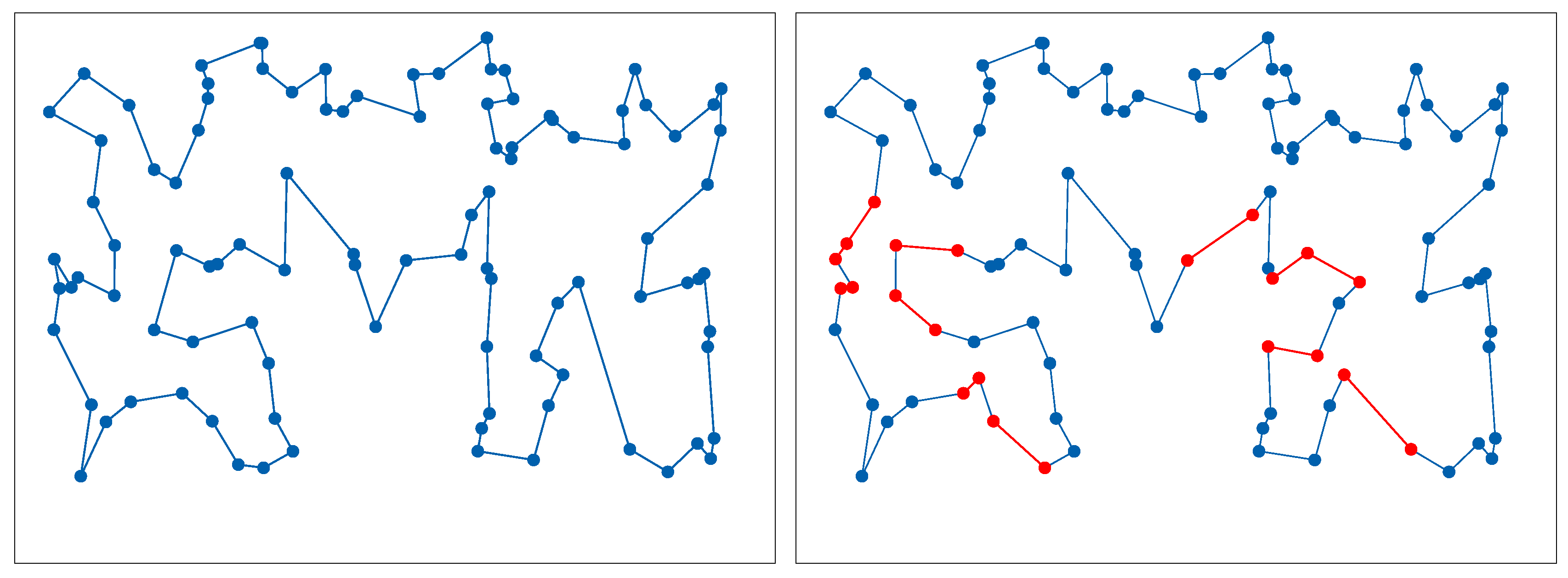
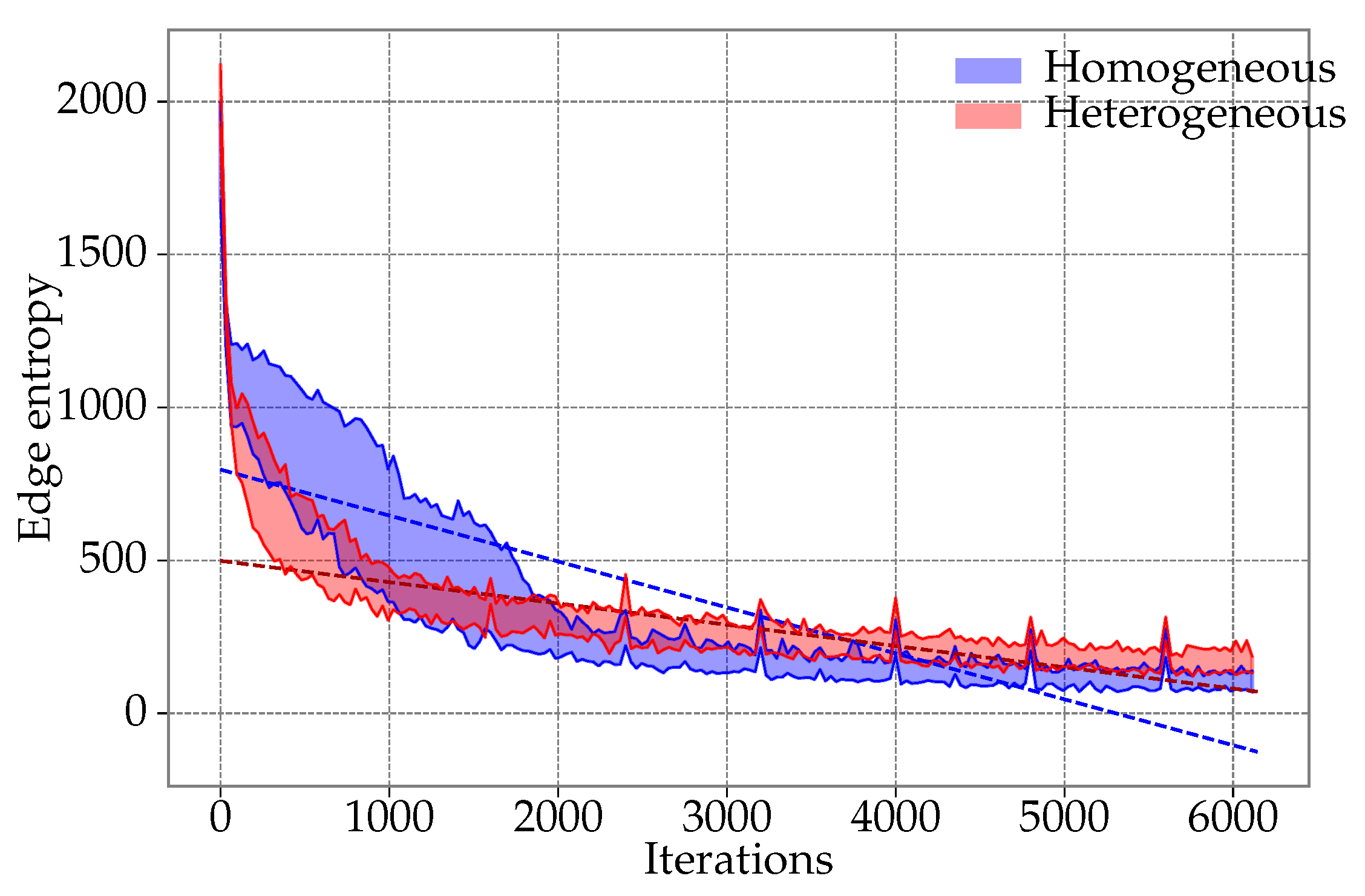
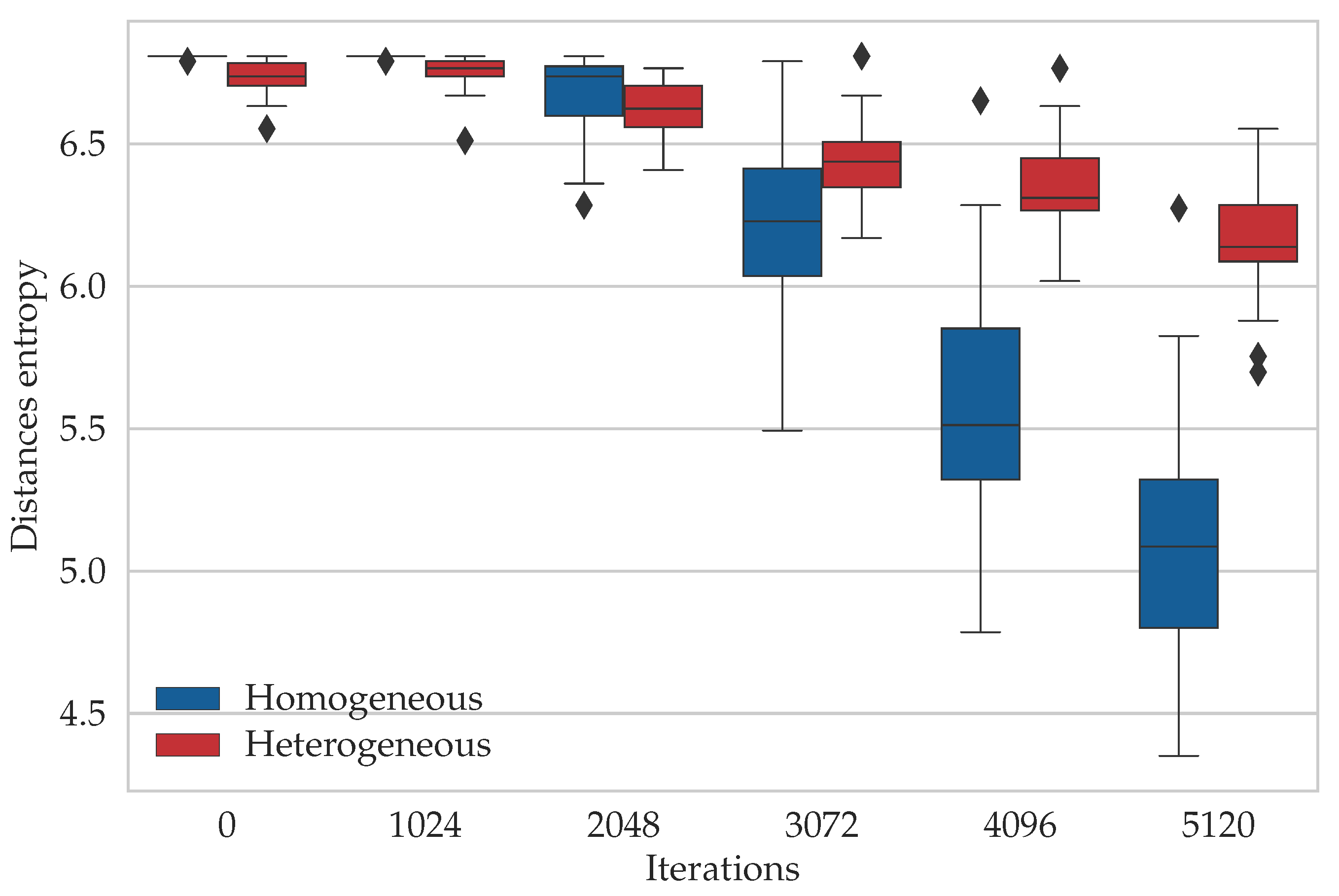
- We study the diversity of the population of particles in the proposed heterogeneous DPSO and the original approach based on the information entropy calculated in two ways. The former method considers the edges, which are building blocks of the solutions to the TSP and DTSP. The latter focuses only on the quality of the solutions
- We compare the efficiency of the proposed heterogeneous DPSO with that of the base DPSO and two algorithms based on ant colony optimization (ACO). The results show that the proposed algorithm outperforms the base DPSO and is competitive with the ACO-based algorithms.
2. Dynamic Traveling Salesman Problem
3. Heterogeneity
- Neighborhood heterogeneity: This concerns cases in which the size of the neighborhood is different for every particle, and hence, the virtual topology of connections between particles is not regular. Some particles can have a wider influence than others on the movement of the swarm.
- Best-particle heterogeneity: Here, there can be variations in the method of selecting the best particle, i.e., the particle whose position is used when updating the current velocity and position. For instance, one particle might update its position following the best particle in its (small) neighborhood, while the second particle might be fully informed and follow the global best particle.
- Heterogeneity of the position update strategy: Here, the particles differ in their patterns of movement (searching) through the solution space. For example, one group of particles might explore the solution space, while the other group might conduct a local search by restricting their velocities or even positions to a certain range. This type of heterogeneity diversifies the population to the greatest extent, since it provides the greatest flexibility in diversifying particle movement.
- Heterogeneity of parameter values: Here, each particle or group of particles in the swarm can have different values of the parameters. For example, some particles might have a large inertia and explore the solution space, whereas other particles might have a small value of and perform the search locally (around the best position found). Although this type of heterogeneity is not as flexible as the heterogeneity of the position update strategy, it requires relatively few changes to the PSO, since only the values of the particle parameters need be set individually. It is this strategy that we apply in the proposed heterogeneous DPSO algorithm.
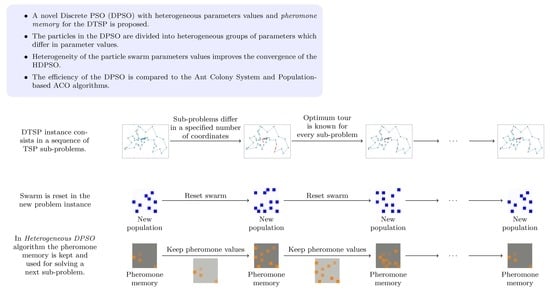
4. DPSO with Pheromone
- It alters the probability of edge selection during the solution construction process; i.e., the higher the value of the pheromone, the greater is the probability of selecting the corresponding edge. In other words, the pheromone serves as an additional memory of the swarm, allowing it to learn the structure of high-quality solutions and, potentially, improve the convergence of the algorithm.
- The pheromone matrix created while solving the current DTSP sub-problem is retained and used when solving the next sub-problem. This allows knowledge about the previous solution search space to be transferred with the aim of helping the construction of high-quality solutions to the current sub-problem. This implicitly assumes that the changes between consecutive sub-problems are not very great, so that the high-quality solutions to the current sub-problem share most of their structure with the high-quality solutions to the previous one.
5. Heterogeneous Swarm
- : = 0.4, = 0.15, = 0.3, = 0.15;
- and : = 0.4, = 0.15, = 0.15, = 0.3;
- : = 0.4, = 0.2, = 0.4.
6. Experimental Results
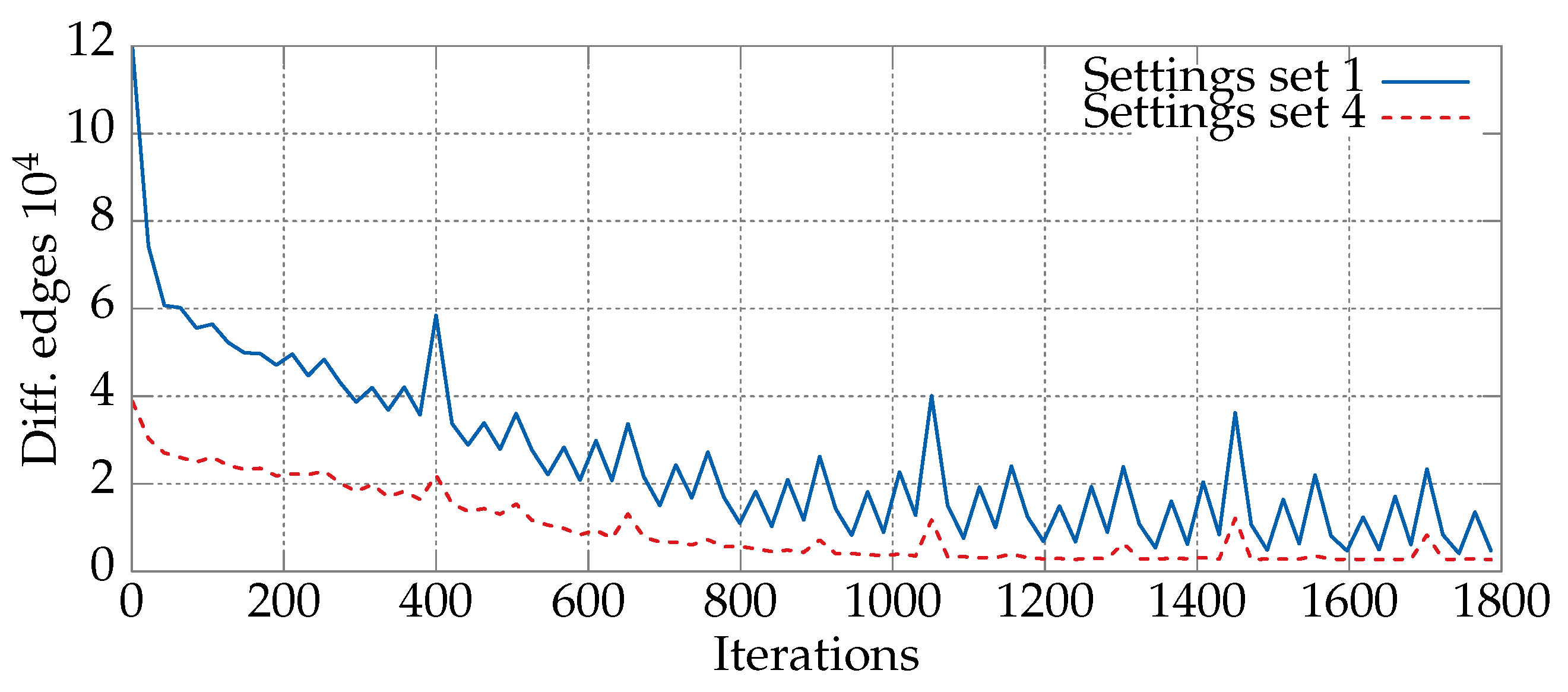
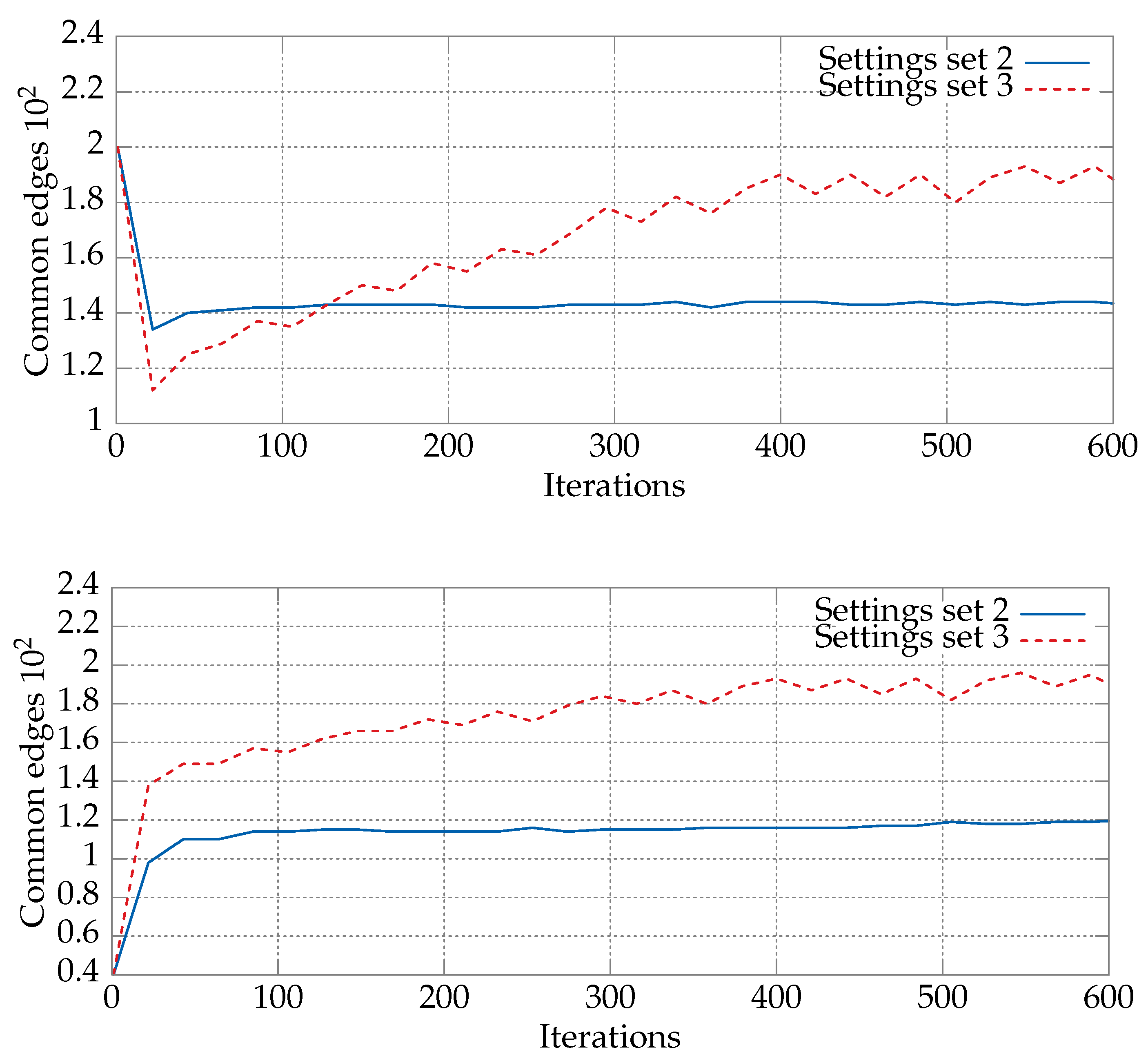
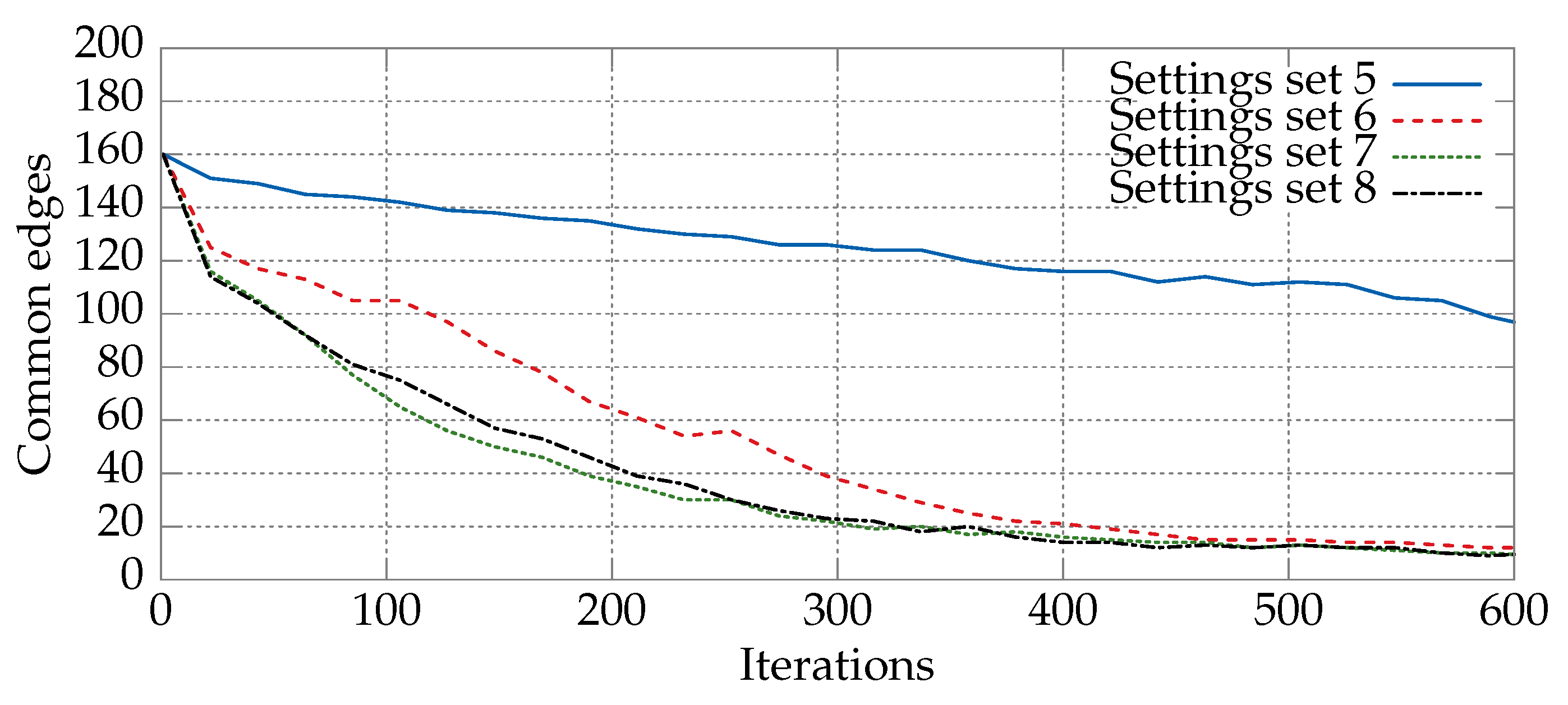
6.1. Convergence Analysis for Various Sets of Parameters
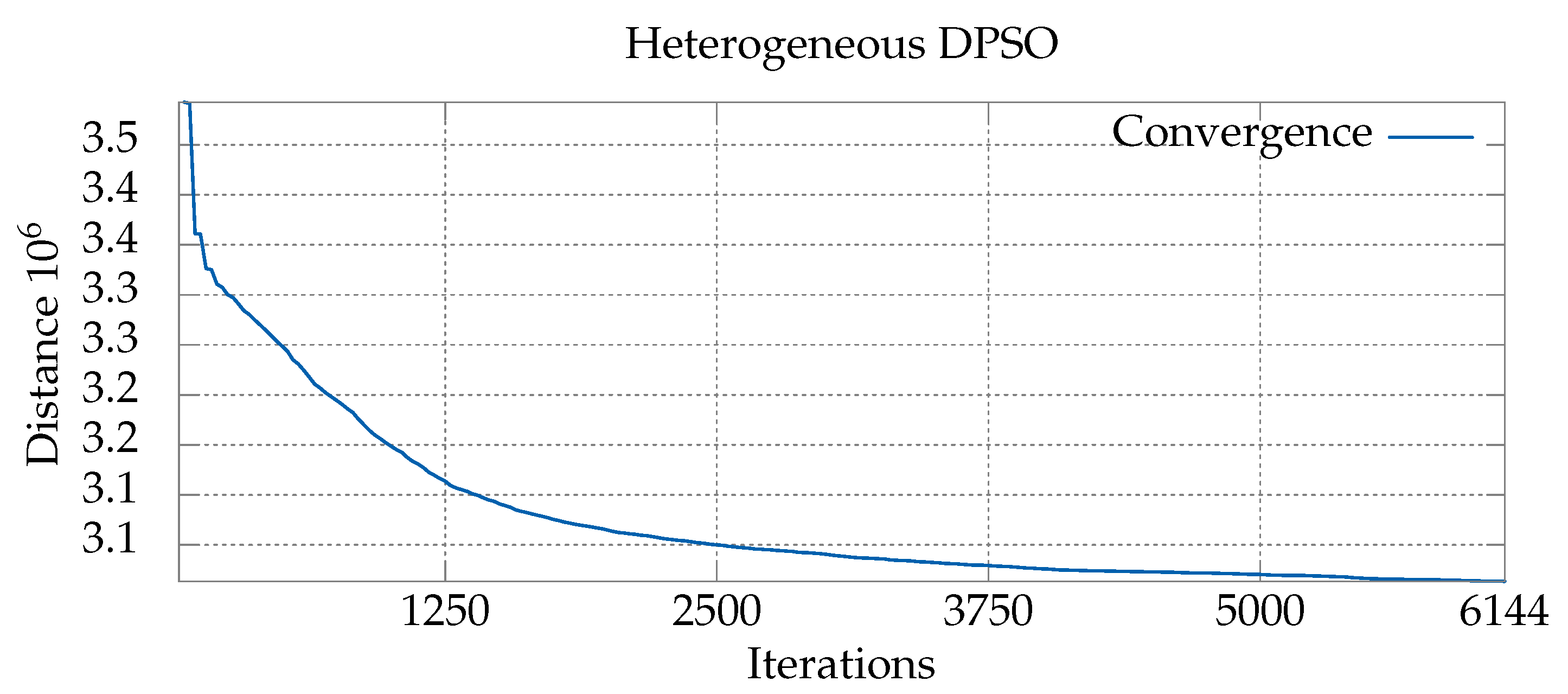
6.2. Comparative Study
| Algorithm 1 Outline of the procedure for solving the DTSP. |
|
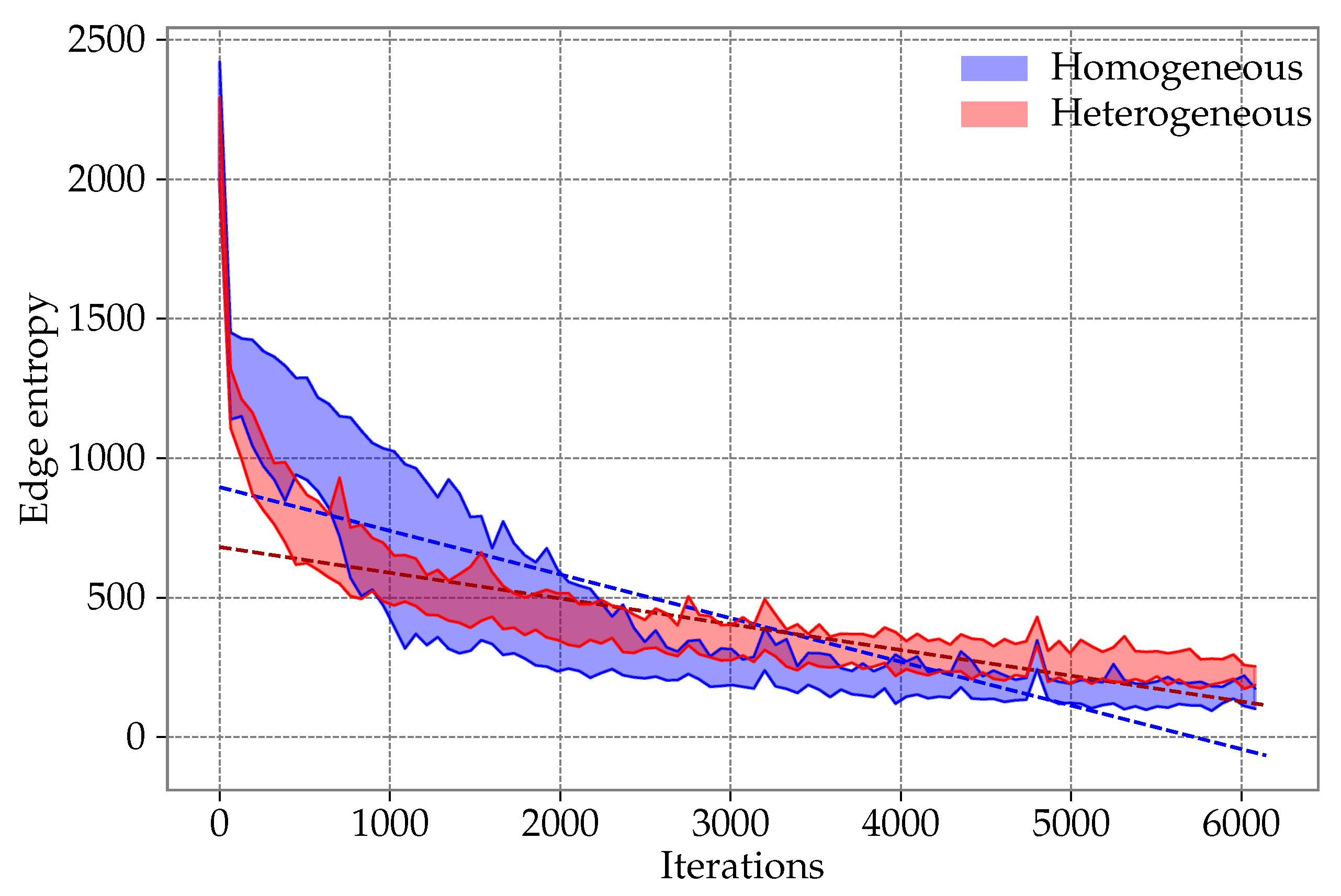
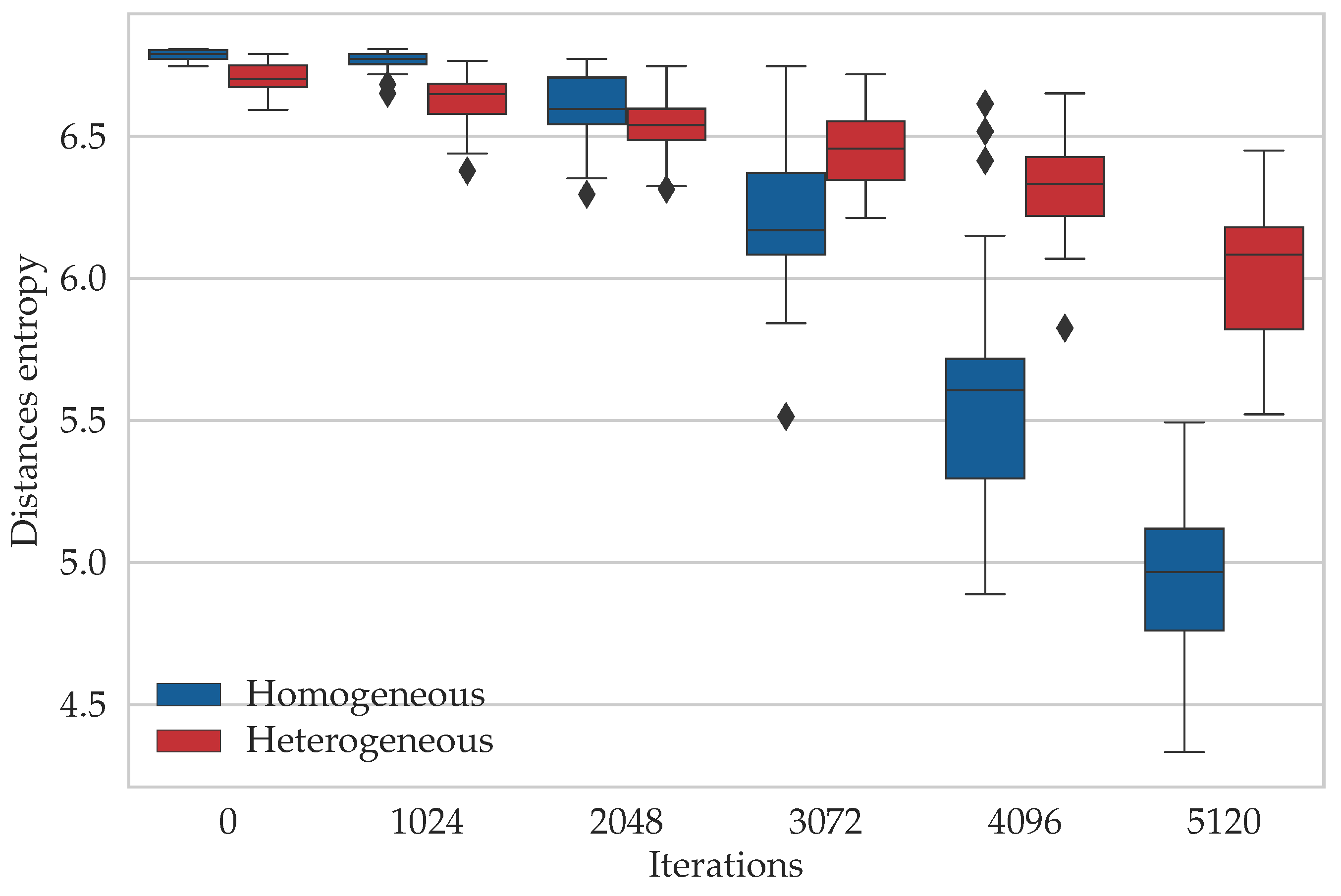
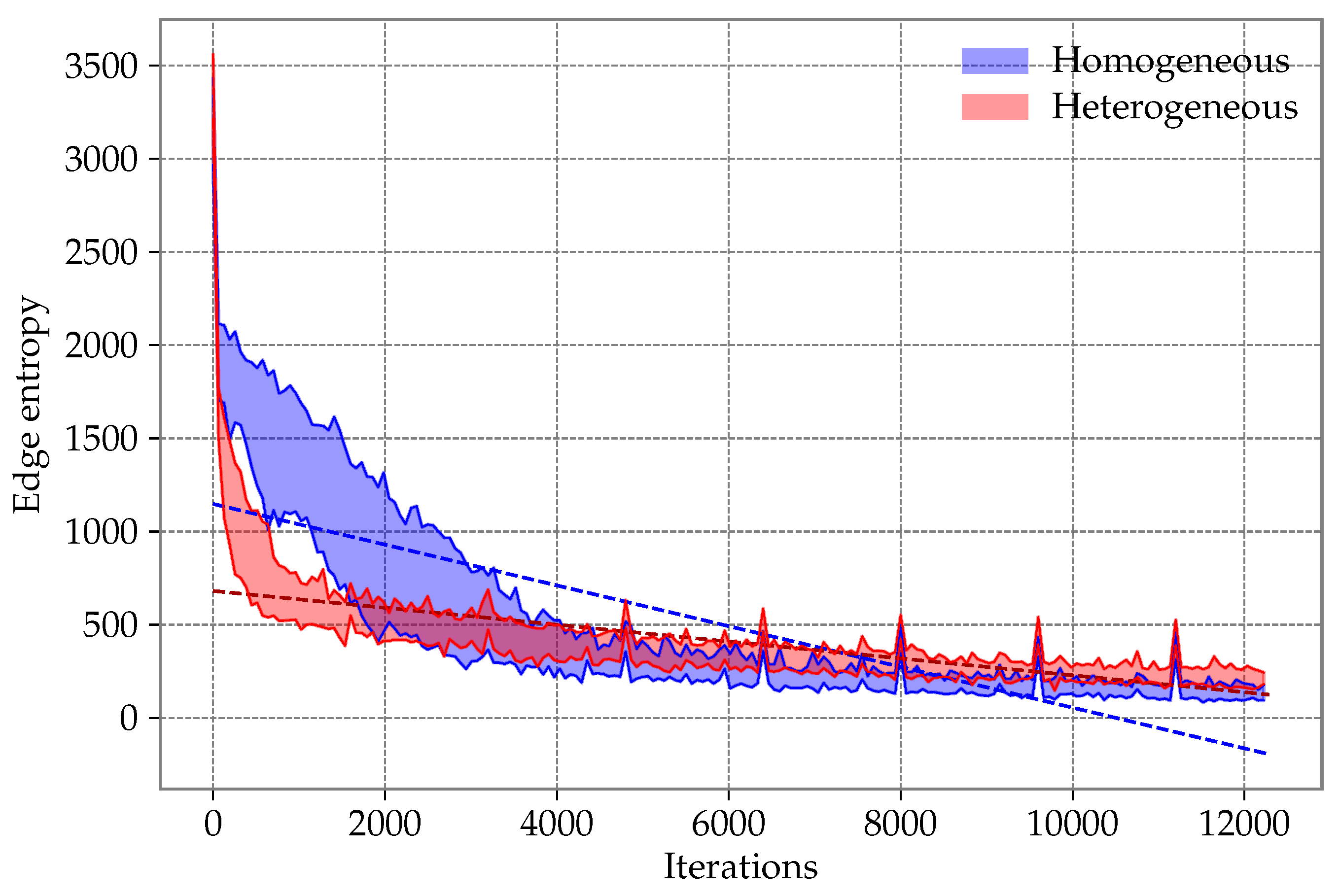
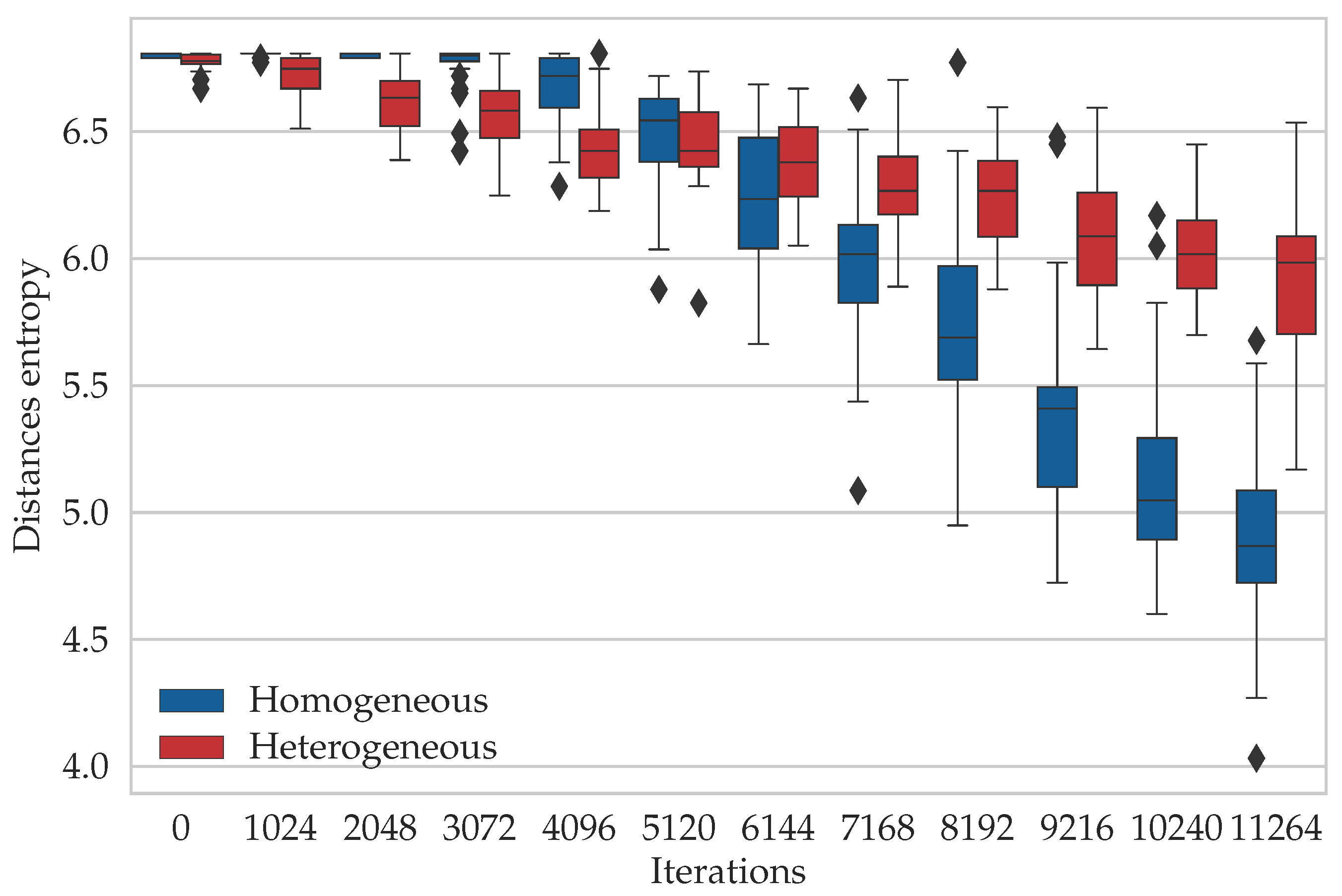
6.3. Entropy Study
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACO | ant colony optimization |
| DPSO | discrete particle swarm optimization |
| DTSP | dynamic traveling salesman problem |
| PACO | population ant colony optimization |
| PSO | particle swarm optimization |
| TSP | traveling salesman problem |
Appendix A. The Entropy Study for the Other TSP Instances
References
- Branke, J. Evolutionary approaches to dynamic environments. In Proceedings of the GECCO Workshop on Evolutionary Algorithms for Dynamics Optimization Problems, San Francisco, CA, USA, 7–11 July 2001. [Google Scholar]
- Li, W. A parallel multi-start search algorithm for dynamic traveling salesman problem. In Proceedings of the International Symposium on Experimental Algorithms, Crete, Greece, 5–7 May 2011; pp. 65–75. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Clerc, M. Discrete Particle Swarm Optimization, illustrated by the Traveling Salesman Problem. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; Volume 141, pp. 219–239. [Google Scholar]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, Q. Particle swarm optimization-based algorithms for TSP and generalized TSP. Inf. Process. Lett. 2007, 103, 169–176. [Google Scholar] [CrossRef]
- Chen, W.N.; Zhang, J.; Chung, H.S.; Zhong, W.L.; Wu, W.G.; Shi, Y.H. A Novel Set-Based Particle Swarm Optimization Method for Discrete Optimization Problems. IEEE Trans. Evol. Comput. 2010, 14, 3283–3287. [Google Scholar]
- Strąk, Ł.; Skinderowicz, R.; Boryczka, U. Adjustability of a discrete particle swarm optimization for the dynamic TSP. Soft Comput. 2018, 22, 7633–7648. [Google Scholar] [CrossRef]
- Hansell, M. Built by Animals; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Nepomuceno, F.V.; Engelbrecht, A.P. A Self-adaptive Heterogeneous PSO Inspired by Ants. In Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7461, pp. 188–195. [Google Scholar] [CrossRef]
- Montes de Oca, M.A.; Peña, J.; Stützle, T.; Pinciroli, C.; Dorigo, M. Heterogeneous Particle Swarm Optimizers. In IEEE Congress on Evolutionary Computation (CEC 2009); Haddow, P., Ed.; IEEE Press: Piscatway, NJ, USA, 2009; pp. 698–705. [Google Scholar]
- Ravindranathan, M.; Leitch, R. Heterogeneous intelligent control systems. IEE Proc. Control Theory Appl. 1998, 145, 551–558. [Google Scholar] [CrossRef]
- Macías-Escrivá, F.D.; Haber, R.; Del Toro, R.; Hernandez, V. Self-adaptive systems: A survey of current approaches, research challenges and applications. Expert Syst. Appl. 2013, 40, 7267–7279. [Google Scholar] [CrossRef]
- Meyer-Nieberg, S.; Beyer, H.G. Self-adaptation in evolutionary algorithms. In Parameter Setting in Evolutionary Algorithms; Springer: Berlin/Heidelberg, Germany, 2007; pp. 47–75. [Google Scholar]
- Qin, A.K.; Suganthan, P.N. Self-adaptive differential evolution algorithm for numerical optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 2, pp. 1785–1791. [Google Scholar]
- Jiang, Y.; Li, X.; Huang, C. Automatic calibration a hydrological model using a master–slave swarms shuffling evolution algorithm based on self-adaptive particle swarm optimization. Expert Syst. Appl. 2013, 40, 752–757. [Google Scholar] [CrossRef]
- Boryczka, U.; Strąk, L. Heterogeneous DPSO Algorithm for DTSP. In Computational Collective Intelligence; Núñez, M., Nguyen, N.T., Camacho, D., Trawiński, B., Eds.; Springer: Cham, Switzerland, 2015; Volume 9330, pp. 119–128. [Google Scholar]
- Psaraftis, H. Dynamic vehicle routing problems. Veh. Routing Methods Stud. 1988, 16, 223–248. [Google Scholar]
- Li, C.; Yang, M.; Kang, L. A new approach to solving dynamic traveling salesman problems. In Proceedings of the 6th international conference on Simulated Evolution And Learning, Hefei, China, 15–18 October 2006; pp. 236–243. [Google Scholar]
- Cook, W.J. In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Guntsch, M.; Middendorf, M. Pheromone Modification Strategies for Ant Algorithms Applied to Dynamic TSP. In Applications of Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2037, pp. 213–222. [Google Scholar]
- Eyckelhof, C.J.; Snoek, M. Ant Systems for a Dynamic TSP. In Ant Algorithms; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2463, pp. 88–99. [Google Scholar]
- Helsgaun, K. An Effective Implementation of the Lin-Kernighan Traveling Salesman Heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Yang, S. Ant Colony Optimization with Immigrants Schemes in Dynamic Environments. In Parallel Problem Solving from Nature, PPSN XI; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6239, pp. 371–380. [Google Scholar]
- Simões, A.; Costa, E. CHC-Based Algorithms for the Dynamic Traveling Salesman Problem. In Applications of Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6624, pp. 354–363. [Google Scholar]
- Younes, A.; Basir, O.; Calamai, P. A Benchmark Generator for Dynamic Optimization. In Proceedings of the 3rd WSEAS International Conference on Soft Computing, Optimization, Simulation & Manufacturing Systems, Malta, 1–3 September 2003. [Google Scholar]
- Tinós, R.; Whitley, D.; Howe, A. Use of Explicit Memory in the Dynamic Traveling Salesman Problem. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 999–1006. [Google Scholar]
- Zhang, Y.; Zhao, G. Research on Multi-service Demand Path Planning Based on Continuous Hopfield Neural Network. In Proceedings of China Modern Logistics Engineering; Springer: Berlin/Heidelberg, Germany, 2015; pp. 417–430. [Google Scholar]
- Eaton, J.; Yang, S.; Mavrovouniotis, M. Ant colony optimization with immigrants schemes for the dynamic railway junction rescheduling problem with multiple delays. Soft Comput. 2016, 20, 2951–2966. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Shengxiang, Y. Empirical study on the effect of population size on MAX-MIN ant system in dynamic environments. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 853–860. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Müller, F.M.; Shengxiang, Y.M.M. Ant Colony Optimization with Local Search for Dynamic Traveling Salesman Problems. IEEE Trans. Cybern. 2017, 47, 1743–1756. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Marufuzzaman, M.; Tunc, H.; Bian, L.; Bullington, W. A Modified Ant Colony Optimization Algorithm to Solve A Dynamic Traveling Salesman Problem: A Case Study with Drones for Wildlife Surveillance. J. Comput. Des. Eng. 2019, 6, 368–386. [Google Scholar] [CrossRef]
- Schmitt, J.P.; Baldo, F.; Parpinelli, R.S. A MAX-MIN Ant System with Short-Term Memory Applied to the Dynamic and Asymmetric Traveling Salesman Problem. In Proceedings of the 2018 7th Brazilian Conference on Intelligent Systems (BRACIS), São Paulo, SP, Brazil, 22–25 October 2018; pp. 1–6. [Google Scholar]
- Wang, Y.; Gao, S.; Todo, Y. Ant colony systems for optimization problems in dynamic environments. Swarm Intell. Princ. Curr. Algorithms Methods 2018, 119, 85. [Google Scholar]
- Huang, Y.W.; Liu, C.F.; Hu, S.F.; Fu, Z.H.; Chen, Y.Q. Dynamic Task Sequencing of Manipulator by Monte Carlo Tree Search. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 569–574. [Google Scholar]
- Yu, S.; Príncipe, J.C. Simple stopping criteria for information theoretic feature selection. Entropy 2019, 21, 99. [Google Scholar]
- Saxena, D.K.; Sinha, A.; Duro, J.A.; Zhang, Q. Entropy-Based Termination Criterion for Multiobjective Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2016, 20, 485–498. [Google Scholar] [CrossRef]
- Boryczka, U.; Strąk, L. Diversification and Entropy Improvement on the DPSO Algorithm for DTSP. In Intelligent Information and Database Systems; Nguyen, N.T., Trawiński, B., Kosala, R., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 9011, pp. 337–347. [Google Scholar]
- Diaz-Gomez, A.P.; Hougen, D. Empirical Study: Initial Population Diversity and Genetic Algorithm Performance. Artif. Intell. Pattern Recogn. 2007, 2007, 334–341. [Google Scholar]
- Cruz Chávez, M.; Martinez, A. Feasible Initial Population with Genetic Diversity for a Population-Based Algorithm Applied to the Vehicle Routing Problem with Time Windows. Math. Probl. Eng. 2016, 2016, 3851520. [Google Scholar] [CrossRef]
- Applegate, D.L.; Bixby, R.E.; Chvatal, V.; Cook, W.J. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2007; ISBN 978-0-691-12993-8. [Google Scholar]
- Cáceres, L.P.; López-Ibánez, M.; Stützle, T. Ant colony optimization on a budget of 1000. In Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; pp. 50–61. [Google Scholar]

| Year | Authors | Algorithm | DTSP Variant |
|---|---|---|---|
| 2001 | Guntsch and Middendorf [21] | ACO with local and global reset of the pheromone | Addition/removal of vertices |
| 2002 | Eyckelhof and Snoek [22] | ACO with various variants of pheromone matrix update to maintain diversity | Changes in edge lengths with time (simulated traffic jam on a road) |
| 2006 | Li et al. [19] | GSInver-over and gene pool with the -measure [23] | CHN145 + 1: 145 cities and one satellite |
| 2010 | Mavrovouniotis and Yang [24] | ACO with immigrants scheme to increase population diversity | Coefficients: frequency and size of changes |
| 2011 | Simões and Costa [25] | CHCalgorithm | A test involving the addition of changes and their subsequent withdrawal [26]. In that way, the optima at the beginning and the end are the same. |
| 2014 | Tinós et al. [27] | EA algorithm | Random changes in the problem |
| 2014 | Zhang and Zhao [28] | Hopfield neural network | Simulation of various types of real random events in a street |
| 2016 | Eaton et al. [29] | ACO with immigrants scheme | Changes in edge lengths. Simulated delays of trains. |
| 2016 | Mavrovouniotis and Yang [30] | MMAS | Encoding of the problem is changed, but the optimal solution remains the same |
| 2017 | Mavrovouniotis et al. [31] | ACO | Distances between cities are changed. The problem can be transformed to an asymmetric one. |
| 2018 | Chowdhury et al. [32] | ACO | Random DTSP, dynamic changes occur randomly. Cyclic DTSP, dynamic changes occur with a cyclic pattern. |
| 2018 | Schmitt et al. [33] | MMAS | Acyclic DTSP with changes in edge lengths with time |
| 2018 | Yirui Wang et al. [34] | ACO | |
| 2018 | Yan-Wei Huang et al. [35] | MCTS | Addition/removal of vertices |
| No. | Description | ||||
|---|---|---|---|---|---|
| 1 | 0.1 | 0.1 | 0.1 | 0.1 | Favors quick changes of position |
| 2 | 2.0 | 0.1 | 0.1 | 0.1 | Emphasis on the information from |
| 3 | 0.1 | 2.0 | 0.1 | 0.1 | Emphasis on the information from |
| 4 | 0.1 | 0.1 | 2.0 | 0.5 | Very slow changes of position |
| 5 | 0.75 | 1.0 | 1.0 | 0.25 | Weak , influence |
| 6 | 1.25 | 1.5 | 1.5 | 0.5 | Stronger , influence |
| 7 | 1.5 | 2.0 | 2.0 | 0.5 | Strong , influence |
| 8 | 1.75 | 2.0 | 2.0 | 0.75 | Very strong , influence |
| Problem | Neighborhood | |||||
|---|---|---|---|---|---|---|
| berlin52 | 0.5 | 0.5 | 0.5 | 0.2 | 32 | 7 |
| kroA100 | 0.5 | 0.5 | 0.5 | 0.5 | 64 | 7 |
| kroA200 | 0.5 | 0.5 | 0.5 | 0.5 | 80 | 7 |
| gr202 | 0.5 | 0.5 | 0.5 | 0.5 | 101 | 10 |
| pcb442 | 0.5 | 1.5 | 0.5 | 0.5 | 104 | 15 |
| gr666 | 0.5 | 1.0 | 1.5 | 0.6 | 112 | 30 |
| Rank | Parameters | Number of Improvements | |||
|---|---|---|---|---|---|
| 1 | 0.1 | 0.1 | 0.1 | 0.5 | 113 |
| 2 | 0.1 | 0.1 | 0.1 | 0.1 | 102 |
| 3 | 0.1 | 2 | 0.1 | 0.1 | 49 |
| 4 | 0.1 | 2 | 2 | 0.5 | 46 |
| 5 | 0.1 | 2 | 2 | 0.1 | 42 |
| 6 | 0.1 | 1.5 | 0.1 | 0.5 | 39 |
| 7 | 0.1 | 1 | 0.1 | 0.1 | 38 |
| 8 | 0.1 | 1 | 0.1 | 0.25 | 34 |
| 9 | 0.75 | 2 | 2 | 0.25 | 27 |
| 10 | 0.1 | 1 | 2 | 0.1 | 26 |
| 11 | 0.1 | 2 | 0.1 | 0.25 | 24 |
| 12 | 0.75 | 2 | 2 | 0.1 | 22 |
| 13 | 1.5 | 1.5 | 2 | 0.5 | 21 |
| 14 | 1.5 | 2 | 0.1 | 0.1 | 21 |
| 15 | 1.5 | 2 | 0.1 | 0.25 | 20 |
| Iterations | Parameters | Number of Improvements | |||
|---|---|---|---|---|---|
| 0–1250 | 0.1 | 0.1 | 0.1 | 0.1 | 94 |
| 0.1 | 0.1 | 0.1 | 0.5 | 93 | |
| 0.1 | 2 | 2 | 0.5 | 38 | |
| 0.1 | 2 | 0.1 | 0.1 | 38 | |
| 0.1 | 2 | 2 | 0.1 | 32 | |
| 1250–2500 | 0.75 | 2 | 2 | 0.25 | 12 |
| 1.5 | 2 | 0.1 | 0.1 | 10 | |
| 0.1 | 2 | 0.1 | 0.1 | 10 | |
| 0.1 | 1.5 | 0.1 | 0.5 | 9 | |
| 0.1 | 1 | 2 | 0.1 | 8 | |
| 2500–3750 | 0.1 | 0.1 | 0.1 | 0.5 | 10 |
| 1.5 | 1.5 | 2 | 0.5 | 4 | |
| 1.5 | 2 | 0.1 | 0.25 | 4 | |
| 0.75 | 2 | 2 | 0.25 | 3 | |
| 0.1 | 1 | 2 | 0.1 | 3 | |
| 3750–5000 | 0.1 | 1 | 0.1 | 0.1 | 2 |
| 0.1 | 1 | 2 | 0.1 | 2 | |
| 0.75 | 0.1 | 2 | 0.5 | 2 | |
| 1.5 | 0.1 | 2 | 0.1 | 2 | |
| 1.5 | 2 | 1.5 | 0.1 | 2 | |
| 5000–6144 | 1.75 | 2 | 1 | 0.5 | 3 |
| 1.5 | 2 | 1.5 | 0.1 | 2 | |
| 1.75 | 0.1 | 2 | 0.5 | 2 | |
| 0.1 | 1.5 | 0.1 | 0.5 | 2 | |
| 1.5 | 1 | 1 | 0.1 | 1 | |
| Homogeneous DPSO | Heterogeneous DPSO | Common Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Problem | Problem | Neighborhood | |||||||||
| berlin52 | 0.5 | 0.5 | 0.5 | 0.2 | berlin52 | Chosen randomly as described in Section 5 | 32 | 7 | |||
| kroA100 | 0.5 | 0.5 | 0.5 | 0.5 | kroA100 | 64 | 7 | ||||
| kroA200 | 0.5 | 0.5 | 0.5 | 0.5 | kroA200 | 80 | 7 | ||||
| gr202 | 0.5 | 0.5 | 0.5 | 0.5 | gr202 | 101 | 10 | ||||
| pcb442 | 0.5 | 1.5 | 0.5 | 0.5 | pcb442 | 104 | 15 | ||||
| gr666 | 0.5 | 1.0 | 1.5 | 0.6 | gr666 | 112 | 30 | ||||
| Problem | Iterations | DPSO Algorithms | Counterparts | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Homogeneous | Heterogeneous | ACS | PACO | ||||||
| T (s) | G (%) | D (%) | T (s) | G (%) | D (%) | G (%) | G (%) | ||
| berlin52 | 104 | 0.13 | 0.15 | 0.32 | 0.13 | 0.13 | 0.15 | 0.96 | 0.96 |
| berlin52 | 416 | 0.3 | 0.01 | 0.04 | 0.28 | 0.01 | 0.05 | 0.5 | 0.5 |
| berlin52 | 1664 | 0.98 | 0 | 0 | 0.89 | 0.01 | 0.05 | 0.46 | 0.46 |
| kroA100 | 100 | 1.03 | 5.44 | 2.47 | 0.86 | 2.68 | 1.4 | 1.8 | 2.97 |
| kroA100 | 400 | 1.63 | 1.28 | 1.02 | 1.27 | 1.05 | 0.81 | 1.31 | 2.13 |
| kroA100 | 1600 | 4.11 | 0.64 | 0.69 | 3.38 | 0.78 | 0.77 | 0.82 | 1.36 |
| kroA200 | 160 | 2.49 | 15.63 | 2.77 | 2.18 | 5.14 | 1.84 | 2.41 | 3.33 |
| kroA200 | 640 | 5.13 | 4.45 | 1.62 | 4.46 | 2.89 | 1.09 | 1.62 | 2.71 |
| kroA200 | 2560 | 15.6 | 1.62 | 0.81 | 13.18 | 2.02 | 0.8 | 1.47 | 2.28 |
| gr202 | 128 | 8.82 | 13.75 | 2.06 | 8.17 | 4.19 | 1.2 | 6.26 | 4.91 |
| gr202 | 512 | 11.54 | 6.81 | 2.11 | 10.88 | 1.97 | 0.66 | 4.88 | 3.9 |
| gr202 | 2048 | 23.01 | 1.52 | 0.6 | 21.98 | 1.53 | 0.55 | 3.93 | 3.34 |
| pcb442 | 272 | 11.22 | 29.31 | 5.33 | 11.16 | 6.73 | 1.68 | 6.18 | 4.44 |
| pcb442 | 1088 | 28.52 | 13.41 | 5 | 30.69 | 2.87 | 0.89 | 4.87 | 3.56 |
| pcb442 | 4352 | 102.78 | 3.13 | 1.52 | 108.25 | 1.92 | 0.79 | 3.91 | 3.3 |
| gr666 | 384 | 85.19 | 10.84 | 1.52 | 91.83 | 9.58 | 0.86 | 9.18 | 5.89 |
| gr666 | 768 | 98.36 | 7.37 | 1.0 | 115.19 | 6.88 | 0.78 | 7.46 | 4.77 |
| gr666 | 1536 | 124.84 | 5.62 | 0.84 | 163.48 | 5.33 | 0.57 | 6.09 | 4.51 |
| gr666 | 3072 | 180.66 | 4.88 | 0.63 | 259 | 4.52 | 0.88 | 5.67 | 4.14 |
| gr666 | 6144 | 296.83 | 3.99 | 0.77 | 453.83 | 3.8 | 0.78 | 4.92 | 4.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strąk, Ł.; Skinderowicz, R.; Boryczka, U.; Nowakowski, A. A Self-Adaptive Discrete PSO Algorithm with Heterogeneous Parameter Values for Dynamic TSP. Entropy 2019, 21, 738. https://doi.org/10.3390/e21080738
Strąk Ł, Skinderowicz R, Boryczka U, Nowakowski A. A Self-Adaptive Discrete PSO Algorithm with Heterogeneous Parameter Values for Dynamic TSP. Entropy. 2019; 21(8):738. https://doi.org/10.3390/e21080738
Chicago/Turabian StyleStrąk, Łukasz, Rafał Skinderowicz, Urszula Boryczka, and Arkadiusz Nowakowski. 2019. "A Self-Adaptive Discrete PSO Algorithm with Heterogeneous Parameter Values for Dynamic TSP" Entropy 21, no. 8: 738. https://doi.org/10.3390/e21080738
APA StyleStrąk, Ł., Skinderowicz, R., Boryczka, U., & Nowakowski, A. (2019). A Self-Adaptive Discrete PSO Algorithm with Heterogeneous Parameter Values for Dynamic TSP. Entropy, 21(8), 738. https://doi.org/10.3390/e21080738