Surrogate Data Preserving All the Properties of Ordinal Patterns up to a Certain Length
Abstract
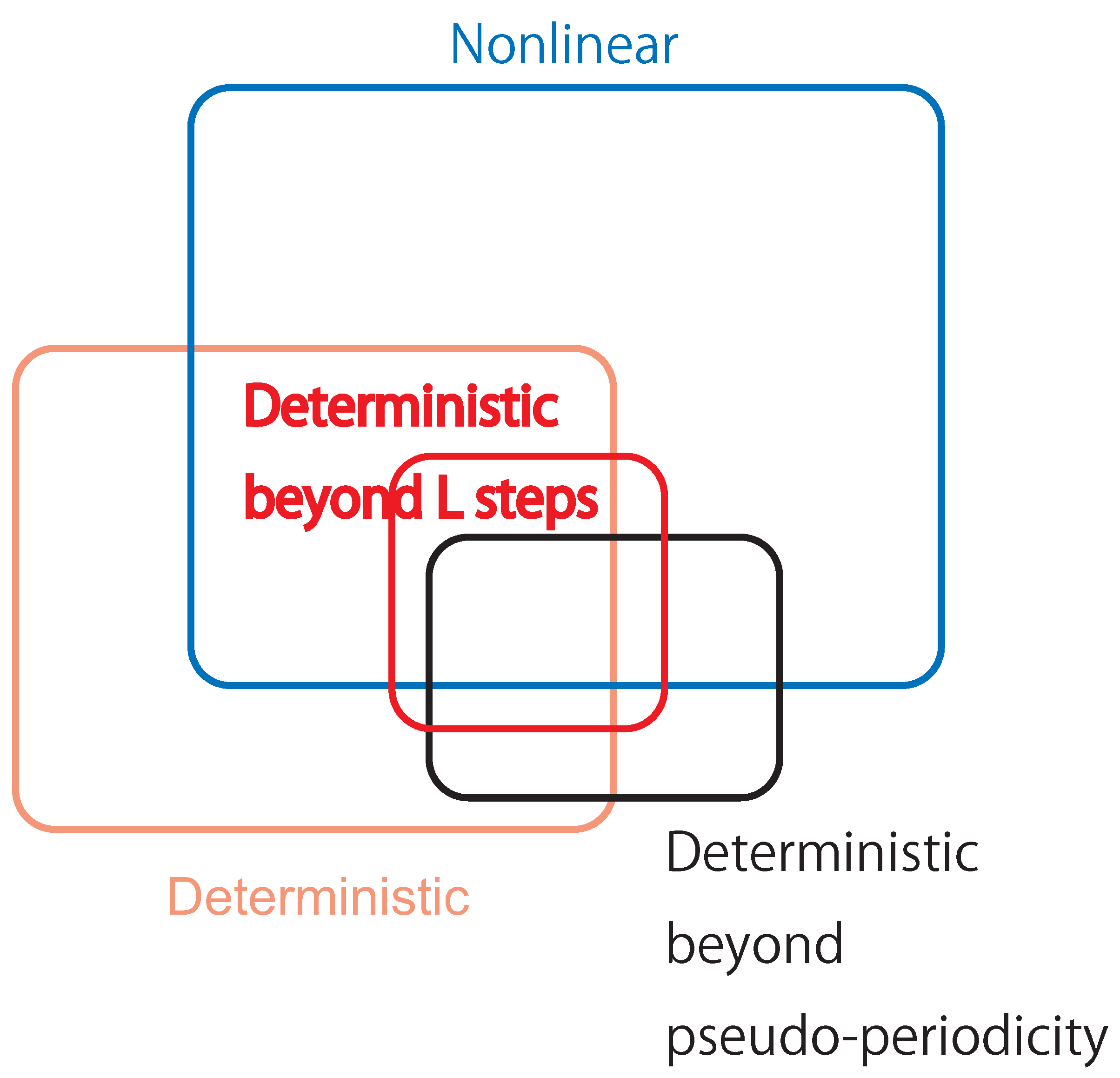
1. Introduction
2. Our Mathematical Settings
3. Background
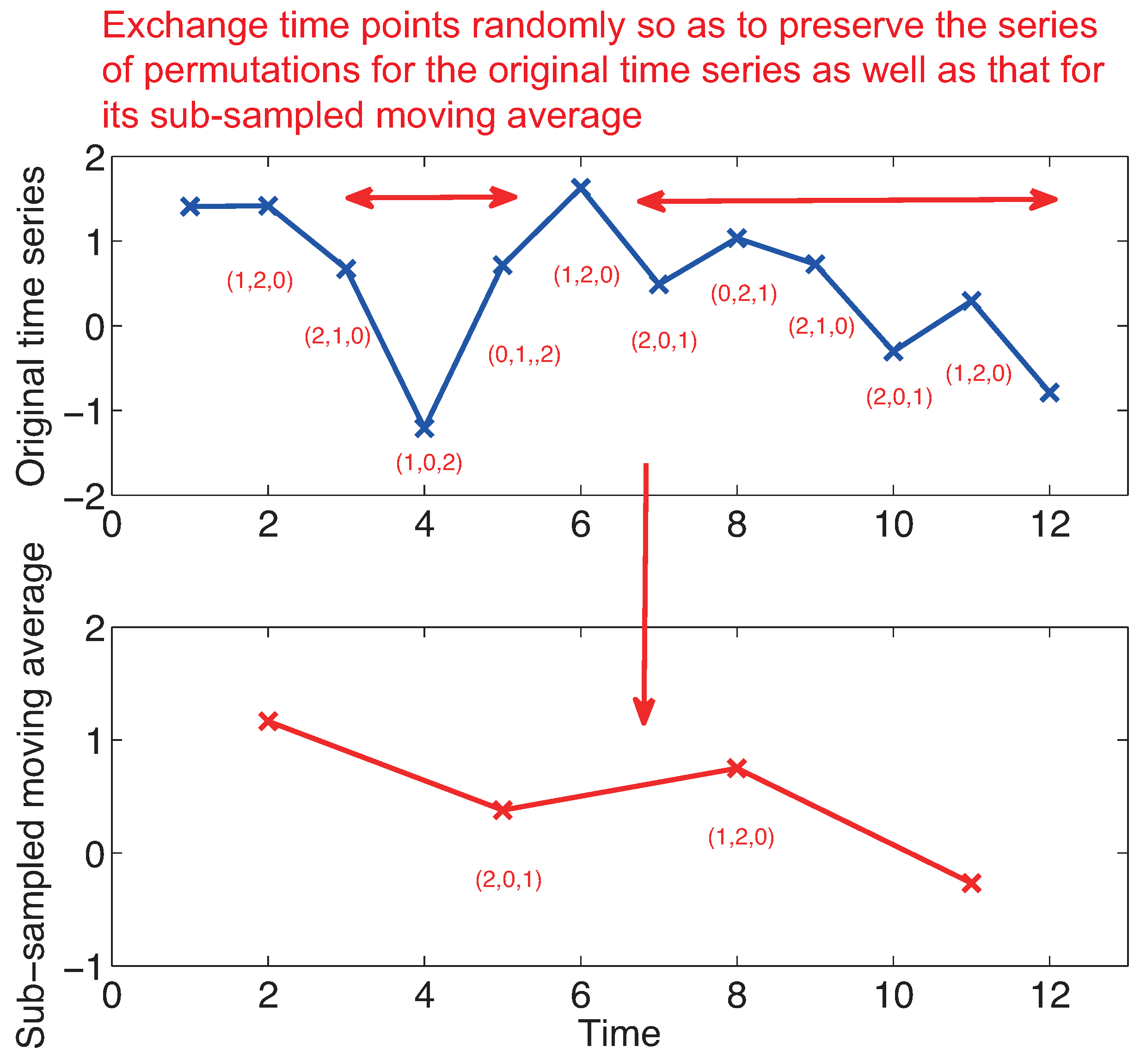
4. Methods
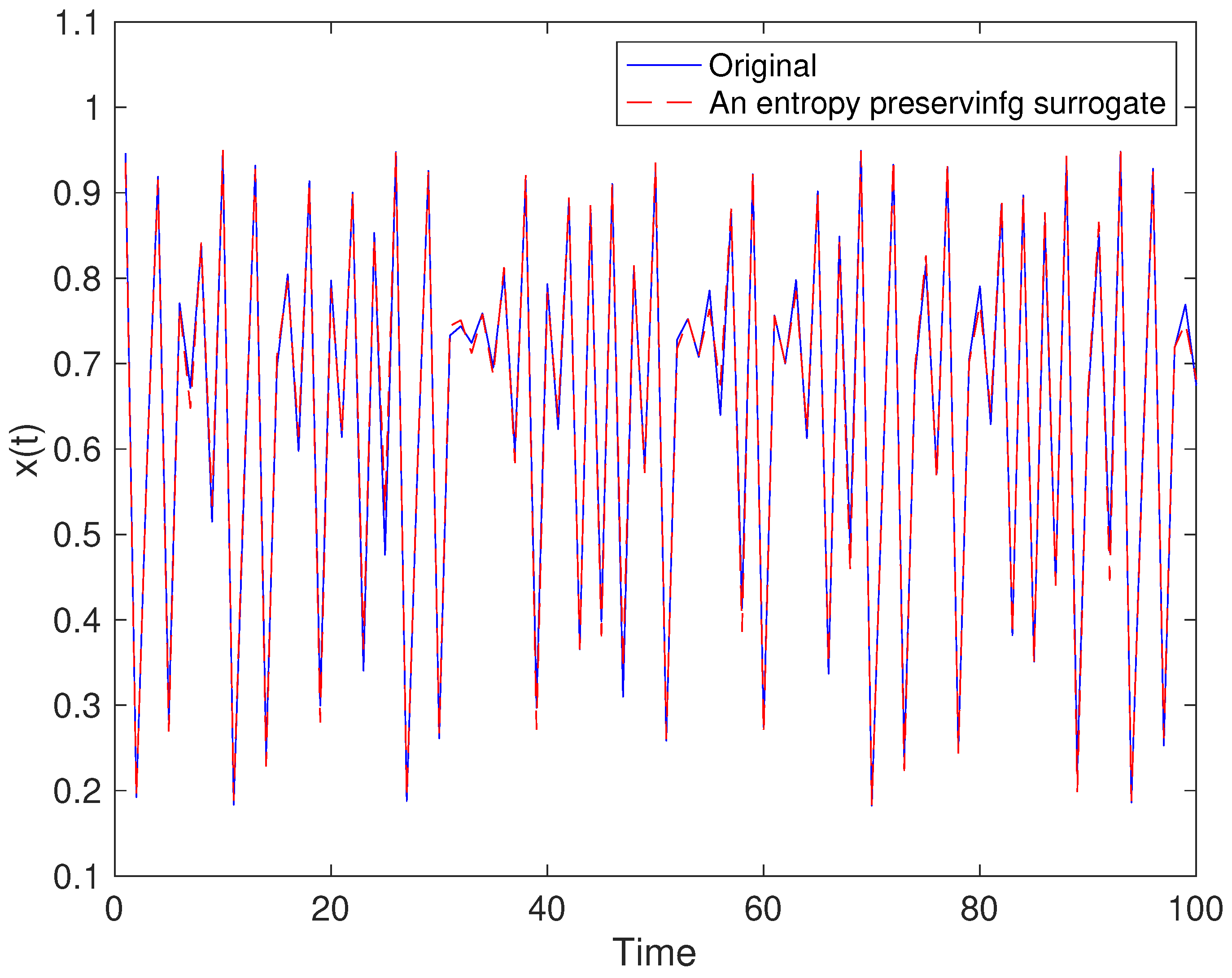
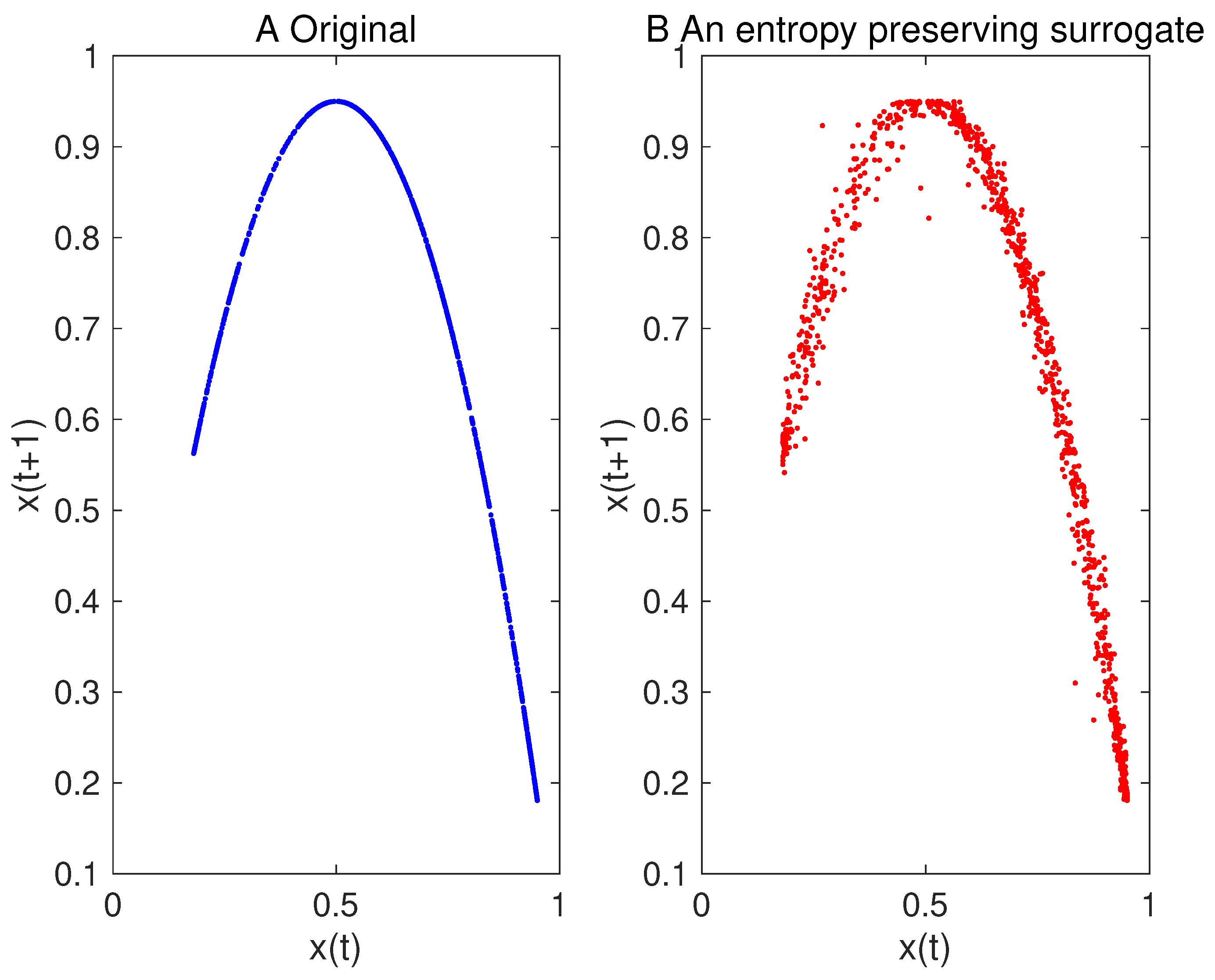
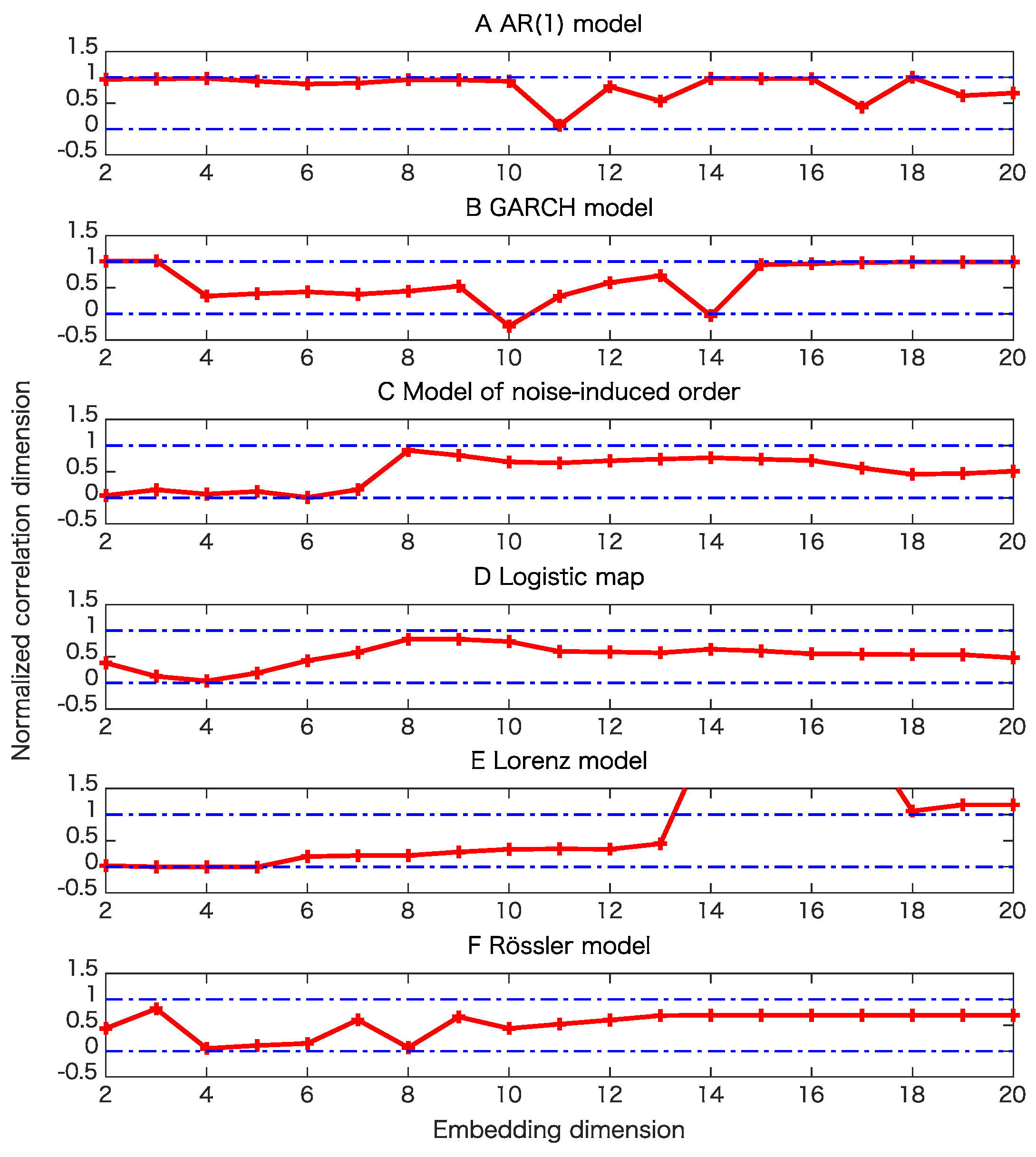
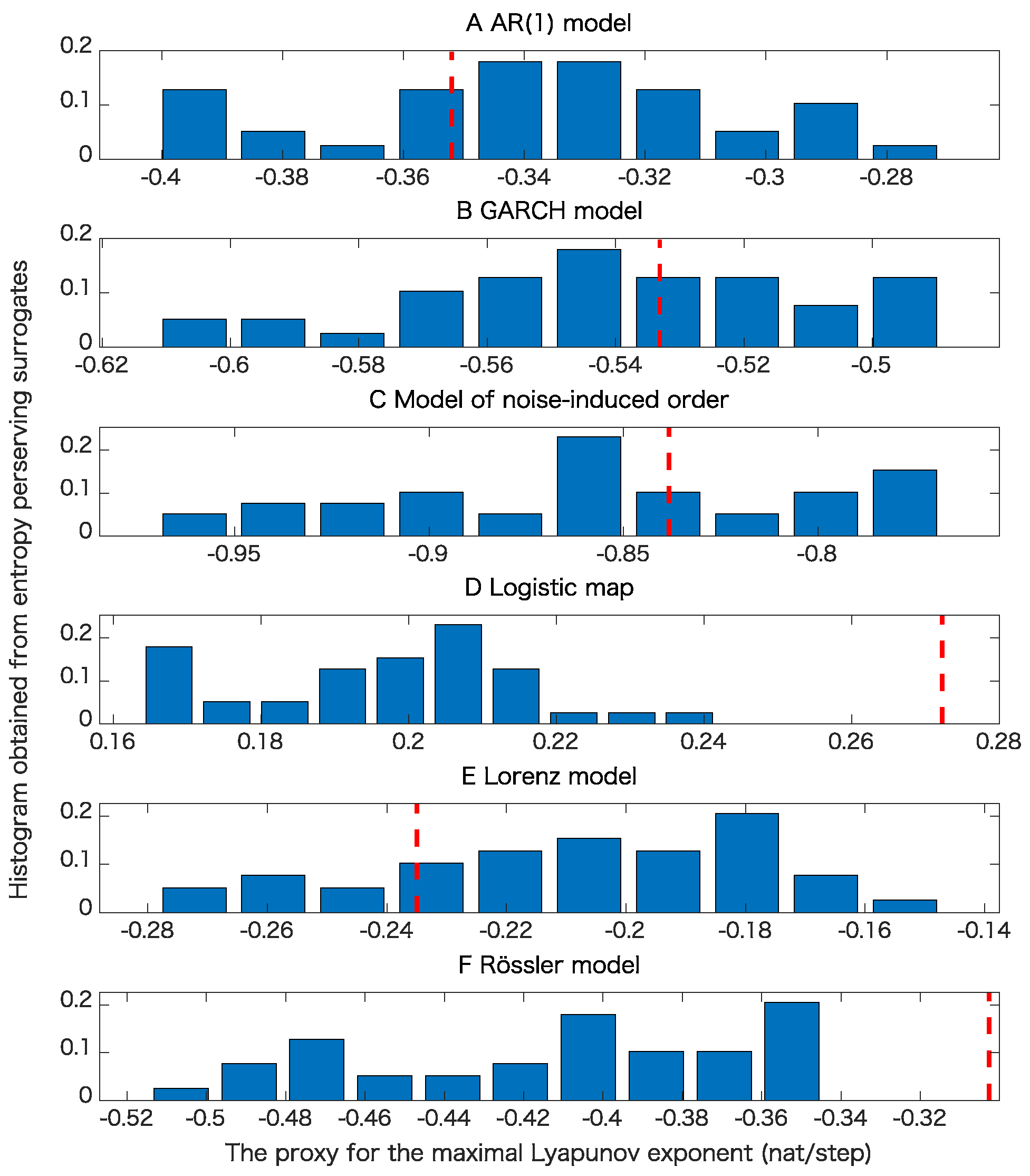
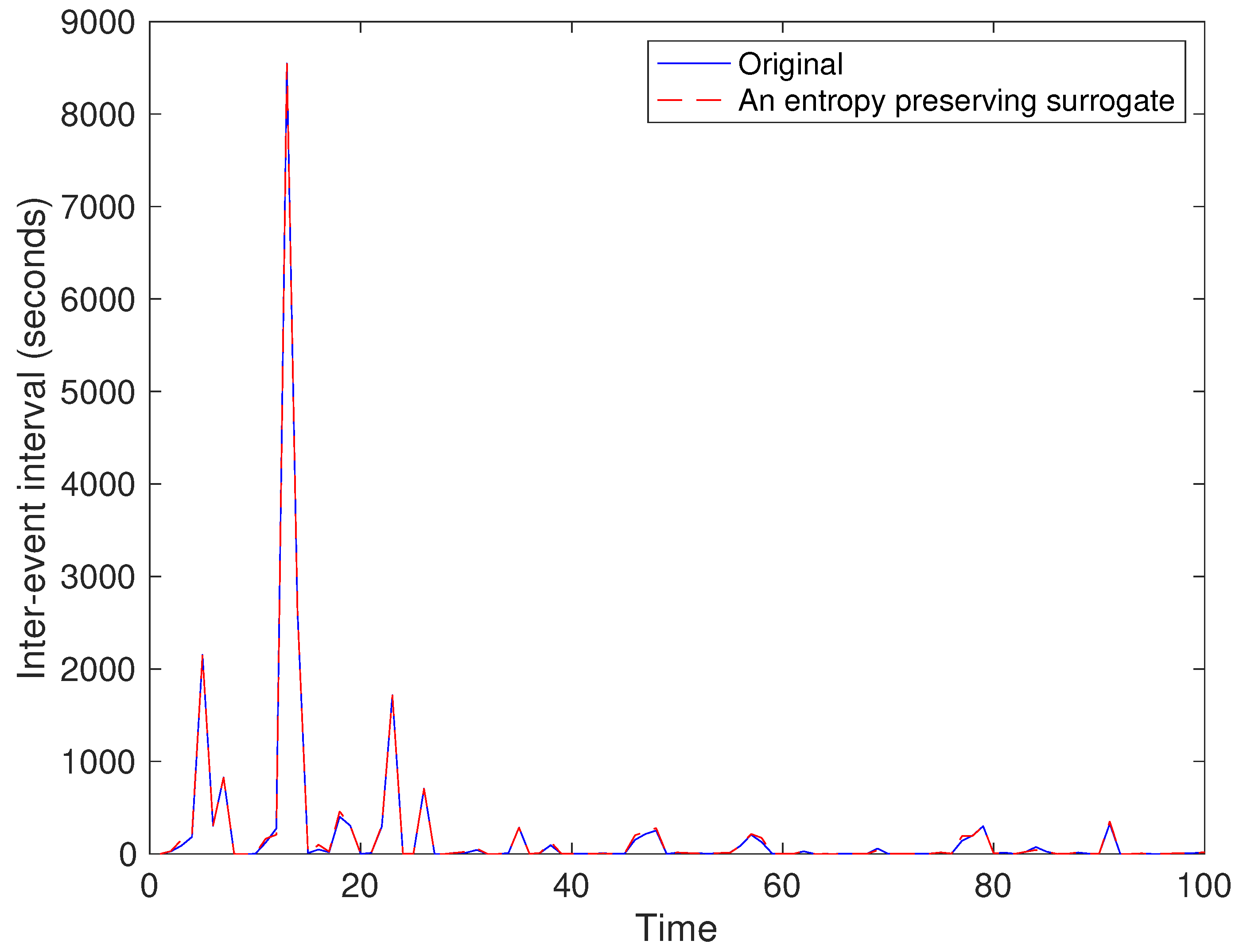
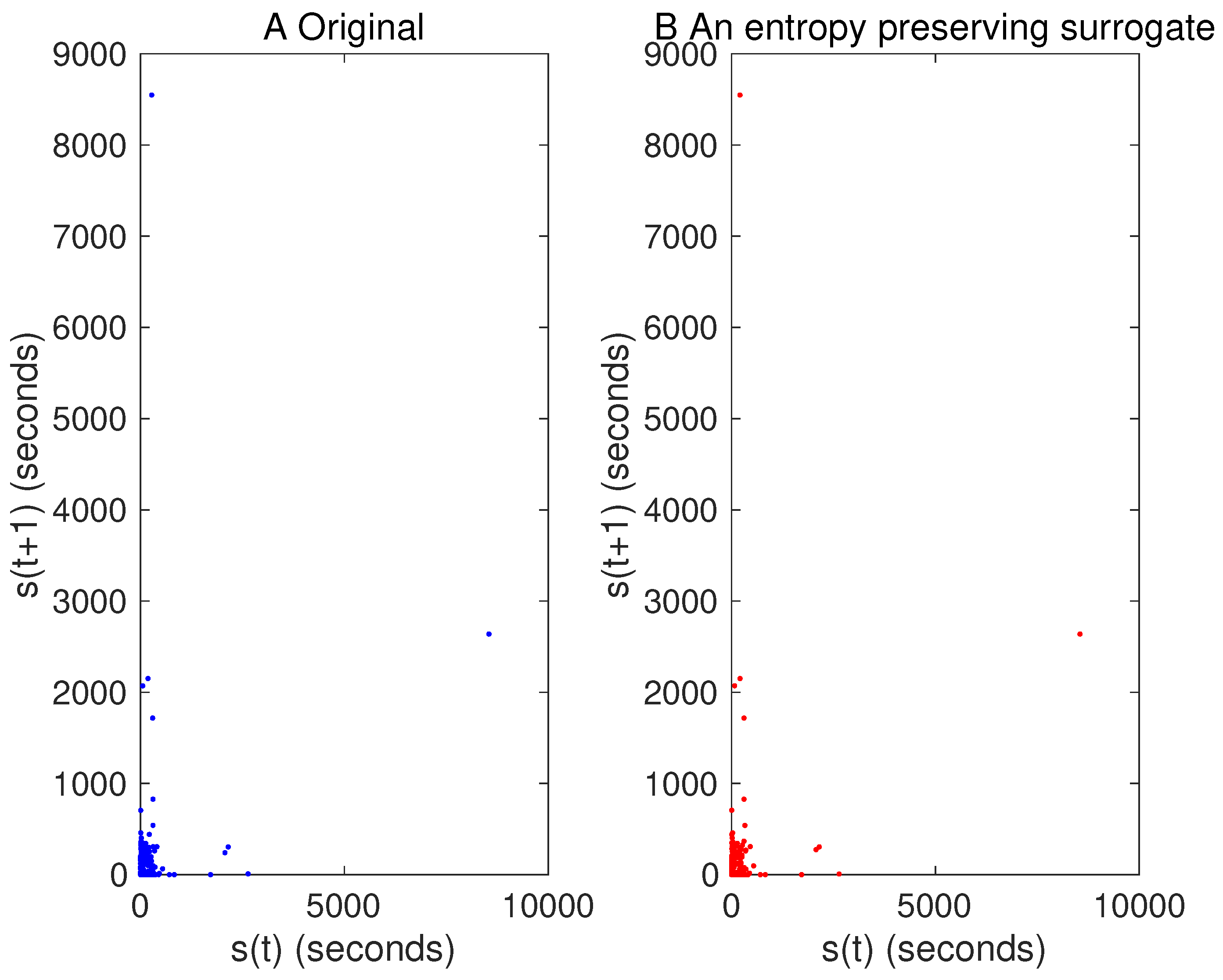
5. Results
5.1. Toy Examples
5.2. Real Data Example of the USD/JPY Market
6. Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Increment the current number i of iterations by 1.
- Prepare an attempt for replacement by swapping two elements of .
- Calculate and .
- Calculate the number of differences between and . Let denote this number.
- Let p be the probability for accepting the attempt, which can be calculated as .
- Generate a uniform random number between 0 and 1. If the random number is less than p, then replace the current time series by the attempt .
- If i is a multiple of S and , then record the current as the -th surrogate data.
References
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Wayl, R.; Bromley, D.; Pickett, D.; Passamante, A. Recognizing determinism in a time series. Phys. Rev. Lett. 1993, 70, 580–582. [Google Scholar]
- Hirata, Y.; Shiro, M. Detecting nonlinear stochastic systems using two independent hypothesis tests. Phys. Rev. E 2019, in press. [Google Scholar]
- Nakamura, T.; Small, M.; Hirata, Y. Testing for nonlinearity in irregular fluctuations with long-term trends. Phys. Rev. E 2006, 74, 026205. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Kennel, M.B. Topological permutation entropy. Phys. D 2007, 231, 137–142. [Google Scholar] [CrossRef]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A.F. Combinatorial detection of determinism in noisy time series. EPL 2008, 83, 60005. [Google Scholar] [CrossRef]
- Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F.; Olson, C.C. An Isserlis’ theorem for mixed Gaussian variables: Application to the auto-bispectral density. J. Stat. Phys. 2009, 136, 89–102. [Google Scholar] [CrossRef]
- Theiler, J.; Prichard, D. Constrained-realization Monte-Carlo method for hypothesis testing. Phys. D 1996, 94, 221–235. [Google Scholar] [CrossRef]
- Kaplan, D.T.; Glass, L. Direct test for determinism in a time series. Phys. Rev. Lett. 1992, 68, 427–430. [Google Scholar] [CrossRef] [PubMed]
- Casdagli, M.C.; Weigend, A.S. Exploring the continuum between deterministic and stochastic modeling. In Time Series Prediction: Forecasting the Future and Understanding the Past; Weigend, A.S., Gershenfeld, N.A., Eds.; Westview Press: New York, NY, USA, 1993; pp. 347–366. [Google Scholar]
- Amigó, J.M.; Kocarev, L.; Szczepansiki, J. Order patterns and chaos. Phys. Lett. A 2006, 355, 27–36. [Google Scholar] [CrossRef]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A.F. Detecting determinism with oridinal patterns: A comparative study. Int. J. Bifurcat. Chaos 2010, 20, 2915–2924. [Google Scholar] [CrossRef]
- Amigó, J.M.; Kennel, M.B.; Kocarev, L. The permutation entropy rate equals the metric entropy rate for ergodic information sources and ergodic dynamical systems. Phys. D 2005, 210, 77–95. [Google Scholar] [CrossRef]
- Schreiber, T. Constrained randomization of time series data. Phys. Rev. Lett. 1998, 80, 2105–2108. [Google Scholar] [CrossRef]
- Gershenfeld, N. The Nature of Mathematical Modeling; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Hirata, Y.; Takeuchi, T.; Horai, S.; Suzuki, H.; Aihara, K. Parsimonious description for predicting high-dimensional dynamics. Sci. Rep. 2015, 5, 15736. [Google Scholar] [CrossRef] [PubMed]
- Small, M.; Yu, D.; Harrison, R.G. Surrogate test for pseudoperiodic time series data. Phys. Rev. Lett. 2001, 87, 188101. [Google Scholar] [CrossRef]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Lamoureux, C.G.; Lastrapes, W.D. Persistence in variance, structural change, and the GARCH model. J. Bus. Econ. Stat. 1990, 8, 225–234. [Google Scholar]
- Matsumoto, K.; Tsuda, I. Noise-induced order. J. Stat. Phys. 1983, 31, 87–106. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. 1976, 57A, 397–398. [Google Scholar] [CrossRef]
- Yu, D.J.; Small, M.; Harrison, R.G.; Diks, C. Efficient implementation of the Gaussian kernel algorithm in estimating invariants and noise level from noisy time series data. Phys. Rev. E 2000, 61, 3750–3756. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Hirata, Y.; Amigó, J.A.; Matsuzaka, Y.; Yokota, R.; Mushiake, H.; Aihara, K. Detecting causality by combined use of multiple methods: climate and brain examples. PLoS ONE 2016, 11, e0158572. [Google Scholar] [CrossRef] [PubMed]
- McCullough, M.; Sakellariou, K.; Stemler, T.; Small, M. Regenerating time series from ordinal networks. Chaos 2017, 27, 035814. [Google Scholar] [CrossRef]
- Small, M.; McCullough, M.; Sakellariou, K. Ordinal network measures: Quantifying determinism in data. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018. [Google Scholar]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100, 158101. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Monetti, R.; Aschenbrenner, T.; Bunk, W. Transcripts: An algebraic approach to coupled time series. Chaos 2012, 22, 013105. [Google Scholar] [CrossRef]
- Hirata, Y.; Aihara, K. Timing matters in foreign exchange markets. Phys. A 2012, 391, 760–766. [Google Scholar] [CrossRef]
Sample Availability: Matlab codes are available from the corresponding author’s following website: https://sites.google.com/view/yoshitohirata/home. |
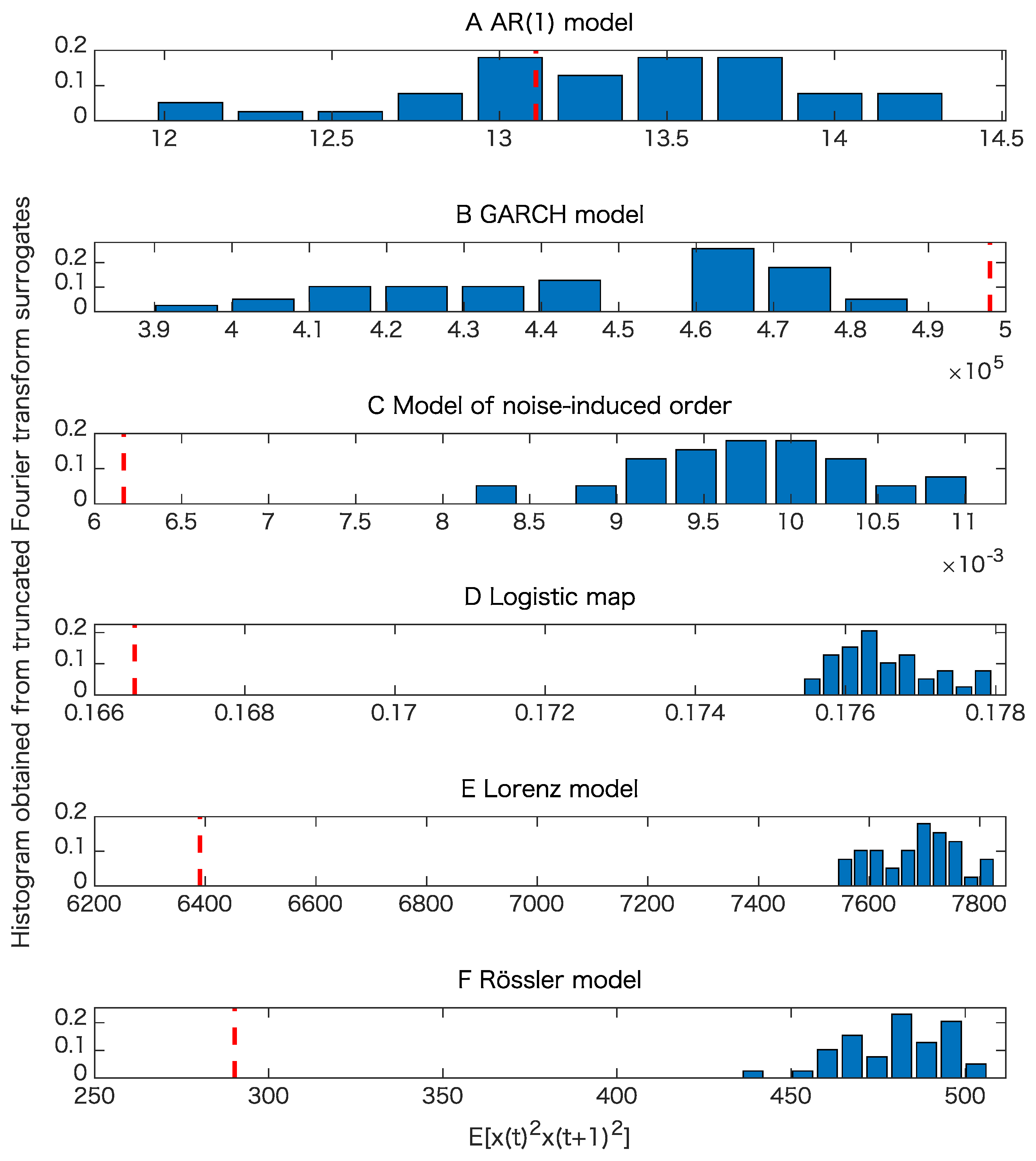
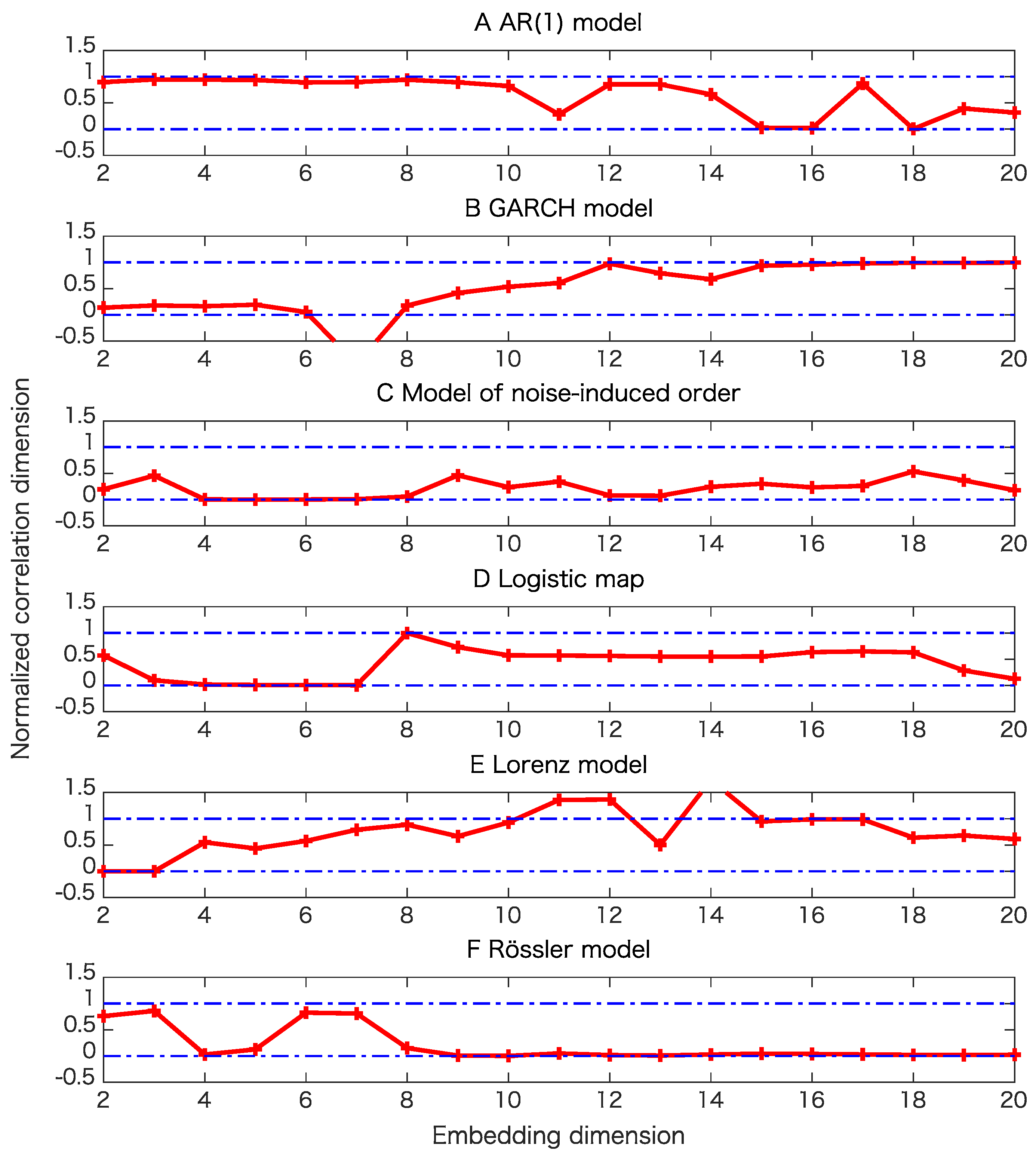
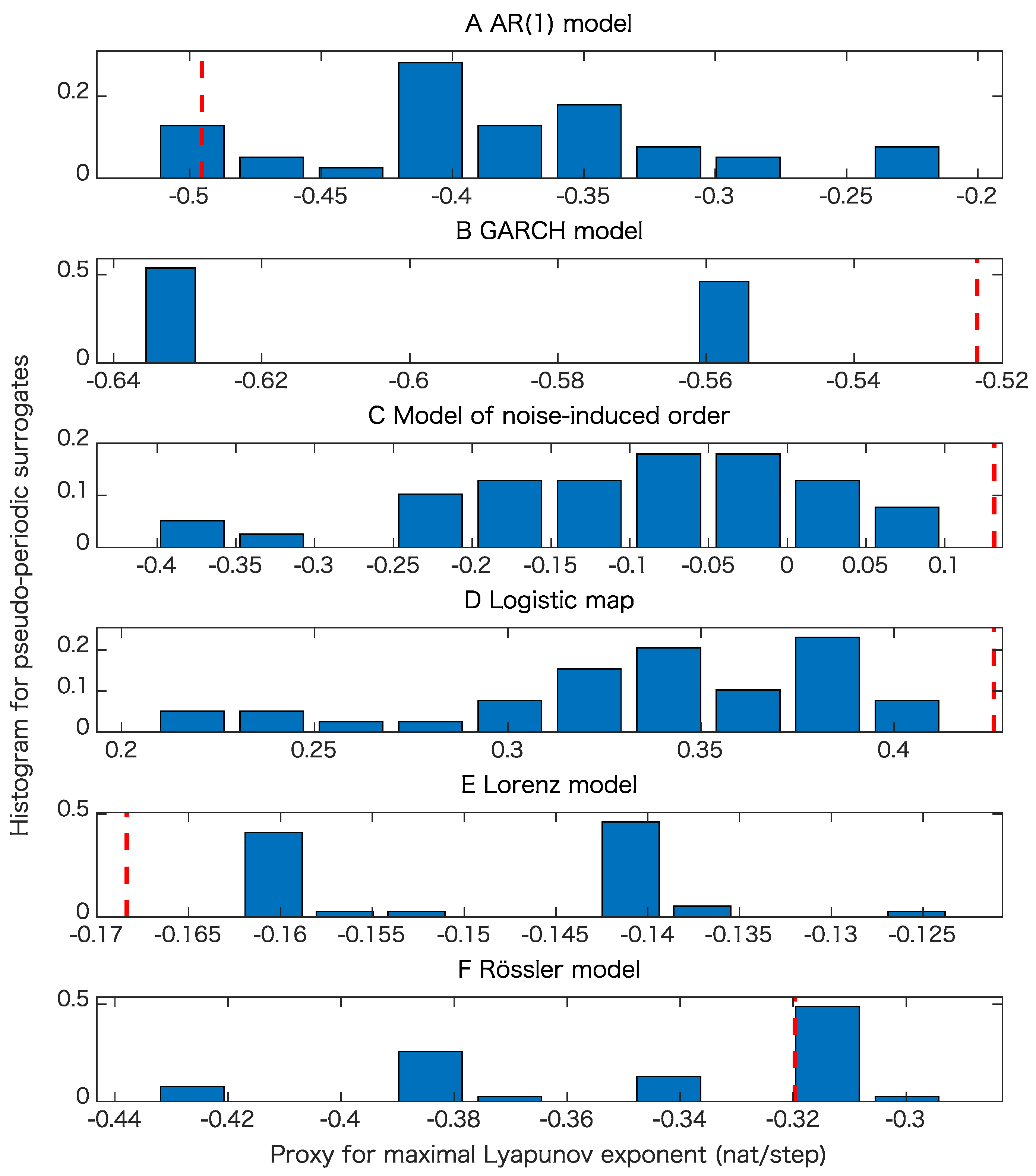
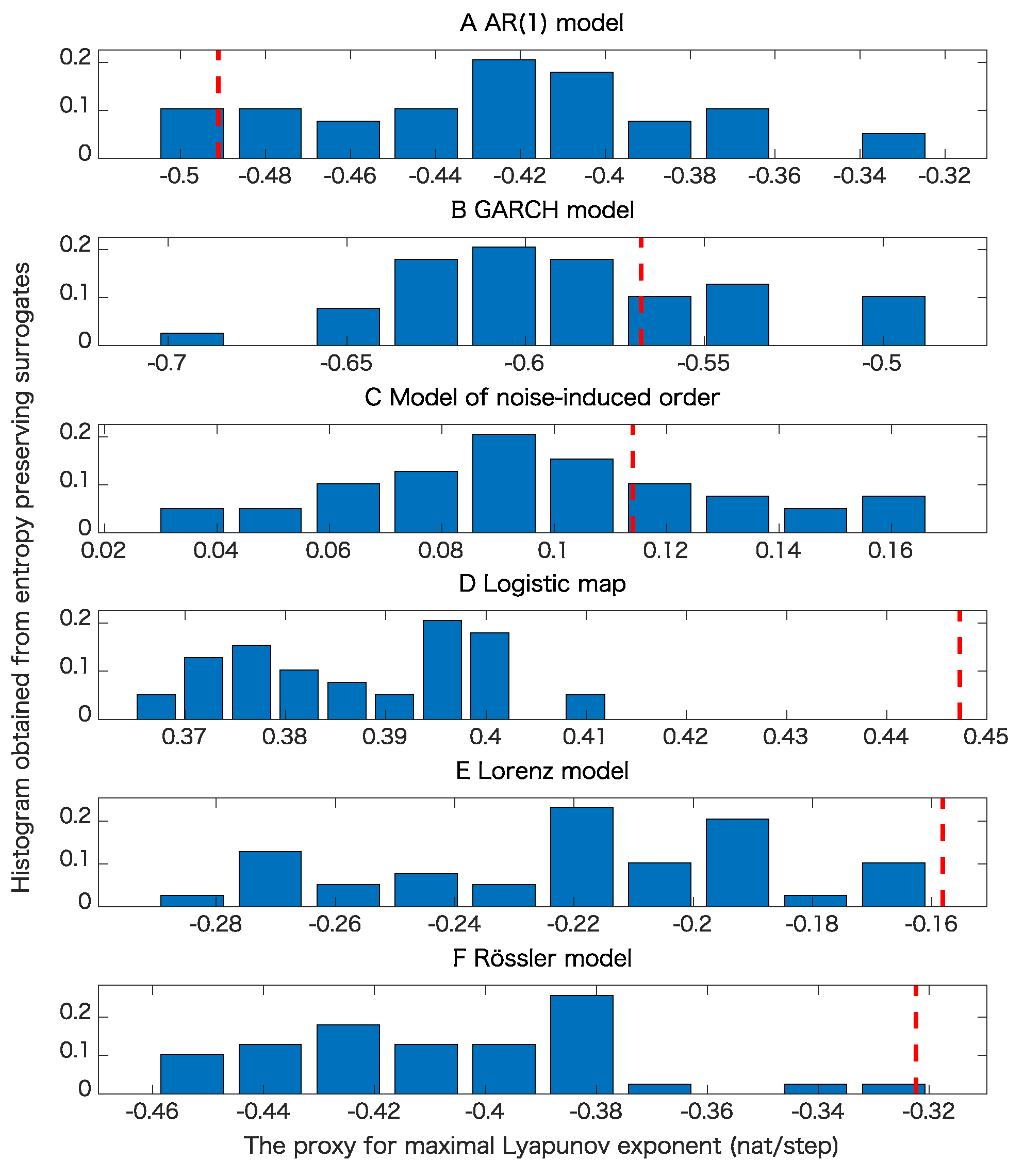
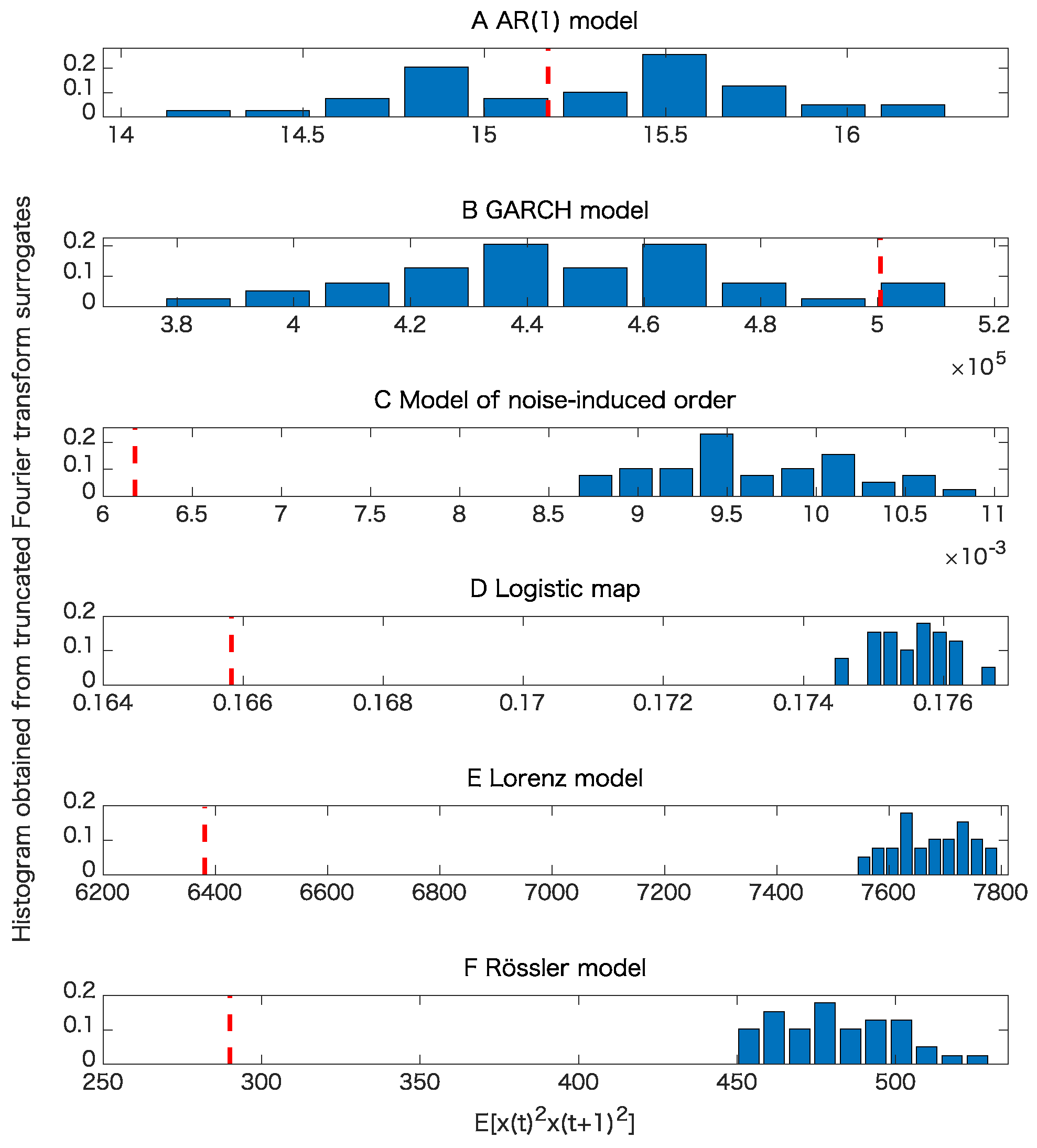
| Property∖Model | AR(1) | GARCH | Noise-Induced Order | Logistic | Lorenz | Rössler |
|---|---|---|---|---|---|---|
| Nonlinearity with | 3 | 20 | 20 | 20 | 20 | 20 |
| Determinism beyond pseudo-periodicity with correlation dimensions | 0 | 20 | 0 | 0 | 0 | 20 |
| Determinism beyond psuedo-periodicity with maximal Lyapunov exponent | 1 | 1 | 7 | 17 | 2 | 0 |
| Determinism beyond 30 steps with maximal Lyapunov exponent | 2 | 1 | 3 | 20 | 8 | 6 |
| Total | 20 | 20 | 20 | 20 | 20 | 20 |
| Property∖Model | AR(1) | GARCH | Noise-Induced Order | Logistic | Lorenz | Rössler |
|---|---|---|---|---|---|---|
| Nonlinearity with | 1 | 19 | 20 | 20 | 20 | 20 |
| Determinism beyond pseudo-periodicity with correlation dimensions | 0 | 20 | 20 | 0 | 20 | 11 |
| Determinism beyond 30 steps with maximal Lyapunov exponent | 3 | 0 | 2 | 16 | 6 | 7 |
| Total | 20 | 20 | 20 | 20 | 20 | 20 |
| Property | Number of Time Segments |
|---|---|
| Nonlinearity with | 24 |
| Determinism beyond pseudo-periodicity with correlation dimensions | 0 |
| Determinism beyond 30 steps with maximal Lyapunov exponent | 12 |
| Total | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirata, Y.; Shiro, M.; Amigó, J.M. Surrogate Data Preserving All the Properties of Ordinal Patterns up to a Certain Length. Entropy 2019, 21, 713. https://doi.org/10.3390/e21070713
Hirata Y, Shiro M, Amigó JM. Surrogate Data Preserving All the Properties of Ordinal Patterns up to a Certain Length. Entropy. 2019; 21(7):713. https://doi.org/10.3390/e21070713
Chicago/Turabian StyleHirata, Yoshito, Masanori Shiro, and José M. Amigó. 2019. "Surrogate Data Preserving All the Properties of Ordinal Patterns up to a Certain Length" Entropy 21, no. 7: 713. https://doi.org/10.3390/e21070713
APA StyleHirata, Y., Shiro, M., & Amigó, J. M. (2019). Surrogate Data Preserving All the Properties of Ordinal Patterns up to a Certain Length. Entropy, 21(7), 713. https://doi.org/10.3390/e21070713






