We begin with an example of our formulation where the players adopt the Nash equilibrium solution concept. We use this example to illustrate how whether DM’s choice is observed or not can change whether they would be willing to pay a positive amount in exchange for an offered change to the game parameters, or would instead have to be paid for the same change. Then we analyze a matching pennies game using both the QRE solution concept and the Nash solution concept. This illustrates how the private offer prices and public offer prices of DM can change with changes to the solution concept of the future game.
4.1. Tragedy of the Commons
We begin with a tragedy of the commons game, modeling two players who simultaneously fish the same region of ocean. Each player
i chooses a continuous value
, which represents how many fish player
i catches. There is a non-strategic regulator that patrols the ocean in a boat, who has a budget
for the fuel of that boat. (It is this parameter that DM will be able to change.) Player
i’s expected utility is
Intuitively, this utility function models the following scenario. The regulator says that players are not allowed to catch a total of more than units of fish. Of course, this could also be a parameter that DM can change but we leave it fixed here, for ease of exposition. However, the regulator’s fuel budget prohibits them from patrolling the entire region of ocean. So a player that fishes more than 0.25 units has some chance of evading the regulator; that probability is the parameter , which is directly determined by the fuel budget of the regulator. However, if player i fishes over the limit and is detected, they incur a cost of . Varying the value of results in four types of pure strategy Nash equilibria in this game. One equilibrium is when both players fish 0.25, two equilibria consist of one player fishing over the limit and the other player fishing the limit and one equilibrium where both players fish over the limit.
Suppose
is low enough so that both players choose to fish over the limit and risk being detected. Then player
i’s best response is
and the symmetric Nash equilibrium is for player
i to fish
. Then the private offer price to player
i is given by:
Since
and
are strictly positive, the RHS Equation (
12) is negative. That means that player
i would
have to be paid in order to agree to an increase in
. To put this result in context, we now consider the public offer price,
where the second equation arises by plugging in the Nash equilibrium values of
and
. For low enough
, the RHS of Equation (
13) is positive. Combining, we see that in this situation, a player would be willing to increase
only if their decision to increase the fuel budget of the regulator was observed by other players.The reason the public and private offer prices differ is based on the fact that this is a tragedy of the commons game. To see this, fix , and suppose both players fish the same amount. The players’ utility decreases if the amount the other player fishes increases. However, each player has an incentive to increase the amount they fish. As a result, both players fish above the social optimum. On the other hand, for higher values of , both players fish less, since they are more likely to be detected and the penalty they face for being detected is increasing in the amount they fish. So an observed increase in the fuel budget decreases the amount both players fish.
Now consider the case when player i’s decision to increase the regulator’s budget is not observed. Suppose i does pay some positive amount to change to and both players best respond accordingly. In this case, the amount that both players fish is less at than it is at . However, player i can benefit by not paying to increase the regulator’s budget, increase the amount they fish, and decreases the probability that they are detected. Crucially, player would not increase the amount that they fish if player i did this, because player i’s decision is unobserved. Therefore, player i would pay rather than . This is true even though player i is worse off for having made that decision. Intuitively, player i is a victim of their own greed, of their inability not to try to save in how much they pay. That is, player i knows that it would have a higher utility when the parameters were but i would never pay to change the parameters because it would always be profitable for i to avoid the cost of paying and cheat.
4.2. Matching Pennies
We now examine how the private and public offer prices are related under the Nash and QRE solution concepts. Consider a version of the matching pennies game depicted in
Table 1 where we once again assume best responses. Without loss of generality assume that DM is the row player and
a is a parameter that controls DM’s preference for matching heads (H). Since players only have two strategies, let
and
represent the probability that DM plays H and −DM plays H, respectively. When
, the unique Nash equilibrium of this game is
and equilibrium expected payoffs are 0.
More generally, when
, the equilibrium profile specifies
and
and the expected utility for DM is given by
where the argument to all
terms is implicity
. Since at the mixed strategy equilibrium players are indifferent among all actions that have support under the equilibrium profile,
is not unique when player
plays the mixed strategy equilibrium profile. Therefore, in this example we need to restrict
to determine the public and private offer price. We do so in the following way: If
is not unique, then
returns
such that −DM is indifferent between its actions. In other words, if DM is indifferent between its two possible actions, it randomizes such that −DM is also indifferent between its actions and therefore,
returns the mixed strategy equilibrium profile for DM when −DM randomizes with probability
.
Furthermore,
is not differentiable with respect to
a when −DM chooses the mixed strategy Nash equilibrium profile. Specifically, for any small increase in
a, DM’s best response would be to place probability 1 on H, holding −DM’s strategy constant. Therefore, we
cannot apply Equation (
3) to determine the private offer price. Instead, we use the definition given in Equation (
2) to derive the private offer price to DM at
:
Line (
15) arises by first taking the derivative of
with respect to
a. The second term results from DM setting
since that is its best response when −DM is best responding as if
but
a actually equals
.
There are several points worth emphasizing in this example. First, even though DM’s best response with respect to a change in a is not continuous, the private offer price is still defined. That is, even though DM’s best response function specifies that DM would change their strategy from to for an infinitesimally small increase in a, the private offer price is still defined in terms of limits of the utility function. The reason is that the change in expected utility with respect to any change in DM’s strategy is 0 holding−DM’s strategy and parameters constant. Consequently any non-differentiable change in DM’s strategy does not affect expected utility.
Second, the private offer price is exactly 0. The reason is that the Nash equilibrium expected utility to DM when is exactly the same as DM’s expected utility when the column player best responds as if a is but a is actually and DM best responds as if . In other words, the utility gained by DM by exploiting a non-equilibrium strategy of −DM is exactly the same as the utility gained by DM for an increase in a.
Now, we derive the public offer price to DM for the matching pennies game for an increase in
a. Again, since
B is not differentiable with respect to
a, we must apply Equation (
7) directly:
Equation (
17) shows that the public offer price to the row player is positive, even though Equation (
16) says the private offer price is zero. This means that DM would be willing to pay to increase
a only if column player was aware that DM paid for the parameter change.
Now, to derive the private and public offer prices under the QRE solution concept, let
be a vector valued function taking
as an input and outputting a probability distribution on
such that for all
,
where
is a scalar parameter. Note that under this assumption the equilibrium profile
is a quantal response equilibrium.
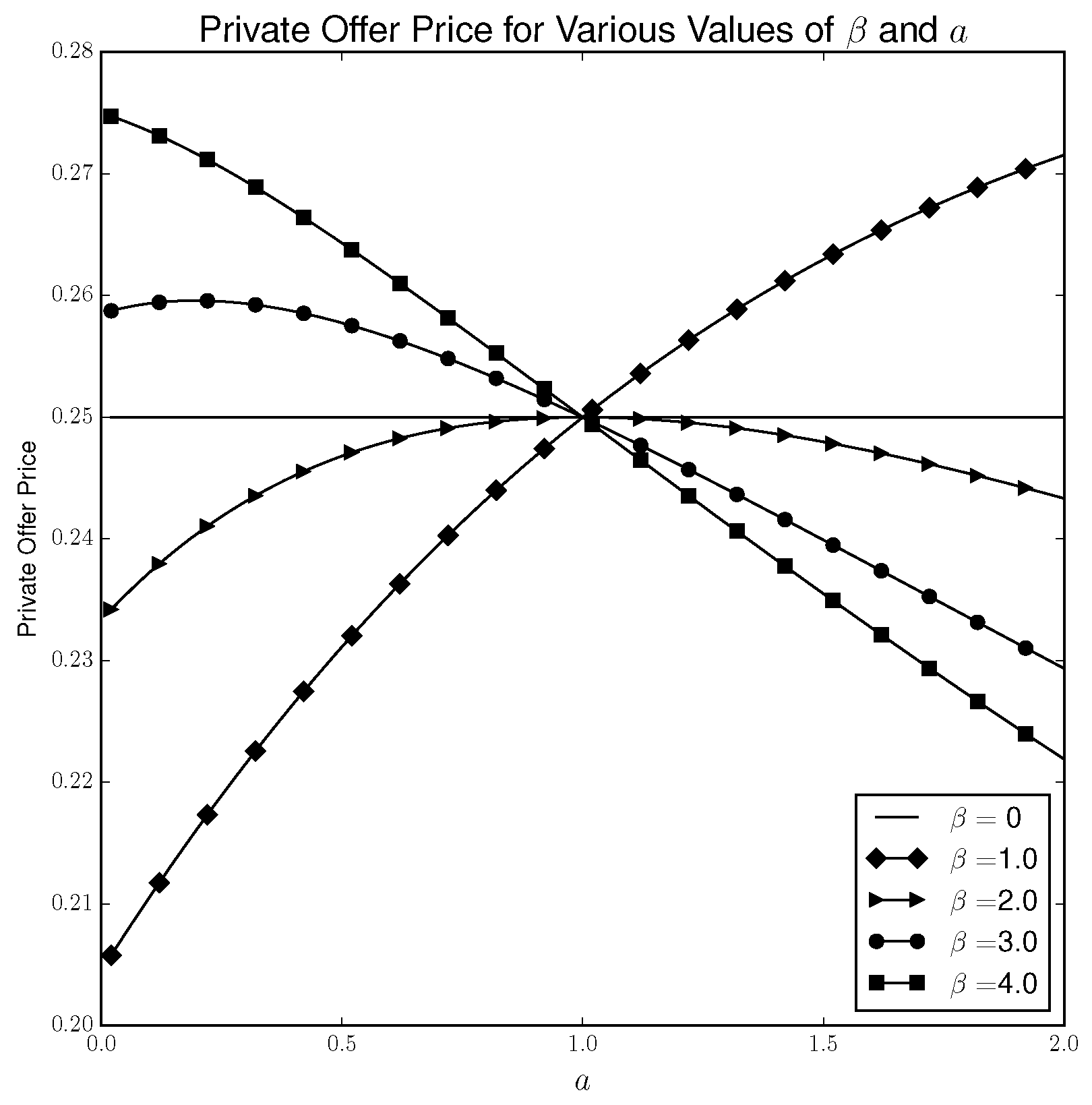
Figure 1 plots the private offer price for different values of
and
a to DM in the matching pennies game under the quantal response equilibrium concept. Recall that
a is DM’s payoff by matching “heads” and
is the rationality parameter. For simplicity, we assume
is common to both players.
As
Figure 1 illustrates, the quantal response private offer price contains more richness than in the Nash case. First, when
, the private offer price is
for all values of
a. The reason for this is that for all values of
a, both players randomize uniformly and the outcome
occurs with probability
. Therefore, increasing
a by amount
increases
a’s expected utility by
for any value of
. Since player’s strategies do not change when
, the second term in Equation (
3) is 0 and the private offer price is
.
However, when
, the private offer price depends on both
and
a.
Figure 1 shows that when
is relatively low, the private offer price is higher for higher values of
a but when
is relatively high, the opposite is true.
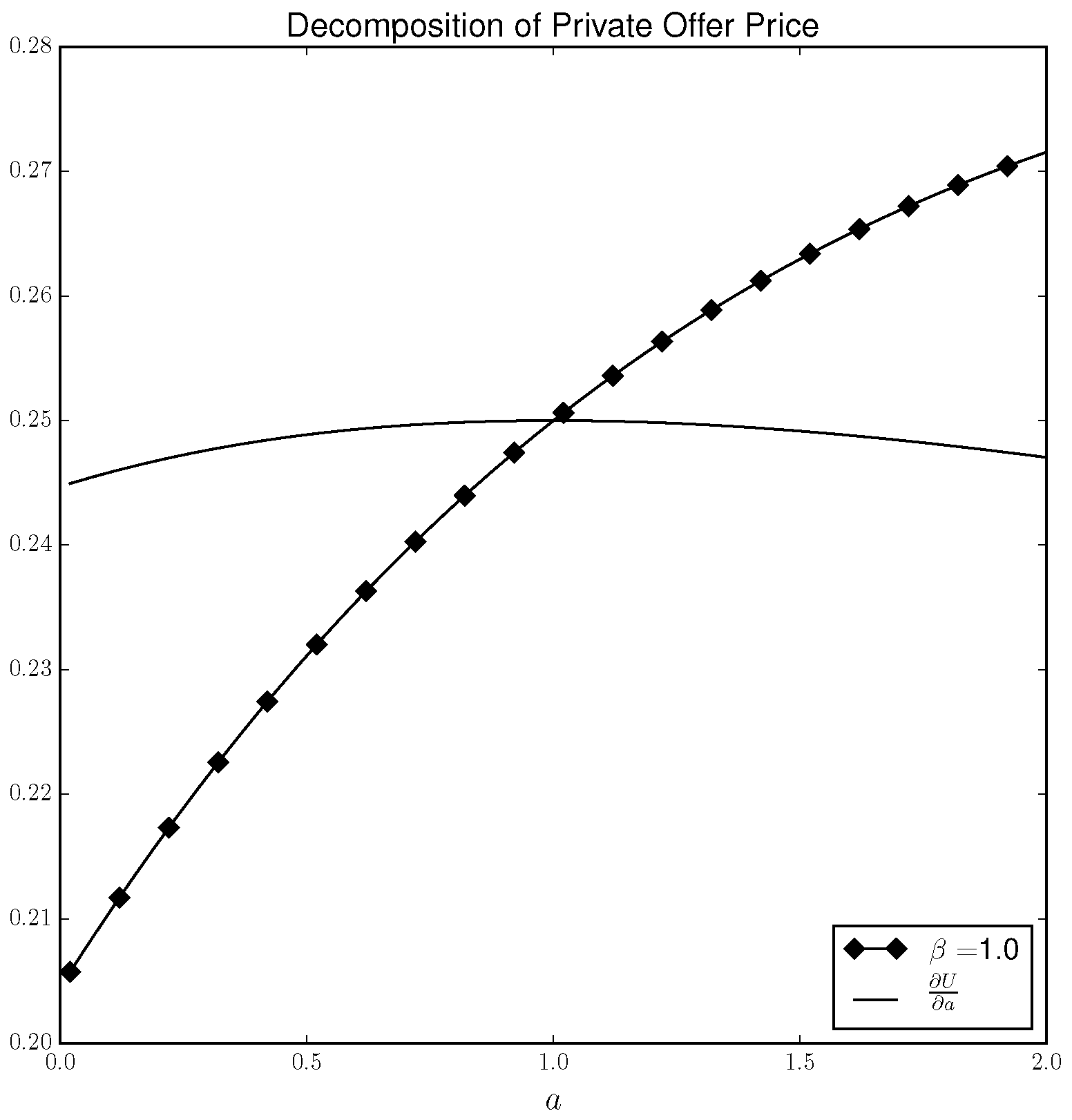
Figure 2 once again plots the private offer price when
as well as the first term (
) of the private offer price. Therefore, the difference between the solid line and the lined marked with diamonds gives the impact on DM’s utility as a result of DM adjusting their strategy in response to a parameter change (i.e., the terms after the second summation in Equation (
3). As the plot shows,
is always positive. However, when
a is low, the impact on DM’s utility due to DM changing their strategy in response to an increase in
a is
negative. The reason is that when
and
is playing the quantal response equilibrium strategy, DM’s
best response would be to always play “T”. However, under the quantal response equilibrium concept DM does not play “T” but instead randomizes according to the logit probabilities given in Equation (
18). Under such a solution concept, increasing
a induces DM to place a
higher probability on “H”, even though it is not DM’s best strategy. On the other hand, when
, DM’s best strategy
is to always play “H” and thus increasing
a makes DM place more weight on “H” and DM increases their utility by adjusting their strategy in response to a change in
a. Put another way, DM would be willing to pay for an increase in
a. However, when
, DM’s willingness to pay is dampened by the fact that increasing
a makes a sub-optimal action more desirable and thus increases the probability that
a will not best respond. That is, DM considers its own future irrationality when determining whether it should pay to change the parameter values.
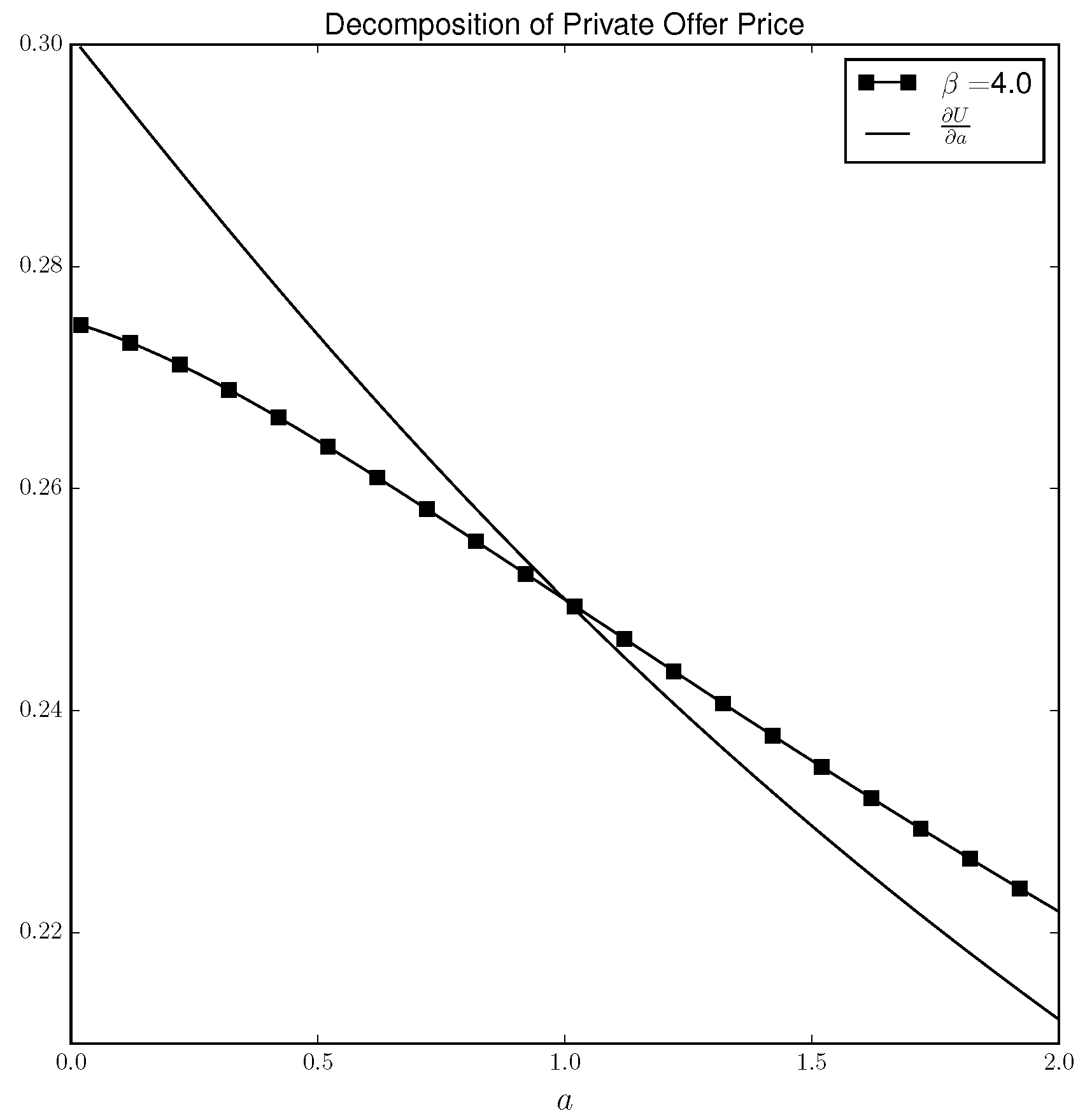
Figure 3 shows the same phenomenon when
. That is,
and the private offer price is less than
when
and greater than
when
. It is the slope of the
curve that accounts for the difference in the private offer price when
and
. As
Figure 3 shows, when
,
is relatively flat but when
, the curve slopes down. To see why, consider the perfectly rational case in which players play the Nash equilibrium. In that case, as
a gets larger, player −DM puts lower probability on ’H’ in order to keep DM indifferent between heads and tails while DM randomizes with probability
for all values of
a. Therefore, the impact of an increase in
a on DM’s utility (holding strategies constant) is less when
a is high. The same logic applies under the QRE solution concept except the player’s mixing probabilities do not respond as strongly to an increase in
a as they do in the Nash case. In other words, as
gets larger, the players move closer to the Nash equilibrium solution and under the Nash solution,
is deceasing in
a.
In the most general sense, it is possible to have DM’s payoffs for all possible outcomes increase but the private offer price actually be negative. For example, let be a vector such that each element of represents DM’s payoff in a specific outcome. Furthermore, suppose that is positive for all components of . Even though DM’s utility would increase under all possible outcomes, it is possible that the change in utilities for each action makes it more likely that DM chooses a sub-optimal action. If the negative effect of DM adjusting their strategy is greater in magnitude than the increase in expected utility due to the parameter change, the private offer price would be negative. Characterizing the games and solution concepts in which this phenomenon occurs is a direction of future work.
Thus far we have considered DM to be the same decision maker in both the first stage and the second stage of the game. An alternative interpretation is that DM in the first stage of the game is a mechanism designer that has the same utility function as DM We thank an anonymous referee for suggesting this interpretation. Then, the private and public offer price determine how much a regulator or policy maker would be willing to pay to change the parameter values. This means that the negative offer prices in the matching pennies game no longer represent DM anticipating its own future irrationality but a regulator anticipating another player’s future bounded rationality.
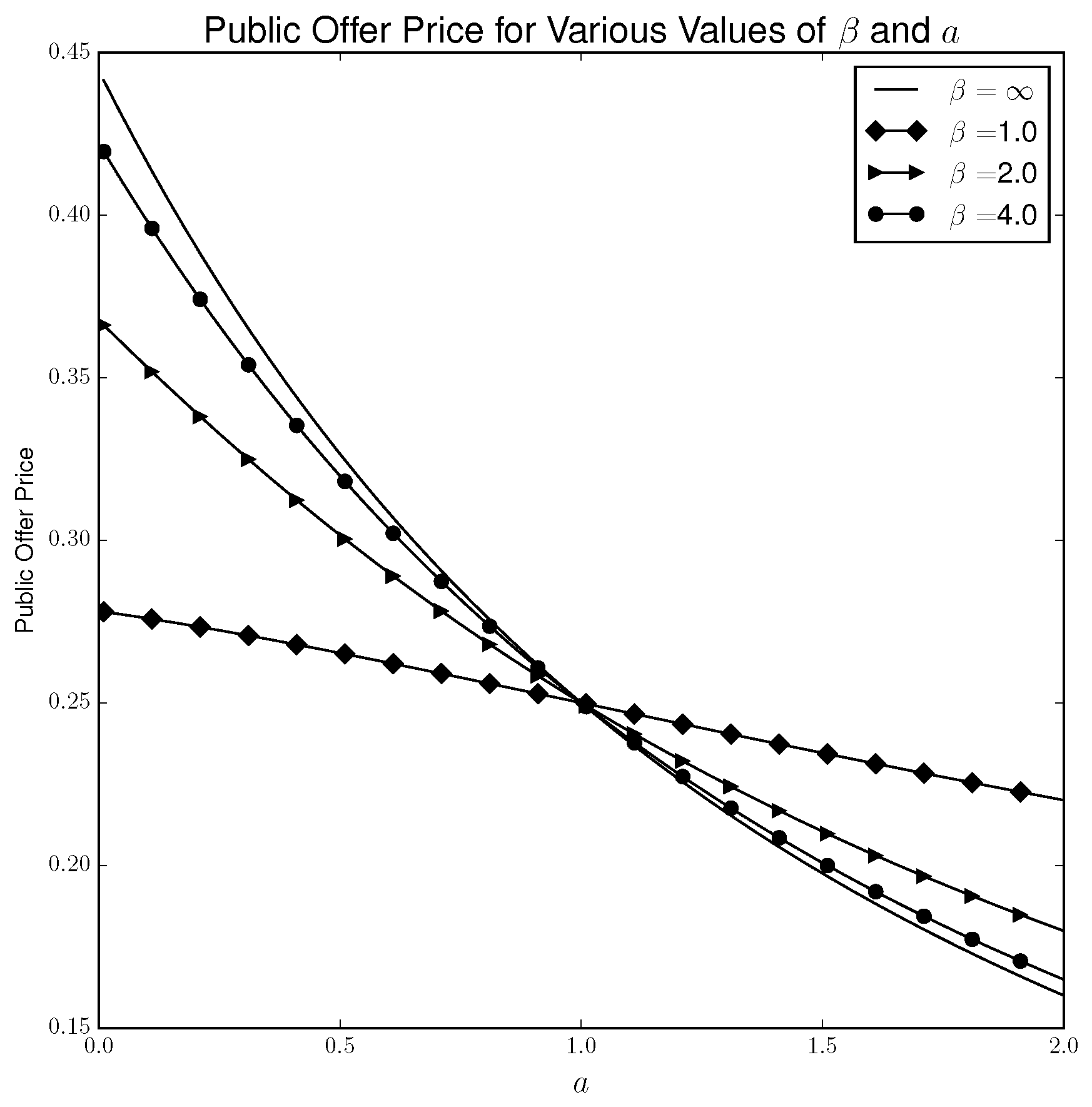
Figure 4 plots the public offer price under the quantal response solution concept for various values of
a and
. In this case, the public offer price behaves qualitatively similar under the quantal response solution concept as under the Nash solution concept. Indeed, as
, the public offer price under quantal response equilibrium approaches the public offer price under the Nash equilibrium.