A Comprehensive Fault Diagnosis Method for Rolling Bearings Based on Refined Composite Multiscale Dispersion Entropy and Fast Ensemble Empirical Mode Decomposition
Abstract
:1. Introduction
2. Basic Theory
2.1. Fast Ensemble Empirical Mode Decomposition (FEEMD)
2.2. Dispersion Entropy and Refined Composite Multiscale Dispersion Entropy
2.2.1. Dispersion Entropy
2.2.2. Refined Composite Multiscale Dispersion Entropy (RCMDE)
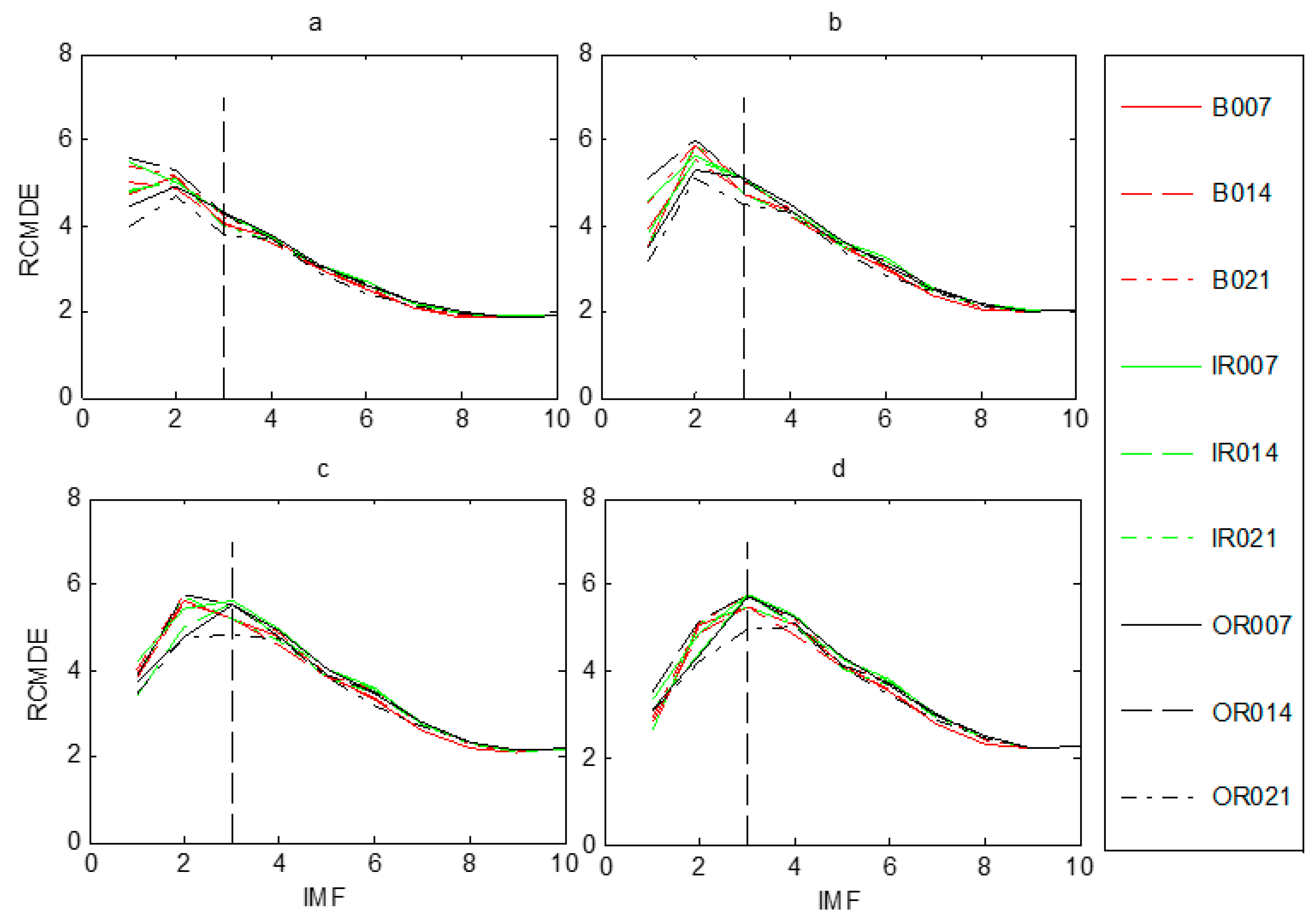
2.2.3. Parameter Settings of RCMDE
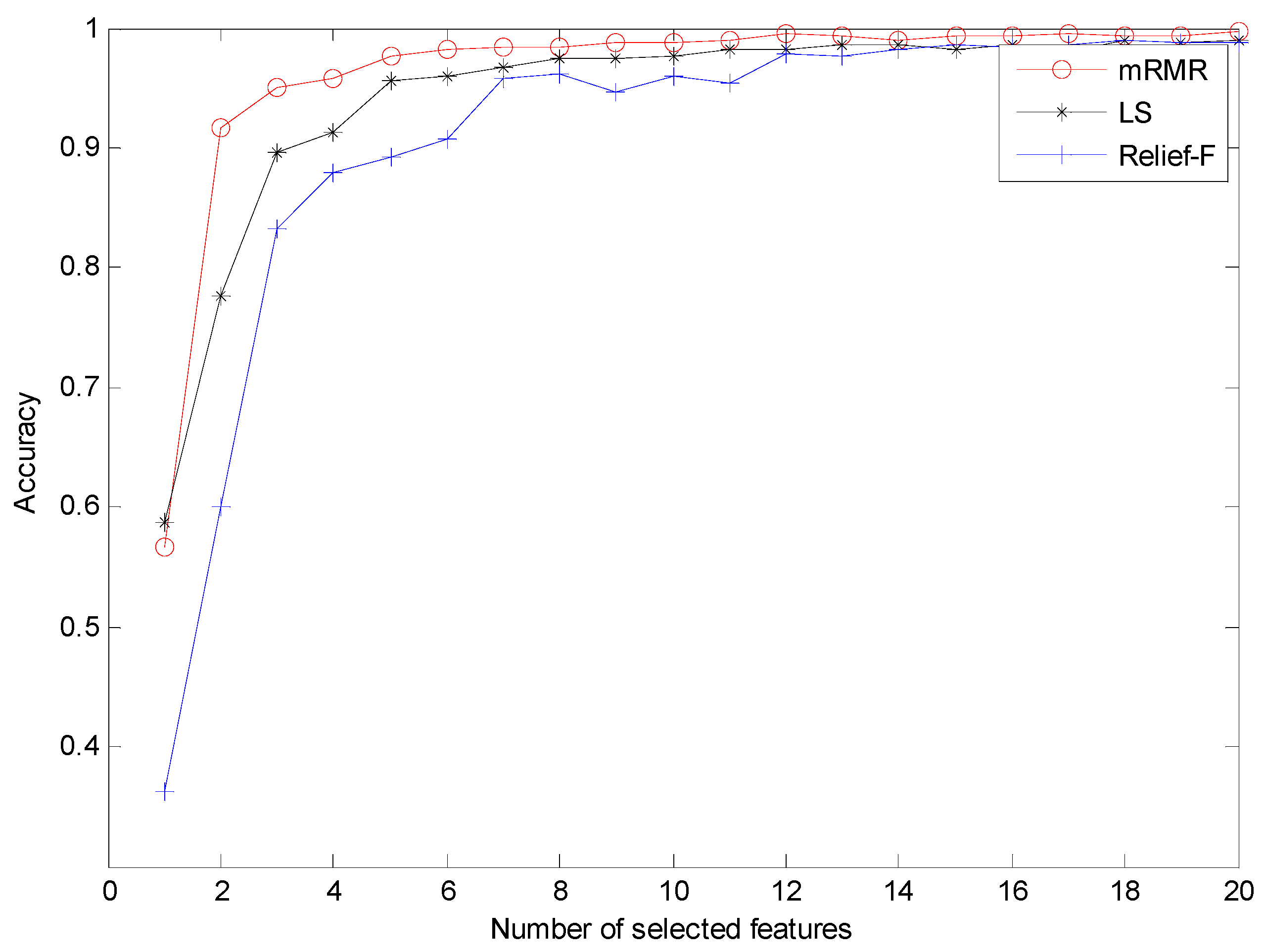
2.3. Max-Relevance And Min-Redundancy (mRMR)
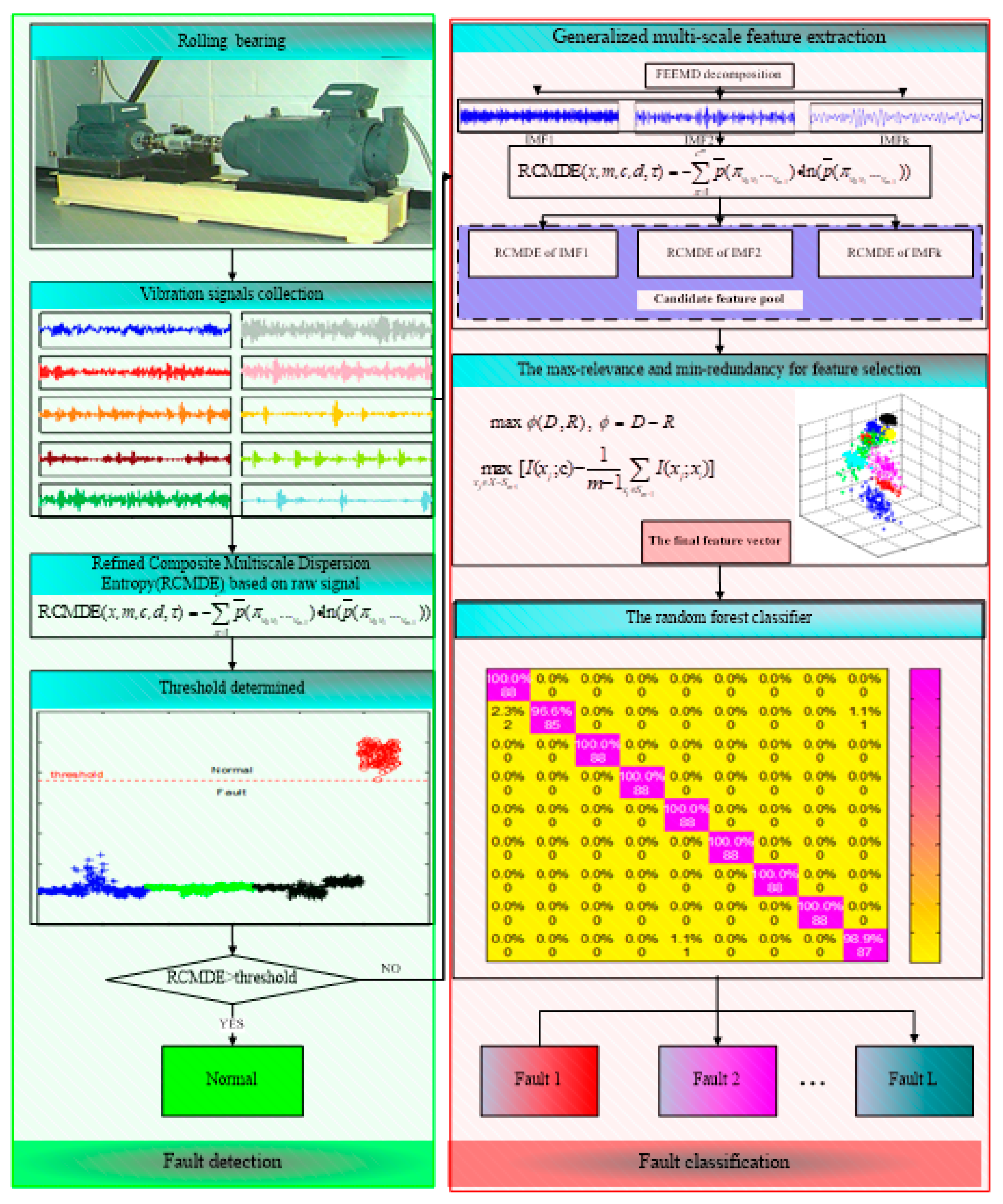
3. The Proposed Method
3.1. Fault Detection
3.2. Fault Classification
- (1)
- Collect the vibration signals under different working conditions of rolling bearings.
- (2)
- Divide the vibration signals into non-overlapped samples.
- (3)
- Calculate the RCMDE values of vibration signals at different scale factors. Find out a threshold based on RCMDE to judge the health status of a bearing. If it is healthy, output normal to present the working condition of the bearing. Otherwise, identify the faults of different types and severity in the next steps.
- (4)
- The fault vibration signals are decomposed into multiple IMFs by FEEMD.
- (5)
- The RCMDE values of the first several IMFs are calculated to construct the candidate feature pool.
- (6)
- The mRMR is employed to select the sensitive features from the candidate feature pool to generate the final feature vectors.
- (7)
- The final feature vectors are fed into the random forest classifier to identify different fault types and severity.
| Algorithm 1. The Pseudocode of the Fault Diagnosis Algorithm |
| 1 Input the vibration signals of N different working conditions 2 Calculate the RCMDE values Ri of different working conditions at scale factor τmax 3 Define a threshold § 4 If Ri > § 5 Output “Normal” 6 Else 7 Decompose the fault vibration signals of L different fault working conditions into m IMFs 8 Calculate the RCMDE values of the first k IMFs at scale factor τ, (τ = 1,2, …, τmax) 9 Then, for fault working conditions, the candidate feature pool is formed with a size of E × F, (E is number of fault sample, F = k × τmax) 10 For training samples Etrain × F, training label Ltrain, select s features from ranked features by mRMR, obtain Etrain × Strain 11 For testing samples Etest × F, select s features according to ranking results of training samples, obtain Etest × Stest 12 Put Etrain × Strain, Ltrain and Etest × Stest into RF classifier 13 Obtain test label Ltest 14 Output fault working condition |
4. Experiment Results
4.1. Experimental Data
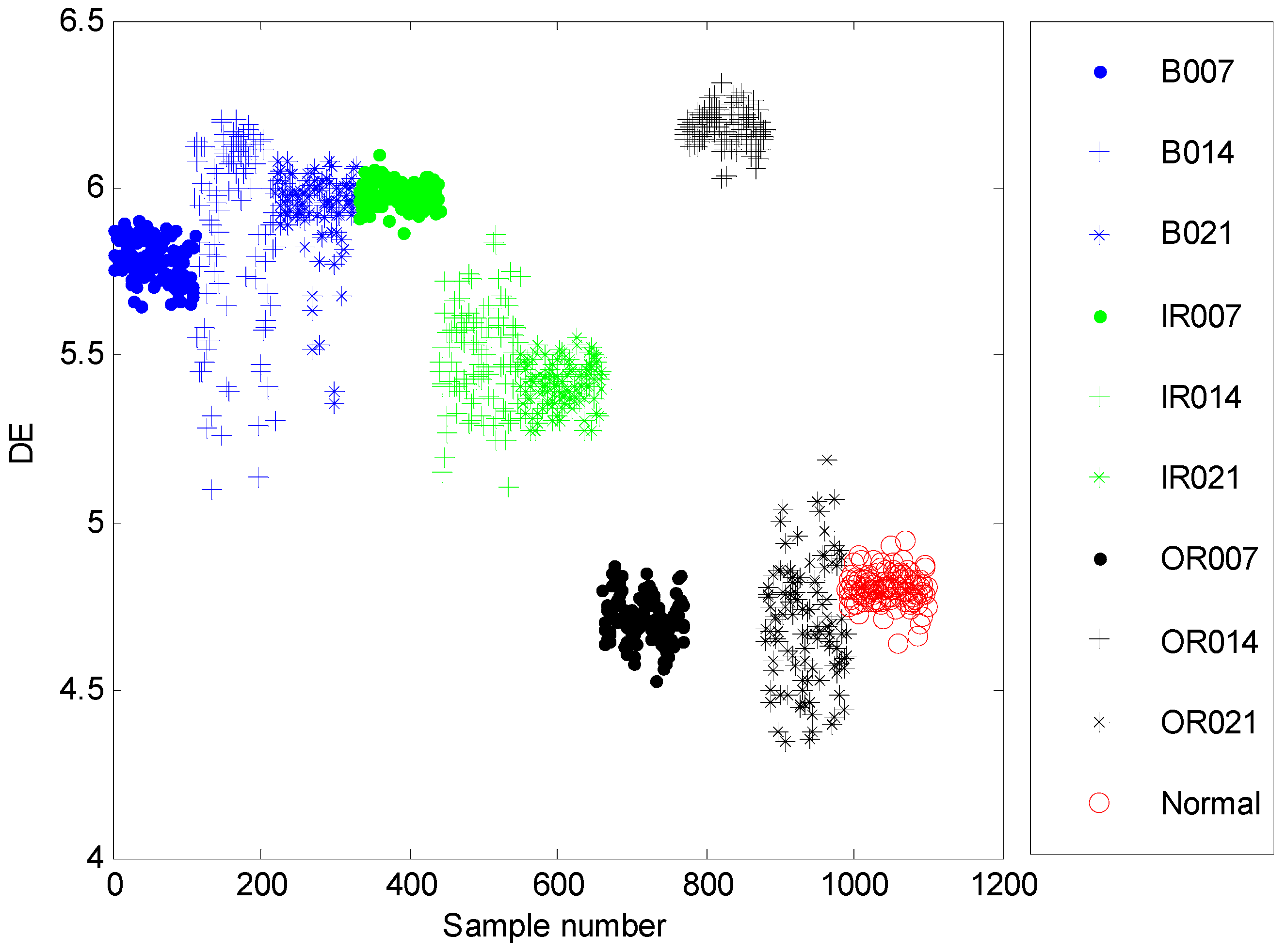
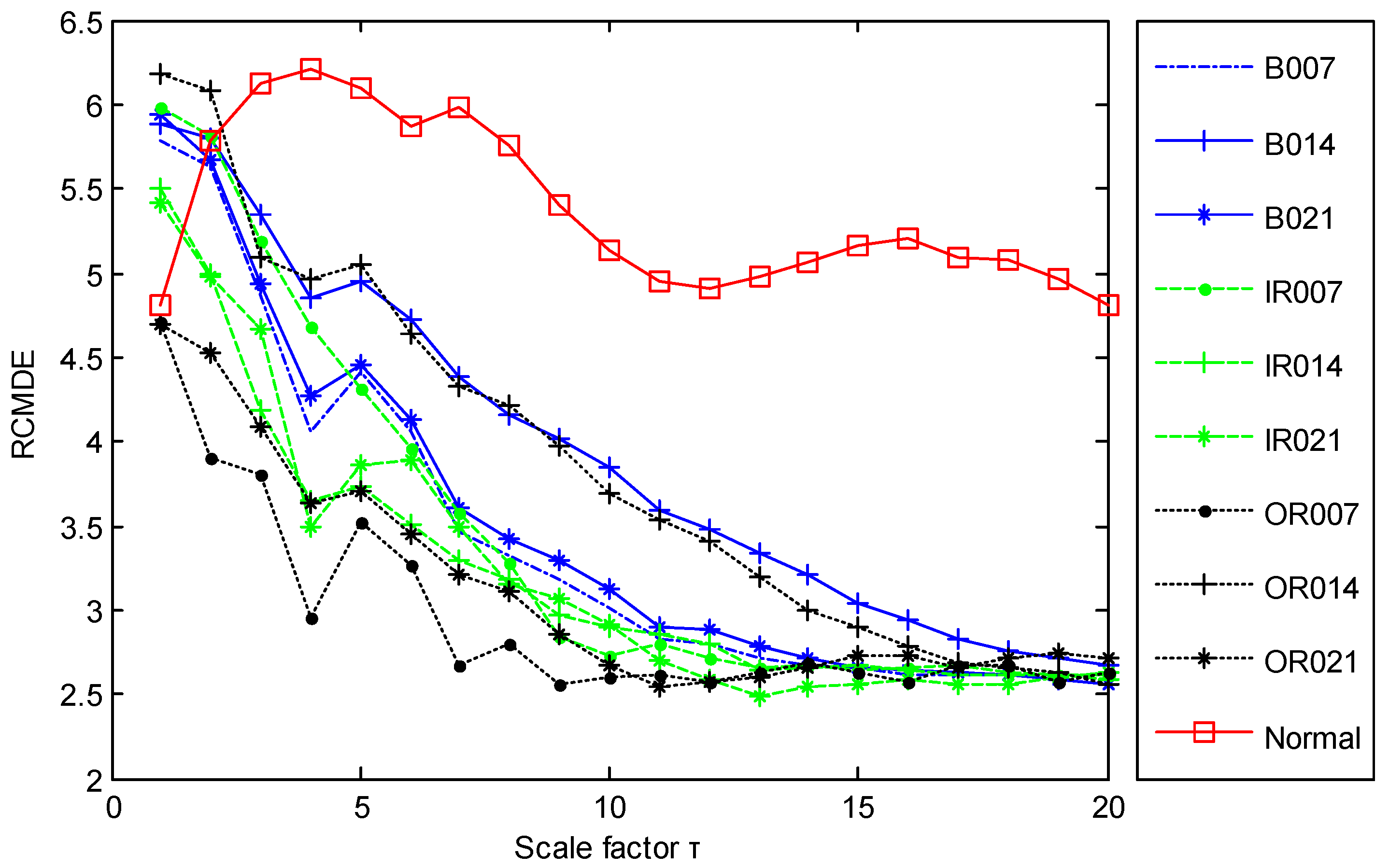
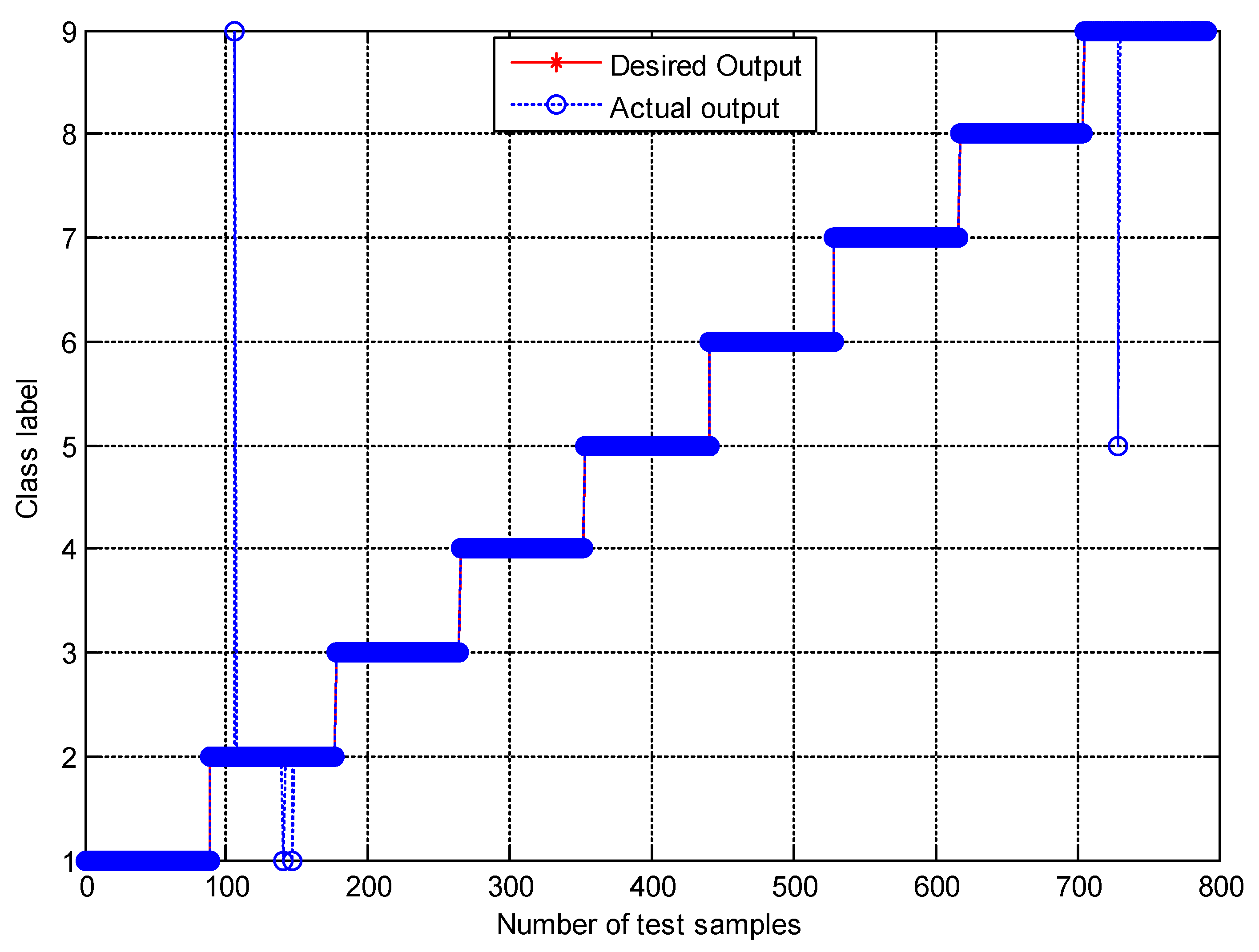
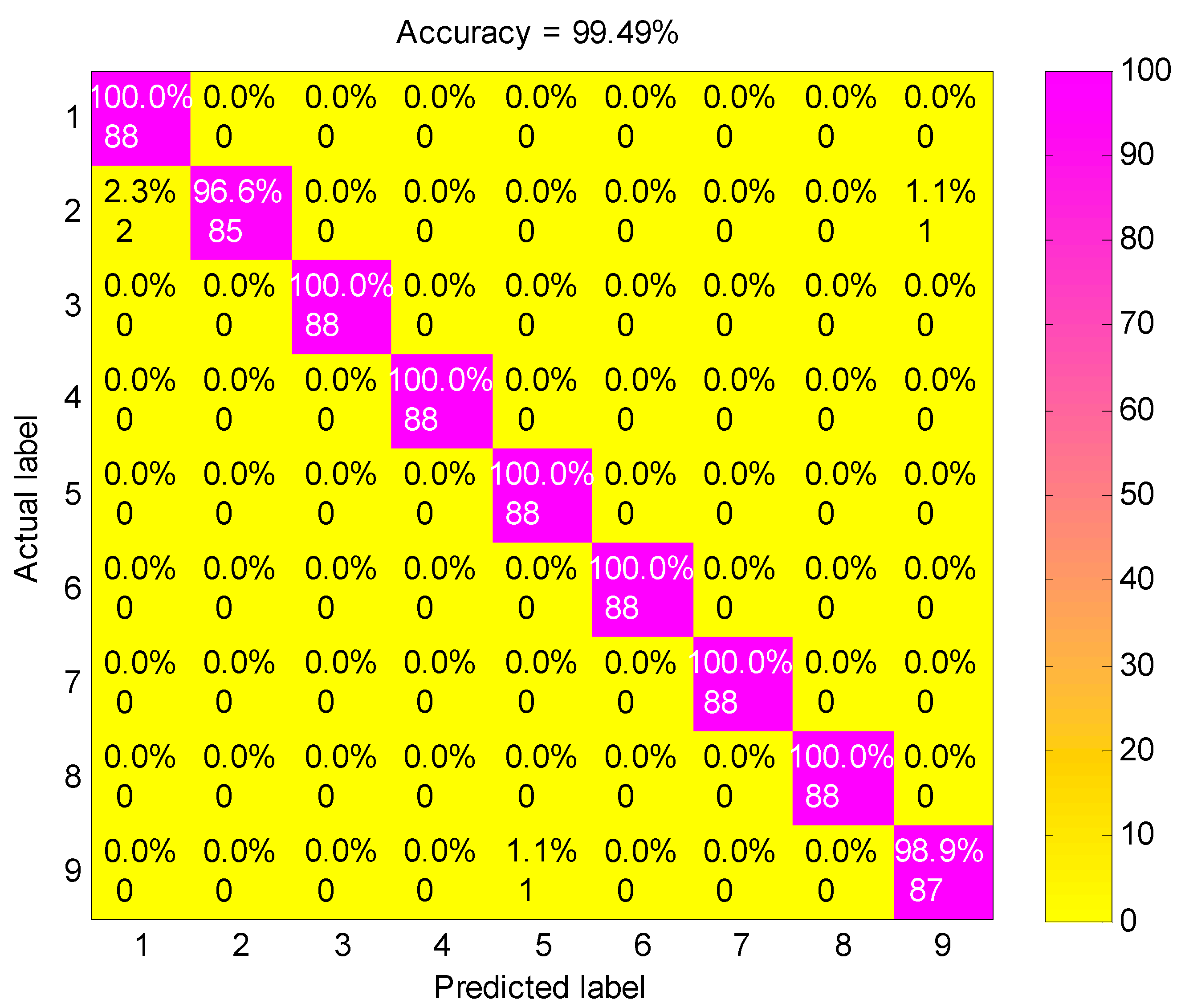
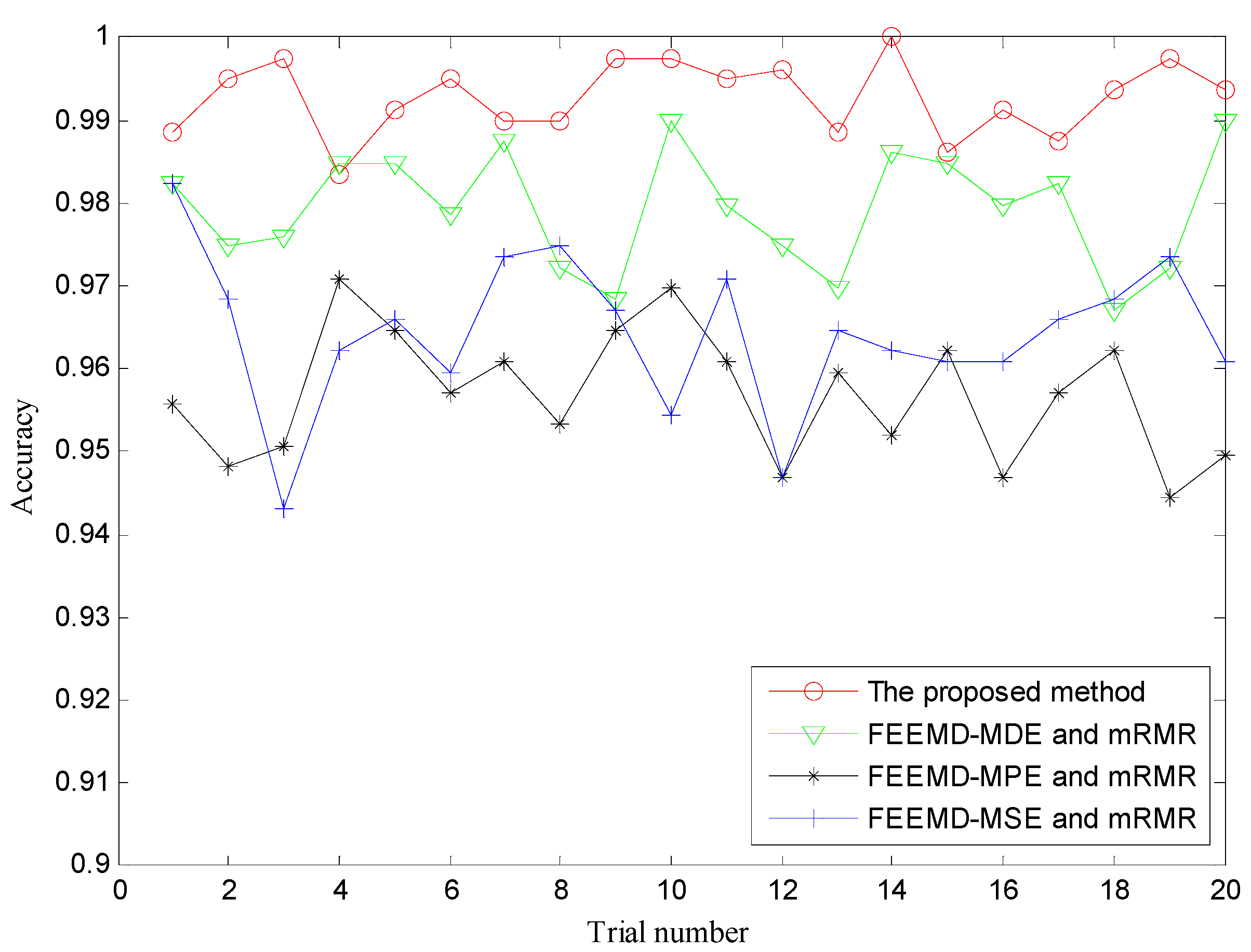
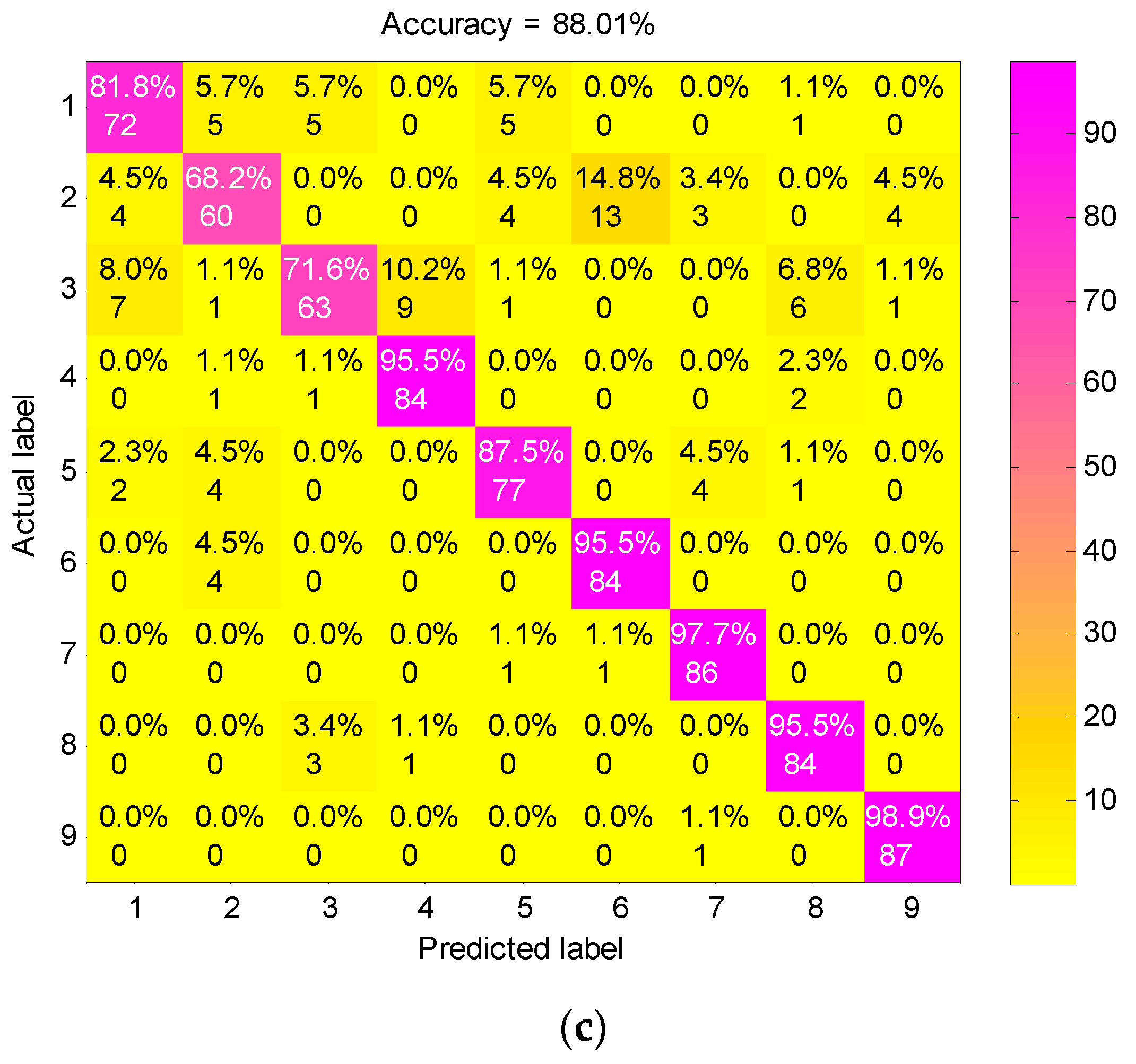
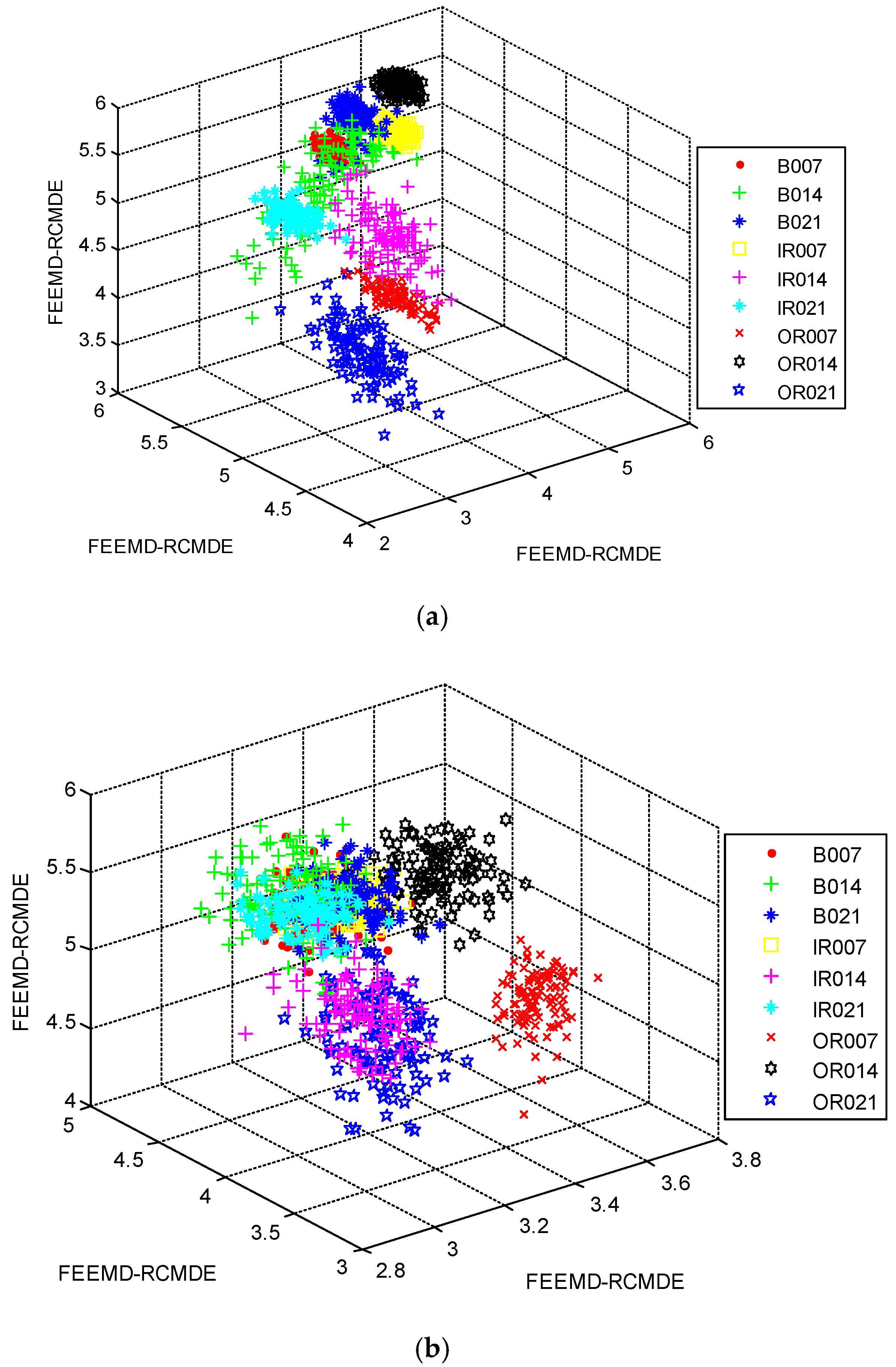
4.2. Result and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Peng, Z.; Tse, P.W.; Chu, F. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Villecco, F. On the evaluation of errors in the virtual design of mechanical systems. Machines 2018, 6, 36. [Google Scholar] [CrossRef]
- Fu, W.; Tan, J.; Zhang, X.; Chen, T.; Wang, K. Blind parameter identification of MAR model and mutation hybrid GWO-SCA optimized SVM for fault diagnosis of rotating machinery. Complexity 2019, 2019, 3264969. [Google Scholar] [CrossRef]
- Torres, L.; Gómez-Aguilar, J.F.; Jiménez, J.; Mendoza, E.; López-Estrada, F.R.; Escobar-Jiménez, R.F. Parameter identification of periodical signals: Application to measurement and analysis of ocean wave forces. Digit. Signal Process. 2017, 69, 59–69. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Zhou, J.; Xu, Y.; Tan, J.; Chen, T. A hybrid approach for multi-step wind speed forecasting based on multi-scale dominant ingredient chaotic analysis, KELM and synchronous optimization strategy. Sustainability 2019, 11, 1804. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Li, C.; Tan, J. Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis, improved hybrid GWO-SCA optimization and ELM. Energy Convers. Manag. 2019, 187, 356–377. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig-Cayuela, V. Diagnosis of fluid leaks in pipelines using dynamic PCA. IFAC-PapersOnLine 2018, 51, 373–380. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Xu, Z.; Shin, B.S.; Klette, R. Accurate and robust line segment extraction using minimum entropy with hough transform. IEEE Trans. Image Process. 2015, 24, 813–822. [Google Scholar]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 1741021–1741024. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Keller, G.; Pompe, B. Entropy of interval maps via permutations. Nonlinearity 2002, 15, 1595–1602. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time-series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Rostaghi, M.; Ashory, M.R.; Azami, H. Application of dispersion entropy to status characterization of rotary machines. J. Sound Vib. 2019, 438, 291–308. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Aziz, W.; Arif, M. Multiscale permutation entropy of physiological time series. In Proceedings of the 9th International Multitopic Conference, Karachi, Pakistan, 24–25 December 2005; pp. 1–6. [Google Scholar]
- Azami, H.; Rostaghi, M.; Abasolo, D.; Escudero, J. Refined composite multiscale dispersion entropy and its application to biomedical signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar]
- Wu, S.; Wu, P.; Wu, C.; Ding, J.; Wang, C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. Intelligent fault diagnosis of rotating machinery using improved multiscale dispersion entropy and mRMR feature selection. Knowl. Based Syst. 2019, 163, 450–471. [Google Scholar] [CrossRef]
- Li, G.; Guan, Q.; Yang, H. Noise reduction method of underwater acoustic signals based on CEEMDAN, effort-to-compress complexity, refined composite multiscale dispersion entropy and wavelet threshold denoising. Entropy 2019, 21, 11. [Google Scholar] [CrossRef]
- Tang, G.; Pang, B.; He, Y.; Tian, T. Gearbox fault diagnosis based on hierarchical instantaneous energy density dispersion entropy and dynamic time warping. Entropy 2019, 21, 593. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Li, C.; Li, X.; Li, Y.; Zhong, H. Vibration trend measurement for a hydropower generator based on optimal variational mode decomposition and an LSSVM improved with chaotic sine cosine algorithm optimization. Meas. Sci. Technol. 2019, 30, 015012. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Tan, J.; Fu, W.; Wang, K.; Xue, X.; Hu, W.; Shan, Y. Fault diagnosis for rolling bearing based on semi-supervised clustering and support vector data description with adaptive parameter optimization and improved decision strategy. Appl. Sci. 2019, 9, 1676. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Physica A 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M. Wind speed forecasting using FEEMD echo state networks with RELM in Hebei, China. Energy Convers. Manag. 2016, 114, 197–208. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, J.; Liu, H.; Shan, Y. A multi-step progressive fault diagnosis method for rolling element bearing based on energy entropy theory and hybrid ensemble auto-encoder. ISA Trans. 2019, 87, 235–250. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Int. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Christopher Culberson, J.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Fault diagnosis in spur gears based on genetic algorithm and random forest. Mech. Syst. Signal Process. 2016, 70–71, 87–103. [Google Scholar] [CrossRef]
- Xue, X.; Li, C.; Cao, S.; Sun, J.; Liu, L. Fault diagnosis of rolling element bearings with a two-step scheme based on permutation entropy and random forests. Entropy 2019, 21, 96. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, J.; Xiao, H.; Zhang, W.; Zhu, W.; Li, C. Multifault diagnosis for rolling element bearings based on intrinsic mode permutation entropy and ensemble optimal extreme learning machine. Adv. Mech. Eng. 2014, 6, 803919. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 15 October 2018).
- He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2005; pp. 507–514. [Google Scholar]
- Liu, H.; Motoda, H. Computational methods of feature selection. IEEE Intell. Inf. Bull. 2008, 9, 39–40. [Google Scholar]
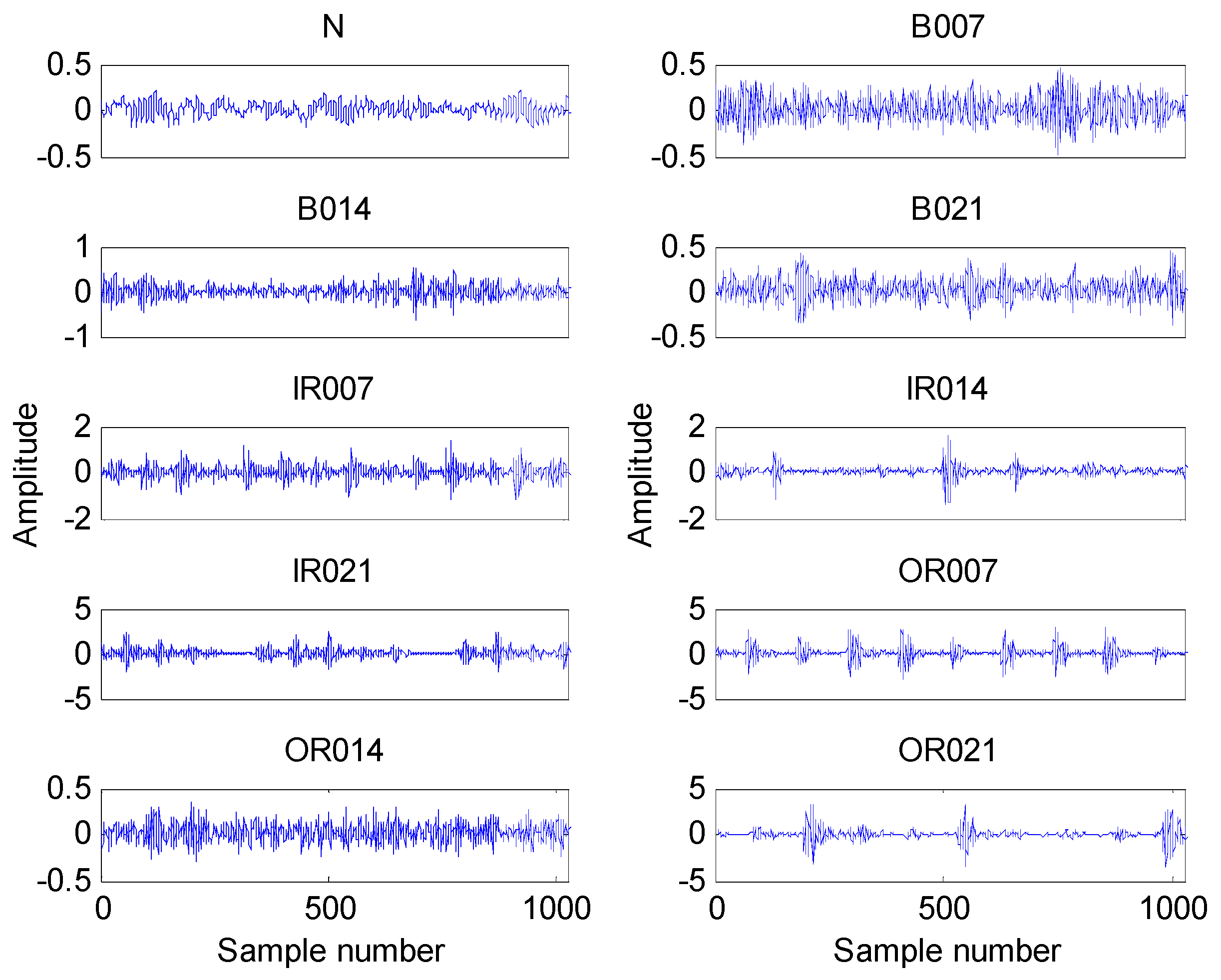


| Working Conditions | Severity (Inches) | Abbreviation | Number of Training Samples (20%) | Number of Testing Samples (80%) | Classification Label |
|---|---|---|---|---|---|
| Normal | None | N | 22 | 88 | 0 |
| Ball fault | 0.007 | B007 | 22 | 88 | 1 |
| 0.014 | B014 | 22 | 88 | 2 | |
| 0.021 | B021 | 22 | 88 | 3 | |
| Inner race fault | 0.007 | IR007 | 22 | 88 | 4 |
| 0.014 | IR014 | 22 | 88 | 5 | |
| 0.021 | IR021 | 22 | 88 | 6 | |
| Outer race fault | 0.007 | OR007 | 22 | 88 | 7 |
| 0.014 | OR014 | 22 | 88 | 8 | |
| 0.021 | OR021 | 22 | 88 | 9 |
| Different Methods | Accuracy (%) | ||
|---|---|---|---|
| Max | Min | Mean | |
| The proposed method | 100 | 98.36 | 99.27 |
| FEEMD-MDE and mRMR | 98.99 | 96.72 | 97.93 |
| FEEMD-MPE and mRMR | 97.10 | 94.44 | 95.69 |
| FEEMD-MSE and mRMR | 98.23 | 93.42 | 96.43 |
| Different Methods | Accuracy (%) | ||
|---|---|---|---|
| Max | Min | Mean | |
| FEEMD-RCMDE | 95.08 | 91.16 | 93.41 |
| FEEMD-MDE | 91.16 | 87.37 | 89.58 |
| FEEMD-MPE | 85.28 | 79.49 | 82.27 |
| FEEMD-MSE | 82.95 | 78.79 | 80.81 |
| Different Classifier | Accuracy (%) | CPU Time (s) | ||
|---|---|---|---|---|
| Max | Min | Mean | ||
| RF | 100 | 98.36 | 99.27 | 0.29 |
| ELM | 99.31 | 96.54 | 97.96 | 0.11 |
| SVM | 100 | 98.75 | 99.42 | 12.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhou, J. A Comprehensive Fault Diagnosis Method for Rolling Bearings Based on Refined Composite Multiscale Dispersion Entropy and Fast Ensemble Empirical Mode Decomposition. Entropy 2019, 21, 680. https://doi.org/10.3390/e21070680
Zhang W, Zhou J. A Comprehensive Fault Diagnosis Method for Rolling Bearings Based on Refined Composite Multiscale Dispersion Entropy and Fast Ensemble Empirical Mode Decomposition. Entropy. 2019; 21(7):680. https://doi.org/10.3390/e21070680
Chicago/Turabian StyleZhang, Weibo, and Jianzhong Zhou. 2019. "A Comprehensive Fault Diagnosis Method for Rolling Bearings Based on Refined Composite Multiscale Dispersion Entropy and Fast Ensemble Empirical Mode Decomposition" Entropy 21, no. 7: 680. https://doi.org/10.3390/e21070680
APA StyleZhang, W., & Zhou, J. (2019). A Comprehensive Fault Diagnosis Method for Rolling Bearings Based on Refined Composite Multiscale Dispersion Entropy and Fast Ensemble Empirical Mode Decomposition. Entropy, 21(7), 680. https://doi.org/10.3390/e21070680




