Time–Energy and Time–Entropy Uncertainty Relations in Nonequilibrium Quantum Thermodynamics under Steepest-Entropy-Ascent Nonlinear Master Equations
Abstract
1. Introduction
2. Assumed Structure of the Nonlinear Dissipative Quantum Master Equation
3. General Uncertainty Relations
4. Characteristic Time of the Rate of Entropy Change
5. Shortest Characteristic Times for Purely-Unitary and Purely-Dissipative Dynamics
6. Occupation Probabilities
7. Example. Steepest-Entropy-Ascent Master Equation for Conservative Dissipative Dynamics
8. Numerical Results for Relaxation within a Single N-Level Qudit or a One-Particle Model of a Dilute Boltzmann Gas of N-Level Particles
9. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Reasons for Not Assuming a Kossakowski–Lindblad form of the Master Equation
Appendix B. How Did Locally Steepest Entropy Ascent Come About?
References
- Aharonov, Y.; Bohm, D. Time in the quantum theory and the uncertainty relation for time and energy. Phys. Rev. 1961, 122, 1649–1658. [Google Scholar] [CrossRef]
- Allcock, G.R. The time of arrival in quantum mechanics I. Formal considerations. Ann. Phys. 1969, 53, 253–285. [Google Scholar] [CrossRef]
- Allcock, G.R. The time of arrival in quantum mechanics II. The individual measurement. Ann. Phys. 1969, 53, 286–310. [Google Scholar] [CrossRef]
- Allcock, G.R. The time of arrival in quantum mechanics III. The measurement ensemble. Ann. Phys. 1969, 53, 311–348. [Google Scholar] [CrossRef]
- Bauer, M.; Mello, P.A. The time-energy uncertainty relation. Ann. Phys. 1978, 111, 38–60. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Kurmyshev, E.V.; Man’ko, V.I. Generalized uncertainty relation and correlated coherent states. Phys. Lett. A 1980, 79, 150–152. [Google Scholar] [CrossRef]
- Busch, P. On the energy-time uncertainty relation. Part I: Dynamical time and time indeterminacy. Found. Phys. 1990, 20, 1–32. [Google Scholar] [CrossRef]
- Busch, P. On the energy-time uncertainty relation. Part II: Pragmatic time versus energy indeterminacy. Found. Phys. 1990, 20, 33–43. [Google Scholar] [CrossRef]
- Landauer, R. Information is physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Hilgevoord, J. The uncertainty principle for energy and time I. Am. J. Phys. 1996, 64, 1451–1456. [Google Scholar] [CrossRef]
- Hilgevoord, J. The uncertainty principle for energy and time. II. Am. J. Phys. 1998, 66, 396–402. [Google Scholar] [CrossRef]
- Hu, B.L.; Zhang, Y. Uncertainty Principle for Quantum Open Systems. Int. J. Mod. Phys. A 1995, 10, 4537–4561. [Google Scholar] [CrossRef]
- Trifonov, D.A. Generalizations of Heisenberg uncertainty relation. Eur. Phys. J. B 2002, 29, 349–353. [Google Scholar] [CrossRef]
- Dodonov, V.V. Purity- and entropy-bounded uncertainty relations for mixed quantum states. J. Opt. B 2002, 4, S98–S108. [Google Scholar] [CrossRef]
- Pfeifer, P.; Fröhlich, J. Generalized time-energy uncertainty relations and bounds on lifetimes of resonances. Rev. Mod. Phys. 1995, 67, 759–779. [Google Scholar] [CrossRef]
- Sackett, C.A.; Kielpinski, D.; King, B.E.; Langer, C.; Meyer, V.V.; Myatt, C.J.; Rowe, M.; Turchette, Q.A.; Itano, W.M.; Wineland, D.J.; et al. Experimental entanglement of four particles. Nature 2000, 404, 256–259. [Google Scholar] [CrossRef]
- Kielpinski, D.; Monroe, C.; Wineland, D.J. Architecture for a large-scale ion-trap quantum computer. Nature 2002, 417, 709–711. [Google Scholar] [CrossRef]
- Ekert, A.K.; Alves, C.M.; Oi, D.K.L.; Horodecki, M.; Horodecki, P.; Kwek, L.C. Direct estimations of linear and nonlinear functionals of a quantum state. Phys. Rev. Lett. 2002, 88, 217901. [Google Scholar] [CrossRef]
- Bovino, F.A.; Castagnoli, G.; Ekert, A.; Horodecki, P.; Alves, C.M.; Sergienko, A.V. Direct measurement of nonlinear properties of bipartite quantum states. Phys. Rev. Lett. 2005, 95, 240407. [Google Scholar] [CrossRef]
- Shull, C.G.; Atwood, D.K.; Arthur, J.; Horne, M.A. Search for a Nonlinear variant of the Schrödinger equation by neutron interferometry. Phys. Lett. Lett. 1980, 44, 765. [Google Scholar] [CrossRef]
- Martinez, J.C.; Polatdemir, E. Measurement of tunneling time via electron interferometry. Appl. Phys. Lett. 2004, 84, 1320–1322. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Czajkowski, J.; Sekatski, P. Adaptive quantum metrology under general markovian noise. Phys. Rev. X 2017, 7, 041009. [Google Scholar] [CrossRef]
- Beau, M.; Del Campo, A. Nonlinear quantum metrology of many-body open systems. Phys. Rev. Lett. 2017, 119, 010403. [Google Scholar] [CrossRef] [PubMed]
- Dodonov, V.V.; Dodonov, A.V. Energy–time and frequency–time uncertainty relations: Exact inequalities. Phys. Scr. 2015, 90, 074049. [Google Scholar] [CrossRef]
- Kraus, K. General state changes in quantum theory. Ann. Phys. 1971, 64, 311–335. [Google Scholar] [CrossRef]
- Kossakowski, A. Necessary and sufficient conditions for a generator of a quantum dynamical semigroup. Bull. Acad. Pol. Sci. Ser. Math. Astr. Phys. 1972, 20, 1021–1025. [Google Scholar]
- Kossakowski, A. On quantum statistical mechanics of non-Hamiltonian systems. Rep. Math. Phys. 1972, 3, 247–274. [Google Scholar] [CrossRef]
- Ingarden, R.S.; Kossakowski, A. On the connection of nonequilibrium information thermodynamics with non-Hamiltonian quantum mechanics of open systems. Ann. Phys. 1975, 89, 451–485. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 119, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Spohn, H. Approach to equilibrium for completely positive dynamical semigroups of N-level systems. Rep. Math. Phys. 1976, 10, 189–194. [Google Scholar] [CrossRef]
- Spohn, H. Entropy production for quantum dynamical semigroups. J. Math. Phys. 1978, 19, 1227–1230. [Google Scholar] [CrossRef]
- Asorey, M.; Kossakowski, A.; Marmo, G.; Sudarshan, E.C.G. Dynamical maps and density matrices. J. Phys. Conf. Ser. 2009, 196, 012023. [Google Scholar] [CrossRef]
- Beretta, G.P. Steepest Entropy Ascent Model for Far-Non-Equilibrium Thermodynamics. Unified Implementation of the Maximum Entropy Production Principle. Phys. Rev. E 2014, 90, 042113. [Google Scholar] [CrossRef] [PubMed]
- Montefusco, A.; Consonni, F.; Beretta, G.P. Essential equivalence of the general equation for the nonequilibrium reversible-irreversible coupling (GENERIC) and steepest-entropy-ascent models of dissipation for nonequilibrium thermodynamics. Phys. Rev. E 2015, 91, 042138. [Google Scholar] [CrossRef] [PubMed]
- Mittnenzweig, M.; Mielke, A. An entropic gradient structure for Lindblad equations and couplings of quantum systems to macroscopic models. J. Stat. Phys. 2017, 167, 205–233. [Google Scholar] [CrossRef]
- Kantner, M.; Mittnenzweig, M.; Koprucki, T. Hybrid quantum-classical modeling of quantum dot devices. Phys. Rev. B 2017, 96, 205301. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; Wiley: New York, NY, USA, 1976; p. 320. [Google Scholar]
- Mandelstam, L.; Tamm, I.G. The uncertainty relation between energy and time in non-relativistic quantum mechanics. In Selected Papers; Bolotovskii, B.M., Frenkel, V.Y., Peierls, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 115–123. [Google Scholar] [CrossRef]
- Ziegler, H. An attempt to generalize Onsager’s principle, and its significance for rheological problems. J. Appl. Math. Phys. 1958, 9, 748–763. [Google Scholar] [CrossRef]
- Swenson, R. Emergent attractors and the law of maximum entropy production: Foundations to a theory of general evolution. Syst. Res. 1989, 6, 187–197. [Google Scholar] [CrossRef]
- Struchtrup, H.; Weiss, W. Maximum of the Local Entropy Production Becomes Minimal in Stationary Processes. Phys. Rev. Lett. 1998, 80, 5048–5051. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A 2005, 38, L371–L381. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Martyushev, L.M. The maximum entropy production principle: Two basic questions. Philos. Trans. R. Soc. B 2010, 365, 1333–1334. [Google Scholar] [CrossRef] [PubMed]
- Martyushev, L.M. Entropy and entropy production: Old misconceptions and new breakthroughs. Entropy 2013, 15, 1152–1170. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. The restrictions of the maximum entropy production principle. Physica A 2014, 410, 17–21. [Google Scholar] [CrossRef]
- Gislason, E.A.; Sabelli, N.H.; Wood, J.W. New form of the time-energy uncertainty relation. Phys. Rev. A 1985, 31, 2078–2081. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 123–132. [Google Scholar] [CrossRef]
- Kobe, D.H.; Aguilera-Navarro, V.C. Derivation of the time-energy uncertainty relation. Phys. Rev. A 1994, 50, 933–938. [Google Scholar] [CrossRef]
- Majernik, V.; Richterek, L. Entropic uncertainty relations. Eur. J. Phys. 1997, 18, 79–89. [Google Scholar] [CrossRef]
- Aharonov, Y.; Reznik, B. “Weighing” a closed system and the time-energy uncertainty principle. Phys. Rev. Lett. 2000, 84, 1368–1370. [Google Scholar] [CrossRef]
- Aharanov, Y.; Massar, S.; Popescu, S. Measuring energy, estimating Hamiltonians, and the time-energy uncertainty relation. Phys. Rev. A 2002, 66, 052107. [Google Scholar] [CrossRef]
- Busch, P. The time-energy uncertainty relation. In Time in Quantum Mechanics; Muga, J., Mayato, R.S., Egusquiza, I., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 734. [Google Scholar] [CrossRef]
- Brunetti, R.; Fredenhagen, K. Remarks on time-energy uncertainty relations. Rev. Math. Phys. 2002, 14, 897–903. [Google Scholar] [CrossRef]
- Gillies, G.T.; Allison, S.W. Experimental test of a time-temperature formulation of the uncertainty principle via nanoparticle fluorescence. Found. Phys. 2005, 18, 65–74. [Google Scholar] [CrossRef]
- Beretta, G.P. On the General Equation of Motion of Quantum Thermodynamics and the Distinction between Quantal and Nonquantal Uncertainties. Ph.D. Thesis, MIT, Cambridge, MA, USA, 1981. [Google Scholar]
- Beretta, G.P.; Gyftopoulos, E.P.; Park, J.L.; Hatsopoulos, G.N. Quantum thermodynamics. A new equation of motion for a single constituent of matter. Nuovo Cimento B 1984, 82, 169–191. [Google Scholar] [CrossRef]
- Beretta, G.P.; Gyftopoulos, E.P.; Park, J.L. Quantum thermodynamics. A new equation of motion for a general quantum system. Nuovo Cimento B 1985, 87, 77–97. [Google Scholar] [CrossRef]
- Maddox, J. Uniting mechanics and statistics. Nature 1985, 316, 11. [Google Scholar] [CrossRef]
- Beretta, G.P. Steepest entropy ascent in quantum thermodynamics. In The Physics of Phase Space, Nonlinear Dynamics and Chaos, Geometric Quantization, and Wigner Function, Proceedings of the First International Conference on the Physics of Phase Space, University of Maryland, College Park, MD, USA, 20–23 May 1986; Kim, Y.S., Zachary, W.W., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 441–443. [Google Scholar] [CrossRef]
- Beretta, G.P. Nonlinear quantum evolution equations to model irreversible adiabatic relaxation with maximal entropy production and other nonunitary processes. Rep. Math. Phys. 2009, 64, 139–168. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Gyftopoulos, E.P. A unified quantum theory of mechanics and thermodynamics. Part I. Postulates. Found. Phys. 1976, 6, 15–31. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Gyftopoulos, E.P. A unified quantum theory of mechanics and thermodynamics. Part IIa. Available energy. Found. Phys. 1976, 6, 127–141. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Gyftopoulos, E.P. A unified quantum theory of mechanics and thermodynamics. Part IIb. Stable equilibrium states. Found. Phys. 1976, 6, 439–455. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Gyftopoulos, E.P. A unified quantum theory of mechanics and thermodynamics. Part III. Irreducible quantal dispersions. Found. Phys. 1976, 6, 561–570. [Google Scholar] [CrossRef]
- Brandão, F.G.L.S.; Horodecki, M.; Oppenheim, J.; Renes, J.M.; Spekkens, R.W. Resource theory of quantum states out of thermal equilibrium. Phys. Rev. Lett. 2013, 111, 250404. [Google Scholar] [CrossRef] [PubMed]
- Cano-Andrade, S.; Beretta, G.P.; von Spakovsky, M.R. Steepest-entropy-ascent quantum thermodynamic modeling of decoherence in two different microscopic composite systems. Phys. Rev. A 2015, 91, 013848. [Google Scholar] [CrossRef]
- Smith, C. Comparing the models of steepest entropy ascent quantum thermodynamics, master equation and the difference equation for a simple quantum system interacting with reservoirs. Entropy 2016, 18, 176. [Google Scholar] [CrossRef]
- Tabakin, F. Model dynamics for quantum computing. Ann. Phys. 2017, 383, 33–78. [Google Scholar] [CrossRef][Green Version]
- Yamada, R.; von Spakovsky, M.R.; Reynolds, W.T., Jr. A method for predicting non-equilibrium thermal expansion using steepest-entropy-ascent quantum thermodynamics. J. Phys. 2018, 30, 325901. [Google Scholar] [CrossRef] [PubMed]
- Yamada, R.; von Spakovsky, M.R.; Reynolds, W.T., Jr. Methodology of an application of the steepest-entropy- ascent quantum thermodynamic framework to physical phenomena in materials science. Comput. Mater. Sci. 2019, 166, 215–264. [Google Scholar] [CrossRef]
- Yamada, R.; von Spakovsky, M.R.; Reynolds, W.T., Jr. Predicting continuous and discontinuous phase decompositions using steepest-entropy-ascent quantum thermodynamics. Phys. Rev. E 2019, 99, 052121. [Google Scholar] [CrossRef]
- Li, G.; von Spakovsky, M.R.; Hin, C. Steepest entropy ascent quantum thermodynamic model of electron and phonon transport. Phys. Rev. B 2018, 97, 024308. [Google Scholar] [CrossRef]
- Kusaba, A.; Li, G.; von Spakovsky, M.R.; Kangawa, Y.; Kakimoto, K. Modeling the non-equilibrium process of the chemical adsorption of ammonia on GaN(0001) reconstructed surfaces based on steepest-entropy-ascent quantum thermodynamics. Materials 2017, 10, 948. [Google Scholar] [CrossRef]
- Militello, B. Steepest entropy ascent for two-state systems with slowly varying Hamiltonians. Phys. Rev. E 2018, 97, 052113. [Google Scholar] [CrossRef] [PubMed]
- Beretta, G.P. A general nonlinear evolution equation for irreversible conservative approach to stable equilibrium. In Frontiers of Nonequilibrium Statistical Physics, Proceedings of the NATO Advanced Study Institute on the Frontiers of Nonequilibrium Statistical Physics, Santa Fe, New Mexico, 3–16 June 1984; Moore, G.T., Scully, M.O., Eds.; NATO ASI Series B; Springer: Boston, MA, USA, 1986; Volume 135, pp. 193–204. [Google Scholar] [CrossRef]
- Beretta, G.P. The role of stability in the unification of mechanics and thermodynamics. In Proceedings of the ANAE-ONERA-CERT International Symposium on Stability, Paris, France, 3–5 November 1987; pp. 87–104. [Google Scholar]
- Beretta, G.P. The Schroedinger-Park paradox about the concept of “state” in quantum statistical mechanics and quantum information theory is still open. One more reason to go beyond? In Beyond the Quantum, Proceedings of the Workshop “Beyond the Quantum”, Lorentz Center of Leiden University, Leiden, The Netherlands, 28 May–3 June 2006; Nieuwenhuizen, T.M., Spicka, V., Mehmani, B., Jafar-Aghdami, M., Khrennikov, A.Y., Eds.; World Scientific: Singapore, 2007; pp. 355–365. ISBN 981-277-117-4. [Google Scholar] [CrossRef]
- Beretta, G.P. Quantum thermodynamics: New light on the physical meaning of entropy and the origin of irreversibility. In Proceedings of the Taormina Conference on Thermodynamics, Taormina, Italy, 18–22 February 1991; Giaquinta, P.V., Vicentini Missoni, M., Wanderlingh, F., Eds.; Atti della Accademia Peloritana dei Pericolanti-Classe di Scienze Fisiche Matematiche e Naturali: Messina, Italy, 1992; Volume 70, pp. 61–99. [Google Scholar]
- Beretta, G.P. Nonlinear extensions of Schroedinger-von Neumann quantum dynamics: A set of necessary conditions for compatibility with thermodynamics. Mod. Phys. Lett. A 2005, 20, 977–984. [Google Scholar] [CrossRef]
- Beretta, G.P. The Hatsopoulos-Gyftopoulos resolution of the Schroedinger-Park paradox about the concept of “state” in quantum statistical mechanics. Mod. Phys. Lett. A 2006, 21, 2799–2811. [Google Scholar] [CrossRef]
- Park, J.L.; Band, W. Generalized two-level quantum dynamics. III. Irreversible conservative motion. Found. Phys. 1978, 8, 239–254. [Google Scholar] [CrossRef]
- Simmons, R.F., Jr.; Park, J.L. The essential nonlinearity of N-level quantum thermodynamics. Found. Phys. 1981, 11, 297–305. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Keenan, J.H. Principles of General Thermodynamics; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Gyftopoulos, E.P.; Beretta, G.P. Thermodynamics: Foundations and Applications; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Beyer, R.T., Ed.; Princeton University Press: Princeton, NJ, USA, 1955; pp. 295–346. [Google Scholar]
- Park, J.L. Nature of quantum states. Am. J. Phys. 1968, 36, 211–226. [Google Scholar] [CrossRef]
- Bóna, P. Geometric formulation of nonlinear quantum mechanics for density matrices. arXiv 1999, arXiv:quant-ph/9910011. [Google Scholar]
- Gheorghiu-Svirschevski, S. Nonlinear quantum evolution with maximal entropy production. Phys. Rev. A 2001, 63, 022105. [Google Scholar] [CrossRef]
- Gheorghiu-Svirschevski, S. Addendum to “Nonlinear quantum evolution with maximal entropy production.”. Phys. Rev. A 2001, 63, 054102. [Google Scholar] [CrossRef]
- Gheorghiu-Svirschevski, S. Quantum nonlocality and quantum dynamics. arXiv 2002, arXiv:quant-ph/0203153. [Google Scholar]
- Gheorghiu-Svirschevski, S. A general framework for nonlinear quantum dynamics. arXiv 2002, arXiv:quant-ph/0207042. [Google Scholar]
- Beretta, G.P. Nonlinear model dynamics for closed-system, constrained, maximal-entropy-generation relaxation by energy redistribution. Phys. Rev. E 2006, 73, 026113. [Google Scholar] [CrossRef] [PubMed]
- Beretta, G.P. Time-energy and time-entropy uncertainty relations in dissipative quantum dynamics. arXiv 2006, arXiv:quant-ph/0511091. [Google Scholar]
- Rigolin, G. A simple derivation of the Schrödinger uncertainty relation. Eur. J. Phys. 2015, 36, 065007. [Google Scholar] [CrossRef]
- Schrödinger, E. About Heisenberg Uncertainty Relation. Proc. Prussian Acad. Sci. Phys. Math. 1930, 19, 296–303. [Google Scholar]
- Robertson, H.P. A general formulation of the uncertainty principle and its classical interpretation. Phys. Rev. 1930, 35, 667. [Google Scholar] [CrossRef]
- Robertson, H.P. An indeterminacy relation for several observables and its classical interpretation. Phys. Rev. 1934, 46, 794. [Google Scholar] [CrossRef]
- Beretta, G.P. Maximum entropy production rate in quantum thermodynamics. J. Phys. Conf. Ser. 2010, 237, 012004. [Google Scholar] [CrossRef]
- Eberly, J.H.; Singh, L.P.S. Time operators, partial stationarity, and the energy-time uncertainty relation. Phys. Rev. D 1973, 7, 359. [Google Scholar] [CrossRef]
- Leubner, C.; Kiener, C. Improvement of the Eberly-Singh time-energy inequality by combination with the Mandelstam-Tamm approach. Phys. Rev. A 1985, 31, 483. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Quantum decay and the Mandelstam-Tamm-energy inequality. J. Phys. A Math. Gen. 1983, 16, 2993. [Google Scholar] [CrossRef]
- Pfeifer, P. How fast can a quantum state change with time? Phys. Rev. Lett. 1993, 70, 3365. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, P. Erratum: How fast can a quantum state change with time? Phys. Rev. Lett. 1993, 71, 306. [Google Scholar] [CrossRef]
- Massieu, F. Sur les fonctions caractéristiques des divers fluides et sur la théorie des vapeurs. C. R. Acad. Sci. 1859, 69, 858–862. [Google Scholar]
- Beretta, G.P. Well-behaved nonlinear evolution equation for steepest-entropy-ascent dissipative quantum dynamics. Int. J. Quantum Inf. 2007, 5, 249–255. [Google Scholar] [CrossRef]
- Rao, R.; Esposito, M. Conservation laws shape dissipation. New J. Phys. 2018, 20, 023007. [Google Scholar] [CrossRef]
- Rao, R.; Esposito, M. Detailed fluctuation theorems: A unifying perspective. Entropy 2018, 20, 635. [Google Scholar] [CrossRef]
- Yunger Halpern, N.; Faist, P.; Oppenheim, J.; Winter, A. Microcanonical and resource-theoretic derivations of the thermal state of a quantum system with noncommuting charges. Nat. Commun. 2016, 7, 12051. [Google Scholar] [CrossRef]
- Bedeauxa, D.; Mazur, P. Mesoscopic non-equilibrium thermodynamics for quantum systems. Physica A 2001, 298, 81–100. [Google Scholar] [CrossRef]
- Beretta, G.P. A theorem on Lyapunov stability for dynamical systems and a conjecture on a property of entropy. J. Math. Phys. 1986, 27, 305308. [Google Scholar] [CrossRef]
- Beretta, G.P. Quantum thermodynamics of nonequilibrium. Onsager reciprocity and dispersion-dissipation relations. Found. Phys. 1987, 17, 365–381. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. Equilibrium microstates which generate second law violating steady states. Phys. Rev. E 1994, 50, 1645. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36, 631. [Google Scholar] [CrossRef]
- Van Zon, R.; Cohen, E.G.D. Extension of the fluctuation theorem. Phys. Rev. Lett. 2003, 91, 110601. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.M.; Sevick, E.M.; Mittag, E.; Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, 050601. [Google Scholar] [CrossRef] [PubMed]
- Nieuwenhuizen, T.M.; Allahverdyan, A.E. Comment on “Experimental violations of the second law of thermodynamics for small systems and short timescales.”. arXiv 2002, arXiv:cond-mat/0207587. [Google Scholar]
- Garnier, N.; Ciliberto, S. Nonequilibrium fluctuations in a resistor. Phys. Rev. E 2005, 71, 060101. [Google Scholar] [CrossRef] [PubMed]
- Ion, D.B.; Ion, M.L.D. Entropic lower bound for the quantum scattering of spinless particles. Phys. Rev. Lett. 1998, 81, 5714. [Google Scholar] [CrossRef]
- Deutsch, D. Uncertainty in quantum measurements. Phys. Rev. Lett. 1983, 50, 631. [Google Scholar] [CrossRef]
- Partovi, M.H. Entropic formulation of uncertainty for quantum measurements. Phys. Rev. Lett. 1983, 50, 1883. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103. [Google Scholar] [CrossRef] [PubMed]
- Simmons, R.F.; Park, J.L. On completely positive maps in generalized quantum dynamics. Found. Phys. 1981, 11, 47–55. [Google Scholar] [CrossRef]
- Prigogine, I.; Mayne, F.; George, C.; De Haan, M. Microscopic theory of irreversible processes. Proc. Natl. Acad. Sci. USA 1977, 74, 4152–4156. [Google Scholar] [CrossRef] [PubMed]
- Grecos, A.; Prigogine, I. On the derivation of linear irreversible thermodynamics for classical fluids. Proc. Natl. Acad. Sci. USA 1978, 75, 1632–1636. [Google Scholar] [CrossRef]
- Misra, B.; Prigogine, I.; Courbage, M. Lyapounov variable: Entropy and measurement in quantum mechanics. Proc. Natl. Acad. Sci. USA 1979, 76, 4768–4772. [Google Scholar] [CrossRef]
- Beretta, G.P. Intrinsic entropy and intrinsic irreversibility for a single isolated constituent of matter: Broader kinematics and generalized nonlinear dynamics. In Frontiers of Nonequilibrium Statistical Physics, Proceedings of the NATO Advanced Study Institute on the Frontiers of Nonequilibrium Statistical Physics, Santa Fe, New Mexico, 3–16 June 1984; Moore, G.T., Scully, M.O., Eds.; NATO ASI Series B; Springer: Boston, MA, USA, 1986; Volume 135, pp. 205–212. [Google Scholar] [CrossRef]
- Beretta, G.P. What if quantum thermodynamics were a fundamental extension of quantum mechanics? In Perimeter Institute Recorded Seminar Archive; PIRSA Quantum Foundations Series; Perimeter Institute of Theoretical Physics: Waterloo, ON, Canada, 2007. [Google Scholar]
- Beretta, G.P. Mechanics and Thermodynamics Can be Fundamentally United by Density Operators with an Ontic Status Obeying a Locally Maximum Entropy Production Dynamics. But at What Price? In Perimeter Institute Recorded Seminar Archive; PIRSA Collection: PIAF 09, New Perspectives on the Quantum State; Perimeter Institute of Theoretical Physics: Waterloo, ON, Canada, 2009. [Google Scholar]
- Hiai, F.; Ohya, M.; Tsukada, M. Sufficiency, KMS condition and relative entropy in von Neumann algebras. Pac. J. Math. 1981, 96, 99–109. [Google Scholar] [CrossRef]
- Beretta, G.P.; Zanchini, E. New definitions of thermodynamic temperature and entropy not based on the concepts of heat and thermal reservoir. Atti della Accademia Peloritana dei Pericolanti-Classe di Scienze Fisiche Matematiche e Naturali 2019, 97 (Suppl. 1), A1. [Google Scholar] [CrossRef]
- Sieniutycz, S. From a least action principle to mass action law and extended affinity. Chem. Eng. Sci. 1987, 42, 2697–2711. [Google Scholar] [CrossRef]
- Beretta, G.P. Quantum thermodynamics: Microscopic foundations of entropy and of entropy generation by Iirreversibility. Atti della Accademia Peloritana dei Pericolanti Classe di Scienze Fisiche Matematiche e Naturali 2008, 86, 1–22. [Google Scholar] [CrossRef]
- Beretta, G.P. Nonlinear dynamical equation for irreversible, steepest-entropy-ascent relaxation to stable equilibrium. In Quantum Theory: Reconsideration of Foundations—4, Proceedings of the IV International Conference on Quantum Theory: Reconsideration of Foundations, Vaxjo, Sweden, 11–16 June 2007; Adenier, G., Khrennikov, A.Y., Lahti, P., Man’ko, V.I., Nieuwenhuizen, T.M., Eds.; American Institute of Physics: Melville, NY, USA, 2007; Volume 962, pp. 233–237. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Beretta, G.P. Where is the entropy challenge? In Meeting the Entropy Challenge, Proceedings of the International Thermodynamics Symposium in Honor and Memory of Professor Joseph H. Keenan, MIT, Cambridge, MA, USA, 4–5 October 2007; Beretta, G.P., Ghoniem, A.F., Hatsopoulos, G.N., Eds.; American Institute of Physics: Melville, NY, USA, 2008; Volume 1033, pp. 34–54. [Google Scholar] [CrossRef]
- Beretta, G.P. Steepest entropy ascent model for far-non-equilibrium dissipative evolution in quantum thermodynamics: A 1984 precursor of GENERIC (1997), gradient flows (1998), maximal entropy production (2001), and SEAQT (2014). In Proceedings of the Workshop on Mathematical Aspects of Non-Equilibrium Thermodynamics, RWTH, Aachen University, Aachen, Germany, 5–7 March 2018. [Google Scholar]
- Beretta, G.P. A new approach to constrained-maximization nonequilibrium problems. In Computer-Aided Engineering of Energy Systems: Second Law Analysis and Modeling, Proceedings of the Winter Annual Meeting of the ASME, Anaheim, CA, USA, 7–12 December 1986; Gaggioli, R.A., Ed.; Book H0341C-AES; ASME: New York, NY, USA, 1986; Volume 3, pp. 129–134. [Google Scholar]
- Beretta, G.P. Steepest-ascent constrained approach to maximum entropy. In Second Law Analysis of Heat Transfer in Energy Systems, Proceedings of the Winter Annual Meeting of the ASME, Boston, MA, USA, 13–18 December 1987; Boehm, R.F., Lior, N., Eds.; Book G00390; ASME: New York, NY, USA, 1987; Volume HTD, pp. 31–38. [Google Scholar]
- Beretta, G.P. Dynamics of smooth constrained approach to maximum entropy. In Second Law Analysis of Thermal Systems, Proceedings of the 4th International Symposium on Second Law Analysis of Thermal Systems, Roma, Italy, 25–29 May 1987; Moran, M.J., Sciubba, E., Eds.; Book I00236; ASME: New York, NY, USA, 1987; pp. 17–24. [Google Scholar]
- Beretta, G.P. Axiomatic definition of entropy for nonequilibrium states. In Proceedings of the 9th Joint European Thermodynamics Conference JETC07, Saint Etienne, France, 12–15 June 2007. [Google Scholar]
- Beretta, G.P. The second law from locally maximal entropy generation quantum dynamics. In Meeting the Entropy Challenge, Proceedings of the International Thermodynamics Symposium in Honor and Memory of Professor Joseph H. Keenan, MIT, Cambridge, MA, USA, 4–5 October 2007; Beretta, G.P., Ghoniem, A.F., Hatsopoulos, G.N., Eds.; American Institute of Physics: Melville, NY, USA, 2008; Volume 1033, pp. 180–187. [Google Scholar] [CrossRef]
- Beretta, G.P.; Hadjiconstantinou, N.G. Steepest entropy ascent models of the Boltzmann equation. Comparisons with hard-sphere dynamics and relaxation-time models for homogeneous relaxation from highly non-equilibrium states. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition IMECE2013, San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Kaufman, A.N. Dissipative hamiltonian systems: A unifying principle. Phys. Lett. A 1984, 100, 419–422. [Google Scholar] [CrossRef]
- Morrison, P.J. Bracket formulation for irreversible classical fields. Phys. Lett. A 1984, 100, 423–427. [Google Scholar] [CrossRef]
- Grmela, M. Bracket formulation of dissipative fluid mechanics equations. Phys. Lett. A 1984, 102, 355–358. [Google Scholar] [CrossRef]
- Jordan, R.; Kinderlehrer, D.; Otto, F. The variational formulation of the Fokker–Planck equation. SIAM J. Math. Anal. 1998, 29, 1–17. [Google Scholar] [CrossRef]
- Otto, F. The geometry of dissipative evolution equations: The porous medium equation. Commun. Partial Differ. Equ. 2001, 26, 101–174. [Google Scholar] [CrossRef]
- Mielke, F. A gradient structure for reaction–diffusion systems and for energy-drift-diffusion systems. Nonlinearity 2011, 24, 1329–1346. [Google Scholar] [CrossRef]
- Mielke, A.; Peletier, M.A.; Renger, D.R.M. On the relation between gradient flows and the large-deviation principle, with applications to Markov chains and diffusion. Potential Anal. 2014, 41, 1293–1327. [Google Scholar] [CrossRef]
- Montefusco, A.; Peletier, M.A.; Öttinger, H.C. Coarse-graining via the fluctuation-dissipation theorem and large-deviation theory. arXiv 2018, arXiv:1809.07253. [Google Scholar]
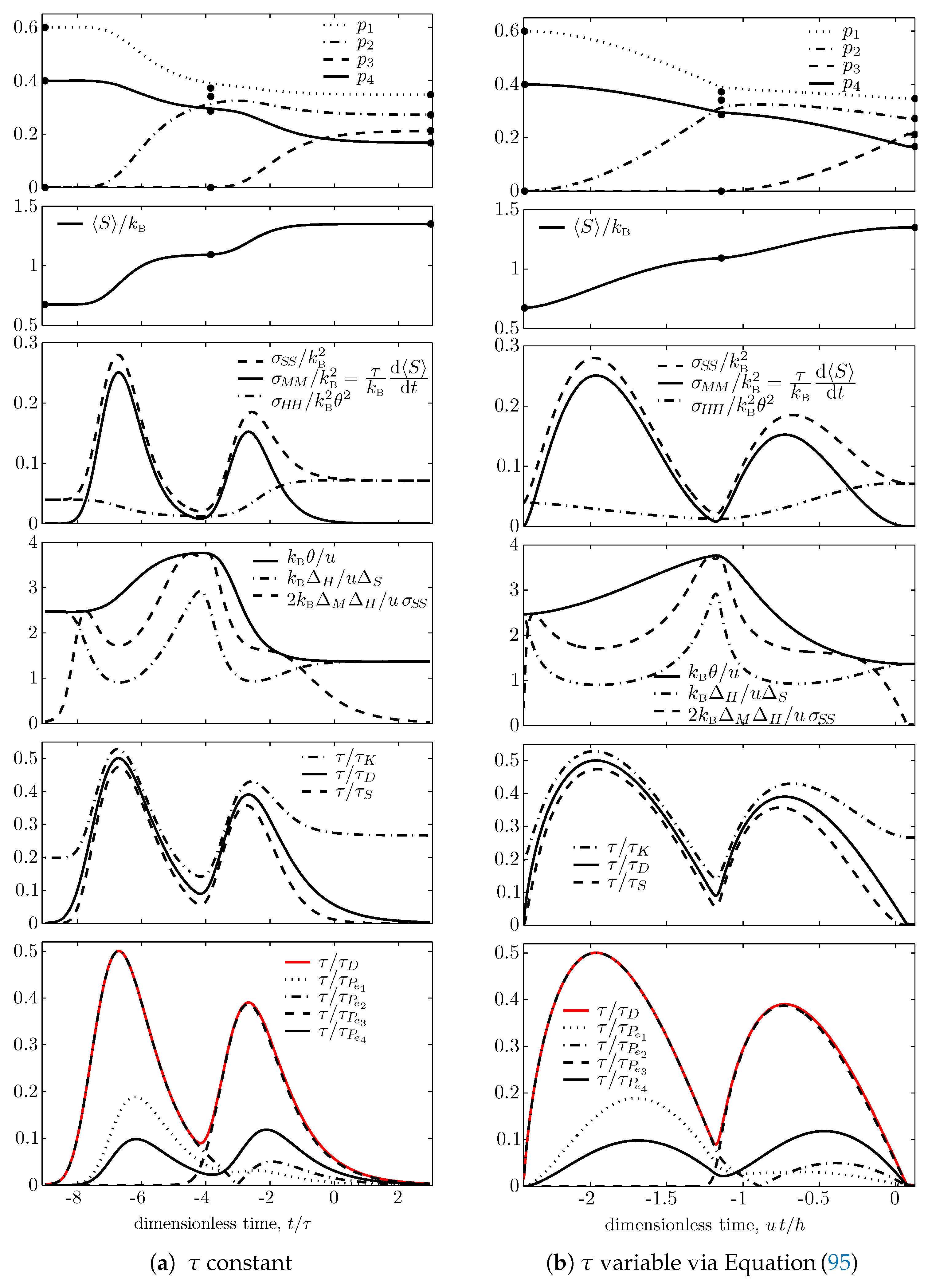
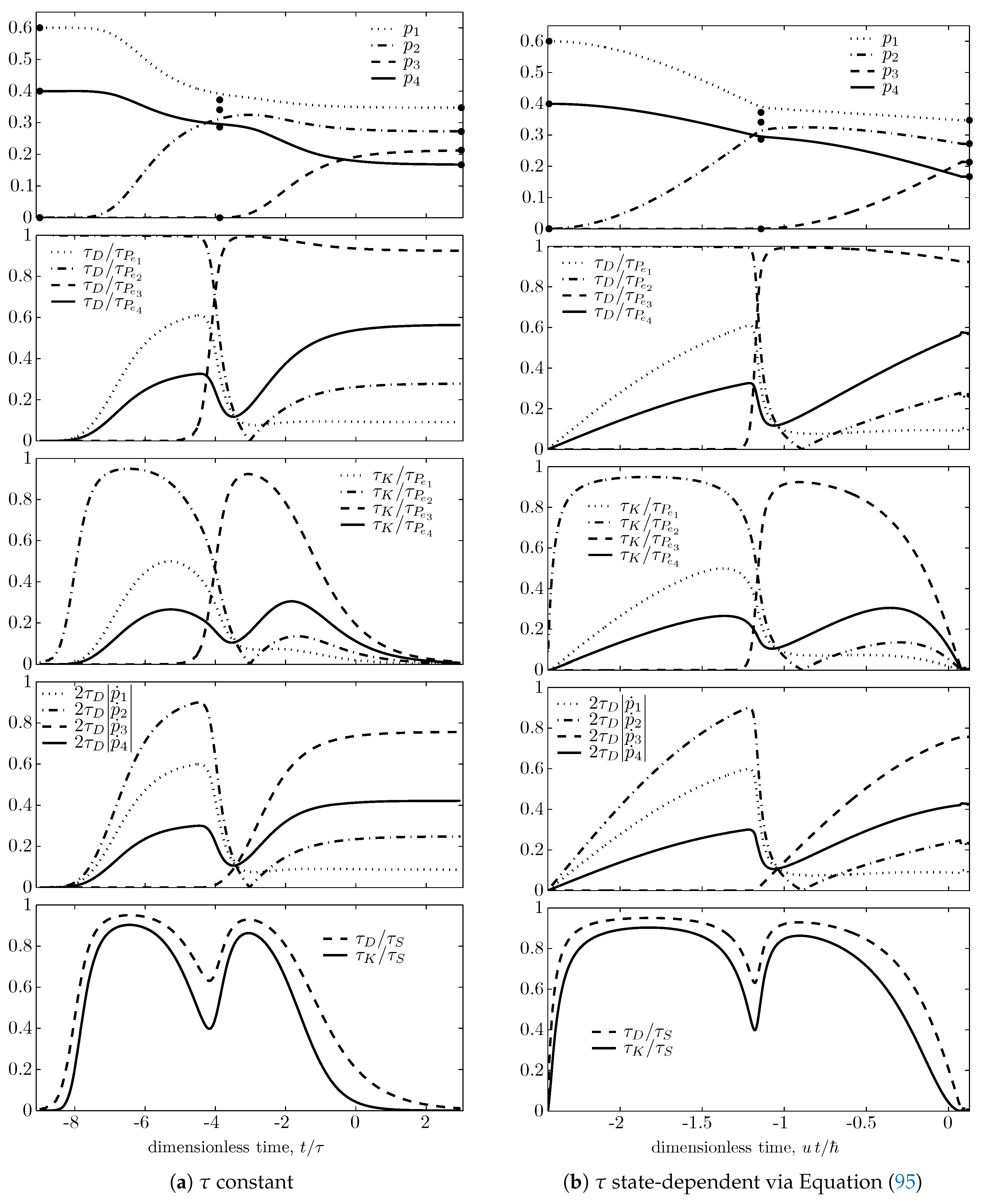
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beretta, G.P. Time–Energy and Time–Entropy Uncertainty Relations in Nonequilibrium Quantum Thermodynamics under Steepest-Entropy-Ascent Nonlinear Master Equations. Entropy 2019, 21, 679. https://doi.org/10.3390/e21070679
Beretta GP. Time–Energy and Time–Entropy Uncertainty Relations in Nonequilibrium Quantum Thermodynamics under Steepest-Entropy-Ascent Nonlinear Master Equations. Entropy. 2019; 21(7):679. https://doi.org/10.3390/e21070679
Chicago/Turabian StyleBeretta, Gian Paolo. 2019. "Time–Energy and Time–Entropy Uncertainty Relations in Nonequilibrium Quantum Thermodynamics under Steepest-Entropy-Ascent Nonlinear Master Equations" Entropy 21, no. 7: 679. https://doi.org/10.3390/e21070679
APA StyleBeretta, G. P. (2019). Time–Energy and Time–Entropy Uncertainty Relations in Nonequilibrium Quantum Thermodynamics under Steepest-Entropy-Ascent Nonlinear Master Equations. Entropy, 21(7), 679. https://doi.org/10.3390/e21070679




