Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit
Abstract
1. Introduction
2. Mathematical Model and DC V–I Plot of the Proposed Memristor
2.1. Mathematical Model
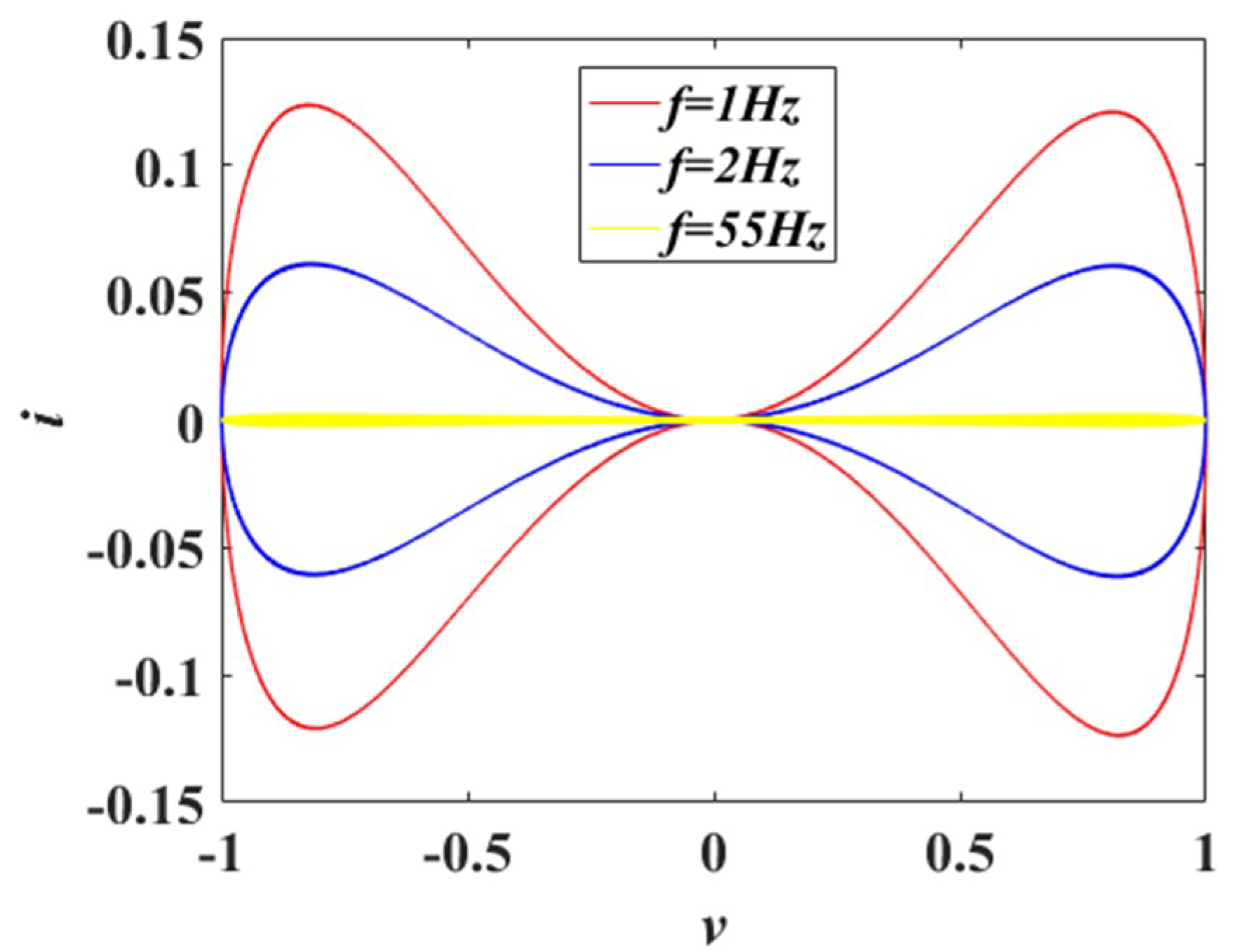
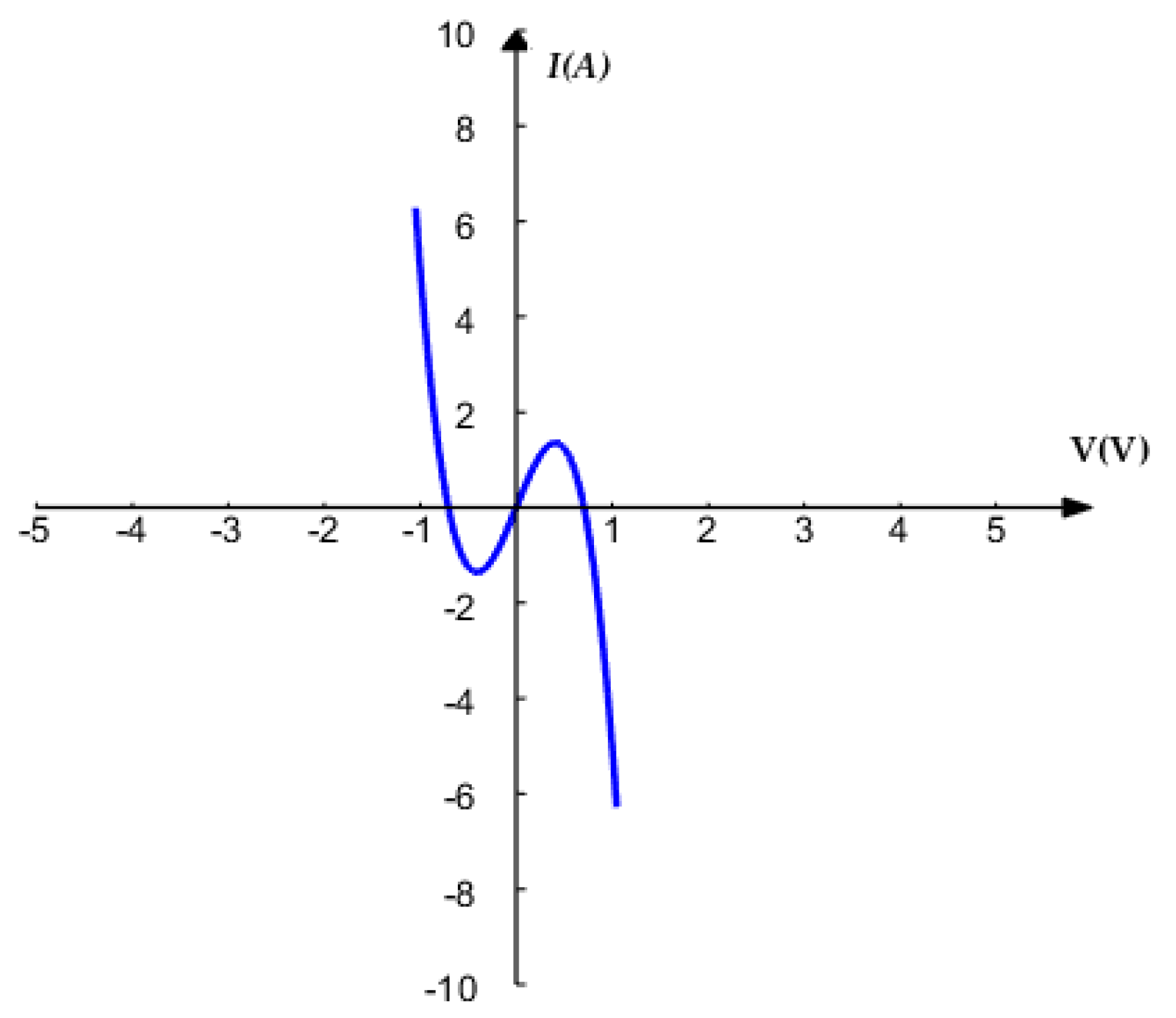
2.2. DC V–I Plot of the Proposed Memristor
3. The Three-Order Memristive Wien-Bridge Chaotic Circuit
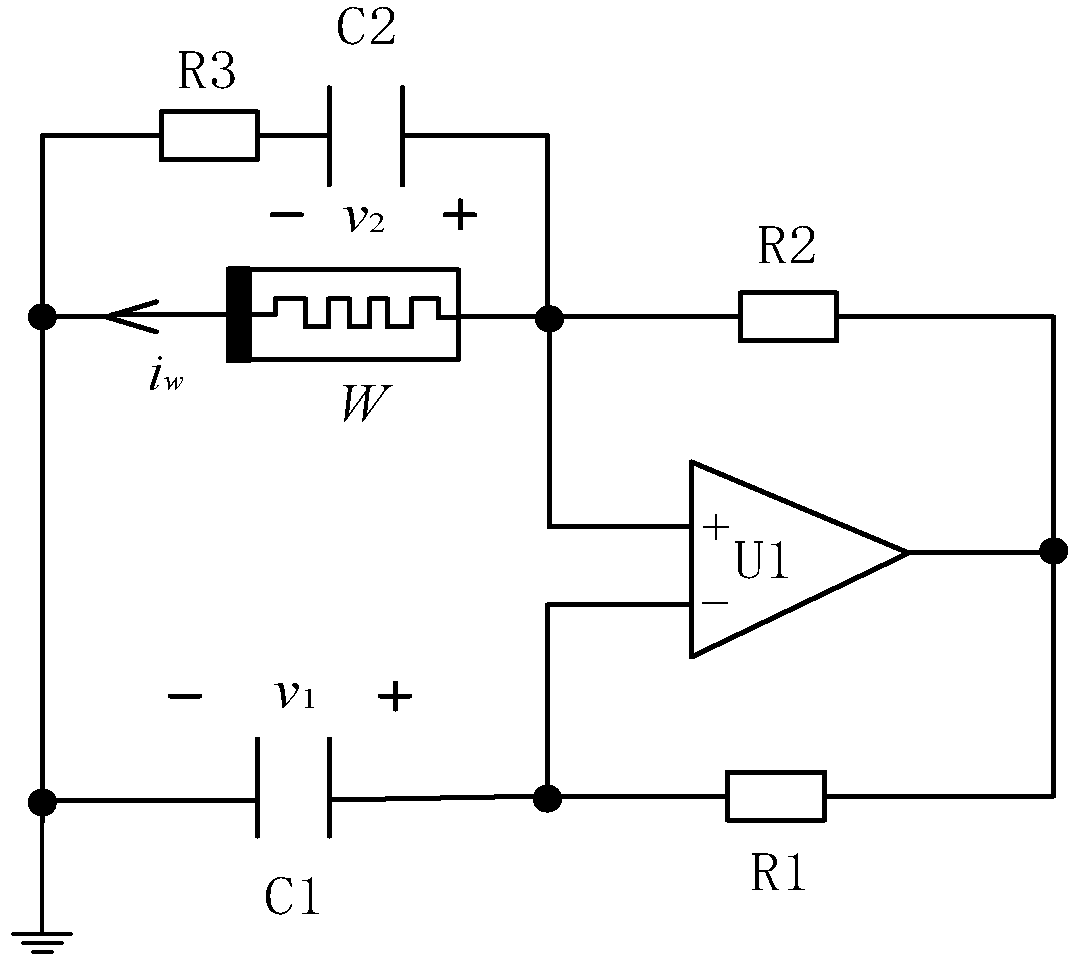
3.1. Circuit Model
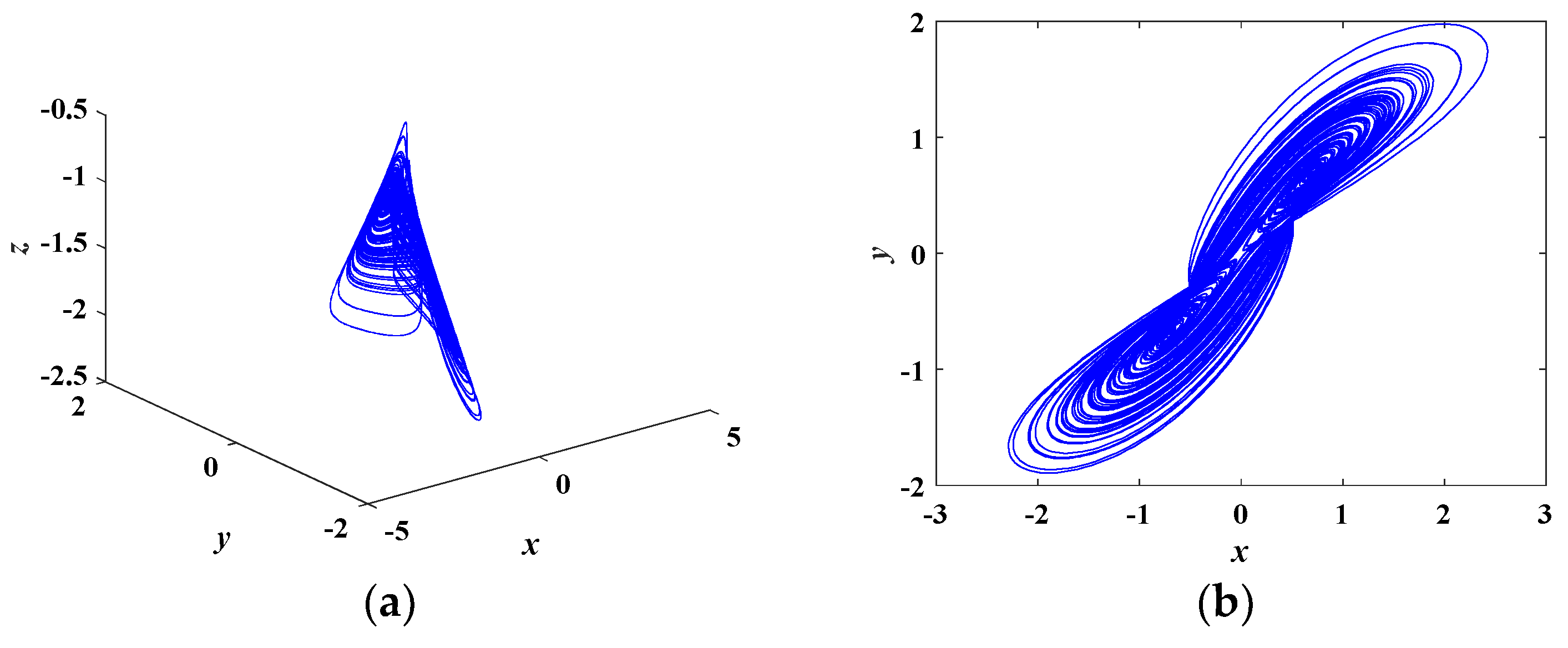
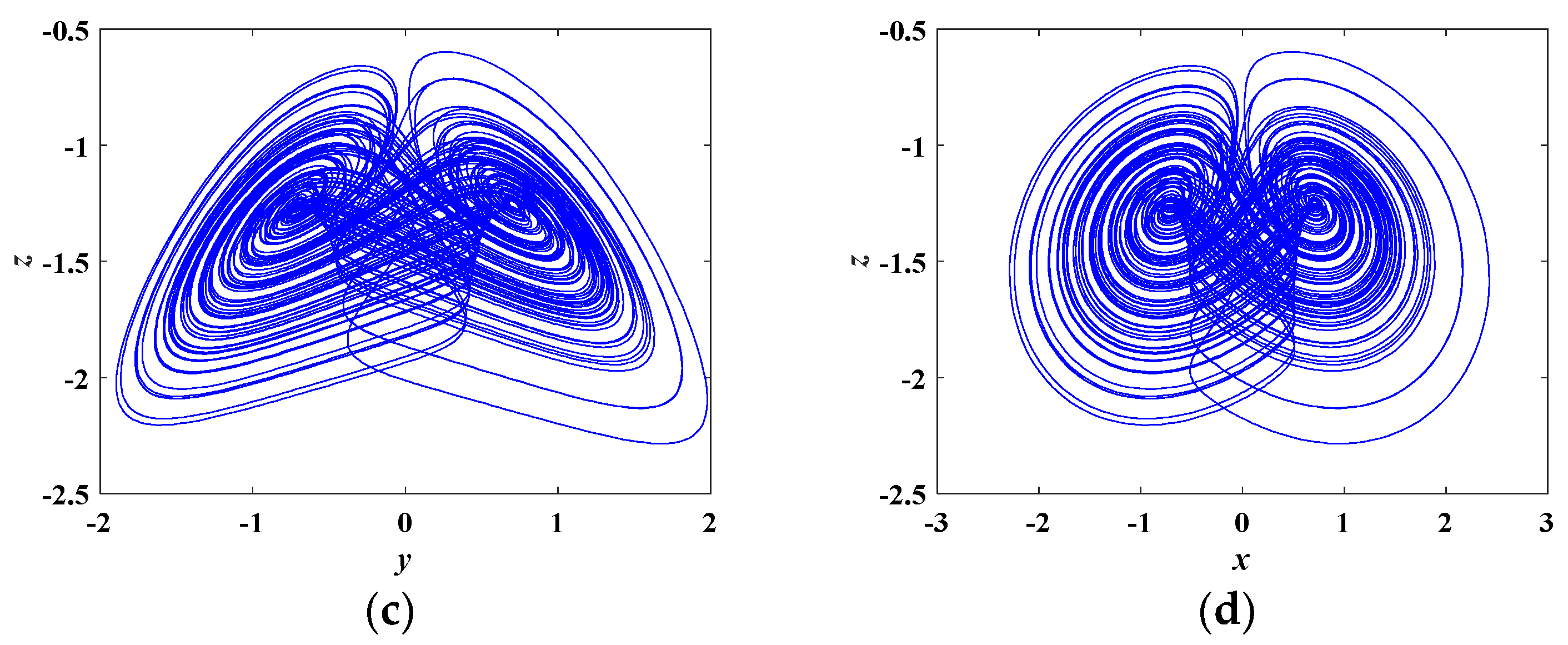
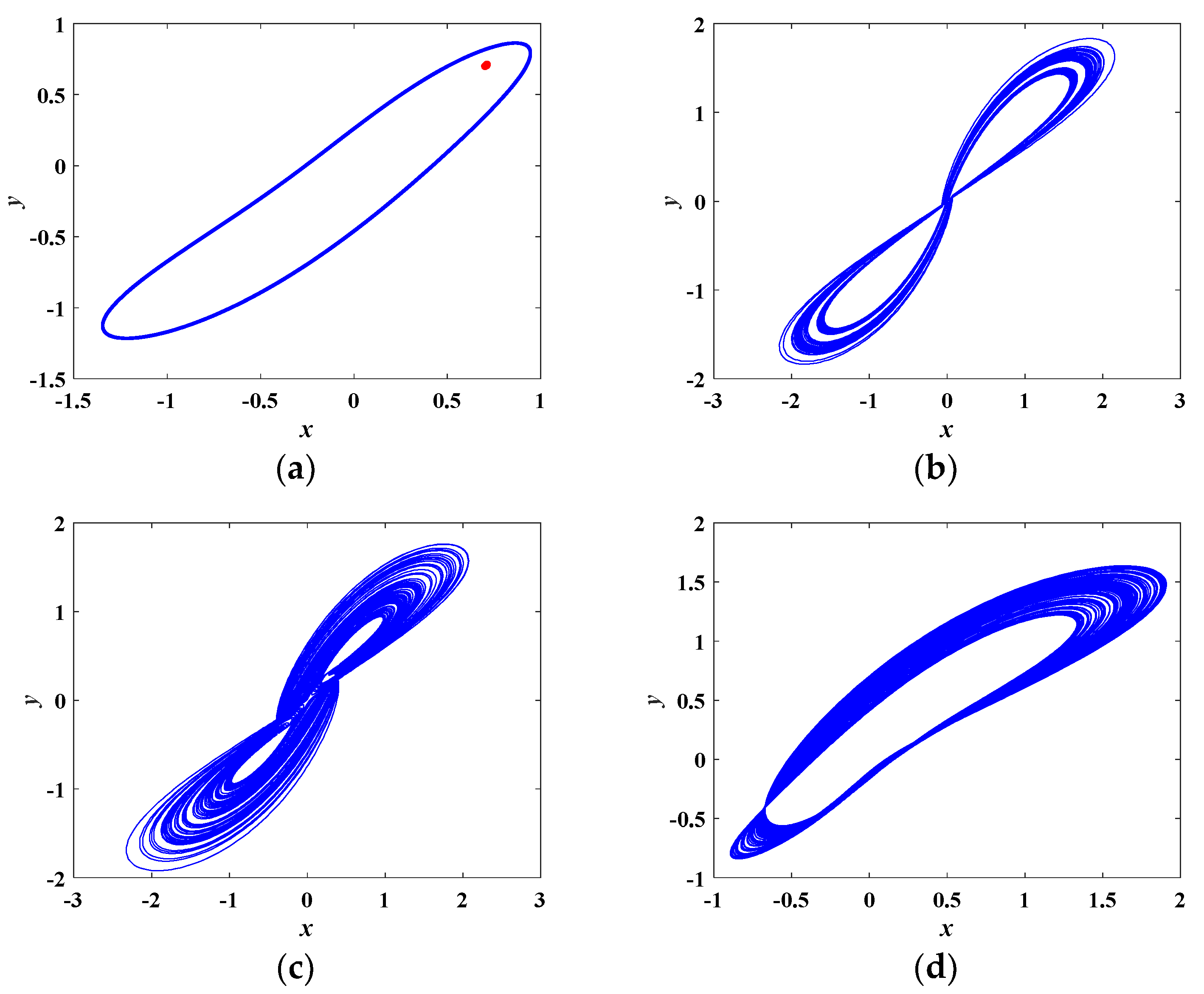
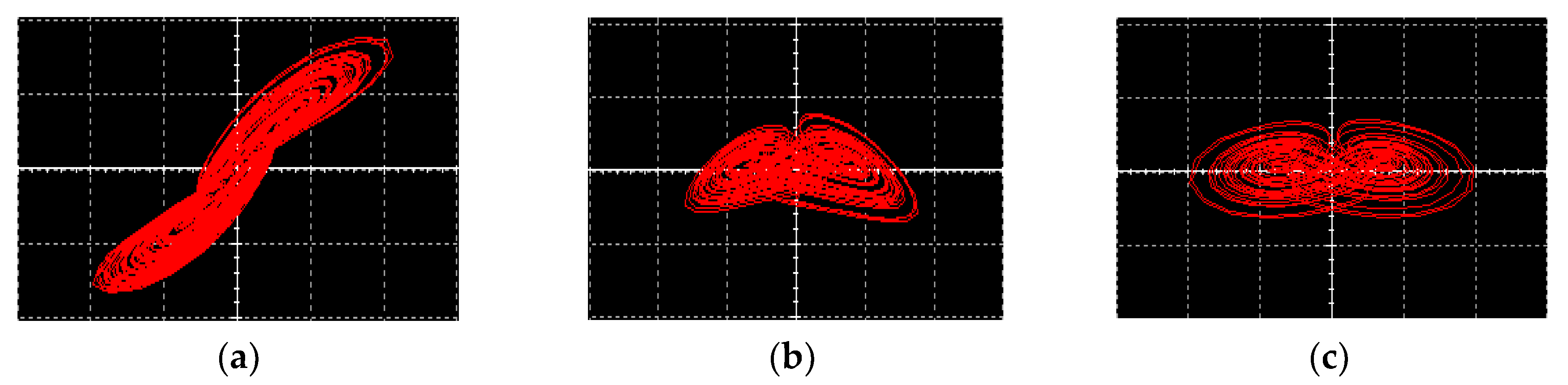
3.2. Typical Chaotic Attractors
4. Dynamical Behaviors of the Proposed Chaotic System
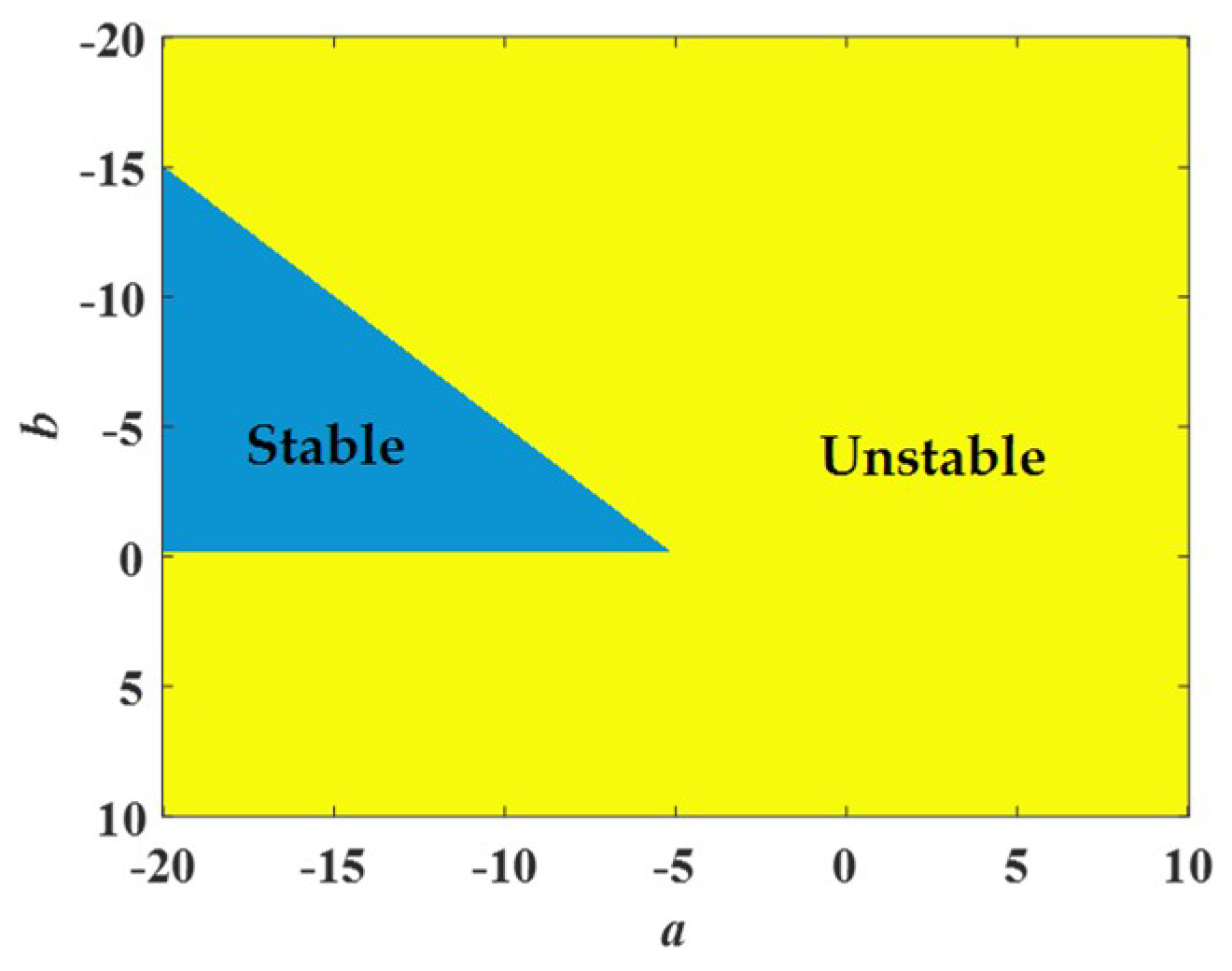
4.1. Dissipativity and Stability
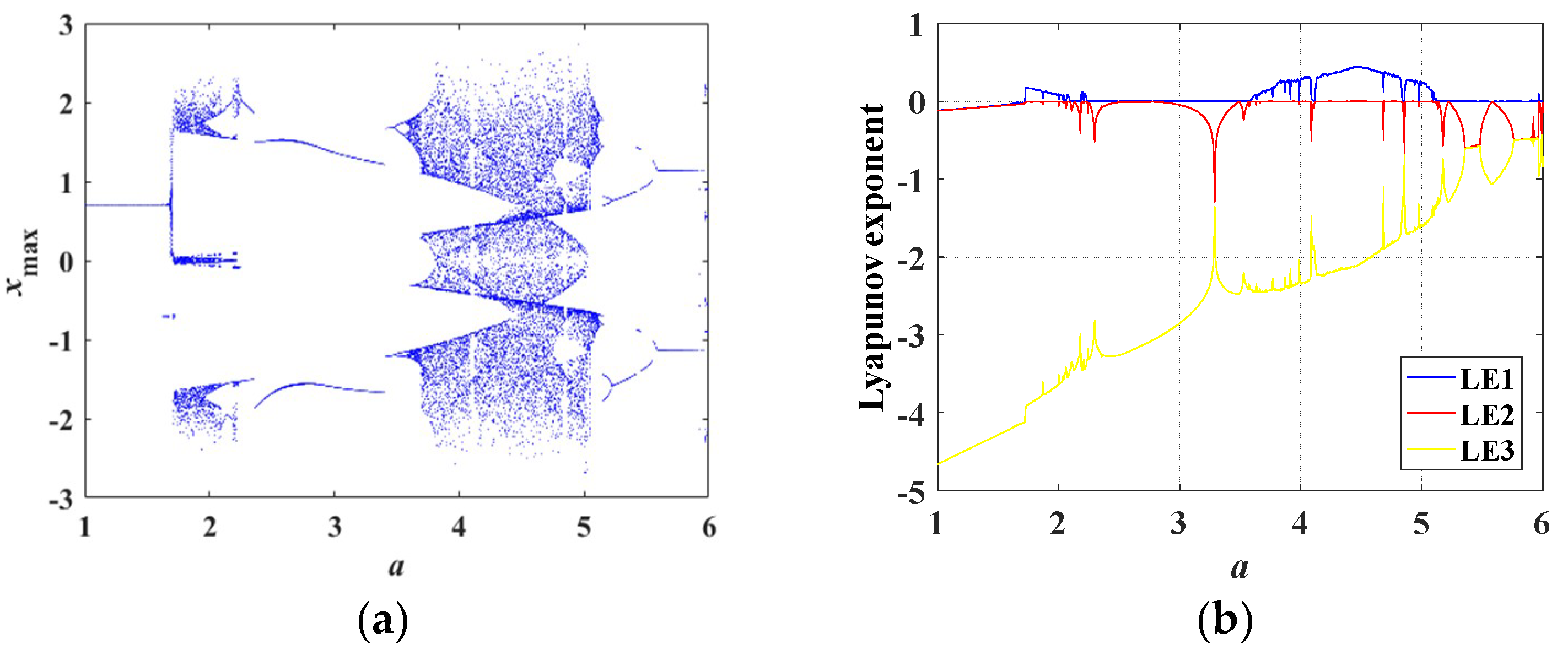
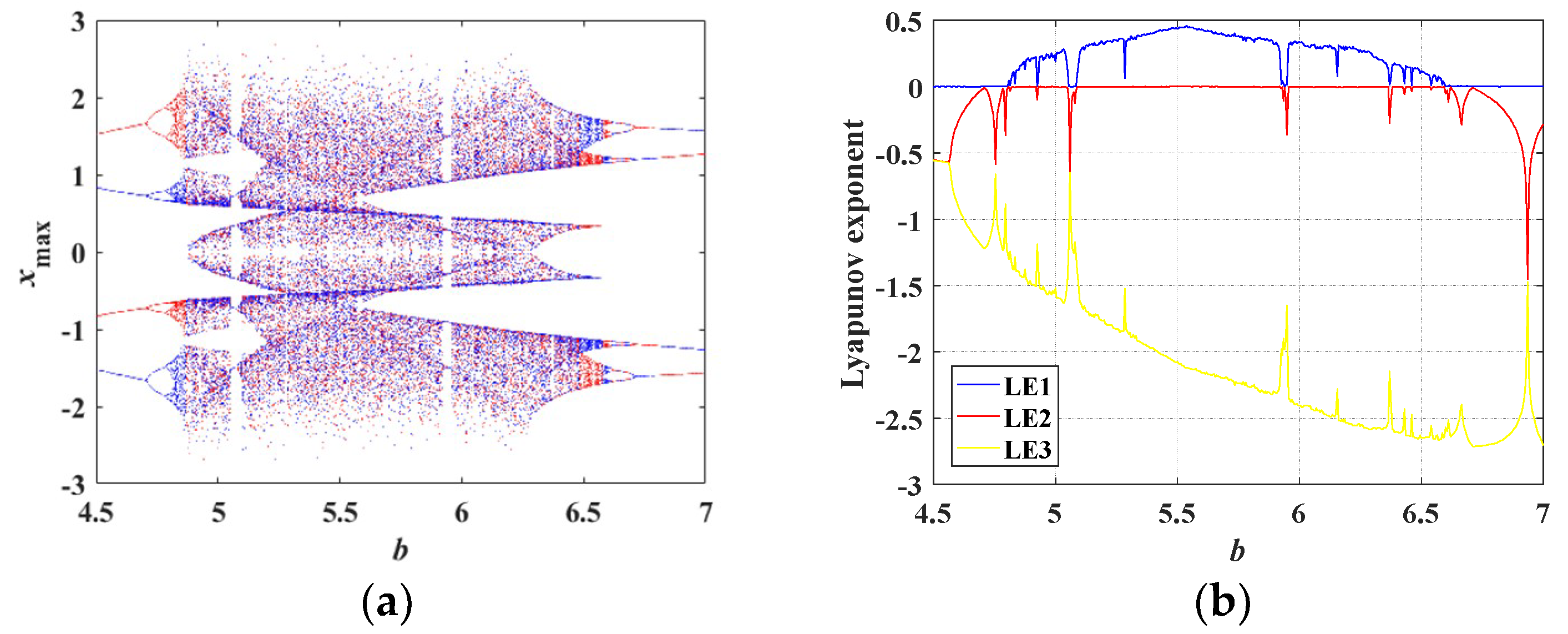
4.2. Bifurcation Diagrams and Lyapunov Exponent Spectra
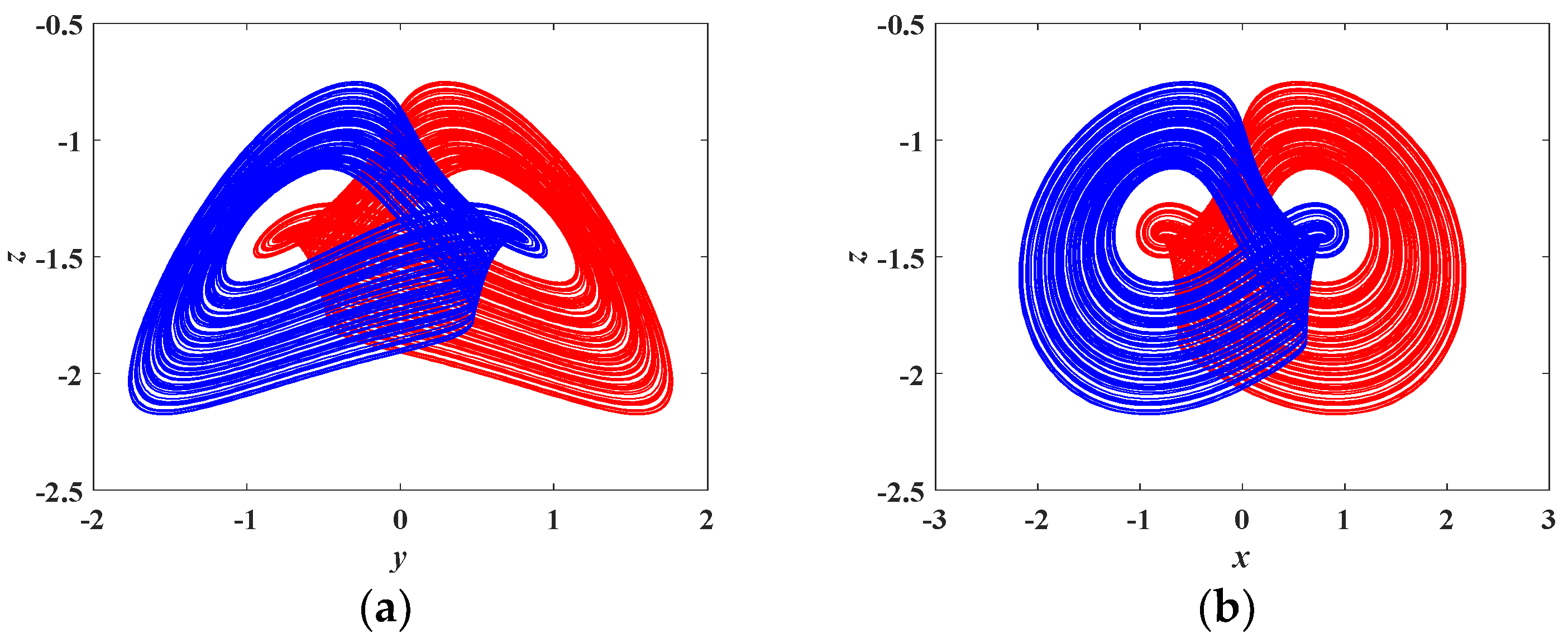
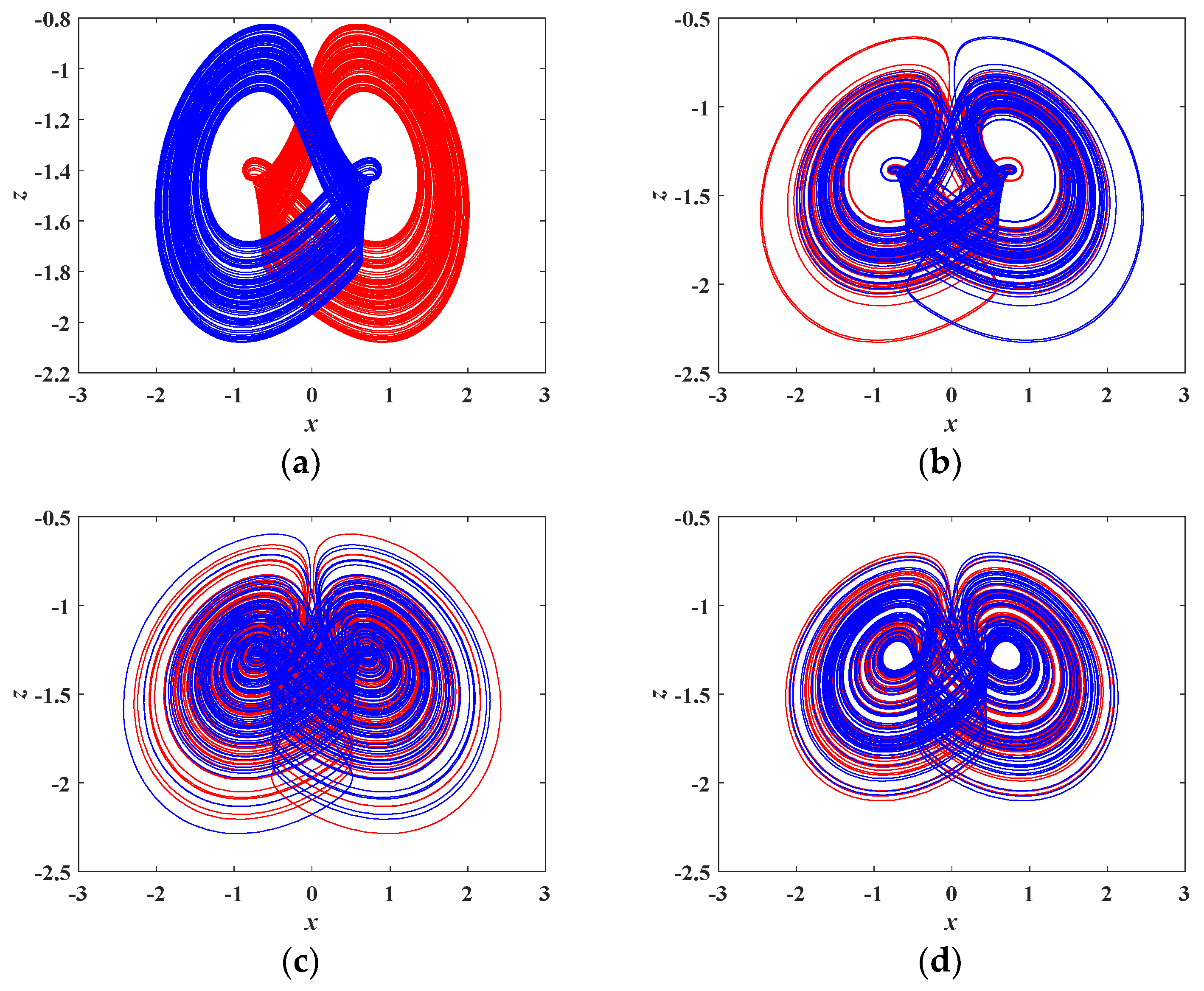
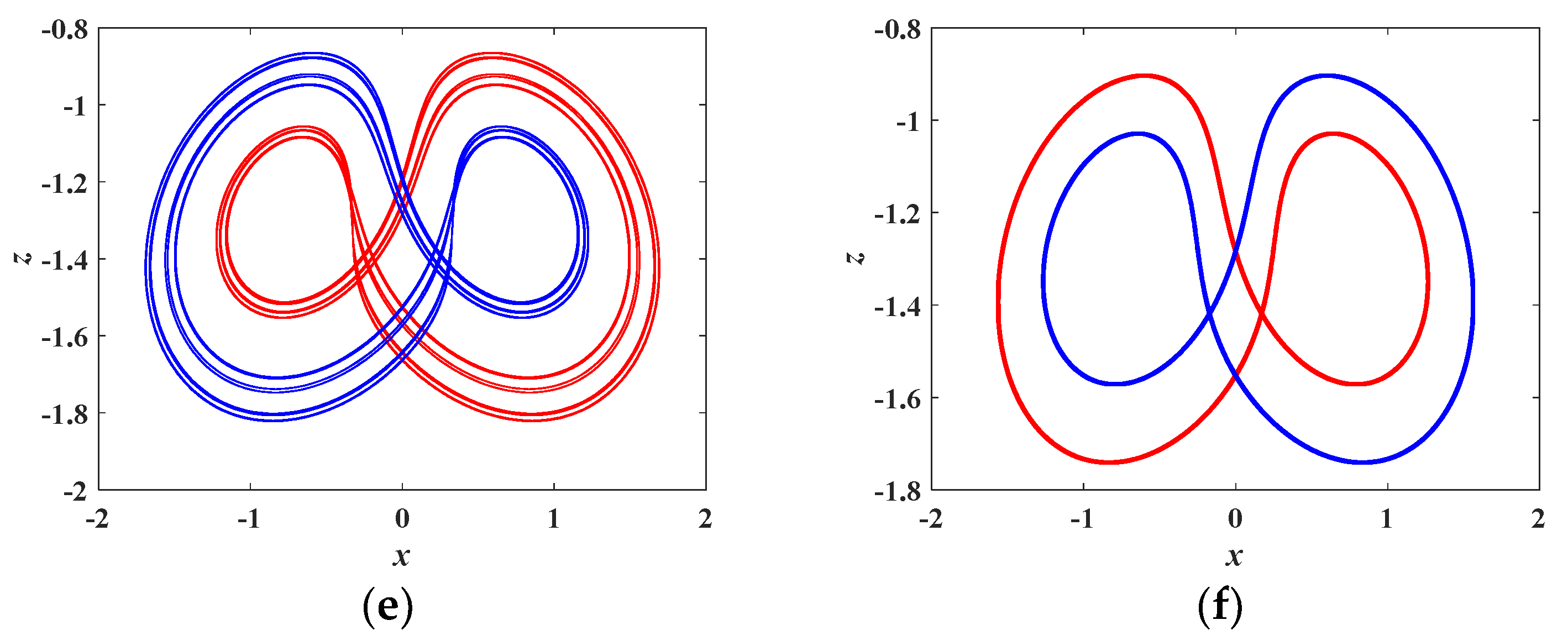
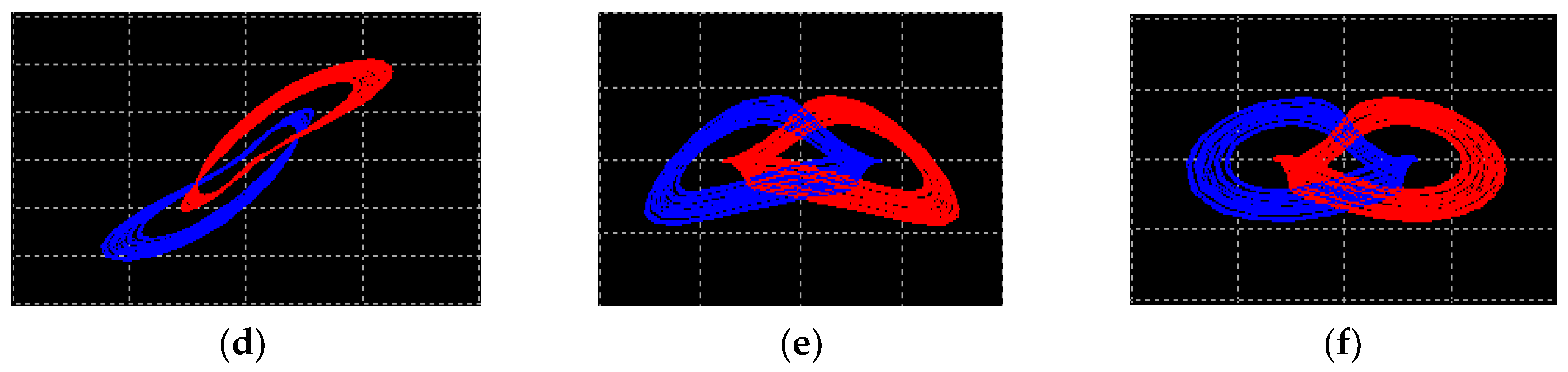
4.3. Coexisting Attractors and Multistability
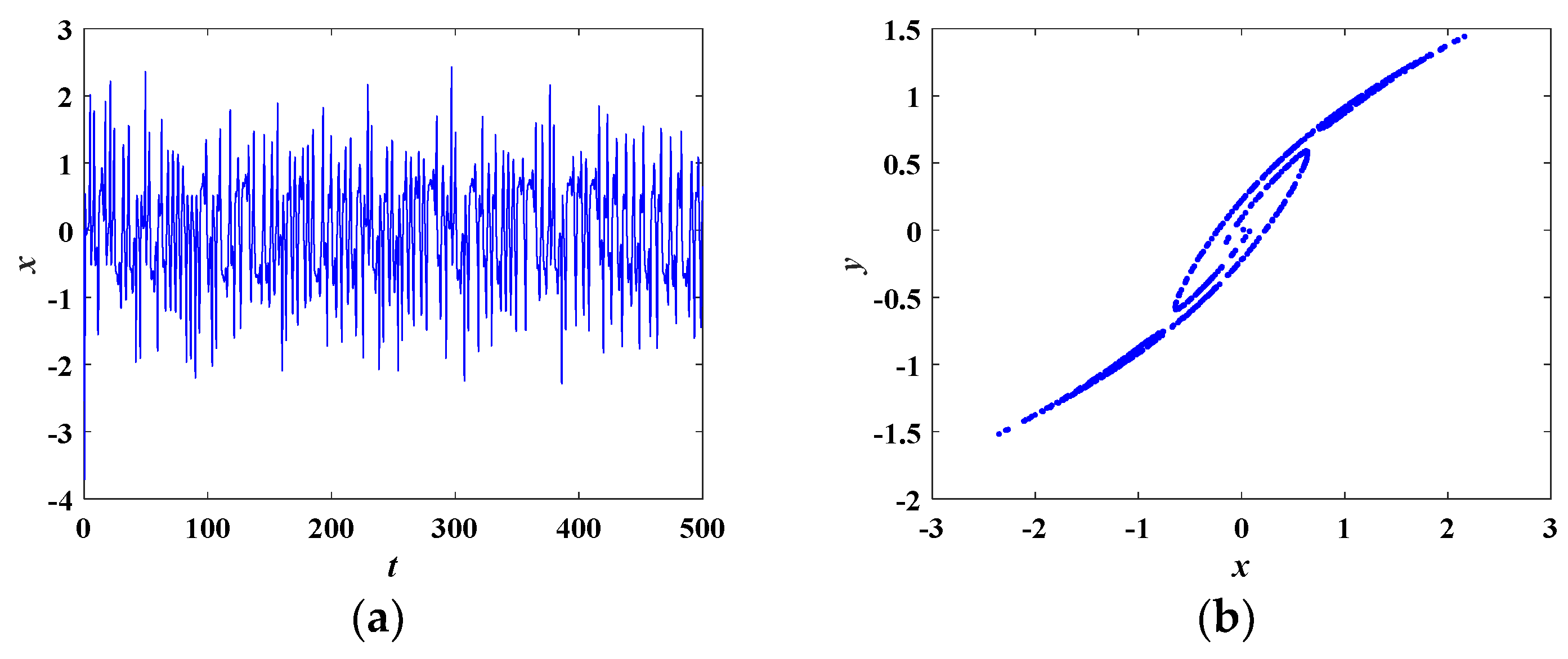
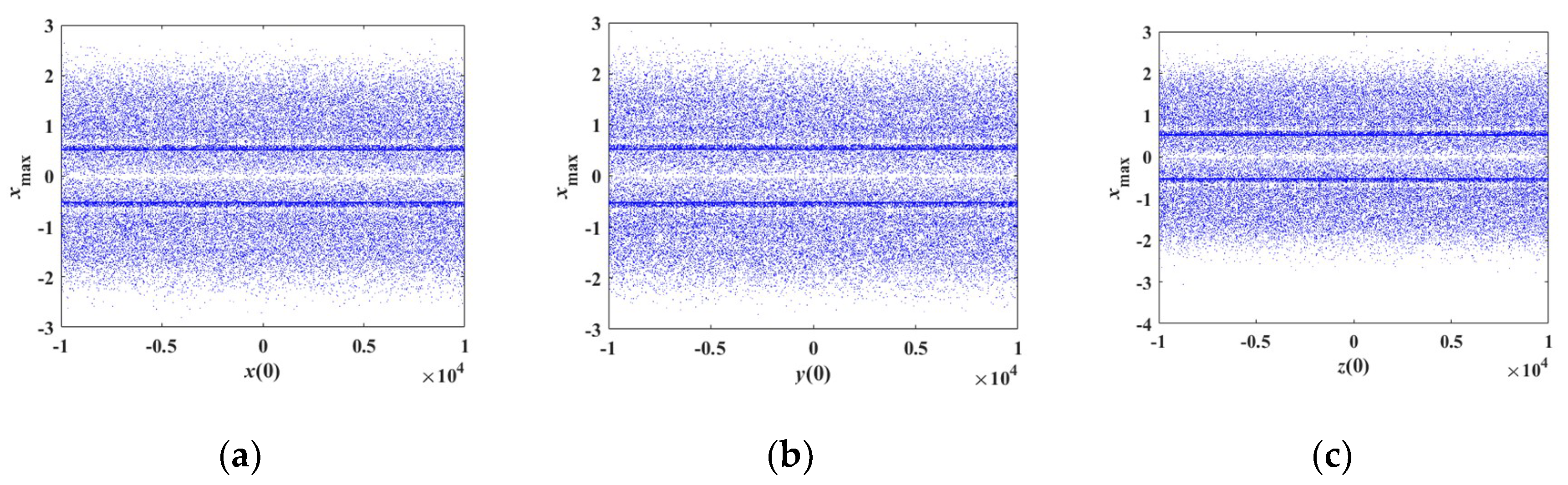
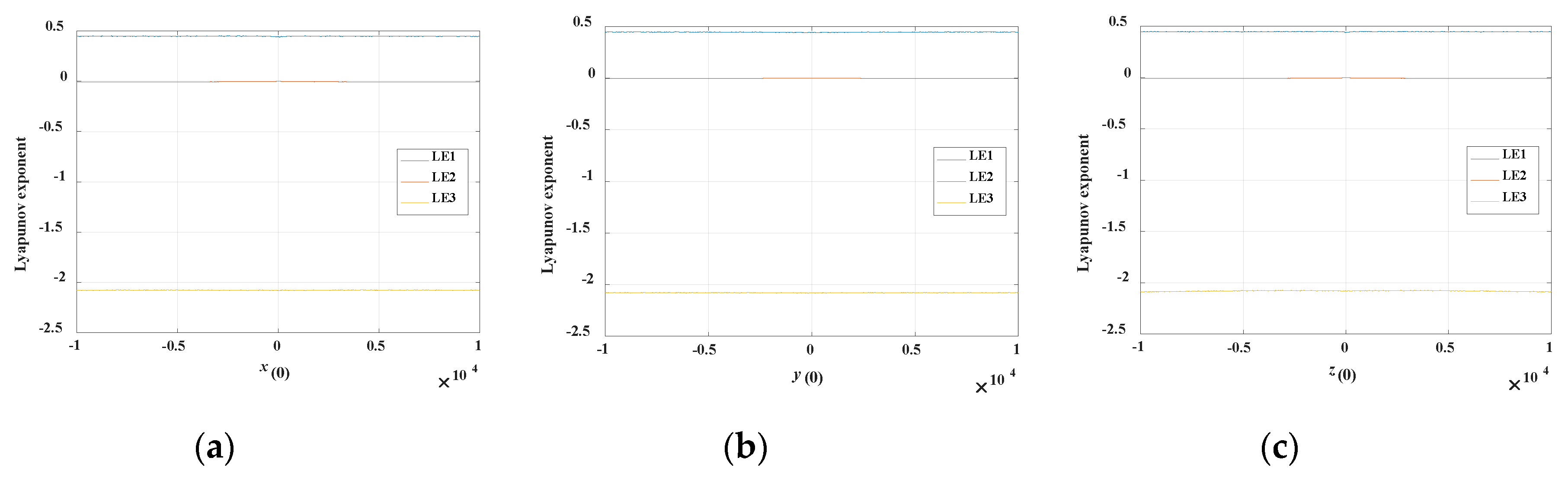
4.4. Sustained Chaos State
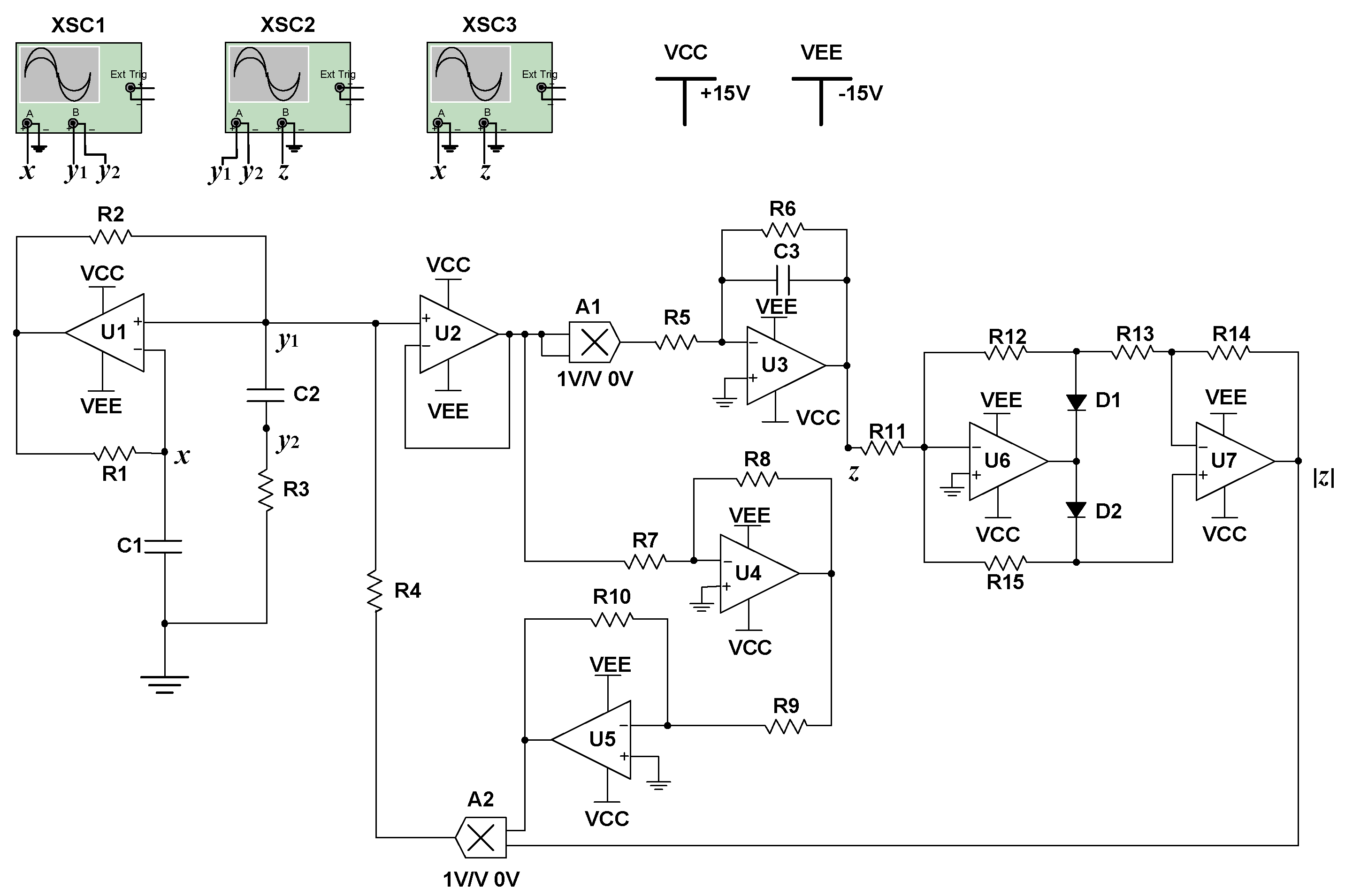
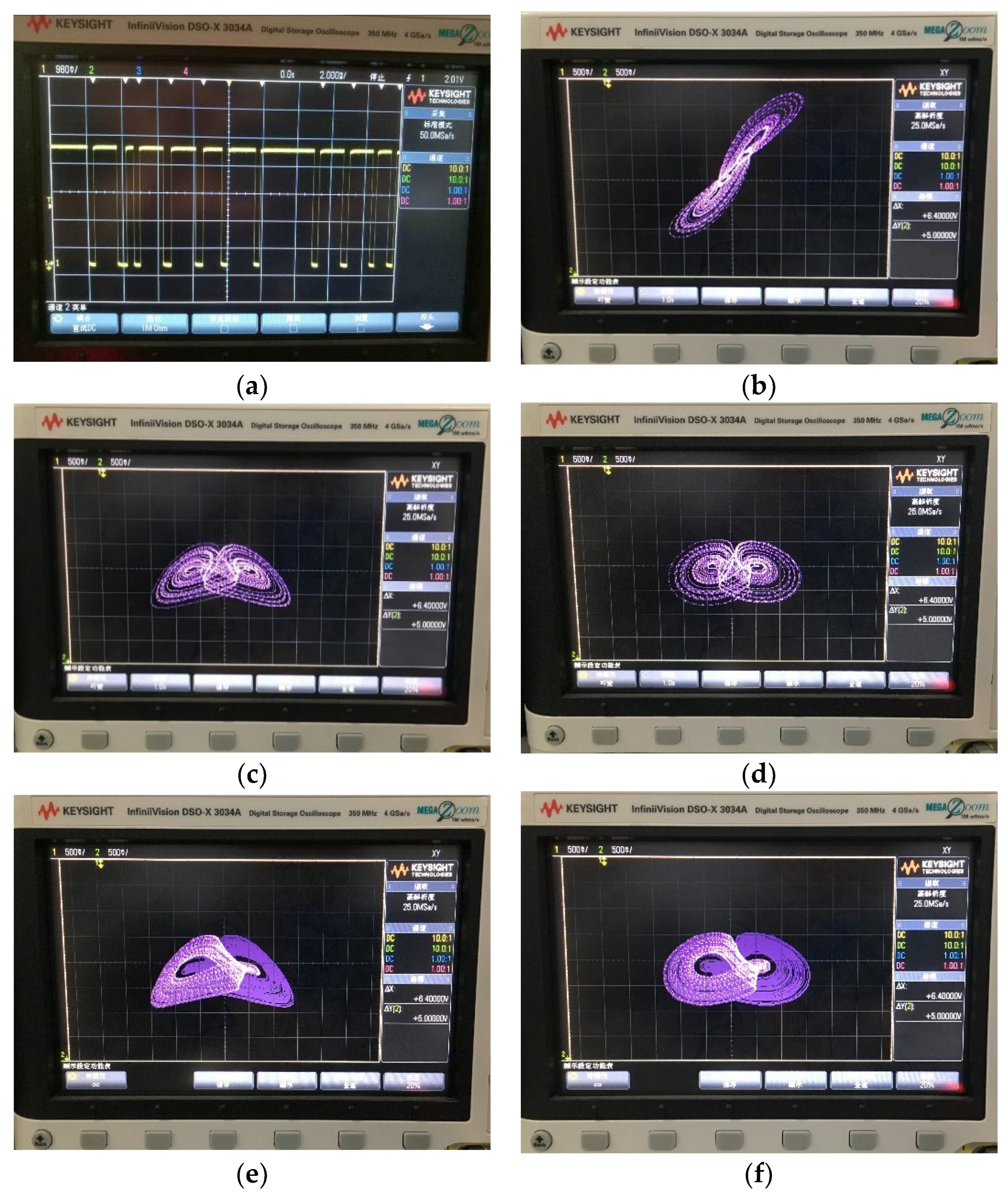
5. Circuit Simulation by the Multisim Software
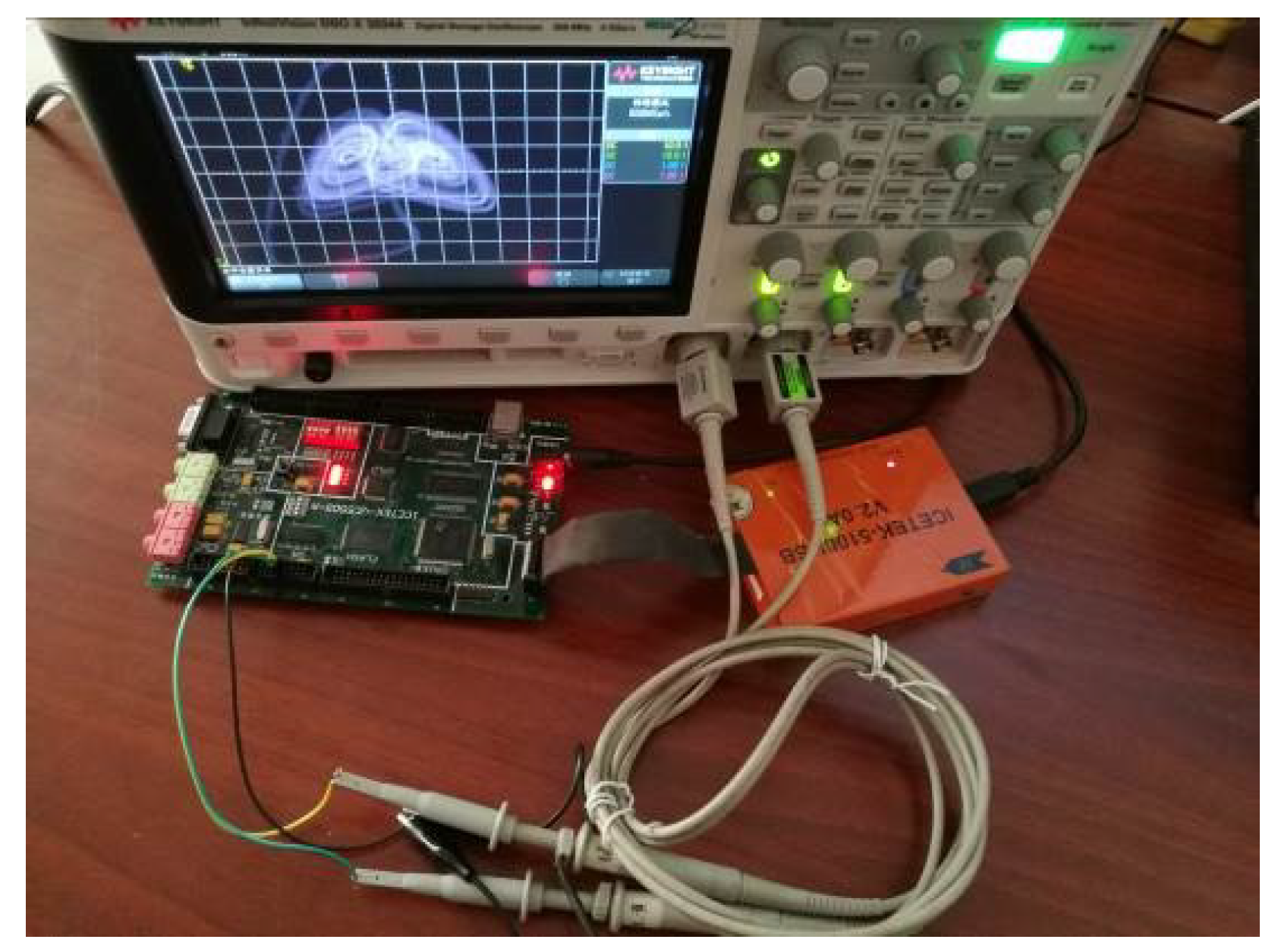
6. Implementation of the Chaotic System by DSP Technology
7. NIST Test Results and Approximate Entropy Analysis of the Proposed Chaotic System
7.1. NIST Test Results
7.2. Approximate Entropy Analysis
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chua, L.O. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Sah, M.P.; Kim, H.; Chua, L.O. Three fingerprints of memristor. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Chua, L.O. Local activity is the origin of complexity. Int. J. Bifurc. Chaos 2005, 15, 3435–3456. [Google Scholar] [CrossRef]
- Chua, L.O. Everything you wish to know about memristors but are afraid to ask. Radioengin 2015, 24, 319–368. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, S.; Zeng, Y.; Li, Z. Generating hidden extreme multistability in memristive chaotic oscillator via micro-perturbation. Electron. Lett. 2018, 54, 808–810. [Google Scholar] [CrossRef]
- Jin, P.; Wang, G.; Iu, H.C.; Fernando, T. A locally-active memristor and its application in chaotic circuit. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 246–250. [Google Scholar] [CrossRef]
- Li, C.; Joo-Chen Thio, W.; Ho-Ching Iu, H.; Lu, T. A memristive chaotic oscillator with increasing amplitude and frequency. IEEE Access 2018, 6, 12945–12950. [Google Scholar] [CrossRef]
- Chang, H.; Wang, Z.; Li, Y.; Chen, G. Dynamic analysis of a bistable bi-local active memristor and its associated oscillator system. Int. J. Bifurc. Chaos 2018, 28, 1850105. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Fardad, M.; Varshney, P.K. A memristor-based optimization framework for artificial intelligence applications. IEEE Circuits Syst. Mag. 2018, 18, 29–44. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, W.; Liu, Q.; Zhao, X.; Wei, J.; Cao, R.; Yao, Z.; Zhu, X.; Zhang, F.; Lv, H.; et al. An artificial neuron based on a threshold switching memristor. IEEE Electron Device Lett. 2018, 39, 308–311. [Google Scholar] [CrossRef]
- Yoon, J.H.; Wang, Z.; Kim, K.M.; Wu, H.; Ravichandran, V.; Xia, Q.; Hwang, C.S.; Yang, J.J. An artificial nociceptor based on a diffusive memristor. Nat. Commun. 2018, 9, 417. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Du Nguyen, H.A.; Taouil, M.; Hamdioui, S.; Bertels, K. A mapping methodology of boolean logic circuits on memristor crossbar. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 37, 311–323. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Q.; Chen, Q.; Zeng, Z. A novel design for memristor-based multiplexer via not-material implication. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 37, 1436–1444. [Google Scholar] [CrossRef]
- Sakib, M.N.; Hassan, R.; Biswas, S.N.; Das, S.R. Memristor-based high-speed memory cell with stable successive read operation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 37, 1037–1049. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Wang, Z.; Li, Y. Nonlinear dynamics and chaos in a simplified memristor-based fractional-order neural network with discontinuous memductance function. Nonlinear Dyn. 2018, 93, 611–627. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Friedman, E.G. Memristor-based circuit design for multilayer neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 677–686. [Google Scholar] [CrossRef]
- Di Marco, M.; Forti, M.; Pancioni, L. New conditions for global asymptotic stability of memristor neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1822–1834. [Google Scholar] [CrossRef]
- Yuan, F.; Deng, Y.; Li, Y.; Wang, G. The amplitude, frequency and parameter space boosting in a memristor–meminductor-based circuit. Nonlinear Dyn. 2019, 96, 389–405. [Google Scholar] [CrossRef]
- Ye, X.; Mou, J.; Luo, C.; Wang, Z. Dynamics analysis of Wien-bridge hyperchaotic memristive circuit system. Nonlinear Dyn. 2018, 92, 923–933. [Google Scholar] [CrossRef]
- Tan, Q.; Zeng, Y.; Li, Z. A simple inductor-free memristive circuit with three line equilibria. Nonlinear Dyn. 2018, 94, 1585–1602. [Google Scholar] [CrossRef]
- Guo, M.; Gao, Z.; Xue, Y.; Dou, G.; Li, Y. Dynamics of a physical SBT memristor-based Wien-bridge circuit. Nonlinear Dyn. 2018, 93, 1681–1693. [Google Scholar] [CrossRef]
- Lai, Q.; Akgul, A.; Li, C.; Xu, G.; Çavuşoğlu, Ü. A New Chaotic System with Multiple Attractors: Dynamic Analysis, Circuit Realization and S-Box Design. Entropy 2018, 20, 12. [Google Scholar] [CrossRef]
- Singh, J.P.; Pham, V.T.; Hayat, T.; Jafari, S.; Alsaadi, F.E.; Roy, B.K. A new four-dimensional hyperjerk system with stable equilibrium point, circuit implementation, and its synchronization by using an adaptive integrator backstepping control. Chin. Phys. B 2018, 27, 100501. [Google Scholar] [CrossRef]
- Yuan, F.; Li, Y.; Wang, G.; Dou, G.; Chen, G. Complex dynamics in a memcapacitor-based circuit. Entropy 2019, 21, 188. [Google Scholar] [CrossRef]
- Chang, H.; Song, Q.; Li, Y.; Wang, Z.; Chen, G. Unstable limit cycles and singular attractors in a two-dimensional memristor-based dynamic system. Entropy 2019, 21, 415. [Google Scholar] [CrossRef]
- Signing, V.R.F.; Kengne, J.; Kana, L.K. Dynamic analysis and multistability of a novel four-wing chaotic system with smooth piecewise quadratic nonlinearity. Chaos Solitons Fractals 2018, 113, 263–274. [Google Scholar] [CrossRef]
- Fonzin, T.F.; Kengne, J.; Pelap, F.B. Dynamical analysis and multistability in autonomous hyperchaotic oscillator with experimental verification. Nonlinear Dyn. 2018, 93, 653–669. [Google Scholar] [CrossRef]
- Wang, G.; Yuan, F.; Chen, G.; Zhang, Y. Coexisting multiple attractors and riddled basins of a memristive system. Chaos 2018, 28, 013125. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z.; Wang, M.; Xiong, L. Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability. Chaos 2018, 28, 013113. [Google Scholar] [CrossRef]
- Xu, B.; Wang, G. Meminductive Wein-bridge chaotic oscillator. Acta Phys. Sin. 2017, 66, 020502. [Google Scholar]
- Xu, G.; Shekofteh, Y.; Akgul, A.; Li, C.; Panahi, S. A new chaotic system with a self-excited attractor: Entropy measurement, signal encryption, and parameter estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]
- Huang, X.; Sun, T.; Li, Y.; Liang, J. A color image encryption algorithm based on a fractional-order hyperchaotic system. Entropy 2015, 17, 28–38. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. A novel image encryption scheme based on self-synchronous chaotic stream cipher and wavelet transform. Entropy 2018, 20, 445. [Google Scholar] [CrossRef]
- Wang, T.; Wang, D.; Wu, K. Chaotic adaptive synchronization control and application in chaotic secure communication for industrial internet of things. IEEE Access 2018, 6, 8584–8590. [Google Scholar] [CrossRef]
- Nwachioma, C.; Perez-Cruz, J.H.; Jimenez, A.; Ezuma, M.; Rivera-Blas, R. A new chaotic oscillator-properties, analog implementation, and secure communication application. IEEE Access 2019, 7, 7510–7521. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications. In NIST Special Publication; Booz-Allen and Hamilton Inc.: McLean, VA, USA, 2010. [Google Scholar]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Ventra, M.D.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors, and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Chua, L.O. Resistance switching memories are memristors. Appl. Phys. A 2011, 102, 765–783. [Google Scholar] [CrossRef]
- Sui, Y.; He, Y.; Yu, W.; Li, Y. Design and circuit implementation of a five-dimensional hyperchaotic system with linear parameter. Int. J. Circuit Theory Appl. 2018, 46, 1503–1515. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, H.; Xiong, W. Analysis and design of digital chaotic systems with desirable performance via feedback control. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 1187–1200. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Muñoz-Pacheco, J.M.; Campos-Cantón, E. Chaos generation in fractional-order switched systems and its digital implementation. Int. J. Electron. Commun. (AEÜ) 2017, 79, 43–52. [Google Scholar] [CrossRef]
- Wheeler, D.D.; Matthews, R. Supercomputer investigations of a chaotic encryption algorithm. Cryptologia 1991, 15, 140–151. [Google Scholar] [CrossRef]
- Heidari-Bateni, G.; McGillem, C.D. A chaotic direct-sequence spread-spectrum communication system. IEEE Trans. Commun. 1994, 42, 1524–1527. [Google Scholar] [CrossRef]
- Cernák, J. Digital generators of chaos. Phys. Lett. A 1996, 214, 151–160. [Google Scholar] [CrossRef]
- Sang, T.; Wang, R.; Yan, Y. Perturbance-based algorithm to expand cycle length of chaotic key stream. Electron. Lett. 1998, 34, 873–874. [Google Scholar] [CrossRef]
- Li, S.; Mou, X.; Cai, Y. Improving security of a chaotic encryption approach. Phys. Lett. A 2001, 290, 127–133. [Google Scholar] [CrossRef]
- Li, C.; Chen, Y.; Chang, T.; Deng, L.; To, K. Period extension and randomness enhancement using high-throughput reseeding-mixing PRNG. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2012, 20, 385–389. [Google Scholar] [CrossRef]
- Nagaraj, N.; Shastry, M.C.; Vaidya, P.G. Increasing average period lengths by switching of robust chaos maps in fifinite precision. Eur. Phys. J. Spec. Top. 2008, 165, 73–83. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.; Liao, X.; Xiang, T.; Chen, G. A chaos-based image encryption algorithm with variable control parameters. Chaos Soliton Fract. 2009, 41, 1773–1783. [Google Scholar] [CrossRef]
- Hu, H.; Xu, Y.; Zhu, Z. A method of improving the properties of digital chaotic system. Chaos Soliton Fract. 2008, 38, 439–446. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| a | 4.5 |
| b | 5.5 |
| c | 0.4 |
| d | 1.0 |
| m | 5.0 |
| n | 4.0 |
| Statistical Test Terms | p-ValueT | Proportion |
|---|---|---|
| Frequency | 0.624627 | 0.9960 |
| Block Frequency | 0.668321 | 0.9940 |
| Cumulative Sums | 0.326749 | 0.9960 |
| Runs | 0.399442 | 0.9900 |
| Longest Run | 0.877083 | 0.9880 |
| Rank | 0.044797 | 0.9900 |
| FFT | 0.887645 | 0.9860 |
| Non-Overlapping Template | 0.993493 | 0.9880 |
| Overlapping Template | 0.476911 | 0.9930 |
| Universal | 0.854708 | 0.9870 |
| Approximate Entropy | 0.272977 | 0.9890 |
| Random Excursions | 0.649066 | 0.9935 |
| Random Excursions Variant | 0.995975 | 0.9951 |
| Serial | 0.007805 | 0.9820 |
| Linear Complexity | 0.755819 | 0.9920 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Yuan, F.; Li, Y. Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit. Entropy 2019, 21, 678. https://doi.org/10.3390/e21070678
Song Y, Yuan F, Li Y. Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit. Entropy. 2019; 21(7):678. https://doi.org/10.3390/e21070678
Chicago/Turabian StyleSong, Yixuan, Fang Yuan, and Yuxia Li. 2019. "Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit" Entropy 21, no. 7: 678. https://doi.org/10.3390/e21070678
APA StyleSong, Y., Yuan, F., & Li, Y. (2019). Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit. Entropy, 21(7), 678. https://doi.org/10.3390/e21070678





