Entropic Regularization of Markov Decision Processes
Abstract
1. Introduction
2. Background
2.1. Policy Gradient Methods
2.2. Entropic Penalties
3. Entropic Proximal Policy Optimization
3.1. Fighting Covariate Shift via Trust Regions
3.2. Policy Optimization with Entropic Penalties
3.3. Value Function Approximation
3.4. Sample-Based Algorithm for Dual Optimization
3.5. Parametric Policy Fitting
3.6. Temperature Scheduling
3.7. Practical Algorithm for Continuous State-Action Spaces
| Algorithm 1: Primal-dual entropic proximal policy optimization with function approximation |
 |
4. High- and Low-Temperature Limits; -Divergences; Analytic Solutions and Asymptotics
4.1. KL Divergence () and Pearson -Divergence ()
Mean Squared Error Minimization with Advantage Reweighting is Equivalent to Pearson Penalty
4.2. High- and Low-Temperature Limits
4.2.1. High Temperatures: All Smooth f-Divergences Tend Towards Pearson -Divergence
4.2.2. Low Temperatures: Linear Programming Formulation Emerges in the Limit
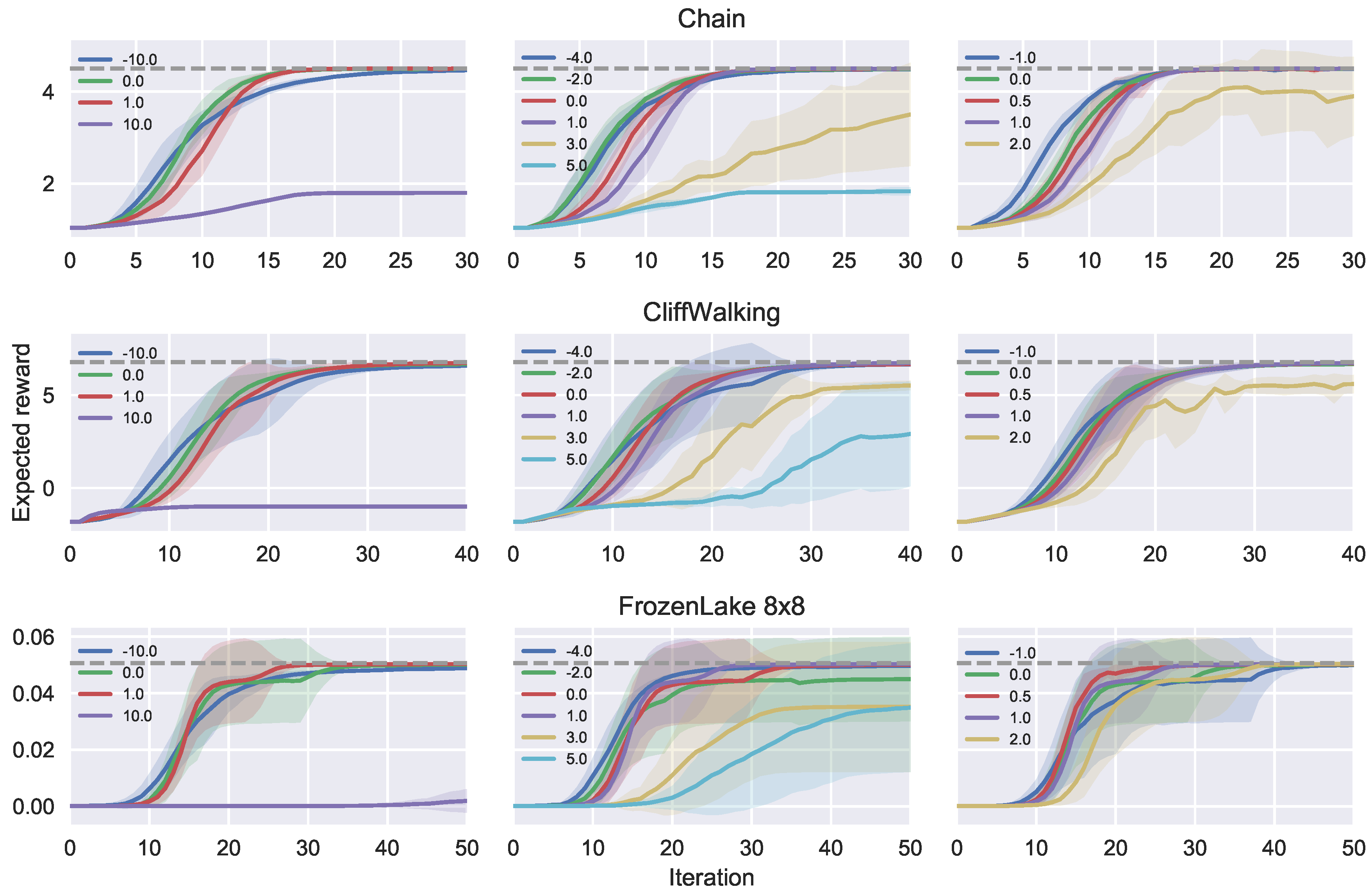
5. Empirical Evaluations
5.1. Illustrative Experiments on Stochastic Multi-Armed Bandit Problems
5.1.1. Effects of on Policy Improvement
5.1.2. Effects of on Regret
5.2. Empirical Evaluations on Ergodic MDPs
6. Related Work
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
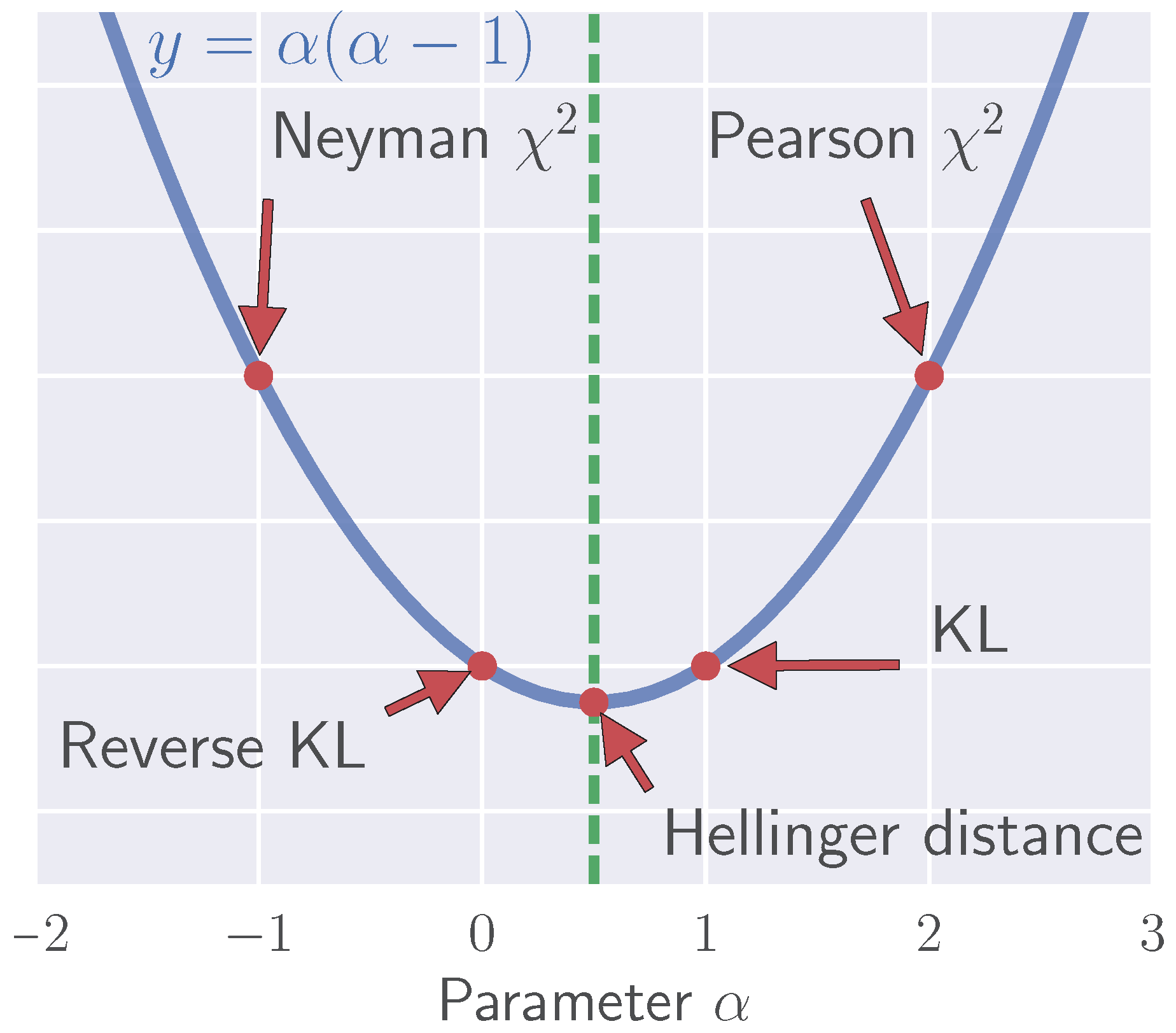
| Divergence | ||||||
|---|---|---|---|---|---|---|
| KL | 1 | |||||
| Reverse KL | 0 | |||||
| Pearson | 2 | |||||
| Neyman | ||||||
| Hellinger |
Appendix B
| Parameter | Value |
|---|---|
| Number of states | 8 |
| Action success probability | 0.9 |
| Small and large rewards | (2.0, 10.0) |
| Number of runs | 10 |
| Number of iterations | 30 |
| Number of samples | 800 |
| Temperature parameters | (15.0, 0.9) |
| Parameter | Value |
|---|---|
| Punishment for falling from the cliff | |
| Reward for reaching the goal | 100 |
| Number of runs | 10 |
| Number of iterations | 40 |
| Number of samples | 1500 |
| Temperature parameters | (50.0, 0.9) |
| Parameter | Value |
|---|---|
| Action success probability | 0.8 |
| Number of runs | 10 |
| Number of iterations | 50 |
| Number of samples | 2000 |
| Temperature parameters | (1.0, 0.8) |
References
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Deisenroth, M.P.; Neumann, G.; Peters, J. A survey on policy search for robotics. Found. Trends® Robot. 2013, 2, 1–142. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1957, 70, 342. [Google Scholar] [CrossRef]
- Kakade, S.M. A Natural Policy Gradient. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; pp. 1531–1538. [Google Scholar]
- Peters, J.; Mülling, K.; Altun, Y. Relative Entropy Policy Search. In Proceedings of the 24th AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 1607–1612. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.; Abbeel, P. Trust Region Policy Optimization. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Shimodaira, H. Improving predictive inference under covariate shift by weighting the log-likelihood function. J. Stat. Plann. Inference. 2000, 227–244. [Google Scholar] [CrossRef]
- Neu, G.; Jonsson, A.; Gómez, V. A unified view of entropy-regularized Markov decision processes. arXiv 2017, arXiv:1705.07798. [Google Scholar]
- Parikh, N. Proximal Algorithms. Found. Trends® Optim. 2014, 1, 127–239. [Google Scholar] [CrossRef]
- Nielsen, F. An elementary introduction to information geometry. arXiv 2018, arXiv:1808.08271. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Bottou, L.; Arjovsky, M.; Lopez-Paz, D.; Oquab, M. Geometrical Insights for Implicit Generative Modeling. Braverman Read. Mach. Learn. 2018, 11100, 229–268. [Google Scholar]
- Nowozin, S.; Cseke, B.; Tomioka, R. f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 271–279. [Google Scholar]
- Teboulle, M. Entropic Proximal Mappings with Applications to Nonlinear Programming. Math. Operations Res. 1992, 17, 670–690. [Google Scholar] [CrossRef]
- Nemirovski, A.; Yudin, D. Problem complexity and method efficiency in optimization. J. Operational Res. Soc. 1984, 35, 455. [Google Scholar]
- Beck, A.; Teboulle, M. Mirror descent and nonlinear projected subgradient methods for convex optimization. Operations Res. Lett. 2003, 31, 167–175. [Google Scholar] [CrossRef]
- Chernoff, H. A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann. Math. Stat. 1952, 23, 493–507. [Google Scholar] [CrossRef]
- Amari, S. Differential-Geometrical Methods in Statistics; Springer: New York, NY, USA, 1985. [Google Scholar] [CrossRef]
- Cichocki, A.; Amari, S. Families of alpha- beta- and gamma- divergences: Flexible and robust measures of Similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Thomas, P.S.; Okal, B. A notation for Markov decision processes. arXiv 2015, arXiv:1512.09075. [Google Scholar]
- Sutton, R.S.; Mcallester, D.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 1999; pp. 1057–1063. [Google Scholar]
- Peters, J.; Schaal, S. Natural Actor-Critic. Neurocomputing 2008, 71, 1180–1190. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Csiszár, I. Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizität von Markoffschen Ketten. Publ. Math. Inst. Hungar. Acad. Sci. 1963, 8, 85–108. [Google Scholar]
- Zhu, H.; Rohwer, R. Information Geometric Measurements of Generalisation; Technical Report; Aston University: Birmingham, UK, 1995. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following methods for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Graphical Models, Exponential Families, and Variational Inference. Found. Trends Mach. Learn. 2007, 1, 1–305. [Google Scholar] [CrossRef]
- Baird, L. Residual Algorithms: Reinforcement Learning with Function Approximation. In Proceedings of the 12th International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 30–37. [Google Scholar]
- Dann, C.; Neumann, G.; Peters, J. Policy Evaluation with Temporal Differences: A Survey and Comparison. J. Mach. Learn. Res. 2014, 15, 809–883. [Google Scholar]
- Sason, I.; Verdu, S. F-divergence inequalities. IEEE Trans. Inf. Theory 2016, 62, 5973–6006. [Google Scholar] [CrossRef]
- Bubeck, S.; Cesa-Bianchi, N. Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems. Found. Trends Mach. Learn. 2012, 5, 1–122. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R. The Non-Stochastic Multi-Armed Bandit Problem. SIAM J. Comput. 2003, 32, 48–77. [Google Scholar] [CrossRef]
- Ghavamzadeh, M.; Mannor, S.; Pineau, J.; Tamar, A. Bayesian Reinforcement Learning: A Survey. Found. Trends Mach. Learn. 2015, 8, 359–483. [Google Scholar] [CrossRef]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Tishby, N.; Polani, D. Information theory of decisions and actions. In Perception-Action Cycle; Cutsuridis, V., Hussain, A., Taylor, J., Eds.; Springer: New York, NY, USA, 2011; pp. 601–636. [Google Scholar]
- Bertschinger, N.; Olbrich, E.; Ay, N.; Jost, J. Autonomy: An information theoretic perspective. Biosystems 2008, 91, 331–345. [Google Scholar] [CrossRef] [PubMed]
- Still, S.; Precup, D. An information-theoretic approach to curiosity-driven reinforcement learning. Theory Biosci. 2012, 131, 139–148. [Google Scholar] [CrossRef]
- Genewein, T.; Leibfried, F.; Grau-Moya, J.; Braun, D.A. Bounded rationality, abstraction, and hierarchical decision-making: An information-theoretic optimality principle. Front. Rob. AI 2015, 2, 27. [Google Scholar] [CrossRef]
- Wolpert, D.H. Information theory—The bridge connecting bounded rational game theory and statistical physics. In Complex Engineered Systems; Braha, D., Minai, A., Bar-Yam, Y., Eds.; Springer: Berlin, Germany, 2006; pp. 262–290. [Google Scholar]
- Geist, M.; Scherrer, B.; Pietquin, O. A Theory of Regularized Markov Decision Processes. arXiv 2019, arXiv:1901.11275. [Google Scholar]
- Li, X.; Yang, W.; Zhang, Z. A Unified Framework for Regularized Reinforcement Learning. arXiv 2019, arXiv:1903.00725. [Google Scholar]
- Nachum, O.; Chow, Y.; Ghavamzadeh, M. Path consistency learning in Tsallis entropy regularized MDPs. arXiv 2018, arXiv:1802.03501. [Google Scholar]
- Lee, K.; Kim, S.; Lim, S.; Choi, S.; Oh, S. Tsallis Reinforcement Learning: A Unified Framework for Maximum Entropy Reinforcement Learning. arXiv 2019, arXiv:1902.00137. [Google Scholar]
- Lee, K.; Choi, S.; Oh, S. Sparse Markov decision processes with causal sparse Tsallis entropy regularization for reinforcement learning. IEEE Rob. Autom. Lett. 2018, 3, 1466–1473. [Google Scholar] [CrossRef]
- Lee, K.; Choi, S.; Oh, S. Maximum Causal Tsallis Entropy Imitation Learning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 4408–4418. [Google Scholar]
- Mahadevan, S.; Liu, B.; Thomas, P.; Dabney, W.; Giguere, S.; Jacek, N.; Gemp, I.; Liu, J. Proximal reinforcement learning: A new theory of sequential decision making in primal-dual spaces. arXiv 2014, arXiv:1405.6757. [Google Scholar]
- Morimoto, T. Markov processes and the H-theorem. J. Phys. Soc. Jpn. 1963, 18, 328–331. [Google Scholar] [CrossRef]
- Ali, S.M.; Silvey, S.D. A General Class of Coefficients of Divergence of One Distribution from Another. J. R. Stat. Soc. Ser. B (Methodol.) 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; 487p. [Google Scholar] [CrossRef]
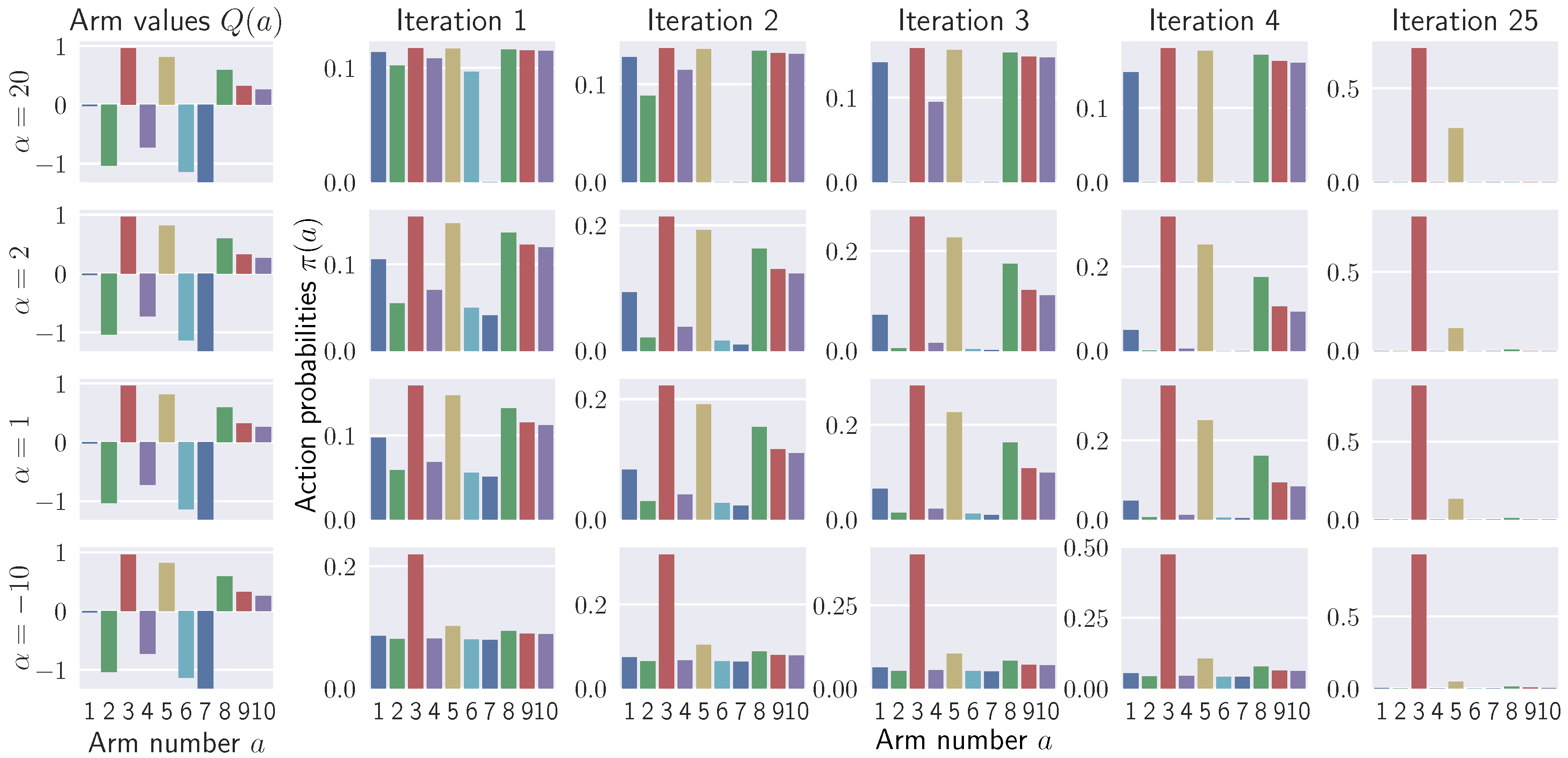
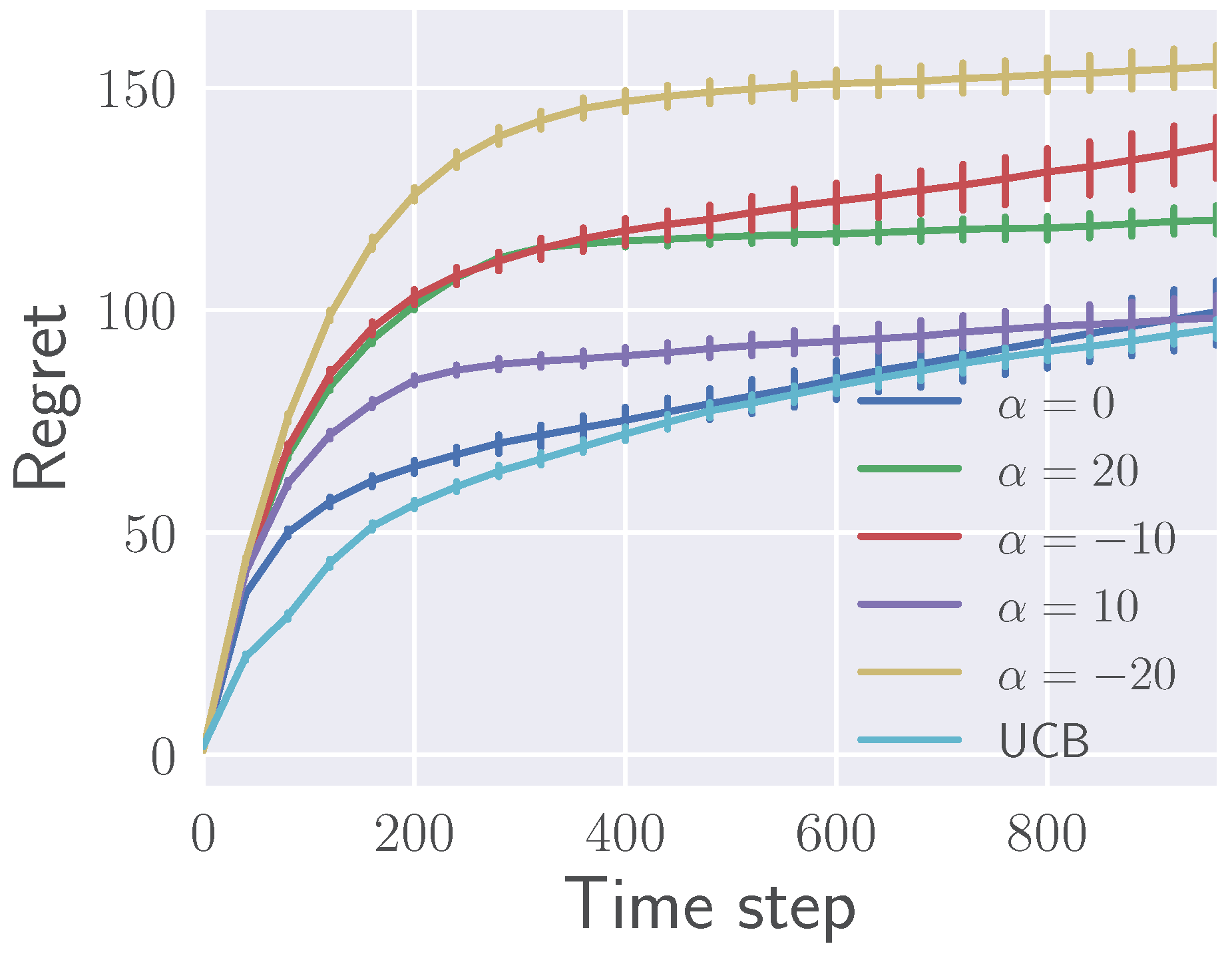
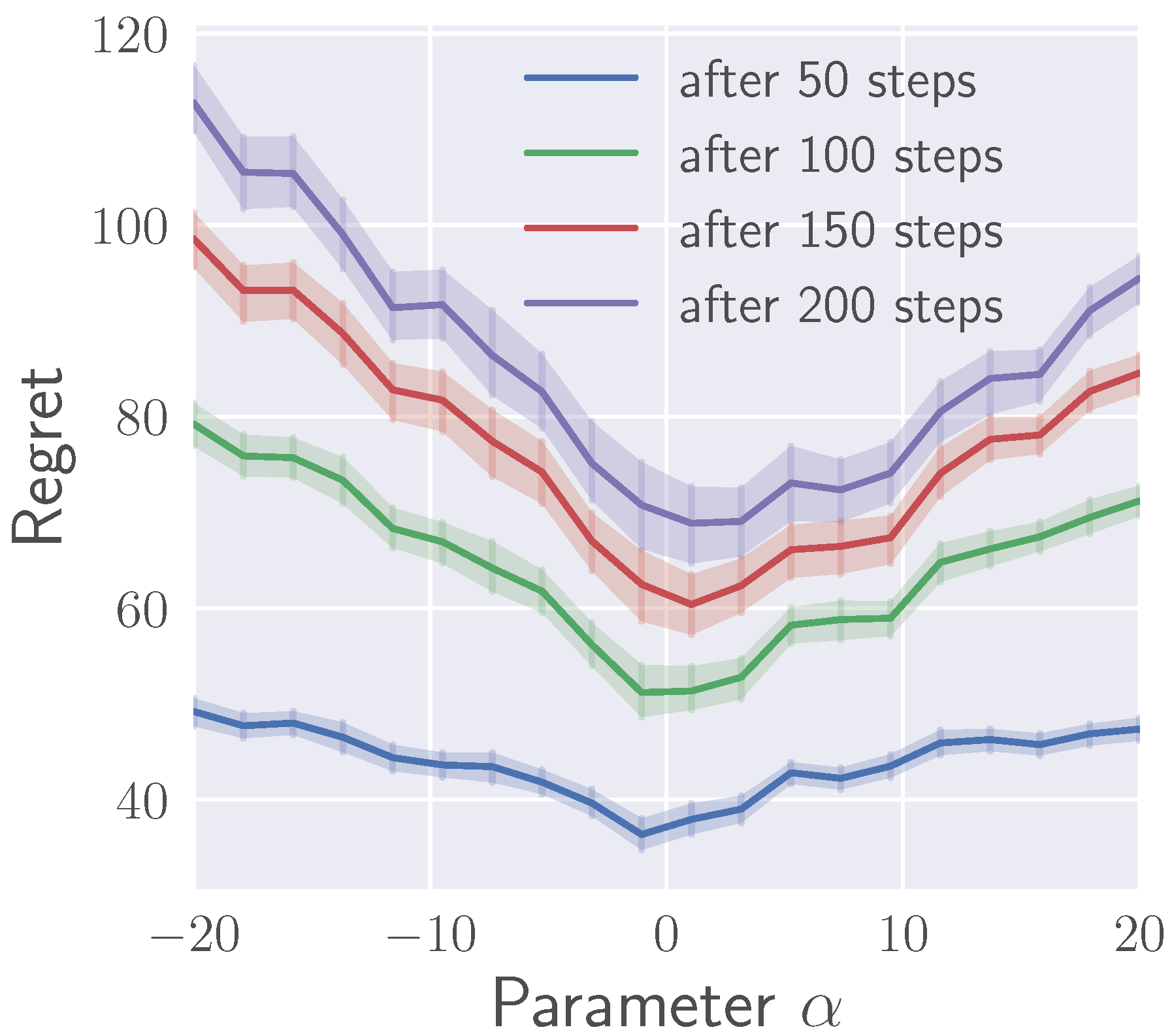
| KL Divergence () | Pearson -Divergence () |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belousov, B.; Peters, J. Entropic Regularization of Markov Decision Processes. Entropy 2019, 21, 674. https://doi.org/10.3390/e21070674
Belousov B, Peters J. Entropic Regularization of Markov Decision Processes. Entropy. 2019; 21(7):674. https://doi.org/10.3390/e21070674
Chicago/Turabian StyleBelousov, Boris, and Jan Peters. 2019. "Entropic Regularization of Markov Decision Processes" Entropy 21, no. 7: 674. https://doi.org/10.3390/e21070674
APA StyleBelousov, B., & Peters, J. (2019). Entropic Regularization of Markov Decision Processes. Entropy, 21(7), 674. https://doi.org/10.3390/e21070674






