Enhancing the Generated Stable Correlation in a Dissipative System of Two Coupled Qubits inside a Coherent Cavity via Their Dipole-Dipole Interplay
Abstract
1. Introduction
2. Time Evolution of Qubits-Cavity Interaction
3. NCC Quantifiers
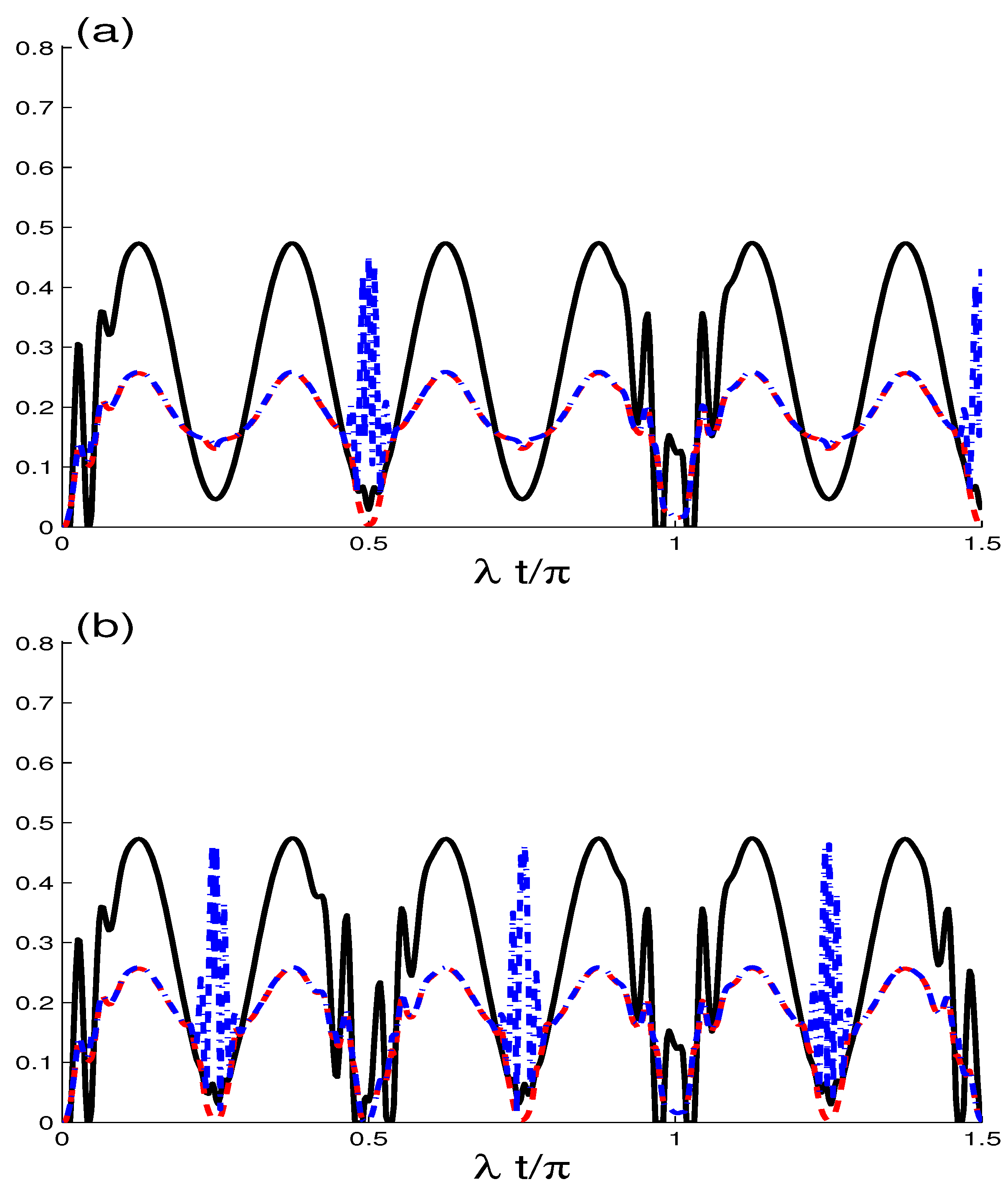
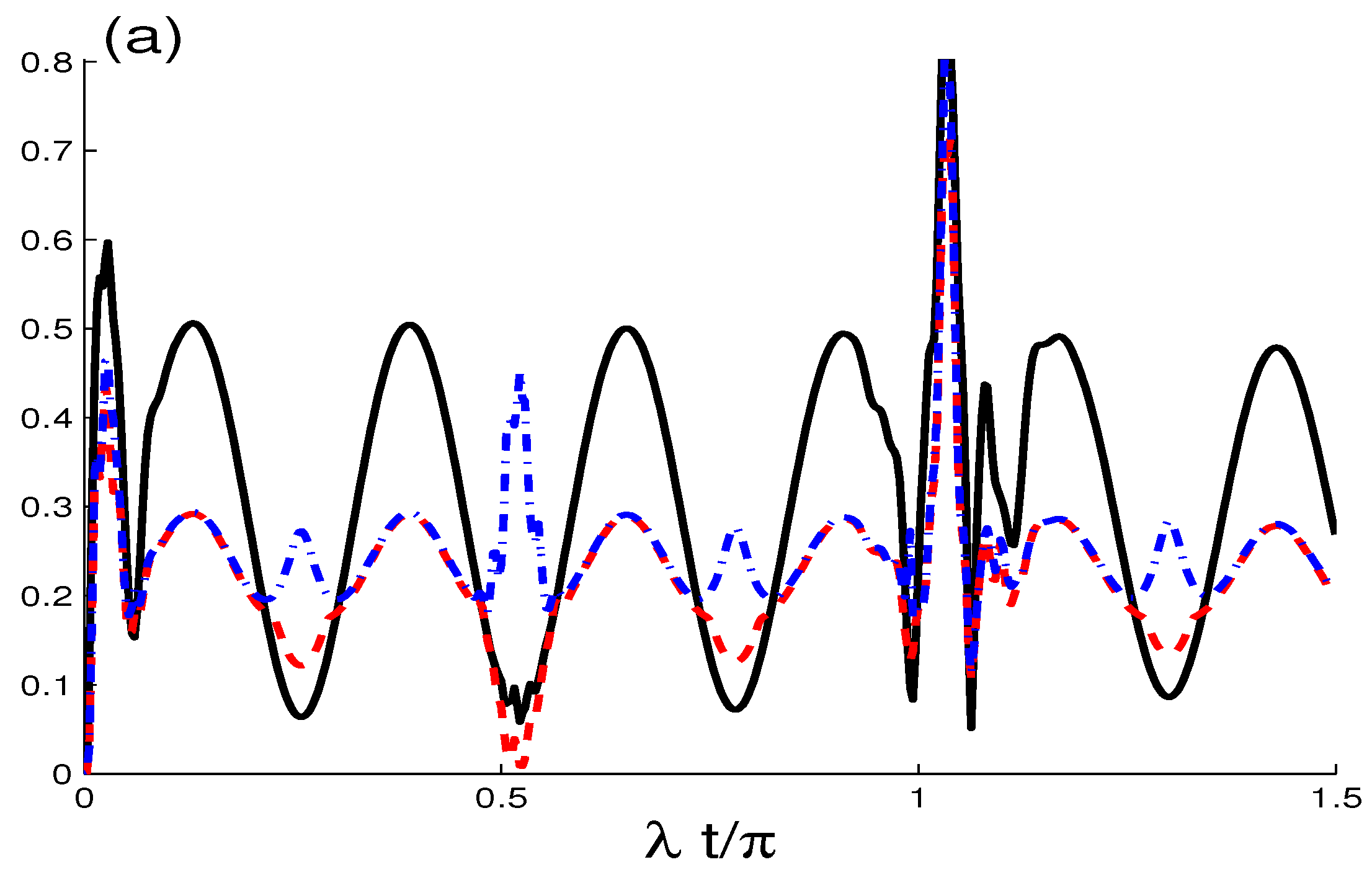
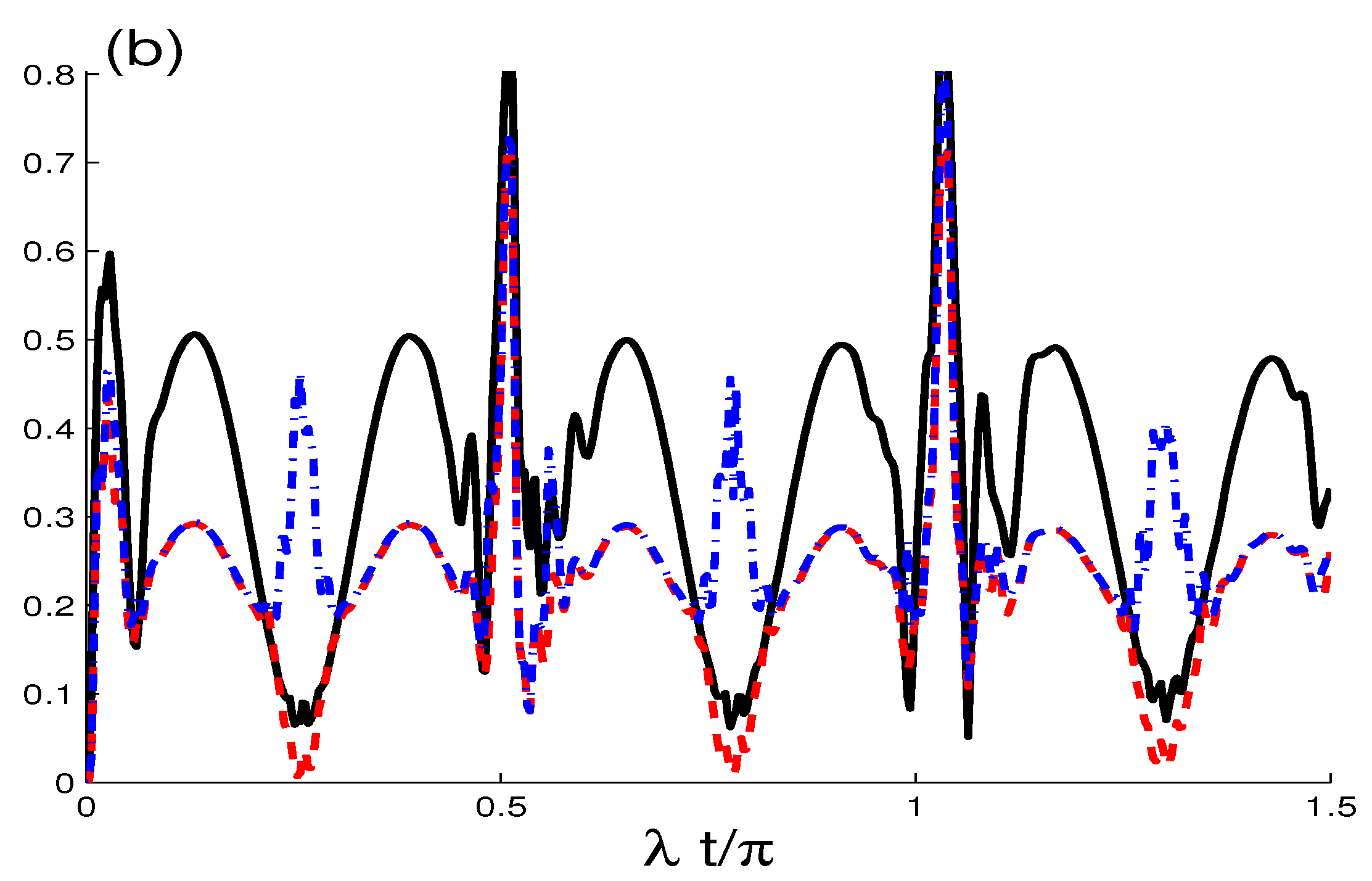
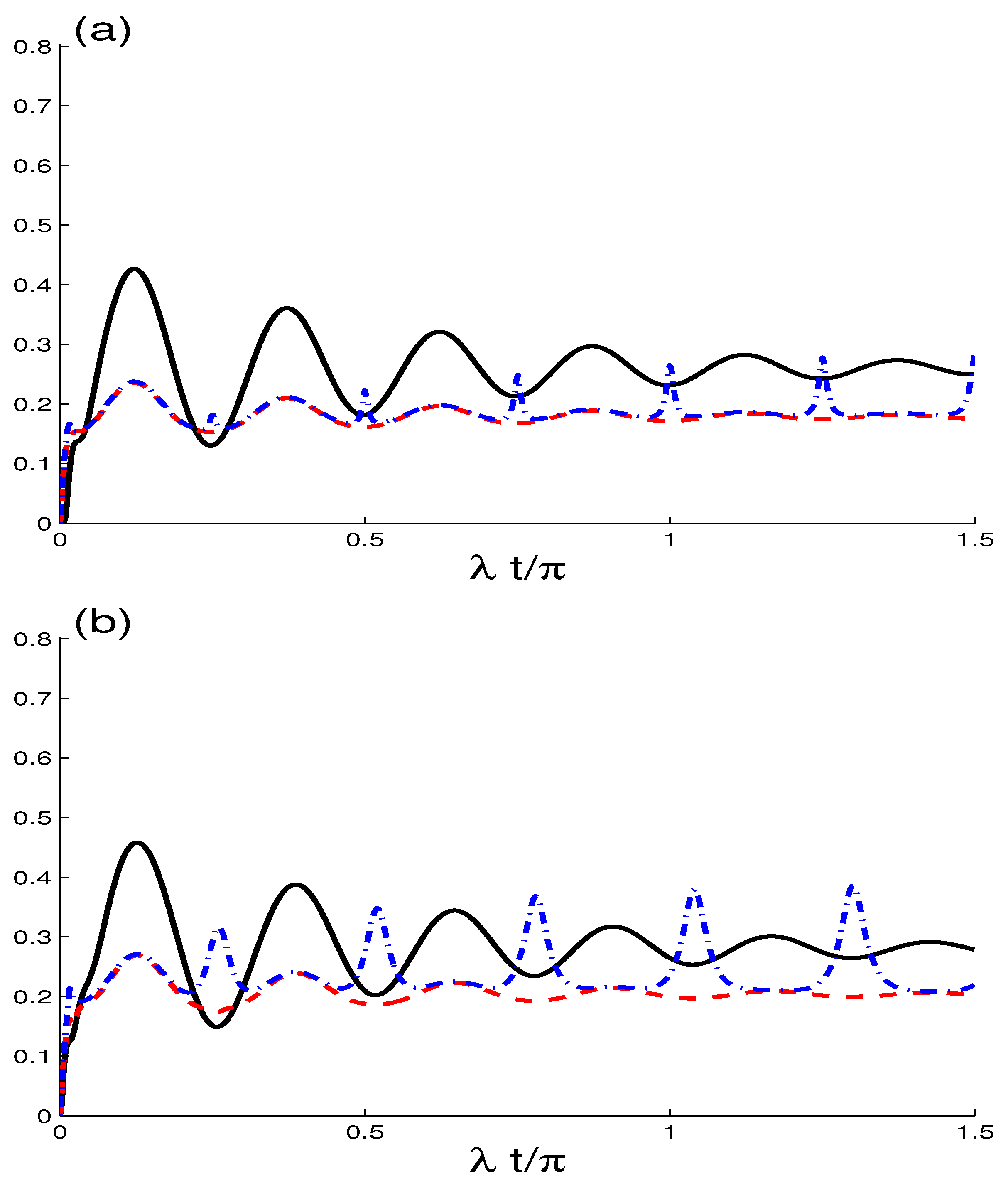
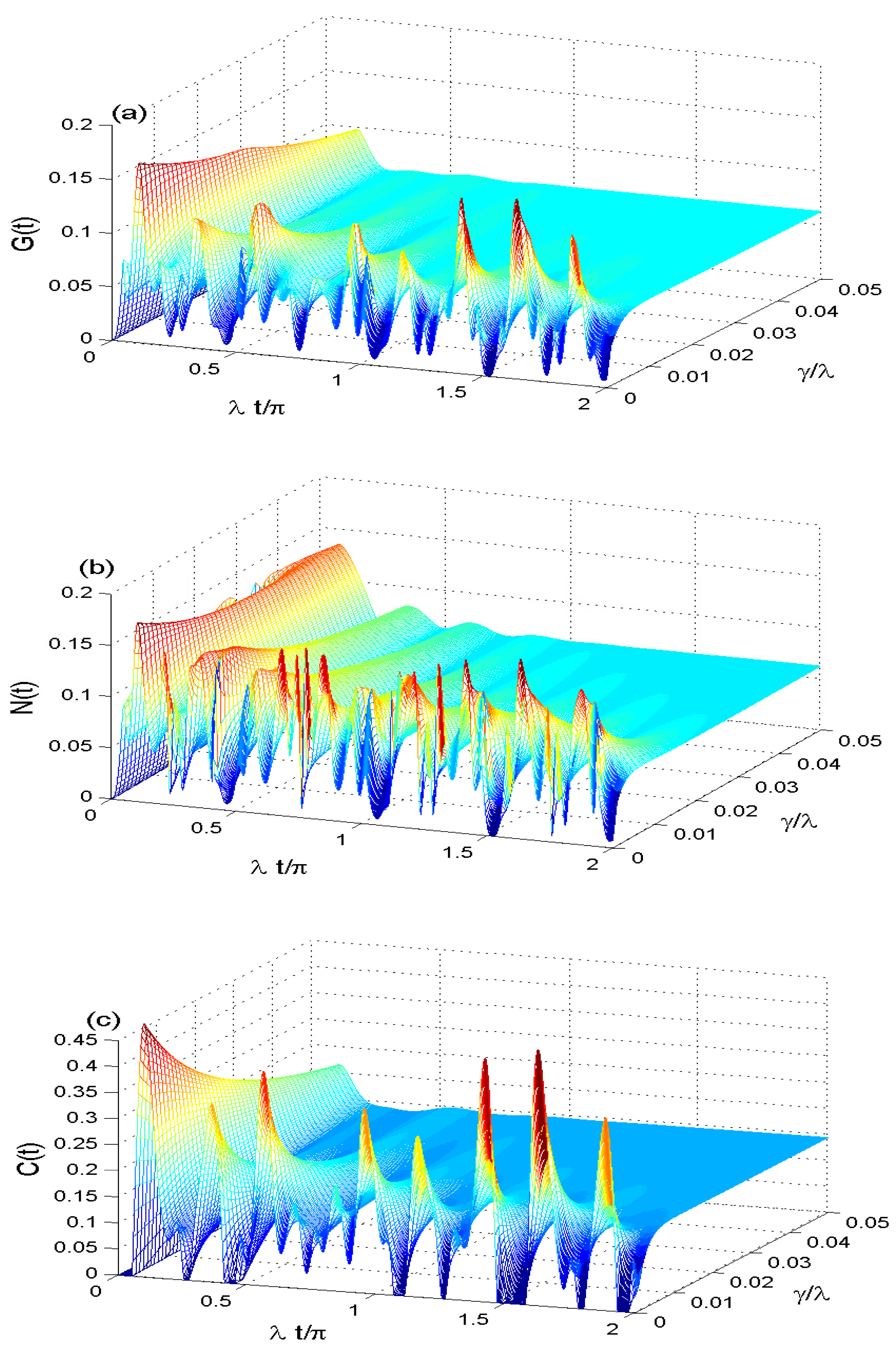
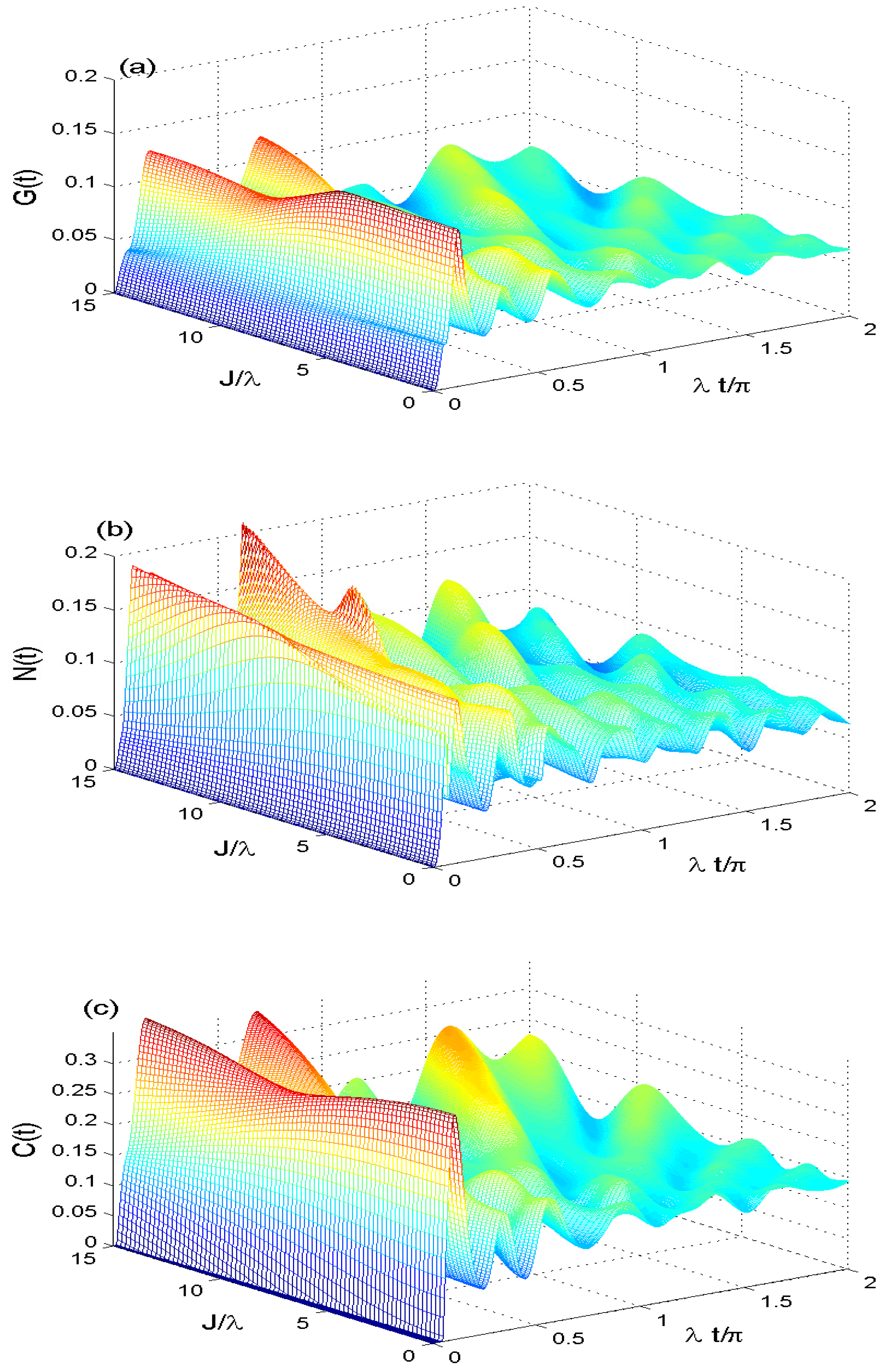
4. Dynamics of the Correlation Quantifiers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Generation and robustness of bipartite non-classical correlations in two nonlinear microcavities coupled by an optical fiber. J. Opt. Soc. Am. B 2018, 35, 47. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Eleuch, H. Dynamical behavior of entanglement in semiconductor microcavities. Physica E 2010, 42, 2091. [Google Scholar] [CrossRef]
- Mohamed, A.B.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Luo, S. Quantum discord for two-qubit systems. Phys. Rev. A 2008, 77, 042303. [Google Scholar] [CrossRef]
- Berrada, K.; Eleuch, H.; Hassouni, Y. Asymptotic dynamics of quantum discord in open quantum systems. J. Phys. B 2013, 44, 145503. [Google Scholar] [CrossRef]
- Dakic, B.; Vedral, V.; Brukner, C. Necessary and sufficient condition for non-zero quantum discord. Phys. Rev. Lett. 2010, 105, 190502. [Google Scholar] [CrossRef] [PubMed]
- Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 2008, 77, 022301. [Google Scholar] [CrossRef]
- Luo, S.; Fu, S. Measurement-induced nonlocality. Phys. Rev. Lett. 2011, 106, 120401. [Google Scholar] [CrossRef]
- Bartkiewicz, K.; Černoch, A.; Lemr, K.; Miranowicz, A.; Nori, F. Temporal steering and security of quantum key distribution with mutually unbiased bases against individual attacks. Phys. Rev. A 2016, 93, 062345. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W. Quantum steering borders in three-qubit systems. Quantum Inf. Process. 2017, 16, 175. [Google Scholar] [CrossRef]
- Ku, H.-Y.; Chen, S.-L.; Budroni, C.; Miranowicz, A.; Chen, Y.-N.; Nori, F. Einstein-Podolsky-Rosen steering: Its geometric quantification and witness. Phys. Rev. A 2018, 97, 022338. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W.; Peřina, J., Jr. Einstein-Podolsky-Rosen steering and coherence in the family of entangled three-qubit states. Phys. Rev. A 2018, 97, 042110. [Google Scholar] [CrossRef]
- Arkhipov, I.I.; Peřina, J., Jr.; Peřrina, J.; Miranowicz, A. Interplay of nonclassicality and entanglement of two-mode Gaussian fields generated in optical parametric processes. Phys. Rev. A 2016, 94, 013807. [Google Scholar] [CrossRef]
- Chen, S.-L.; Lambert, N.; Li, C.-M.; Chen, G.-Y.; Chen, Y.-N.; Miranowicz, A.; Nori, F. Spatio-Temporal Steering for Testing Nonclassical Correlations in Quantum Networks. Sci. Rep. 2017, 7, 3728. [Google Scholar] [CrossRef]
- Kalaga, J.K.; Leoński, W.; Szczȩśniak, R. Quantum steering and entanglement in three-mode triangle Bose-Hubbard system. Quantum Inf. Process. 2017, 16, 265. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Pairwise quantum correlations of a three-qubit XY chain with phase decoherence. Quantum Inf. Process. 2013, 12, 1141. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Joshi, A.; Hassan, S.S. Bipartite non-local correlations in a doublequantum- dot excitonic system. J. Phys. A Math. Theor. 2014, 47, 335301. [Google Scholar] [CrossRef]
- Tian, Z.; Jing, J. Measurement-induced-nonlocality via the Unruh effect. Ann. Phys. 2013, 333, 76. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Quantum correlation of correlated two qubits interacting with a thermal field. Phys. Scr. 2012, 85, 055013. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Metwally, N. Non-classical correlations based on skew information for an entangled two qubit-system with non-mutual interaction under intrinsic decoherence. Ann. Phys. 2017, 381, 137. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A. Thermal effect on the generated quantum correlation between two superconducting qubits. Laser Phys. Lett. 2016, 13, 085202. [Google Scholar] [CrossRef]
- Paula, F.M.; Oliveira, T.R.; Sarandy, M.S. Geometric quantum discord through the Schatten 1-norm. Phys. Rev. 2013, 87, 064101. [Google Scholar] [CrossRef]
- Spehner, D.; Orszag, M. Geometric quantum discord with Bures distance. New J. Phys. 2013, 15, 103001. [Google Scholar] [CrossRef]
- Behzadi, N.; Faizi, E.; Heibati, O. Quantum discord protection of a two-qutrit V-type atomic system from decoherence by partially collapsing measurements. Quantum Inf. Process. 2017, 16, 257. [Google Scholar] [CrossRef]
- Slaoui, A.; Daoud, M.; Laamara, R.A. The dynamics of local quantum uncertainty and trace distance discord for two-qubit X states under decoherence: A comparative study. Quantum Inf. Process. 2018, 17, 178. [Google Scholar] [CrossRef]
- Golkar, S.; Tavassoly, M.K. Coping with attenuation of quantum correlations of two qubit systems in dissipative environments: Multi-photon transitions. Eur. Phys. J. D 2018, 72, 184. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Obada, A.-S.F. Non-classical correlations in two quantum dots coupled in a coherent resonator field under decoherence. Quantum Inf. Process. 2018, 17, 277. [Google Scholar] [CrossRef]
- Sha, Y.-T.; Wang, Y.; Sun, Z.-H.; Hou, X.-W. Thermal quantum coherence and correlation in the extended XY spin chain. Ann. Phys. 2018, 392, 229. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Quantum correlation control for two semiconductor microcavities connected by an optical fiber. Phys. Scr. 2017, 92, 065101. [Google Scholar] [CrossRef]
- Jha, P.K.; Eleuch, H.; Rostovtsev, Y.V. Coherent control of atomic excitation using off-resonant strong few-cycle pulses. Phys. Rev. A 2010, 82, 045805. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Eleuch, H. Stationary quantum correlation and coherence of two-mode Kerr nonlinear coupler interdicting with Su(2)-system under intrinsic damping. J. Mod. Opt. 2018, 65, 2213. [Google Scholar] [CrossRef]
- Datta, A.; Shaji, A.; Caves, C.M. Quantum Discord and the Power of One Qubit. Phys. Rev. Lett. 2008, 100, 050502. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Barbieri, M.; Almeida, M.P.; White, A.G. Experimental Quantum Computing without Entanglement. Phys. Rev. Lett. 2008, 101, 200501. [Google Scholar] [CrossRef]
- Viola, L.; Knill, E.; Lloyd, S. Dynamical Decoupling of Open Quantum Systems. Phys. Rev. Lett. 1999, 82, 2417. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Resonances in open quantum systems. Phys. Rev. A 2017, 95, 022117. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Nearby states in non-Hermitian quantum systems II: Three and more states. Eur. Phys. J. D 2015, 69, 230. [Google Scholar] [CrossRef]
- Gardiner, C.W. Quantum Noise; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Milburn, G.J. Intrinsic decoherence in quantum mechanics. Phys. Rev. A 1991, 44, 5401. [Google Scholar] [CrossRef]
- Janszky, J.; Domokos, P.; Adam, P. oherent states on a circle and quantum interference. Phys. Rev. A 1993, 48, 2213. [Google Scholar] [CrossRef]
- Miry, S.R.; Tavassoly, M.K. Generation of a class of SU(1,1) coherent states of the Gilmore–Perelomov type and a class of SU(2) coherent states and their superposition. Phys. Scr. 2012, 85, 035404. [Google Scholar] [CrossRef]
- Brune, M.; Hagley, E.; Dreyer, J.; Maitre, X.; Maali, A.; Wunderlich, C.; Raimond, J.M.; Haroche, S. Observing the Progressive Decoherence of the “Meter” in a Quantum Measurement. Phys. Rev. Lett. 1996, 77, 4887. [Google Scholar] [CrossRef] [PubMed]
- Monroe, C.; Meekhof, D.M.; King, B.E.; Wineland, D.J. A “Schrödinger Cat” Superposition State of an Atom. Science 1996, 272, 1131. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.B. High-speed generation of macroscopic quantum-interference states for the motion of a trapped ion. Phys. Rev. A 2004, 69, 055801. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, G.-F. Intrinsic decoherence in Jaynes-Cummings model with Heisenberg exchange interaction. Eur. Phys. J. D 2017, 71, 288. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Obada, A.-S.F.; Mohamed, A.-B.A. Quantum correlations of two non-interactingion’s internalelectronic states with intrinsic decoherence. Opt. Commun. 2012, 285, 3027. [Google Scholar] [CrossRef]
- Życzkowski, K.; Horodecki, P.; Horodecki, M.; Horodecki, R. Dynamics of quantum entanglement. Phys. Rev. A 2001, 65, 012101. [Google Scholar] [CrossRef]
- Ficek, Z.; Tanaś, R. Dark periods and revivals of entanglement in a two-qubit system. Phys. Rev. A 2006, 74, 024304. [Google Scholar] [CrossRef]
- Mohamed, A.-B.A.; Hessian, H.A.; Obada, A.-S.F. Entanglement sudden death of a SC-qubit strongly coupled with a quantized mode of a lossy cavity. Physica A 2011, 390, 519. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.-B.A.; Hashem, M.; Eleuch, H. Enhancing the Generated Stable Correlation in a Dissipative System of Two Coupled Qubits inside a Coherent Cavity via Their Dipole-Dipole Interplay. Entropy 2019, 21, 672. https://doi.org/10.3390/e21070672
Mohamed A-BA, Hashem M, Eleuch H. Enhancing the Generated Stable Correlation in a Dissipative System of Two Coupled Qubits inside a Coherent Cavity via Their Dipole-Dipole Interplay. Entropy. 2019; 21(7):672. https://doi.org/10.3390/e21070672
Chicago/Turabian StyleMohamed, Abdel-Baset A., Mostafa Hashem, and Hichem Eleuch. 2019. "Enhancing the Generated Stable Correlation in a Dissipative System of Two Coupled Qubits inside a Coherent Cavity via Their Dipole-Dipole Interplay" Entropy 21, no. 7: 672. https://doi.org/10.3390/e21070672
APA StyleMohamed, A.-B. A., Hashem, M., & Eleuch, H. (2019). Enhancing the Generated Stable Correlation in a Dissipative System of Two Coupled Qubits inside a Coherent Cavity via Their Dipole-Dipole Interplay. Entropy, 21(7), 672. https://doi.org/10.3390/e21070672



