Entropy and the Tolman Parameter in Nucleation Theory
Abstract
1. Introduction
2. Thermodynamic Aspects of Nucleation: Some General Considerations
2.1. Thermodynamic Driving Force in Nucleation
2.2. Temperature and Pressure Dependence of the Surface Tension
2.3. Tolman Equation and Tolman Parameter
3. Application to Crystal Nucleation
3.1. Peculiarities of the Application of the Tolman Equation to Crystal Nucleation
3.2. Tolman Equation and Its Generalization in the Application to Crystallization: The Tolman Parameter
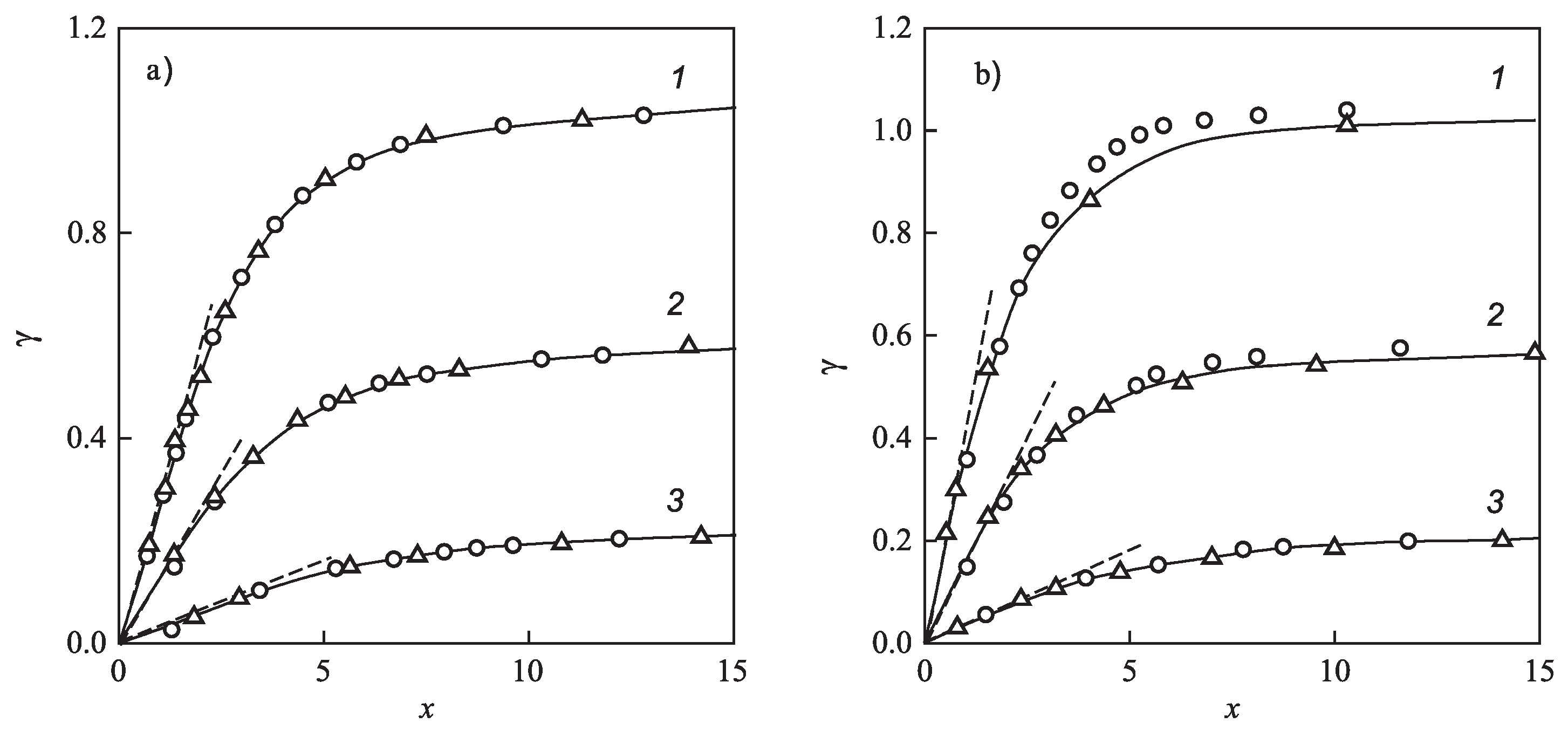
3.3. Brief Comparison with Experimental Data and Computer Simulation Studies
3.4. Critical Analysis of Some Alternative Approaches
4. Application to Condensation and Boiling
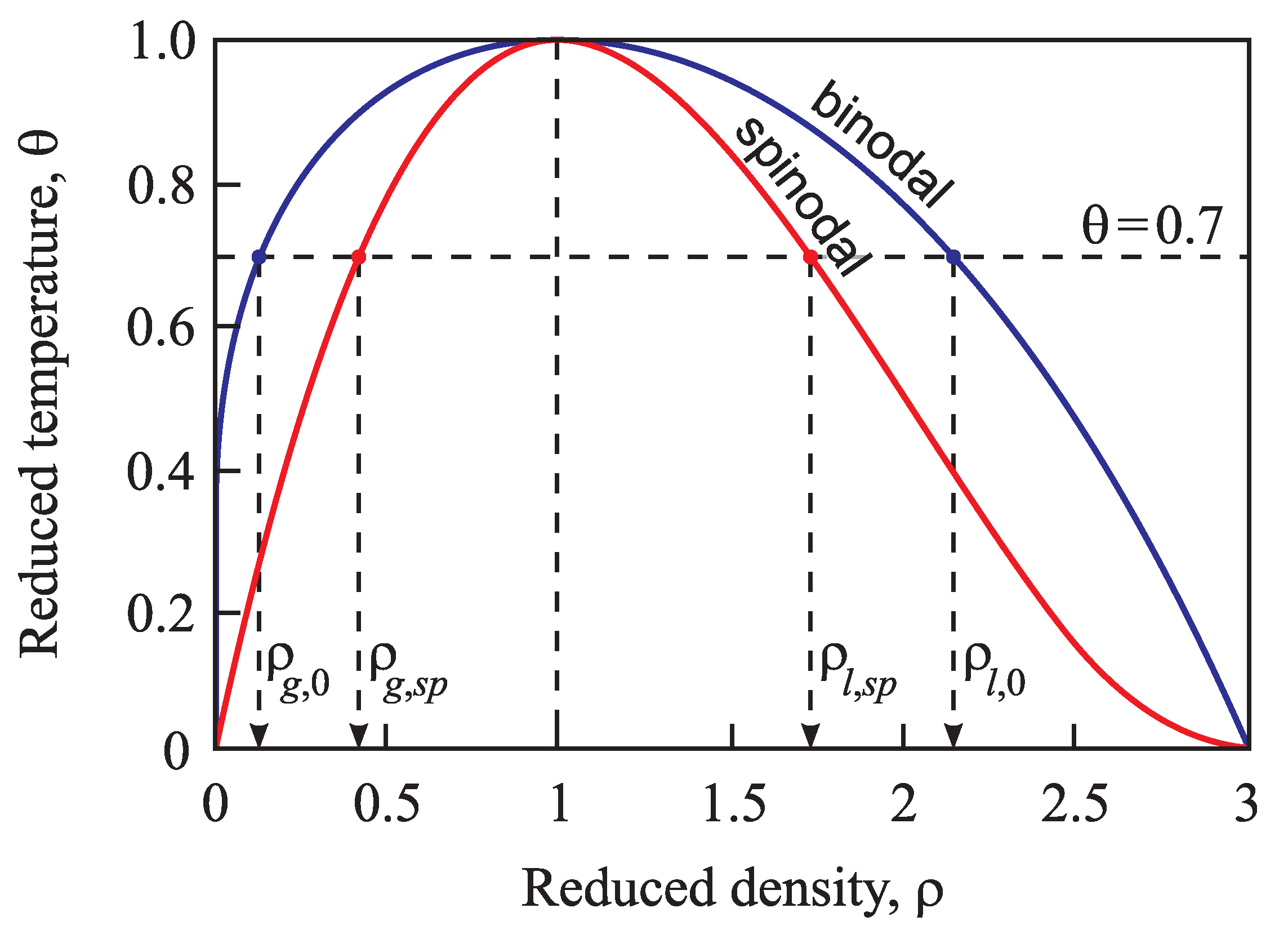
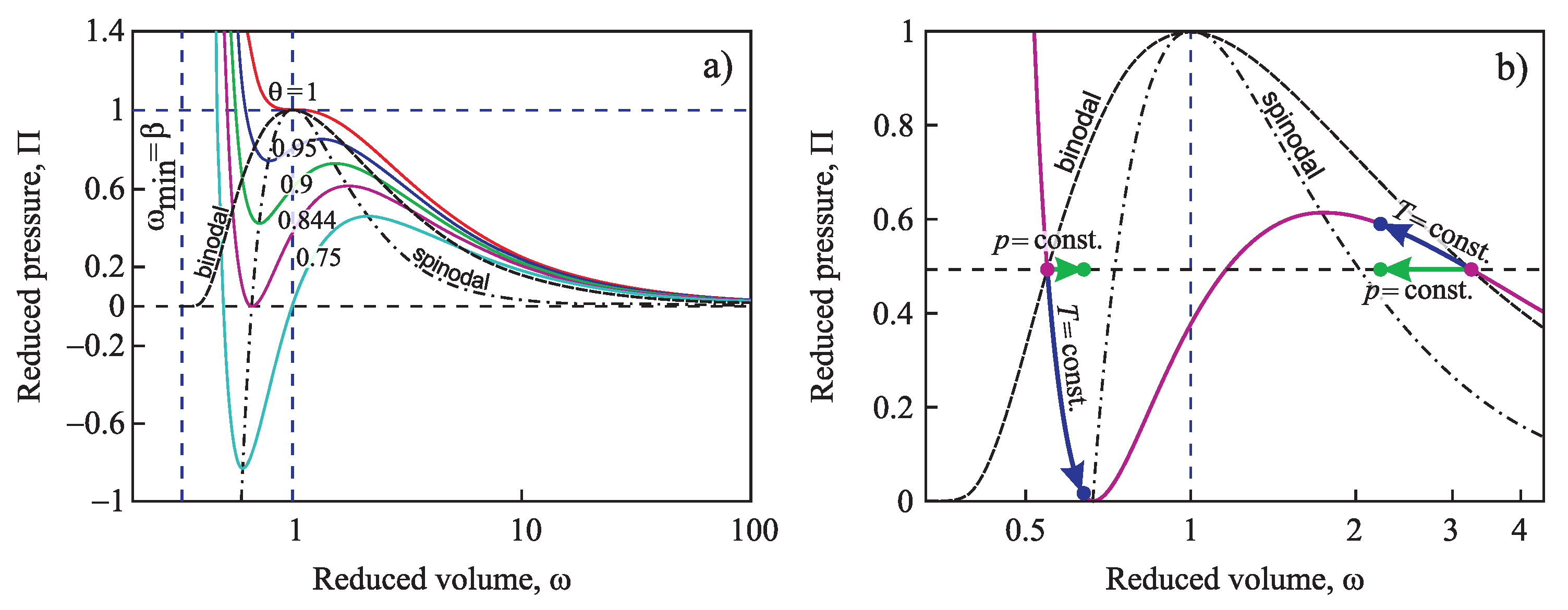
4.1. Bulk Properties of Ambient and Newly-Evolving Phases, Binodal and Spinodal Curves
4.2. Surface Tension
4.2.1. Dependence of the Surface Tension on Pressure and Temperature
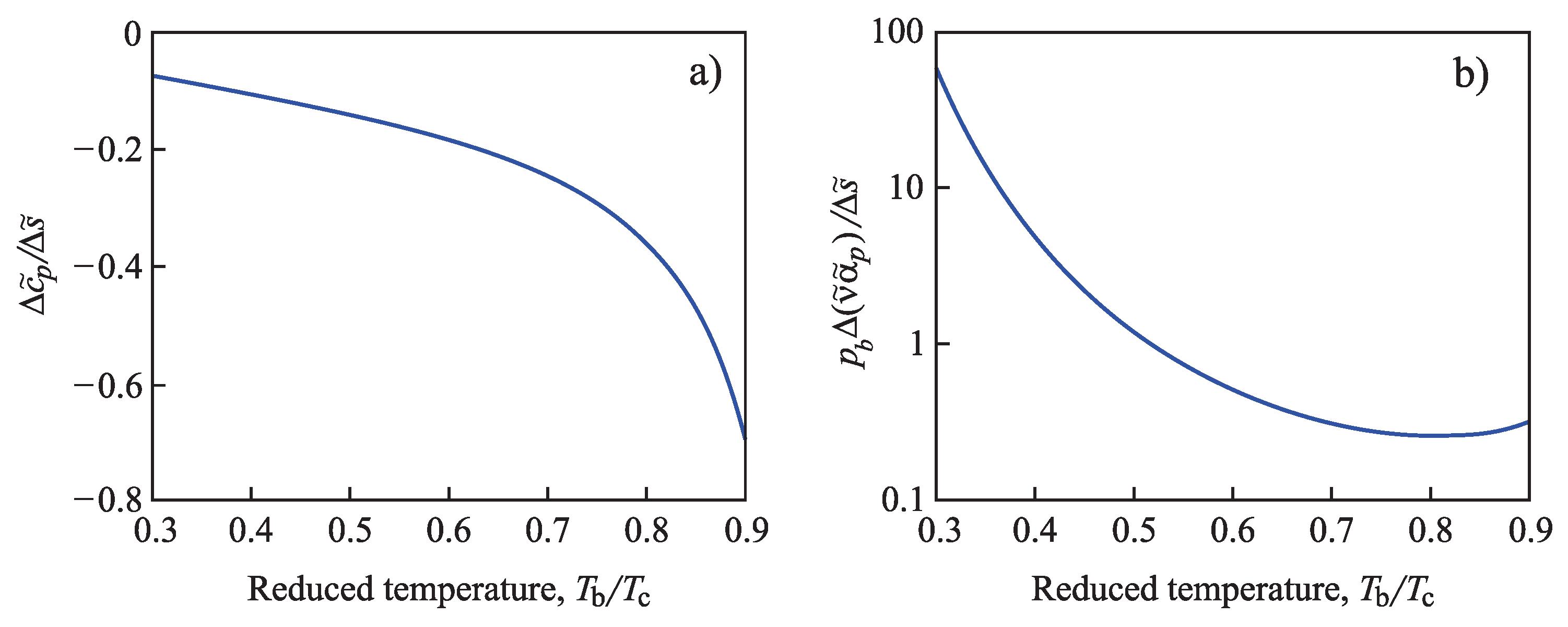
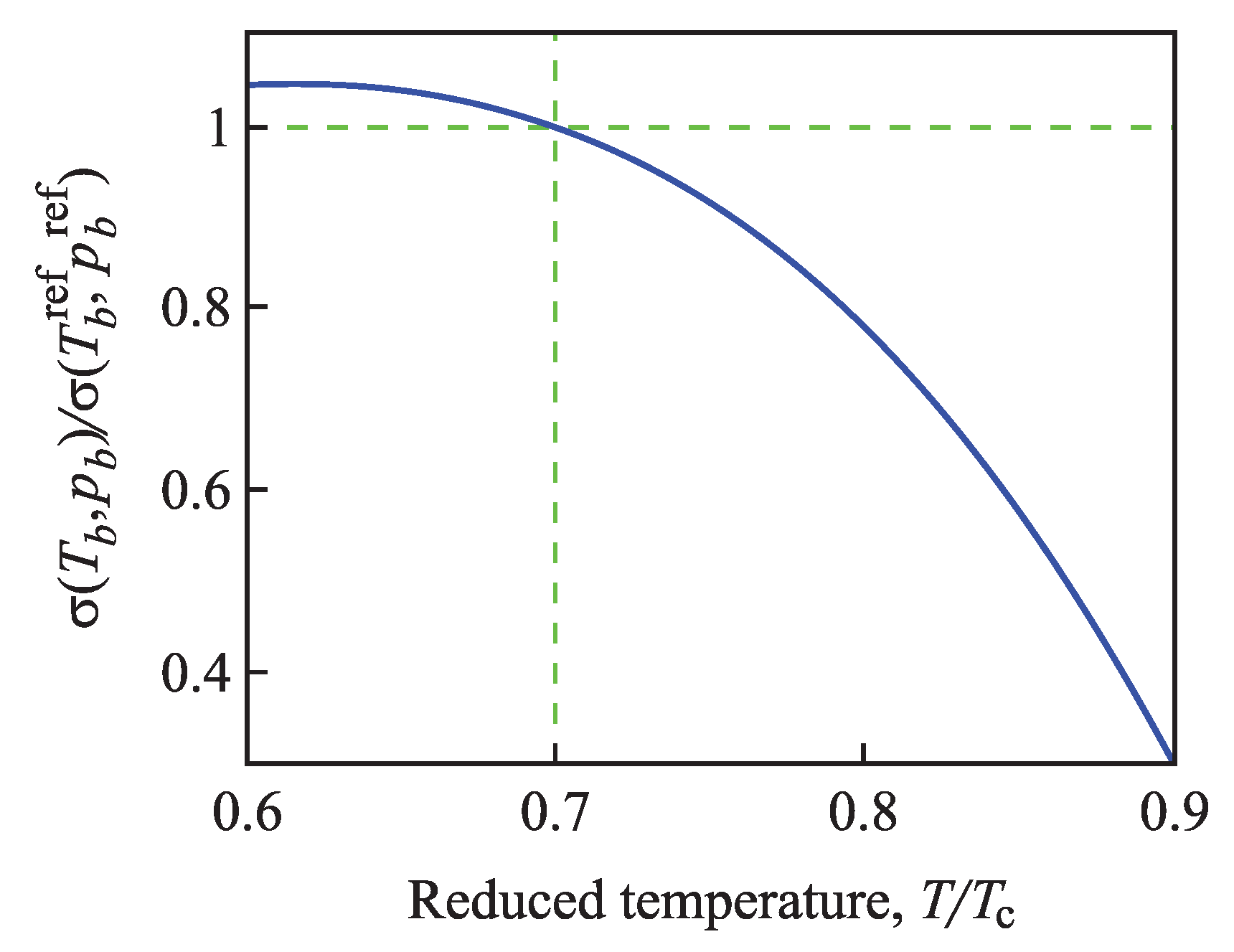
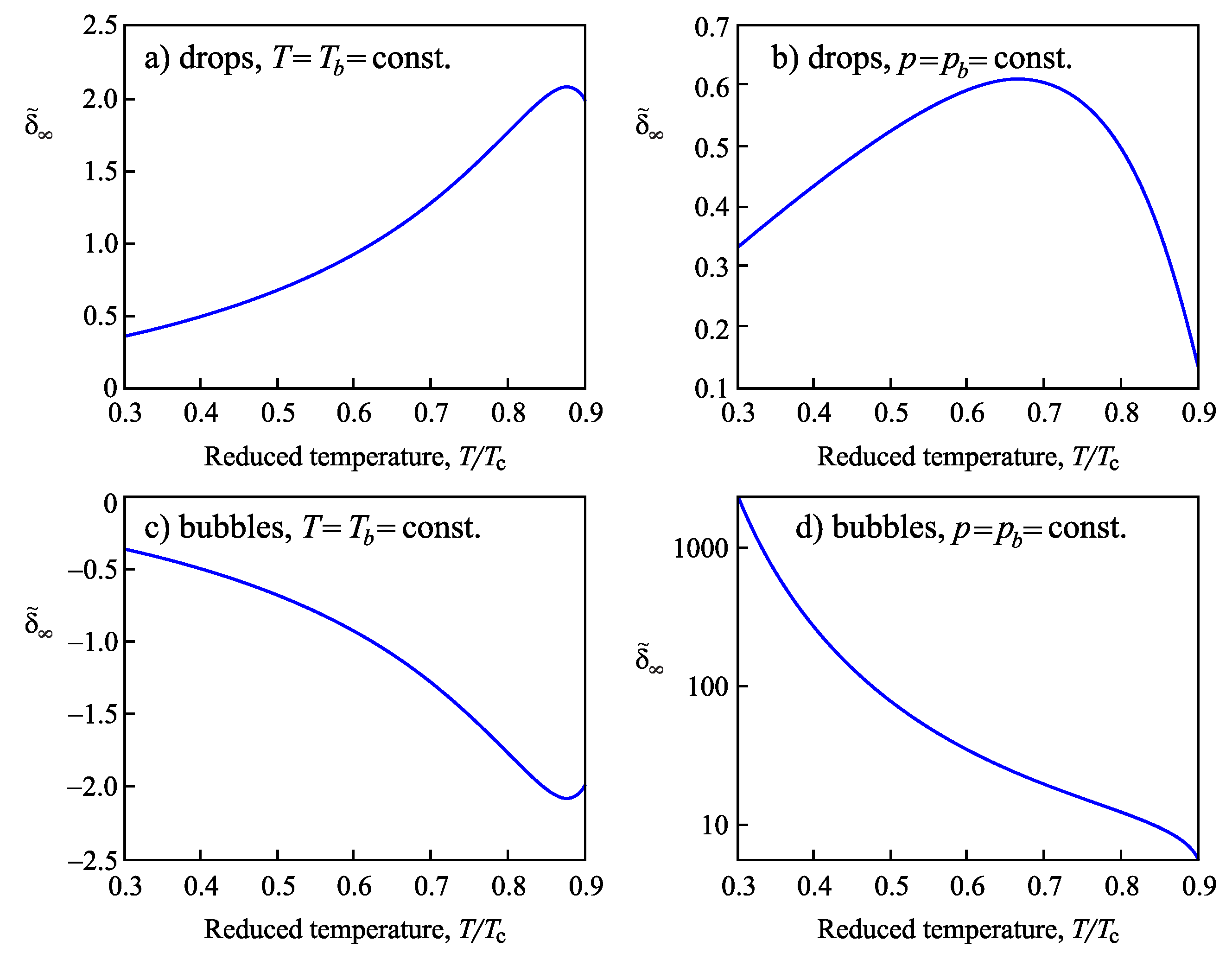
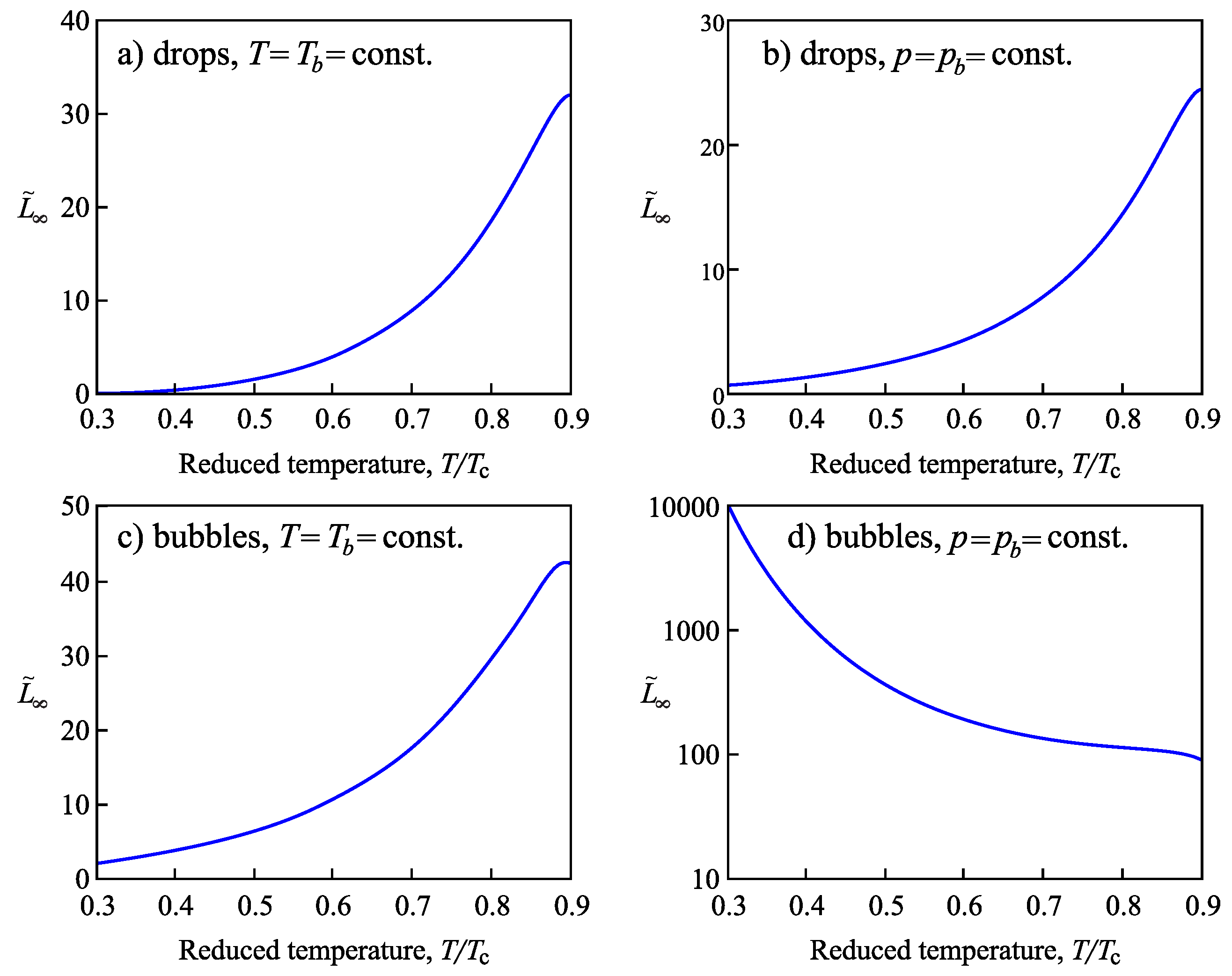
4.2.2. Determination of the Tolman Parameter
4.2.3. Generalization of the Tolman Equation in the Application to Condensation and Boiling: Account of the Existence of the Spinodal Curve
4.3. Comparison with Density Functional Studies: The van der Waals Approach
4.3.1. Some Introductory Comments
4.3.2. Planar Interfaces
4.3.3. Determination of the Tolman Parameter in van der Waals’ Theory of Capillarity
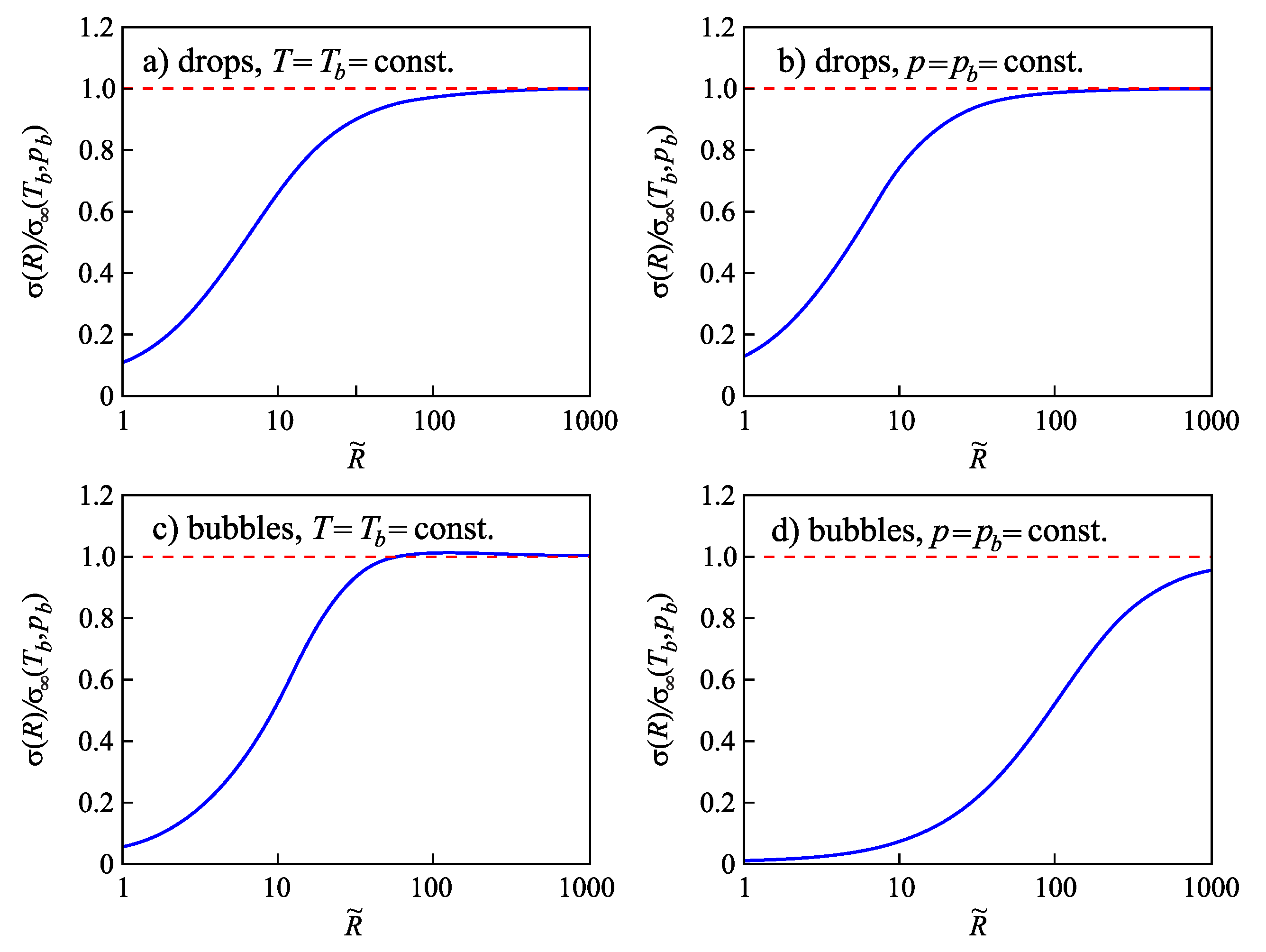
4.3.4. Dependence of the Surface Tension of Bubbles and Droplets on the Radius of the Dividing Surface
5. Results and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gibbs, J.W. On the Equilibrium of Heterogeneous Substances. Trans. Conn. Acad. Arts Sci. 1875–1878, 108, 343. [Google Scholar] [CrossRef]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization, 1st ed.; Springer: Berlin, Germany, 1995; (Second enlarged edition, Springer, Heidelberg, 2013). [Google Scholar]
- Schmelzer, J.W.P.; Boltachev, G.S.; Baidakov, V.G. Is Gibbs’ Thermodynamic Theory of Heterogeneous Systems Really Perfect. In Nucleation Theory and Applications; Schmelzer, J.W.P., Ed.; WILEY-VCH: Berlin/Weinheim, Germany, 2005; pp. 418–446. [Google Scholar]
- Schmelzer, J.W.P.; Boltachev, G.S.; Baidakov, V.G. Classical and Generalized Gibbs’ Approaches and the Work of Critical Cluster Formation in Nucleation Theory. J. Chem. Phys. 2006, 124, 194503. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P.; Fokin, V.M.; Abyzov, A.S.; Zanotto, E.D.; Gutzow, I. How do crystals form and grow in glass-forming liquids: Ostwald’s rule of stages and beyond. Int. J. Appl. Glass Sci. 2010, 1, 16–26. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M. Crystallization of glass: What we know, what we need to know. Int. J. Appl. Glass Sci. 2016, 7, 253–261. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. Crystallization of glass-forming melts: New answers to old questions. J. Non-Crystalline Solids 2018, 501, 11–20. [Google Scholar] [CrossRef]
- Bakker, G. Kapillarität und Oberflächenspannung. In Handbuch der Experimentalphysik; Wien, W., Harms, F., Lenz, H., Eds.; Akademische Verlagsgesellschaft: Leipzig, Germany, 1928; Volume 6. [Google Scholar]
- Ono, S.; Kondo, S. Molecular theory of surface tension in liquids. In Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin/Göttingen/Heidelberg, Germany, 1960; Volume 10. [Google Scholar]
- Rowlinson, J.S.; Widom, B. Molecular Theory of Capillarity; Clarendon Press: Oxford, UK, 1982. [Google Scholar]
- Tolman, R. The Effect of Droplet Size on Surface Tension. J. Chem. Phys. 1949, 17, 333–337. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Mahnke, R. General Formulae for the Curvature Dependence of Droplets and Bubbles. J. Chem. Soc. Faraday Trans. I 1986, 82, 1413–1420. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P. The Curvature Dependence of Surface Tension of Small Droplets. J. Chem. Soc. Faraday Trans. I 1986, 82, 1421–1428. [Google Scholar] [CrossRef]
- Hollomon, J.H.; Turnbull, D. Nucleation. Prog. Metal Phys. 1953, 4, 333–388. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Ferreira, E.B.; Fokin, V.M. Curvature dependence of the surface tension and crystal nucleation in liquids. Int. J. Appl. Glass Sci. 2019, 10, 57–68. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Boltachev, G.S. Curvature dependence of the surface tension of liquid and vapor nuclei. Phys. Rev. E 1999, 59, 469–475. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Boltachev, G.S. Extended version of the van der Waals theory of capillarity. J. Chem. Phys. 2004, 121, 8594–8601. [Google Scholar] [CrossRef] [PubMed]
- Van Giessen, A.E.; Blokhuis, E.M. Direct determination of the Tolman length from the bulk pressures of liquid drops via molecular dynamics simulations. J. Chem. Phys. 2009, 131, 164705. [Google Scholar] [CrossRef] [PubMed]
- Joswiak, M.N.; Do, R.; Doherty, M.F.; Peters, B. Energetic and entropic components of the Tolman length for mW and TIP4P/2005 water nanodroplets. J. Chem. Phys. 2016, 145, 204703. [Google Scholar] [CrossRef] [PubMed]
- Gunawardana, K.G.S.H.; Song, X. Theoretical prediction of crystallization kinetics of a supercooled Lennard-Jones fluid. J. Chem. Phys. 2018, 148, 204506. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Ceriotti, M. Computing the Tolman length for solid-liquid interfaces. J. Chem. Phys. 2018, 148, 231102. [Google Scholar] [CrossRef] [PubMed]
- Malek, M.A.; Poole, P.H.; Saika-Voivod, I. Surface tension of supercooled water nanodroplets from computer simulations. J. Chem. Phys. 2019, 150, 234507. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R. Thermodynamics; North-Holland-Publishing Company: Amsterdam, The Netherlands, 1968. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S. Crystallization of glass-forming liquids: Specific surface energy. J. Chem. Phys. 2016, 145, 064512. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M. Thermodynamic aspects of pressure-induced crystallization: Kauzmann pressure. Int. J. Appl. Glass Sci. 2016, 7, 474–485. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C. Kauzmann paradox and the crystallization of glass-forming melts. J. Non-Crystalline Solids 2018, 501, 21–35. [Google Scholar] [CrossRef]
- Koga, K.; Zeng, X.C.; Shchekin, A.K. Validity of Tolman’s equation: How large should a droplet be? J. Chem. Phys. 1998, 109, 4063–4070. [Google Scholar] [CrossRef]
- Baidakov, V.G. Explosive Boiling of Superheated Cryogenic Liquids; WILEY-VCH: Berlin/Weinheim, Germany, 2007. [Google Scholar]
- Schmelzer, J.W.P.; Baidakov, V.G. Comment on “Simple improvements to classical nucleation models”. Phys. Rev. E 2016, 94, 026801. [Google Scholar] [CrossRef] [PubMed]
- Kelton, K.F.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials and Biology; Pergamon: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Herlach, D.; Galenko, P.; Holland-Moritz, D. Metastable Solids from Undercooled Melts; Pergamon Materials Series; Cahn, R.W., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 10. [Google Scholar]
- Abyzov, A.S.; Fokin, V.M.; Rodrigues, A.M.; Zanotto, E.D.; Schmelzer, J.W.P. The effect of elastic stresses on the thermodynamic barrier for crystal nucleation. J. Non-Crystalline Solids 2016, 432, 325–333. [Google Scholar] [CrossRef]
- Fokin, V.M.; Abyzov, A.S.; Zanotto, E.D.; Cassar, D.R.; Rodrigues, A.M.; Schmelzer, J.W.P. Crystal nucleation in glass-forming liquids: Variation of the size of the “structural units” with temperature. J. Non-Crystalline Solids 2016, 447, 35–44. [Google Scholar] [CrossRef]
- Abyzov, A.S.; Fokin, V.M.; Yuritsyn, N.S.; Rodrigues, A.M.; Schmelzer, J.W.P. The effect of heterogeneous structure of glass-forming liquids on crystal nucleation. J. Non-Crystalline Solids 2017, 462, 32–40. [Google Scholar] [CrossRef]
- Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.E.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy 2018, 20, 956. [Google Scholar] [CrossRef]
- Chen, S.; Tong, Y.; Liaw, P.K. Additive Manufacturing of High-Entropy Alloys: A Review. Entropy 2018, 20, 937. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Glass transition, crystallization of glass-forming melts, and entropy. Entropy 2018, 20, 103. [Google Scholar] [CrossRef]
- Johari, G.P. Source of JG-relaxation in the entropy of glass. J. Phys. Chem. 2019, 123, 3010–3023. [Google Scholar] [CrossRef]
- Dyre, J. Perspective: Excess-entropy scaling. J. Chem. Phys. 2018, 149, 210901. [Google Scholar] [CrossRef]
- Perez-Diaz, J.L.; Alvarez-Valenzuela, M.A.; Sanchez-Garcia-Casarrubios, J.; Jimenez-Lopez, S. Ice surface entropy induction or how humidity prompts freezing. J. Multidiscip. Eng. Sci.Technol. (JMEST) 2016, 3, 3825–3828. [Google Scholar]
- Perez-Diaz, J.L.; Ivanov, O.; Peshev, Z.; Alvarez-Valenzuela, M.A.; Valiente-Blanco, I.; Evgenieva, T.; Dreischuh, T.; Gueorguiev, O.; Todorov, P.V.; Vaseashta, A. Fogs: Physical Basis, Characteristic Properties, and Impacts on the Environment and Human Health. Water 2017, 9, 807. [Google Scholar] [CrossRef]
- Hellmuth, O.; Schmelzer, J.W.P.; Feistel, R. Ice-crystal nucleation in water: Thermodynamic driving force and surface tension. Entropy, in preparation.
- Stefan, J. Über die Beziehung zwischen den Theorien der Capillarität und der Verdampfung (English: On the relation between the theories of capillarity and evaporation). Annalen der Physik 1886, 94, 4–14. [Google Scholar]
- von der Waals, J.; Kohnstamm, P. Lehrbuch der Thermodynamik (Engl.: Textbook on Thermodynamics); Johann-Ambrosius-Barth Verlag: Leipzig, Germany; Amsterdam, The Netherlands, 1908. [Google Scholar]
- Rowlinson, J.S. Translation of J. D. van der Waals’ “The Thermodynamic Theory of Capillarity Under the Hypothesis of a Continuous Variation of Density”. J. Stat. Phys. 1979, 20, 197–244. [Google Scholar] [CrossRef]
- Rusanov, A.I. Phasengleichgewichte und Grenzflächenerscheinungen (Translation: Phase Equilibria and Surface Phenomena); Akademie-Verlag: Berlin, Germany, 1978. [Google Scholar]
- Ulbricht, H.; Schmelzer, J.W.P.; Mahnke, R.; Schweitzer, F. Thermodynamics of Finite Systems and the Kinetics of First-Order Phase Transitions; Teubner-Texte zur Physik; Teubner-Verlag: Leipzig, Germany, 1988; Volume 17. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S. Crystallization of glass-forming liquids: Thermodynamic driving force. J. Non-Crystalline Solids 2016, 449, 41–49. [Google Scholar] [CrossRef]
- Kauzmann, W. The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures. Chem. Rev. 1948, 43, 219–256. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Gutzow, I.S. Glasses and the Glass Transition; WILEY-VCH: Berlin/Weinheim, Germany, 2011. [Google Scholar]
- Spaepen, F. A structural model for the solid-liquid interface in monatomic systems. Acta Metall. 1975, 23, 729–743. [Google Scholar] [CrossRef]
- Spaepen, F. Homogeneous Nucleation and the Temperature Dependence of the Crystal-Melt Interfacial Tension. Solid State Phys. 1994, 23, 1–32. [Google Scholar] [CrossRef]
- Spaepen, F.; Fransaer, J. Advances in Modeling of Crystal Nucleation from the Melt. Adv. Eng. Mater. 1994, 2, 593–596. [Google Scholar] [CrossRef]
- Turnbull, D. Thermodynamics and Kinetics of Formation of the Glassy State and Initial Devitrification. In Physics of Non-Crystalline Solids, Proceedings of the International Conference, Boston, MA, USA 27–30 September 1964; Prins, J.A., Ed.; North-Holland Publisher: Amsterdam, The Netherlands, 1965; pp. 41–56. [Google Scholar]
- Skapski, A.S. The Surface Tension of Liquid Metals. J. Chem. Phys. 1948, 16, 389–393. [Google Scholar] [CrossRef]
- Skapski, A.S. A next neighbors theory of maximum undercooling. Acta Metall. 1956, 4, 583–585. [Google Scholar] [CrossRef]
- Fokin, V.M.; Yuritsyn, N.S.; Zanotto, E.D.; Schmelzer, J.W.P. Homogeneous crystal nucleation in silicate glasses: A 40 years perspective. J. Non-Crystalline Solids 2006, 352, 2681–2714. [Google Scholar] [CrossRef]
- Wulff, G.V. Zur Frage der Geschwindigkeit des Wachsthums und der Auflösung der Krystallflächen (Translation: On the question of speed of growth and dissolution of crystal surfaces). Zeitschrift für Kristallographie und Mineralogie 1901, 34, 449–530. [Google Scholar]
- van Laue, M. Der Wulffsche Satz für die Gleichgewichtsform von Kristallen (Translation: Wulff’s theorem for the equilibrium shape of crystals). Zeitschrift für Kristallographie 1943, 105, 124–133. [Google Scholar] [CrossRef]
- Dirksen, J.A.; Ring, T.A. Fundamentals of crystallization: Kinetic effects on particle size distributions and morphology. Chem. Eng. Sci. 1991, 46, 2389–2427. [Google Scholar] [CrossRef]
- Markov, I. Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth, and Epitaxy; World Scientific: Singapore, 2002. [Google Scholar]
- Skripov, V.P.; Koverda, V.P. Spontaneous Crystallization of Undercooled Liquids; Nauka: Moscow, Russia, 1984. [Google Scholar]
- Baidakov, V.G. Crystallization of Undercooled Liquids: Results of Molecular Dynamics Simulations. In Glass: Selected Properties and Crystallization; Schmelzer, J.W.P., Ed.; de Gruyter: Berlin, Germany; Boston, MA, USA, 2014; pp. 481–520. [Google Scholar]
- Cammarata, R.C. Generalized Thermodynamics of Surfaces with Applications to Small Solid Systems. Solid State Phys. 2009, 61, 1–75. [Google Scholar] [CrossRef]
- Komatsu, T. Design and control of crystallization in oxide glasses. J. Non-Crystalline Solids 2015, 428, 156–175. [Google Scholar] [CrossRef]
- Skripov, V.P.; Baidakov, V.G. Absence of a spinodal in undercooled liquids. Teplofiz. Vys. Temp. 1972, 10, 1226–1230, (English version is available in High Temp. 1972, 10, 1102.). [Google Scholar]
- Skripov, V.P.; Faizullin, M.Z. Crystal-Liquid-Gas Phase Transitions and Thermodynamic Similarity; Wiley: Weinheim, Germany, 2006. [Google Scholar]
- Schmidt, M.; Kusche, R.; von Issendorff, B.; Haberland, H. Irregular variations in the melting point of size-selected atomic clusters. Nature 1998, 939, 238–240. [Google Scholar] [CrossRef]
- Kusche, R.; Hippler, T.; Schmidt, M.; von Issendorff, B.; Haberland, H. Melting of free sodium clusters. Eur. Phys. J. D 1999, 9, 1–4. [Google Scholar]
- Samsonov, V.M.; Sdobnyakov, N.Y.; Vasilyev, S.A.; Sokolov, D.N. On the Size Dependence of the Heats of Melting of Metal Nanoclusters. Bull. Russ. Acad. Sci. Phys. 2016, 80, 494–496. [Google Scholar] [CrossRef]
- Breaux, G.A.; Benirschke, R.C.; Sugai, T.; Kinnear, B.S.; Jarrold, M.F. Hot and Solid Gallium Clusters: Too Small to Melt. Phys. Rev. Lett. 2003, 91, 215508. [Google Scholar] [CrossRef] [PubMed]
- Fokin, V.M.; Zanotto, E.D. Crystal Nucleation in Silicate Glasses: The Temperature and Size Dependence of Crystal-Liquid Surface Energy. J. Non-Cryst. Solids 2000, 256, 105–112. [Google Scholar] [CrossRef]
- James, P.F. Kinetics of Crystal Nucleation in Silicate Glasses. J. Non-Cryst. Solids 1985, 73, 517–540. [Google Scholar] [CrossRef]
- Turnbull, D. Kinetics of Solidification of Supercooled Liquid Mercury Droplets. J. Chem. Phys. 1952, 20, 411–424. [Google Scholar] [CrossRef]
- Miyazawa, Y.; Pound, G.M. Homogeneous Nucleation of Crystalline Gallium from Liquid Gallium. J. Cryst. Growth 1974, 23, 45–57. [Google Scholar] [CrossRef]
- Rowlands, E.G.; James, P.F. Analysis of Steady-State Crystal Nucleation Rates in Glasses. Part 1: Methods of Analysis and Application to Lithium Disilicate Glass. Phys. Chem. Glass 1979, 20, 1–8. [Google Scholar]
- Rowlands, E.G.; James, P.F. Analysis of Steady-State Crystal Nucleation Rates in Glasses. Part 2: Further Comparison between Theory and Experiment for Lithium Disilicate Glass. Phys. Chem. Glass 1979, 20, 9–14. [Google Scholar]
- Fokin, V.M.; Kalinina, A.M.; Filipovich, V.N. Nucleation in Silicate Glasses and Effect of Preliminary Heat Treatment on It. J. Cryst. Growth 1981, 52, 115–121. [Google Scholar] [CrossRef]
- Potapov, O.V.; Fokin, V.M.; Filipovich, V.N. Nucleation and Crystal Growth in Water Containing Soda-Lime-Silica Glasses. J. Non-Cryst. Solids 1999, 247, 74–78. [Google Scholar] [CrossRef]
- Abyzov, A.S.; Fokin, V.M.; Zanotto, E.D. Predicting homogeneous nucleation rates in silicate glass-formers. J. Non-Cryst. Solids 2018, 500, 231–234. [Google Scholar] [CrossRef]
- Tanaka, K.K.; Kimura, Y. Theoretical Analysis of Crystallization by Homogeneous Nucleation of Water Droplets. Phys. Chem. Chem. Phys. 2019, 21, 2410–2418. [Google Scholar] [CrossRef] [PubMed]
- Baidakov, V.G.; Protsenko, S.P. Computer simulation of nucleation under tension. Dokl. Akad. Nauk Russ. Fed. Phys. 2004, 49, 69–72. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Tipeev, A.O.; Bobrov, K.S.; Ionov, G.V. Crystal nucleation rate isotherms in Lennard-Jones liquids. J. Chem. Phys. 2010, 132, 234505. [Google Scholar] [CrossRef] [PubMed]
- Baidakov, V.G.; Tipeev, A.O. Crystal Nucleation and the Solid-Liquid Interfacial Free Energy. J. Chem. Phys. 2012, 136, 074510. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Protsenko, S.P.; Tipeev, A.O. Temperature dependence of the crystal-liquid interfacial free energy and the endpoint of the melting line. J. Chem. Phys. 2013, 139, 224703. [Google Scholar] [CrossRef]
- Tipeev, A.O. Crystallization of Undercooled Liquids in Molecular-Dynamics Models. Ph.D. Thesis, Russian Academy of Sciences, Yekaterinburg, Russia, 2016. (In Russian). [Google Scholar]
- Tipeev, A.O.; Zanotto, E.D.; Rino, J.P. Diffusivity, Interfacial Free Energy, and Crystal Nucleation in a Supercooled Lennard-Jones Liquid. J. Phys. Chem. C 2018, 122, 28884–28894. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, F.; Song, H.; Mendelev, M.I.; Wang, C.Z.; Ho, K.M. Temperature dependence of the solid-liquid interface free energy of Ni and Al from molecular dynamics simulation of nucleation. J. Chem. Phys. 2018, 149, 174501. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Sanz, E.; Valeriani, C.; Vega, C. Homogeneous Ice Nucleation Evaluated for Several Water Models. J. Chem. Phys. 2014, 141, 18C529. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Zaragoza, A.; Rosales-Pelaez, P.; Navarro, C.; Valeriani, C.; Vega, C.; Sanz, E. Interfacial Free Energy as the Key to the Pressure-Induced Deceleration of Ice Nucleation. Phys. Rev. Lett. 2016, 117, 135702. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Soria, G.D.; Ramirez, J.; Valeriani, C.; Vega, C.; Sanz, A.E. Role of Salt, Pressure, and Water Activity on Homogeneous Ice Nucleation. Phys. Chem. Lett. 2017, 8, 4486–4491. [Google Scholar] [CrossRef] [PubMed]
- Zaragoza, A.; Espinosa, J.R.; Ramos, R.; Cobos, J.A.; Aragones, J.L.; Vega, C.; Sanz, E.; Ramirez, J.; Valeriani, C. Phase boundaries, nucleation rates, and speed of crystal growth of the water-to-ice transition under an electric field: A simulation study. J. Phys. Condens. Matter 2018, 30, 174002. [Google Scholar] [CrossRef] [PubMed]
- Yuritsyn, N.S. Influence of preformed nuclei on crystal nucleation kinetics in soda-lime-silica glass. J. Non-Crystalline Solids 2015, 427, 139–145. [Google Scholar] [CrossRef]
- Potapov, O.V.; Fokin, V.M.; Ugolkov, V.L.; Suslova, L.Y.; Filipovich, V.N. Influence of Na2O content on the nucleation kinetics in glasses of compositions close to the Na2O · 2CaO · 3SiO2 stoichiometry. Glass Phys. Chem. 2000, 26, 27–32. [Google Scholar]
- Yuritsyn, N.S. Nucleation of crystals in sodium-calcium-silicate glasses of the metasilicate section. Glass Phys. Chem. 2015, 41, 112–115. [Google Scholar] [CrossRef]
- Gonzalez-Oliver, C.J.R.; James, P.F. Crystal nucleation and growth in a Na2O · 2CaO · 3SiO2 glass. J. Non-Crystalline Solids 1980, 38, 699–704. [Google Scholar] [CrossRef]
- Kalinina, A.M.; Filipovich, V.N.; Fokin, V.M. Stationary and non-stationary crystal nucleation rate in a glass of 2Na2O · CaO · 3SiO2 stoichiometric composition. J. Non-Crystalline Solids 1980, 38, 723–728. [Google Scholar] [CrossRef]
- Nascimento, M.L.F.; Fokin, V.M.; Zanotto, E.D.; Abyzov, A.S. Dynamic processes in a silicate liquid from above melting to below the glass transition. J. Chem. Phys. 2011, 135, 194703. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, A.M. Diffusion Processes, Crystallization, and Viscous Flow in Barium Disilicate Glass. Ph.D. Thesis, Federal University of São Carlos, São Carlos, Brazil, 2014. [Google Scholar]
- Tipeev, A.O. Comment on “Theoretical prediction of crystallization kinetics of a supercooled Lennard-Jones fluid” [J. Chem. Phys. 2018, 148, 204506]. J. Chem. Phys. 2019, 151, 017101. [Google Scholar] [CrossRef]
- Slezov, V.V. Kinetics of First-Order Phase Transitions; WILEY-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Van der Waals, J. D. Sijthoff, Leiden 1873; German translation: Die Kontinuität des gasförmigen und flüssigen Zustandes (Engl.: On the Continuity of the Gaseous and Liquid States). Ph.D. Thesis, Johann-Ambrosius Barth Publishers, Leipzig, Germany, 1881. [Google Scholar]
- Schmelzer, J.W.P.; Schmelzer, J., Jr. Kinetics of condensation of gases: A new approach. J. Chem. Phys. 2001, 114, 5181–5193. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Schmelzer, J., Jr. Kinetics of bubble formation and the tensile strength of liquids. Atmos. Res. 2003, 65, 303–324. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Baidakov, V.G. Kinetics of Condensation and Boiling: Comparison of Different Approaches. J. Phys. Chem. B 2001, 105, 11595–11604. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Schmelzer, J., Jr.; Gutzow, I. Reconciling Gibbs and van der Waals: A New Approach to Nucleation Theory. J. Chem. Phys. 2000, 112, 3820–3831. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. How do crystals nucleate and grow: Ostwald’s rule of stages and beyond. In Thermal Physics and Thermal Analysis: From Macro to Micro Highlighting Thermodynamics, Kinetics, and Nano-Materials; Sestak, J., Hubik, P., Mares, J.J., Eds.; Springer: Cham, Switzerland, 2017; pp. 195–211. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a non-uniform system: III. Nucleation in a two-component incompressible fluid. J. Chem. Phys. 1959, 31, 688–699. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Kagan, Y. Quantum kinetics of phase transitions at temperatures near to the absolute zero. Soviet J. Exp. Theor. Phys. 1972, 62, 385–402. (In Russian) [Google Scholar]
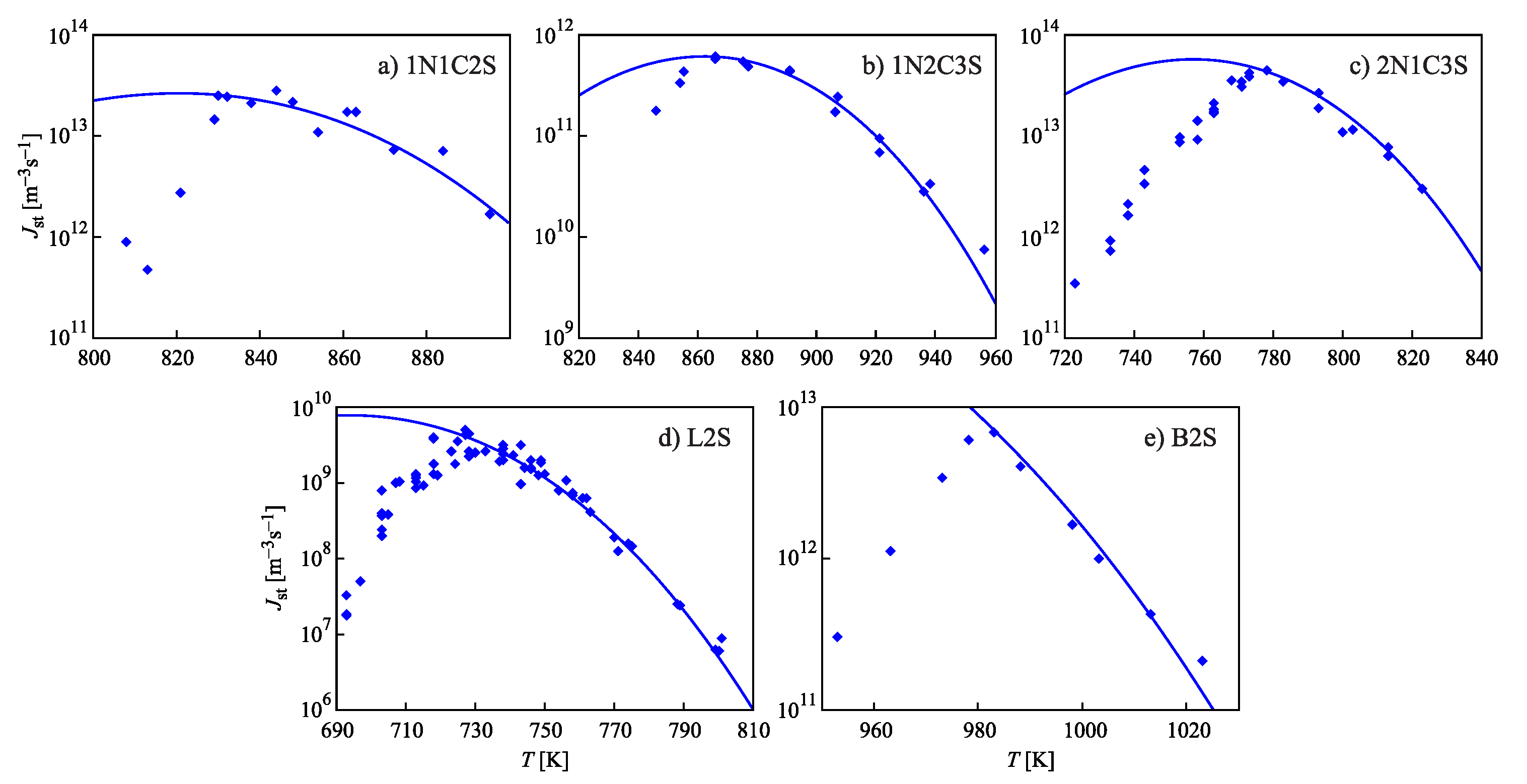
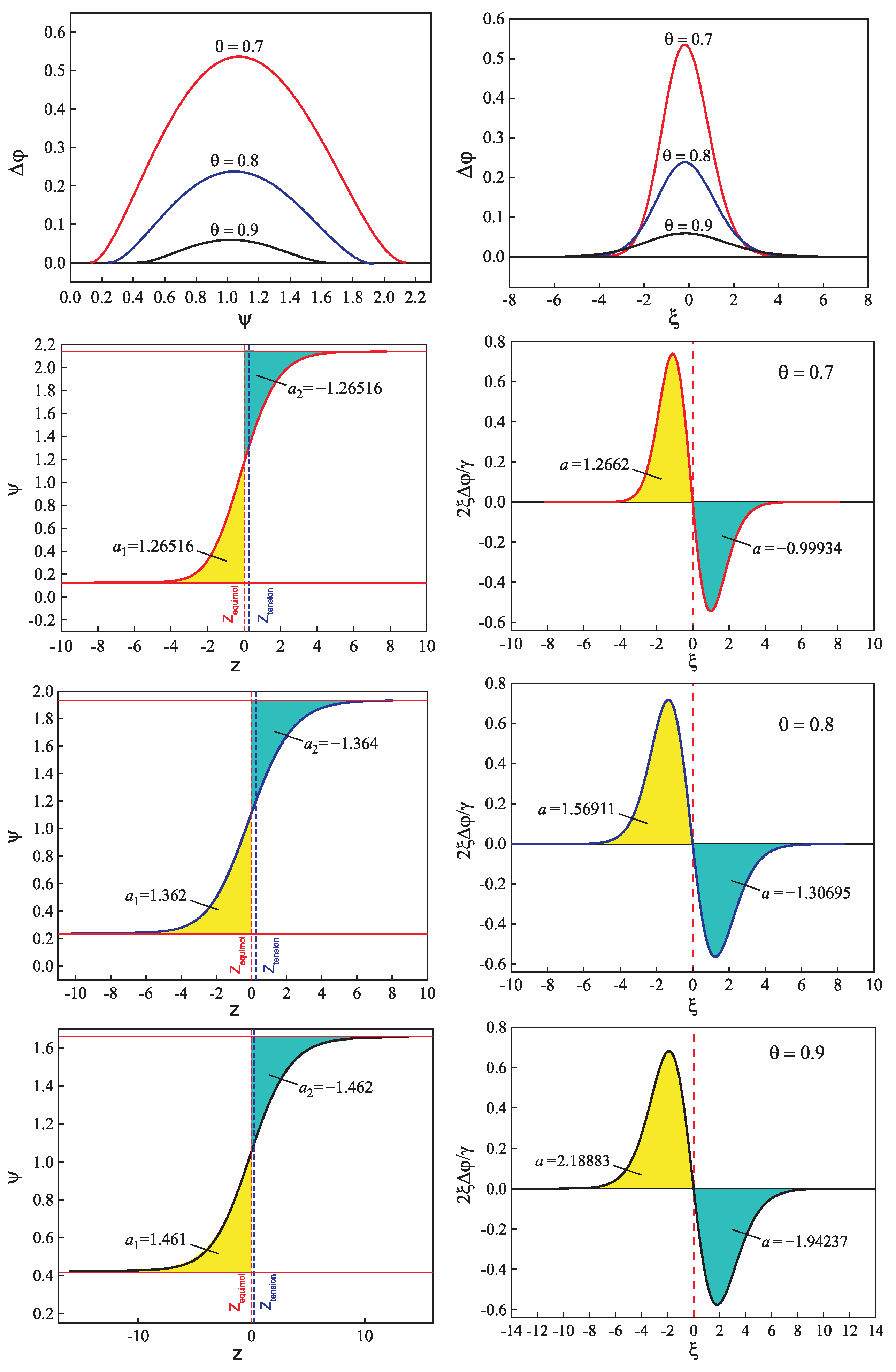
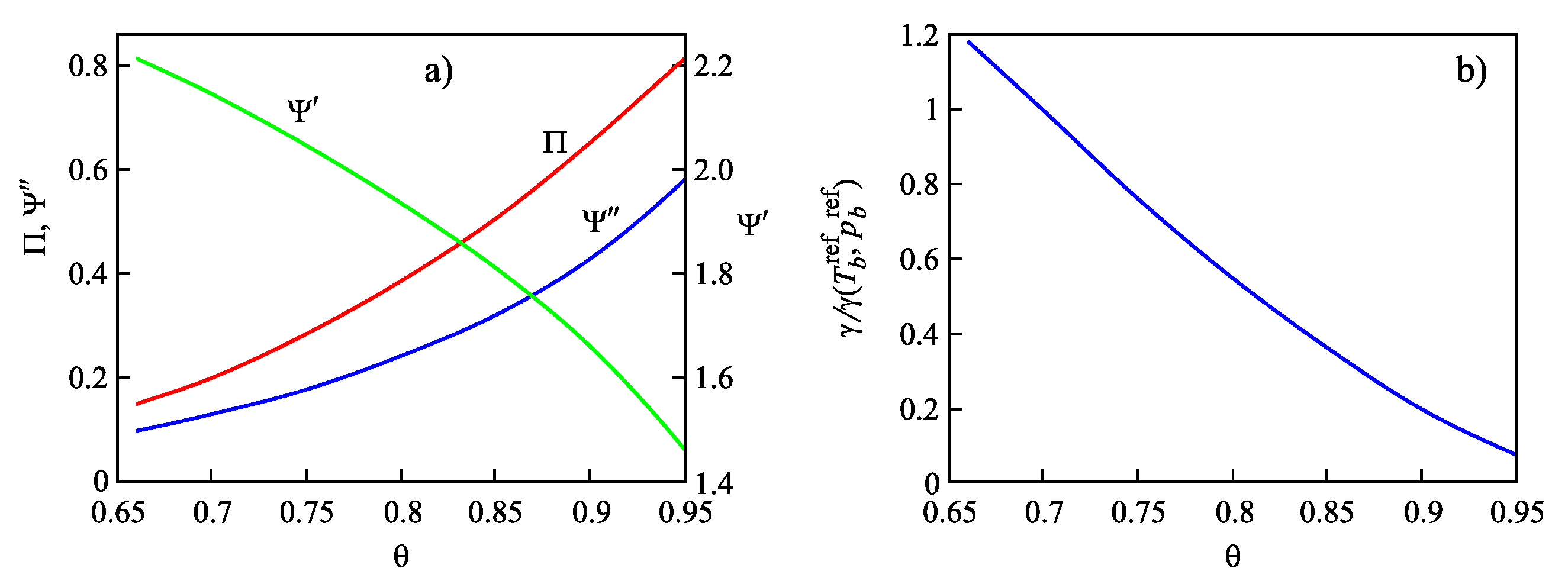
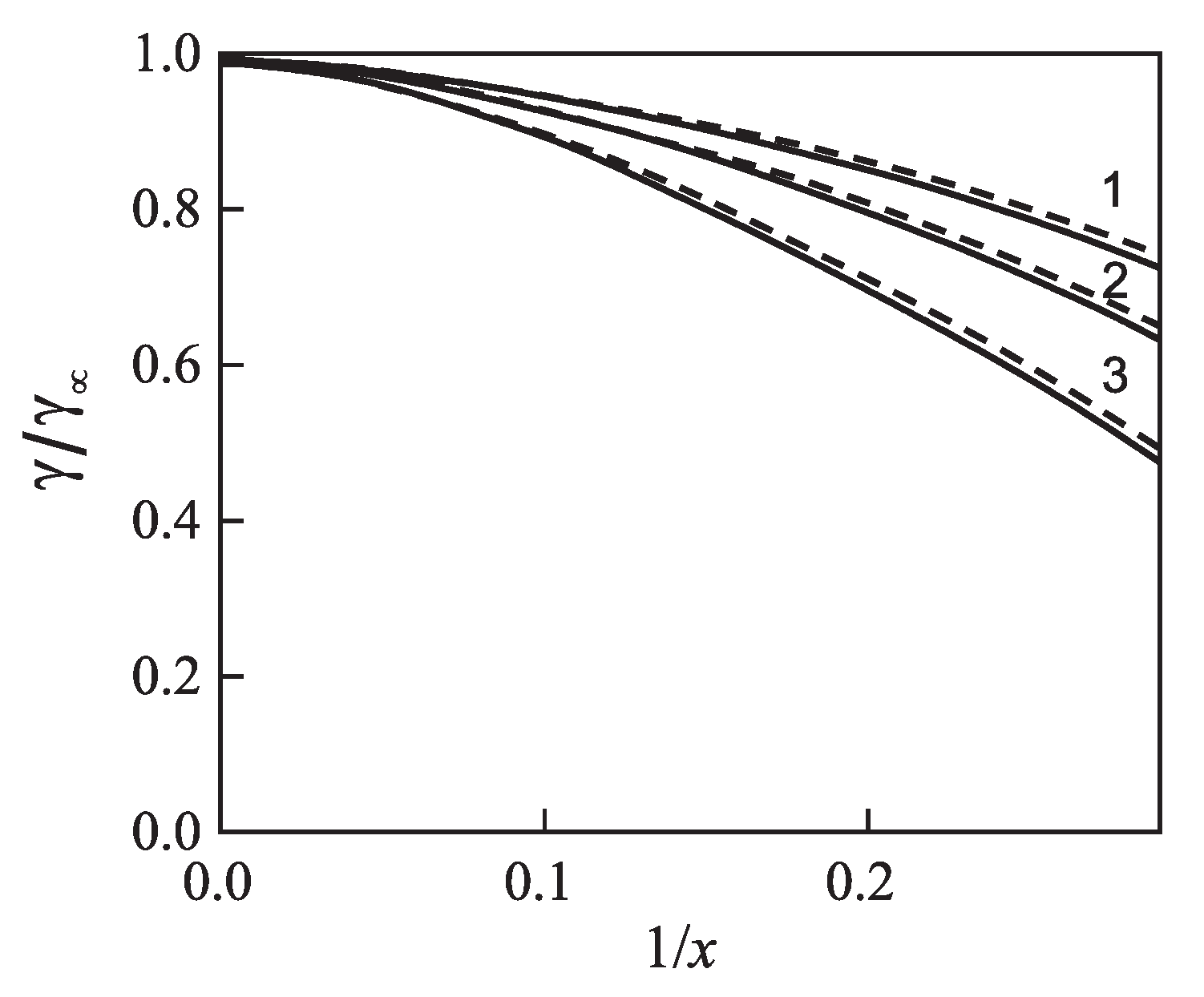
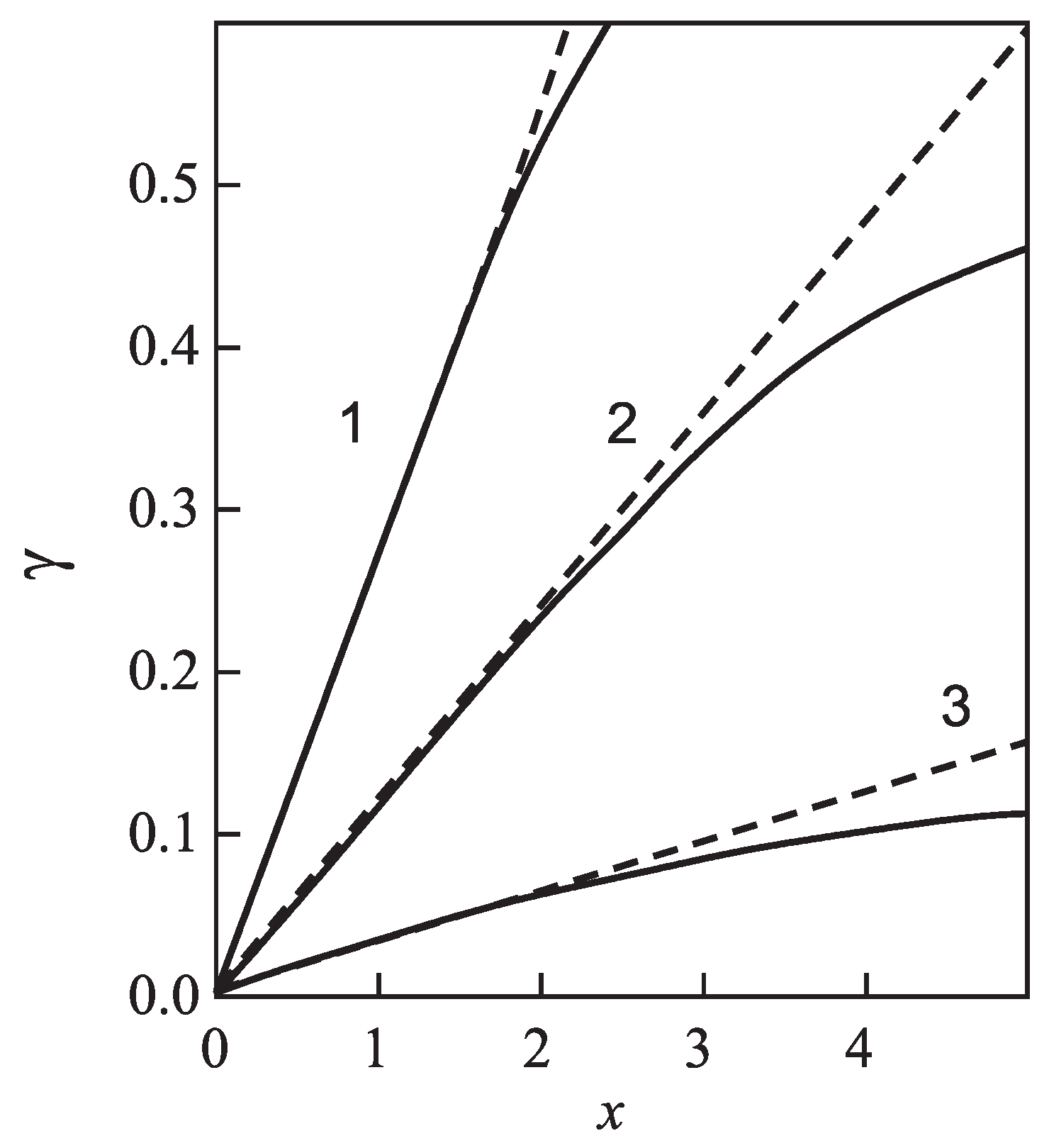
| Glass | Fit of Nucleation Rate Data | Equation (69) | |||
|---|---|---|---|---|---|
| (nm) | |||||
| 1N1C2S | 0.243 | 0.588 | 1.15 | 0.21 | 0.17 |
| 1N2C3S | 0.235 | 0.588 | 1.1 | 0.214 | 0.17 |
| 2N1C3S | 0.225 | 0.599 | 1.7 | 0.133 | 0.118 |
| L2S | 0.238 | 0.480 | 0.455 | 0.524 | 0.24 |
| B2S | 0.197 | 0.496 | 1.04 | 0.189 | 0.112 |
| 0.66 | 0.147 | 2.212 | 0.096 | 1.26 |
| 0.70 | 0.200 | 2.140 | 0.128 | 1.06 |
| 0.75 | 0.283 | 2.042 | 0.177 | 0.81 |
| 0.80 | 0.383 | 1.933 | 0.240 | 0.58 |
| 0.85 | 0.504 | 1.807 | 0.320 | 0.38 |
| 0.90 | 0.647 | 1.657 | 0.426 | 0.21 |
| 0.95 | 0.812 | 1.462 | 0.579 | 0.075 |
| 2.14035 | 0.12802 | 1.06 | −0.1335 | |
| 1.93334 | 0.239667 | 0.58 | −0.13108 | |
| 1.657 | 0.426 | 0.21 | −0.123235 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmelzer, J.W.P.; Abyzov, A.S.; Baidakov, V.G. Entropy and the Tolman Parameter in Nucleation Theory. Entropy 2019, 21, 670. https://doi.org/10.3390/e21070670
Schmelzer JWP, Abyzov AS, Baidakov VG. Entropy and the Tolman Parameter in Nucleation Theory. Entropy. 2019; 21(7):670. https://doi.org/10.3390/e21070670
Chicago/Turabian StyleSchmelzer, Jürn W. P., Alexander S. Abyzov, and Vladimir G. Baidakov. 2019. "Entropy and the Tolman Parameter in Nucleation Theory" Entropy 21, no. 7: 670. https://doi.org/10.3390/e21070670
APA StyleSchmelzer, J. W. P., Abyzov, A. S., & Baidakov, V. G. (2019). Entropy and the Tolman Parameter in Nucleation Theory. Entropy, 21(7), 670. https://doi.org/10.3390/e21070670






